计算机图形学--圆的的生成算法的实现

画圆环算法c程序全文共四篇示例，供读者参考第一篇示例：画圆环是计算机图形学中常见的基本图形之一，常用于游戏开发、动画制作等领域。

在计算机中，画圆环的算法有多种，其中最常用的是中点画圆算法。

本文将介绍使用C语言实现中点画圆算法的程序，并进行详细分析和讲解。

1. 算法原理中点画圆算法是一种简单而高效的算法，其基本原理是通过逐渐逼近圆形的方法，利用对称性和中点的位置进行迭代计算。

具体步骤如下：（1）给定圆的半径r和圆心坐标(x0, y0)，设置初始点P(0, r)作为起点，并计算判别式d=1-r。

（2）在每次迭代中，分别取直线y=x和y=-x两侧的中点，分别计算两种情况下的判别式值，并根据判别式值的大小决定下一个中点的位置。

（3）重复进行上述步骤，直到计算完整个圆的一周。

2. C程序实现下面是使用C语言实现中点画圆算法的程序代码：```c#include <stdio.h>#include <graphics.h>void plot_circle_points(int x0, int y0, int x, int y) { // 绘制圆的八个对称点putpixel(x0 + x, y0 + y, WHITE);putpixel(x0 - x, y0 + y, WHITE);putpixel(x0 + x, y0 - y, WHITE);putpixel(x0 - x, y0 - y, WHITE);putpixel(x0 + y, y0 + x, WHITE);putpixel(x0 - y, y0 + x, WHITE);putpixel(x0 + y, y0 - x, WHITE);putpixel(x0 - y, y0 - x, WHITE);}void midpoint_circle(int x0, int y0, int r) { int x = 0, y = r;int d = 1 - r;plot_circle_points(x0, y0, x, y); while (x < y) {if (d < 0) {d = d + 2 * x + 3;x++;} else {d = d + 2 * (x - y) + 5;x++;y--;}plot_circle_points(x0, y0, x, y);}}delay(5000);closegraph();return 0;}```以上是一个简单的使用C语言实现中点画圆算法的程序代码。

计算机图形学实验报告实验二Bresenham算法画圆并填充学号：09009202 姓名：陶园成绩：东南大学计算机科学与工程学院二〇一一年十一月一．实验题目Bresenham算法画圆并填充二．算法思想1.首先，真实的线条是连续的，但是计算机中的线条是离散的，是由很多点组成的，那么画线的重点就是如何高效地找到这些离散的点来更好地画出想要的图形。

2.实验要求用Bresenham算法实现画圆。

那么首先先要了解Bresenham算法是一种什么算法。

经过查阅，我找到Bresenham直线算法和画圆算法。

直线是圆的基础。

Bresenham直线算法是用来描绘由两点所决定的直线的算法，它会算出一条线段在 n 维光栅上最接近的点。

这个算法只会用到较为快速的整数加法、减法和位元移位，常用于绘制电脑画面中的直线。

是计算机图形学中最先发展出来的算法。

Bresenham画圆算法又称中点画圆算法，与Bresenham 直线算法一样，其基本的方法是利用判别变量来判断选择最近的像素点，判别变量的数值仅仅用一些加、减和移位运算就可以计算出来。

为了简便起见，考虑一个圆心在坐标原点的圆，而且只计算八分圆周上的点，其余圆周上的点利用对称性就可得到。

Bresenham直线算法流程图圆的八对称性所以，只需要知道圆上的一个点的坐标 (x, y) ，利用八对称性，就能得到另外七个对称点的坐标。

和直线算法类似，Bresenham画圆算法也是用一系列离散的点来近似描述一个圆。

Bresenham画圆算法的流程图三．源代码#include "stdlib.h"#include "math.h"#include <gl/glut.h>//按坐标画点void draw(GLint xCoord, GLint yCoord){glBegin(GL_POINTS);//以点的形式glVertex2i(xCoord, yCoord);//在（xCoord, yCoord）坐标下画点glEnd();glFlush();//强制刷新}void Circle(GLint x,GLint y){int a=abs(x);//将x的绝对值赋给aint b=abs(y);//将y的绝对值赋给bint c=a*-1;//使c=a的相反数int d=b*-1;//使d=b的相反数draw(x, y); draw(y, x);draw(-x, y); draw(y, -x);draw(x, -y); draw(-y, x);draw (-x, -y); draw(-y, -x);//按照圆的对称性以圆心为对称点将四个象限的圆周画出for(int i=c;i<=a;i++){for(int j=d;j<=b;j++){draw(i,j);}}//以a,b,c,d为边界用点填充该圆}//主函数void BresenhamCircle(GLint r){int d, d1, d2, direct;GLint x,y;x=0;y=r;d = 2*(1-r);while(y>=0){Circle(x,y);if(d < 0){d1 = 2* (d+ y) -1;if(d1 <=0)direct = 1;elsedirect = 2;}else{if( d > 0){d2 = 2*(d-x)-1;if(d2 <= 0)direct = 2;elsedirect = 3;}elsedirect = 2;}switch(direct){case 1:x++;d+=2*x + 1;break;case 2:x++; y--;d+=2*(x-y+1) + 1;break;case 3:y--;d+=-2*y + 1;break;}}}void RenderScene(void){BresenhamCircle(50);//主函数调用}//当窗口大小改变时由GLUT函数调用void ChangeSize(GLsizei width, GLsizei Height){GLfloat aspectRatio;if (Height == 0){Height = 1;}glViewport(0, 0, width, Height);//指定视口矩形左下角glMatrixMode(GL_PROJECTION);//指定当前矩阵，对投影矩阵应用随后的矩阵操glLoadIdentity();// 装载单位矩阵aspectRatio = (GLfloat)width / (GLfloat) Height;if (width <= Height){glOrtho(-100.0, 100.0, -100.0 / aspectRatio, 100.0 / aspectRatio, 1.0, -1.0);}else{glOrtho(-100.0 * aspectRatio, 100.0 * aspectRatio, -100.0, 100.0, 1.0, -1.0);}glMatrixMode(GL_MODELVIEW);//指定当前矩阵，对模型视景矩阵堆栈应用随后的矩阵操作glLoadIdentity();// 装载单位矩阵}//主程序入口void main(void){glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);//设置初始显示模式,指定单缓存窗口,指定RGB 颜色模式的窗口glutCreateWindow("圆");//创建窗口，窗口名称为“圆”glutDisplayFunc(RenderScene);//进行画图glutReshapeFunc(ChangeSize);//重画回调函数glutMainLoop();//进入GLUT事件处理循环，让所有的与“事件”有关的函数调用无限循环}四．结果截屏五．出现问题及解决方案1.对于如何填充整个圆一开始没有好的方法，后来决定每画一个点，就将该横坐标的所有纵坐标点画出，从下到上，整个填充圆从中间到两边形成。

计算机图形学实验03
《计算机图形学》实验报告
圆（椭圆）的生成算法
一、实验教学目标与基本要求
1．实现圆的生成算法；
2．实现椭圆的生成算法；
二、实验课程内容 (2学时)
1．写出完整的圆的Bresenham生成算法；
2．写出完整的椭圆的中点生成算法；
三、算法思想
1．圆的Bresenham生成算法：
如果我们构造函数 F(_,y)=_+y-R，则对于圆上的点有F(_,y)=0，对于圆外的点有F(_,y)_gt;0，对于圆内的点F(_,y)_lt;0 。

与中点画线法一样，构造判别式:d=F(M)=F(_p+1,yp-0.5)=(_p+1)+(yp-0.5)-R。

若d_lt;0，则应取P1为下一象素，而且再下一象素的判别式为：
222d=F(_p+2,yp-0.5)=(_p+2)+(yp-0.5)-R=d+2_p+3
若d≥0，则应取P2为下一象素，而且下一象素的判别式为：
d=F(_p+2,yp-1.5)=(_p+2)+(yp-
1.5)-R=d+2(_p-yp)+5我们这里讨论的第一个象素是（0,R），判别式d的初始值为：d0=F(1,R-0.5)=1.25-R。

为了进一步提高算法的效率，将上面的算法中的浮点数改写成整数，将乘法运算改成加法运算，即仅用整数实现中点画圆法。

2．椭圆的中点生成算法：
椭圆中点生成算法是将椭圆在第一象限中分为两个部分：
1)对于斜率绝对值小于1的区域内在_方向取单位量；
2)对于斜率绝对值大于1的区域内在y方向取单位量；
斜率可以通过椭圆的标准方程中获得为K = - (ry_ry)__/(r__r_)_y;这里中点椭圆222222222。

信息与计算科学专业基础课ComputerReport Of course 计算机图形学课程实验报告实验题目设计算法绘制直线与圆班级姓名学号指导教师日期实验说明 试验目的： 掌握直线和圆的基本生成算法思想，并上机编程实现相应的算法。

试验地点： 教九楼401 数学系机房实验要求(Direction): 1. 每个学生单独完成；2.开发语言为TurboC 或C++，也可使用其它语言；3.请在自己的实验报告上写明姓名、学号、班级；4.每次交的实验报告内容包括：题目、试验目的和意义、程序制作步骤、主程序、运行结果图以及参考文件；5. 自己保留一份可执行程序,考试前统一检查和上交。

实验内容实验题一实验题目1).用DDA 法在屏幕上画一条具有三个像素宽的直线段L1。

要求：(1)直线段L1的两个端点坐标和画线颜色都要求可以随机输入；(2)要求输出直线段L1上的各点坐标；(3)画出直线的同时要求标明两端点坐标。

2).将课堂所讲的斜率0<K<1的中点画线算法推广到斜率K>1、-1<K<0和K<-1的情况，编写一通用的中点画线算法。

实验目的和意义1.了解如何利用C 语言和图形函数进行绘图；2. 熟悉并掌握C 语言的图形模式控制函数，图形屏幕操作函数，以及基本图形函数；3. 通过对Turbo C 进行图形程序设计的基本方法的学习，能绘制出简单的图形；4. 熟悉并掌握DDA 法在屏幕上画一条具有三个像素宽的直线段L1以及通用的中点画线算法。

通过DDA 法及用的中点画线算法，了解图形系统初始化、图形系统关闭和图设计算法绘制直线与圆实验2形模式的控制，并熟练运用图形坐标的设置，包括定点、读取光标以及图形颜色的设置。

程序制作步骤(包括算法思想、算法流程图等)1.自动搜索显示器类型和显示模式，初始化图形系统，通过printf 、scanf 语句控制线段的端点坐标和画线颜色的自由输入；2. DDAline:设直线之起点为（x1，y1），终点为（x2，y2），则斜率k 为： 则有：⑴.可通过计算由x 方向的增量x ∆引起y 的改变生成直线。

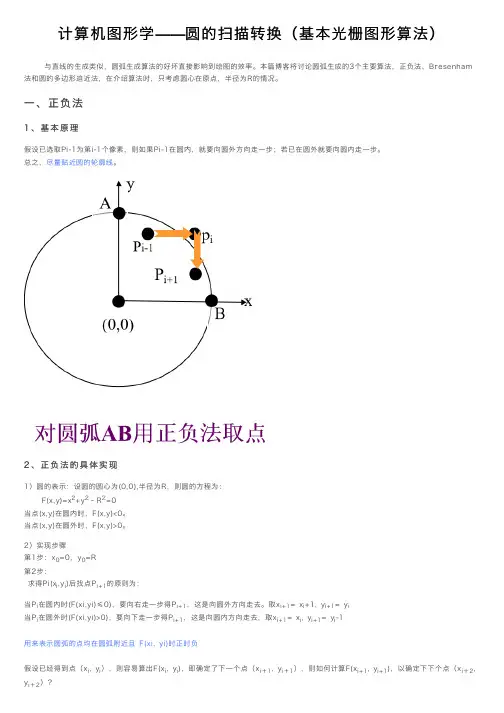
计算机图形学——圆的扫描转换（基本光栅图形算法）与直线的⽣成类似，圆弧⽣成算法的好坏直接影响到绘图的效率。

本篇博客将讨论圆弧⽣成的3个主要算法，正负法、Bresenham 法和圆的多边形迫近法，在介绍算法时，只考虑圆⼼在原点，半径为R的情况。

⼀、正负法1、基本原理假设已选取Pi-1为第i-1个像素，则如果Pi-1在圆内，就要向圆外⽅向⾛⼀步；若已在圆外就要向圆内⾛⼀步。

总之，尽量贴近圆的轮廓线。

2、正负法的具体实现1）圆的表⽰：设圆的圆⼼为(0,0),半径为R，则圆的⽅程为：F(x,y)=x2+y2–R2=0当点(x,y)在圆内时，F(x,y)<0。

当点(x,y)在圆外时，F(x,y)>0。

2）实现步骤第1步：x0=0，y0=R第2步：求得Pi(x i,y i)后找点P i+1的原则为：当P i在圆内时(F(xi,yi)≤0)，要向右⾛⼀步得P i+1，这是向圆外⽅向⾛去。

取x i+1= x i+1, y i+1= y i当P i在圆外时(F(xi,yi)>0)，要向下⾛⼀步得P i+1，这是向圆内⽅向⾛去，取x i+1= x i, y i+1= y i-1⽤来表⽰圆弧的点均在圆弧附近且 F(xi, yi)时正时负假设已经得到点（x i, y i），则容易算出F(x i, y i)，即确定了下⼀个点（x i＋1, y i＋1），则如何计算F(x i+1, y i+1)，以确定下下个点（x i＋2, y i＋2）？分为两种情况：右⾛⼀步后：x i+1=x i+1，y i+1=y i，此时：F(x i+1, y i+1)=x i+12+y i2-R2=x i2+y i2-R2+2x i+1 = F(x i, y i)+2x i+1下⾛⼀步后：x i+1=x i，y i+1=y i-1， 此时：F(x i+1, y i+1)=x i2+（y i-1)2-R2= F(x i, y i)-2y i+1由此可得：确定了F(xi+1, yi+1)之后，即可决定下⼀个点(xi+2, yi+2)，选择道理同上。

计算机图形学期中作业姓名：学号:专业：计算机科学与技术班级：2班基本算法：#include <graphics.h>#include<stdio.h>#include <conio.h>#include<math.h>#define ROUND(a) ((int)(a+0.5))void lineDDA (int x1, int y1, int x2, int y2,int color) //DDA 画直线 int ROUND(float a) {return (int)(a+0.5);} {int i;float x,y,k;k=(float)(y2-y1)/(x2-x1);x=(float)x1, y=(float)y1;if (k<=1)for (i=x1 ; i<=x2 ; i++){ putpixel (ROUND(x), ROUND(y),color);x=x+1;y=y+k;}elsefor (i=y1;i<=y2;i++){ putpixel (ROUND(x), ROUND(y),color);x=x+1/k;y=y+1;}void lineBre(int xs, int ys, int xe, int ye,int color) //Bresenham画直线{ int x,y, k, steps;float m, e;m=(float)(ye-ys)/(xe-xs);e=m-0.5;steps=xe-xs;x=xs;y=ys;for (k=0; k<steps; k++){putpixel(x,y,color);if(e>=0){y=y+1;e= e-1;}x=x+1;e=e+m;}void Bs_Mid_Line(int x1,int y1,int x2,int y2,int color) //笔刷画直线{int i,j; int x,y;int a,b; a=y1-y2;b=x2-x1;int cy=(a<=0 ? 1:(a=-a,-1));int cx=(b>=0 ? 1:(b=-b,-1));x=x1; y=y1; for(i=-2; i<=2;i++)for(j=-2; j<=2;j++)putpixel(x,y,color);int d,d1,d2;if(-a<=b) //直线斜率绝对值小于等于1{ d=2*a+b;d1=2*a;d2=2*(a+b);while(x!=x2){if(d<0){x+=cx;y+=cy;d+=d2;}else{x+=cx;d+=d1;}for(i=-2; i<=2;i++)for(j=-2; j<=2;j++)putpixel(x+i,y+j,color);}}else //直线斜率绝对值大于1{ d=2*b+a;d1=2*b;d2=2*(a+b);while(y!=y2){ if(d<0){y+=cy;d+=d1;}else{x+=cx;y+=cy;d+=d2;}for(i=-2; i<=2;i++)for(j=-2; j<=2;j++)putpixel(x+i,y+j,color);}}}void line (int x1,int y1,int x2,int y2,int color)//驻点比较画直线{int x,y,n;int f;n=(x2-x1)+(y2-y1);x=x1;y=y1;f=y*x2-y2+x;for (int i=1; i<=n; i++){ putpixel(x,y,color);if (f>=0){x=x+1;y=y;}else{x=x;y=y+1;}f=y*x2-y2*x;}}void circleMidpoint (int xc, int yc, int r)//中点画圆法{int x=0;int y=r;int p=1-r;void circleplotpoints(int, int, int, int);circleplotpoints(xc, yc, x,y);while(x<y){x++;if ( p<0)p+=2*x+1;else{y--;p+=2*(x-y)+1;}circleplotpoints(xc, yc, x,y);}}void circleplotpoints (int xc, int yc, int x, int y){putpixel(xc+x, yc+y,YELLOW);putpixel(xc-x, yc+y,YELLOW);putpixel(xc+x, yc-y,YELLOW);putpixel(xc-x, yc-y,YELLOW);putpixel(xc+y, yc+x,YELLOW);putpixel(xc-y, yc+x,YELLOW);putpixel(xc+y, yc-x,YELLOW);putpixel(xc-y, yc-x,YELLOW);}arc(int xc, int yc, double r, double ts, double te) //数值微分法产生园弧（DDA算法）{ double rad, tsl ,tel, deg, dte,ta, ct,st;int x,y,n,i;rad=0.0174533;tsl=ts*rad;tel=te*rad;if (r<5.08)deg=0.015;else if (r<7.62)deg=0.06;else if (r<25.4)deg=0.075;elsedeg=0.15;dte=deg*25.4/r;if (tel<tsl)tel=tel+6.28319;n=(int)((tel-tsl)/dte+0.5);if (n==0)n=(int)(6.28319/dte+0.5);ta=tsl;x=xc+r*cos(tsl);y=yc+r*sin(tsl);moveto (x,y);for ( i=1; i<=n; i++){ta=ta+dte;ct=cos(ta);st=sin(ta);x=xc+r*ct;y=yc+r*st;lineto (x,y);}x=xc+r*cos(tel);y=yc+r*sin(tel);lineto (x,y);return (0);}void circleBre(int r) //Bresenham画园算法{ int x=0, y=r, d=3-2*r;while (x<y){putpixel (x,y,RED);if (d<0)d=d+4*x+6;else{d=d+4*(x-y)+10;y=y-1;}x=x+1;}if (x==y)putpixel(x,y,RED);}ellipse (int xc, int yc, double a, double b, double alp, double ts, double te) //角度DDA法产生椭圆弧{double rad, tsl, tel, alpl, deg, dte, r, ta, a1,a2,b1,b2; int x,y,n,i;rad=0.0174533;tsl=ts*rad;tel=te*rad;alpl=alp*rad;a1=a*cos(tsl);b1=cos(alpl);a2=b*sin(tsl);b2=sin(alpl);r=(a>b)?a:b;if (r<5.08)deg=0.015;else if (r>7.62)deg=0.06;else if (r<25.4)deg=0.075;elsedeg=0.15;dte=deg*25.4/r;if (tel<tsl)tel+=6.28319;n=(int)(6.28319/dte+0.5); ta=tsl;x=xc+a1*b1-a2*b2;y=yc+a1*b2+a2*b1;moveto (x,y);for (i=1;i<=n;i++){ta+=dte;a1=a*cos(ta);a2=b*sin(ta);x=xc+a1*b1-a2*b2;y=yc+a1*b2+a2*b1;lineto (x,y);}a1=a*cos(tel);a2=b*sin(tel);x=xc+a1*b1-a2*b2;y=(int)yc+a1*b2+a2*b1;lineto (x,y);return(0);}void ellipse (int x0, int y0, int a, int b, int dt) {int x,y,n,i;float t1, t=0.0;t1=(float)dt*0.0174533;n=360/dt;moveto (x0+a, y0);for (i=1;i<n; i++){t=t+t1;x=(int)x0+a*cos(t);y=(int)y0+b*sin(t);lineto (x,y);}lineto (x0+a, y0);}Par(int xs, int ys, int xm, int ym, int xe, int ye) //二次曲线的参数拟合法{double d, d1, ax, ay, bx,by;int n,i;ax=(xe-2*xm+xs)*2.0;ay=(ye-2*ym+ys)*2.0;bx=(xe-xs-ax);by=(ye-ys-ay);n=(int)sqrt(ax*ax+ay*ay)/4;n=(int)sqrt(n*100);moveto (xs,ys);d=1.0/n;d1=d;for (i=0; i<=n;i++){ lineto ((int)( ax*d1*d1+bx*d1+xs), (int) (ay*d1*d1+by*d1+ys));d1=d1+d;}lineto (xe, ye);return (0);}void main(){printf("1: DDA画直线.\n");printf("2: Bresenham 画直线.\n");printf("3: 笔刷画直线.\n");printf("4: 驻点比较画直线.\n");printf("5: 中点画圆法.\n");printf("6: 数值微分法产生园弧（DDA算法）.\n");printf("7: Bresenham画园算法.\n");printf("8: 角度DDA法产生椭圆弧.\n");printf("9: 二次曲线的参数拟合法.\n");printf("0: 退出.\n\n");while(true){printf("请输入你要选择的方法：\n");int a;scanf("%d",&a);switch(a){case 0:exit(0);case 1:initgraph(640, 480);lineDDA(100,100,400,450,YELLOW);break;case 2:initgraph(640, 480);lineBre(100, 100, 450, 500,YELLOW);break;case 3:initgraph(640, 480);Bs_Mid_Line(100,100,450,500,YELLOW);break;case 4:initgraph(640, 480);line (100,100,450,500,YELLOW);break;case 5:initgraph(640, 480);circleMidpoint (100, 100, 50) ;break;case 6:initgraph(640, 480);arc(200, 200, 100, 30, 90);break;case 7:initgraph(640, 480);circleBre(100);break;case 8:initgraph(640, 480);ellipse (100, 100, 50, 60, 20, 30, 90) ; break;case 9:initgraph(640, 480);Par(100, 100, 300, 350, 50, 100);break;case 10:default :printf("错误\n");}getch();cleardevice();closegraph();}}程序运行截图如下：。

《计算机图形学》实验报告一、实验目的计算机图形学是一门研究如何利用计算机生成、处理和显示图形的学科。

通过本次实验，旨在深入理解计算机图形学的基本原理和算法，掌握图形的生成、变换、渲染等技术，并能够运用所学知识解决实际问题，提高对图形学的应用能力和编程实践能力。

二、实验环境本次实验使用的编程语言为 Python，使用的图形库为 Pygame。

开发环境为 PyCharm。

三、实验内容1、直线的生成算法DDA 算法（Digital Differential Analyzer）Bresenham 算法DDA 算法是通过计算直线的斜率来确定每个像素点的位置。

它的基本思想是根据直线的斜率和起始点的坐标，逐步计算出直线上的每个像素点的坐标。

Bresenham 算法则是一种基于误差的直线生成算法。

它通过比较误差值来决定下一个像素点的位置，从而减少了计算量，提高了效率。

在实验中，我们分别实现了这两种算法，并比较了它们的性能和效果。

2、圆的生成算法中点画圆算法中点画圆算法的核心思想是通过判断中点的位置来确定圆上的像素点。

通过不断迭代计算中点的位置，逐步生成整个圆。

在实现过程中，需要注意边界条件的处理和误差的计算。

3、图形的变换平移变换旋转变换缩放变换平移变换是将图形在平面上沿着指定的方向移动一定的距离。

旋转变换是围绕一个中心点将图形旋转一定的角度。

缩放变换则是改变图形的大小。

通过矩阵运算来实现这些变换，可以方便地对图形进行各种操作。

4、图形的填充种子填充算法扫描线填充算法种子填充算法是从指定的种子点开始，将相邻的具有相同颜色或属性的像素点填充为指定的颜色。

扫描线填充算法则是通过扫描图形的每一行，确定需要填充的区间，然后进行填充。

在实验中，我们对不同形状的图形进行了填充，并比较了两种算法的适用情况。

四、实验步骤1、直线生成算法的实现定义直线的起点和终点坐标。

根据所选的算法（DDA 或Bresenham）计算直线上的像素点坐标。