初三物理压强压轴题-从甲乙丙中选择放入薄壁轻质圆柱形容器内计算最大压强
- 格式:docx
- 大小:229.08 KB
- 文档页数:3

专题10 液体的抽取与倒入选择题一、常见题目类型1.分别从两柱形容器中抽出液体,抽出某一厚度(体积或质量)(图1)。
注意抽出的厚度(体积或质量)可能相同,也可能不同。
2.分别向两容器中倒入液体,倒入某一深度(体积或质量)(图2)。
注意倒入的深度(体积或质量)可能相同,也可能不同。
3.向甲容器中倒入液体,从乙容器抽取液体(图3)。
二、分析此类题目常用到的知识:①液体的压强:p=F/S=G/S=mg/S P =ρg h变化的压强△P=△F / S △P =ρg△h②密度:ρ=m/V③柱形液体产生的压力大小等于液体自身的重力大小。
即:F =G = mg④柱体的体积:V= sh(长方体) V= h3(立方体)柱体的底面积:S= ab S= h2三、例题【例题1】A、B两个轻质薄壁圆柱形容器放置在水平桌面上,它们内部分别盛有质量相等的甲、乙两种液体,如图1所示。
若再向两容器内分别注入体积相同的各自原有液体后(都没有液体溢出)。
关于甲、乙的密度和容器底部增加的压强的正确判断的是()A.ρ甲>ρ乙,Δp甲>Δp乙。
B.ρ甲<ρ乙,Δp甲>Δp乙。
C.ρ甲<ρ乙,Δp甲<Δp乙。
D.ρ甲>ρ乙,Δp甲<Δp乙。
【答案】A【解析】第一步:先比较甲、乙液体密度的大小关系。
根据m甲=m乙ρ甲V甲=ρ乙V乙因为V甲<V乙,所以甲、乙的密度ρ甲>ρ乙。
第二步:比较液体增加的深度的大小关系。
向两容器内分别注入体积相同的各自原有液体后,因为ΔV甲=ΔV乙S甲<S乙,所以液体升高的高度为Δh甲>Δh乙。
第三步:比较增加的压强的大小关系。
根据△P=ρg△h可以比较液体对容器底部增加的压强:因为ρ甲>ρ乙,Δh甲>Δh乙,所以Δp甲>Δp乙。
故答案为A。
【例题2】如图2所示,两个足够高的薄壁轻质圆柱形容器A、B(底面积S A>S B)置于水平地面上,容器中分别盛有体积相等的液体甲和乙,它们对各自容器底部的压强相等。
下列选项中,一定能使甲液体对容器底部的压强大于乙液体对容器底部压强的操作方法是()①分别倒入相同深度的液体甲和乙②分别倒入相同质量的液体甲和乙③分别倒入相同体积的液体甲和乙④分别抽出相同体积的液体甲和乙A.①B.②③C.①④D.①②③【答案】A【解析】第一步,先比较甲与乙密度大小的关系:因为甲和乙它们对各自容器底部的压强相等,p甲=p乙根据p=ρgh可知:ρ甲gh甲=ρ乙gh乙。
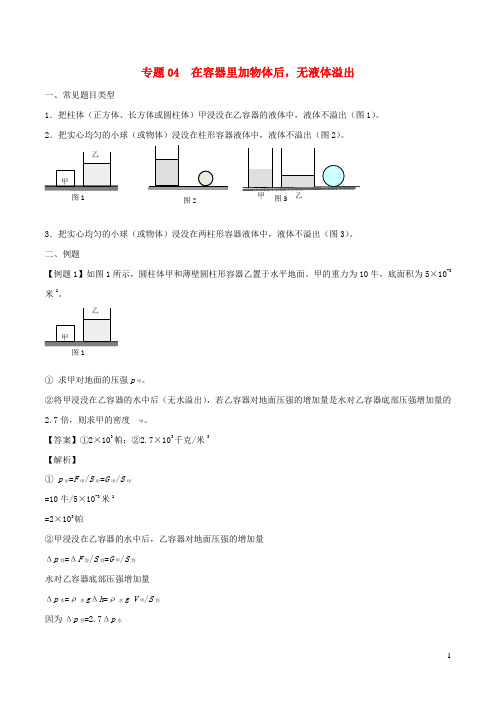
专题04 在容器里加物体后,无液体溢出一、常见题目类型1.把柱体(正方体、长方体或圆柱体)甲浸没在乙容器的液体中,液体不溢出(图1)。
2.把实心均匀的小球(或物体)浸没在柱形容器液体中,液体不溢出(图2)。
3.把实心均匀的小球(或物体)浸没在两柱形容器液体中,液体不溢出(图3)。
二、例题【例题1】如图1所示,圆柱体甲和薄壁圆柱形容器乙置于水平地面。
甲的重力为10牛,底面积为5×10-3米2。
① 求甲对地面的压强p 甲。
②将甲浸没在乙容器的水中后(无水溢出),若乙容器对地面压强的增加量是水对乙容器底部压强增加量的2.7倍,则求甲的密度甲。
【答案】①2×103帕;②2.7×103千克/米3【解析】① p 甲=F 甲/S 甲=G 甲/S 甲 =10牛/5×10-3米2=2×103帕②甲浸没在乙容器的水中后,乙容器对地面压强的增加量 Δp 容=ΔF 容/S 容=G 甲/S 容 水对乙容器底部压强增加量 Δp 水=ρ水g Δh =ρ水g V 甲/S 容 因为Δp 容=2.7Δp 水乙图1甲图2 乙图1甲 图3G 甲/S 容=2.7ρ水g V 甲/S 容G 甲=ρ水g V 甲 ρ甲g V 甲=2.7ρ水g V 甲所以 ρ甲=2.7ρ水 =2.7×103千克/米3【例题2】如图2所示,有一薄壁柱形容器置于水平地面上,容器中装有水。
现将一只质量为2千克的实心小球浸没在容器的水中,水不溢出,分别测出小球浸入前和浸没后水对容器底部的压强p 水、小球浸入前和浸没后容器对水平地面的压强p 地,如下表所示。
求:① 小球浸入前,容器中水的深度h 水。
② 容器中水的重力G 水。
③ 实心球的密度ρ球。
【答案】①0.2米;②39.2牛;③2.5×103千克/米3。
【解析】① 由p 水=ρ水gh 水可求小球浸入前,容器中水的深度h 水:h 水=p 水/(ρ水g )=1960帕/(103千克/米3×9.8牛/千克)=0.2米② 容器对水平地面增大的压强为Δp 地=p’地-p 地=3430帕-2450帕=980帕 容器的底面积为S 容=△F 地/ △P 地= m 地g /△P 地=(2千克×9.8牛/千克)/980帕=2×10-2米2∵容器是柱形∴G 水=F 水=p 水S =1960帕×2×10-2米2=39.2牛 ③ 水对容器底部增大的压强Δp 水=p ´水-p 水=2352帕-1960帕=392帕 根据Δp 水=ρ水g Δh 可求升高的高度Δh 水△h 水=△p 水/(ρ水g )=392帕/(103千克/米3×9.8牛/千克)=0.04米 ∵小球浸没∴实心球的体积V 球=ΔV 水=S 容Δh 水=2×10-2米2×0.04米=8×10-4米3实心球的密度ρ球=m 球/V 球 = 2.千克/8×10-4米3=2.5×103千克/米3【例题3】如图3(a )所示,底面积为2×10-2米2的薄壁轻质圆柱形容器放在水平地面上。

一、初中物理压力与压强问题1.如图所示,甲、乙两个均匀实心正方体放在水平地面上时对水平地面的压强相等,若分别在两物体上沿竖直方向截去厚度相同的部分并分别叠放在对方剩余部分的上方,此时压强p 甲、p 乙比较,正确的是( )A .可能是p 甲> p 乙B .一定是p 甲> p 乙C .可能是p 甲= p 乙D .一定是p 甲< p 乙【答案】B 【解析】 【详解】甲、乙两个均匀实心正方体放在水平地面上时对水平地面的压强相等,则3G a 甲甲=3G a 乙乙,设a 甲=5cm ,a 乙=10cm ,截去厚度为2cm , 则G 甲=18G 乙,叠放在对方剩余部分的上方后的压强p 甲=33251035G G a +甲乙甲=3G a 甲甲+313G a ⨯乙甲=3G a 甲甲+13×38G a 甲甲=3113G a ⨯甲甲 p 乙=382105810G G a +乙甲乙=3G a 乙乙+312G a ⨯甲乙=3G a 乙乙+12×318G a 乙乙=1716×3G a 乙乙 故p 甲> p 乙。
故选B 。
2.甲、乙两个实心均匀正方体放在水平地面上,他们对地面压强相等,已知ρ甲<ρ乙,在两个正方体上部分别沿水平方向切去相同的高度,切去部分的质量分别为m ′甲和m ′乙,则下列说法中正确的是 A . m ′甲一定大于m ′乙 B . m ′甲一定小于m ′乙 C . m ′甲一定等于m ′乙 D . m ′甲可能等于m ′乙【答案】A 【解析】 【详解】据最初压强相等有:ρ甲gh 甲=ρ乙gh 乙,ρ甲h甲=ρ乙h乙ρ甲<ρ乙,故:h甲>h乙。
甲的横截面积:S甲=h2甲,乙的横截面积:S乙=h2乙.设切去的高度为△h,要比较切去部分的质量,切去部分的质量=密度×切去部分的体积:m′甲=ρ甲S甲∆h=ρ甲h2甲∆h=ρ甲h甲h甲∆hm′乙=ρ乙S乙∆h=ρ乙h2乙∆h=ρ乙h乙h乙∆h则:m′甲>m′乙。

一、初中物理压力与压强问题1.如图所示,水平桌面上放置有甲、乙两个完全相同的圆柱形烧杯,分别装入适量的密度不同但质量相等的盐水,将同一个鸡蛋先后放入甲、乙两个烧杯中,鸡蛋在甲烧杯中处于悬浮状态,在乙烧杯中处于漂浮状态。
下列判断正确的是( )A .甲杯中盐水密度为ρ甲,乙杯中盐水密度为ρ乙,则ρ甲>ρ乙B .鸡蛋在甲、乙两烧杯中受到的浮力分别为F 浮和F′浮,则F 浮>F′浮C .放入鸡蛋后,甲、乙两烧杯对桌面的压力分别为F 甲和F 乙,则F 甲>F 乙D .放入鸡蛋后,甲、乙两烧杯底部受到的压强分别为p 甲和p 乙,则p 甲=p 乙 【答案】D 【解析】 【分析】(1)同一只鸡蛋无论漂浮或悬浮,其浮力都等于排开盐水的重,也等于自身的重力;在浮力相同时,排开的液体体积越大,说明液体的密度是越小的;(2)水平面上物体的压力和自身的重力相等,据此可知甲、乙两烧杯对桌面的压力关系; (3)粗细均匀容器底部受到的压力等于液体的重力和漂浮(或悬浮)物体的重力之和,根据Fp S =判断甲、乙两烧杯底部受到的压强关系。
【详解】 AB .因为鸡蛋在甲中悬浮、乙中漂浮,所以浮力都等于自身的重力,即鸡蛋在甲、乙两烧杯中受到的浮力相等,根据F gV ρ=浮液排可知,在浮力相同时,甲杯中的V 排大,则ρ甲小于ρ乙,故AB 错误;C .因甲、乙两个烧杯完全相同,装入密度不同但质量相等的盐水,且鸡蛋一样,根据水平面上物体的压力和自身的重力相等和G mg =可知,放入鸡蛋后甲、乙两烧杯对桌面的压力相等,故C 错误;D .烧杯粗细均匀,装入密度不同但质量相等的盐水,且鸡蛋一样,所以甲、乙两烧杯底部受到的压力相等,因两烧杯底面积S 相同,根据Fp S=可知,两只杯子底部受到液体的压强相同,故D 正确。
故选D 。
2.甲、乙两个实心正方体物块放在相同的海绵上,甲的凹陷程度比较深.将它们沿水平方向切去一部分后,剩余部分对海绵的凹陷程度如图所示,则A .甲切去的质量一定比乙小B .它们切去的质量一定相同C .甲切去的高度一定比乙大D .它们切去的高度一定相同 【答案】C 【解析】 【分析】 【详解】甲、乙两个实心正方体物块放在相同的海绵上,甲的凹陷程度比较深, 所以,P 甲>P 乙,而F G m g ==甲甲甲,F G m g 乙乙乙==,所以,m g m gS S =甲乙甲乙将它们沿水平方向切去一部分后,海绵的凹陷程度相同,则甲乙对海绵压强相等,P 甲剩=P 乙剩,即:m g m gm g m g S S --=乙甲乙剩甲切甲乙所以,m 甲切>m 乙切,故AB 错误;放在水平面上的柱体的压强可用P ρgh =求解. 因为P 甲剩=P 乙剩,所以,gh gh ρρ=甲乙甲剩乙剩, 由图可知,h h 甲剩乙剩>,所以ρρ<甲乙. 因为m 甲切>m 乙切,V Sh =,m V ρ=所以:m m g g S S >甲切乙切甲乙,即:S h g S h g S S ρρ>甲甲乙乙甲切乙切甲乙所以,h 甲切>h 乙切,C 正确,D 错误. 故选C.3.如图,形状、体积相同的长方体甲、乙至于水平地面,对地面的压力分别为F 甲、F 乙,将他们顺时针旋转90°,此时甲乙对地面的压强为p '甲、p '乙,对地面的压强变化量分别为p ∆甲、p ∆乙。

一、初中物理压力与压强问题1.如图所示,轻质圆柱形容器A 、B 、C 分别盛有质量相同的不同液体(S A <S B <S c ),现有质量相同的甲、乙两实心物体(ρ甲>ρ乙),若选择其中一个物体放入某个容器中,物体浸没且液体没有溢出,此时液体对容器底部的压强为p 液,则( )A .甲放入B 中p 液最小 B .甲放入C 中p 液最小 C .乙放入A 中p 液最大D .乙放入B 中p 液最大【答案】B 【解析】 【分析】由题意可知,本题意在比较容器底受到液体压强的大小关系,可由压强的计算公式Fp S=、液体内部压强的计算公式p gh ρ=液液、阿基米德原理、力的平衡、作用力与反作用力,综合进行分析判断,合理进行受力分析是解决此题的关键 【详解】 浸在液体中的物体,会受到竖直向上的浮力;由于力的作用是相互的,所以物体会对液体产生竖直向下的压力,相互作用力大小相等1F F =压浮①对杯中液体体进行受力分析:竖直向上的方向上,液体受容器底部的支持力F 支;竖直向下的方向上,受重力G 液和物体对其的压力1F 压,由力的平衡条件可得1F G F =+压支液②容器底部对液体的支持力F 支,和液体对容器底部的压力2F 压为相互作用力,其大小相等2F F =压支③由①②③式和阿基米德原理可得,液体对容器底部的压力为2F F G V g G ρ=+=+压浮液液物液若容器底面积为S ,则容器底受到液体的压强为2m gF V gG V gG G p SSSSSSρρρρ+===+=+物液压液物液液物液液物上式也可写成m g Gp SSρρ=+液物液物由于三容器中液体质量相等、物体质量也相等,由上式不难看出液体对容器底部压强的大小取决于ρ液、ρ物和容器底面积S 的大小关系;AB .ρ液最小、ρ物最大、S 最大时,此时容器底部受到的液体压强最小,所以将甲放入C 中时容器受到的液体压强最小,故A 不符合题意,B 符合题意;CD .ρ液最大、ρ物最小、S 最小时,此时容器底部受到的液体压强最大;但由图形不能判断出A 、B 中液体密度谁大谁小,故CD 不符合题意。

一、初中物理压力与压强问题1.如图(a )所示,底面积不同的圆柱形容器分别盛有甲、乙两种液体,其密度为ρ甲和ρ乙。
已知液体对各自容器底部的压强相等。
现将甲、乙液体互换容器(均不溢出),如图(b )所示,甲、乙液体对容器底部压强的变化量分别为Δp 甲、Δp 乙,则( )A .ρ甲>ρ乙,Δp 甲>Δp 乙B .ρ甲<ρ乙,Δp 甲<Δp 乙C .ρ甲<ρ乙,Δp 甲=Δp 乙D .ρ甲>ρ乙,Δp 甲=Δp 乙 【答案】A 【解析】 【详解】液体对各自容器底部的压强相等,即p p =甲乙,即gh gh ρρ=甲甲乙乙从图(a)可以看到,h h <甲乙,那么可知ρρ甲乙>现将甲、乙液体互换容器,那么可得''p gh ρ=甲甲甲、''p gh ρ=乙乙乙,甲、乙液体对容器底部压强的变化量分别为()'''p p p gh gh g h h ρρρ∆=-=-=-甲甲甲甲甲甲甲甲甲甲 ()'''p p p gh gh g h h ρρρ∆=-=-=-乙乙乙乙乙乙乙乙乙乙还可以知道甲液体、乙液体在大底面积1S 和小底面积2S 的容器中时的体积关系式是''12V V S h S h ===甲甲甲甲 ''21V V S h S h ===乙乙乙乙式子变换可以得到'21S h h S =⋅甲甲,'12S h h S =⋅乙乙,代入上面的式子可以得到 '''21211S S S p g h h gh S S ρρ⎛⎫-∆=-⋅=⋅ ⎪⎝⎭甲甲甲甲甲甲'''11222S S S p g h h gh S S ρρ⎛⎫-∆=-=⋅ ⎪⎝⎭乙乙乙乙乙乙两式相减可得到()''''211212121212-----h S h S S S S S p p gh gh g S S S S S S ρρρρ-∆∆=⋅⋅=⋅甲甲乙乙甲乙甲甲乙乙因为p p =甲乙,12S S >,那么12p S p S >甲乙即在(a)图甲液体对容器底的压力大于乙液体对容器底的压力,也可知G G >甲乙因为'2G h S ρ=甲甲甲、'1G h S ρ=乙乙乙,可知''21-0h S h S ρρ>甲甲乙乙所以-0p p ∆∆>甲乙即p p ∆>∆甲乙;故选A 。
上海市备战2020年中考物理压强压轴题 专题01 柱体切割、液体抽取(倒入)一、常见题目类型1.在柱形物体沿水平方向切切割:切去某一厚度(体积或质量)(图1)。
2.在柱形容器中抽取(或加入)液体:某一深度(体积或质量)(图2)。
3.在柱形固体切去一部分,同时在柱形容器的液体中抽取(或加入)液体:某一深度(体积或质量)(图3)。
二、例题【例题1】如图1所示,实心均匀正方体甲、乙放置在水平地面上,它们的重力G 均为90牛,甲的边长a 为0.3米,乙的边长b 为0.2米。
求:① 正方体甲对地面的压强p 甲;② 若沿水平方向将甲、乙截去相同的厚度Δh 后,它们剩余部分对地面的压强p 甲′和 p 乙′相等,请计算截去的厚度Δh 。
【答案】①1000帕;②0.16米。
【解析】① p 甲=F 甲/s 甲=G /a 2==90牛/9×10-2米2=1000帕② 先比较原来两个立方体压强的大小关系:它们的重力G 均为90牛,对地面的压力均为90牛,因为甲的底面积大于乙的底面积,根据p =F /S =G /S 所以原来两个立方体的压强 p 甲´ <p 乙´。
可以先求出甲乙两立方体密度的大小关系:它们的重力G 均为90牛,所以m 甲=m 乙 ρ甲V 甲=ρ乙V 乙 ρ甲(0.3米)3 = ρ乙(0.2米)3图2B图3图1图1甲乙两立方体密度的大小关系ρ甲︰ρ乙=8︰:27设截去的厚度Δh时,它们剩余部分对地面的压强相等,即p甲´=p乙´ρ甲g(a−Δh)=ρ乙g(b−Δh)8 ×(0.3米−Δh)= 27 ×(0.2米−Δh)Δh=0.16米【例题2】(2019上海中考题)如图7所示,足够高的薄壁圆柱形容器甲、乙置于水平桌面上,容器甲、乙底部所受液体的压强相等。
容器甲中盛有水,水的深度为0.08米,容器乙中盛有另一种液体。
①若水的质量为2千克,求容器甲中水的体积V水。
专题05 在容器里加物体后,有液体溢出一、常见题目类型1.将物体甲浸没在柱形容器乙的液体中(图1)。
2.将物块丙放入容器甲的液体中、叠放在柱体乙的上方(图2)。
3.将甲、乙两个实心均匀光滑小球先后分别放入容器中(图3). 4.在柱形物体乙上方沿水平方向切去一部分,并将切去部分竖直放在甲容器内(浸没或不浸没)(图4).二、例题【例题1】柱形轻质薄壁容器的底面积为1×10—2米2,如图1所示,甲图4图3 乙图1甲乙甲乙图2丙内盛0。
2米深度的水后置于水平地面上。
① 求容器底部受到水的压强p 水。
② 现将一块质量为1.5千克、体积为1×10—3米3的物体完全浸没在容器的水中后,测得容器底部受到水的压强为2450帕。
求此时容器对水平桌面的压强p 容。
【答案】①1960帕;②2940帕。
【解析】 ①p 水=ρ水g h=1×103千克/米3×9.8牛/千克×0.2米3=1960帕②物体浸没在容器的水中后,容器底部受到水的压强为2450帕可求现在水的深度h ':p '水=ρ水g h ' h '= p '/ρ水gh '=2450帕/1×103千克/米3×9。
8牛/千克=0。
25米容器内剩余水的体积为V 剩余水= S h '-V 物=0。
25米×1×10—2米2-1×10-3米3=1。
5×10-3米3现在容器对水平桌面的压力图1F 容=G 容=(m 剩余水+m 物)g=(1。
5×10—3米3×1×103千克/米3+1.5千克)×9.8牛/千克=29.4牛对水平桌面的压强P 容= F 容/S =29。
4牛/ 1×10-2米2=2940帕(注意:此题不计算溢出水的质量,更简单。
也可用其他方法求解) 【例题2】如图2所示,盛有水的轻质薄壁圆柱形容器甲和实心均匀圆柱体乙均放置于水平地面上,它们的底面积分别为1×10-2米2和0.5×10—2米2.现将两完全相同物块分别放入容器甲中和叠在圆柱体乙的上方,放置前后容器甲、圆柱体乙对水平地面的压强大小p 甲、p 乙如下表所示。
上海市备战2020年中考物理压强选择题专项大剖析专题12 在柱形的液体中放入物体一、常见题目类型1.把甲、乙两个实心小球分别放入液体中且浸没(图1)。
2.把甲、乙两个实心小球分别放入两种液体中且浸没(或从液体中取出)(图2)。
3.将小球从液体A 中取出并浸没在液体B 中(图3)。
二、分析此类题目常用到的知识与方法:① 液体对柱形容器底部的压强: p =F /S P =ρg h变化(增大或减小)的压强: △P =△F / S △P =ρg △h②把物体放入柱形液体中浸没时,液体对容器底部产生的压力:F=PS =ρg hS+ρg △h S =G 液+ G 排(F 浮)等于原来液体的重力与物体受到的浮力之和。
增大的压力△F :就是物体排开的液体所受到的重力(即浮力)。
即△F =F 浮=ρ液gV 排三、例题【例题1】如图1所示,两个底面积不同的圆柱形容器A 和B (S A <S B ),容器足够高,分别盛有两种液体,且两种液体对容器底部的压力相等。
若在容器A 中浸没金属球甲,在容器B 中浸没金属球乙后,两种液体对容器底部的压强相等,则甲、乙两金属球相比,不可能存在的是( )A .甲的质量大B .甲的密度大C .乙的体积小D .乙的密度小【答案】C A B 图1 甲 乙图2 图3A B图1【解析】①原来甲、乙液体对各自容器底部的压力相等:F A=F B,质量相等,m A=m B,即ρA V A=ρB V B。
因为V A<V B 所以A、B液体密度的关系为ρA>ρB。
②根据P=F/S,因为F A =F B,S A<S B,所以原来A、B液体的压强P A>P B。
③在容器A中浸没金属球甲,在容器B中浸没金属球乙后,液体对容器底部的压强相等,P'A=P'B。
增大的压强△P= P原来− P剩余,因为原来P A>P B,现在P'A=P'B,所以△P A<△ P B。
④根据△P A<△ P B可得:ρA g△h A<ρB g△h B,因为ρA>ρB,所以△h A<△h B,又因为S A<S B,所以△V A<△V B,即A液体升高的体积小于B液体升高的体积,也就是金属球甲的体积小于乙的体积。
2022年中考物理复习之挑战压轴题(选择题):压强一.选择题(共10小题)1.(2021秋•青浦区期末)均匀正方体甲、乙置于水平地面上,对水平地面的压强分别为p、p乙,如图所示。
现沿水平方向分别切去相同高度的部分后,甲、乙剩余部分对水平甲地面的压强相等。
下列关于甲、乙的密度ρ甲、ρ乙和甲、乙正方体对水平地面的压强p、p乙大小的判断,正确的是()甲A.ρ甲=ρ乙,p甲>p乙B.ρ甲=ρ乙,p甲<p乙C.ρ甲>ρ乙,p甲>p乙D.ρ甲>ρ乙,p甲<p乙2.(2021秋•闵行区期末)实心均匀正方体甲、乙按如图所示放置在水平桌面上,已知它们对桌面的压强相等。
现将乙在桌面外的部分沿竖直方向切去,切去的比例为n。
甲按相同比例n沿水平方向切去一部分,并将切去部分叠放在对方剩余的上方,此时甲、乙对桌面的压力分别为F甲、F乙,压强分别为p甲、p乙。
关于压力、压强的大小关系,下列判断正确的是()A.F甲=F乙、p甲>p乙B.F甲>F乙、p甲<p乙C.F甲=F乙、p甲<p乙D.F甲<F乙、p甲>p乙3.(2021•闵行区二模)实心均匀柱体甲、圆台乙放置于水平地面上,已知它们高度相同、底面积S甲>S乙,如图所示。
若在甲、乙上方沿水平方向截去相同体积,将切下部分竖放在对方剩余部分正上方后,甲、乙上方受到的压强p甲′<p乙′。
则截去前甲、乙对地的压力F甲、F乙,压强p甲、p乙的大小关系是()A.F甲>F乙,p甲>p乙B.F甲>F乙,p甲<p乙C.F甲<F乙,p甲>p乙D.F甲<F乙,p甲<p乙4.(2018•陕西二模)如图所示,完全相同的甲、乙两个烧杯内分别装有密度不同的液体。
在两烧杯中,距离杯底同一高度处有A、B两点,已知A、B两点压强相等,烧杯甲、乙对桌面的压强为p甲、p乙,若将两个体积相等的实心物体M、N分别轻轻地放入甲、乙量容器中,发现M漂浮在甲液面上,N悬浮在乙液体中,两容器中液体均未溢出。
则下列说法正确的是()A.甲、乙两烧杯对桌面的压强p甲与p乙的大小无法确定B.M、N两物体的密度关系为ρM>ρNC.放入M、N两物体后,容器底增加的压强为△p甲<△p乙D.放入M、N两物体后,容器对桌面增加的压力为△F甲=△F乙5.(2021秋•普陀区期末)如图所示,甲、乙两个实心均匀正方体放在水平地面上,沿竖直方向在两个正方体上分别切去相同宽度,甲、乙剩余部分对地面的压强相等,则下列关于甲、乙正方体切去部分质量m甲'和m乙'的大小关系正确的是()A.m甲'一定大于m乙'B.m甲'一定等于m乙'C.m甲'可能小于m乙'D.m甲'可能不等于m乙'6.(2021秋•鹿城区期末)在图所示装置中,粗细均匀的细玻璃管上端塞有橡皮塞,管内一段水银柱将一部分气体封闭在玻璃管内。