苏教版九下三角函数复习练习

苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习锐角三角函数—知识讲解【学习目标】1．结合图形理解记忆锐角三角函数定义；2．会推算30°、45°、60°角的三角函数值，并熟练准确的记住特殊角的三角函数值； 3．理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c ∠==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边；cos B aB c∠==的邻边斜边；tan B b B B a ∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化． (2)sinA ，cosA ，tanA 分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin 与∠A ，cos 与∠A ，tan 与∠A 的乘积．书写时习惯上省略∠A 的角的Ca b记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°<∠A<90°间变化时，，，tanA＞0．要点二、特殊角的三角函数值(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；②余弦值随锐角度数的增大(或减小)而减小(或增大)．要点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．【典型例题】类型一、锐角三角函数值的求解策略1．（2016•安顺）如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC 的正切值是（）A．2 B．C．D．【思路点拨】根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案．【答案】D．【解析】解：如图：，由勾股定理，得AC=，AB=2，BC=，∴△ABC为直角三角形，∴tan∠B==，故选：D．【总结升华】本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数．举一反三：【课程名称：锐角三角函数395948：例1（1）-（2）】【变式】在RtΔABC中，∠C=90°，若a=3，b=4，则c=，sinA=，cosA=，sinB=，cosB=．a【答案】c = 5 ，sinA = 35 ， cosA =45，sinB =45， cosB =35．类型二、特殊角的三角函数值的计算2．求下列各式的值：(1)（2015•茂名校级一模） 6tan 230°﹣sin60°﹣2sin45°；(2)（2015•乐陵市模拟） sin60°﹣4cos 230°+sin45°•tan60°；(3)（2015•宝山区一模） +tan60°﹣．【答案与解析】 解：（1）原式==12(2) 原式=×﹣4×（）2+×=﹣3+3；(3) 原式=+﹣=2+﹣=3﹣2+2【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值，先代入特殊角的三角函数值，再进行化简．举一反三：【课程名称： 锐角三角函数 395948 ：例1（3）-（4）】 【变式】在Rt ΔABC 中，∠C =90°，若∠A=45°，则∠B = ，sinA=，cosA=，sinB=，cosB=．【答案】∠B=45°，sinA=，cosA=，sinB=cosB=．类型三、锐角三角函数之间的关系3．（2015•河北模拟）已知△ABC中的∠A与∠B满足（1﹣tanA）2+|sinB﹣|=0（1）试判断△ABC的形状．（2）求（1+sinA）2﹣2﹣（3+tanC）0的值．【答案与解析】解：（1）∵|1﹣tanA）2+|sinB﹣|=0，∴tanA=1，sinB=，∴∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴△ABC是锐角三角形；（2）∵∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴原式=（1+）2﹣2﹣1=．【总结升华】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．类型四、锐角三角函数的拓展探究与应用4．如图所示，AB是⊙O的直径，且AB＝10，CD是⊙O的弦，AD与BC相交于点P，若弦CD＝6，试求cos∠APC的值．【答案与解析】连结AC，∵ AB是⊙O的直径，∴∠ACP＝90°，又∵∠B＝∠D，∠PAB＝∠PCD，∴△PCD∽△PAB，∴PC CDPA AB=． 又∵ CD ＝6，AB ＝10， ∴ 在Rt △PAC 中，63cos 105PC CD APC PA AB ∠====．【总结升华】直角三角形中，锐角的三角函数等于两边的比值，当这个比值无法直接求解，可结合相似三角形的性质，利用对应线段成比例转换，间接地求出这个比值．锐角的三角函数是针对直角三角形而言的，故可连结AC ，由AB 是⊙O 的直径得∠ACB ＝90°，cos PC APC PA ∠=，PC 、PA 均为未知，而已知CD ＝6，AB ＝10，可考虑利用△PCD ∽△PAB 得PC CDPA AB=．5．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图1①，在△ABC 中，AB ＝AC ，顶角A 的正对记作sadA ，这时sadA BCAB==底边腰．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：(1)sad60°＝________．(2)对于0＜A ＜180°，∠A 的正对值sadA 的取值范围是_______．(3)如图1②，已知sinA ＝35，其中∠A 为锐角，试求sadA 的值．【答案与解析】(1)1； (2)0＜sadA ＜2；(3)如图2所示，延长AC 到D ，使AD ＝AB ，连接BD ．设AD ＝AB ＝5a ，由3sin 5BC A AB ==得BC ＝3a ，∴ 4AC a ==，∴ CD ＝5a-4a ＝a ，BD ==，∴ sadA BD AD == 【总结升华】(1)将60°角放在等腰三角形中，底边和腰相等，故sadA ＝1；(2)在图①中设想AB ＝AC的长固定，并固定AB 让AC 绕点A 旋转，当∠A 接近0°时，BC 接近0，则sadA 接近0但永远不会等于0，故sadA ＞0，当∠A 接近180°时，BC 接近2AB ，则sadA 接近2但小于2，故sadA ＜2；(3)将∠A 放到等腰三角形中，如图2所示，根据定义可求解．。

天津市2020年〖苏科版〗九年级数学下册复习综合试卷锐角三角函数创作人：百里六条 创作日期：202X.04.01 审核人： 北堂规中创作单位： 博恒中英学校1．如图28－1－1，在△ABC 中，∠C ＝90°，AB ＝5，BC ＝3，则sin A 的值是( C ) 图28－1－1 A.34B.43C.35D.452．把△ABC 三边的长度都扩大为原来的3倍，则锐角A 的正弦函数值( A ) A ．不变 B ．缩小为原来的13C ．扩大为原来的3倍D ．不能确定3．如图28－1－2，在Rt △ABC 中，∠C ＝90°，AB ＝2BC ，则sin B 的值为( C ) 图28－1－2 A.12 B.22 C.32D ．1 4．在Rt △ABC 中，∠C ＝90°，AC ＝9，sin B ＝35，则AB ＝( A ) A ．15 B ．12 C ．9 D ．6 【解析】 AB ＝AC sinB ＝935＝15，选A. 5．如图28－1－3所示，△ABC 的顶点是正方形网格的格点，则sin A 的值为( B ) 图28－1－3A.12B.55C.1010D.2556．如图28－1－4，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边上有一点P (3，4)，则sin α的值是( D )图28－1－4 A.25 B.55 C.35 D.45【解析】 OP ＝32＋42＝5，∴sin α＝45.故选D. 7．△ABC 中，∠C ＝90°，sin A ＝25，则sin B ＝__215__． 【解析】 由sin A ＝25可得BC AB ＝25，故可设BC ＝2a ，AB ＝5a ，由勾股定理求得AC ＝21a ，再由正弦定义求得sin B ＝AC AB ＝21a 5a ＝215.8. 如图图28－1－5，在⊙O 中，过直径AB 延长线上的点C 作⊙O 的一条切线，切点为D ，若AC ＝7，AB ＝4，则sin C 的值为__25__．图28－1－59．Rt △ABC 中，若∠C ＝90°，a ＝15，b ＝8，求 sin A ＋sin B . 解：由勾股定理有c ＝a2＋b2＝152＋82＝17， 于是sin A ＝1517，sin B ＝817， 所以sin A ＋sin B ＝1517＋817＝2317.图28－1－610．如图28－1－6所示，△ABC 中，∠C ＝90°，sin A ＝13，AC ＝2，求AB ，BC 的长． 解：∵sin A ＝13，∴BC AB ＝13，∴AB ＝3BC . ∵AC 2＋BC 2＝AB 2，∴22＋BC 2＝(3BC )2， ∴BC ＝22，∴AB ＝322. 11. 在Rt △ABC 中，∠C ＝90°，若AB ＝4，sin A ＝35，则斜边上的高等于( B ) A.6425B.4825C.165D.12512．如图28－1－7，在菱形ABCD 中，DE ⊥AB 于E ，DE ＝6 cm ，sin A ＝35，则菱形ABCD 的面积是__60__cm 2. 图28－1－7【解析】 在Rt △ADE 中，sin A ＝DE AD， ∴AD ＝DE sinA ＝635＝10(cm)，∴AB ＝AD ＝10 cm ， ∴S 菱形ABCD ＝DE ·AB ＝6×10＝60(cm 2)．13．如图28－1－8，⊙O 的半径为3，弦AB 的长为4，求sin A 的值． 图28－1－8 第13题答图【解析】 要求sin A 的值，必将∠A 放在直角三角形中，故过O 作OC ⊥AB 于C ，构造直角三角形，然后根据正弦的定义求解．解：过点O 作OC ⊥AB ，垂足为C ，如图所示， 则有AC ＝BC .∵AB ＝4，∴AC ＝2.在Rt △AOC 中，OC ＝OA2－AC2＝32－22＝5，∴sin A ＝OC OA ＝53. 14．如图28－1－9，在Rt △ABC 中，∠ACB ＝90°，D 是AB 的中点，过D 点作AB 的垂线交AC 于点E ，BC ＝6，sin A ＝35，求DE .图28－1－9解：∵BC ＝6，sin A ＝35， ∴AB ＝10，∴AC ＝102－62＝8， ∵D 是AB 的中点， ∴AD ＝12AB ＝5， ∵△ADE ∽△ACB ， ∴DE BC ＝AD AC ，即DE 6＝58， 解得：DE ＝154.15．如图28－1－10，是一个半圆形桥洞截面示意图，圆心为O ，直径AB 是河底线，弦CD 是水位线，CD ∥AB ，且CD ＝24 m ，OE ⊥CD 于点E ，已测得sin ∠DOE ＝1213.(1)求半径OD ；(2)根据需要，水面要以每小时0.5 m 的速度下降，则经过多长时间才能将水排干？ 图28－1－10解：(1)∵OE ⊥CD 于点E ，CD ＝24 m ， ∴ED ＝12CD ＝12 m. 在Rt △DOE 中，sin ∠DOE ＝ED OD ＝1213， ∴OD ＝13 m.(2)OE ＝OD2－ED2＝132－122＝5(m)， ∴将水排干需5÷0.5＝10(小时)．16．如图28－1－11，已知⊙O 的半径为2，弦BC 的长为23，点A 为弦BC 所对优弧上任意一点(B ，C 两点除外)． (1)求∠BAC 的度数；(2)求△ABC 面积的最大值．⎝ ⎛⎭⎪⎫参考数据：sin60°＝32，cos30°＝32，tan30°＝33 图28－1－11解：(1)过点O 作OD ⊥BC 于点D ，连接OC ，OB . 因为BC ＝23， 所以CD ＝12BC ＝3. 又因为OC ＝2， 所以sin ∠DOC ＝CD OC ＝32， 所以∠DOC ＝60°，所以∠BOC ＝2∠DOC ＝120°， 所以∠BAC ＝12∠BOC ＝60°.(2)因为△ABC 中的边BC 的长不变，所以底边上的高最大时，△ABC 的面积最大，即点A 是BAC ︵的中点时，△ABC 的面积最大，此时AB ︵＝AC ︵，所以AB ＝AC . 又因为∠BAC ＝60°，所以△ABC 是等边三角形．连接AD ，易证AD 是△ABC 的高． 在Rt △ADC 中，AC ＝BC ＝23，CD ＝3，所以AD ＝AC2－CD2＝（23）2－（3）2＝3， 所以△ABC 面积的最大值为12×23×3＝33.第2课时 锐角三角函数[见A 本P80]1．在Rt △ABC 中，∠C ＝90°，AB ＝5，BC ＝3，则∠A 的余弦值是( C ) A.35B.34C.45D.432. 如图28－1－12，将∠AOB 放置在5×5的正方形网格中，则tan ∠AOB 的值是( B ) 图28－1－12 A.23 B.32C.21313 D.313133．如图28－1－13是教学用直角三角板，边AC ＝30 cm ，∠C ＝90°，tan ∠BAC ＝33，则边BC 的长为( C ) A ．303 cm B ．203 cm C ．103 cm D ．53 cm 【解析】 BC ＝AC ·tan ∠BAC ＝30×33＝103(cm)． 图28－1－13 图28－1－144．在Rt △ABC 中，∠C ＝90°，cos B ＝45，则AC ∶BC ∶AB ＝( A ) A ．3∶4∶5 B ．5∶3∶4 C ．4∶3∶5 D ．3∶5∶4【解析】 由cos B ＝BC AB ＝45，设BC ＝4x ，AB ＝5x ， 则AC ＝AB2－BC2＝（5x ）2－（4x ）2＝3x ， ∴AC ∶BC ∶AB ＝3x ∶4x ∶5x ＝3∶4∶5，故选A.5．如图28－1－14，在Rt △ABC 中，∠C ＝90°，AB ＝6，cos B ＝23，则BC 的长为( A ) A ．4 B ．25C.181313 D.121313【解析】 ∵cos B ＝23，∴BC AB ＝23.∵AB ＝6，∴BC ＝23×6＝4，故选A.6．如图28－1－15，P 是∠α的边OA 上一点，点P 的坐标为(12，5)，则tan α等于( C )图28－1－15A.513B.1213C.512D.1257．在Rt △ABC 中，∠C ＝90°，BC ＝8，AC ＝6，则sin B ＝__35__，cos B ＝__45__，sin A ＝__45__，cos A ＝__35__，tan A ＝__43__，tan B ＝__34__． 【解析】 AB ＝BC2＋AC2＝82＋62＝10. sin B ＝AC AB ＝610＝35，cos B ＝BC AB ＝810＝45， sin A ＝BC AB ＝810＝45，cos A ＝AC AB ＝610＝35， tan A ＝BC AC ＝86＝43，tan B ＝AC BC ＝68＝34.8. [·杭州]在Rt △ABC 中，∠C ＝90°，AB ＝2BC ，现给出下列结论：①sin A ＝32；②cos B ＝12；③tan A ＝33；④tan B ＝3，其中正确的结论是__②③④__．(只需填上正确结论的序号)9. [·安顺]在Rt △ABC 中，∠C ＝90°，tan A ＝43，BC ＝8，则Rt △ABC 的面积为__24__． 10．(1)在△ABC 中，∠C ＝90°，BC ＝2，AB ＝5，求sin A ，cos A ，tan A .(2)在△ABC 中，若三边BC ，CA ，AB 满足BC ∶CA ∶AB ＝5∶12∶13，求sin A ，cos B ，tan A . 解：(1)由勾股定理，知AC ＝AB2－BC2＝25－4＝21， ∴sin A ＝BC AB ＝25，tan A ＝BC AC＝221＝22121，cos A ＝AC AB ＝215.(2)设BC ＝5k ，CA ＝12k ，AB ＝13k .∵BC 2＋CA 2＝25k 2＋144k 2＝169k 2＝AB 2， ∴△ABC 为直角三角形，∠C ＝90°，∴sin A ＝BC AB ＝513，cos B ＝BC AB ＝513，tan A ＝BC AC ＝512.11．(1)若∠A 为锐角，且sin A ＝35，求cos A ，tan A .(2)已知如图28－1－16，在Rt △ABC 中，∠C ＝90°，tan A ＝12，求∠B 的正弦、余弦值．图28－1－16解：(1)设在△ABC 中，∠C ＝90°，∠A 为已知锐角，∵sin A ＝a c ＝35，设a ＝3k ，c ＝5k ，∴b ＝c2－a2＝（5k ）2－（3k ）2＝4k ， ∴cos A ＝b c ＝4k 5k ＝45，tan A ＝a b ＝3k 4k ＝34. (2)∵∠C ＝90°，tan A ＝BC AC ＝12， ∴设BC ＝x ，AC ＝2x ， ∴AB ＝AC2＋BC2＝5x ， ∴sin B ＝AC AB＝2x 5x＝255，cos B ＝BCAB＝x 5x ＝55. 12．如图28－1－17，在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD ＝5，AC ＝6，则tan B 的值是( C ) A.45 B.35 C.34 D.43图28－1－17 图28－1－1813．如图28－1－18，在半径为5的⊙O 中，弦AB ＝6，点C 是优弧AB 上一点(不与点A ，B 重合)，则cos C 的值为__45__．【解析】 连接AO 并延长交⊙O 于点D ，连接BD ， 可得AD 为⊙O 直径，故∠ABD ＝90°. ∵⊙O 的半径为5，弦AB ＝6，∴BD ＝AD2－AB2＝102－62＝8.∵∠D ＝∠C ， ∴cos C ＝cos D ＝BD AD ＝810＝45.14．如图28－1－19，在△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AC ＝8，AB ＝10，求cos ∠BCD 的值． 图28－1－19解：∵∠ACB ＝90°，CD ⊥AB ， ∴∠BDC ＝∠ACB ＝90°， ∴∠B ＋∠BCD ＝90°， ∠B ＋∠A ＝90°， ∴∠BCD ＝∠A . ∵AB ＝10，AC ＝8，∴cos ∠BCD ＝cos A ＝AC AB ＝810＝45. 15．已知α为锐角，且tan α＝2，求sinα－22cosα＋sinα的值．【解析】 根据锐角三角函数的定义，结合图形设参数即可求出各边的比，从而得出sin α、cos α的值进行计算．解：如图所示，作Rt △ABC ，使∠C ＝90°， 设AC ＝k ，BC ＝2k ，则∠A ＝α. ∵AB ＝AC2＋BC2＝ k2＋（2k ）2＝5k ， ∴sin α＝2k 5k ＝255，cos α＝k 5k ＝55，∴sinα－22cosα＋sinα＝255－2255＋255＝1－52.16．如图28－1－20，定义：在直角三角形ABC 中，锐角α的邻边与对边的比叫做角α的余切，记作cot α，即cot α＝角α的邻边角α的对边＝ACBC，根据上述角的余切定义，解下列问题：(1)cot30°＝________；(2)如图，已知tan A ＝34，其中∠A 为锐角，试求cot A 的值． 图28－1－20 解：(1)3(2)∵tan A ＝BC AC ＝34，∴cot A ＝AC BC ＝43. 第3课时 特殊角三角函数值 [见B 本P80] 1. 3tan30°的值等于(A) A.3 B ．33 C.33 D.322. 计算6tan45°－2cos60°的结果是(D)A ．43B ．4C ．53D ．53．如图28－1－21，在Rt △ABC 中，∠C ＝90°，AB ＝2BC ，则sin B 的值为( C ) A.12 B.22C.32D ．1 【解析】 ∵Rt △ABC 中，∠C ＝90°，AB ＝2BC ， ∴sin A ＝BC AB ＝BC 2BC ＝12，∴∠A ＝30°，∴∠B ＝60°，∴sin B ＝32.图28－1－21图28－1－224．如果在△ABC 中，sin A ＝cos B ＝22，则下列最确切的结论是( C ) A ．△ABC 是直角三角形B ．△ABC 是等腰三角形 C ．△ABC 是等腰直角三角形D ．△ABC 是锐角三角形 【解析】 ∵sin A ＝cos B ＝22，∴∠A ＝∠B ＝45°，∴∠C ＝90°，AC ＝BC ，∴△ABC 是等腰直角三角形．5．如图28－1－22，当太阳光线与水平地面成30°角时，一棵树的影长为24 m ，则该树高为( A )A ．83 mB ．123 mC ．122 m D. 12 m【解析】 树高为24×tan30°＝24×33＝83(m)． 6．(1)3cos30°的值是__32__．(2)计算：sin30°·cos30°－tan30°＝__－12结果保留根号)． 【解析】 原式＝12×32－33＝－312. (3)cos 245°＋tan30°·sin60°＝__1__．【解析】cos 245°＋tan30°·sin60°＝⎝ ⎛⎭⎪⎫222＋33×32＝12＋12＝1.7．根据下列条件，求出锐角A 的度数．(1)sin A ＝32，则∠A ＝__60°__； (2)cos A ＝12，则∠A ＝__60°__；(3)cos A ＝22，则∠A ＝__45°__； (4)cos A ＝32，则∠A ＝__30°__． 8．如图28－1－23是引拉线固定电线杆的示意图，已知CD ⊥AB ，CD ＝3 m ，∠CAD ＝∠CBD ＝60°，求拉线AC 的长． 图28－1－23解：在Rt △ACD 中sin ∠CAD ＝CD AC， 则AC ＝CD sin∠CAD ＝332＝23(m)．答：拉线AC 的长是23 m.9．式子2cos30°－tan45°－（1－ta n60°）2的值是( B ) A. 23－2 B ．0 C ．23 D ．210．在△ABC 中，若⎪⎪⎪⎪⎪⎪sinA －12＋(cos B －12)2＝0，则∠C 的度数是( D )A ．30°B ．45°C ．60°D ．90° 【解析】 ⎪⎪⎪⎪⎪⎪sinA －12＋(cos B －12)2＝0∴sin A ＝12，cos B ＝12，∴∠A ＝30°，∠B ＝60°，则∠C ＝180°－30°－60°＝90° 故选D.11．如图28－1－24，测量河宽AB (假设河的两岸平行)，在C 点测得∠ACB ＝30°，在D 点测得∠ADB ＝60°，又CD ＝60 m ，则河宽AB 为结果保留根号)． 图28－1－24【解析】 因为∠ACB ＝30°，∠ADB ＝60°，所以∠ACB ＝∠CAD ＝30°，所以AD ＝CD ＝60 m ，所以AB ＝AD ·sin ∠ADB ＝60×32＝303(m)． 12．计算： (1)cos45°sin45°＋2sin60°tan60°－1tan30°＋tan45°；(2)sin45°＋cos30°3－2cos60°－sin60°(1－sin30°)；(3)sin 260°tan45°－⎝ ⎛⎭⎪⎫－1tan60°－2＋(tan30°)0.(4)(－1)2 011－⎝ ⎛⎭⎪⎫12－3＋⎝⎛⎭⎪⎫cos68°＋5π0＋||33－8sin60°. 解：(1)原式＝1＋2×32×3－3＋1＝5－3； (2)原式＝22＋323－2×12－32×⎝ ⎛⎭⎪⎫1－12＝2＋34－34＝24； (3)原式＝⎝ ⎛⎭⎪⎫322×1－⎝ ⎛⎭⎪⎫－13－2＋1＝34－3＋1＝－114；(4)原式＝－1－8＋1＋⎪⎪⎪⎪⎪⎪33－8×32＝－8＋3. 13．已知α是锐角，且sin(α＋15°)＝32，计算8－4cos α－(π－3.14)0＋tan α＋⎝ ⎛⎭⎪⎫13－1的值．【解析】 由sin60°＝32，从而可求出α. 解：由sin(α＋15°)＝32得α＋15°＝60°， 即α＝45°，原式＝22－4×22－1＋1＋3＝3. 14．如图28－1－25，在△ABC 中，AD ⊥BC 于点D ，AB ＝8，∠ABD ＝30°，∠CAD ＝45°，求BC 的长．图28－1－25解：∵AD ⊥BC 于点D ， ∴∠ADB ＝∠ADC ＝90°.在Rt △ABD 中，∵AB ＝8，∠ABD ＝30°， ∴AD ＝12AB ＝4，BD ＝3AD ＝43.在Rt △ADC 中，∵∠CAD ＝45°，∠ADC ＝90°， ∴DC ＝AD ＝4，∴BC ＝BD ＋DC ＝43＋4.15．阅读下面的材料，先完成阅读填空，再按要求答题： sin30°＝12，cos30°＝32，则sin 230°＋cos 230°＝__1__；① sin45°＝22，cos45°＝22，则sin 245°＋cos 245°＝__1__；② sin60°＝32，cos60°＝12，则sin 260°＋cos 260°＝__1__；③ …观察上述等式，猜想：对任意锐角A ，都有sin 2A ＋cos 2A ＝__1__．④(1)如图28－1－26，在锐角三角形ABC 中，利用三角函数的定义及勾股定理对∠A 证明你的猜想； 图28－1－26(2)已知：∠A 为锐角(cos A >0)且sin A ＝35，求cos A . 解：(1)如图，过点B 作BH ⊥AC 于点H ，BH 2＋AH 2＝AB 2则sin A ＝BH AB ，cos A ＝AH AB所以sin 2A ＋cos 2A ＝BH2AB2＋AH2AB2＝BH2＋AH2AB2＝1. (2)∵sin 2A ＋cos 2A ＝1，sin A ＝35， ∴cos 2A ＝1－(35)2＝1625∵cos A >0，∴cos A ＝45. 第4课时 利用计算器求锐角三角函数值和锐角度数 [见A 本P82] 1．利用计算器求sin30°时，依次按键：sin 30＝，则计算器上显示的结果是( A )A ．0.5B ．0.707C ．0.866D ．1【解析】 因为sin30°＝12，故选A.2．下列计算不正确的是( D )A ．sin α＝0.327 5，则α≈19°7′2″B ．sin β＝0.054 7，则β≈3°8′8″C ．tan γ＝5，则γ≈78°41′24″D ．sin A ＝0.726，则A ≈46°36′8″3．如图28－1－27，A ，B 两点在河的两岸，要测量这两点之间的距离，测量者在与A 同侧的河岸边选定一点C ，测出AC ＝a 米，∠A ＝90°，∠C ＝40°，则AB 等于( C )A ．a sin40° 米B ．a cos40°米C ．a tan40°米 D.a tan40°米 图28－1－27图28－1－284．如图28－1－28，在“测量旗杆的高度”的数学课题学习中，某学习小组测得太阳光线与水平面的夹角为27°，此时旗杆在水平地面上的影子的长度为24米，则旗杆的高度约为( D )A ．24米B ．20米C ．16米D ．12米5．用计算器计算(保留4个有效数字)：(1)sin35°≈__0.573__6__；(2)cos63°17′≈__0.449__6__；(3)tan27.35°≈__0.517__2__；(4)sin39°57′6″≈__0.642__1__．【解析】 (1)用计算器计算得sin35°≈0.573 576 436≈0.573 6；(2)按键顺序：cos 63°′″17°′″＝，结果：cos63°17′≈0.449 6；(3)按键顺序：tan 27·35＝，结果：tan 27.35°≈0.517 2；(4)按键顺序：sin 39°′″57°′″6°′″＝，结果：sin 39°57′6″≈0.642 1.6．若cos α＝0.501 8，则锐角α≈__59.88°__；若tan A ＝0.375，则锐角A ≈__20.56°__．7．如图28－1－29，某游乐场内滑梯的滑板与地面所成的角∠A ＝35°，滑梯的高度BC ＝2米，滑板AB 的长约为__3.5__米(精确到0.1米)．图28－1－29【解析】 ∵sin A ＝BC AB ，∴AB ＝BC sinA ＝2sin35°≈3.5(米)． 8．比较大小：8cos 31°__>__35.(填“＞”“＝”或“＜”)9．利用计算器求下列各角(精确到1′)．(1)sin A ＝0.75，求A ；(2)cos B ＝0.888 9，求B ； (3)tan C ＝45.43，求C ；(4)tan D ＝0.974 2，求D.解：(1)∵sin A ＝0.75，∴∠A ≈48°35′；(2)∵cos B ＝0.888 9，∴∠B ≈27°16′；(3)∵tan C ＝45.43，∴∠C ≈88°44′；(4)∵tan D ＝0.974 2，∴∠D ≈44°15′.10．如图28－1－30，小明以3米/秒的速度从山脚A 点爬到山顶B 点，已知B 点到山脚的垂直距离BC 为24米，且山坡坡角∠A 的度数为28°，问小明从山脚爬上山顶需要多少时间？(结果精确到0.1秒，参考数据：sin 28°≈0.47，cos 28°≈0.88，tan 28°≈0.53) 图28－1－30解：∵sin A ＝BC AB， ∴AB ＝BC sinA ＝24sin28°≈240.47≈51.06(米)， ∴所需时间t ≈51.06÷3≈17.0(秒)．答：小明从山脚爬上山顶大约需要17.0秒．11．如图28－1－31，在Rt △ABO 中，斜边AB ＝1.若OC ∥BA ，∠AOC ＝36°，则( C ) A ．点B 到AO 的距离为sin 54°B ．点B 到AO 的距离为tan 36°C ．点A 到OC 的距离为sin 36°sin 54°D ．点A 到OC 的距离为cos 36°sin 54°图28－1－31图28－1－3212．如图28－1－32，沿AC 方向开修一条公路，为了加快施工进度，要在小山的另一边寻找点E 同时施工，从AC 上的一点B 取∠ABD ＝127°，沿BD 的方向前进，取∠BDE ＝37°，测得BD ＝520 m ，并且AC ，BD 和DE 在同一平面内．(1)施工点E 离点D 多远正好能使A ，C ，E 成一条直线(结果保留整数)?(2)在(1)的条件下，若BC ＝80 m ，求公路CE 段的长(结果保留整数，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)．解：(1)∵∠ABD ＝127°，∠BDE ＝37°，∴∠DEB ＝127°－37°＝90°.在Rt △BDE 中，cos D ＝DE BD， ∴DE ＝BD·cos D ＝520×cos 37°≈520×0.80＝416(m )，即施工点E 离点D416 m 正好能使A ，C ，E 成一条直线．(2)在(1)的条件下可得BE ＝BD·sin D ＝520×sin 37°≈520×0.60＝312(m )，∴CE ＝BE －BC ≈312－80＝232(m )．13．如图(1)，某超市从一楼到二楼的电梯AB 的长为16.50米，坡角∠BAC 为32°.(1)求一楼与二楼之间的高度BC(精确到0.01米)；(2)电梯每级的水平级宽均是0.25米，如图(2)，小明跨上电梯时，该电梯以每秒上升2级的高度运行，10秒后他上升了多少米(精确到0.01米)？(备用数据：sin 32°≈0.529 9，cos 32°≈0.848 0，tan 32°≈0.624 9)(1) (2)图28－1－33【解析】 (1)在直角三角形ABC 中利用∠BAC 的正弦值和AB 的长求得BC 的长即可；(2)首先根据题意求得级高，然后根据10秒钟上升的级数求小明上升的高度即可．解：(1)在Rt △ABC 中，∵sin ∠BAC ＝BC AB ， ∴BC ＝AB·sin ∠BAC ≈16.50×0.529 9≈8.74(米)．(2)∵tan 32°＝级高级宽， ∴级高＝级宽×tan 32°≈0.25×0.624 9＝0.156 225(米)．∵10秒钟电梯上升了2×10＝20(级)，∴小明上升的高度为0.156 225×20≈3.12(米)．14．已知：如图28－1－34，在△ABC 中，AB ＝8，AC ＝9，∠A ＝48°.求：(1)AB 边上的高(精确到0.01)；(2)∠B 的度数(精确到1′)．图28－1－34第14题答图解：(1)如图，过点C 作AB 边上的高CH ，垂足为H ，∵在Rt △ACH 中，sin A ＝CH AC， ∴CH ＝AC·sin A ＝9sin 48°≈6.69.(2)∵在Rt △ACH 中，cos A ＝AH AC， ∴AH ＝AC·cos A ＝9cos 48°，∴在Rt △BCH 中，tan B ＝CH BH ＝CH AB －AH ＝9sin48°8－9cos48°≈3.382， ∴∠B ≈73°32′.15．如图28－1－35，伞不论张开还是收紧，伞柄AM 始终平分同一平面内两条伞架所成的角∠BAC ，当伞收紧时，动点D 与点M 重合，且点A ，E ，D 在同一条直线上。

7.6 锐角三角函数的简单应用（1）1、如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，AC =22，BC =1， 那么sin ABD 的值是________2、一艘观光游船从港口A 以北偏东60°的方向出港观光，航行80海里至C 处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到大事故船C 处所需的大约时间．（温馨提示：sin 53°≈0.8，cos 53°≈0.6）3、如图，某数学兴趣小组想测量一棵树CD 的高度，他们先在点A 处测得树顶C 的仰角为30°，然后沿AD 方向前行10m ，到达B 点，在B 处测得树顶C 的仰角高度为60°（A 、B 、D 三点在同一直线上）．请你根据他们测量数据计算这棵树CD 的高度（结果精确到0.1m ）．（参考数据：≈1.414，≈1.732）4、如图，一艘海轮在A 点时测得灯塔C 在它的北偏东42°方向上，它沿正东方向航行80海里后到达B 处，此时灯塔C 在它的北偏西55°方向上．（1）求海轮在航行过程中与灯塔C 的最短距离（结果精确到0.1）； （2）求海轮在B 处时与灯塔C 的距离（结果保留整数）．（参考数据：sin 55°≈0.819，cos 55°≈0.574，tan 55°≈1.428，tan 42°≈0.900，tan 35°≈0.700，tan 48°≈1.111）学校 班级 姓 考试-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------参考答案：1.22 32.解：如图，过点C作CD⊥AB交AB延长线于D．在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，∴CD=AC=40海里．在Rt△CBD中，∵∠CDB=90°，∠CBD=90°﹣37°=53°，∴BC=≈=50（海里），∴海警船到大事故船C处所需的时间大约为：50÷40=（小时）．3. 解：∵∠CBD=∠A+∠ACB，∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°，∴∠A=∠ACB，∴BC=AB=10（米）．在直角△BCD中，CD=BC•sin∠CBD=10×=5≈5×1.732=8.7（米）．答：这棵树CD的高度为8.7米．4.解：（1）C作AB的垂线，设垂足为D，根据题意可得：∠1=∠2=42°，∠3=∠4=55°，设CD的长为x海里，在Rt△ACD中，tan42°=，则AD=x•tan42°，在Rt△BCD中，tan55°=，则BD=x•tan55°，∵AB=80，∴AD+BD=80，∴x•tan42°+x•tan55°=80，解得：x≈34.4，答：海轮在航行过程中与灯塔C的最短距离是34.4海里；（2）在Rt△BCD中，cos55°=，∴BC=≈60海里，答：海轮在B处时与灯塔C的距离是60海里．7.6 锐角三角函数的简单应用(2)1．如图，小明在M 处用高1米（DM =1米）的测角仪测得旗杆AB 的顶端B 的仰角为30°，再向旗杆方向前进10米到F 处，又测得旗杆顶端B 的仰角为60°，请求出旗杆AB 的高度（取≈1.73，结果保留整数）2．如图，在建筑平台CD 的顶部C 处，测得大树AB 的顶部A 的仰角为45°，测得大树AB 的底部B 的俯角为30°，已知平台CD 的高度为5m ，则大树的高度为 m （结果保留根号）3．如图，某学校新建了一座吴玉章雕塑，小林站在距离雕塑2.7米的A 处自B 点看雕塑头顶D 的仰角为45°，看雕塑底部C 的仰角为30°，求塑像CD 的高度．（最后结果精确到0.1米，参考数据：）4．如图，梯子斜靠在与地面垂直（垂足为O ）的墙上，当梯子位于AB 位置时，它与地面所成的角∠ABO =60°；当梯子底端向右滑动1m （即BD =1m ）到达CD 位置时，它与地面所成的角∠CDO =51°18′，求梯子的长．（参考数据：sin 51°18′≈0.780，cos 51°18′≈0.625，tan 51°18′≈1.248）学校 班级 姓 考试-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------参考答案：1. 解：∵∠BDE=30°，∠BCE=60°，∴∠CBD=60°﹣∠BDE=30°=∠BDE，∴BC=CD=10米，在Rt△BCE中，sin60°=，即=，∴BE=5，AB=BE+AE=5+1≈10米．答：旗杆AB的高度大约是10米．2. 解：作CE⊥AB于点E，在Rt△BCE中，BE=CD=5m，CE==5m，在Rt△ACE中，AE=CE•tan45°=5m，AB=BE+AE=（5+5）m．故答案为：（5+5）．3. 解：在Rt△DEB中，DE=BE•tan45°=2.7米，在Rt△CEB中，CE=BE•tan30°=0.9米，则CD=DE﹣CE=2.7﹣0.9≈1.2米．故塑像CD的高度大约为1.2米．4. 解：设梯子的长为xm．在Rt△ABO中，cos∠ABO=，∴OB=AB•cos∠ABO=x•cos60°=x．在Rt△CDO中，cos∠CDO=，∴OD=CD•cos∠CDO=x•cos51°18′≈0.625x．∵BD=OD﹣OB，∴0.625x﹣x=1，解得x=8．故梯子的长是8米．7.6 锐角三角函数的简单应用(3)1、已知：如图，河旁有一座小山，从山顶A 处测得河对岸点C 的俯角为30°，测得岸边点D 的俯角为45°，又知河宽CD 为50m ．现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ，求山的高度及缆绳AC 的长(答案可带根号)．2、已知：如图，在一次越野比赛中，运动员从营地A 出发，沿北偏东60°方向走了500m 3到达B 点，然后再沿北偏西30°方向走了500m ，到达目的地C 点．求 (1)A 、C 两地之间的距离；(2)确定目的地C 在营地A 的什么方向?3、在一次暑假旅游中，小亮在仙岛湖的游船上(A 处)，测得湖西岸的山峰太婆尖(C 处)和湖东岸的山峰老君岭(D 处)的仰角都是45°，游船向东航行100米后(B 处)， 测得太婆尖、老君岭的仰角分别为30°、60°. 试问太婆尖、老君岭的高度为多少米？(3 1.732 ，结果精确到米).4、已知：如图，在1998年特大洪水时期，要加固全长为10000m 的河堤．大堤高5m ，坝顶宽4m ，迎水坡和背水坡都是坡度为1∶1的等腰梯形．现要将大堤加高1m ，背水坡坡度改为1∶1.5．已知坝顶宽不变，求大坝横截面面积增加了多少平方米，完成工程需多少立方米的土石?学校 班级 姓 考试-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------5、已知：如图，斜坡PQ的坡度i＝1∶3，在坡面上点O处有一根1m高且垂直于水平面的水管OA，顶端A处有一旋转式喷头向外喷水，水流在各个方向沿相同的抛物线落下，水流最高点M比点A高出1m，且在点A测得点M的仰角为30°，以O点为原点，OA所在直线为y轴，过O点垂直于OA的直线为x轴建立直角坐标系．设水喷到斜坡上的最低点为B，最高点为C．(1)写出A点的坐标及直线PQ的解析式；(2)求此抛物线AMC的解析式；(3)求｜x C－x B｜；(4)求B点与C点间的距离．6、如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12m，塔影长DE=18m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为多少？参考答案1、答案：山高m )31(50,m )31(25+=+AC2、答案：(1)1000m ； (2)C 点在A 点的北偏东30°方向上．3、答案：137米，237米4、答案：面积增加24m 2，需用240 000m 2土石．5、答案：(1)A (0，1)，;y x =(2).1332312)3(3122++-=+--=x x x y(3)m 15．(4) 6、答案：24m。

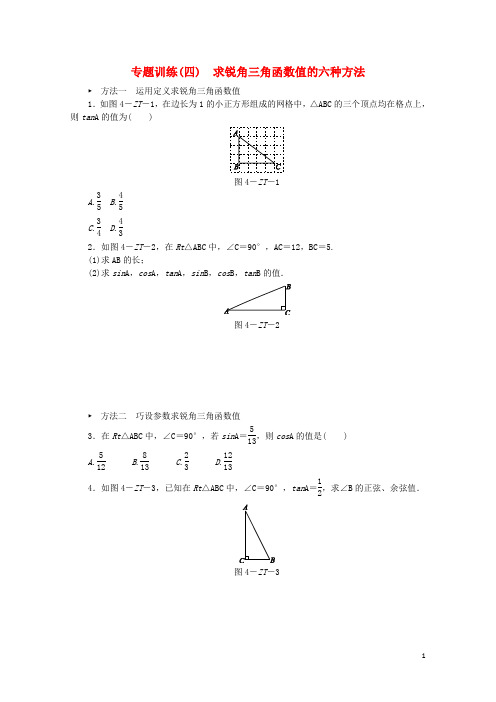
专题训练(四) 求锐角三角函数值的六种方法► 方法一 运用定义求锐角三角函数值1．如图4－ZT －1，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则tan A 的值为( )图4－ZT －1A .35B .45C .34D .432．如图4－ZT －2，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝5. (1)求AB 的长；(2)求sin A ，cos A ，tan A ，sin B ，cos B ，tan B 的值．图4－ZT －2► 方法二 巧设参数求锐角三角函数值3．在Rt △ABC 中，∠C ＝90°，若sin A ＝513，则cos A 的值是( )A .512B .813C .23D .12134．如图4－ZT －3，已知在Rt △ABC 中，∠C ＝90°，tan A ＝12，求∠B 的正弦、余弦值．图4－ZT －35．已知α为锐角，且cos α＝13，求tan α＋cos α1＋sin α的值．► 方法三 利用同角三角函数的关系求锐角三角函数值6．已知在Rt △ABC 中，∠C ＝90°，cos B ＝23，则sin B 的值为( )A .2 53 B .53 C .2 55 D .55► 方法四 利用互余两角三角函数的关系求锐角三角函数值 7．已知0°＜∠A ＜90°，那么cos (90°－∠A)等于( ) A ．cos A B ．sin (90°＋∠A) C ．sin A D ．sin (90°－∠A)8．(1)在△ABC 中，∠C ＝90°，cos A ＝715，求sin B 的值；(2)若∠A ＝35°，∠B ＝65°，试比较cos A 与sin B 的大小，并说明理由．► 方法五 构造直角三角形求锐角三角函数值9．如图4－ZT －4，在四边形ABCD 中，E ，F 分别是AB ，AD 的中点，若EF ＝2，BC ＝5，CD ＝3，则tan C 等于( )图4－ZT －4A .34B .43C .35D .4510．由小正方形组成的网格如图4－ZT －5，A ，B ，C 三点都在格点上，则∠ABC 的正切值为( )图4－ZT －5A .55 B .2 55 C .12 D .5211．2017·山西一副三角尺按图4－ZT －6所示的方式摆放，得到△ABD 和△BCD ，其中∠ADB ＝∠BCD ＝90°，∠A ＝60°，∠CBD ＝45°.E 为AB 的中点，过点E 作EF ⊥CD 于点F.若AD ＝4 cm ，则EF 的长为________cm .图4－ZT －612．如图4－ZT －7，在△ABC 中，∠C ＝150°，AC ＝4，tan B ＝18.(1)求BC 的长；(2)利用此图形求tan 15°的值(精确到0.1，参考数据：2≈1.41，3≈1.73，5≈2.24)图4－ZT －7► 方法六 利用等角求锐角三角函数值13．如图4－ZT －8，已知AB 是⊙O 的直径，CD 是⊙O 的弦，且CD ⊥AB ，BC ＝6，AC ＝8，求sin ∠ABD 的值．图4－ZT －814．如图4－ZT－9，在矩形ABCD中，AB＝10，BC＝8，E为AD边上一点，沿CE将△CDE 对折，使点D正好落在AB边上的点F处，求tan∠AFE的值．图4－ZT－9详解详析1．[解析] D 在Rt △ABC 中，∠A 的对边BC ＝4，∠A 的邻边AB ＝3，因此tan A ＝BC AB ＝43.故选D .2．解： (1)AB ＝AC 2＋BC 2＝13.(2)sin A ＝BC AB ＝513，cos A ＝AC AB ＝1213，tan A ＝BC AC ＝512，sin B ＝AC AB ＝1213，cos B ＝BC AB ＝513，tan B＝AC BC ＝125. 3．D4．解： ∵∠C ＝90°，tan A ＝12，∴设BC ＝x ，则AC ＝2x ， ∴AB ＝5x ，∴sin B ＝AC AB ＝2x 5x ＝2 55，cos B ＝BC AB ＝x 5x ＝55.5．解： 如图，设α为直角三角形的一个锐角．∵cos α＝13，∴设α的邻边中的直角边长为k ，斜边长为3k. 由勾股定理，得α的对边长为（3k ）2－k 2＝2 2k ， ∴tan α＝2 2，sin α＝2 23，故tan α＋cos α1＋sin α＝2 2＋131＋2 23＝2 2＋3－2 2＝3.6．[解析] B 在△ABC 中，∠C ＝90°，cos B ＝23，∴sin B ＝1－（23）2＝53，故选B .7．C8．解： (1)∵在△ABC 中，∠C ＝90°， ∴∠A ＋∠B ＝90°， ∴sin B ＝cos A ＝715.(2)cos A ＜sin B.理由：∵cos A ＝cos 35°＝sin 55°＜sin 65°＝sin B ， ∴cos A ＜sin B.9．[解析] B 连接BD.∵E ，F 分别是AB ，AD 的中点， ∴BD ＝2EF ＝4.∵BC ＝5，CD ＝3，CD 2＋BD 2＝BC 2， ∴△BCD 是直角三角形， ∴tan C ＝BD CD ＝43.10．[解析] C 如图，过点C 作CD ⊥AB 于点D ，则D 在网格的格点上，且CD ＝ 2.∵BD ＝22＋22＝2 2， ∴tan ∠ABC ＝CD BD ＝22 2＝12.故选C .11．(6＋2)12．[解析] (1)过点A 作AD ⊥BC ，交BC 的延长线于点D ，由含30°角的直角三角形的性质得AD ＝12AC ＝2，由三角函数求出CD ＝2 3，在Rt △ABD 中，由三角函数求出BD ＝16，即可得出结果；(2)在BC 边上取一点M ，使得CM ＝AC ，连接AM ，求出∠AMC ＝∠MAC ＝15°，由tan 15°＝tan ∠AMD ＝AD MD即可得出结果．解：(1)过A 作AD ⊥BC ，交BC 的延长线于点D ，如图①所示：在Rt △ADC 中，AC ＝4， ∵∠ACB ＝150°， ∴∠ACD ＝30°， ∴AD ＝12AC ＝2.在△ACD 中，CD ＝AC·cos 30°＝4×32＝2 3. 在Rt △ABD 中，tan B ＝AD BD ＝2BD ＝18，∴BD ＝16，∴BC ＝BD －CD ＝16－2 3.(2)在BC 边上取一点M ，使得CM ＝AC ，连接AM ，如图②所示：∵∠ACB ＝150°，∴∠AMC ＝∠MAC ＝15°，∴tan 15°＝tan ∠AMD ＝AD MD ＝24＋2 3＝12＋3＝2－3≈0.27≈0.3.13．解： ∵AB 是⊙O 的直径，CD ⊥AB ， ∴∠ACB ＝90°，∠AC ︵＝AD ︵，∴∠ABD ＝∠ABC.在Rt △ABC 中，根据勾股定理，得AB ＝10， ∴sin ∠ABD ＝sin ∠ABC ＝810＝45.14．解： 根据图形有∠AFE ＋∠EFC ＋∠BFC ＝180°， 根据折叠的性质有∠EFC ＝∠EDC ＝90°， 则∠AFE ＋∠BFC ＝90°.在Rt △BCF 中，有∠BCF ＋∠BFC ＝90°， 所以∠AFE ＝∠BCF.在Rt △BFC 中，CF ＝CD ＝AB ＝10，BC ＝8， 由勾股定理易得BF ＝6， 则tan ∠BCF ＝34，故tan ∠AFE ＝tan ∠BCF ＝34.。

〖苏科版〗九年级数学下册 1.1 锐角三角函数同步训练一、选择题（本题共计 8 小题，每题 3 分，共计24分，）1. 如图，的三个顶点都在方格纸的格点上，则A. B. C. D.2. 若为锐角，且，则A.小于B.大于C.大于且小于D.大于3. 若，则下列说法不正确的是（）A.随的增大而增大B.随的增大而减小C.随的增大而增大D.、、的值都随的增大而增大4. 如果在中，，，，那么下列各式正确的是（）A. B.C. D.5. 若把一个直角三角形的两条直角边都扩大倍，（是大于的自然数），则两个锐角的三角函数值（）A.都变大为原来的倍B.都缩小为原来的C.不变化D.各个函数值变化不一致6. 比较，，的大小关系是（）A.B.C.D.7. 如图，在中，，，的平分线与的外角平分线交于，连接，则的值是（）A. B. C. D.8. 如图，在中，点在上，，垂足为，若，，则等于（）A. B. C. D.二、填空题（本题共计 8 小题，每题 3 分，共计24分，）9. ________ （填大小关系）10. 在中，，如果，，那么________．11. 在中，，当已知和时，求，则、、关系式是________．12. 已知在中，为直角，，，________．13. 已知为锐角，且，那么的范围是________．14. 在中，，、、分别是、、的对边，下列式子：①，②，③，④，必定成立的是________．15. 如图，是的边上一点，且点坐标为，则________________．16. 如图，直角三角形纸片的两直角边长分别为，，现将如图那样折叠，使点与点重合，折痕为，则的值是________．三、解答题（本题共计 8 小题，每题 9 分，共计72分，）17. 在中，，若，写出的四个三角函数的值．18. 分别求出图中、的正弦值、余弦值和正切值．19. 在中，，、、分别是、、的对边．请利用三角函数的定义探讨能否用边的式子表示？请写出你必要的理由．20. 如图，点在第一象限，与轴所夹的锐角为，，求的值．21. 在中，，，，求的值．22. 如图，在中，，是直角边上一点，于点，，，求的值．23. 如图，在中，，，．求的长；利用此图形求的值（精确到，参考数据：，，）24. 如图，在四边形中，平分，，，求的值．答案1. D2. D3. D4. A5. C6. D7. D8. D9.10.11.12.13.14. ②15.16.17. 解：，，由勾股定理，得，，，．18. 解：如图，，，，，，，．如图，，，，，，，．如图，，，，，，，．19. 解：∵，，∴，即．20. 解：过作轴于．∴，∵，∴，∵，∴，∴，∴．21. 解：在中，，，，∵，∴，则．22. 解：∵，，∴，又∵，∴，∴，设，，由勾股定理得：，在中，．23. 解：过作，交的延长线于点，如图所示：在中，，∵，∴，∴，，在中，，∴，∴；在边上取一点，使得，连接，如图所示：∵，∴，．24. 解：∵平分，∴．又∵，∴．∴，在中，∵，∴．。

7.6用锐角三角函数解决问题同步习题一．选择题1．如图，大楼高30m，远处有一塔BC，某人爬到楼顶D测得塔顶的仰角为30°，且测得D、B相距30m，则塔高BC为（）m．A．40B．45C．30+D．302．如图，已知点C从点B出发，沿射线BD方向运动，运动到点D后停止，则在这个过程中，从A观测点C的俯角将（）A．增大B．减小C．先增大后减小D．先减小后增大3．如图是某河坝横断面示意图，AC为迎水坡，AB为背水坡，过点A作水平面的垂线AD，BD ＝2CD，设斜坡AC的坡度为i AC，坡角为∠ACD，斜坡AB的坡度为i AB，坡角为∠ABD，则下列结论正确的是（）A．i AC＝2i AB B．∠ACD＝2∠ABD C．2i AC＝i AB D．2∠ACD＝∠ABD 4．如图，小王在山坡上E处，用高1.5米的测角仪EF测得对面铁塔顶端A的仰角为25°，DE 平行于地面BC，若DE＝2米，BC＝10米，山坡CD的坡度i＝1：0.75，坡长CD＝5米，则铁塔AB的高度约是（）（参考数据：sin25°≈0.42，cos25°≈0.91，tan25°≈0.47 ）A．11.1米B．11.8米C．12.0米D．12.6米5．如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为10m，DE的长为5m，则树AB的高度是（）m．A．10B．15C．15D．15﹣56．如图是某市一座人行天桥的示意图，天桥离地面的高BC是10米，坡面AC的倾斜角∠CAB ＝45°，在距A点10米处有一建筑物HQ．为了方便行人推车过天桥，市政府部门决定降低坡度，使新坡面DC的倾斜角∠BDC＝30°，若新坡面下D处与建筑物之间需留下HD长的人行道，问人行道HD的长度是（）米．（计算最后结果保留一位小数）．（参考数据：≈1.414，≈1.732）A．2.7B．3.4C．2.5D．3.17．如图，一个直角梯形的堤坝坡长AB为6米，斜坡AB的坡角为60°，为了改善堤坝的稳固性，准备将其坡角改为45°，则调整后的斜坡AE的长度为（）A．3米B．3米C．（3﹣2）米D．（3﹣3）米8．为加快5G网络建设，某移动通信公司在一个坡度为2：1的山腰上建了一座5G信号通信塔AB，在距山脚C处水平距离39米的点D测得通信塔底B处的仰角是35°，测得通信塔顶A 处的仰角是49°（如图），则通信塔AB的高度约为（）参考数据：sin35°＝0.57，tan35°＝0.70，sin49°＝0.75，tan49°＝1.15）A．27米B．31米C．48米D．52米9．如图，某货船以24海里/时的速度从A处向正东方向的D处航行，在点A处测得某岛C在北偏东60°的方向．该货船航行30分钟后到达B处，此时测得该岛在北偏东30°的方向上．则货船在航行中离小岛C的最短距离是（）A．12海里B．6海里C．12海里D．24海里10．“五一”期间，小明和妈妈到某景区游玩，小明想利用所学的数学知识，估测景区里的观景塔DE的高度．他从点D处的观景塔出来走到点A处．沿着斜坡AB从A点走了8米到达B 点，此时回望观景塔，更显气势宏伟．在B点观察到观景塔顶端的仰角为45°且AB⊥BE，再往前走到C处，观察到观景塔顶端的仰角30°，测得BC之间的水平距离BC＝10米，则观景塔的高度DE约为（）米．（＝1.41，＝1.73）A．14B．15C．19D．20二．填空题11．如图，在坡角为30°的斜坡上有两棵树，它们间的水平距离AC为3m，则这两棵树间的坡面距离AB的长为m．12．如图，在一次测绘活动中，在港口A的位置观测停放于B、C两处的小船，测得船B在港口A北偏东75°方向12海里处，船C在港口A南偏东15°方向9海里处，则船B与船C之间的距离为海里．13．如图，为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD，在与M相距4米的A处，测得警示牌下端D的仰角为45°，再笔直往前走8米到达B处，在B处测得警示牌上端C的仰角为30°，则警示牌CD的高度为米（结果保留根号）．14．水务人员为考察水情，乘快艇以每秒10米的速度沿平行于岸边的航线AB由西向东行驶．如图所示，在A处测得岸边一建筑物P在北偏东30°方向上，继续行驶40秒到达点B处，测得建筑物P在北偏西60°方向上，则建筑物P到航线AB的距离为米．15．2019年，徐州马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅度提升了徐州市的国际影响力，如图，在一场马拉松比赛中，某人在大楼A处，测得起点拱门CD的顶部C的俯角为35°，底部D的俯角为45°，如果A处离地面的高度AB＝20米，求起点拱门CD的高度m．（结果精确到1米；参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）．三．解答题16．如图，某办公大楼正前方有一根高度是15米的旗杆ED，从办公大楼顶端A测得旗杄顶端E 的俯角α是45°，旗杄底端D到大楼前梯坎底边的距离DC是10米，梯坎坡长BC是10米，梯坎坡度i BC＝1：，求大楼AB的高．17．如图，在瞭望塔AB前有一段坡比为1：的斜坡BC，经测量BC＝8米，在海岸上取点D，使CD＝45米，在点D测得瞭望塔顶端A的仰角为40°，求瞭望塔AB的高度约为多少米．（结果精确到0.1米，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，≈1.41）18．某数学兴趣小组要测量实验大楼部分楼体的高度（如图1所示，CD部分），在起点A处测得大楼部分楼体CD的顶端C点的仰角为45°，底端D点的仰角为30°，在同一剖面沿水平地面向前走16米到达B处，测得顶端C的仰角为63.4°（如图2所示），求大楼部分楼体CD的高度约为多少米？（精确到1米）（参考数据：sin63.4°≈0.89，cos63.4°≈0.45，tan63.4°≈2.00，≈1.41，≈1.73）参考答案一．选择题1．解：过点D作DE⊥BC于点E，∵∠BDE＝30°，BD＝30m，∴BE＝BD＝15m，∵AD＝30m，∴CE＝30m，∴BC＝CE+BE＝30+15＝45m．故选：B．2．解：点C从点B出发，沿射线BD方向运动，运动到点D后停止，则在这个过程中，从A观测点C的俯角将增大，故选：A．3．解：斜坡AC的坡度i AC＝，斜坡AB的坡度i AB＝，∵BD＝2CD，∴i AC＝2i AB，A正确，C错误；∠ACD≠2∠ABD，B错误；2∠ACD≠∠ABD，D错误；故选：A．4．解：如图，过点E、F分别作AB的垂线，垂足分别为G、H，得矩形EFHG，∴GH＝EF＝1.5，HF＝GE＝GD+DE＝GD+2，过点D作BC延长线的垂线，垂足为M，得矩形DMBG，∵CD的坡度i＝1：0.75＝4：3，CD＝5，∴DM＝4，CM＝3，∴DG＝BM＝BC+CM＝10+3＝13，BG＝DM＝4，∴HF＝DG+2＝15，在Rt△AFH中，∠AFH＝25°，∴AH＝FH•tan25°≈15×0.47≈7.05，∴AB＝AH+HG+GB≈7.05+1.5+4≈12.6（米）．答：铁塔AB的高度约是12.6米．故选：D．5．解：在Rt△CDE中，∵CD＝10m，DE＝5m，∴sin∠DCE＝，∴∠DCE＝30°．∵∠ACB＝60°，DF∥AE，∴∠BGF＝60°∴∠ABC＝30°，∠DCB＝90°．∵∠BDF＝30°，∴∠DBF＝60°，∴∠DBC＝30°，∴BC＝＝＝10（m），∴AB＝BC•sin60°＝10×＝15（m）．故选：B．6．解：根据题意可知：∠CBA＝90°，∠CAB＝45°，∴∠ACB＝45°，∴AB＝CB＝10，AH＝10，设DH＝x米，则AD＝AH﹣DH＝（10﹣x）米，∴BD＝AD+AB＝（20﹣x）米，在Rt△DCB中，∠CDB＝30°，∴tan30°＝，即＝，解得x≈2.7．所以人行道HD的长度是2.7米．故选：A．7．解：作AH⊥BC于H，在Rt△ABH中，sin∠ABH＝，cos∠ABH＝，则AH＝AB•sin∠ABH＝6×＝3，∵∠E＝45°，∴AE＝AH＝×3＝3，故选：A．8．解：设CE＝x米，∵斜坡BC的坡度为2：1，∴BE＝2x米，在Rt△BDE中，tan∠BDE＝，则＝0.7，解得，x＝21，∴DE＝39+x＝60，在Rt△ADE中，tan∠ADE＝，则AE＝DE•tan∠ADE＝69，∴AB＝AE﹣BE＝69﹣42＝27（米），故选：A．9．解：作CE⊥AB交AB的延长线于E，由题意得，AB＝24×＝12，∠CBE＝60°，∠CAE＝30°，∴∠ACB＝30°，∴∠CAE＝∠ACB，∴BC＝AB＝12，在Rt△CBE中，sin∠CBE＝，∴CE＝BC×sin∠CBE＝12×＝6（海里），故选：B．10．解：作BF⊥DE于F，AH⊥BF于H，∵∠EBF＝45°，∴∠ABH＝45°，∴AH＝BH＝8×＝4，在Rt△ECF中，tan∠ECF＝，则CF＝EF，在Rt△EBF中，∠EBF＝45°，∴BF＝EF，由题意得，EF﹣EF＝10，解得，EF＝5+5，则DE＝EF+DF＝5+5+4≈19，故选：C．二．填空题11．解：由题意知，在Rt△ABC中，AC＝3m，∠A＝30°，∵cos∠A＝，∴AB＝＝＝6（m），故答案为：6．12．解：根据题意得：∠BAC＝90°，AB＝12海里，AC＝9海里，在Rt△ABC中，BC＝＝15海里，故答案为：15．13．解：在Rt△ADM中，∵AM＝4，∠MAD＝45°，∴DM＝AM＝4，∵AB＝8，∴MB＝AM+AB＝12，在Rt△BCM中，∵∠MBC＝30°，∴MC＝MB tan30°＝4，∴DC＝MC﹣DM＝（4﹣4）（米）答：警示牌的高度CD为（4﹣4）米，故答案为：（4﹣4）．14．解：过P点作PC⊥AB于C，由题意可知：∠P AC＝60°，∠PBC＝30°，在Rt△P AC中，＝tan∠P AC＝tan60°，∴AC＝PC，在Rt△PBC中，＝tan∠PBC＝tan30°，∴BC＝PC，∵AB＝AC+BC＝PC＝10×40＝400，∴PC＝100（米），故答案为：100．15．解：作CE⊥AB于E，则四边形CDBE为矩形，∴CE＝DB，CD＝BE，在Rt△ADB中，∠ADB＝45°，∴AB＝DB＝20，∴CE＝20，在Rt△ACE中，tan∠ACE＝，∴AE＝CE•tan∠ACE≈20×0.70＝14，∴CD＝BE＝AB﹣AE＝6m，故答案为：6．三．解答题16．解：如图，过点E作EF⊥AB于点F，作BG⊥CD于点G，∵ED⊥CD，∴四边形DEFG是矩形，∴EF＝DG，ED＝FG，根据题意可知：∠AEF＝α＝45°，∴AF＝EF，∵坡度，∴BG：CG＝3：4，设BG＝3x，CG＝4x，则BC＝5x，∴5x＝10，解得x＝2，∴CG＝8，BG＝6，∴EF＝DG＝CG+CD＝8+10＝18，∴AF＝EF＝18，∵FG＝ED＝15，∴FB＝FG﹣BG＝15﹣6＝9，∴AB＝AF+FB＝18+9＝27（米）．答：大楼AB的高为27米．17．解：如图，延长AB，交直线DC于点F．∵在Rt△BCF中，，∴设BF＝k，则，．又∵，∴k＝8，∴BF＝8，．∵DF＝DC+CF，∴．∵在Rt△ADF中，，∴（米）．∵AB＝AF﹣BF，∴AB＝47.28﹣8≈39.3（米）．答：瞭望塔AB的高度约为39.3米．18．解：设楼高CE为x米，∵在Rt△AEC中，∠CAE＝45°，∴AE＝CE＝x，∵AB＝16，∴BE＝x﹣16，在Rt△CEB中，CE＝BE•tan63.4°≈2（x﹣16），∴2（x﹣16）＝x，解得：x＝32（米），在Rt△DAE中，DE＝AE tan30°＝32×＝，∴CD＝CE﹣DE＝32﹣≈14（米），答：大楼部分楼体CD的高度约为14米．。

苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习锐角三角函数—巩固练习【巩固练习】一、选择题1. （2016•乐山）如图，在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于点D ，则下列结论不正确的是（ ）A ．B ．C ．D ．2.（2015•山西）如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是（ ）A ．2B ．C ．D ．3. 已知锐角α满足sin25°＝cos α，则α＝( )A ．25°B ．55°C ．65°D ．75°4．如图所示，直径为10的⊙A 经过点C(0，5)和点O(0，0)，B 是y 轴右侧⊙A 优弧上一点，则∠OBC 的余弦值为 ( )A ．12B ．34C ．45第4题 第5题5．如图，在△ABC 中，∠A ＝120°，AB ＝4，AC ＝2，则sinB 的值是( )A B C D 6．在Rt △ABC 中，∠C ＝90°，若将各边长度都扩大为原来的2倍，则∠A 的正弦值( )A ．扩大2倍B ．缩小2倍C ．扩大4倍D ．不变7．如图所示是教学用具直角三角板，边AC ＝30cm ，∠C ＝90°，tan ∠BAC BC 的长为( )A ．cmB ．．．第7题 第8题8. 如图所示，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB ，垂足为D ，若AC ，BC ＝2，则sin ∠ACD 的值为( )A ．3B ．3C ．2D ． 23二、填空题9．（2016•临夏州）如图，点A （3，t ）在第一象限，OA 与x 轴所夹的锐角为α，tan α=，则t 的值是 ．10. 用不等号连接下面的式子．(1)cos50°________cos20° (2)tan18°________tan21°11．在△ABC 中，若2sin cos 0A B ⎫-+-=⎪⎪⎝⎭，∠A 、∠B 都是锐角，则∠C 的度数为 . 12．如图所示，△ABC 的顶点都在方格纸的格点上，则sinA ＝________．13．已知：正方形ABCD 的边长为2，点P 是直线CD 上一点，若DP ＝1，则tan ∠BPC 的值是________．第12题 第15题14．如果方程2430x x -+=的两个根分别是Rt △ABC 的两条边，△ABC 的最小角为A ，那么tanA 的值为________．15．如图所示，△ABC 的内心在y 轴上，点C 的坐标为(2，0)，点B 的坐标是(0，2)，直线AC 的解析式为112y x =-，则tanA 的值是________． 16.（2014•高港区二模）若α为锐角，且，则m 的取值范围是 ．三、解答题17．如图所示，△ABC 中，D 为AB 的中点，DC ⊥AC ，且∠BCD ＝30°，求∠CDA 的正弦值、余弦值和正切值．18. 计算下列各式的值．(1) （2015•普陀区一模）；(2) （2015•常州模拟）sin45°+tan45°﹣2cos60°． (3) （2015•奉贤区一模）﹣cos60°．19．如图所示，在矩形ABCD 中，E 是BC 边上的点，AE ＝BC ，DF ⊥AE ，垂足为F ，连接DE ．(1)求证：AB ＝DF ；(2)若AD ＝10，AB ＝6，求tan ∠EDF 的值．20. 如图所示，已知⊙O 的半径为2，弦BC 的长为A 为弦BC 所对优弧上任意一点(B 、C 两点除外)．(1)求∠BAC 的度数；(2)求△ABC 面积的最大值．(参考数据：sin 602=°，cos302=°，tan 303=°．【答案与解析】一、选择题1.【答案】C.【解析】在Rt △ABC 中，∠BAC=90°，sinB=， ∵AD ⊥BC ，∴sinB=，sinB=sin ∠DAC=， 综上，只有C 不正确故选：C ．2.【答案】D ；【解析】如图：由勾股定理得，AC=，AB=2，BC=，∴△ABC 为直角三角形， ∴tan∠B==， 故选：D ．3. 【答案】C ；【解析】由互余角的三角函数关系，cos sin(90)αα=-°，∴ sin25°-sin(90°-α)，即90°-α＝25°，∴ α＝65°．4.【答案】C ；【解析】设⊙A 交x 轴于另一点D ，连接CD ，根据已知可以得到OC ＝5，CD ＝10，∴ OD == ∠OBC ＝∠ODC ，∴ cos OB cos 102OD C ODC CD ∠=∠===．5.【答案】D ；【解析】如图所示，过点C 作CD ⊥AB 于D ，∵ ∠BAC ＝120°，∴ ∠CAD ＝60°，又∵ AC ＝2，∴ AD ＝1，CD ，∴ BD ＝BA+AD ＝5，在Rt △BCD 中，BC ===∴ sin 14CD B BC ===．6.【答案】D ； 【解析】根据锐角三角函数的定义，锐角三角函数值等于相应边的比，与边的长度无关，而只与边的比值或角的大小有关．7.【答案】C ；【解析】由tan BC BAC AC ∠==，∴ 30BC AC ===8. 【答案】A ；【解析】 ∵ 3AB =，∴ sin sin 3AC ACD B AB ∠=∠==二、填空题9.【答案】．【解析】过点A 作AB ⊥x 轴于B ，∵点A （3，t ）在第一象限，∴AB=t ，OB=3，又∵tan α===， ∴t=． 故答案为：．10.【答案】(1)＜； (2)＜；【解析】当α为锐角时，其余弦值随角度的增大而减小，∴ cos50°＜cos20°；当α为锐角时，其正切值随角度的增大而增大，∴ tan18°＜tan21°．11．【答案】105°；【解析】∵ 2sin cos 0A B ⎫+-=⎪⎪⎝⎭，∴ sin 02A -=cos 0B -=即sin 2A =，cos B =又∵ ∠A 、∠B 均为锐角，∴ ∠A ＝45°，∠B ＝30°，在△ABC 中，∠A+∠B+∠C ＝180°，∴ ∠C ＝105°．12．【解析】假设每一个小正方形的边长为1，利用网格，从C 点向AB 所在直线作垂线CH ．垂足为H ，则∠A 在直角△ACH 中，利用勾股定理得AC ==∴sin 5CH A AC ===． 13．【答案】2或23【解析】此题为无图题，应根据题意画出图形，如图所示，由于点P 是直线CD 上一点，所以点P 既可以在边CD 上，也可以在CD 的延长线上，当P 在边CD 上时，tan 2BC BPC PC ∠==；当P 在CD 延长线上时，2tan 3BC BPC PC ∠==．14．【答案】13或4； 【解析】由2430x x -+=得11x =，23x =，①当3为直角边时，最小角A 的正切值为1tan 3A =；②当3为斜边时，=∴ 最小角A的正切值为tan 4A ==. 故应填13或4． 15．【答案】13； 【解析】由△ABC 的内心在y 轴上可知OB 是∠ABC 的角平分线，则∠OBA ＝45°，易求AB 与x 轴的交点为(-2，0)，所以直线AB 的解析式为：2y x =+， 联立2112y x y x =+⎧⎪⎨=-⎪⎩可求A 点的坐标为(-6，-4)， ∴AB ==OC ＝OB ＝2，∴ BC＝．在Rt △ABC中，1tan 3BC A AB ===．16.【答案】 ； 【解析】∵0＜cos α＜1， ∴0＜＜1， 解得.三、解答题17.【答案与解析】过D 作DE ∥AC ，交BC 于点E ．∵ AD ＝BD ，∴ CE ＝EB ，∴ AC ＝2DE ．又∵ DC ⊥ AC ，DE ∥AC ，∴ DC ⊥DE ，即∠CDE ＝90°．又∵ ∠BCD ＝30°，∴ EC ＝2DE ，DC DE ．设DE ＝k ，则CD ，AC ＝2k ．在Rt △ACD 中，AD ．∴ sinAC CDA AD ∠===cos 7CD CDA AD ∠===．tanAC CDA CD ∠===．18.【答案与解析】解：（1）原式=4×﹣×+× =1+3． (2) 原式=×+1﹣2× =1+1﹣1=1．(3) 原式=﹣× =﹣=14． 19.【答案与解析】(1)证明：∵ 四边形ABCD 是矩形，∴ AD ∥BC ，AD ＝BC∴ ∠DAF ＝∠AEB又∵ AE ＝BC ，∴ AE ＝AD又∵ ∠B=∠DFA ＝90°，∴ △EAB ≌△ADF ．∴ AB ＝DF ．(2)解：在Rt △ABE 中，8BE =∵ △EAB ≌△ADF ，∴ DF ＝AB ＝6，AF ＝EB ＝8，∴ EF ＝AE-AF ＝10-8＝2．∴ 21tan 63EF EDF DF ∠===．20.【答案与解析】(1)连接BO 并延长，交⊙O 于点D ，连接CD ．∵ BD 是直径，∴ BD ＝4，∠DCB ＝90°．在Rt △DBC 中，sin 42BC BDC BD ∠=== ∴ ∠BDC ＝60°，∴ ∠BAC ＝∠BDC ＝60°．(2)因为△ABC 的边BC 的长不变，所以当BC 边上的高最大时，△ABC 的面积最大，此时点A 应落在优弧BC 的中点处．过O 作OE ⊥BC 于点E ，延长EO 交⊙O 于点A ，则A 为优孤BC 的中点．连结AB ，AC ， 则AB ＝AC ，∠BAE 12=∠BAC ＝30°．在Rt △ABE 中，∵ BE =BAE ＝30°，∴3tan303BEAE===°，∴132ABCS=⨯=△答：△ABC面积的最大值是。

【文库独家】第七章锐角函数测试1 锐角三角函数定义学习要求理解一个锐角的正弦、余弦、正切的定义．能依据锐角三角函数的定义，求给定锐角的三角函数值．课堂学习检测一、填空题1．如图所示，B 、B ′是∠MAN 的AN 边上的任意两点，BC ⊥AM 于C 点，B ′C ′⊥AM 于C ′点，则△B 'AC ′∽______，从而ACB A BC C B )()(='=''，又可得 ①='''BA CB ______，即在Rt △ABC 中(∠C ＝90°)，当∠A 确定时，它的______与______的比是一个______值； ②=''B AC A ______，即在Rt △ABC 中(∠C ＝90°)，当∠A 确定时，它的______与______的比也是一个______； ③='''CA CB ______，即在Rt △ABC 中(∠C ＝90°)，当∠A 确定时，它的______与______的比还是一个______．第1题图2．如图所示，在Rt △ABC 中，∠C ＝90°．第2题图①斜边)(sin =A ＝______， 斜边)(sin =B ＝______； ②斜边)(cos =A ＝______，斜边)(cos =B ＝______；③的邻边A A ∠=)(tan ＝______，)(tan 的对边B B ∠=＝______．3．因为对于锐角α 的每一个确定的值，sin α 、cos α 、tan α 分别都有____________与它______，所以sin α 、cos α 、tan α 都是____________．又称为α 的____________． 4．在Rt △ABC 中，∠C ＝90°，若a ＝9，b ＝12，则c ＝______， sin A ＝______，cos A ＝______，tan A ＝______， sin B ＝______，cos B ＝______，tan B ＝______．5．在Rt △ABC 中，∠C ＝90°，若a ＝1，b ＝3，则c ＝______， sin A ＝______，cos A ＝______，tan A ＝______， sin B ＝______，cos B ＝______，tan B ＝______．6．在Rt △ABC 中，∠B ＝90°，若a ＝16，c ＝30，则b ＝______， sin A ＝______，cos A ＝______，tan A ＝______， sin C ＝______，cos C ＝______，tan C ＝______．7．在Rt △ABC 中，∠C ＝90°，若∠A ＝30°，则∠B ＝______， sin A ＝______，cos A ＝______，tan A ＝______， sin B ＝______，cos B ＝______，tan B ＝______．二、解答题8．已知：如图，Rt △TNM 中，∠TMN ＝90°，MR ⊥TN 于R 点，TN ＝4，MN ＝3． 求：sin ∠TMR 、cos ∠TMR 、tan ∠TMR ．9．已知Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．综合、运用、诊断10．已知：如图，Rt △ABC 中，∠C ＝90°．D 是AC 边上一点，DE ⊥AB 于E 点．DE ∶AE ＝1∶2．求：sin B 、cos B 、tan B ．11．已知：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠43sin AOC 求：AB 及OC 的长．12．已知：⊙O 中，OC ⊥AB 于C 点，AB ＝16cm ，⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ； (2)求cos ∠AOC 及tan ∠AOC ． 13．已知：如图，△ABC 中，AC ＝12cm ，AB ＝16cm ，⋅=31sin A(1)求AB 边上的高CD ； (2)求△ABC 的面积S ； (3)求tan B ．14．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．拓展、探究、思考15．已知：如图，Rt △ABC 中，∠C ＝90°，按要求填空：(1),sin ca A =∴=⋅=c A c a ,sin ______； (2),cos cb A =∴b ＝______，c ＝______；(3),tan ba A =∴a ＝______，b ＝______；(4),23sin =B ∴=B cos ______，=B tan ______； (5),53cos =B ∴=B sin ______，=A tan ______；(6)∵=B tan 3，∴=B sin ______，=A sin ______．16．已知：如图，在直角坐标系xOy 中，射线OM 为第一象限中的一条射线，A 点的坐标为(1，0)，以原点O 为圆心，OA 长为半径画弧，交y 轴于B 点，交OM 于P 点，作CA ⊥x 轴交OM 于C 点．设∠XOM ＝α ．求：P 点和C 点的坐标．(用α 的三角函数表示)17．已知：如图，△ABC 中，∠B ＝30°，P 为AB 边上一点，PD ⊥BC 于D ．(1)当BP ∶PA ＝2∶1时，求sin ∠1、cos ∠1、tan ∠1； (2)当BP ∶PA ＝1∶2时，求sin ∠1、cos ∠1、tan ∠1．测试2 锐角三角函数学习要求1．掌握特殊角(30°，45°，60°)的正弦、余弦、正切三角函数值，会利用计算器求一个锐角的三角函数值以及由三角函数值求相应的锐角．2．初步了解锐角三角函数的一些性质．课堂学习检测一、填空题二、解答题2．求下列各式的值．(1)o 45cos 230sin 2-︒(2)tan30°－sin60°·sin30°(3)cos45°＋3tan30°＋cos30°＋2sin60°－2tan45°(4)︒+︒+︒+︒-︒45sin 30cos 30tan 130sin 145cos 2223．求适合下列条件的锐角α ． (1)21cos =α (2)33tan =α(3)222sin =α(4)33)16cos(6=- α4．用计算器求三角函数值(精确到0.001)． (1)sin23°＝______； (2)tan54°53′40″＝______．5．用计算器求锐角α (精确到1″)． (1)若cos α ＝0.6536，则α ＝______；(2)若tan(2α ＋10°31′7″)＝1.7515，则α ＝______．综合、运用、诊断6．已知：如图，在菱形ABCD 中，DE ⊥AB 于E ，BE ＝16cm ，⋅=1312sin A 求此菱形的周长．7．已知：如图，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5． 求：sin ∠ACB 的值．8．已知：如图，Rt △ABC 中，∠C ＝90°，∠BAC ＝30°，延长CA 至D 点，使AD ＝AB ．求：(1)∠D 及∠DBC ； (2)tan D 及tan ∠DBC ；(3)请用类似的方法，求tan22.5°．9．已知：如图，Rt △ABC 中，∠C ＝90°，3==BC AC ，作∠DAC ＝30°，AD 交CB 于D 点，求：(1)∠BAD ；(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD ．10．已知：如图△ABC 中，D 为BC 中点，且∠BAD ＝90°，31tan =∠B ，求：sin ∠CAD 、cos ∠CAD 、tan ∠CAD ．拓展、探究、思考11．已知：如图，∠AOB ＝90°，AO ＝OB ，C 、D 是上的两点，∠AOD ＞∠AOC ，求证：(1)0＜sin ∠AOC ＜sin ∠AOD ＜1； (2)1＞cos ∠AOC ＞cos ∠AOD ＞0；(3)锐角的正弦函数值随角度的增大而______； (4)锐角的余弦函数值随角度的增大而______．12．已知：如图，CA ⊥AO ，E 、F 是AC 上的两点，∠AOF ＞∠AOE ．(1)求证：tan ∠AOF ＞tan ∠AOE ；(2)锐角的正切函数值随角度的增大而______．13．已知：如图，Rt △ABC 中，∠C ＝90°，求证：(1)sin 2A ＋cos 2A ＝1； (2)⋅=AAA cos sin tan14．化简：ααcos sin 21⋅-(其中0°＜α ＜90°)15．(1)通过计算(可用计算器)，比较下列各对数的大小，并提出你的猜想：①sin30°______2sin15°cos15°； ②sin36°______2sin18°cos18°； ③sin45°______2sin22.5°cos22.5°； ④sin60°______2sin30°cos30°； ⑤sin80°______2sin40°cos40°； ⑥sin90°______2sin45°cos45°． 猜想：若0°＜α ≤45°，则sin2α ______2sin α cos α ．(2)已知：如图，△ABC 中，AB ＝AC ＝1，∠BAC ＝2α ．请根据图中的提示，利用面积方法验证你的结论．16．已知：如图，在△ABC 中，AB ＝AC ，AD ⊥BC 于D ，BE ⊥AC 于E ，交AD 于H 点．在底边BC 保持不变的情况下，当高AD 变长或变短时，△ABC 和△HBC 的面积的积S △ABC ·S △HBC 的值是否随着变化?请说明你的理由．测试3 解直角三角形(一)学习要求理解解直角三角形的意义，掌握解直角三角形的四种基本类型．课堂学习检测一、填空题1．在解直角三角形的过程中，一般要用的主要关系如下(如图所示)： 在Rt △ABC 中，∠C ＝90°，AC ＝b ，BC ＝a ，AB ＝c ，第1题图①三边之间的等量关系：__________________________________． ②两锐角之间的关系：__________________________________． ③边与角之间的关系：==B A cos sin ______； ==B A sin cos _______；==B A tan 1tan _____； ==B Atan tan 1______． ④直角三角形中成比例的线段(如图所示)．第④小题图在Rt △ABC 中，∠C ＝90°，CD ⊥AB 于D ． CD 2＝_________；AC 2＝_________； BC 2＝_________；AC ·BC ＝_________． ⑤直角三角形的主要线段(如图所示)．第⑤小题图直角三角形斜边上的中线等于斜边的_________，斜边的中点是_________． 若r 是Rt △ABC (∠C ＝90°)的内切圆半径，则r ＝_________＝_________．⑥直角三角形的面积公式． 在Rt △ABC 中，∠C ＝90°， S △ABC ＝_________．(答案不唯一)2．关于直角三角形的可解条件，在直角三角形的六个元素中，除直角外，只要再知道_________(其中至少_________)，这个三角形的形状、大小就可以确定下来．解直角三角形的基本类型可分为已知两条边(两条_________或斜边和_________)及已知一边和一个锐角(_________和一个锐角或_________和一个锐角) 3二、解答题4．在Rt △ABC 中，∠C ＝90°．(1)已知：a ＝35，235=c ，求∠A 、∠B ，b ；(2)已知：32=a ，2=b ，求∠A 、∠B ，c ；(3)已知：32sin =A ，6=c ，求a 、b ；(4)已知：,9,23tan ==b B 求a 、c ；(5)已知：∠A ＝60°，△ABC 的面积,312=S 求a 、b 、c 及∠B ．综合、运用、诊断5．已知：如图，在半径为R 的⊙O 中，∠AOB ＝2α ，OC ⊥AB 于C 点．(1)求弦AB的长及弦心距；(2)求⊙O的内接正n边形的边长a n及边心距r n．6．如图所示，图①中，一栋旧楼房由于防火设施较差，想要在侧面墙外修建一外部楼梯，由地面到二楼，再从二楼到三楼，共两段(图②中AB、BC两段)，其中CC′＝BB′＝3.2m．结合图中所给的信息，求两段楼梯AB与BC的长度之和(结果保留到0.1m)．(参考数据：sin30°＝0.50，cos30°≈0.87，sin35°≈0.57，cos35°≈0.82)7．如图所示，某公司入口处原有三级台阶，每级台阶高为20cm，台阶面的宽为30cm，为了方便残疾人士，拟将台阶改为坡角为12°的斜坡，设原台阶的起点为A，斜坡的起点为C，求AC的长度(精确到1cm)．拓展、探究、思考8．如图所示，甲楼在乙楼的西面，它们的设计高度是若干层，每层高均为3m，冬天太阳光与水平面的夹角为30°．(1)若要求甲楼和乙楼的设计高度均为6层，且冬天甲楼的影子不能落在乙楼上，那么建筑时两楼之间的距离BD至少为多少米?(保留根号)(2)由于受空间的限制，甲楼和乙楼的距离BD＝21m，若仍要求冬天甲楼的影子不能落在乙楼上，那么设计甲楼时，最高应建几层?9．王英同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地多少距离?10．已知：如图，在高2m，坡角为30°的楼梯表面铺地毯，地毯的长度至少需要多少米?(保留整数)测试4 解直角三角形(二)学习要求能将解斜三角形的问题转化为解直角三角形．课堂学习检测1．已知：如图，△ABC中，∠A＝30°，∠B＝60°，AC＝10cm．求AB及BC的长．2．已知：如图，Rt△ABC中，∠D＝90°，∠B＝45°，∠ACD＝60°．BC＝10cm．求AD的长．3．已知：如图，△ABC中，∠A＝30°，∠B＝135°，AC＝10cm．求AB及BC的长．4．已知：如图，Rt △ABC 中，∠A ＝30°，∠C ＝90°，∠BDC ＝60°，BC ＝6cm ．求AD 的长．综合、运用、诊断5．已知：如图，河旁有一座小山，从山顶A 处测得河对岸点C 的俯角为30°，测得岸边点D 的俯角为45°，又知河宽CD 为50m ．现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ，求山的高度及缆绳AC 的长(答案可带根号)．6．已知：如图，一艘货轮向正北方向航行，在点A 处测得灯塔M 在北偏西30°，货轮以每小时20海里的速度航行，1小时后到达B 处，测得灯塔M 在北偏西45°，问该货轮继续向北航行时，与灯塔M 之间的最短距离是多少?(精确到0.1海里，732.13 )7．已知：如图，在两面墙之间有一个底端在A 点的梯子，当它靠在一侧墙上时，梯子的顶端在B 点；当它靠在另一侧墙上时，梯子的顶端在D 点．已知∠BAC ＝60°，∠DAE ＝45°．点D 到地面的垂直距离m 23 DE ，求点B 到地面的垂直距离BC ．8．已知：如图，小明准备测量学校旗杆AB 的高度，当他发现斜坡正对着太阳时，旗杆AB 的影子恰好落在水平地面和斜坡的坡面上，测得水平地面上的影长BC ＝20m ，斜坡坡面上的影长CD ＝8m ，太阳光线AD 与水平地面成26°角，斜坡CD 与水平地面所成的锐角为30°，求旗杆AB 的高度(精确到1m)．9．已知：如图，在某旅游地一名游客由山脚A 沿坡角为30°的山坡AB 行走400m ，到达一个景点B ，再由B 地沿山坡BC 行走320米到达山顶C ，如果在山顶C 处观测到景点B 的俯角为60°．求山高CD (精确到0.01米)．10．已知：如图，小明准备用如下方法测量路灯的高度：他走到路灯旁的一个地方，竖起一根2m 长的竹竿，测得竹竿影长为1m ，他沿着影子的方向，又向远处走出两根竹竿的长度，他又竖起竹竿，测得影长正好为2m ．问路灯高度为多少米?3到达B点，11．已知：如图，在一次越野比赛中，运动员从营地A出发，沿北偏东60°方向走了500m 然后再沿北偏西30°方向走了500m，到达目的地C点．求(1)A、C两地之间的距离；(2)确定目的地C在营地A的什么方向?12．已知：如图，在1998年特大洪水时期，要加固全长为10000m的河堤．大堤高5m，坝顶宽4m，迎水坡和背水坡都是坡度为1∶1的等腰梯形．现要将大堤加高1m，背水坡坡度改为1∶1.5．已知坝顶宽不变，求大坝横截面面积增加了多少平方米，完成工程需多少立方米的土石?拓展、探究、思考13．已知：如图，在△ABC中，AB＝c，AC＝b，锐角∠A＝α ．(1)BC的长；(2)△ABC的面积．14．已知：如图，在△ABC中，AC＝b，BC＝a，锐角∠A＝α ，∠B＝β ．(1)求AB 的长；(2)求证：.sin sin βαb a =15．已知：如图，在Rt △ADC 中，∠D ＝90°，∠A ＝α ，∠CBD ＝β ，AB ＝a ．用含a 及α 、β 的三角函数的式子表示CD 的长．16．已知：△ABC 中，∠A ＝30°，AC ＝10，25=BC ，求AB 的长．17．已知：四边形ABCD 的两条对角线AC 、BD 相交于E 点，AC ＝a ，BD ＝b ，∠BEC ＝α (0°＜α ＜90°)，求此四边形的面积．测试5 综合测试1．计算． (1)45tan 260tan 60cos 2- (2)60cos 30cos 60tan 30tan 45sin 30sin 2222+⋅++2．已知：如图，△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AB ＝32，BC ＝12．求：sin ∠ACD 及AD 的长．3．已知：Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于D 点，AB ＝2m ，BD ＝m －1，⋅=54cos A (1)用含m 的代数式表示BC ；(2)求m 的值；4．已知：如图，矩形ABCD 中，AB ＝3，BC ＝6，BE ＝2EC ，DM ⊥AE 于M 点．求DM 的长．5．已知：如图，四边形ABCD 中，∠A ＝45°，∠C ＝90°，∠ABD ＝75°，∠DBC ＝30°，AB ＝2a ．求BC 的长．6．已知：如图，四边形ABCD 中，∠A ＝∠C ＝90°，∠D ＝60°，35=AD ．AB ＝3，求BC 的长．7．已知：如图，△ABC 内接于⊙O ，BC ＝m ，锐角∠A ＝α ，(1)求⊙O 的半径R ；(2)求△ABC 的面积的最大值．8．已知：如图，矩形纸片ABCD 中，BC ＝m ，将矩形的一角沿过点B 的直线折叠，使A 点落在DC 边上，落点记为A ′，折痕交AD 于E ，若∠A ′BE ＝α ． 求证：⋅⋅=αα2sin cos m EB第七章锐角函数全章测试一、选择题1．Rt △ABC 中，∠C ＝90°，若BC ＝4，,32sin =A 则AC 的长为( ) A ．6B ．52C ．53D ．132 2．⊙O 的半径为R ，若∠AOB ＝α ，则弦AB 的长为( )A ．2sin 2αRB ．2R sin αC ．2cos 2αR D ．R sin α 3．△ABC 中，若AB ＝6，BC ＝8，∠B ＝120°，则△ABC 的面积为( )A ．312B ．12C ．324D ．3484．若某人沿倾斜角为α 的斜坡前进100m ，则他上升的最大高度是( )A ．m sin 100αB ．100sin α mC ．m cos 100βD ．100cos β m5．铁路路基的横断面是一个等腰梯形，若腰的坡度为2∶3，顶宽为3m ，路基高为4m ，则路基的下底宽应为( )A ．15mB ．12mC ．9mD ．7m6．P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B 点，若∠APB ＝2α ，⊙O 的半径为R ，则AB 的长为( )A ．ααtan sin R B ．ααsin tan R C ．ααtan sin 2R D ．ααsin tan 2R 7．在Rt △ABC 中，AD 是斜边BC 上的高，若CB ＝a ，∠B ＝β ，则AD 等于( )A ．a sin 2βB ．a cos 2βC ．a sin β cos βD ．a sin β tan β 8．已知：如图，AB 是⊙O 的直径，弦AD 、BC 相交于P 点，那么ABDC 的值为( )A ．sin ∠APCB ．cos ∠APC C ．tan ∠APCD ．APC∠tan 1 9．如图所示，某人站在楼顶观测对面的笔直的旗杆AB ．已知观测点C 到旗杆的距离(CE 的长度)为8m ，测得旗杆的仰角∠ECA 为30°，旗杆底部的俯角∠ECB 为45°，那么，旗杆AB 的高度是( )第9题图A ．m )3828(+B ．m )388(+C ．m )33828(+D ．m )3388(+ 10．如图所示，要在离地面5m 处引拉线固定电线杆，使拉线和地面成60°角，若考虑既要符合设计要求，又要节省材料，则在库存的l 1＝5.2m 、l 2＝6.2m 、l 3＝7.8m 、l 4＝10m ，四种备用拉线材料中，拉线AC 最好选用( )第10题图 A ．l 1 B ．l 2 C ．l 3 D ．l 4二、填空题11．在△ABC 中，∠C ＝90°，∠ABC ＝60°，若D 是AC 边中点，则tan ∠DBC 的值为______．12．在Rt △ABC 中，∠C ＝90°，a ＝10，若△ABC 的面积为3350，则∠A ＝______度． 13．如图所示，四边形ABCD 中，∠B ＝90°，AB ＝2，CD ＝8，AC ⊥CD ，若,31sin =∠ACB 则cos ∠ADC ＝______．第13题图14．如图所示，有一圆弧形桥拱，拱的跨度m 330=AB ，拱形的半径R ＝30m ，则拱形的弧长为______．第14题图15．如图所示，半径为r 的圆心O 在正三角形的边AB 上沿图示方向移动，当⊙O 的移动到与AC 边相切时，OA 的长为______．第15题图三、解答题16．已知：如图，AB ＝52m ，∠DAB ＝43°，∠CAB ＝40°，求大楼上的避雷针CD 的长．(精确到0.01m)17．已知：如图，在距旗杆25m 的A 处，用测角仪测得旗杆顶点C 的仰角为30°，已知测角仪AB的高为1.5m ，求旗杆CD 的高(精确到0.1m)．18．已知：如图，△ABC 中，AC ＝10，,31sin ,54sin ==B C 求AB ．19．已知：如图，在⊙O 中，∠A ＝∠C ，求证：AB ＝CD (利用三角函数证明)．20．已知：如图，P 是矩形ABCD 的CD 边上一点，PE ⊥AC 于E ，PF ⊥BD 于F ，AC ＝15，BC ＝8，求PE＋PF ．21．已知：如图，一艘渔船正在港口A 的正东方向40海里的B 处进行捕鱼作业，突然接到通知，要该船前往C 岛运送一批物资到A 港，已知C 岛在A 港的北偏东60°方向，且在B 的北偏西45°方向．问该船从B 处出发，以平均每小时20海里的速度行驶，需要多少时间才能把这批物资送到A 港(精确到1小时)(该船在C 岛停留半个小时)?)45.26,73.13,41.12(≈≈≈22．已知：如图，直线y ＝－x ＋12分别交x 轴、y 轴于A 、B 点，将△AOB 折叠，使A 点恰好落在OB的中点C 处，折痕为DE ．(1)求AE 的长及sin ∠BEC 的值； (2)求△CDE 的面积．23．已知：如图，斜坡PQ 的坡度i ＝1∶3，在坡面上点O 处有一根1m 高且垂直于水平面的水管OA ，顶端A 处有一旋转式喷头向外喷水，水流在各个方向沿相同的抛物线落下，水流最高点M 比点A 高出1m ，且在点A 测得点M 的仰角为30°，以O 点为原点，OA 所在直线为y 轴，过O 点垂直于OA 的直线为x 轴建立直角坐标系．设水喷到斜坡上的最低点为B ，最高点为C ．(1)写出A点的坐标及直线PQ的解析式；(2)求此抛物线AMC的解析式；(3)求｜x C－x B｜；(4)求B点与C点间的距离．答案与提示第七章锐角函数测试11．△BAC ，AB ，AC ′．①ABBC，对边，斜边，固定； ②ABAC，邻边，斜边，固定值； ③ACBC，对边，邻边，固定值． 2．①∠A 的对边，,c a∠B 的对边，;c b ②∠A 的邻边，,cb ∠B 的邻边，;c a③∠A 的对边，,b a ∠B 的邻边，⋅ab3．唯一确定的值，对应，α 的函数，锐角三角函数． 4．⋅34,53,54,43,54,53,15 5．.3,1010,10103,31,10103,1010,10 6．⋅815,178,1715,158,1715,178,34 7．.3,21,23,33,23,21,60o8．⋅==∠=∠=∠==∠37tan tan ,43cos cos ,47sin sin N TMR N TMR N TMR 9．⋅===53cos ,20,16B AB AC 10．.2tan ,55cos ,552sin ===B B B 11．AB ＝2AC ＝2AO ·sin ∠AOC ＝24cm ，cm 7422=-=AC OA OC12．⋅=∠=∠==43tan ,54cos )2(;cm 332,cm 340)1(AOC AOC OC OA 13．(1)CD ＝AC ·sin A ＝4cm ；(2);cm 32212=⨯=CD AB S(3)⋅+=422tan B14．⋅=31sin B15．(1);sin Aa (2);cos ,cos AbA c ⋅ (3);tan ,tan Aa Ab ⋅ (4);3,21(5);43,54 (6)⋅1010,10103 16．P (cos α ，sin α )，C (1，tan α )．提示：作PD ⊥x 轴于D 点． 17．(1).31tan ,211cos ,231sin =∠=∠=∠ (2),231tan ,7721cos ,7211sin =∠=∠=∠ 提示：作AE ⊥BC 于E ，设AP ＝2．测试21．2．(1)0； (2);123(3);222325-+ (4)⋅-413 3．(1)α ＝60°；(2)α ＝30°；(3)22.5°；(4)46°．4．(1)0.391；(2)1.423．5．(1)49°11＇11″；(2)24°52＇44″．6．104cm ．提示：设DE ＝12x cm ，则得AD ＝13x cm ，AE ＝5x cm ．利用BE ＝16cm ． 列方程8x ＝16．解得x ＝2． 7．,721提示：作BD ⊥CA 延长线于D 点． 8．(1)∠D ＝15°，∠DBC ＝75°；(2);32tan ,32tan +=∠-=DBC D (3).125.22tan -= 9．(1)15°； (2).32tan ,426cos ,426sin -=∠+=∠-=∠BAD BAD BAD10．⋅23,13132,13133提示：作DE ∥BA ，交AC 于E 点，或延长AD 至F ，使DF ＝ AD ，连结CF ．11．提示：作CE ⊥OA 于E ，作DF ⊥OA 于F ． (3)增大， (4)减小． 12．(2)增大．13．提示：利用锐角三角函数定义证． 14．原式ααααcos sin 2cos sin 22-+=2)cos (sin αα-=|cos sin |αα-=⎩⎨⎧<<-<≤-=).450(sin cos ),9045(cos sinαααααα 15．(1)①～⑥略．sin2α ＝2sin α cos α ．(2),2sin 212sin 12121αα=⨯⨯=⋅=∆BE AC S ABC ,cos sin 21αα⋅=⨯=⋅=∆AD BD AD BC S ABC ∴sin2α ＝2sin α cos α ．16．不发生改变，设∠BAC ＝2α ，BC ＝2m ，则.)tan (tan 422m m m S S HBCABC =⋅=⋅∆∆αα测试31．①a 2＋b 2＝c 2； ②∠A ＋∠B ＝90°； ③;,,,abb ac b c a④AD ·BD ，AD ·AB ，BD ·BA ，AB ·CD ： ⑤一半，它的外心，2c b a -+(或⋅++cb a ab) ⑥ab 21或ch 21(h 为斜边上的高)或A bc sin 21或B ac sin 21或).(21c b a r ++ (r 为内切圆半径)2．两个元素，有一个是边，直角边，一条直角边，斜边，一条直角边． 3．90°－∠A ，sin A ，cos A ；;sin ,tan ,90o Aa A a A ∠- ;90,tan ,22Ab a A b ac ∠-=+=.90,sin ,22B caA a c b ∠-=-=4．(1)∠A ＝45°，∠B ＝45°，b ＝35； (2)∠A ＝60°，∠B ＝30°，c ＝4；(3);52,4==b a (4);133,6==c a(5).30,64,62,26 =∠===B c b a 5．(1)AB ＝2R ·sin α ，OC ＝R ·cos α ；(2)⋅⋅=⋅=n R r n R a n n180cos ,180sin 26．AB ≈6.40米，BC ≈5.61米，AB ＋BC ≈12.0米． 7．约为222cm ． 8．(1)318米．(2)4层，提示：设甲楼应建x 层则.2130tan 3≤x9．m 3100 10．6米．1．cm 3310,cm 3320==BC AB 2．)3515(+cm ．3．cm 25;cm )535(=-=BC AB 提示：作CD ⊥AB 延长线于D 点． 4．34cm ．5．山高m )31(50,m )31(25+=+AC 6．约为27.3海里． 7．m 33．8．约为17m ，提示：分别延长AD 、BC ，设交点为E ，作DF ⊥CE 于F 点．9．约477.13m ． 10．10m ．11．(1)AC ＝1 000m ； (2)C 点在A 点的北偏东30°方向上． 12．面积增加24m 2，需用240 000m 2土石．13．(1).cos 222α⋅-+=bc c b BC 提示：作CD ⊥AB 于D 点，则CD ＝b ·sin α ，AD ＝b ·cos α ．再利用BC 2＝CD 2＋DB 2的关系，求出BC ． (2)a bc sin 21⋅ 14．(1)AB ＝b ·cos α ＋a ·cos β . 提示：作CD ⊥AB 于D 点．(2)提示：由b sin α ＝CD ＝a sin β 可得b sin α ＝a sin β ，从而βαsin sin ba =． 15．提示：AB ＝AD －BD ＝CD tan(90°－α )－CD tan(90°－β )＝CD 〔tan(90°－α )－tan(90°－β )〕，)90tan()90tan(βα---=∴ a CD 或⋅-=αββαtan tan tan tan a CD 16．535+或.535-提示：AB 边上的高CD 的垂足D 点可能在AB 边上(这时AB ＝)535+，也可能在AB 边的延长线上(这时535-=AB )．17．.sin 21αab1．(1);23+ (2)⋅252．⋅==∠255,855sin AD ACD 3．(1))1(2-=m m BC 或⋅=56m BC (2)⋅=725m4．⋅5185．a BC 2=．提示：作BE ⊥AD 于E 点．6．BC ＝6．提示：分别延长AB 、DC ，设它们交于E 点． 7．(1)⋅=αsin 2mR 提示：作⊙O 的直径BA ＇，连结A ＇C ． (2)⋅2tan42αm 提示：当A 点在优弧BC 上且AO ⊥BC 时，△ABC 有面积的最大值．8．提示：⋅⋅=∠⋅='=αααα2sin cos 'sin cos cos mB CA BC B A EB 答案与提示第七章锐角函数全章测试1．B ． 2．A ． 3．A ． 4．B ． 5．A ． 6．C ． 7．C ． 8．B ． 9．D ． 10．B ． 11．⋅23 12．60． 13．⋅54 14．20πm ． 15．.332r 16．约4.86 m ． 17．约15.9m ．18．AB ＝24．提示：作AD ⊥BC 于D 点．19．提示：作OE ⊥AB 于E ，OF ⊥CD 于F ．设⊙O 半径为R ，∠A ＝∠C ＝α ．则AB ＝2R cos α ，CD ＝2R cos α ，∴AB ＝CD ． 20．⋅151618提示：设∠BDC ＝∠DCA ＝α ．PE ＋PF ＝PC sin α ＋PD sin α ＝CD sin α ． ,158sin =α ⋅=⨯=+∴151618158161PF PE21．约3小时，提示：作CD ⊥AB 于D 点．设CD ＝x 海里． 22．(1)⋅=∠=53sin .25BEC AE 提示：作CF ⊥BE 于F 点，设AE ＝CE ＝x ，则EF .29x -= 由CE 2＝CF 2＋EF 2得.25=x (2)⋅475提示：.4245sin 21o AE AD AE AD S S AED CDE ⋅=⋅==∆∆ 设AD ＝y ，则CD ＝y ，OD ＝12－y ，由OC 2＋OD 2＝CD 2可得⋅=215y 23．(1)A (0，1)，;33x y =(2).1332312)3(3122++-=+--=x x x y(3)m 15． (4).m 5230cos ||=-=B C x x BC。