当前位置：文档之家 › 用积分法求梁的变形

用积分法求梁的变形

  • 格式：ppt
  • 大小：724.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

工程力学第2节 确定梁位移的积分法

工程力学第2节 确定梁位移的积分法


例10-3 如图图示简支梁， l 4m ，弯曲刚度EI 1640N m2。在无限接近右支座 B 处受到矩为的集中 力偶 M e 120 N m 作用，试求 (1)转角方程和位移方 程；(2)梁的最大挠度。
解：(1)转角方程和 位移方程 x
Me FA FB l
梁的弯矩方程为
5
3
4
令 x 0，得B截面的挠度为
ql yB （ ） 30 EI
Me 2 x C (1) 将上式一次积分得转角 y' 2EIl
Me M ( x) x l
转角方程
Me 2 y' x C 2EIl
(1)
再次积分，可得挠度方程：
Me 3 y x Cx D (2) 6EIl 边界条件： x 0 时，y0 0 ； x l 时，yl 0 M el D0 C 6EI M e 2 M el 2 0 . 00915 x 0.0488 x 2EIl 6EI M e 3 M el 3 x 0.0488x y x x 0.00305 6EIl 6EI
再次积分，可得挠度方程：
1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24
1 1 1 3 2 ( qlx qx ) C EI 4 6 1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24 边界条件： x 0 时，y0 0 ； x l 时，yl 0
补充例 悬臂梁AB在三角形分布载荷作用下，跨 度为l，抗弯刚度为EI，如图所示。试求B截面的挠度。 解：与B截面距离为 x 的任一截面的载荷集度为
x q( x) q l
(0 x l )
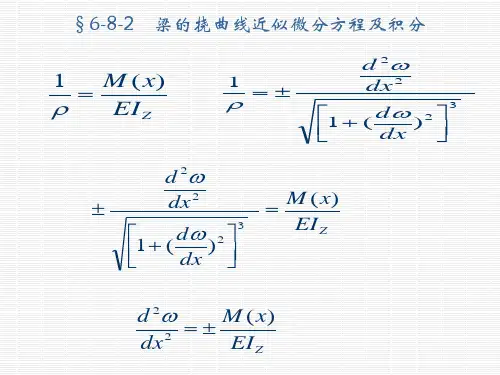
用积分法求梁的变形

用积分法求梁的变形

3

M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0


x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接，挠曲线在 中间铰处，挠度连续，但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C

B

x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1

M ( x ) 在小变形情况下，任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征： 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
结构位移和刚度—梁的刚度计算(建筑力学)

结构位移和刚度—梁的刚度计算(建筑力学)


二、用积分法求梁的变形
1.挠曲线近似微分方程
y( x)
M (x) EI
2.用积分法求变形 EI (x) M (x)dx C1
三、用叠加法求梁的变形
EIy(x) [ M (x)dx C1]dx C2
叠加法—梁截面的总变形，就等于各个荷载单独作用时产生变形的代数和。
四、梁的刚度计算 ymax [ f ]
梁的刚度计算
主要内容
梁的刚度条件和设计准则 梁的刚度计算 梁的刚度计算工程实例
梁的刚度计算
➢ 如果梁的弯曲变形过大，即使强度满足要求，也不能正常工作。例如：房 屋的楼面板或者梁长时间受较大荷载作用，导致变形过大，会造成抹灰面 出现裂缝，工业厂房的吊车梁变形过大，会影响吊车梁的正常使用等。设 计梁时，除了进行强度计算外，还应考虑进行刚度计算，需要把梁的最大 挠度和最大转角限制在一定的允许范围内。
l
l
课后作业：《建筑力学练习册》 练习二十五
3.6 4 4
3.6kN m
2、按正应力强度设计。查强度准则
3.6kNm
max
M max Wz
M max 0.1d 3
[ ]
得：
d3
M max
3
3.6 106 mm 153.3mm
0.1[ ] 0.110
取d=160mm
梁的刚度计算
3、按梁的刚度准则校核。
查变形表得
ymax
Fl 3 48EI
为:
ymax [ f ]
l
l
式中 ymax 为最大相对挠度，[ f ] 为许用相对挠度，其值可
l
l
根据梁的工作情况及要求查阅有关设计手册。土建工程中的许
用相对挠度值 [ f ] 常限制在
10.2 梁的挠曲线近似微分方程及其积分

10.2 梁的挠曲线近似微分方程及其积分

10.2 梁的挠曲线近似微分方程及其积分纯弯曲 EIM =ρ1挠曲线曲率()322"1w w κ=⎡⎤'+⎣⎦EIM ±=d θFFxd xyxρ O正负号的确定xyOxyOM > 0w ″< 0M < 0w ″>0M 与 w ″异号()322"1w w κ=⎡⎤'+⎣⎦EIM ±=()3221w M EIw ''=-⎡⎤'+⎣⎦小变形：转角 w ′ ≈ 0 适用条件： 1. 坐标系，正负号；2. 忽略剪力 F S 对变形的影响；3. 线弹性，小变形，w′ ≈ 0。

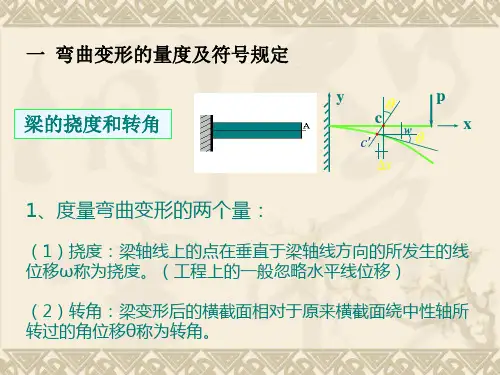
M w EI''=-EI ——梁的抗弯刚度， 若为等直梁，EI ＝C ，则 EIw M''=-挠曲线近似微分方程1'd Mw x C EIθ==-+⎰12d d M w x x C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰一次积分：二次积分：积分法计算梁的变形BAlw A = 0 w B = 0BAlw A = 0 θA =0EIw M''=-挠曲线近似微分方程 由边界条件，确定积分常数光滑连续条件——相邻挠曲线必须光滑连续。

挠曲线近似微分方程及其积分w C2= w C3θC2=θC2w B1= w B2θB1=θB2挠曲线近似微分方程及其积分——例题[例题1] 已知悬臂梁的抗弯刚度为EI，求在荷载P 作用下梁的挠曲线方程，并确定梁上的最大挠度和转角。

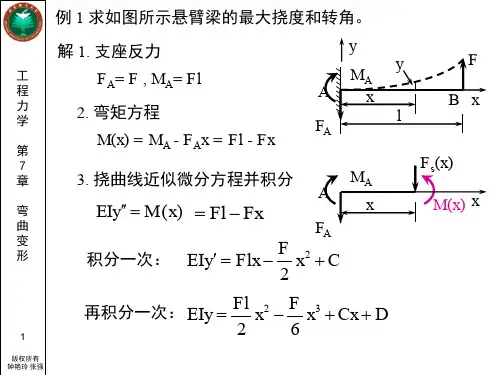
BAxL P有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）[解] （1）建立弯矩方程 ()()M x P L x =-()()E Iw M x P L x ''=-=--21()2xEIw P Lx C '=--+2312()26Lx x EIw P C x C =--++（3）确定积分常数 0,0x w ==0,0x w '==20C=10C=挠曲线近似微分方程及其积分——例题BALxPx（2）代入挠曲线方程并积分挠曲线近似微分方程222PLx Pxw EIθ-'==-23(3)6P Lx x w EI-=-最大挠度和转角3max()3PL f EI=↑2max2PL EIθ=挠曲线近似微分方程及其积分——例题B ALxPxmaxθmaxw挠曲线近似微分方程及其积分——例题[例题2] 已知：EI = 常数，求：1. 挠度、转角方程； 2. |θmax |, |w max |。

积分法计算梁的变形

积分法计算梁的变形

工程力学
积分法计算梁的变形
步骤：（EI为常量） 1、根据荷载分段列出弯矩方程 M（x）。 2、根据弯矩方程列出挠曲线的近似微分方程并进行积分
EIw(x) M (x)
EIw(x) M (x)dx C1 EIw (x) ( M (x)dx)dx C1x C2
积分法计算梁的变形
3、根据弯曲梁变形的边界条件和连续条件确
C1
C2
Fb 6L
(L2
b2 );
D1 D2 0
确定挠曲线和转角方程
w1
F b x1 6LEI
L2 b2 x12
w2
Fb 6LEI
L b
(x2
a)3
x23
(L2
b2
)x2
1
w1
Fb 6LEI
(L2 b2 ) 6x12
2
w2
Fb 2LEI
L b
(x2
a)2
x22
1 3
(L2
5、计算任意截面的挠度、转角；挠度的最大 值、转角的最大值。
例：求图示悬臂梁自由端的挠度及转角( EI=常数）。
w
x
L
F
x
解：建立坐标系并写出弯矩方程
M (x) F(L x)
写出微分方程并积分 EIw FL Fx
EIw
FLx
1 2
Fx
2
C1
EIw
FLx2 2
Fx3 6
C1x
C2
EIw
q
确定积分常数
x =0 , w=0 ; x=L , w=0 .
C1
ql3 24,C2 0A NhomakorabeaB
L
最大挠度及最大转角
确定挠曲线和转角方程 w qx (l3 2lx2 x3 )
讲梁的挠曲线方程与积分解法

讲梁的挠曲线方程与积分解法


②积分常数的确定——边界条件和连续条件：
边界条件：梁在其支承处的挠度或转角是已知的， 这样的已知条件称为边界条件。 连续条件：梁的挠曲线是一条连续、光滑、平坦 的曲线。因此，在梁的同一截面上不可能有两个 不同的挠度值或转角值，这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入（1）（2）得：
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得：
A
qL3 6EI
（与C比较知E：I A C）
A
qL4 8EI
（与D比较知E：IA ）D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次： EI' EI 1 qx3 C （1）
积分二次：
6
EI 1 qx4 Cx D （2）
24
B X``
3、确定常数C、D.
由边界条件： x L, 0 代入（1）得： C 1 qL3
6
x L, y 0 代入（2）得： D 1 qL4
支座反力，分段列弯矩方程； 分段的原则:
①凡载荷有突变处（包括中间支座），应作为分段点；
②凡截面有变化处，或材料有变化处，应作为分段点；
③中间铰视为两个梁段间的联系，此种联系体现为两部分之间 的相互作用力，故应作为分段点；
(2)分段列出梁的挠曲线近似微分方程，并对其积分 两次
积分法求变形

积分法求变形

15
版权所有 钟艳玲 张强
(3) 确定转角和挠度方程 (AB 段)
0 x1 l :
EI z
y1
M (x1)


Fx1 2
EIz1 EIz y1 M (x1) dx1

Fx1 2
dx1


Fx12 4
C1
1

1 EI z
(
Fx12 4
C1)
EIz y1
26
2
2
版权所有 钟艳玲 张强
例 1 求如图所示悬臂梁的最大挠度和转角。
y
工 程 力 学
第 7 章
弯 曲 变
5. 挠曲线和转角方程
EIy Fl x2 F x3 26
EI EIy ' Flx F x2
2
6. 最大挠度和转角 (在 B 截面处)
xl:
MA y
F
Ax
Bx
FA
l
MA A

1 2
M
0x2

Cx

D
y

1 EI z
(1 2
M0x2
Cx
D)


1 EI z
(M 0 x
C)
工 程 力
y

1 EI z
(1 2
M0x2

Cx

D)
学 (3) 确定积分常数
M0
第
A
7
x 0: 0 C 0
B
章
y0 D0
l
弯 曲 变 形
M0x
EI z
y M0x2 2EI z
F
用积分法求梁的挠和转角

用积分法求梁的挠和转角

§8-3 用积分法求梁的挠度和转角 梁的挠曲线近似微分方程：
d2y dx 2
M (x) EI
EI
d2y dx2
M
(x)
积分一次得转角方程为：
EIy M (x)
dy dx
M (x) EI
dx
C
再积分一次得挠度方程为：
y
M (x) EI
dx
dx
Cx
D
§8-3 用积分法求梁的挠度和转角
梁截面的已知位移条件或位移约束条件，称为梁位移的边界条件。 积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
5ql 4
ymax
y
x l 2
384EI
max
A
B
ql3 24 EI
§8-3 用积分法求梁的挠度和转角 外伸梁，承受集中载荷作用，试绘制挠曲线的大致形状图。
设弯矩刚度EI为常数。
§8-3 用积分法求梁的挠度和转角
解：1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区，确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处，应满足位移边界条件；在分段处，则 应满足位移连续条件。
§8-3 用积分法求梁的挠度和转角
三、使用视频 1.可使用的视频文件类型 常用格式为AVI,另一种为RealAudio。 2.加入视频 1）定位光标 2）选择“插入/图片/视频”菜单命令，弹出
“视频”对话框 3）选择视频文件 3.修改视频属性 1）选定视频位置上出现的图片 2）单击右键选择“图片属性” 3）在“图片属性”对话框中设置视频的属性
C ql3 24
EIy ql x3 q x4 Cx D 12 24
材料力学 积分法求梁的变形

材料力学 积分法求梁的变形

一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段，共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点： A = 0, q A = 0
B 点 ： w B 左 = w B 右
C点 ： w C左 = w C右
D点：w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
积分法是求解梁变形的基本方法

积分法是求解梁变形的基本方法


C
BC刚化C
l
C
F
F
F
a
B
A
B
wA A1
B Fa w3
A
B
1. AB弯曲(BC刚化） Fa 3
w A1 3EI () 2. BC扭转(AB刚化)
wA2
B
a
Fal GI p
a
Fa 2l GI p
3. BC弯曲(AB刚化)
Fl 3
wA3 wB 3EI
wA wA1 wA2 wA3 Fa2l Fl 3 Fa3
Page5
BUAA
MECHANICS OF MATERIALS
例2：E常数, I 2 2I1 ,求 wC ， C
I2
I1
A B
刚化AB段：
A B
P
C
仅考虑BC段变形：
P C
C1
Pa 2 2EI1
Pa3 wC1 3EI1
BC段刚化：
M Pa
B
C
A
B
FP
仅考虑AB段变形：
C2 B B,F B,M
材料物质点应力状况·应力微体 材态
通过构件内一点，所作各微截面的 应力状况，称为该点处的应力状态
三、怎么研究应力状态
x
研究构件内的一点的应力状态时， z
通常是围绕该点取出一个微小立方体（简 称微体）作为研究对象
y
y y
d
x
x
d
y
x
d
x
z
y
Page18
BUAA
BUAA
MECHANICS OF MATERIALS
上讲回顾
挠曲轴的近似微分方程
d 2w M(x) dx2 = EI
梁的弯曲-变形刚度计算

梁的弯曲-变形刚度计算


一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x

y
1'
y
C'
1
在小变形下： 即：
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al ， AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0

04-8.2 积分法求梁的变形

材料力学大连理工大学王博积分法求梁的变形积分法计算梁的变形每段弯矩方程积分后出现两个积分常数，须确定它们积一次分： 积两次分：挠曲线微分方程： EIMw"=C x EIMw'+==⎰d θ⎰⎰++⎪⎭⎫ ⎝⎛=DCx x x EI M w d d积分常数的确定1.边界条件 —— 约束条件挠曲线必须正确地通过约束点2. 连续条件 —— 相邻挠曲线必须光滑连接x = 0, w = 0 x = l , w = 0 x = 0 , w = 0 θ = 0lxBAlxBA例题1：写出确定积分常数的条件边界条件 : x = 0, w 1 = 0w 1′ = 0 x=a+l , w 2= Δl CDa l l xABC Dyq12连续条件 : x = a , w 1= w 2例题2已知：EI = 常数求：1. 挠度、转角方程 2. w max , θmax3. 画挠曲线大致形状 解：1. 建立坐标系EIw = -Flx 2/2 + Fx 3/6+C x+DEIw ′ = -Flx +Fx 2/2+CEIw ″ = M(x)= - Fl + Fx 4.列挠曲线近似微分方程并积分M(x)= -Fl+Fx （0<x ≤l ）3.列弯矩方程2. 求支反力 Fxy F lx BA F AM AF A =F （↑）, M A =Fl （ ）5. 确定积分常数6. 确定转角方程和挠曲线方程7. 求w max , θmaxx = 0 , w = 0 D = 0x = 0 , w’ = 0 C = 0xy FlxB A )2(2x l EI Fxw'--==θ)3(62x l EIFx w --=EIFll x B 2,2max-===θθ33max Fl x l ,w EI ==-（ ） （ ）EIw = -Flx 2/2 + Fx 3/6 +C x+DEIw ′ = -Flx +Fx 2/2+C例题3已知：EI = 常数求：1. 挠度、转角方程 2. w max , θmax 3. 画挠曲线大致形状 解：1. 建立坐标系F A =2F /3（↑）, F B =F /3（↑） EIw 1= F A x 3/6＋C 1 x ＋D 1 EIw 1′= F A x 2/2＋C 1EIw 1″= F A x 4.列挠曲线近似微分方程并积分M 1=F A x （0≤x ≤a ） 3.列弯矩方程 EIw 2″= F A x －F (x －a )EIw 2′= F A x 2/2 －F (x －a )2/2 ＋C 2EIw 2= F A x 3/6 －F (x －a )3/6＋C 2x ＋D 2M 2= F A x －F (x －a ) （ a ≤x ≤3a ） 2.求支反力2aay xA F C BxxF A F B5. 确定积分常数x= 0 , w 1= 0 —D 1= 0x = 3a , w 2 = 0 —C 1 = C 2 = －5Fa 2/96. 确定转角方程和挠曲线方程EI θ1=Fx 2/3－ 5Fa 2/9 EIθ2=Fx 2/3－F (x －a )2/2－ 5Fa 2/9 EIw 1=Fx 3/9－ 5Fa 2x /9 EIw 2=Fx 3/9－F (x －a )3/6－ 5Fa 2x /9 （0≤x ≤ a ） （ a ≤ x ≤3a ）x =a , w 1′= w 2′ —C 1 = C 2w 1 = w 2 — D 1 = D 2 = 0EIw 1= F A x 3/6＋C 1 x ＋D 1EIw 2= F A x 3/6 －F (x －a )3/6＋C 2x ＋D 22aa y x A F C Bx xF A F B2aay xA F CB xxF AF B8.画挠曲线大致形状 可根据约束和载荷画出7. 求w max , θmax)(95,02max ↵===EI Fa x A θθEIFa a x B 94,32==θ00'22=⇒=θw )(4838.03max↓=EIFa w ax 367.1=简支梁在挠曲线无拐点时 可用中点挠度代替最大挠度对比, 梁的中点D接近最大挠度（误差1％）1，最大挠度的计算2aay xAF CB F A F B1.5a1.367a w maxw D)(4838.0,367.13max↓==EIFa w a x )(4792.03↓=EIFa w D 讨论：2.画挠曲线大致形状依据如下条件：1. 约束条件2. 载荷情况，作出M图3. 凹凸情况——由w″即M的正负号决定M>0,则凹M<0,则凸一段M= 0,直线一点M= 0,拐点4. 光滑连续特性《咏挠曲线》挠挠挠曲线弯矩图光连和支座正负有凹凸13FlFlMM e M eA B C Dl l l哪一个是正确的？DCA BMM e。

梁的挠曲线近似微分方程


由边界条件：
x 0，yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
q
A
x θA
θB
y
l
B
x
EIy ql x3 q x4 Cx D 12 24
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
ql x3 q x4 ql3 x 12 24 24
24EI
最大转角和最大挠度分别为：
y qx (l3 2lx2 x3) 24EI
ymax
y
x l 2
5ql 4 384EI
max
A
B
ql3 24 EI
外伸梁，承受集中载荷作用，试绘制挠曲线的大致形状图。 设弯矩刚度EI为常数。
§6-3 用积分法求梁的变形
解：1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区，确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处，应满足位移边界条件；在分段处，则 应满足位移连续条件。
载荷作用。试求此梁的转角方程和挠度方程，并确定最大转角
和最大挠度。
y
q
解：
FRA
FRB
ql 2
A
B
x
M(x) ql x q x2 22
x
l
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
§6-3 用积分法求梁的变形
§6-3 用积分法求梁的变形
梁的挠曲线近似微分方程：
d 2 y M (x) dx2 EI

梁的变形

1 2 1 3 C1 PL ; C 2 PL 2 6
2
写出挠曲线方程和转角方程，并画出挠曲线
P v( x ) ( L x )3 3 L2 x L3 6 EI P q ( x ) v' ( L x )2 L2 2 EI
最大挠度及最大转角


v
P L
度量梁变形的两个基本量
1.挠度：横截面形心沿垂直于轴线方向的线位移。用v 表示。
v向下为正，反之为负。
2.转角：横截面绕其中性轴转动的角度。用q 表示， 顺时针转动为正，反之为负。
C v v
q
P x
C’
转角与挠度的关系
挠曲线上任一点的纵坐标 v（x）即为该点的
横截面的挠度。
dv tgq v' dx
qmax
x


vmax
PL3 v ( L) ( ) 3 EI
q max
PL2 q ( L) ( ) 2 EI
例： 简支梁受集中力F作用，求梁的转角方程和挠度方程， 并求C截面的挠度和A截面的转角。已知梁的EI，l=a+b，a>b。 解：1）由梁整体平衡分析得： HA
H A 0, RA Fb Fa , RB l l
前面讨论了(梁）弯曲 内力、弯曲应力，接下
来讨论弯曲变形。
第10章
梁的变形
梁在外力作用下除了限制其应力，使其满 足强度条件外，还必须限制它的变形，即必须 具有足够的刚度，满足刚度条件。 例如：楼板弯曲变形太大.则平顶下面的粉 刷层就会剥落，不但影响美观，而且给人以不 安全的感觉；高速铁路桥梁变形过大，就无法 提高行车速度。
2、尽量减小梁的跨度或长度，减少弯矩数值

梁的变形



Fl2(l 6EI
a)
Fa2 (a l) ()
3EI
A


Fa(l a)2 2EIl

F (l a) EIl
(l
a)2 2
l(l

a)

Fl(3l 4a) 6EI
Fa (2l 3a) () 6EI
5.3 用叠加法求图示梁的挠度yc和θc。
B
c
ql3 24 EI

ql3 3EI

ql 2a EI

ql3 24 EI

ql2 (l 3a) 3EI
yc

yc

yc
yc
ql3a 24 EI

ql 2a 2 2EI

ql3a 3EI


ql2a(7l 12a) 24 EI
5.5 简支圆木梁, 跨长l=4m, 受均布载荷q=1.82kN/m的作用。 己知[ ] 10MPa ，E=1.0GPa，许可挠度[δ]=l/200，试确定 梁截面的最小直径。
4

l 200

4000 200
20
64

d
4

51.82 4000 4 64
384 103 20

d 280 .39mm
取d=280mm，(280.37-280)/280.37=0.13%，故取d=280mm。
3)实取d=280mm。
5.8 试求图示梁的约束反力，并画剪力图、弯矩图。
M0
A
l/2 C l/2
B
解：这是一次超静定问题。解除B点约束, 受力如图

工程力学中设计到分部积分法的案例

工程力学中设计到分部积分法的案例咱就说那个工程力学里用分部积分法的事儿哈。

就想象有这么个场景，你要计算一个弯曲梁的变形。

这个梁啊，它受到了一个很奇怪的力的作用，这个力的分布不是那种简单的均匀分布啥的，是个随着梁的长度变化的函数。

比如说这个力的函数是F(x) = x e^x（这里的x就是沿着梁的长度方向啦），然后你想要求这个力沿着梁做的功。

根据功的计算公式，那就是力乘以位移的积分。

可这个积分可不好直接求啊。

这时候分部积分法就闪亮登场啦。

咱们把x e^x这个函数看成是两个部分，就像把一个复杂的小怪兽拆成两个小一点的怪兽。

设u = x，dv = e^x dx。

为啥这么设呢？因为e^x的积分咱们比较熟悉呀，就是它自己e^x。

然后根据分部积分法的公式∫ u dv = uv ∫ v du。

v就是e^x积分之后的结果还是e^x，du就是x求导之后的结果，也就是1。

那这个积分就变成了x e^x ∫ e^x dx，后面这个积分就好求啦，就是e^x。

所以最终这个积分的结果就是x e^x e^x + C（C是常数啦，在工程实际问题里，根据具体的边界条件啥的来确定这个常数的值）。

通过这个结果，咱们就能算出这个力在梁上做的功啦，就好像把一个隐藏在复杂函数后面的谜底给揭开了一样。

再比如说计算一些非对称截面的轴的扭转角的时候。

这个扭转角的计算公式里面可能会涉及到一个函数的积分，这个函数是两个函数相乘的形式，就像x sin x这样的（这里的x可能是和轴的某个几何参数有关的变量哦）。

咱们还是用分部积分法，设u = x，dv = sin x dx。

v就是-cos x（因为sin x积分是-cos x），du = 1。

然后根据分部积分公式一算，就可以把这个复杂的积分搞定，这样就能算出轴的扭转角啦。

就好比把一个拧巴的问题给捋直了，你看，分部积分法在工程力学里是不是很神奇呢？。

材料力学A_(梁弯曲变形的描述,挠曲线近似微分方程,积分法和叠加法)

2
w
(x) 挠曲线(轴) (x) w(x)
x x F (13.9) (13.10)
2.挠曲线近似微分方程 由变形几何关系：
1
( x)

M ( x) EI
平面曲线w = w(x) 的曲率为 小变形简化：
( x)
1
( x)

w( x) [1 (w( x))2 ]2
w M>0
§5.5 弯曲时挠曲线的近似微分方程
1.弯曲变形的描述
第5章 弯曲 弯曲变形
w
(x) 挠曲线(轴) (x) w(x)
x x F
季葆华
北京理工大学宇航学院力学系
弯曲使梁的任意 x 截面产生弯曲位移： （1）截面形心的铅垂位移 ——挠度w(x)(向上为正) （2）截面绕中性轴转过的角度 ——转角(x)(为正)
例题
例 题 5-12
l
a
§5
梁的弯曲
D 求图示结构C点的挠度。 解：该梁由梁AB和 拉杆BD组成 1.BD刚化(拉杆不变 形)，仅AB变形 B点相当于简支座：
(a)AB段刚化,BC段变形
BC段相当于 Fa 3 f CF 1 悬臂梁： 3EI

A
B
F C
(b)BC段刚化，AB段变形 F力向B点平移后， A 仅有M=Fa使AB段弯曲变形： Ml Fal Fa2l fCF 2 B2 a a a 3EI 3EI 3EI f C f Cq f CF 1 f CF 2 A
2.弯曲位移计算的载荷叠加法
17
称为叠加原理 叠加原理 利用基本变形表13.2
18
3
例题
例 题 5-8
求图示梁的 f c ?
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Me
共有四个积分常数
A
EI z
a
B
C
L
x
边界条件
x0 x aL
A 0
y
A 0 C 0
连续条件
xa
B1 B 2
Fb 2 Fb EI C1 x z 1 M x x EI z 1 1L 2 L Fb 3 EI z1 x C1 x D1








例题 5.3
求图示简支梁在集中荷载F的作用下（F力在右半跨）的最大挠度。
a
F
A
Fb L
b
B
l
C
x x
最大转角
Fb L b A 6 EI z L
2
Fb 3 Fb L2 b 2 EI z1 x x 6L 6L Fa Fb 2 1 Fb L2 b 2 2 L EI z 2 x F x a 2L 2 6L
x
Fb 2 Fb L2 b 2 EI z1 x 2L 6L
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2ห้องสมุดไป่ตู้ 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
y
A
C

B

x
C
B
tan
d dx
挠曲线方程应分两段AB,BC.
F A
a
q
B
L
共有四个积分常数
EI z
C
x
边界条件
xa
x aL
连续条件
B 0
C 0
y
xa
B1 B 2
B1 B 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
§6-8-2 梁的挠曲线近似微分方程及积分
M ( x) EI Z
d 2 dx 2 d 2 1 ( ) dx
3
1
1


d 2 dx 2 d 2 1 ( ) dx
3

M ( x) EI Z
d 2 M ( x) 2 dx EI Z
q 3 L x L3 6 EI z


qL4 B 8EI z
q L x 4 4 L3 x L4 24 EI z

例题 5.3
求图示简支梁在集中荷载F的作用下（F力在右半跨）的最大挠度。
a
F
A
Fb L
b
B
x
M 1 x
Fb x L
0 xa
3、积分常数由位移边界条件确定。
积分常数C1、C2由边界条件确定
X
x0
xL
0
X
0
y
x0
0
y
0
例题 5.1
F A A
A
求图所示悬臂梁A端的挠度与转角。
x
l
M x Fx
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z






最大挠度 0
令x=a
力靠近哪个支座，哪边的转角最大。
C
Faba b 3L
2 2
Fb 2 Fb L2 b 2 EI z C a 2L 6L Fb 2 Fb L2 b 2 x0 0 2L 6L


转角为零的点在AC段
1 b L 2 x0
l
C
x x
CB段
Fa L
M 2 x
Fb x F x a L axL
AC段
y
6L Fb 2 1 Fb 2 EI zz x F x xC M 2x xa F 22 2 a D 0 2L 2 L x 0 1 0 0 x L L 0 Fb 3 1 3 EI z2 x F x a C2 x D2 a1 D 22 a 1 aC 1 C a x a 1 D 2 2 6L 6 FbFb 1 2 2 3 Fb Fb 1a 3 C L3 0 2 F3 2 3 L Fb Fb L b EI L L 2 C C L b Z 2 Fb a 62 a 1 F a a Fb 2 C2 a D2 1 2D 3C1a 1 EI z1 x 6 L a C a F a a C2 6L 6 6L 6L 1 2L 6L 2L 2L 2 2 2 Fb 2 1 Fb L b 2 EI z 2 x F x a Fb 3 Fb L2 b 2 EI z1 x x 2L 2 6L 6L 6L 2 2 Fb 3 1 Fb L b 3 EI z2 x F x a x 6L 6 6L
挠曲线方程应分两段AB,BC.
EIz1
F
EI z 2
B
共有四个积分常数 x
边界条件
A
L2 L2
C
x0
连续条件
A 0
A 0
L x 2
y
B1 B 2
B1 B 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
1 q Lx 2


2
1 3 EI z EI z qL x C1 6
y
边界条件
EI z
1 4 qL x C1 x C2 24
x0 x0 xL
0
qL3 C1 6 EI z
0
qL3 B 6 EI z
qL3 C2 24 EI z
d dx
M ( x) EI Z dx C1

M ( x ) 在小变形情况下，任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征： 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
2、积分应遍及全梁。在梁的弯矩方程或弯曲刚度不连续处，其挠曲线的近似 微分方程应分段列出，并相应地分段积分。
x0


x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接，挠曲线在 中间铰处，挠度连续，但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
挠曲线方程应分两段AB,BC. 共有四个积分常数
q
A
B
EI z
C
x
边界条件
k
l 2
x0 xL
L x 2
A 0
l 2
y
Fc qL C k 8k
连续条件
B1 B 2
B1 B 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
xL xL x0
B 0
B 0
A
FL 2 EI z
2
FL2 C1 2 EI z FL3 C2 3EI z
Fx 2 FL2 2 EI z 2 EI z Fx3 FL2 FL3 x 6 EI z 2 EI z 3EI z
FL3 A 3EI z
例题 5.2
求图所示悬臂梁B端的挠度与转角。
B
1 2 M x q L x 2
A
x
l
x
EI z M x






y

0
2
FabL b
6 EI z L
M x 0
x0
Fb 2 Fab 1 L a 2 Fb L2 b 2 EI z B B L F L a 2L 2 6 EI z L 6L
xL
Fb 3 1 Fb L2 b 2 3 EI z2 x F x a x 6L 6 6L
全梁仅一个挠曲线方程 共有两个积分常数
L1
q
C EA
边界条件
B
A
x
x0 xL
A 0
EIZ
L
y
qLL1 B LBC 2 EA
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
挠曲线方程应分两段AB,BC.