综上可知 y≥2 6或 y≤-2 6,
即函数的值域为(-∞,-2 6]∪[2 6,+∞).
3
时,等号成
2
(3)已知函数式可变形为:yx2+2yx+3y=2x2+4x-7.
(y-2)x2+2(y-2)x+3y+7=0,
当y≠2时,将上式视为关于x的一元二次方程.
∵x∈R,∴Δ≥0,即[2(y-2)]2-4(y-2)(3y+7)≥0.
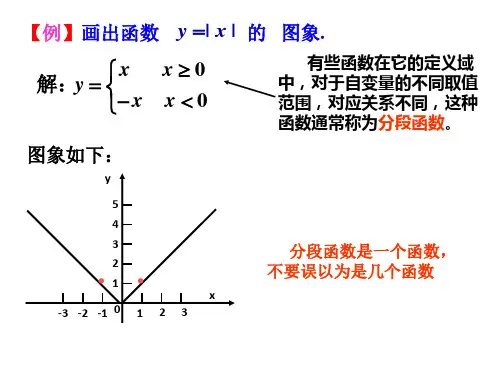
(1)因为分段函数在定义域的不同区间内解析式不一样,所以它的图象也由
几部分构成,有的可以是光滑的曲线段,有的也可以是一些孤立的点或几段
线段,画图时要特别注意区间端点处对应点的实虚之分.
(2)对含有绝对值的函数,要作出其图象,首先根据绝对值的意义去掉绝对
值符号,将函数转化为分段函数来画图象.
变式训练1已知函数f(x)=|x-1|-2.
每个站点之间的距离为1千米,如果某空调公共汽车运行路线中设20个站
点,求票价y(单位:元)关于里程x(单位:千米)的函数解析式,并画出图象.
解 根据题意,
如果某空调汽车运行路线中设20个站点(包括起点站和终点站),那么汽车
行驶的里程约为19千米,所以自变量x的取值范围是{x∈N*|x≤19}.
由空调汽车票价制定的规则,
选取相应的对应关系.要注意写解析式时各区间的端点能否取到,做到不重
复、不遗漏.
(3)分段函数的定义域是各段定义域的并集,值域是分别求出各段上的值域
后取并集.
微练习
-x,x ≤ 0,
f(x)= 2
x ,x > 0.
(1)求f(f(-2))的值;
(2)若f(a)=4,求实数a的值.