《信号与系统分析基础》第1章习题解答
- 格式:doc
- 大小:352.00 KB
- 文档页数:6
第1章信号与系统的概述1.1 学习要求(1)了解信号与系统的基本概念与定义,会画信号的波形;(2)了解常用基本信号的时域描述方法、特点与性质,并会灵活应用性质;(3)深刻理解信号的时域分解、运算的方法,会求解;(4)深刻理解线性是不变系统的定义与性质,会应用性质求解系统1.2 本章重点(1)基本的连续时间信号的时域描述和时域特性;(2)单位冲激信号的定义、性质与应用;(3)信号的时域运算及其综合应用;(4)线性时不变系统的性质与应用。
1.3 本章的知识结构1.4 本章的内容摘要1.4.1信息、消息和信号的概念所谓信息,是指存在于客观世界的一种事物形象,一般泛指消息、情报、指令、数据和信号等有关周围环境的知识。
消息是指用来表达信息的某种客观对象,如电报中的电文、电话中的声音、电视中的图像和雷达探测的目标距离等等都是消息。
所谓信号,是指消息的表现形式,是带有信息的某种物理量,如电信号、光信号和声信号等等。
信号代表着消息,消息中又含有信息,因此信号可以看作是信息的载体。
1.4.2信号的分类以信号所具有的时间函数特性来加以分类,可以将信号分为确定信号与随机信号、连续时间信号与离散时间信号、周期信号与非周期信号、能量信号与功率信号、实信号与复信号等等。
1.4.3 常用信号 (1)正弦型信号)cos()(ϕω+=t A t f (1-3)(2)指数信号st Ae t f =)( (1-8)(3)矩形脉冲⎪⎩⎪⎨⎧><=2/02/1)(ττt t t f(4)三角脉冲⎪⎩⎪⎨⎧>≤-=2/02/21)(τττt t tt f (1-18)(5)抽样信号ttt sin )Sa(=(1-19)性质:(1))Sa()Sa(t t =-,偶函数 (2)1)Sa(,0==t t ,即1)Sa(lim 0=→t t(3)π,0)Sa(n t t ±==, 3,2,1=n (4)⎰∞=02πd sin t t t ,⎰∞∞-=πd sin t tt(5)0)Sa(lim =±∞→t t该函数的另一表示式是辛格函数,其表示式为ttsi t c ππn )(sin =(1-20) (6) 斜变信号⎩⎨⎧≥<=000)(t t t t f (1-24)(7)单位阶跃信号⎩⎨⎧><=0100)(t t t u 或⎩⎨⎧><=-0100)(000t t t t u如果矩形脉冲对于纵坐标左右对称,则可用)(t G T)2()2()(Tt u T t u t G T --+= 下标T 表示其矩形脉冲宽度。


习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。


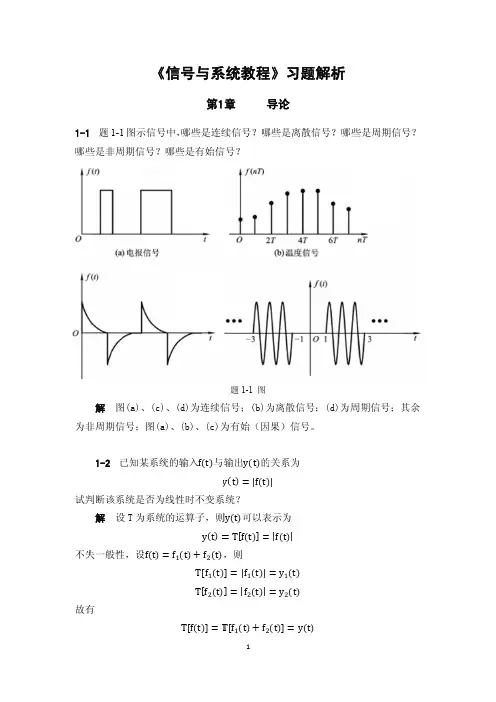
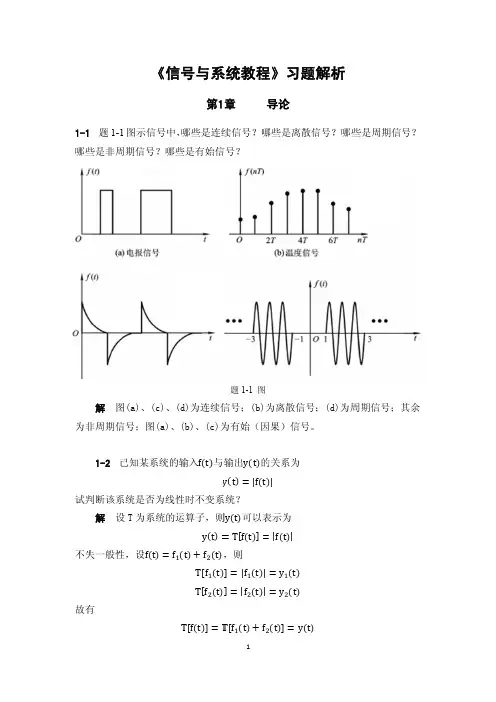
第1章 习题答案1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?解: ① 连续信号:图(a )、(c )、(d ); ② 离散信号:图(b ); ③ 周期信号:图(d );④ 非周期信号:图(a )、(b )、(c ); ⑤有始信号:图(a )、(b )、(c )。
1-2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。
解: 设T 为此系统的运算子,由已知条件可知: y(t)=T[f(t)]=|f(t)|,以下分别判定此系统的线性和时不变性。
① 线性1)可加性不失一般性,设f(t)=f 1(t)+f 2(t),则y 1(t)=T[f 1(t)]=|f 1(t)|,y 2(t)=T[f 2(t)]=|f 2(t)|,y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|,而|f 1(t)|+|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下,不存在f 1(t)+f 2(t)→y 1(t)+y 2(t),因此系统不具备可加性。
由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。
2)齐次性由已知条件,y(t)=T[f(t)]=|f(t)|,则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) (其中a 为任一常数)即在f(t)→y(t)前提下,不存在af(t)→ay(t),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|,则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|,即由f(t)→y(t),可推出f(t-t 0)→y(t-t 0),因此,此系统具备时不变特性。
依据上述①、②两点,可判定此系统为一非线性时不变系统。

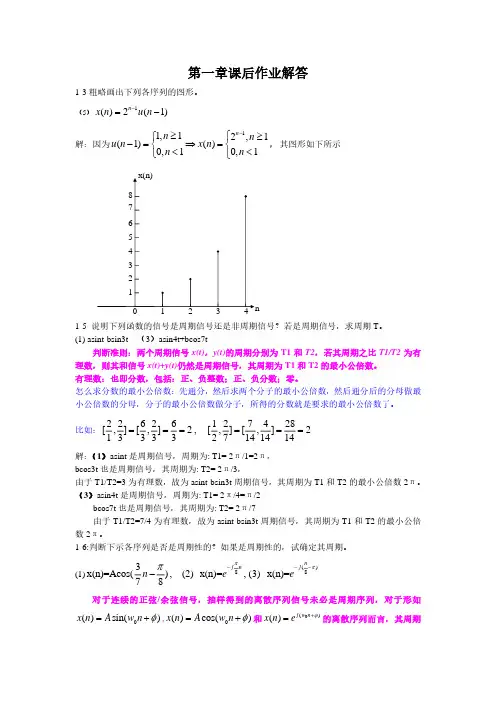
第一章课后作业解答1-3粗略画出下列各序列的图形。
(5)1()2(1)n x n u n −=−解:因为11,12,1(1)()0,10,1n n n u n x n n n −≥⎧≥⎧−=⇒=⎨⎨<<⎩⎩,其图形如下所示1-5 说明下列函数的信号是周期信号还是非周期信号?若是周期信号,求周期T 。
(1) asint-bsin3t (3)asin4t+bcos7t判断准则:两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T1/T2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T1和T2的最小公倍数。
有理数:也即分数,包括:正、负整数;正、负分数;零。
怎么求分数的最小公倍数:先通分,然后求两个分子的最小公倍数,然后通分后的分母做最小公倍数的分母,分子的最小公倍数做分子,所得的分数就是要求的最小公倍数了。
比如:22626[,][,]213333===, 127428[,][,]227141414=== 解:(1)asint 是周期信号,周期为: T1= 2π/1=2π,bcos3t 也是周期信号,其周期为: T2= 2π/3,由于T1/T2=3为有理数,故为asint-bsin3t 周期信号,其周期为T1和T2的最小公倍数2π。
(3)asin4t 是周期信号,周期为: T1= 2π/4=π/2bcos7t 也是周期信号,其周期为: T2= 2π/7由于T1/T2=7/4为有理数,故为asint-bsin3t 周期信号,其周期为T1和T2的最小公倍数2π。
1-6:判断下示各序列是否是周期性的?如果是周期性的,试确定其周期。
(1)3x(n)=Acos()78n π−, (2) 8x(n)=j n e π−, (3) ()8x(n)=n j e π−−对于连续的正弦/余弦信号,抽样得到的离散序列信号未必是周期序列,对于形如0()sin()x n A w n φ=+,0()cos()x n A w n φ=+和0()()j w n x n e ϕ+=的离散序列而言,其周期性判断准则如下: (1)当02Pw Qπ=为有理数时(P 、Q 为互素的整数),x(n) 为周期性且周期为P. (2)当02Pw Qπ=为无理数时,x(n)为非周期性序列 解:(1)022143/73w πππ==为无理数,x(n)为非周期性序列 (2)02216/8w πππ==为有理数,x(n)为周期性序列,其周期为16 (3)022161/8w πππ==为无理数,x(n)为非周期性序列 1-10应用冲激信号的筛选特性(又称抽样特性),求下列各表达式的函数值。

∑ {δ [n + 4m - 4k ] - δ [n + 4m - 1 - 4k ]}∑ {δ [n - 4(k - m )] - δ [n - 1 - 4(k - m )]}∑ {δ [n - 4k ] - δ [n - 1 - 4k ]}s Because g (t ) =∑ δ (t - 2k ) ,Chapter 1 Answers1.6 (a).NoBecause when t<0, x (t ) =0. 1(b).NoBecause only if n=0, x [n ] has valuable.2(c).Y esBecause x[n + 4m ] ===∞ k =-∞ ∞ k =-∞ ∞ k =-∞N=4.1.9 (a). T=π /5Because w =10, T=2π /10= π /5.(b). Not periodic.Because x (t ) = e -t e - jt , while e -t is not periodic, x (t ) is not periodic.2 2(c). N=2Because w =7 π , N=(2 π / w )*m, and m=7.0 0(d). N =10Because x (n) = 3e j 3π / 10 e j (3π / 5)n , that is w =3 π /5, N=(2 π / w )*m, and m=3.4 0(e). Not periodic.Because w =3/5, N=(2 π / w )*m=10π m/3 , it ’not a rational number .1.14 A1=3, t1=0, A2=-3, t2=1 or -1Solution: x(t) isdx(t )dtis∞ k =-∞1.15. (a). y[n]=2x[n-2]+5x[n-3]+2x[n-4]dx(t ) dx(t )=3g(t)-3g(t -1) or =3g(t)-3g(t+1)d t dt2 22 12Solution:y [n ] = x [n - 2] + 1x [n - 3] 2 2 1= y [n - 2] + y [n - 3]1 1= {2 x [n - 2] + 4 x [n - 3]} + {2 x [n - 3] + 4 x [n - 4]}1 1 1 1 =2 x [n - 2] + 5x [n - 3] + 2 x [n - 4]1 11Then, y[n ] = 2 x [n - 2] + 5x[n - 3] + 2 x [n - 4](b).No. For it ’s linearity .the relationship be tw e en y [n ] and x [n ] is the same in-out relationship with (a).1 2you can have a try.1.16. (a). No.For example, when n=0, y[0]=x[0]x[-2]. So the system is memory . (b). y[n]=0.When the input is A δ [n ] ,then, y[n] = A 2δ [n]δ [n - 2] , so y[n]=0.(c). No.For example, when x[n]=0, y[n]=0; when x[n]= A δ [n ] , y[n]=0.So the system is not invertible.1.17. (a). No.For example, y(-π ) = x(0) . So it ’s not causal.(b). Y es.Because : y (t ) = x (sin(t )) ,y (t ) = x (sin(t ))1 122ay (t ) + by (t ) = ax (sin(t )) + bx (sin(t ))1 2121.21. Solution:W e(a).have known:(b).(c).(d).1.22.Solution:W e have known:(a).(b).(e).22 E {x(t )} =(g)1.23. Solution:For1[ x (t ) + x(-t )] v 1O {x(t )} = [ x (t ) - x(-t )] dthen, (a).(b).(c).1.24.2Solution:For:E {x[n ]} = v 1 2( x [n ] + x[-n ])1O {x[n]} = ( x [n ] - x[-n ]) dthen,(a).(b).Solution: x(t ) = E {cos(4π t )u(t )}s(c).1.25. (a). Periodic. T=π /2.Solution: T=2π /4= π /2. (b). Periodic. T=2.Solution: T=2π / π =2. (d). Periodic. T=0.5.v1= {cos(4πt )u (t ) + cos(4π (-t ))u (-t )}2 1= cos(4π t ){u (t ) + u(-t )}2 1= cos(4π t )2So, T=2π /4 π =0.51.26. (a). Periodic. N=7Solution: N= 2π* m =7, m=3.6π / 7(b). Aperriodic.Solution: N= 2π 1/ 8* m = 16m π , it ’not rational number .(e). Periodic. N =16Solution as follow:2 cos( n ) , it ’s period is N=2π *m/( π /4)=8, m=1.sin( n ) , it ’s period is N=2π *m/( π /8)=16, m=1.(2). g (t ) ∑δ (t - 2k )π π π πx[n ] = 2 cos( n ) + sin( n ) - 2 cos( n + 4 8 2 6)in this equation,π4 π8π π- 2 cos( n + 2 6) , it ’s period is N=2π *m/( π /2)=4, m=1.So, the fundamental period of x[n ] is N=(8,16,4)=16.1.31. SolutionBecausex (t ) = x (t ) - x (t - 2), x (t ) = x (t + 1) + x (t ) .2 11311According to LTI property ,y (t ) = y (t ) - y (t - 2), y (t ) = y (t + 1) + y (t )2 11311Extra problems:1. SupposeSketch y(t ) = ⎰t-∞x(t )dt .Solution:2. SupposeSketch:(1). g (t )[δ (t + 3) + δ (t + 1) - 2δ (t - 1)]∞k =-∞Because x[n]=(1 2 0 –1) , h[n]=(2 0 2) , the nSolution: (1).(2).Chapter 22.1 Solution:-1(a).So,y [n ] = 2δ [n + 1] + 4δ [n ] + 2δ [n - 1] + 2δ [n - 2] - 2δ [n - 4]1(b). according to the property of convolutioin:y [n ] = y [n + 2]2 1(c). y [n] = y [n + 2]31=∑ x[k ]h [n - k ]( ) 0 - ( ) (n +2)-2+1= ∑ ( ) k -2 u[n] = 2 u[n]2 ⎩0, elsewhere W e have known: x[n] = ⎨ ⎩0,elsewhere , h[n] = ⎨ ,( N ≤ 9 ), , ∑ h[k ]u[n - k ]∑ (u[k ] - u[k - N - 1])(u[n - k ] - u[n - k - 10])∑ (u[k ] - u[k - N - 1])(u[4 - k ] - u[-k - 6])⎧∑ 1,...N ≤ 4⎪∑1,...N ≥ 4 ⎪⎩∑ (u[k ] - u[k - N - 1])(u[14 - k ] - u[4 - k ])2.3 Solution:y[n ] = x[n ]* h [n ]∞ k =-∞ ∞1= ∑ ( ) k -2 u [k - 2]u [n - k + 2]2k =-∞1 1 n +2 121 k =2 1 -21= 2[1 - ( ) n +1 ]u [n ]2the figure of the y[n] is:2.5 Solution:⎧1 ....0 ≤ n ≤ 9 ....⎧1 0≤ n ≤ N .... Then,x[n] = u[n] - u[n - 10] , h[n] = u[n] - u[n - N - 1]y[n] = x[n]* h[n] =∞k =-∞=∞ k =-∞So, y[4] =∞ k =-∞N⎪ ⎪ = ⎨k =04k =0=5, the n N ≥ 4And y[14] =∞ k =-∞⎧∑ 1,...N ≤ 14⎪∑1,...N ≥ 14 ⎪⎩ ∑ x[k ]g [n - 2k ]∑ x[k ]g [n - 2k ] = ∑ δ [k - 1]g [n - 2k ] = g [n - 2]∑ x[k ]g [n - 2k ] = ∑ δ [k - 2]g [n - 2k ] = g [n - 4]∑ x[k ]g [n - 2k ] = ∑ u[k ]g [n - 2k ] = ∑ g [n - 2k ]N⎪ ⎪= ⎨ k =514k =5∴N = 4=0, the n N < 52.7 Solution:y[n] =∞k =-∞(a ) x[n] = δ [n - 1] , y[n] =∞∞k =-∞ k =-∞ (b)x[n] = δ [n - 2] , y[n] =∞∞k =-∞k =-∞(c) S is not LTI system..(d) x[n] = u[n] , y[n] =∞ ∞∞k =-∞k =-∞ k =02.8 Solution:y(t ) = x(t ) * h (t ) = x(t ) *[δ (t + 2) + 2δ (t + 1)]= x(t + 2) + 2 x (t + 1)Then,⎩ = ⎰ u(τ - 3)e -3(t -τ )u(t - τ )d τ - ⎰ u(τ - 5)e -3(t -τ )u(t - τ )d τ⎩= u(t - 3)⎰ e -3(t -τ ) d τ - u(t - 5)⎰ e -3(t -τ ) d τ⎧t + 3,..... - 2 < t < -1 ⎪4,.......... t = -1 ⎪⎪That is, y(t ) = ⎨t + 4,..... - 1 < t ≤ 0⎪2 - 2t,....0 < t ≤ 1 ⎪ ⎪0,....... others2.10 Solution:(a). W e know:Then,h '(t ) = δ (t ) - δ (t - α )y '(t ) = x(t ) * h '(t ) = x(t ) *[δ (t ) - δ (t - α )]= x(t ) - x(t - α )that is,⎧t,.....0 ≤ t ≤ α ⎪α ,....α ≤ t ≤ 1So, y(t ) = ⎨⎪1 + α - t,.....1 ≤ t ≤ 1 + α ⎪0,.....others(b). From the figure of y '(t ) , only if α = 1 , y '(t ) would contain merely therediscontinuities.2.11 Solution:(a).y(t ) = x(t ) * h(t ) = [u (t - 3) - u (t - 5)]* e -3t u (t )∞ ∞-∞-∞tt35= ⎨⎰ e -3(t -τ ) d τ = ,.....3 ≤ t < 5 ⎪ 3 ⎪⎰ e -3(t -τ ) d τ - ⎰ e -3(t -τ ) d τ = - e ⎪ t9-3t + e 15-3t ⎪⎩ s y(t ) = e -t u (t ) * ∑ δ (t - 3k ) = ∑ [e = ∑ e -(t -3k )u (t - 3k )y(t ) = e -t [ ∑ e 3k u (t - 3k )] = e -t∑ ew [n ] = 1w [n - 1] + x[n ]⎧⎪ ⎪0,................. t < 3⎪ t1 - e 9-3t3t353,...... t ≥ 5(b). g (t ) = (dx(t ) / dt ) * h(t ) = [δ (t - 3) - δ (t - 5)]* e -3t u (t )= e -3(t -3) u (t - 3) - e -3(t -5) u (t - 5)(c). It ’obvious that g (t ) = d y (t ) / dt .2.12 Solution∞∞k =-∞k =-∞∞k =-∞Considering for 0 ≤ t < 3 ,we can obtain-t u (t ) * δ (t - 3k )]∞k =-∞0 k =-∞3k= e -t 11 - e -3.(Because k mu st be negetive , u (t - 3k ) = 1 for 0 ≤ t < 3 ).2.19 Solution:(a). W e have known:2 (1)y[n ] = αy[n - 1] + βw [n ](2)then, H ( E ) = H ( E ) H ( E ) =βE 2= .... or : (α + ) = ∴⎨ 2 8 ⎝ 2 = - E ∴ h [n ] = ⎢2( ) n - ( ) n ⎥u [n ] ⎩Θ⎰⎰ sin(2πt )δ (t + 3)dt has value only on t = -3 , but - 3 ∉ [0,5]⎰ sin(2πt )δ (t + 3)dt =0Θ⎰-4from (1), H ( E ) =E1E -1 2from (2), H ( E ) =2 βEE - α121 ( E - α )(E - )2 = β1 α 1 - (α + ) E -1 + E -22 21 α∴ y[n ] - (α + ) y[n - 1] + y[n - 2] = βx[n ]2 21 3but, y[n ] = - y[n - 2] + y[n - 1] + x[n ]8 4⎧α 1 ⎛1 ⎪ 3 ⎫ ⎪4 ⎭ ⎧ 1 ⎪α = ∴⎨ 4⎪β = 1(b). from (a), we know H ( E ) = H ( E ) H ( E ) =1 22E +1 1 E - E -4 2⎡ 1 1 ⎤ ⎣ 24 ⎦2.20 (a). 1⎪⎩β = 1E 21 1 ( E - )(E - ) 4 2(b). 0∞-∞ u (t ) cos(t )dt =⎰∞ δ (t ) cos(t )dt = cos(0) = 1-∞Θ∴(c). 05 0 5 05-5 u (1 - τ ) cos(2πτ )d τ = -⎰6 u (t ) cos(2πt )dt1 1= -⎰6 δ '(t ) cos(2πt )dt-4= cos '(2π t ) |t =0= -2π sin(2πt ) |t =0= 0∑ δ (t - kT ) * h (t )∑ h (t - kT )⎰ y(t )d t , A = ⎰ x(t )dt ,A = ⎰ h(t )d t .⎰ x(τ ) x (t - τ )d τ⎰ y(t )dt = ⎰ ⎰ x(τ ) x (t - τ )d τd t= ⎰ ⎰ x(τ ) x (t - τ )dtd τ = ⎰ x(τ ) ⎰ x(t - τ )dtd τ⎰ x(τ ) ⎰ x(ξ )d ξ d τ = ⎰ x(τ )d τ{ ⎰ x(ξ )d ξ}2.23 Solution:Θ y(t ) = x(t ) * h (t ) =∞k =-∞=∞ k =-∞∴2.27 SolutionA = y∞ ∞ ∞ x h-∞ y(t ) = x(t )* h(t ) = -∞ -∞ ∞-∞A = y∞ ∞ ∞-∞ -∞ -∞∞ ∞∞∞-∞ -∞-∞ -∞= ∞ ∞ ∞ ∞-∞= A Ax h-∞ -∞ -∞⎰e ⎰ eδ (τ - 2)d τ = ⎰ e⎰ u(τ + 1)eu(t - 2 - τ )d τ - ⎰ u(τ - 2)e= u(t - 1) ⎰ ed τ - u(t - 4) ⎰ e-(t -2-τ )d τ2.40 Solution(a) y(t ) = t-(t -τ) x(τ - 2)d τ ,Let x(t ) = δ (t ) ,then y(t ) = h (t ) .-∞So , h(t ) = t t -2-(t -τ ) -∞-∞-(t -2-ξ )δ (ξ )d ξ = e -(t -2)u(t - 2)(b)y(t ) = x(t )* h(t ) = [u(t + 1) - u(t - 2)]* e -(t -2)u(t - 2)=∞ ∞ -(t -2-τ )-∞-∞-(t -2-τ )u(t - 2 - τ )d τt -2-1-(t -2-τ ) t -2 2= u(t - 1)[e -(t -2) e τ ]| t -2 -u(t - 4)[e -(t -2) e τ ]| t -2-1 2= [1- e -(t -1) ]u(t - 1) - [1- e -(t -4) ]u(t - 4)2.46 SolutionBecaused d dx(t ) = [ 2e -3t ]u (t - 1) + 2e -3t [ u (t - 1)] d t dt d t= -3x(t ) + 2e -3t δ (t - 1) = -3x(t ) + 2e -3δ (t - 1) .From LTI property ,we knowdd tx(t ) → -3 y (t ) + 2e -3 h (t - 1)whereh (t ) is the impulse response of the system.So ,following equation can be derived.2e -3h(t - 1) = e -2t u (t )Finally, h (t ) = 12e 3e -2(t +1)u (t + 1)2.47 SoliutionAccording to the property of the linear time-invariant system:(a). y(t ) = x(t ) * h(t ) = 2 x (t ) * h (t ) = 2 y (t )0 0(b). y(t ) = x(t ) * h(t ) = [ x (t ) - x (t - 2)]* h(t )1y(t)= x (t ) * h (t ) - x (t - 2) * h (t )0 2 4t= [ y (t )] = y (1). Because H ( P ) = 1so h (t ) = (1= 2 + E - E ⎪ [ ]⎪δ [k ] = i (-1 - i) n- (-1 + i) n u [n] so h [n ] = 2 2 i= y (t ) - y (t - 2)0 0(c). y(t ) = x(t ) * h(t ) = x (t - 2) * h (t + 1) = x (t - 2) * h (t ) * δ (t + 1) = y (t - 1)0 0(d). The condition is not enough.(e). y(t ) = x(t ) * h(t ) = x (-t ) * h (-t )0 0= ⎰∞ x (-τ )h (-t + τ )d τ-∞ = ⎰∞x (m )h (-t - m )dm = y (-t )-∞(f). y(t ) = x(t ) * h (t ) = x ' (-t ) * h ' (-t ) = [ x ' (-t ) * h (-t )] ' ' ' " (t )Extra problems:1. Solute h(t), h[n](1). d 2 dy(t ) + 5 y(t ) + 6 y(t ) = x(t )dt 2 dt(2). y[n + 2] + 2 y[n + 1] + 2 y[n ] = x[n + 1]Solution:1 1 - 1= = +P 2 + 5P + 6 ( P + 2)( P + 3) P + 2 P + 3- 1+)δ (t ) = (e -2t - e -3t )u (t )P + 2P + 3(2). Because H ( E ) = E E E= =E 2 + 2E + 2 ( E + 1) 2 + 1 ( E + 1 + i)( E + 1 - i)i i E - E2E + 1 + i E + 1 - i⎛ i ⎫+E + 1 + i E + 1 - i ⎪ 2 ⎪ ⎝ ⎭x(t ) = ∑ for the period of cos( 5πt ) is T = 63the period of sin( 22⎰ x 2 (t )e - jkw 2t d t = ⎰ ( x 1 (1- t ) + x 1 (t - 1))e - jkw 1t dtT T TChapter 33.1 Solution:Fundamental period T = 8 . ω = 2π / 8 = π / 4∞a e j ω0kt = a e j ω0t + a e - j ω0t + a e j 3ω0t + a e - j 3ω0tk 1 -1 3 -3k =-∞ = 2ej ω0t+ 2e - j ω0t + 4 je j 3ω0t - 4 je - j3ω0t π 3π= 4cos( t ) - 8sin( t )4 43.2 Solution:for , a = 1 , a0 -2= e - j π / 4 , a = e j π / 4 , a 2-4= 2e - j π / 3 , a = 2e j π / 34x[n] = ∑ a e jk (2π / N )nkk =< N >= a + a e j (4π / 5)n + a e - j (4π / 5)n + a e j (8π / 5)n + a e - j (8π / 5)n0 2-24-4= 1 + e j π / 4 e j (4π / 5)n + e - j π / 4 e - j (4π / 5)n + 2e j π / 3e j (8π / 5)n + 2e - j π / 3e - j (8π / 5)n4 π 8 π= 1 + 2 cos( πn + ) + 4 cos( πn + )5 4 5 3 4 3π 8 5π= 1 + 2sin( πn + ) + 4sin( πn + )5 4 5 63.3 Solution:2πt ) is T= 3 , 3so the period of x(t ) is 6 , i.e. w = 2π / 6 = π / 32π 5π x(t ) = 2 + cos(t ) + 4sin(t )331= 2 + cos(2w t ) + 4sin(5w t )0 0 1= 2 + (e j 2w 0t + e - j 2w 0t ) - 2 j(e j5w 0t - e - j5w 0t )2 then, a = 2 , a 0 -2 1= a = , a 2 -5 = 2 j , a = -2 j 53.5 Solution:(1). Because x (t ) = x (1 - t ) + x (t - 1) , the n x (t ) has the same period as x (t ) ,21121that is T = T = T ,w = w2121(2). b = 1 k⎰ x 1 (1- t )e - jkw 1t d t + 1 ⎰ x 1 (t - 1)e - jkw 1t dt ∑∑⎰ x(t ) 2 dt = a 0 2 + a -1 2 + a 1 2 = 2 a 1 2 = 1 Fundamental period T = 8 . ω = 2π / 8 = π / 4∑∑ a H ( jkw )ejkw 0tk ω ⎩0,......k ≠ 0⎧ ∑t Because a =⎰ x(t )d t = 1⎰4 1d t + 1 ⎰ 8(-1)d t = 0TT88 4= 1 T T T T= a e - jkw 1 + a e - jkw 1 = (a -k k3.8 Solution:-k+ a )e - jkw 1 kΘx(t ) =∞ k =-∞a e jw 0ktkwhile:andx(t ) is real and odd, the n a = 0 , a = -a 0 kT = 2 , the n w = 2π / 2 = πa = 0 for k > 1k-ksox(t ) =∞ a e jw 0kt = a + a e - jw 0t + a e jw 0tk 0 -1 1k =-∞= a (e j πt - e - j πt ) = 2a sin(π t )11for1 2 2 0∴∴a = ± 2 /21x(t ) = ± 2 sin(π t )3.13 Solution:Θx(t ) =∞ k =-∞a e jw 0ktk∴ y(t ) =∞k 0k =-∞H ( jk ω ) = sin(4k ω0 ) =⎨4,...... k = 00 0 ∴ y(t ) =∞a H ( jkw )e jkw 0= 4a k 00 k =-∞1Soy(t ) = 0 .∑∑a H(jkw)e jkw0tT t H(jw)=⎨if a=0,it needs kw>100T ⎰T⎰t dt=0T ⎰x(t)e-jkw0t dt=⎰te-jk22t dt=1⎰1te-jkπt dt11⎰1tde-jkπt2jkπ⎢-1⎦⎢(e-jkπ+e jkπ)-⎥-jkπ2c os(kπ)+-jkπ⎥⎦[2cos(kπ)]=j cos(kπ)=j(-1)k............k≠03.15Solution:Θx(t)=∞k=-∞a e jw0kt k∴y(t)=∞k=-∞k0∴a=1k ⎰Ty(t)H(jkw)e-jkw0d tfor⎧⎪1,......w≤100⎪⎩0,......w>100∴k0that is k2π100 >100,.......k>π/612and k is integer,so K>8 3.22Solution:a=10x(t)dt=112-1a= k 1T2-12-1π=-1 2jkπ-1=-1⎡⎢te-jkπt⎣1-1-e-jkπt-jkπ1⎤⎥⎥=-=-12jkπ12jkπ⎡(e-jkπ-e jkπ)⎤⎣⎦⎡2sin(kπ)⎤⎢⎣=-12jkπkπkπ⎰ h (t )e - j ωt d t = ⎰ e -4 t e - j ωt d t= ⎰ e e d t + ⎰ e -4t e - j ωt d t∑0 ∑∑Ta = ⎰ x(t )e - jkw 0t d t = ⎰1/ 2 δ(t )e - jk 2πt d t = 1T T-1/ 2 ∑T∑ (-1) δ (t - n ) .T=2, ω = π , a = 1T a = ⎰ x(t )e - jkw 0t d t = ⎰ δ (t )e - jk πt d t + ⎰ 3/ 2 (-1)δ (t - 1)e - jk πt d tT 2 -1/ 2 2 1/ 2 T 16 + (k π )23.34 Solution:∞ ∞H ( j ω ) =-∞-∞0 ∞ 4t - j ωt-∞118=+=4 - j ω 4 + j ω 16 + ω 2A periodic continous-signal has Fourier Series:. x(t ) =T is the fundamental period of x(t ) . ω = 2π / T∞ k =-∞a e j ω ktkThe output of LTI system with inputed x(t ) is y(t ) =Its coefficients of Fourier Series: b = a H ( jk ω )k k 0∞ k =-∞a H ( jk ω )e jk ω tk 0(a) x(t ) =∞ n =-∞ δ (t - n ) .T=1, ω = 2π a = 1 = 1 .0 k1 k(N ot e :If x(t ) =∞ n =-∞δ (t - nT ) , a =1 k)So b = a H ( jk 2π ) = k k 8 2=16 + (2k π )2 4 + (k π )2(b) x(t ) = ∞n =-∞n0 k= 11 1 1/2 1 k1= [1- (-1)k ] 24[1-(-1)k ]So b = a H ( jk π ) = ,k k(c) T=1, ω = 2π⎰ x(t )e - jk ω0t d t = ⎰1/ 4e - jk 2πt d t =∑∑ a H ( jkw )ejkw 0t⎪⎩0,......otherwise ⎩0,......otherwise H ( jw) = ⎨⎪, 14Let y(t ) = x(t ) , b = a , it needs a = 0 ,for k < 18..or .. k ≤ 17 .∑∑∑ 2n e - j ωn + ∑ ( )n e - j ωn1 =2 41 1 5∑a ejk ( N )n .a = k1 T T -1/ 4 k π sin(2 k π)b = a H ( jk π ) =k k k π8sin( )2 k π [16 + (2k π )2 ]3.35 Solution: T= π / 7 , ω = 2π / T = 14 .Θx(t ) =∞a e jw 0ktk∴y(t ) =k =-∞ ∞ k =-∞k 0∴b = a H ( jkw )k k 0for ⎧1,...... w ≥ 250 ⎧1,...... k ≥ 170 that is k ω 0 < 250,....... k < 250, and k is integer , so k < 18..or .. k ≤ 17 .kkk3.37 Solution:H (ej ω) = ∞n =-∞h [n ]e- j ωn=∞ n =-∞1 ( ) ne - j ωn 2-1∞1= 2n =-∞ n =0 1 3e j ω+ =1 - e j ω 1 - e - j ω - cos ω2 2 4A periodic sequen ce has Fourier Series: x [n ] =N is the fundamental period of x[n ] .k =< N >k2πThe output of LTI system with inputed x[n ] is y[n ] =∑ a H (ekj 2π k N)ejk ( 2π )n N .k =< N >∑4 .So b = a H (e j N k ) = 1 4 45 - cos( 2π k ) k =2 21 T ' 1 3T '-1 = ⎰ x(3t - 1)e T ' dt = ⎰ x(m )e = ⎰ x(m )e e⎡ 1T -1 T ⎢⎰∑a e jk (2π/T )t ,where a = 0 for every2π Its coefficients of Fourier Series: b = a H (ejN k )kk3(a) x[n ] =∞ k =-∞δ [n - 4k ] .N=4, a = 1 k k k 2π 4 4b =k3 165 π- cos( k ) 4 23.40 Solution:According to the property of fourier series:(a). a k '= a e - jkw 0t 0 + a e jkw 0t 0 = 2a cos(kw t ) = 2a cos(k k k k 0 0 k 2π t )T 0(b). Because E {x(t )} =v x(t ) + x(-t )2a ' a + a k 2-k= E {a }v k(c). Because R {x(t )} = x(t ) + x * (t )e'a + a *a = k-k k(d). a '= ( jkw ) 2 a = ( jk k 0 k 2πT) 2 ak(e). first, the period of x(3t - 1) is T ' =T3th e n ak ' 2π - jk t T ' 0 T ' -11 T -12π 2π - jkm - jk dmT TT -1- jk 2π m +1 dm T ' 3 3= e- jk 2π ⎣ T -1x(m )e2π- jk m T⎤dm ⎥⎦2π = a e- jk Tk3.43 (a) Proof:( i ) Because x(t ) is odd harmonic , x(t ) =non-zer o even k.∞ k =-∞k kx(t + ) = ∑ a e jk (2π /T )(t + 2 )T 2∑= - ∑ a e jk (2π /T )t(ii )Because of x(t ) = - x (t + ) ,we get the coefficients of Fourier Seriesa = ⎰ x(t )e - jk 2T π t d t = 1 ⎰ T / 2 x(t )e - jk 2T π t d t + 1 ⎰ T x(t )e - jk 2T π t d tT 0 T 0 T T /2 1 T /2 1 T /2 = ⎰ T dt + ⎰ x(t + T / 2)e x(t )e 1 T /2 1 T /2 = ⎰ x(t )eT dt - ⎰ x(t )(-1)k e T dt 1T /2It is obvious that a = 0 for every non-zer o even k. So x(t ) is odd harmonic ,-11x(t ) = ∑ δ (t - kT ) , T = π∞ T k k =-∞= ∞a e jk π e jk (2π /T )tkk =-∞∞kk =-∞It is noticed that k is odd integers or k=0.That meansTx(t ) = - x (t + )2T21 T k2π - jk t T 0 T 0 2π- jk (t +T / 2) Tdt2π 2π- jk t - jk t T 0 T 0= [1- (-1)k ] ⎰T 02π x(t )e- jk Tt d tk(b) x(t )1......-2-12 tExtra problems:∞ k =-∞(1). Consider y(t ) , when H ( jw) isx(t ) = ∑ δ (t - kT ) ↔T π T∑ a H ( jkw )ejkw 0t=1k =-∞ π∑∑π∑1(2). Consider y(t ) , when H ( jw) isSolution:∞k =-∞ 1 1 2π= , w = = 2 0(1).y(t ) =∞k 0∞k =-∞a H ( j 2k )e j 2ktk=2π (for k can only has value 0)(2).y(t ) =∞ k =-∞a H ( jkw )e jkw 0t =1k 0∞k =-∞a H ( j 2k )e j 2ktk=1π (e - j 2t + e j 2t ) =2 cos 2tπ(for k can only has value – and 1)。
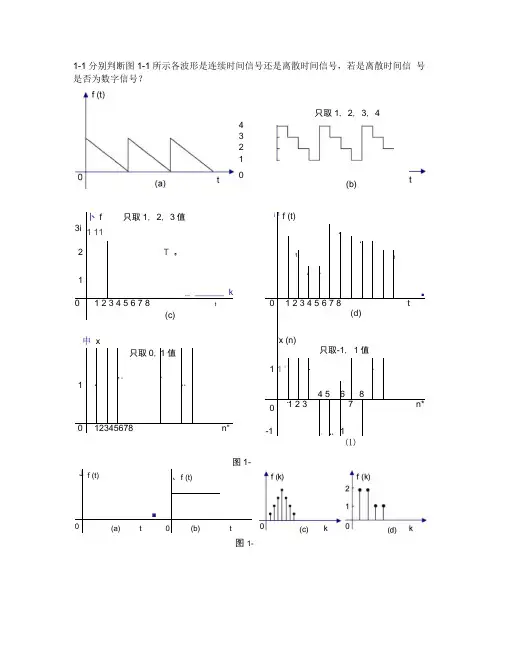
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?4321(b)卜f (t)只取1, 2, 3值3i 1 112T 口1_ ______ k0 1 2 3 4 5 6 7 8 t(c)11只取0,卩11值11 1012345678 n"j1f (t)1卜11111卜■0 1 2 3 4 5 6 7 8t(d)'x (n)只取-1,1值11 'c14 568011 2 37n*-1' « 1 111⑴图1-1 J°f (t)、f (t)■0(a)t 0(b)t 只取1, 2, 3, 4值申x(n)图1-2解信号分类如下:模拟:幅值、时间均连 续(例见图1 2( a ))幅值离散,时间连续(例见图12( b ))图1 1所示信号分别为 图1-1所示信号分力别为时间离散,幅值连续(例见图1 2( c ))幅值、时间均离散(例见图1 2(d )) (a) 连续信号(模拟信号); (b) 连续(量化)信号; (c) 离散信号,数字信号; (d) 离散信号;(e) 离散信号,数字信号; (f) 离散信号,数字信号。
1-2分别判断下列各函数式属于何种信号?(重复 1-1题所示问)(1) e at sin( t);(2) e nT ; (3) cos(n );(4) sin(n 0)( 0为任意值);2(5) - o2解由1-1题的分析可知: (1) 连续信号; (2) 离散信号;(3) 离散信号,数字信号; (4) 离散信号; (5) 离散信号。
1-3分别求下列各周期信号的周期T : (1) cos(10t) cos(30t); (2) e j10t ; (3) [5sin(8t)]2 ; (4)( 1)n u(t nT) u(t nT T) (n 为整数)。
n 0解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号, 需要考察各 分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若 不存在,则该复合信号为非周期信号。
1-4 分析过程:(1)例1-1的方法:()()()()23232f t f t f t f t →−→−→−− (2)方法二:()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦(3)方法三:()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程:(1)方法一:方法二:(1)()−f at 左移0t :()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at (2)()f at 右移0t :()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at (3)()f at 左移0t a :()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a (4)()f at 右移0t a :()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故(4)运算可以得到正确结果。
注:1-4、1-5题考察信号时域运算:1-4题说明采用不同的运算次序可以得到一致的结果;1-5题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 解题过程: (1)()()()2tf t eu t −=− (2)()()()232tt f t ee u t −−=+(3)()()()255ttf t e eu t −−=− (4)()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程:((((注:1-9、1-12题中的时域信号均为实因果信号,即()()()=f t f t u t 1-18 分析过程:任何信号均可分解为奇分量与偶分量之和的形式,即()()()()1e o f t f t f t =+其中,()e f t 为偶分量,()o f t 为奇分量,二者性质如下:()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程:(a-1) (a-2)(a-3)(a-4)f t为偶函数,故只有偶分量,为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性(1)线性(Linearity):基本含义为叠加性和均匀性即输入()1x t ,()2x t 得到的输出分别为()1y t ,()2y t ,()()11T x t y t =⎡⎤⎣⎦,()()22T x t y t =⎡⎤⎣⎦,则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦(1c ,2c 为常数)。
第1章 习 题 解 答1-1.判断下列信号是否是周期性的,如果是周期性的,试确定其基波周期(1)()⎪⎭⎫⎝⎛+=43cos 2πt t f 解:对于()k Z ∈()222cos 32cos 322cos 333444f t k t k t k t f t ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=++=++=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∴原函数是周期函数,令1k =,则基波周期为23π。
(2)()26sin ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=πt t f解:对于()k Z ∈()()22sin sin 66f t k t k t f t ππππ⎡⎤⎡⎤⎛⎫⎛⎫+=+-=-= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦∴原函数是周期函数,令1k =,则基波周期为π。
(3)()[]()t u t t f π2cos =解:设其存在周期,令周期为T()()()cos 2f t T t T u t T π+=++⎡⎤⎣⎦在0T ≠的情况下函数不为零的部分发生了平移,故()()f t T f t +≠∴原函数不是周期函数。
(4)())(42π+=t j et f解:对于()k Z ∈())()(())(()224442222j t k j t j t j k f t k eeeef t ππππππ+++++==⨯==∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.求信号())14sin()110cos(2--+=t t t f 的基波周期。
解:cos(101)t +的基波周期为15π, s i n (41)t -的基波周期为12π二者的最小公倍数为π,故())14sin()110cos(2--+=t t t f 的基波周期为π。
1-3.设()3,0<=t t f , 对以下每个信号确定其值一定为零的t 值区间。
(1)()t f -1 (2)()()t f t f -+-21 (3))()(t f t f --21 (4)()t f 3 (5)()3tf解:(1)()t f -1为()f t 反折后向右平移一个单位得到,故当()2t >-时()10f t -=(2)()2f t -为()f t 反折后向右平移两个单位得到,故当()1t >-时()20f t -=。
《信号与系统》习题参考答案(1)2—1(1) 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ (2) 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰(3) 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= (4) 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ (5) 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ (6)()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2(1) [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--(2) 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑(3) 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ (4) 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑(5) 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3(1) 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- (2) 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---(3) 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5(1) 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰(2) 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质,先对()x t 积分,对()h t 微分,'()()()y t x t dt h t =*⎰(3) 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰(4) 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰(5) 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7(1) 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =(2) 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- (3) 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8(1) 0()3()y t y t =(2) 00()()(2)y t y t y t =-- (3) 0()(1)y t y t =- (4) 0()()y t y t =-(5) 0()()dy t y t dt=(6) 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10(1) 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ (2) 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ (3) 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11(1) 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ (2) 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---(1)'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- (2)当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13(1)213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--(2)1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14(1)因果、稳定 (2)非因果、非稳定 (3)非因果、稳定 (4)非因果、稳定 (5)非因果、稳定 (6)因果、稳定 (7)因果、非稳定 2—15(1)因果、稳定 (2)非因果、稳定 (3)非因果、非稳定 (4)非因果、稳定 (5)因果、非稳定 (6)非因果、稳定 (7)因果、稳定 2—16(1)对 (2)对()h t dt ∞-∞=+∞⎰(3)错 例如单位冲激响应(1)t δ-是因果的,但LTI 系统的逆系统(1)t δ+不是因果的。
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章(无) (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号,由f (t )求f (−3t − 2),但改变运算顺序,先求f (3t )或先求f (−t ),讨论所得结果是否与原例之结果一致。
解:(1). 例1-1的方法: f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二:f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三:f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三:1-5 已知()f t ,为求0()f t at −应按下列哪种运算求得正确结果(式中0t ,a 都为正值)?(1)()f at −左移0t (2)()f at 右移0t (3)()f at 左移0t a (4)()f at −右移0ta解:(4)()f at −右移t a:故(4)运算可以得到正确结果。
注:1-4、1-5 题考察信号时域运算:1-4 题说明采用不同的运算次序可以得到一致的结果; 1-5 题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 粗略绘出下列各函数式的波形图: (1)()(2)()t f t e u t −=− (2)2()(36)()t t f t e e u t −−=+ (3)3()(55)()t t f t e e u t −−=−(4)()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解:(1)()(2)()tf t e u t −=−(2)2()(36)()ttf t e eu t −−=+(3)3()(55)()ttf t e eu t −−=−(4)()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图,注意它们的区别:(1)[()(1)]−−;t u t u t(2)(1)�;t u t−(3)[()(1)](1)−−+−;t u t u t u t(4)(1)(1)−−;t u t(5)(1)[()(1)]−−−−;t u t u t(6)[(2)(3)]−−−;t u t u t(7)(2)[(2)(3)]t u t u t−−−−。
《信号与系统分析基础(第2版)》部分习题解答
姜建国,曹建中,高玉明著,清华大学出版社,2006年7月
第一章
1-3 粗略画出下列各序列的图形。
(5)1
()2
(1)n x n u n -=-
1-5 说明下列函数的信号是否是周期信号,若是,求周期T 。
(本题属于连续情况) (1)sin sin3a t b t - 解:12222, T 13
T ππ
π=
==
1
2
3T T =,为有理数
∴是周期信号,2T π=
(3)sin 4cos7a t b t + 解:122, 27T T π
π=
=
1
2
7
224
7
T T π
π=
=
为有理数 ∴是周期信号,2T π=
1-6 判断下列各序列是否是周期性的,若是,试确定其周期。
(本题属于离散情况) (1)3
()cos()7
8
x n A n π
=-
解:周期条件:22 =m kN m N k
πωπω=⋅ 本题中,314 =73m N k
πω=⋅为无理数,非周期。
(2)8
()n j x n e π-=
解: =168
N π
ω=,是周期信号,周期为16.
(3)()8
()n j x n e π-=
解:12 =168N m m πωπω
=
⋅=为无理数,非周期。
1-7 绘出下列各时间函数的波形图,注意它们的区别。
设01
= 2
t ωπ=
, 12030040(1) ()sin ()(2) ()sin ()(3) ()sin ()()(4) ()sin ()()
f t t u t f t t u t t f t t t u t t f t t t u t ωωωω=⋅=⋅-=-⋅-=-⋅
t
t
t
1-10 应用冲激信号的筛选特征(又称抽样特性),求下列个表达式的函数值。
000
0000000000 ()()()
()(2)0
-2 ()()(0)
1 (sin )()sin 6666210 ()()()()0222t f t t t dt f t e t t dt t f t t t t dt f t t t dt t t t t t t u t dt u t u t δδδππππδδ--+∞
-∞+∞
-+∞-∞
+∞-∞+∞-=-++==--=+-=+=+
≥--=-==⎰
⎰⎰
⎰⎰(1)(2) 只有在处有值,但不在积分区间。
(3)(4)(5)00
000
[()()]1j t j t j t e t t t dt e e e ωωωδδ+∞
----∞
⎧⎨
<⎩--=-=-⎰(6)
1-12 绘出下列各时间函数的波形图。
10(10-1)
1
()()11
10(10-1)10(-)(-0.1)1010
0.1t at t a
t t t t δδδδδδ==⋅
=∴=(3) 由尺度特性: 知在处有一个脉冲。
t
2()3()2
u t t π
δ+-(4)
1-13 计算下列积分:
202
020
(2)cos[(3)]cos (3)0 (1)(2)22 ()(2)2
2(2)(2) 2(42)12
j t t t dt t e dt t t dt
t t dt
t t dt
ωδωω
δδδδ-----∞
∞
∞
∞∞
--=+=-+-=+=-+=+=⎰⎰⎰⎰⎰(1)(2),t=-3不在积分区间内。
(3)
2
2
2000
1 (2)()22tu t u t dt tdt t --∞
-===⎰⎰(4)
2220
()|0
t t
t e e t dt e
λ
λλδλλ--∞
--=⎧≥-==⎨
<⎩⎰(5) 00000
2
sin10 '()
10 '()()'()sin10sin10 '()
[]1010cos10sin10 10 t t t
t dt t
t t f t dt f t t d t
t dt t dt t t t
t t δδδ--∞
+∞-∞
∞
==-=-=-=-+⎰⎰⎰(6)由得:()1
1
10 '(1)()t t
t t t d t e u t dt e e e dt
δ-∞
----===∞-=-
==⎰(7)
1-14 已知系统具有初始值0()y t ,其响应()y t 与激励()x t 有如下关系:
0023000001 ()()()()
2 ()()()
3 ()()3()
4 ()3()2()
5 ()()sin 5()
6 ()()t
y t ay t bx t dx t y t y t x t dt
y t y t t x t y t y t x d y t y t t tx t y t y t ττ=+=+=+=+=+=+⎰(), 线性时不变
(), 非线性系统(), 非线性系统,时变系统(), 线性系统,时不变系统
(), 线性系统,时变系统()23()t x t , 线性系统,时变系统
试判断它是线性系统还是非线性系统,并注明其理由。
解:判断是否线性时,应从三个方面来判断:
①可分解性,即系统的输出响应可分解为零输入与零状态响应之和;
②零输入线性,系统的零输入的响应必须对所有的初始状态呈现线性特征;
③零状态线性,系统的零状态响应必须对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
(1)0() () zi zs y y t y bx t ==∴满足可分解性 判别零输入线性: 显然 判别零状态线性: 显然 ∴是线性系统
02 (),() (), y t dx t x t dt
⋅∴()响应满足分解性
零输入为具备线性特性
零状态为不具备线性特性
是非线性系统
∴(3) 满足可分解性,但零输入不符合迭加性是非线性系统
01211220
312331204 (),()() ()2(), ()2()()()() ()2()2[()()]t
t
zs zs t zs y t x t x t y t x d y t x d x t ax t bx t y t x d ax bx ττττ
ττττ===+==+⎰⎰⎰()响应满足分解性
零输入为3具备线性特性 判别零状态线性:
设输入为、时系统的零状态响应分别为 当系统起始状态为时,系统的零状态响应为:
120
12 2()2() ()() t
t
t
zs zs d x d x d ay t by t τ
ττττ
=+=+∴⎰⎰⎰满足零状态线性
三个特性都满足,是线性系统。
005 y y , , zi zs ∴()(t)=y(t )sin5t (t)=tx(t)响应满足分解性零输入为y(t )sin5t 具备线性特性零状态为tx(t)具备线性特性是线性系统,但是时变系统。
02
6 (), 3(), y t t x t ∴()响应满足分解性
零输入为具备线性特性
零状态为具备线性特性,但是时变的是线性时变系统。