坐标系与平面直角坐标系

空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系本篇学习了空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系。

这个个坐标系有时很容易弄混淆！（一）空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心，Z轴指向参考椭球的北极，X轴指向起始子午面与赤道的交点，Y轴位于赤道面上切按右手系于X轴呈90度夹角，某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用如下图所示：（二）大地坐标系大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。

地面点的高程和国家高程基准(1)绝对高程。

地面点沿垂线方向至大地水准面的距离称为绝对高程或称海拔。

过去我国采用青岛验潮站(tide gauge station)1950～1956年观测成果求得的黄海平均海水面作为高程的零点，称为“1956年黄海高程系”(Huanghai height system 1956水准原点高程为72.289m)。

后经复查，发现该高程系的验潮资料时间过短，准确性较差，改用青岛验潮站1950～1979年的观测资料重新推算，并命名为“1985年国家高程基准”（Chinese height datum 1985）。

国家水准原点(leveling origin高程为72.260m)设于青岛市观象山附近，作为我国高程测量的依据。

它的高程值是以“1985年国家高程基准”所确定的平均海水面为零点测算而得。

在使用原“1956年黄海高程系”的高程成果时，应注意将其换算为新的高程基准系统。

(2)相对高程。

地面点沿铅垂线方向至任意假定的水准面的距离称为该点的相对高程，亦称假定高程。

在图l—5中，地面点A和B的相对高程分别为H'A 和H'B 。

高斯平面直角坐标系是数学中一个重要的概念，它与平面直角坐标系有着一定的区别。

下面我们通过以下几个方面来详细分析高斯平面直角坐标系与数学中的平面直角坐标系的区别。

1. 坐标系定义：高斯平面直角坐标系是由德国数学家高斯在复数分析中引入的一种坐标系，它是复平面上的直角坐标系，以复数的实部和虚部作为坐标轴的坐标值。

而数学中的平面直角坐标系是由两条垂直的坐标轴构成的，其中横轴为x轴，纵轴为y轴，以点的横纵坐标来确定点的位置。

2. 坐标轴单位：在高斯平面直角坐标系中，横轴和纵轴的单位都是复数单位i，而在数学中的平面直角坐标系中，横轴和纵轴的单位分别是实数单位和虚数单位。

3. 笛卡尔坐标系变换：在高斯平面直角坐标系中，可以将复平面上的点(x, y)表示为复数z=x+iy的形式，而在数学中的平面直角坐标系中，点(x, y)的坐标可以表示为(x, y)。

4. 应用领域：高斯平面直角坐标系主要应用于复数分析、电磁学、控制论等领域，在这些领域中，复数的运算和分析是非常重要的。

而数学中的平面直角坐标系则主要应用于几何、代数、微积分等数学学科中，其中二维平面上的点的位置关系是重要的研究对象。

5. 图形表示：在高斯平面直角坐标系中，图形通常表示为复平面上的曲线和点，通过复数的实部和虚部来确定图形的位置和形状。

而在数学中的平面直角坐标系中，图形表示为二维平面上的曲线、点和图形，通过点的横纵坐标来确定图形的位置和形状。

总结起来，高斯平面直角坐标系与数学中的平面直角坐标系有着明显的区别，主要体现在坐标系定义、坐标轴单位、笛卡尔坐标系变换、应用领域和图形表示等方面。

了解这些区别有助于我们更深入地理解复数分析和坐标系的概念，同时也有助于我们更好地应用和理解这些概念在不同领域中的具体问题。

高斯平面直角坐标系与数学中的平面直角坐标系之间的区别并不仅仅体现在其定义、坐标轴单位、坐标系转换、应用领域和图形表示方面。

事实上，它们之间的差异还体现在许多其他重要方面，这些区别对于我们理解和应用这两种坐标系都具有重要意义。

平面直角坐标系和直角坐标方程一、平面直角坐标系的定义与构成1.平面直角坐标系是由两条互相垂直的数轴（横轴和纵轴）组成的平面图形。

2.横轴（x轴）与纵轴（y轴）相交于原点（O点），原点是坐标的起点。

3.坐标轴上的点用数值表示，横轴上的点用x表示，纵轴上的点用y表示。

二、坐标值的表示方法1.点的坐标值用一对有序实数（x, y）表示，其中x为横坐标，y为纵坐标。

2.坐标值可以是正数、负数或零。

3.坐标轴上的点，其坐标值有一个为零，另一个为无穷大。

三、坐标系的性质与特点1.坐标系具有原点、轴、象限、坐标轴正方向等基本元素。

2.任意一点在坐标系中的位置都可以用其坐标值（x, y）来表示。

3.坐标系将平面分成四个部分，称为象限，每个象限具有特定的坐标符号特征。

四、直角坐标方程的概念1.直角坐标方程是描述平面直角坐标系中点的位置关系的方程，形式为f(x, y)=0。

2.直角坐标方程可以表示直线、圆、椭圆、双曲线等平面图形。

3.直角坐标方程由函数、变量、常数等数学符号组成。

五、直角坐标方程的分类1.线性方程：最高次项为一次的方程，如ax + by + c = 0。

2.二次方程：最高次项为二次的方程，如ax^2 + bxy + cy^2 + dx + ey +f = 0。

3.三次方程：最高次项为三次的方程，如ax^3 + bx^2y + cx2y2 + dx^3+ ey^3 + f = 0。

4.函数方程：含有自变量和因变量的方程，如y = f(x)。

六、直角坐标方程的求解方法1.线性方程的求解：通过解析式求出x、y的值。

2.二次方程的求解：利用求根公式、配方法、图像法等求解。

3.三次方程的求解：利用代数方法、因式分解、图像法等求解。

4.函数方程的求解：通过代入法、图像法、解析法等求解。

七、直角坐标方程的应用1.描述几何图形的位置和形状。

2.解决实际问题，如物体的运动轨迹、平面几何题等。

3.数学分析、物理学、工程学等领域的建模和求解。

直角坐标系与平面直角坐标系直角坐标系是一种用于描述平面上点的特定坐标系。

它由两条相互垂直的坐标轴组成，通常为水平的x轴和垂直的y轴。

这两条坐标轴相交于一个起点，称为原点，通常表示为O。

平面直角坐标系是直角坐标系在平面上的具体应用。

它由两个相交的直线（坐标轴）及其所有可能的点所组成。

其中一条直线是水平的，叫作x轴；另一条是垂直的，叫作y轴。

x轴和y轴的交点是原点O，原点是该坐标系的起点。

在平面直角坐标系中，每个点都可以用一对有序实数(x, y)来表示。

其中，x是该点在x轴上的坐标，y是该点在y轴上的坐标。

这种表示方式称为点的笛卡尔坐标。

在平面直角坐标系中，x轴和y轴将整个平面分为四个象限，分别命名为第一象限、第二象限、第三象限和第四象限。

第一象限位于x轴和y轴的正方向上方，其中x轴和y轴上的坐标值都为正数。

第二象限位于x轴的负方向上方，y轴的正方向的左侧，x轴上的坐标值为负数，y轴上的坐标值为正数。

第三象限位于x轴和y轴的负方向上方，x轴和y轴上的坐标值都为负数。

第四象限位于x轴的正方向的右侧，y轴的负方向下方，x轴上的坐标值为正数，y轴上的坐标值为负数。

平面直角坐标系广泛应用于数学、物理、工程等领域。

它的使用方便且直观，可以准确描述平面上点的位置和运动。

在平面直角坐标系中，我们可以进行各种运算和推导。

例如，求两点之间的距离可以使用勾股定理来计算。

设A(x1, y1)和B(x2, y2)是平面直角坐标系中的两个点，它们之间的距离d可以通过以下公式求得：d=sqrt((x2-x1)^2+(y2-y1)^2)。

另外，平面直角坐标系也可以用来表示线段、直线、曲线、图形等。

通过设定合适的方程或条件，我们可以在平面直角坐标系中描述并解决各种几何问题。

总结来说，直角坐标系是一种用于描述平面上点位置的坐标系，而平面直角坐标系是直角坐标系在平面上的具体应用。

它们是数学研究和实际问题求解中不可或缺的工具。

坐标系与平面直角坐标系坐标系是数学中用来表示和描述点和线的工具。

它由坐标轴和原点组成，并利用数值组合来确定点的位置。

坐标系被广泛应用于几何学、物理学、经济学等领域，特别是在平面直角坐标系中，它的重要性更加突出。

一、坐标系简介坐标系是由一个或多个坐标轴组成，坐标轴可以是直线、圆、球或其他几何形状。

通常情况下，坐标轴是直线，用来表示一个维度上的数值变化。

一个坐标系可以是一维、二维或多维的，取决于坐标轴的数量。

在平面直角坐标系中，坐标系由水平的x轴和垂直的y轴组成，它们相交于原点O。

二、平面直角坐标系平面直角坐标系是二维坐标系中最基本和最常用的一种。

x轴和y轴分别垂直于彼此，并且固定在平面上。

这一坐标系被广泛应用于几何学、物理学、计算机图形学等领域。

在平面直角坐标系中，每个点的位置可以由一对有序数值(x, y)来表示，其中x表示点在x轴上的位置，y表示点在y轴上的位置。

三、确定坐标点的方法在平面直角坐标系中，确定一个点的位置可以使用两种方法：绝对坐标和相对坐标。

1. 绝对坐标：绝对坐标是指将点的位置与坐标轴上的数值直接对应。

例如，点A的绝对坐标为(3, 4)，表示它在x轴上的位置为3，y轴上的位置为4。

这种方法适用于直接给出点的坐标。

2. 相对坐标：相对坐标是指将点的位置与其他已知点或线段的关系来确定。

例如，点B相对于点A的位置为(-2, 1)，表示它在x轴上的位置比点A小2个单位，在y轴上的位置比点A大1个单位。

这种方法适用于推导和计算点的位置。

使用绝对坐标和相对坐标，我们可以在平面直角坐标系中准确地定位和描述任意点。

四、坐标系的应用平面直角坐标系在许多学科和行业中都起着重要作用。

1. 几何学：平面直角坐标系可以用来研究和解决几何形状的性质和问题。

例如，通过确定点的坐标，我们可以计算两点之间的距离或计算线段的长度。

2. 物理学：平面直角坐标系在物理学中广泛应用于描述和分析物体的运动。

通过在坐标系中绘制物体的位置随时间的变化，我们可以得到物体的速度、加速度等重要信息。

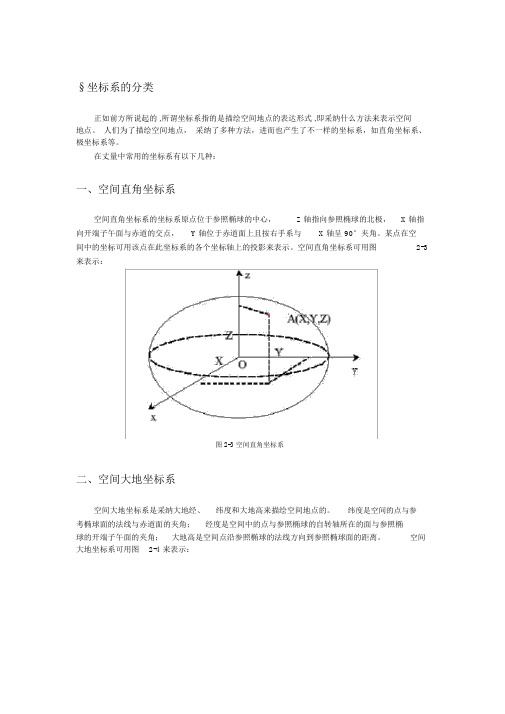
§坐标系的分类正如前方所说起的 ,所谓坐标系指的是描绘空间地点的表达形式 ,即采纳什么方法来表示空间地点。

人们为了描绘空间地点，采纳了多种方法，进而也产生了不一样的坐标系，如直角坐标系、极坐标系等。

在丈量中常用的坐标系有以下几种：一、空间直角坐标系空间直角坐标系的坐标系原点位于参照椭球的中心，Z 轴指向参照椭球的北极，X 轴指向开端子午面与赤道的交点，Y 轴位于赤道面上且按右手系与X 轴呈 90°夹角。

某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用图2-3来表示：图 2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采纳大地经、纬度和大地高来描绘空间地点的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参照椭球的自转轴所在的面与参照椭球的开端子午面的夹角；大地高是空间点沿参照椭球的法线方向到参照椭球面的距离。

空间大地坐标系可用图2-4 来表示：图 2-4 空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换，将空间坐标空间直角坐标或空间大地坐标经过某种数学变换映照到平面上，这类变换又称为投影变换。

投影变换的方法有好多，如横轴墨卡托投影、 UTM 投影、兰勃特投影等。

在我国采纳的是高斯-克吕格投影也称为高斯投影。

UTM 投影和高斯投影都是横轴墨卡托投影的特例，不过投影的个别参数不一样而已。

高斯投影是一种横轴、椭圆柱面、等角投影。

从几何意义上讲，是一种横轴椭圆柱正切投影。

如图左边所示，假想有一个椭圆柱面横套在椭球外面，并与某一子午线相切（此子午线称为中央子午线或轴子午线），椭球轴的中心轴CC’经过椭球中心而与地轴垂直。

高斯投影知足以下两个条件：1、它是正形投影；2、中央子午线投影后应为x 轴，且长度保持不变。

将中央子午线东西各必定经差（一般为 6 度或 3 度）范围内的地域投影到椭圆柱面上，再将此柱面沿某一棱线睁开，便组成了高斯平面直角坐标系，以以下图２－５右边所示。

测量平面直角坐标系与数学坐标系的区别在数学和测量领域中，我们常常会涉及到平面直角坐标系和数学坐标系。

这两个概念很相似，但又有一些不同之处。

本文将深入探讨平面直角坐标系和数学坐标系的区别。

平面直角坐标系平面直角坐标系是一种通过两条互相垂直的数轴构建的坐标系统。

通常，垂直的数轴称为x轴和y轴。

这种坐标系以原点O为起点，x轴向右为正方向，y轴向上为正方向。

在平面直角坐标系中，点的位置由其在x轴和y轴上的坐标确定。

例如，点A的坐标为(x,y)，其中x是A点到原点O的水平距离，y是A点到原点O的垂直距离。

在坐标系中，我们通常使用方括号来表示坐标，即\[x,y\]。

平面直角坐标系常用于表示几何图形的位置和形状。

通过在坐标系中的点之间绘制直线和曲线，我们可以描述各种几何图形，如直线、抛物线、圆等。

此外，平面直角坐标系还用于解决方程组和函数的图像表示。

数学坐标系数学坐标系可以指代不同的坐标系统，如球坐标系、极坐标系等。

这些坐标系可以用来描述平面或空间中的点的位置。

每个数学坐标系都具有其特殊的坐标轴和坐标表示方法。

在球坐标系中，点的位置由距离原点的距离、与正x轴的夹角和与正z轴的夹角来确定。

而在极坐标系中，点的位置由此点到原点的距离和此点与正x轴的夹角确定。

数学坐标系在几何学、物理学、工程学等领域具有广泛的应用。

通过使用不同的数学坐标系，我们可以更方便地研究和解决一些特定的问题，如球面上的运动、天体测量等。

区别与应用尽管平面直角坐标系和数学坐标系都是以坐标为基础的坐标系统，但它们之间存在一些明显的区别。

首先，平面直角坐标系是一种二维坐标系，而数学坐标系可以是二维或三维的。

平面直角坐标系仅包含x轴和y轴，用于描述平面内的点的位置。

而数学坐标系可以包含多个坐标轴，可以用于描述空间中的点的位置。

其次，平面直角坐标系中的坐标表示为\[x,y\]，其中x和y分别表示水平和垂直方向的距离。

而数学坐标系中的坐标表示方式会根据不同的坐标系而有所变化。

认识小学数学中的坐标与平面直角坐标系数学是一门抽象而又实用的学科，其中的坐标与平面直角坐标系是数学中重要的概念之一。

在小学数学中，我们就要开始认识和应用这些概念，它们能够帮助我们更好地理解和解决各种数学问题。

本文将为大家介绍小学数学中的坐标与平面直角坐标系的基本概念和应用。

一、坐标的概念在小学数学中，我们经常会遇到“坐标”的概念。

坐标是用来确定一个点在平面上位置的一对有序数。

通常用括号表示，如(3, 5)。

其中第一个数表示点在平面直角坐标系的横坐标，也称为x坐标；第二个数表示点在平面直角坐标系的纵坐标，也称为y坐标。

举个例子来说明，假设在一个平面上有一个点P，我们想要确定它的位置，可以通过确定它的横坐标和纵坐标来实现。

比如，如果点P 的横坐标为3，纵坐标为5，那么我们可以表示为P(3, 5)。

这样，我们就通过坐标的方式明确了点P在平面上的位置。

二、平面直角坐标系了解了坐标的概念后，我们就需要引入平面直角坐标系。

平面直角坐标系是一个平面上的点与坐标之间的一种对应关系。

它由两条相互垂直的直线构成，一条叫x轴，另一条叫y轴。

交点O称为原点，它的坐标为(0, 0)。

x轴和y轴将平面分成了四个象限，依次从第一象限、第二象限、第三象限和第四象限。

每个象限都有对应的坐标数值范围。

在平面直角坐标系中，点的位置可以通过坐标的正负值来确定。

如坐标(3, 5)表示横坐标为3，纵坐标为5的一个点。

如果横坐标或纵坐标为负数，如(-3, -5)，则表示该点在平面上的位置相对于原点的相应象限。

三、坐标的应用坐标与平面直角坐标系在小学数学中有着广泛的应用。

它们可以帮助我们更好地理解和解决各种数学问题。

1.图形的位置通过坐标和平面直角坐标系，我们可以准确地描述一个图形在平面上的位置。

比如，如果我们想知道某个点在一个图形内部还是外部，可以通过坐标的方式判断。

如果该点的坐标满足某个条件，例如某条直线方程或不等式，那么该点就在图形内部，否则在图形外部。

平面直角坐标系与空间直角坐标系直角坐标系是数学中常用的坐标系统，用于确定点在平面或空间中的位置。

其中，平面直角坐标系是用来描述平面上的点的位置，而空间直角坐标系则是用来描述三维空间中的点的位置。

一、平面直角坐标系平面直角坐标系由两条互相垂直的坐标轴组成，分别为x轴和y轴。

这两条轴相交于原点O，分别向右和上延伸。

在平面直角坐标系中，任意点的位置可以由其在x轴和y轴上的坐标来确定。

标记一个点P在平面直角坐标系上，可以使用一个有序数对(x, y)表示，其中x为点P在x轴上的坐标，y为点P在y轴上的坐标。

例如，若点P的坐标为(3, 4)，则表示点P横坐标为3，纵坐标为4，将点P与(3, 4)这个数对对应起来。

在平面直角坐标系中，直角坐标满足右手定则。

向右和向上的方向分别被定义为正方向，向左和向下的方向分别被定义为负方向。

根据这个规则，可以定义出平移、旋转等运算。

二、空间直角坐标系空间直角坐标系是平面坐标系的扩展，它由三条互相垂直的轴组成，分别为x轴、y轴和z轴。

这三条轴相交于原点O，在各自的轴上分别向右、上和外延伸。

在空间直角坐标系中，任意点的位置可以由其在x 轴、y轴和z轴上的坐标来确定。

和平面直角坐标系类似，标记一个点P在空间直角坐标系上，可以使用一个有序数组(x, y, z)表示，其中x为点P在x轴上的坐标，y为点P在y轴上的坐标，z为点P在z轴上的坐标。

例如，若点P的坐标为(1, 2, 3)，则表示点P横坐标为1，纵坐标为2，高度为3。

在空间直角坐标系中，同样满足右手定则。

向右、向上和指向观察者外延的方向被定义为正方向，向左、向下和指向观察者内缩的方向被定义为负方向。

这样的定义使得在空间直角坐标系中可以进行平移、旋转、缩放等几何变换。

三、平面直角坐标系与空间直角坐标系的区别与联系平面直角坐标系和空间直角坐标系有许多相似之处，但也存在一些显著的不同。

首先，平面直角坐标系只有两个轴，用来描述平面上的点的位置，而空间直角坐标系有三个轴，用来描述三维空间中的点的位置。

平面直角坐标系与数学坐标系的区别我们在学习数学时，对于“平面直角坐标系”和“数学坐标系”并不陌生，而大家最为困惑的是这两种坐标系有什么样的区别呢？下面我就来跟大家分享一下。

一、平面直角坐标系与数学坐标系的联系初中学过的许多几何概念，如点、线、直线、平面、简单几何体等，都是通过建立坐标系来定义的。

在初中教材中，一个完整的公式和定理，往往以建立坐标系的方法为前提的。

如证明：点P（ x， y）的坐标是点P在(x， y)直线上方的横坐标、点P在(x， y)直线下方的纵坐标、点P在(-y， y)直线上方的横坐标、点P在(-y， y)直线下方的纵坐标，还有以点P为原点的与x轴垂直的直线（实线）与y 轴垂直的直线（虚线）所组成的二维坐标系；又如，由点A（ x， y）和点B（ y， x）构成的平面ABCD，称为二维的直角坐标系。

二、平面直角坐标系与数学坐标系的区别从平面直角坐标系到数学坐标系的转化要经过“化实为虚”和“虚实结合”两个步骤。

“化实为虚”就是将数学坐标系的原点移至参照系中心O上。

在建立了平面直角坐标系后，在其中加入直角符号和坐标原点，则可表示成：这里x(0， 0)， y(0， 0)， z(0， 0)，叫做坐标原点，（ a， b， c，d）叫做参考三要素，正x，正y，负z，它们的位置关系为： x(a，b)=y(c， d)=z(e， f)。

若取某一点为坐标原点，则该点的坐标即为平面直角坐标系的坐标，此点的坐标也就是相应的函数值或自变量的取值范围。

当然，把数学坐标系的原点移至参考系中心O上之后，必须保持参考系的选择性。

例如，当取直角坐标系的原点作为参考系中心时，只能用于地球上的任意一点，因为在地球上没有绝对静止的物体存在。

再者，直角坐标系的原点移至参考系中心O上，会使得参考系发生旋转，但在计算机上显示图像时却看不出来。

从平面直角坐标系到数学坐标系，既需要化实为虚，又需要虚实结合。

同时，随着数学知识的不断增长，我们必须用多元化思想对待坐标问题，解决问题时，不能仅满足于一种方法，而应根据问题的不同情况，寻找多种途径解决问题。