四川省2014级普通高中学业水平考试(自扫描)

2014年普通高等学校招生全国统一考试理科参考答案〔四川卷〕一．选择题：本大题共10小题，每一小题5分，共50分．在每一小题给出的四个选项中，只有一个是符合题目要求的。

1．集合2{|20}A x x x =--≤，集合B 为整数集，如此A B ⋂= A ．{1,0,1,2}- B ．{2,1,0,1}-- C ．{0,1} D ．{1,0}- 【答案】A【解析】{|12}A x x =-≤≤，B Z =，故A B ⋂={1,0,1,2}- 2．在6(1)x x +的展开式中，含3x 项的系数为A ．30B ．20C ．15D ．10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3．为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上 所有的点A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度 【答案】A【解析】因为，故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4．假设0a b >>，0c d <<，如此一定有A ．a b c d >B ．a b c d <C ．a b d c >D ．a b d c < 【答案】D【解析】由1100c d d c <<⇒->->，又0a b >>，由不等式性质知：0a b d c ->->，所以a bd c <5．执行如图1所示的程序框图，如果输入的,x y R ∈，如此输出的S 的最大值为A ．0B ．1C ．2D ．3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时，函数2S x y =+的最大值为2，否如此，S 的值为1.6．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能拍甲，如此不同的排法共有 A ．192种 B ．216种 C ．240种 D ．288种 【答案】B【解析】当最左端为甲时，不同的排法共有55A 种；当最左端为乙时，不同的排法共有14C 44A 种。

四川省2014级普通高中学业水平考试历史试题参考答案及评分意见第Ⅰ卷一、选择题(共有30小题，每小题2分，共60分。

每小题中只有一个选项符合题目要求。

不选、多选、错选均不得分)1. B2. A3. A4. D5. B6. C7. A8. C9. D 10. C11. A 12. D 13. B 14. A 15. C 16. B 17. B 18. B 19. A 20. A21. A 22. D 23. B 24. A 25. D 26. B 27. D 28. B 29. B 30. C第Ⅱ卷二、非选择题(本大题有4小题，每小题10分，共40分)31.（10分)(1)立法权、司法权、税收权(或财政权)、军权i(3分，任答三点即可) 《权利法案》。

(2分)(2)君主立宪制。

(2分) 特点：皇帝是实际上的政府首脑，掌握国家最高权力，(1分)议会受制于皇帝和宰相，权力有限；(1分)保留了浓厚的专制残余，专制是实，立宪为虚。

(1分) 32. ( 10 分)(1)上海、广东、天津等沿海地区；(2分。

只答“上海、广东、天津”其中一个地点，给1分；答“沿海地区”而无具体地点同样给2分)使用机器，雇用工人生产。

(2分)(2)原因：１)清政府放宽了对民间设厂的限制(1分)２）民间出现办厂热潮；(1分)３）列强侵略加剧，进一步破坏了中国的自然经济。

(1分)(3)民族资产阶级力量发展，(1分)无产阶级力量壮大(1分)新文化运动发生。

33. (10 分)(1)智者学派，(1分)人是万物的尺度。

(1分)(2)意大利。

(2分)突破上流社会、知识阶层；传播、发展人文主义；为启蒙运动的到来做了思想准备。

(2分，任答两点)(3)理性。

(2分)天赋人权，三权分立，社会契约，人民主权，主权在民等。

(2分，任举2点即可)34.(10分)探究题(1)毕昇。

(1分) 作用：为欧洲走出黑暗的中世纪以及文艺复兴运动的出现准备了条件。

(传播新教的工具和科学复兴的手段)(2分)(2)方面：运载火箭研究领域、空间技术领域、信息技术领域、生物工程领域。

四川省2014级普通高中学业水平考试语文试题时间：120分钟满分：100分第Ⅰ卷（共10分）注意事项：⑴答第Ⅰ卷前，考生务必用蓝、黑墨水钢笔或圆珠笔将自己的姓名、准考证号、考试科目等填写在答题卡上，考试结束时，由监考人员将试卷和答题卡一并收回。

⑵每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试卷上。

一、（6分，每小题2分）1.下列各句中，加点的词语使用不恰当的一句是A.从当当网到亚马逊再到拇指阅读，太多的平台跃跃欲试．．．．地满足了我们的阅读好奇心。

B.我细细观赏它纤细的脉络，嫩芽，以揠苗助长．．．．的心情，巴不得它长得快，长得茂绿。

C.马克思在他研究的每一个领域，都有独到的发现，而且任何一个领域都不是浅尝辄止．．．．。

D.现实生活中动人心弦的场景并不少见，只是我们习以为常．．．．，才没有产生情感的共鸣。

2.下列说法，不正确的一项是A.关于汉字的构成有“六书”说，即象形、指示、会意、形声、转注、假借六种方法。

B.《祝福》选自鲁迅的小说集《呐喊》，作者塑造了祥林嫂这一普通劳动妇女的形象。

C.古人常并用帝王纪年和干支纪年，例如《兰亭集序中》有“永和九年，岁在癸丑”。

D.古人见面常用的礼仪是拜礼和揖礼，前者以叩头跪拜为主，后者以拱手示意为主。

3.下列句子中没有语病的一项是A.在过去三五十年的这三个节目里，如何兴奋了这地方的人，直到现在，还毫无什么变化，仍旧是那地方居民们最有意义的几个日子。

B.鲍勃·迪伦能够获得2016年诺贝尔文学奖，是因为他把美国的乡土气和欧洲的精致风巧妙结合，满足评委对作品文学性要求的原因。

C.若想用自己建筑上的优良传统建设适合新中国的建筑，先得熟悉自己建筑上的“文法”和“词法”，否则是不能写出一篇中国“文章”的。

D.从那时起，“藏獒”开始成为张继科的代号，没有什么比这种看上去沉默迟钝，关键时刻疯狂爆发的动物更能恰如其分的形容他的个性。

四川省高2014级普通高中学业水平考试语文试卷四川省2014级普通高中学业水平考试语文试题，共分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷为选择题，共10分。

考生需在答题卡上填写姓名、准考证号和考试科目等信息。

每小题需用2B铅笔涂黑答案标号，如需更改，需先用橡皮擦干净。

第Ⅱ卷总分为100分。

一、选择题，共6分，每小题2分。

1.以下加点词语使用不恰当的一句是：B.我细细观赏它纤细的脉络，嫩芽，以揠苗助长的心情，巴不得它长得快，长得茂绿。

2.以下说法不正确的一项是：B.《祝福》选自XXX的小说集《呐喊》，作者塑造了XXX这一普通劳动妇女的形象。

3.以下句子中没有语病的一项是：C.若想用自己建筑上的优良传统建设适合新中国的建筑，先得熟悉自己建筑上的“文法”和“词法”，否则是不能写出一篇中国“文章”的。

二、阅读理解，共4分，每小题2分。

游褒禅山记》是XXX的一篇游记。

XXX又称华山，唐代XXX褒在此舍身修行，后葬于此，因而得名“褒禅”。

如今所说的XXX就是褒禅山上的庐冢。

华山洞则是距离XXX东五里的地方，因在华山之阳而得名。

此时，我还有足够的力气进入洞内，火也还能照亮。

⑵于是XXX。

（1分）于是我叹息。

⑶其下平旷，有泉侧出，而记游者甚众，所谓前洞也。

（2分）在山下平坦的地方，有泉水从旁边流出来，游客们经常来这里，这就是所谓的前洞。

2.此所以学者不可以不深思而慎取之也。

这就是为什么学者们不能不深思熟虑地选择的原因。

7.XXX说“此余之所得也”，他有怎样的心得？请简要概括。

XXX在这里表达了他对于研究知识的态度和方法，即需要深思熟虑、慎重选择。

8.下列对本诗的理解和分析，不正确的一项是（）A.不正确。

虽然诗中有“野老”这一自称，但并不代表这是XXX的自称，而是诗中所描写的一个形象。

B.正确。

诗中的“柴门不正”反映了诗人生活的贫困和窘迫。

C.不正确。

诗中并没有出现“片云”自喻的情节。

D.正确。

诗歌后四句的抒情表达了诗人内心的悲哀和无奈。

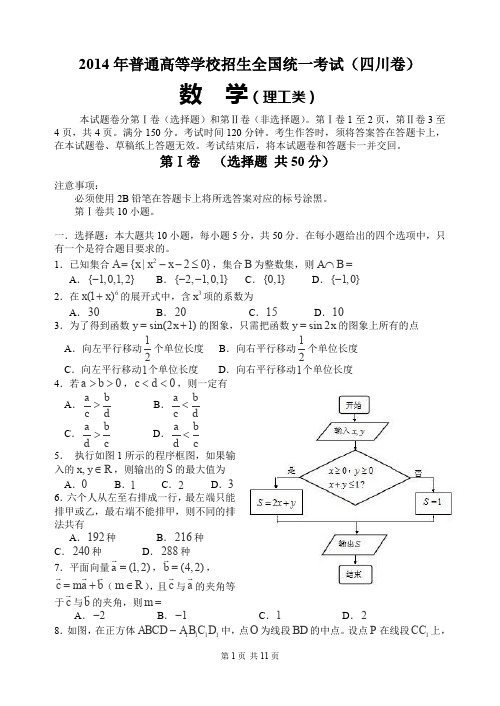
2014年普通高等学校招生全国统一考试（四川卷）数 学（理工类）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）。

第Ⅰ卷1至2页，第Ⅱ卷3至4页，共4页。

满分150分。

考试时间120分钟。

考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效。

考试结束后，将本试题卷和答题卡一并交回。

第Ⅰ卷 （选择题 共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。

第Ⅰ卷共10小题。

一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的。

1．已知集合2{|20}A x x x =--≤，集合B 为整数集，则A B ⋂= A ．{1,0,1,2}- B ．{2,1,0,1}-- C ．{0,1} D ．{1,0}- 2．在6(1)x x +的展开式中，含3x 项的系数为A ．30B ．20C ．15D ．103．为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上所有的点A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度 C ．向左平行移动1个单位长度 D ．向右平行移动1个单位长度 4．若0a b >>，0c d <<，则一定有A ．a b c d >B ．a b c d <C ．a b d c >D ．a b d c<5． 执行如图1所示的程序框图，如果输入的,x y R ∈，则输出的S 的最大值为A ．0B ．1C ．2D ．3 6．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有A ．192种B ．216种C ．240种D ．288种 7．平面向量(1,2)a =，(4,2)b =，c ma b =+（m R ∈），且c 与a 的夹角等于c 与b 的夹角，则m =A ．2-B ．1-C ．1D ．2 8．如图，在正方体1111ABCD A B C D -中，点O 为线段BD 的中点。

!"#!"#!"#$$%&’()*+,-./012%3#&’(【45】(“!”"#$%&“!"”。

!&%(【45】(’&’—(；)&)—*，+—,；*&-—.，/—0。

+&%(【45】(“1234”"567“89:;<=>?@AB C1DEFG%HIJ"KL”，MNO，PQRSTUVWXY。

$&)(【45】(%Z[\“]^”_‘\“abcde”fgXY；’ZhiXj,，jklmkXnopq%；*ZaKrs，s“tu”"‘\“5v”。

,&*(【45】(w：xy，yz。

-&’(【45】(’Z{7|}，“~”；%Z j “ ” }，“ "”， “ ”\ }， \ ；)Z j “C”}， ， “C” }， ；*Z j “ ”}， “ ”， “ ” }，“ ”。

.&)(【45】(“ "6 _ v ，7 j, "”X¡¢5。

/&（#）!"#$%&：“’%()，*+,-./01。

”（23456#7，“8”“-”9:45，;"&,7，<!7）（!）=>?@A，BC=DEFG。

（23456#7，“HI”“C”9:45，;"&,7，<!7）0&（#）$JKLM(%NOPQLR(&STUVWXY（!）《Z[\]》：^_‘abcc，defghLi。

jk1Z lmn，oUpqrst。

《uvwxyz{|》：}~X l ， ? " ；4[ % ， u 。

［ #7（ L67），! 、 、 ， L67。

< -7］#"& ， D 。

（ C D 。

¡¢L£D ¤C b D ）（q31¥¦§。

2014年普通高等学校招生全国统一考试(四川卷)数学(理工类)第Ⅰ卷(选择题 共50分)注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑． 一、选择题．1．已知集合A ＝{x |x 2－x －2≤0}，集合B 为整数集，则A ∩B ＝( ) A ．{－1,0,1,2} B ．{－2，－1,0,1} C ．{0,1} D ．{－1,0}2．在x (1＋x )6的展开式中，含x 3项的系数为( ) A ．30 B ．20 C ．15 D ．103．为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin 2x 的图象上所有的点( ) A ．向左平行移动12 个单位长度B ．向右平行移动12 个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度4．若a >b >0，c <d <0，则一定有( ) A.a c >b d B.a c <b d C.a d >b c D.a d <b c5．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )A ．0B ．1C ．2D ．36．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有( )A ．192种B ．216种C ．240种D ．288种7．平面向量a ＝(1,2)，b ＝(4,2)，c ＝m a ＋b (m ∈R )，且c 与a 的夹角等于c 与b 的夹角，则m ＝( )A ．－2B ．－1C ．1D ．28.如图，在正方体ABCD -A 1B 1C 1D 1中，点O 为线段BD 的中点，设点P 在线段CC 1上，直线OP 与平面A 1BD 所成的角为α，则sin α的取值范围是( )A.⎣⎡⎦⎤33，1B.⎣⎡⎦⎤63，1C.⎣⎡⎦⎤63，223 D.⎣⎡⎦⎤223，19．已知f (x )＝ln(1＋x )－ln(1－x )，x ∈(－1,1)，现有下列命题：①f (－x )＝－f (x )；②f ⎝⎛⎭⎫2x1＋x 2＝2f (x )；③|f (x )|≥2|x |.其中的所有正确命题的序号是( )A ．①②③B ．②③C ．①③D ．①②10．已知F 为抛物线y 2＝x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，＝2(其中O 为坐标原点)，则△ABO 与△AFO 面积之和的最小值是( )A ．2B ．3 C.1728 D.10第Ⅱ卷 (非选择题 共100分)二、填空题．11．复数2－2i1＋i ＝________.12．设f (x )是定义在R 上的周期为2的函数，当x ∈[－1,1)时， f (x )＝⎩⎪⎨⎪⎧－4x 2＋2， －1≤x <0x ， 0≤x <1，则f ⎝⎛⎭⎫32＝________.13.如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67°，30°，此时气球的高是46 m ，则河流的宽度BC 约等于________m ．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80，3≈1.73)14．设m ∈R ，过定点A 的动直线x ＋my ＝0和过定点B 的动直线mx －y －m ＋3＝0交于点P (x ，y )，则|P A |·|PB |的最大值是________．15．以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数φ(x )组成的集合：对于函数φ(x )，存在一个正数M ，使得函数φ(x )的值域包含于区间[－M ，M ]．例如，当φ1(x )＝x 3，φ2(x )＝sin x 时，φ1(x )∈A ，φ2(x )∈B .现有如下命题：①设函数f (x )的定义域为D ，则“f (x )∈A ”的充要条件是“∀b ∈R ，∃a ∈D ，f (a )＝b ”； ②函数f (x )∈B 的充要条件是f (x )有最大值和最小值；③若函数f (x )，g (x )的定义域相同，且f (x )∈A ，g (x )∈B ，则f (x )＋g (x )∉B ； ④若函数f (x )＝a ln(x ＋2)＋xx 2＋1(x >－2，a ∈R )有最大值，则f (x )∈B .其中的真命题有________．(写出所有真命题的序号)三、解答题．16．(本小题满分12分) 已知函数f (x )＝sin ⎝⎛⎭⎫3x ＋π4. (1)求f (x )的单调递增区间；(2)若α是第二象限角，f ⎝⎛⎭⎫α3＝45cos ⎝⎛⎭⎫α＋π4cos 2α，求cos α－sin α的值．17．(本小题满分12分)一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分(即获得－200分)．设每次击鼓出现音乐的概率为12，且各次击鼓出现音乐相互独立．(1)设每盘游戏获得的分数为X ，求X 的分布列； (2)玩三盘游戏，至少有一盘出现音乐的概率是多少？(3)玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．18．(本小题满分12分)三棱锥A -BCD 及其侧视图、俯视图如图所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP .(1)证明：P 是线段BC 的中点； (2)求二面角A -NP -M 的余弦值．19．(本小题满分12分)设等差数列{a n }的公差为d ，点(a n ，b n )在函数f (x )＝2x 的图象上(n ∈N *)． (1)若a 1＝－2，点(a 8,4b 7)在函数f (x )的图象上，求数列{a n }的前n 项和S n ；(2)若a 1＝1，函数f (x )的图象在点(a 2，b 2)处的切线在x 轴上的截距为2－1ln 2，求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .20．(本小题满分13分)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．(1)求椭圆C 的标准方程；(2)设F 为椭圆C 的左焦点，T 为直线x ＝－3上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q .①证明：OT 平分线段PQ (其中O 为坐标原点)； ②当|TF ||PQ |最小时，求点T 的坐标．21．(本小题满分14分)已知函数f (x )＝e x －ax 2－bx －1，其中a ，b ∈R ，e ＝2.718 28…为自然对数的底数． (1)设g (x )是函数f (x )的导函数，求函数g (x )在区间[0,1] 上的最小值； (2)若f (1)＝0，函数f (x )在区间(0,1)内有零点，求a 的取值范围．答案第Ⅰ卷(选择题 共50分)注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑．一、选择题．1．解析：选A 因为A ＝{x |－1≤x ≤2}，B ＝Z ，故A ∩B ＝{－1,0,1,2}．2．解析：选C 只需求(1＋x )6的展开式中含x 2项的系数即可，而含x 2项的系数为C 26＝15，故选C.3．解析：选A 因为y ＝sin(2x ＋1)＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋12，故可由函数y ＝sin 2x 的图象上所有的点向左平行移动12个单位长度得到，选A.4．解析：选D 由c <d <0⇒－1d >－1c >0，又a >b >0，故由不等式性质，得－a d >－bc >0，所以a d <bc，选D. 5．解析：选C 当⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1时，由线性规划的图解法知，目标函数S ＝2x ＋y 的最大值为2，否则，S 的值为1.所以输出的S 的最大值为2.6．解析：选B 当最左端排甲时，不同的排法共有A 55种；当最左端排乙时，甲只能排在中间四个位置之一，则不同的排法共有C 14A 44种．故不同的排法共有A 55＋C 14A 44＝9×24＝216种．7．解析：选D 解法一 由已知得c ＝(m ＋4,2m ＋2)，因为cos 〈c ，a 〉＝c ·a|c |·|a |，cos 〈c ，b 〉＝c ·b |c |·|b |，所以c ·a |c |·|a |＝c ·b|c |·|b |，又由已知得|b |＝2|a |，所以2c ·a ＝c ·b ，即2[(m ＋4)＋2(2m ＋2)]＝4(m ＋4)＋2(2m ＋2)，解得m ＝2.解法二 易知c 是以m a ，b 为邻边的平行四边形的对角线向量，因为c 与a 的夹角等于c 与b 的夹角，所以该平行四边形为菱形，又由已知得|b |＝2|a |，故m ＝2.8.解析：选B 易证AC 1⊥平面A 1BD ，当点P 在线段CC 1上从C 运动到C 1时，直线OP 与平面A 1BD 所成的角α的变化情况：∠AOA 1→π2→∠C 1OA 1点P 为线段CC 1的中点时，α＝π2，由于sin ∠AOA 1＝63，sin ∠C 1OA 1＝223>63，sin π2＝1，所以sin α的取值范围是⎣⎡⎦⎤63，1. 9．解析：选A f (－x )＝ln(1－x )－ln(1＋x )＝－f (x )，故①正确；因为f (x )＝ln(1＋x )－ln(1－x )＝ln 1＋x 1－x ，又当x ∈(－1,1)时，2x 1＋x 2∈(－1,1)，所以f ⎝⎛⎭⎫2x 1＋x 2＝ln 1＋2x1＋x 21－2x 1＋x 2＝ln ⎝ ⎛⎭⎪⎫1＋x 1－x 2＝2ln 1＋x 1－x ＝2f (x )，故②正确；当x ∈[0,1)时，|f (x )|≥2|x |⇔f (x )－2x ≥0，令g (x )＝f (x )－2x ＝ln(1＋x )－ln(1－x )－2x (x ∈[0,1))，因为g ′(x )＝11＋x ＋11－x －2＝2x 21－x 2>0，所以g (x )在区间[0,1)上单调递增，g (x )＝f (x )－2x ≥g (0)＝0，即f (x )≥2x ，又f (x )与y ＝2x 都为奇函数，所以|f (x )|≥2|x |成立，故③正确，故选A.10．解析：选B 设点A (x 1，y 1)，B (x 2，y 2)(不妨假设y 1>0，y 2<0)，直线AB 的方程为x＝ty ＋m ，且直线AB 与x 轴的交点为M (m,0)．由⎩⎪⎨⎪⎧x ＝ty ＋my 2＝x 消去x ，得y 2－ty －m ＝0，所以y 1y 2＝－m .又＝2，所以x 1x 2＋y 1y 2＝2，(y 1y 2)2＋y 1y 2－2＝0，因为点A ，B 在抛物线上且位于x 轴的两侧，所以y 1y 2＝－2，故m ＝2.又F ⎝⎛⎭⎫14，0，于是S △ABO ＋S △AFO ＝12×2×(y 1－y 2)＋12×14×y 1＝98y 1＋2y 1≥298y 1×2y 1＝3，当且仅当98y 1＝2y 1，即y 1＝43时取“＝”，所以△ABO 与△AFO 面积之和的最小值是3.第Ⅱ卷 (非选择题 共100分)二、填空题．11．解析：2－2i 1＋i ＝2(1－i )2(1＋i )(1－i )＝(1－i)2＝－2i.答案：－2i12．解析：f ⎝⎛⎭⎫32＝f ⎝⎛⎭⎫2－12＝f ⎝⎛⎭⎫－12＝－4×⎝⎛⎭⎫－122＋2＝1. 答案：113. 解析：过A 作BC 边上的高AD ，D 为垂足．在Rt △ACD 中，AC ＝92，在△ABC 中，由正弦定理，得BC ＝AC sin ∠ABC×sin ∠BAC ＝92sin 67°×sin 37°≈920.92×0.60＝60(m)．答案：6014．解析：易求定点A (0,0)，B (1,3)．当P 与A 和B 均不重合时，不难验证P A ⊥PB ，所以|P A |2＋|PB |2＝|AB |2＝10，所以|P A |·|PB |≤|P A |2＋|PB |22＝5(当且仅当|P A |＝|PB |＝5时，等号成立)，当P 与A 或B 重合时，|P A |·|PB |＝0，故|P A |·|PB |的最大值是5.答案：515．解析：对于①，根据题中定义，f (x )∈A ⇔函数y ＝f (x )，x ∈D 的值域为R ，由函数值域的概念知，函数y ＝f (x )，x ∈D 的值域为R ⇔∀b ∈R ，∃a ∈D ，f (a )＝b ，所以①正确；对于②，例如函数f (x )＝⎝⎛⎭⎫12|x |的值域(0,1]包含于区间[－1,1]，所以f (x )∈B ，但f (x )有最大值1，没有最小值，所以②错误；对于③，若f (x )＋g (x )∈B ，则存在一个正数M 1，使得函数f (x )＋g (x )的值域包含于区间[－M 1，M 1]，所以－M 1≤f (x )＋g (x )≤M 1，由g (x )∈B 知，存在一个正数M 2，使得函数g (x )的值域包含于区间[－M 2，M 2]，所以－M 2≤g (x )≤M 2，亦有－M 2≤－g (x )≤M 2，两式相加得－(M 1＋M 2)≤f (x )≤M 1＋M 2，于是f (x )∈B ，与已知“f (x )∈A ”矛盾，故f (x )＋g (x )∉B ，即③正确；对于④，如果a >0，那么x →＋∞，f (x )→＋∞，如果a <0，那么x →－2，f (x )→＋∞，所以f (x )有最大值，必须a ＝0，此时f (x )＝xx 2＋1在区间(－2，＋∞)上，有－12≤f (x )≤12，所以f (x )∈B ，即④正确，故填①③④.答案：①③④ 三、解答题．16．解：(1)因为函数y ＝sin x 的单调递增区间为－π2＋2k π，π2＋2k π，k ∈Z ，由－π2＋2k π≤3x ＋π4≤π2＋2k π，k ∈Z ，得－π4＋2k π3≤x ≤π12＋2k π3，k ∈Z .所以，函数f (x )的单调递增区间为－π4＋2k π3，π12＋2k π3，k ∈Z .(2)由已知，有sin ⎝⎛⎭⎫α＋π4＝45cos ⎝⎛⎭⎫α＋π4(cos 2α－sin 2α)， 所以sin αcos π4＋cos αsin π4＝45cos αcos π4－sin α·sin π4(cos 2α－sin 2α)，即sin α＋cos α＝45(cos α－sin α)2(sin α＋cos α)．当sin α＋cos α＝0时，由α是第二象限角，知α＝3π4＋2k π，k ∈Z .此时，cos α－sin α＝－ 2.当sin α＋cos α≠0时，有(cos α－sin α)2＝54.由α是第二象限角，知cos α－sin α<0，此时cos α－sin α＝－52. 综上所述，cos α－sin α＝－2或－52. 17．解：(1)X 可能的取值为：10,20,100，－200.根据题意，有P (X ＝10)＝C 13×⎝⎛⎭⎫121×⎝⎛⎭⎫1－122＝38， P (X ＝20)＝C 23×⎝⎛⎭⎫122×⎝⎛⎭⎫1－121＝38， P (X ＝100)＝C 33×⎝⎛⎭⎫123×⎝⎛⎭⎫1－120＝18，P (X ＝－200)＝C 03×⎝⎛⎭⎫120×⎝⎛⎭⎫1－123＝18. 所以X 的分布列为(2)设“第i 盘游戏没有出现音乐”为事件A i (i ＝1,2,3)，则P (A 1)＝P (A 2)＝P (A 3)＝P (X ＝－200)＝18.所以，“三盘游戏中至少有一次出现音乐”的概率为1－P (A 1A 2A 3)＝1－⎝⎛⎭⎫183＝1－1512＝511512. 因此，玩三盘游戏至少有一盘出现音乐的概率是511512.(3)X 的数学期望为EX ＝10×38＋20×38＋100×18－200×18＝－54.这表明，获得分数X 的均值为负，因此，多次游戏之后分数减少的可能性更大． 18．解：(1)如图，取BD 中点O ，连接AO ，CO .由侧视图及俯视图知，△ABD ，△BCD 均为正三角形， 因此AO ⊥BD ，OC ⊥BD .因为AO ，OC ⊂平面AOC ，且AO ∩OC ＝O ， 所以BD ⊥平面AOC .又因为AC ⊂平面AOC ，所以BD ⊥AC . 取BO 的中点H ，连接NH ，PH .又M ，N 分别为线段AD ，AB 的中点，所以NH ∥AO ，MN ∥BD . 因为AO ⊥BD ，所以NH ⊥BD . 因为MN ⊥NP ，所以NP ⊥BD .因为NH ，NP ⊂平面NHP ，且NH ∩NP ＝N ，所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ，所以BD ⊥HP .又OC ⊥BD ，HP ⊂平面BCD ，OC ⊂平面BCD ，所以HP ∥OC . 因为H 为BO 中点， 故P 为BC 中点．(2)法一：如图，作NQ ⊥AC 于Q ，连接MQ .由(1)知，NP ∥AC ， 所以NQ ⊥NP .因为MN ⊥NP ，所以∠MNQ 为二面角A -NP -M 的一个平面角． 由(1)知，△ABD ，△BCD 为边长为2的正三角形，所以AO ＝OC ＝ 3. 由俯视图可知，AO ⊥平面BCD .因为OC ⊂平面BCD ，所以AO ⊥OC ，因此在等腰Rt △AOC 中，AC ＝6， 作BR ⊥AC 于R .在△ABC 中，AB ＝BC ，所以BR ＝AB 2－⎝⎛⎭⎫AC 22＝102. 因为在平面ABC 内，NQ ⊥AC ，BR ⊥AC ，所以NQ ∥BR . 又因为N 为AB 的中点，所以Q 为AR 的中点， 因此NQ ＝BR 2＝104.同理，可得MQ ＝104.所以在等腰△MNQ 中，cos ∠MNQ ＝MN 2NQ ＝BD 4NQ ＝105.故二面角A -NP -M 的余弦值是105. 法二：由俯视图及(1)可知，AO ⊥平面BCD .因为OC ，OB ⊂平面BCD ，所以AO ⊥OC ，AO ⊥OB . 又OC ⊥OB ，所以直线OA ，OB ，OC 两两垂直． 如图，以O 为坐标原点，以的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O -xyz .则A (0,0，3)，B (1,0,0)，C (0，3，0)，D (－1,0,0)． 因为M ，N 分别为线段AD ，AB 的中点， 又由(1)知，P 为线段BC 的中点，所以M ⎝⎛⎭⎫－12，0，32，N ⎝⎛⎭⎫12，0，32，P ⎝⎛⎭⎫12，32，0.从而⎩⎪⎨⎪⎧x 2＝0，32y 2－32z 2＝0. 取z 2＝1，所以n 2＝(0,1,1)． 设二面角A -NP -M 的大小为θ.则cos θ＝⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝⎪⎪⎪⎪⎪⎪(3，1，1)·(0，1，1)5×2＝105. 故二面角A -NP -M 的余弦值是105. 19．解：(1)由已知，b 7＝2a 7，b 8＝2a 8＝4b 7，有2a 8＝4×2a 7＝2a 7＋2， 解得d ＝a 8－a 7＝2.所以，S n ＝na 1＋n (n －1)2d ＝－2n ＋n (n －1)＝n 2－3n .(2)函数f (x )＝2x 在(a 2，b 2)处的切线方程为y －2a 2＝(2a 2ln 2)(x －a 2)， 它在x 轴上的截距为a 2－1ln 2.由题意知，a 2－1ln 2＝2－1ln 2，解得a 2＝2.所以，d ＝a 2－a 1＝1.从而a n ＝n ，b n ＝2n ，所以T n ＝12＋222＋323＋…＋n －12n －1＋n 2n ， 2T n ＝11＋22＋322＋…＋n 2n －1. 因此，2T n －T n ＝1＋12＋122＋…＋12n －1－n 2n ＝2－12n －1－n 2n ＝2n ＋1－n －22n . 所以，T n ＝2n ＋1－n －22n . 20．解：(1)由已知可得⎩⎨⎧ a 2＋b 2＝2b ，2c ＝2a 2－b 2＝4，解得a 2＝6，b 2＝2，所以椭圆C 的标准方程是x 26＋y 22＝1. (2)①由(1)可得，F 的坐标是(－2,0)，设T 点的坐标为(－3，m )，则直线TF 的斜率k TF ＝m －0－3－(－2)＝－m . 当m ≠0时，直线PQ 的斜率k PQ ＝1m，直线PQ 的方程是x ＝my －2. 当m ＝0时，直线PQ 的方程是x ＝－2，也符合x ＝my －2的形式．设P (x 1，y 1)，Q (x 2，y 2)，将直线PQ 的方程与椭圆C 的方程联立，得⎩⎪⎨⎪⎧ x ＝my －2，x 26＋y 22＝1， 消去x ，得(m 2＋3)y 2－4my －2＝0，其判别式Δ＝16m 2＋8(m 2＋3)>0.所以y 1＋y 2＝4m m 2＋3，y 1y 2＝－2m 2＋3， x 1＋x 2＝m (y 1＋y 2)－4＝－12m 2＋3. 所以PQ 的中点M 的坐标为⎝ ⎛⎭⎪⎫－6m 2＋3，2m m 2＋3， 所以直线OM 的斜率k OM ＝－m 3. 又直线OT 的斜率k OT ＝－m 3，所以点M 在直线OT 上， 因此OT 平分线段PQ .②由①可得，|TF |＝m 2＋1，|PQ |＝(x 1－x 2)2＋(y 1－y 2)2＝(m 2＋1)[(y 1＋y 2)2－4y 1y 2] ＝(m 2＋1)⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫4m m 2＋32－4·－2m 2＋3＝24(m 2＋1)m 2＋3.所以|TF ||PQ |＝124·(m 2＋3)2m 2＋1＝124·⎝⎛⎭⎫m 2＋1＋4m 2＋1＋4≥124·(4＋4)＝33. 当且仅当m 2＋1＝4m 2＋1，即m ＝±1时，等号成立，此时|TF ||PQ |取得最小值． 所以当|TF ||PQ |最小时，T 点的坐标是(－3,1)或(－3，－1)． 21．解：(1)由f (x )＝e x －ax 2－bx －1，有g (x )＝f ′(x )＝e x －2ax －b ，所以g ′(x )＝e x －2a .因此，当x ∈[0,1]时，g ′(x )∈[1－2a ，e －2a ]．当a ≤12时，g ′(x )≥0，所以g (x )在[0,1]上单调递增． 因此g (x )在[0,1]上的最小值是g (0)＝1－b ；当a ≥e 2时，g ′(x )≤0，所以g (x )在[0,1]上单调递减， 因此g (x )在[0,1]上的最小值是g (1)＝e －2a －b ；当12<a <e 2时，令g ′(x )＝0，得x ＝ln(2a )∈(0,1)． 所以函数g (x )在区间[0，ln(2a )]上单调递减，在区间(ln(2a )，1]上单调递增． 于是，g (x )在[0,1]上的最小值是g (ln(2a ))＝2a －2a ln(2a )－b .综上所述，当a ≤12时，g (x )在[0,1]上的最小值是g (0)＝1－b ； 当12<a <e 2时，g (x )在[0,1]上的最小值是g (ln(2a ))＝2a －2a ln(2a )－b ； 当a ≥e 2时，g (x )在[0,1]上的最小值是g (1)＝e －2a －b . (2)设x 0为f (x )在区间(0,1)内的一个零点，则由f (0)＝f (x 0)＝0可知，f (x )在区间(0，x 0)上不可能单调递增，也不可能单调递减．则g (x )不可能恒为正，也不可能恒为负．故g (x )在区间(0，x 0)内存在零点x 1.同理g (x )在区间(x 0,1)内存在零点x 2.所以g (x )在区间(0,1)内至少有两个零点．由(1)知，当a ≤12时，g (x )在[0,1]上单调递增，故g (x )在(0,1)内至多有一个零点． 当a ≥e 2时，g (x )在[0,1]上单调递减，故g (x )在(0,1)内至多有一个零点． 所以12<a <e 2. 此时g (x )在区间[0，ln(2a )]上单调递减，在区间(ln(2a )，1]上单调递增． 因此x 1∈(0，ln(2a )]，x 2∈(ln(2a )，1)，必有g (0)＝1－b >0，g (1)＝e －2a －b >0. 由f (1)＝0有a ＋b ＝e －1<2，有g (0)＝1－b ＝a －e ＋2>0，g (1)＝e －2a －b ＝1－a >0.解得e －2<a <1.当e －2<a <1时，g (x )在区间[0,1]内有最小值g (ln(2a ))．若g (ln(2a ))≥0，则g (x )≥0(x ∈[0,1])，从而f(x)在区间[0,1]上单调递增，这与f(0)＝f(1)＝0矛盾，所以g(ln(2a))<0.又g(0)＝a－e＋2>0，g(1)＝1－a>0，故此时g(x)在(0，ln(2a))和(ln(2a)，1)内各只有一个零点x1和x2.由此可知f(x)在[0，x1]上单调递增，在(x1，x2)上单调递减，在[x2,1]上单调递增．所以f(x1)>f(0)＝0，f(x2)<f(1)＝0，故f(x)在(x1，x2)内有零点．综上可知，a的取值范围是(e－2,1)．。

绝密·启用前 2014年6月20日14:00~15:00本试题由四川省三台中学王良勇老师收集整理。

一个字一个字的打的哟！！！！！四川省2014年6月普通高中学业水平考试通用技术试卷（考试时间：60分钟；满分：100分）本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷为选择题，第Ⅱ卷为非选择题。

第Ⅰ卷 选择题（共60分）本部分共20小题，，每小题3分，共60分。

从每小题列出的四个备选项中选出最符合题目要求的一项。

1.短短几十年时间，打印机经历了针式打印机、喷墨打印机、激光打印机、3D打印机的发展历程。

下列说法不正确的是A．技术源于人类的需求和愿望B．技术的发展离不开设计者精心的设计C．设计需要不断改进D．3D打印技术已完全取代其它打印技术2.食品添加剂的使用推动了食品工业的发展，但也带来食品的一些安全隐患。

这说明技术的应用具有 A．创新性　B. 两面性　C. 综合性 D. 实践性3．下列选项主要为科学活动的是A．广义相对论的发现 B．“辽宁号”航母战斗群的形成C．移动信息平台的建立 D．小木凳的制作4．轿车座椅靠背的倾斜度能够调节，这主要体现了人机关系的目标是A．舒适 B．安全 C．健康 D．高效5．如右图所示，某公司利用单片机技术设计制作了一款有利于青少年学习机器人技术的小车。

该设计可以申请A．发明专利 B．实用新型专利C．著作权 D．商标权6．下列关于标准件的描述，错误是的A．标准件是统一了技术要求的零部件　B．标准件的使用可以降低产品成本C．标准件质量性能可靠，具有互换性D．经国家检验合格的零部件都属于标准件7．某公司生产的“老人代步车”，其设计未采用标准化技术。

该产品的设计违背了A．经济性原则 B．创新性原则C．技术规范性原则D．可持续发展原则8．微波炉的产品说明书内容可以不包括A．使用说明 B．维护与保养C．生产工艺 D．安全注意事项9．小刚对如右图所示的凳子进行下列技术测试，其中最不合理的是A．在凳子上逐步加上适当重物，测试其强度B．将凳子放在平整处，用手前后左右摇晃，测试其稳定性C．坐在凳子上体验，测试其舒适性D．用木工锯锯凳子，直到凳子被锯开，测试其材料性能10.如下图所示的零部件对应的主视图是11．小龙要在木工板上钻孔，需要用到的工具是12．下列尺寸标注不正确的是13．如右图所示，赵州桥是中国现存最著名的古代石拱桥。

四川高中普通高中学业水平考试四川高中普通高中学业水平考试，简称四川高中会考，是对四川省普通高中学生学业成果的重要检验。

该考试旨在评估学生在各学科领域的知识掌握程度、应用能力和综合素质，帮助学生检验自身学业水平，为后续学习和发展奠定基础。

四川高中会考涵盖了语文、数学、英语、物理、化学、生物、政治、历史、地理、体育与健康、音乐、美术等学科。

考试内容紧密结合教材，注重考察学生对基础知识的掌握和基本技能的应用。

通过考试，学生可以了解自己在各学科中的优势和不足，为今后的学习制定更有针对性的计划。

四川高中会考分为两个阶段：第一阶段为学科基础知识测试，主要考察学生对各学科基本概念、原理的理解和运用；第二阶段为学科能力测试，着重考察学生在实际问题中运用知识解决问题的能力。

两个阶段均采用闭卷笔试形式，考试时间为150分钟。

参加四川高中会考的学生需具备较强的学术能力和心理素质。

为了取得理想成绩，学生在备考过程中需系统复习各学科知识点，强化基础知识和基本技能训练，提高自身综合素质。

此外，培养解题技巧、增强应试心理素质同样至关重要。

四川高中会考成绩对学生的学业发展和综合素质评价具有重要参考价值。

高中学校、高校和社会各界对学生学业水平考试的成绩给予高度重视。

学生通过努力提高会考成绩，有助于进入理想高中和大学，为实现人生目标奠定坚实基础。

总之，四川高中普通高中学业水平考试是对学生学业成果的全面检验。

学生应把握考试机会，展示自身学术实力，为未来发展铺平道路。

同时，考试也为学生提供了自我认知、调整学习策略的平台，有助于提高个人综合素质。

在我国教育体系的背景下，四川高中会考对于培养全面发展的人才具有重要意义。