基本和常用逻辑运算

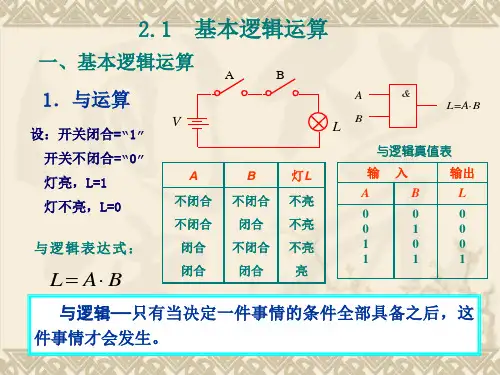
与基本逻辑运算和常见逻辑运算相对应,
基本逻辑运算包括与、或、非三种运算，常见逻辑运算包括条件、双条件、蕴含等运算。

下面是它们之间的对应关系：
- 与运算对应常见逻辑运算中的条件运算（→），即p 且 q（p and q）对应p→q；
- 或运算对应常见逻辑运算中的双条件运算（↔），即p 或 q （p or q）对应p↔q；
- 非运算对应常见逻辑运算中的否定运算（¬），即非p（not p）对应 ¬p。

同时，还有以下常见逻辑运算的对应关系：
- 异或运算对应常见逻辑运算中的异或运算（⊕），即p 异或
q（p xor q）；
- 蕴含运算对应常见逻辑运算中的蕴含运算（⇒），即p 蕴含
q（p ⇒ q）；
- 等价运算对应常见逻辑运算中的等价运算（≡），即p 等价
于 q（p ≡ q）。

这些逻辑运算在数理逻辑、计算机科学、哲学和数学等领域中具有重要的应用。

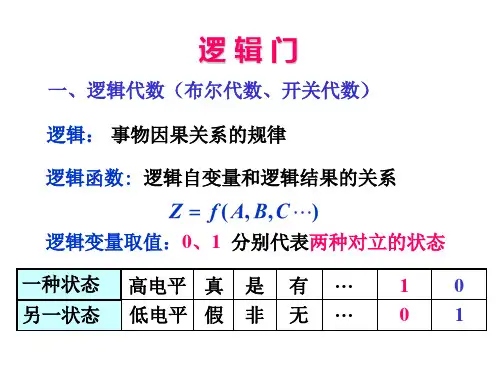
第二节算术运算和逻辑运算一、二进制的算术运算1、加法运算规则：0+0=0 0+1=1 1+0=1 1+1=102、减法运算规则：0-0=0 0-1=1（向高位借1） 1-0=1 1-1=03、乘法运算规则：0×0=0 0×1=0 1×0=0 1×1=1二、逻辑运算1、基本运算① 逻辑乘，也称“与”运算，运算符为“·”或“∧”0·0=0 0·1=0 1·0=0 1·1=1使用逻辑变量时，A·B可以写成AB② 逻辑加，也乘“或”运算，运算符为“+”或“∨”0+0=0 0+1=1 1+0=1 1+1=1③ 逻辑非，也称“反”运算，运算符是在逻辑值或变量符号上加“—”0 = 1 1 = 02、常用运算异或运算：A⊕B = A·B＋A·B2、基本公式① 0，1律A·0=0A·1=AA＋0=AA＋1=1② 交换律A＋B=B＋AA·B=B·A③ 结合律A＋B＋C =（A＋B）＋C = A＋（B＋C）A·B·C =（A·B）·C = A·（B·C）④ 分配律A·（B＋C）= A·B ＋A·C⑤ 重叠律A＋A＋...＋A = AA·A·...·A = A⑥ 互补律A + A = 1 A·A = 0⑦ 吸收律A＋A·B = A A·（A＋B） = AA＋A·B = A＋B A·（A＋B） = A·B⑧ 对合律对一个逻辑变量两次取反仍是它本身⑨ 德·摩根定理A+B = A·BA·B = A＋B三、逻辑代数的应用1、逻辑表达式化简例如： F = A·B＋A·B＋A·B=A·B＋A（B＋B）（利用分配律）=A·B＋A （利用互补律以及0，1律） = A＋B （利用吸收律）2、对指定位进行运算，假设变量A有八位，内容是d7d6d5d4d3d2d1d0① 将变量A的d5位清零A·（11011111）→A② 将变量A的各位置1A＋（11111111）→A。

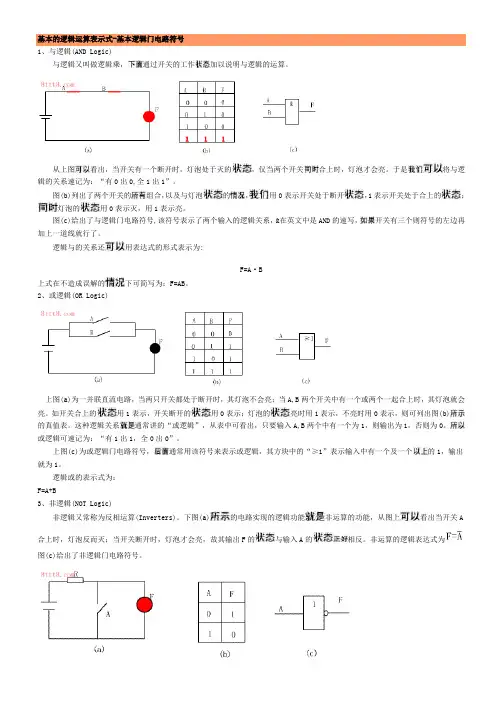
基本的逻辑运算表示式-基本逻辑门电路符号1、与逻辑(AND Logic)与逻辑又叫做逻辑乘，通过开关的工作加以说明与逻辑的运算。

从上图看出，当开关有一个断开时，灯泡处于灭的，仅当两个开关合上时，灯泡才会亮。

于是将与逻辑的关系速记为：“有0出0,全1出1”。

图(b)列出了两个开关的组合，以及与灯泡的，用0表示开关处于断开，1表示开关处于合上的；灯泡的用0表示灭，用1表示亮。

图(c)给出了与逻辑门电路符号,该符号表示了两个输入的逻辑关系，&在英文中是AND的速写，开关有三个则符号的左边再加上一道线就行了。

逻辑与的关系还用表达式的形式表示为:F=A·B上式在不造成误解的下可简写为：F=AB。

2、或逻辑(OR Logic)上图(a)为一并联直流电路，当两只开关都处于断开时，其灯泡不会亮；当A,B两个开关中有一个或两个一起合上时，其灯泡就会亮。

如开关合上的用1表示，开关断开的用0表示；灯泡的亮时用1表示，不亮时用0表示，则可列出图(b)的真值表。

这种逻辑关系通常讲的“或逻辑”，从表中可看出，只要输入A,B两个中有一个为1，则输出为1，否则为0。

或逻辑可速记为：“有1出1，全0出0”。

上图(c)为或逻辑门电路符号，通常用该符号来表示或逻辑，其方块中的“≥1”表示输入中有一个及一个的1，输出就为1。

逻辑或的表示式为：F=A+B3、非逻辑(NOT Logic)非逻辑又常称为反相运算(Inverters)。

下图(a)的电路实现的逻辑功能非运算的功能，从图上看出当开关A 合上时，灯泡反而灭；当开关断开时，灯泡才会亮，故其输出F的与输入A的相反。

非运算的逻辑表达式为图(c)给出了非逻辑门电路符号。

复合逻辑运算在数字系统中，除了与运算、或运算、非运算之外，使用的逻辑运算还有是通过这三种运算派生出来的运算，这种运算通常称为复合运算，的复合运算有：与非、或非、与或非、同或及异或等。

4、与非逻辑(NAND Logic)与非逻辑是由与、非逻辑复合而成的。

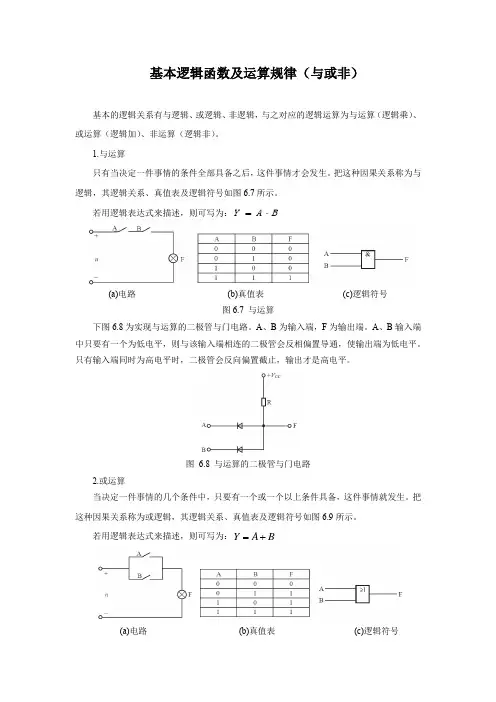
基本逻辑函数及运算规律（与或非）基本的逻辑关系有与逻辑、或逻辑、非逻辑，与之对应的逻辑运算为与运算（逻辑乘）、或运算（逻辑加）、非运算（逻辑非）。

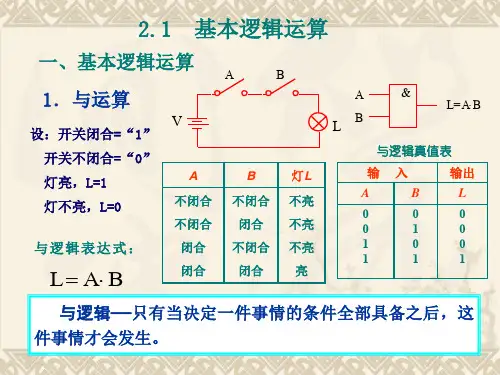
1.与运算只有当决定一件事情的条件全部具备之后，这件事情才会发生。

把这种因果关系称为与逻辑，其逻辑关系、真值表及逻辑符号如图6.7所示。

若用逻辑表达式来描述，则可写为：B A Y ⋅=(a)电路 (b)真值表 (c)逻辑符号图6.7 与运算下图6.8为实现与运算的二极管与门电路。

A 、B 为输入端，F 为输出端。

A 、B 输入端中只要有一个为低电平，则与该输入端相连的二极管会反相偏置导通，使输出端为低电平。

只有输入端同时为高电平时，二极管会反向偏置截止，输出才是高电平。

图 6.8 与运算的二极管与门电路2.或运算当决定一件事情的几个条件中，只要有一个或一个以上条件具备，这件事情就发生。

把这种因果关系称为或逻辑，其逻辑关系、真值表及逻辑符号如图6.9所示。

若用逻辑表达式来描述，则可写为：B A Y +=(a)电路 (b)真值表 (c)逻辑符号图6.9 或运算下图6.10为实现与运算的二极管或门电路。

A、B为输入端，F为输出端。

A、B输入端中只要有一个为高电平，则输出端为高电平。

只有当A、B同时为低电平，输出端才会输出低电平。

图 6.10或运算的二极管与门电路3.非运算某事情发生与否，仅取决于一个条件，而且是对该条件的否定，即条件具备时事情不发生；条件不具备时事情才发生，其逻辑关系、真值表及逻辑符号如图6.11所示。

(a)电路(b)真值表(c)逻辑符号图6.11 或运算Y若用逻辑表达式来描述，则可写为：A下图6.12为晶体管非门电路。

当输入为高电平，晶体管饱和，输出为低电平；当输入为电平，晶体管截止，输出为高电平，实现了非门功能。

图 6.12 非运算的二极管与门电路二、常用逻辑运算1.与非运算下图6.13为2输入与非运算的电路、逻辑符号及真值表。

它由二极管与门和晶体管非门串接而成，当输入中至少有一个为低电平，P点输出为低电平，晶体管截止，F输出为高电平；当输入全为高电平时，P点输出为高电平，晶体管饱和，F输出为低电平，实现了与非的逻辑功能。

计算机基础逻辑运算计算机基础逻辑运算是计算机科学中非常重要的一部分，它涉及到计算机处理信息的核心机制。

逻辑运算是指基于逻辑判断进行的运算，它包括逻辑与、逻辑或、逻辑非等操作。

逻辑与运算是指对两个逻辑表达式进行运算，只有当两个表达式都为真时，结果才为真。

逻辑与运算可以用符号“&&”表示。

例如，表达式A && B表示A和B都为真时，结果为真，否则为假。

逻辑或运算是指对两个逻辑表达式进行运算，只要其中一个表达式为真，结果就为真。

逻辑或运算可以用符号“||”表示。

例如，表达式A || B表示A或B中有一个为真时，结果为真，否则为假。

逻辑非运算是指对一个逻辑表达式进行运算，将真变为假，将假变为真。

逻辑非运算可以用符号“!”表示。

例如，表达式!A表示A为真时，结果为假，A为假时，结果为真。

逻辑运算在计算机中被广泛应用。

在程序设计中，逻辑运算常用于控制程序的流程和判断条件。

通过逻辑与、逻辑或、逻辑非等运算，可以实现复杂的逻辑判断和逻辑控制。

除了基本的逻辑运算，计算机还可以进行位运算和比较运算。

位运算是指对二进制数据的每一位进行运算，常用的位运算包括与运算、或运算、异或运算等。

比较运算是指对两个数据进行比较，常用的比较运算包括等于、不等于、大于、小于等。

这些运算在计算机中被广泛应用于数据处理和算法设计中。

在计算机中，逻辑运算和其他运算一起构成了计算机的基本运算能力。

计算机通过逻辑运算和其他运算，可以进行复杂的数据处理和逻辑判断，实现各种各样的功能。

逻辑运算是计算机科学中的基础，对于理解计算机工作原理和设计计算机程序非常重要。

总结一下，计算机基础逻辑运算是计算机科学中非常重要的一部分。

逻辑运算包括逻辑与、逻辑或、逻辑非等操作，通过逻辑运算可以实现复杂的逻辑判断和逻辑控制。

逻辑运算在计算机中被广泛应用，是计算机的基本运算能力之一。

了解和掌握逻辑运算对于理解计算机工作原理和设计计算机程序非常重要。

逻辑代数的运算规则逻辑代数的基本定律逻辑代数的三个规则1、代入规则在任一逻辑等式中，如果将等式两边所有出现的某一变量都代之以一个逻辑函数，则此等式仍然成立，这一规则称之为代入规则。

2、反演规则已知一逻辑函数F，求其反函数时，只要将原函数F中所有的原变量变为反变量，反变量变为原变量；“＋”变为“·”,“·”变为“＋”；“0”变为“1”；“1”变为“0”。

这就是逻辑函数的反演规则。

3、对偶规则已知一逻辑函数F，只要将原函数F中所有的“＋”变为“·”,“·”变为“＋”；“0”变为“1”；“1”变为“0”，而变量保持不变、原函数的运算先后顺序保持不变，那么就可以得到一个新函数，这新函数就是对偶函数F'。

其对偶与原函数具有如下特点：1.原函数与对偶函数互为对偶函数；2.任两个相等的函数，其对偶函数也相等。

这两个特点即是逻辑函数的对偶规则。

逻辑运算的常用公式逻辑代数的总结基本逻辑运算：与（或称“积”）---符号（&、•、无、∧、∩）或（或称“和”）---符号（| 、＋、∨、∪）非（或称“反”）---符号（! 、）10-1律：0•A=0 0＋A=11•A=A 1＋A=A同一律：A•A=A A＋A=A互补律：A•A=0 A＋A=0反演律A•B =A＋B A＋B=A•还原律A =A√⊕⊙••＋A=02、常用公式交换律：A•B=B•A A+B=B+A结合律：A•(A•B)=(A•B)•C A＋(A＋B)=(A＋B)＋C 分配律：A•(A＋B)=A•B＋A•C A＋(A•B)=(A＋B)•(A＋C) 吸收律：A•(A+B)=AB A+(A•B)=ABA•B+(A•B)=A (A+B)•(A+B)=A。