轴承基本额定动载荷和静载荷计算

轴承的额定静载荷与额定动载荷嗨喽，各位，交叉滚子轴承研究者带着各种宝贝又回来了，本研究者发现平时我们在查询轴承型号时，常会看到Cr和Cor两个选项，这两组字母代表的什么呢？其实，Cr指的是轴承额定动载荷，Cor指的是轴承额定静载荷。

那什么是轴承额定静载荷和额定动载荷呢？这两者之间有什么关系和区别呢？那么今天我们就来看看轴承额定动载荷和轴承额定静载荷，→_→，一起来看满满的干货呀。

在设计中滚动轴承中经常用到的三个基本参数是：满足一定疲劳寿命要求的基本额定动载荷Cr（径向）或Ca（轴向）；满足一定静强度要求的基本额定静强度Cor（径向）或Coa（轴向）和控制轴承磨损的极限转速No。

（1）什么是轴承额定静载荷？滚动轴承的基本额定静载荷（径向Cor，轴向Coa）是指轴承最大载荷滚动体与滚道接触中心处引起一定接触应力时所相当的假象径向载荷或中心轴向静载荷。

额定静载荷是在假定的载荷条件下决定的，对向心轴承，额定静载荷是指径向载荷，对向心推力轴承（角接触球轴承）是指使轴承中半圈滚道受载的载荷的径向分量，对推力轴承是指中心轴向载荷。

也就是说轴承的径向基本额定静负荷与轴向基本额定静负荷指轴承在静态或旋转时，最大能承受的载重。

深沟球轴承在静止或缓慢旋转(转速n≤10r/min)时的承载能力为额定静载荷。

（2）什么是轴承额定动载荷？轴承额定动载荷是指：滚动轴承理论上能承受的恒定径向载荷（恒定轴向载荷），在该载荷的作用下基本额定的寿命为100W转，轴承的基本额定动载荷体现轴承的耐滚动疲劳的能力。

向心轴承和推力轴承的基本额定动载荷反别称作径向基本额定动负荷与轴向基本额定动负荷，用Cr和Ca表示。

沟球轴承在旋转（转速n>10r/mim)时的承载能力为基本额定动载荷。

（3）为何轴承额定动载荷大于额定静载荷？额定动负荷是指额定寿命为100万转时轴承所承受的负荷。

额定静负荷是指轴承承受该负荷作用下,静止时受负荷最大的滚动体和套圈滚道接触处,滚动体和套圈滚道的永久变形量之和为滚动体直径的万分之一。

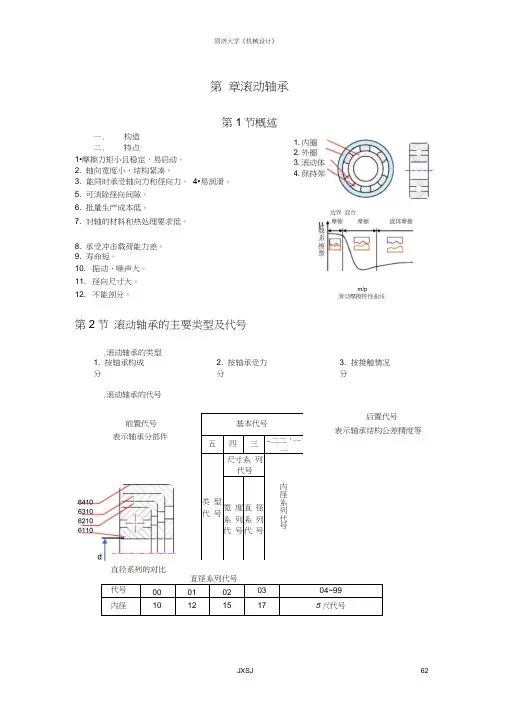
同济大学《机械设计》第 章滚动轴承第1节概述一. 构造 二. 特点1•摩擦力矩小且稳定，易启动。

2. 轴向宽度小，结构紧凑。

3. 能同时承受轴向力和径向力。

4•易润滑。

5. 可消除径向间隙。

6. 批量生产成本低。

7. 对轴的材料和热处理要求低。

8. 承受冲击载荷能力差。

9. 寿命短。

10. 振动、噪声大。

11. 径向尺寸大。

12. 不能剖分。

第2节 滚动轴承的主要类型及代号.滚动轴承的类型1. 按轴承构成分2. 按轴承受力分3. 按接触情况分.滚动轴承的代号代号 00 01 02 03 04~99 内径101215175代代号前置代号 表示轴承分部件基本代号 五四三 -二二 '一一类 型代 号尺寸系 列代号 内径系列代号宽 度 系 列 代 号 直 径 系 列 代 号后置代号表示轴承结构公差精度等1. 内圈2. 外圈3. 滚动体4. 保持架边界 混合m/p滑动摩擦特性曲线圆锥滚子轴承角接触球轴承7OOOC(G=150)7000AC(G =25°)7000B(a=40°) S=R/(2Y)S=eRS=0.68RS=1.14R注：1）Y 对应A/R>e 的Y 2）e 由轴承样本查取第3节滚动轴承的类型选择选择轴承类型时考虑的因素：二.轴承的转速 .轴承的载荷载荷大小、方向是决定轴承类型的重要依据三.安装方便性 四•轴承的调心性能第4节 滚动轴承的工作情况一. 轴承元件上的载荷分布 1 .推力轴承设轴承受到轴向力 S,则每个滚动体受力： 3.失效形式：疲劳点蚀F i =S/Z4.设计计算准则：保证一定的接触疲劳强度二.向心推力轴承的派生轴向 力（附加轴向力）1.派生轴向力的产生 R ■■ Ni ■■ Si ■■ S — A2向心轴承1）力分布2.轴向力对接触情况的影响A/R=tan 二 A/R=1.25tan F i2）轴承元件上应力A/R>1.7tan 用第5节滚动轴承的尺寸选择一.滚动轴承的失效形式及基本额定寿命1. 失效形式滚动体或内外圈滚道上的疲劳点蚀。

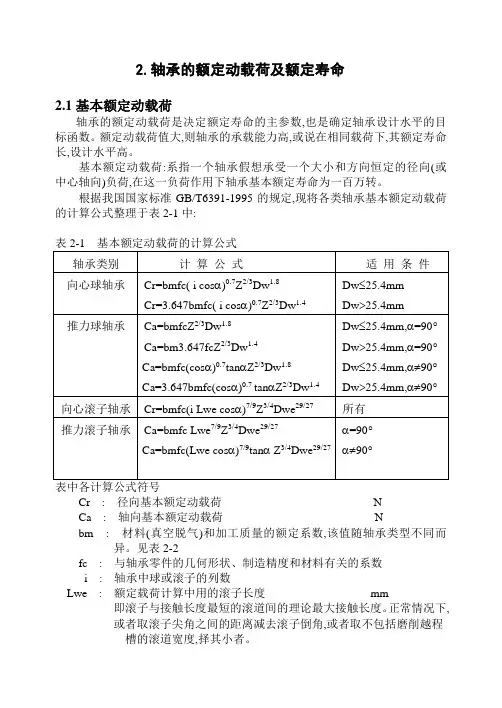
2.轴承的额定动载荷及额定寿命2.1基本额定动载荷轴承的额定动载荷是决定额定寿命的主参数,也是确定轴承设计水平的目标函数。

额定动载荷值大,则轴承的承载能力高,或说在相同载荷下,其额定寿命长,设计水平高。

基本额定动载荷:系指一个轴承假想承受一个大小和方向恒定的径向(或中心轴向)负荷,在这一负荷作用下轴承基本额定寿命为一百万转。

根据我国国家标准GB/T6391-1995的规定,现将各类轴承基本额定动载荷的计算公式整理于表2-1中:Cr : 径向基本额定动载荷NCa : 轴向基本额定动载荷Nbm : 材料(真空脱气)和加工质量的额定系数,该值随轴承类型不同而异。

见表2-2fc : 与轴承零件的几何形状、制造精度和材料有关的系数i : 轴承中球或滚子的列数Lwe : 额定载荷计算中用的滚子长度mm即滚子与接触长度最短的滚道间的理论最大接触长度。

正常情况下,或者取滚子尖角之间的距离减去滚子倒角,或者取不包括磨削越程槽的滚道宽度,择其小者。

α: 轴承的公称接触角度Z: 单列轴承中的球或滚子数。

每列球或滚子数相同的多列轴承中每列的球或滚子数Dw : 球直径mmDwe : 额定载荷计算中用的滚子直径mm对于圆锥滚子取滚子端面和小端面理论尖角处直径的平均值。

对于非对称外凸滚子近似地取零载荷下滚子与无挡边滚道间接触点处滚子的直径现将GB/T6391-1995所定的额定系数bm值列于表2-22.2 额定动载荷的修正滚动轴承基本额定动载荷的计算方法适用于优质淬硬钢(系指真空脱气钢),按良好的加工方法制造,且滚动接触表面的形状为常规设计。

超越上述规定,额定动载荷应予修正。

2.2.1 材质轴承钢因冶炼方法不同,材料中夹杂物的大小、分布、含量亦不同。

夹杂物是造成金属材料疲劳裂纹产生的主要成因,是影响滚动轴承疲劳寿命的主要因素。

如采用夹杂物含量高于真空脱气的普通电炉冶炼轴承钢,则轴承的载荷能力将会有不同程度的下降。

当采用诸如真空重熔、电渣重熔等方法冶炼的轴承钢或其它等效材质的钢材时,其夹杂物的含量显著减少,轴承的载荷能力将会得到提高。

圆锥滚子轴承是一种常用的滚动轴承，广泛应用于工业领域。

在选用圆锥滚子轴承时，其基本额定动载荷是一个重要的参数。

本文将介绍圆锥滚子轴承的基本概念，以及如何计算其基本额定动载荷。

一、圆锥滚子轴承的基本概念圆锥滚子轴承是一种滚动轴承，其内圈和外圈滚道均为圆锥面，滚子为圆锥形，因此具有内径和外径相对较大的特点。

由于其结构的特殊性，圆锥滚子轴承能够承受径向和轴向的双向载荷，因此在工程机械等领域有着广泛的应用。

二、基本额定动载荷的定义基本额定动载荷是指在标准条件下，滚动轴承在长期运转（或者说1百万转）后仍能保证其基本性能的载荷。

对于圆锥滚子轴承而言，其基本额定动载荷是指在轴承内部滚道和滚子上所承受的一组标准化载荷。

基本额定动载荷通常由制造厂商根据其内部的一套标准化试验得出，并在轴承的产品手册中进行了公布。

三、基本额定动载荷的计算计算圆锥滚子轴承的基本额定动载荷需要考虑多个因素，其中最主要的是轴承的基本额定静载荷和基本额定动载荷。

在一般情况下，基本额定动载荷一般是基本额定静载荷的0.1倍至0.3倍。

具体的计算方法可以参考国际轴承制造工程师协会（ABMA）或者国际标准化组织（ISO）的相关标准和手册，这里就不做过多赘述。

四、基本额定动载荷的意义基本额定动载荷是评价圆锥滚子轴承性能的重要指标之一。

在工程设计和选用中，通过比较轴承的基本额定动载荷和实际工作载荷，可以判断轴承在特定工况下的工作性能，为工程机械的可靠性和安全性提供依据。

了解和准确计算圆锥滚子轴承的基本额定动载荷对于工程设计和选用具有重要意义。

五、圆锥滚子轴承基本额定动载荷的应用在工程实践中，圆锥滚子轴承的基本额定动载荷可用于轴承选型、寿命预测和工作状态评估等方面。

通过对轴承的基本额定动载荷进行合理的计算和应用，可以提高工程机械设备的可靠性和安全性，减少故障率，延长轴承的使用寿命，降低设备的维护成本。

六、结语圆锥滚子轴承的基本额定动载荷是评价其性能与可靠性的重要参数，通过合理计算和应用基本额定动载荷，可以为工程设计和选用提供科学依据。

滚动轴承的选择及校核计算根据条件，轴承的预计寿命 h L h45568283568=⨯⨯⨯=' 一.蜗杆轴上的轴承的选择和寿命计算1.轴承的选择采用角接触球轴承，其型号为7212AC ，主要参数如下： mm mm mm B D d 2211060⨯⨯=⨯⨯基本额定静载荷kN C or 2.46=基本额定动载荷kN C r 2.58=极限转速m in /5300max r V =2.寿命计算因为蜗杆所受的轴向力向左N d T F F a t 49021121===N d T F F t a 323222221===N F F F t r r 1507tan 221===α该轴承所受的径向力N F F r r 5.753211== 对于7000AC 型轴承，查P322表13-7轴承派生轴向力r d F F 68.0=12d ae d F F F =+kN F F d a 4.51222=='kN F F F ae d a 4.374421=+=' 又e F F r a =>=68.03.4所以可得出87.0,41.0==Y X当量动载荷N YF XF P a r 6.3566=+=因为是球轴承，所以取指数3ε=轴承寿命计算h P C n L h 50498)57.32.58(14306010)(6010366=⨯⨯=='ε 所以该轴承满足寿命要求。

二.涡轮轴上轴承的选择和寿命计算1.轴承的选择选择角接触轴承，其型号为7213AC ，主要参数如下： mm mm mm B D d 2312065⨯⨯=⨯⨯基本额定静载荷kN C or 5.52=基本额定动载荷kN C r 5.66=2.计算涡轮轴的径向力N F F F a r V r 75.373160224880221=⨯-⨯= N F F F V r r V r 25.1133122=-=N F F t H r 16161608021== N F F F H r r H r 1616122=-=所以可以得出N F F F H r V r r 7.165821211=+=N F F F H r V r r 8.197322222=+=对于7000AC 型号的轴承r d F F 68.0=N F F r d 9.112768.011==N F F r d 2.134268.022==所以可得N F F F d ae a 2.1832221=+=N F F d a 2.134222== 又68.08.19732.134222==r a F F 所以可以得出0,1==Y X 轴承的当量动载荷N F P r 8.197322==h P C n L h 445726)97.15.66(14306010)(6010363262=⨯⨯== 68.093.08.19732.183211>==r a F F 所以有87.0,41.0==Y X 当量动载荷N YF XF P a r 2274111=+=h P C n L h 291478)(60103161==。

轴承基本额定静载荷一、什么是轴承基本额定静载荷轴承基本额定静载荷是指在静止状态下，轴承能够承受的最大力量。

它是根据轴承的设计、材料及制造工艺来确定的，是轴承使用的安全边界。

轴承基本额定静载荷通常由制造商提供，并以标准单位kN（千牛顿）表示。

二、轴承基本额定静载荷的意义轴承基本额定静载荷是选取合适轴承的重要参数。

在设计和选择使用轴承时，需要根据实际工况下的载荷情况与轴承的基本额定静载荷进行比较，以确保轴承在运行中不会过载。

如果超过了轴承的基本额定静载荷，就会导致轴承损坏、破裂甚至事故发生。

三、轴承基本额定静载荷的计算方法轴承基本额定静载荷的计算方法是经过理论推导和实验验证得出的。

通常包括以下几个方面的因素：3.1 材料的强度与硬度轴承的材料强度和硬度是决定其额定静载荷的重要因素。

材料具有一定的强度极限，超过这个极限就会发生塑性变形或破坏。

因此，合理选择高强度、高硬度的材料可以提高轴承的基本额定静载荷。

3.2 轴承接触面的几何形状和曲率半径轴承接触面上的几何形状和曲率半径会影响轴承的承载能力。

通常情况下，接触面越大，承载能力越大。

而曲率半径越小，轴承承载能力越大。

因此，在轴承设计和制造过程中，需要合理选择几何形状和曲率半径来满足要求的额定静载荷。

3.3 轴承的结构和制造工艺轴承的结构设计和制造工艺对其额定静载荷也有影响。

合理的结构设计可以提高轴承的刚性和承载能力，而优良的制造工艺可以保证轴承的精度和质量。

因此，通过优化结构设计和制造工艺，可以提高轴承的额定静载荷。

四、如何读取轴承基本额定静载荷轴承制造商通常会在产品目录或技术手册中提供轴承的基本额定静载荷。

读取轴承基本额定静载荷时，需要注意以下几点：4.1 了解额定静载荷的单位和数值额定静载荷的单位通常为kN（千牛顿），数值表示轴承所能承受的最大力量。

在选择轴承时，需要根据实际工况下的载荷情况，与轴承的额定静载荷进行比较，确保轴承不会过载。

4.2 考虑使用环境和工作条件在读取轴承基本额定静载荷时，还需考虑使用环境和工作条件对轴承的影响。

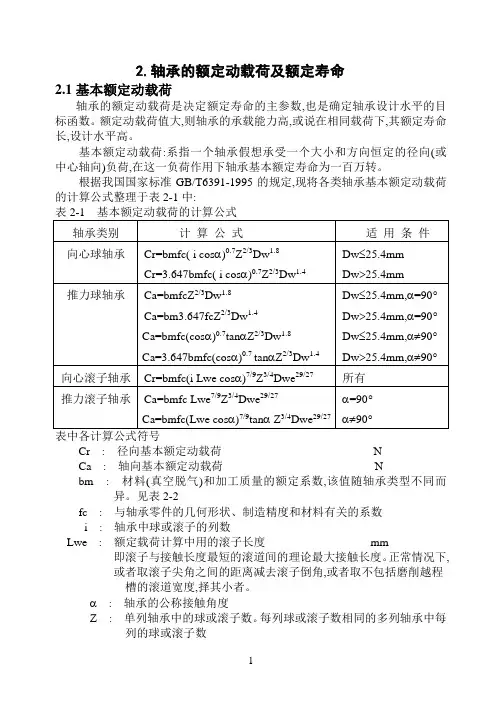
2.轴承的额定动载荷及额定寿命2.1基本额定动载荷轴承的额定动载荷是决定额定寿命的主参数,也是确定轴承设计水平的目标函数。

额定动载荷值大,则轴承的承载能力高,或说在相同载荷下,其额定寿命长,设计水平高。

基本额定动载荷:系指一个轴承假想承受一个大小和方向恒定的径向(或中心轴向)负荷,在这一负荷作用下轴承基本额定寿命为一百万转。

根据我国国家标准GB/T6391-1995的规定,现将各类轴承基本额定动载荷的计算公式整理于表2-1中:Cr : 径向基本额定动载荷NCa : 轴向基本额定动载荷Nbm : 材料(真空脱气)和加工质量的额定系数,该值随轴承类型不同而异。

见表2-2fc : 与轴承零件的几何形状、制造精度和材料有关的系数i : 轴承中球或滚子的列数Lwe : 额定载荷计算中用的滚子长度mm即滚子与接触长度最短的滚道间的理论最大接触长度。

正常情况下,或者取滚子尖角之间的距离减去滚子倒角,或者取不包括磨削越程槽的滚道宽度,择其小者。

α: 轴承的公称接触角度Z: 单列轴承中的球或滚子数。

每列球或滚子数相同的多列轴承中每列的球或滚子数Dw : 球直径mmDwe : 额定载荷计算中用的滚子直径mm对于圆锥滚子取滚子端面和小端面理论尖角处直径的平均值。

对于非对称外凸滚子近似地取零载荷下滚子与无挡边滚道间接触点处滚子的直径现将GB/T6391-1995所定的额定系数bm值列于表2-2滚动轴承基本额定动载荷的计算方法适用于优质淬硬钢(系指真空脱气钢),按良好的加工方法制造,且滚动接触表面的形状为常规设计。

超越上述规定,额定动载荷应予修正。

2.2.1 材质轴承钢因冶炼方法不同,材料中夹杂物的大小、分布、含量亦不同。

夹杂物是造成金属材料疲劳裂纹产生的主要成因,是影响滚动轴承疲劳寿命的主要因素。

如采用夹杂物含量高于真空脱气的普通电炉冶炼轴承钢,则轴承的载荷能力将会有不同程度的下降。

当采用诸如真空重熔、电渣重熔等方法冶炼的轴承钢或其它等效材质的钢材时,其夹杂物的含量显著减少,轴承的载荷能力将会得到提高。

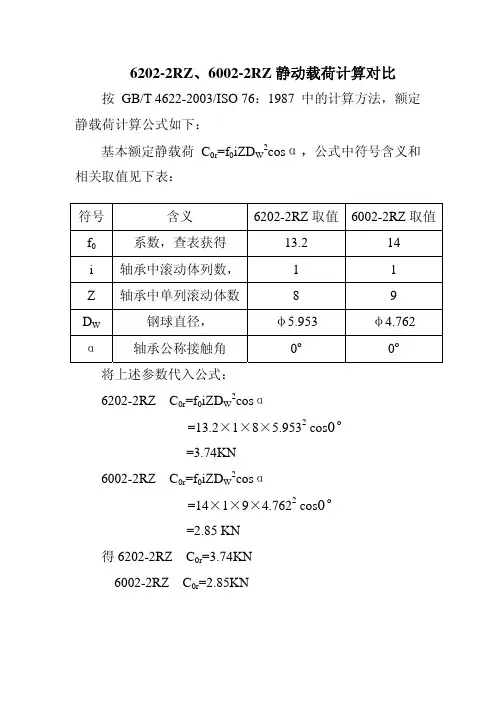
6202-2RZ、6002-2RZ静动载荷计算对比按 GB/T 4622-2003/ISO 76：1987 中的计算方法，额定静载荷计算公式如下：基本额定静载荷C0r=f0iZD W2cosα，公式中符号含义和相关取值见下表：符号含义 6202-2RZ取值6002-2RZ取值f0系数，查表获得 13.2 14i 轴承中滚动体列数， 1 1 Z 轴承中单列滚动体数8 9 D W钢球直径，φ5.953 φ4.762α轴承公称接触角0o0o将上述参数代入公式：6202-2RZ C0r=f0iZD W2cosα=13.2×1×8×5.9532 cos0 o=3.74KN6002-2RZ C0r=f0iZD W2cosα=14×1×9×4.7622 cos0 o=2.85 KN得6202-2RZ C0r=3.74KN6002-2RZ C0r=2.85KN按 GB/T 6391-2003/ISO 281：1990 中的计算方法，额定动载荷计算公式如下：额定动载荷C r=b m f c(icosα)0.7 Z2/3 D W1.8公式中符号含义和相关取值见下表：符号含义 6202-2RZ取值6002-2RZ取值b m系数，查表获得 1.3 1.3f c系数，查表获得 59.3 59.9i 轴承中滚动体列数， 1 1 Z 轴承中单列滚动体数8 9 D W钢球直径，φ5.953 φ4.762α轴承公称接触角0o0o6202-2RZ C r=b m f c(icosα)0.7 Z2/3 D W1.8=1.3×59.3×(cos0o)0.7×82/3×5.9531.8=7.64 KN6002-2RZ C r=b m f c(icosα)0.7 Z2/3 D W1.8=1.3×59.9×(cos0o)0.7×92/3×4.7621.8=5.59 KN综上，6202-2RZ与6002-2RZ静动载荷对比如下：项目6202-2RZ 6002-2RZ基本额定静载荷C0r 3.74 2.85 额定动载荷C r 7.64 5.59。

滚动轴承的校核计算及公式1 基本概念1．轴承寿命：轴承中任一元件出现疲劳剥落扩展迹象前运转的总转数或一定转速下的工作小时数。

批量生产的元件，由于材料的不均匀性，导致轴承的寿命有很大的离散性，最长和最短的寿命可达几十倍，必须采用统计的方法进行处理。

2．基本额定寿命：是指90%可靠度、常用材料和加工质量、常规运转条件下的寿命，以符号L10（r）或L10h（h）表示。

3．基本额定动载荷（C）：基本额定寿命为一百万转（106）时轴承所能承受的恒定载荷。

即在基本额定动载荷作用下，轴承可以工作106 转而不发生点蚀失效，其可靠度为90%。

基本额定动载荷大，轴承抗疲劳的承载能力相应较强。

4．基本额定静载荷（径向C0r，轴向C0a）：是指轴承最大载荷滚动体与滚道接触中心处引起以下接触应力时所相当的假象径向载荷或中心轴向静载荷。

在设计中常用到滚动轴承的三个基本参数：满足一定疲劳寿命要求的基本额定动载荷Cr（径向）或Ca（轴向），满足一定静强度要求的基本额定静强度C0r（径向）或C0a（轴向）和控制轴承磨损的极限转速N0。

各种轴承性能指标值C、C0、N0等可查有关手册。

2 寿命校核计算公式图17-6滚动轴承的寿命随载荷的增大而降低，寿命与载荷的关系曲线如图17-6，其曲线方程为PεL10=常数其中 P-当量动载荷，N；L10-基本额定寿命，常以106r为单位（当寿命为一百万转时，L10=1）；ε-寿命指数，球轴承ε=3，滚子轴承ε=10/3。

由手册查得的基本额定动载荷C是以L10=1、可靠度为90%为依据的。

由此可得当轴承的当量动载荷为P时以转速为单位的基本额定寿命L10为Cε×1=Pε×L10L10=(C/P)ε 106r (17.6)若轴承工作转速为n r/min，可求出以小时数为单位的基本额定寿命h （17.7）应取L10≥L h'。

L h '为轴承的预期使用寿命。

通常参照机器大修期限的预期使用寿命。

轴的负载载荷计算公式在工程设计和制造中，轴的负载承载能力是一个非常重要的参数。

轴的负载承载能力直接影响着机械设备的使用寿命和安全性能。

因此，正确计算轴的负载载荷是非常重要的。

本文将介绍轴的负载载荷计算公式以及其应用。

轴的负载载荷计算公式可以分为静载荷和动载荷两种情况。

静载荷是指轴承在静止状态下所受的载荷，而动载荷是指轴承在运动状态下所受的载荷。

在实际工程中，通常需要考虑轴的静载荷和动载荷两种情况。

首先我们来看轴的静载荷计算公式。

轴的静载荷计算公式可以表示为：P = F / A。

其中，P表示轴的静载荷，单位为N；F表示轴承所受的力，单位为N；A表示轴承的有效截面积，单位为m^2。

在实际工程中，轴承所受的力可以通过受力分析或者实验测量得到。

而轴承的有效截面积可以通过轴的几何尺寸和材料性质来计算得到。

接下来我们来看轴的动载荷计算公式。

轴的动载荷计算公式可以表示为：P = F / A + M / I。

其中，P表示轴的动载荷，单位为N；F表示轴承所受的力，单位为N；A表示轴承的有效截面积，单位为m^2；M表示轴承所受的弯矩，单位为N·m；I表示轴承的截面惯性矩，单位为m^4。

在实际工程中，轴承所受的弯矩可以通过受力分析或者实验测量得到。

而轴承的截面惯性矩可以通过轴的几何尺寸和材料性质来计算得到。

除了上述的静载荷和动载荷计算公式外，还需要考虑一些特殊情况下的轴的负载载荷计算。

比如在轴的工作过程中可能会受到冲击载荷，这时需要考虑冲击载荷对轴的影响，可以通过冲击载荷系数来修正轴的负载载荷计算公式。

另外，在高速运转的轴上，还需要考虑轴的离心力对轴的负载载荷的影响，可以通过离心力系数来修正轴的负载载荷计算公式。

总的来说，轴的负载载荷计算公式是一个非常重要的工程问题。

正确的轴的负载载荷计算可以保证轴承的安全可靠运行，延长设备的使用寿命，提高设备的安全性能。

因此，在工程设计和制造中，需要认真对待轴的负载载荷计算问题，确保轴的负载承载能力符合工程要求。

基本额定动载荷一．滚动轴承基本额定动载荷和当量动载荷的概念区别能承受纯轴向载荷的推力轴承，只要分别令式中的Fr 或Fa 为0，即可计算P 。

二．滚动轴承基本额定动载荷与寿命的关系 一．额定动载荷的修正轴承工作温度与试验温度不同时应修正额定动载荷。

C t =f t C二． 滚动轴承寿命的计算公式1.载荷和额定寿命的关系2.寿命计算公式1) 用转数表示的寿命公式：10C L P ε⎛⎫= ⎪⎝⎭球轴承 滚子轴承 ε33.3332) 用小时表示的寿命公式：61060h C L n P ε⎛⎫= ⎪⎝⎭额定寿命值10H L 的例子：工作条件基本额定寿命L 10H不频繁操作。

500 短期或间歇操作。

故障影响不大功能。

4,000 8,000 间歇操作。

失败有重大影响功能。

8,000 12,000 非连续运行8小时的 12,000 20,000 8小时的连续运转。

20,000 30,000 24小时连续运行。

40,000 60,000 24小时保证无故障运行。

100,000200,0003) 设计式：012345678910L 10(106)载荷额定寿命4 3 2C三． 滚动轴承基本额定动载荷计算式Basic dynamic radial load rating for single bearingsThe basic dynamic radial load rating for radial ball bearings is given by the equations.0.72/3 1.80.72/31.4(cos )25.43.647(cos )25.4r m c w w r c ww C b f i Z D forD mmC f i ZD forD mmαα=≤=≥where the values of bm and fc are given in Tables 1 and 2 respectively. They apply to bearings with a cross-sectional raceway groove radius not larger than 0.52 Dw in radial and angular contact ball bearing inner rings and not larger than 0.53 Dw in radial and angular contact ball bearing outer rings and self-aligning ball bearing inner rings.The load-carrying ability of a bearing is not necessarily increased by the use of a smaller groove radius, but it is reduced by the use of a groove radius larger than those indicated in the previous paragraph. In the lattercase, a correspondingly reducedvalue of fc shall be used. Calculation of this reduced value of fc can be carried out by means of Equation (3–15) given in ISO/TR 8646:1985.。