信号与系统作业答案
- 格式:doc
- 大小:730.50 KB
- 文档页数:19


1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
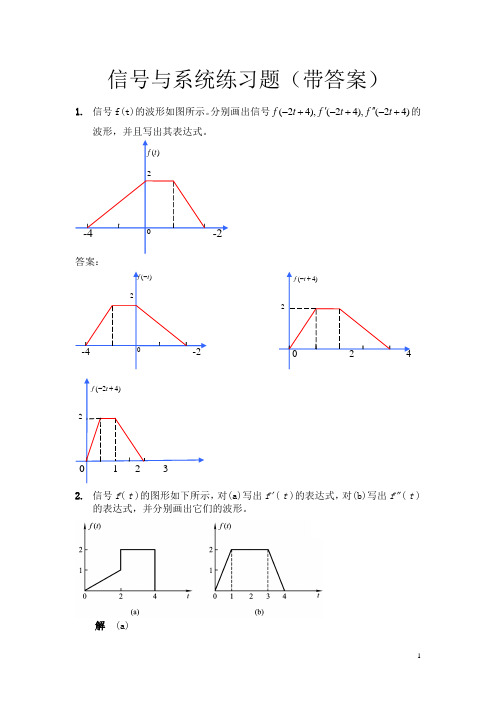
信号与系统练习题(带答案)1. 信号f(t)的波形如图所示。
分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形,并且写出其表达式。
答案:2. 信号f ( t )的图形如下所示,对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
解 (a)20,21≤≤tf ' (t)= δ(t -2), t = 2-2δ(t -4), t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示,试画出f(t)的波形。
52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析()右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得-2t ,即f(5-2t)左移(52)(2)f t f t -−−−→-时移由(2)反转:f(-2t)中以-t 代替t ,可求得f(2t),表明f(-2t)的波形 以t =0的纵轴为中心线对褶,注意()t δ是偶数,故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由(3)尺度变换:以12t 代替f(2t)中的t ,所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。
4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。
解:{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。

信号与系统练习及答案一、单项选择题1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( )A .tu(t)B .(t-1)u(t-1)C .tu(t-1)D .2(t-1)u(t-1)2.积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是( ) A .14 B .24 C .26 D .283.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )4.周期矩形脉冲的谱线间隔与( )A .脉冲幅度有关B .脉冲宽度有关C .脉冲周期有关D .周期和脉冲宽度有关 5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( ) A .不变 B .变窄 C .变宽D .与脉冲宽度无关 6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号()A .一定相同 B .一定不同 C .只能为零 D .可以不同7.f(t)=)(t u e t 的拉氏变换为F (s )=11-s ,且收敛域为( ) A .Re[s]>0B .Re[s]<0C .Re[s]>1D .Re[s]<1 8.函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F (s )等于( ) A .1 B .s 1 C .e -2s D .s1e -2s 9.单边拉氏变换F (s )=22++-s e )s (的原函数f(t)等于( ) A .e -2t u(t-1) B .e -2(t-1)u(t-1) C .e -2t u(t-2)D .e -2(t-2)u(t-2)答案: BCCCBDCDA二.填空题1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
3.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。


第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e = (5)()()cos2y t f t t = (8)()()2y t f t = 解:(2)()()2f t y t e = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f t f t y t ey t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f t y t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t 1,()()121f t y t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦, 显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
)t t)](23--t δt解ttt1.27(a ))2()2()(t x t x t y -+-=① 因为)2()2()0(x x y +-=,在0=t 的输出与前后时刻的输入都有关,所以系统是记忆的。
② 已知)2()2()(111t x t x t y -+-=,)2()2()(222t x t x t y -+-=。
当)()(012t t x t x -=时,)2()2()(01012t t x t t x t y --+--=,而)2()2()(010101t t x t t x t t y +-+--=-,所以:)()(012t t y t y -≠。
因而系统是时变的。
③已知)2()2()(111t x t x t y -+-=,)2()2()(222t x t x t y -+-=,)2()2()(333t x t x t y -+-=,当)()()(213t x t x t x +=时,)]2()2([)]2()2([)(21213t x t x t x t x t y -+-+-+-= 所以)()()(213t y t y t y +=,因而系统是可加的。
当)()(12t ax t x =时,)()2()2()(1112t ay t ax t ax t y =-+-=,因而系统是齐次的。
综合系统的可加性与齐次性,所以系统是线性的。
④因为)2()2()0(x x y +-=,在0=t 的输出与2=t 的输入也有关,所以系统是非因果的。
⑤若+∞<≤B t x )(,即输入有界,则:+∞<≤-+-≤-+-=B t x t x t x t x t y 2)2()2()2()2()(,即输出有界。
所以系统是稳定的。
(d )⎩⎨⎧≥-+<=0),2()(0,0)(t t x t x t t y①)2()0()0(-+=x x y ,即)0(y 与2,0-==t t 的输入有关, ∴系统是记忆系统。
②令)()(01t t x t x -=,则⎩⎨⎧≥--+-<=⎩⎨⎧≥-+<=0),2()(0,00),2()(0,0)(00111t t t x t t x t t t x t x t t y而⎩⎨⎧≥--+-<=⎩⎨⎧≥---+-<-=-000000000),2()(,00),2()(0,0)(t t t t x t t x t t t t t t x t t x t t t t y)()(01t t y t y -≠∴,系统是时变的。
③令)()(1t ax t x =,则)(0),2()(0,0)(1t ay t t ax t ax t t y =⎩⎨⎧≥-+<=,所以,系统是齐次的。
已知⎩⎨⎧≥-+<=0),2()(0,0)(111t t x t x t t y ,⎩⎨⎧≥-+<=0),2()(0,0)(222t t x t x t t y当)()()(213t x t x t x +=时,)()(0),2()(0,00),2()(0,00),2()2()()(0,00),2()(0,0)(2122112121333t y t y t t x t x t t t x t x t t t x t x t x t x t t t x t x t t y +=⎩⎨⎧≥-+<+⎩⎨⎧≥-+<=⎩⎨⎧≥-+-++<=⎩⎨⎧≥-+<=综上,所以,系统是线性的。
④考察0t t=点,若00<t ,则0)(0=t y若00≥t ,则)2()()(000-+=t x t x t y ,满足因果的定义,所以系统是因果的。
⑤若∞<≤B t x )(,即输入有界,则:∞<≤⎩⎨⎧≥+<=B t t x t x t t y 20,)2()(0,0)(,有界,所以系统是稳定的。
2.23 解:∑∑∑+∞-∞=+∞-∞=+∞-∞=-=-=-==k k k kT t h kT t t h kT t t h t h t x t y )()(*)()(*)()(*)()(δδ(a) 当4=T 时,)2()()(112--=t x t x t x 解31.1.的系统是又LTI )2()()(112--=∴t y t y t y)()1()(113t x t x t x ++= .的系统是又LTI )()1()(113t y t y t y ++=∴)8()4()()4()8()4()(-+-++++++=-=∑+∞-∞=t h t h t h t h t h k t h t y k a(b) 当2=T 时,)4()2()()2()4()2()(-+-++++++=-=∑+∞-∞=t h t h t h t h t h k t h t y k b(c) 当23=T 时,)2()()()()2()()(2323232323⋅-+-++++⋅++=-=∑+∞t h t h t h t h t h k t h t y c(d) 当1=T 时,1)2()1()()1()2()()(=-+-++++++=-=∑+∞-∞= t h t h t h t h t h k t h t y k d2.40解:依题意)()(t y t x LTI −→−,⎰∞----=tt d x et y τττ)2()()(。
(a) 而)()()()(t h t y t t x LTI=−−→−=δ, ∴)2()2()2()()2()2()(-=-=-=--∞---∞---⎰⎰t u ed ed et h t tt tt ττδττδτ(b) )(t x )2()1()('--+=t t t x δδ波形如图。
令)()(t u e t w t-=,则)2(*)()2()(-=-=t t w t w t h δ,21tx'(t)-1 -1而)()1()()()()(0)1(t u e t u d e d u ed w t wtttt--∞--∞---=⎥⎦⎤⎢⎣⎡===⎰⎰⎰λλλλλλλ,所以)4(]1[)]1()1[)4()1()]4()1([*)()2(*)]2()1([*)()2(*)('*)()2(*)(*)()(*)()()4()1()1()1()1()1()1(-----=---=---=---+=-=-==---------t u e t u et wt wt t t w t t t t w t t x t wt t w t x t h t x t y t t δδδδδδδ3.34解:168)()(,)(2||4+==∴=⎰+∞∞---ωωωdt et h j H et h tj t (a)ππωδω22,)()(00==∑=-∑=-+∞-∞=+∞-∞=Tea n t t x tjk k k n1)(10==⎰dt et x Ta tjk Tk ωtjk k et x 0)(ω+∞-∞=∑=∴则ktj k ktj k tjk k k ek ek ejk H a t y ππωππω2222204216)2(8)()(0+∑=+∑=∑=+∞-∞=+∞-∞=+∞-∞=。
(b)tjk k k nk e a n t t x 0)()1()(ωδ+∞-∞=+∞-∞=∑=--∑=,ππω==T20 []⎥⎦⎤⎢⎣⎡--==⎰⎰-5.15.0)1()(21)(10dt e t t dt et x Ta tjk tjk Tk πωδδ⎩⎨⎧±±=+=⋅⋅⋅⋅⋅⋅⋅±±===--=-=......2,1,0,12,12,1,0,2,0])1(1[21)1(21m m k m m k ekjk πtm j m m tm j m m tjk k k em j H a em j H a ejk H a t y ππωππω22)12(120)2(])12([)()(0+∞-∞=+++∞-∞=+∞-∞=∑++∑=∑=∴tk j k tm j m ek em ππππ)12(2)12(216])12[(816])12[(8++∞-∞=++∞-∞=++∑=++∑=(c)tjk k k ea t x 0)(ω+∞-∞=∑=,ππω220==T)2(21sin][21)(1222414120k Sa kkeekj dt edt e t x Ta kjkjktj tjk Tk πππππππω==--===----⎰⎰ktj k ktj k tjk k k ek k k ek kk ejk H a t y ππππωππππω22222220)4()sin(416)2(8)sin()()(0+∑=+∑=∑=∴+∞-∞=+∞-∞=+∞-∞=3.35解:ktj k k tjk k k ea ea t x 140)(+∞-∞=+∞-∞=∑=∑=ω,142270===πππωT,⎩⎨⎧≥=otherj H ,0250||,1)(ωωktj k k ktj k k tjk k k ea ek j H a ejk H a t y 1418||140)14()()(0≥+∞-∞=+∞-∞=∑=∑=∑=∴ωω 要使)()()(t x t y t x S=−→−,则要求k a 满足:⎩⎨⎧≥=other k a a k k ,018,4.21解: (a)[]0),(cos )(0>=-a t u t et x atωωj a FTatt u e +-−→←1)( ;)()(cos 000ωωπδωωπδω-++−−→←FTt ()20200][)]()([)()(1)(12100121ωωωωωωωωπωωπδωωπδω+++-++++=+=-++*=∴j a j a j a j a j a j X(h))(1t x 如图所示:则2111)(==−→←Tk FSa t x ;∑∑+∞-∞=+∞-∞=-=-=−−→←k k TkFTk kaj X t x )()(2)()(211πωδπωδπωπ而)1()(2)(11-+=t x t x t x∑∑+∞-∞=+∞-∞=----+=-+=+=∴k kk j j k k eej X j X j X )(])1(2[)()2()()(2)(11πωδππωδπωωωωω4.22解:(c )令: )()()(11ωωj X j X t x FT=−→←,则:⎰⎰⎰⎰=+-==-+∞∞-11111)cos(1][21)(21)(ωωωπωωωωπωωπωωωd t d ed ed ej X t x tj tj tj211101cos sin ]cos 1[sin 1])sin()sin([1tt ttt tt td t t tππωπωωωωπ-+=+=-=⎰而)3(1)()()()(ωωωωω-∠⋅==j j X j ej X e j X j X ,21)3(1)3cos()3()3sin()3()(---+--=-=∴t t t t t x t x ππ(d ))]2()2([3)]1()1([2)(πωδπωδωδωδω++-++--=j X)]}2()2([{3)]}1()1([{2πωδπωδππωδωδππ-+++--+=j jtt jt x πππ2cos 3sin 2)(+=∴4.25 解:(a )令)(1t x 如图所示,)(1111)()()(ωωωj X j FTe j X j X t x ∠=−→←。