第三章:量子力学导论
- 格式:ppt
- 大小:6.64 MB
- 文档页数:76

三、薛定谔方程的讨论
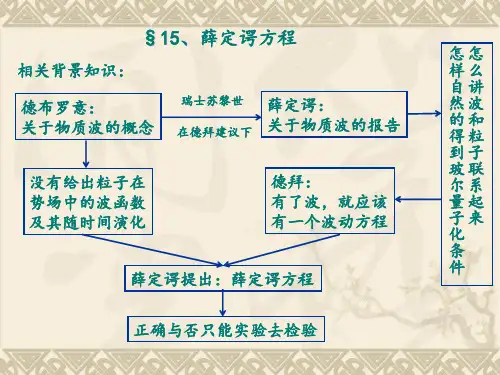
1.薛定谔方程描述了微观粒子的运动状态),(t r →ψ在势场 ),(t r U →中随时间变化的 规律 规律;
2.薛定谔方程是量子力学的基本方程,它不能从更基本的假设中推导出来。
它的 正确性只有通过与实验结果相一致来得到证明。
3.具体的势场 ),(t r U →决定粒子状态变化的情况,如果给出势能函数 ),(t r U → 的具体形式,只要我们知道了微观粒子初始时刻的状态),(00t r →ψ原则上说,只要通
过 薛定谔方程,就可以求出任意时刻的状态 ),(t r →ψ。
4.薛定谔方程中有虚数单位i ,所以),(t r →ψ一般是复数形式。
),(t r →
ψ表
示概率波, 2),(t r →ψ是表示粒子在时刻t 、在空间某处出现的概率。
因而薛定谔方程所描述的态随时间变化的规律,是一种统计规律。
5.在薛定谔方程的建立中,应用了),(22
t r U p E →+=μ,所以是非相对论的结果;同 时方程不适合一切0=μ的粒子,这是方程的局限性。

第三章量⼦⼒学导论1第三章:量⼦⼒学导论§1 玻尔理论的困难 §2 波粒⼆象性 §3 不确定关系 §4 波函数及其统计解释 §5 薛定谔⽅程 §6 平均值与算符 §7 量⼦⼒学对氢原⼦的处理1. 玻尔氢原⼦理论的成绩第⼀节玻尔理论的困难成功地解释了原⼦的稳定性、⼤⼩及氢原⼦光谱的规律性。
从理论上计算了⾥德伯常量;解决了近30年之久的巴⽿末公式之迷,打开了⼈们认识原⼦结构的⼤门,⽽且玻尔提出的⼀些概念,如能量量⼦化、量⼦跃迁及频率条件等,⾄今仍然是正确的。
能对类氢原⼦的光谱给予说明。
冲破了经典物理的束缚,提供了描述微观体系的新⽅法,为⼈们认识微观世界以及对量⼦理论的建⽴打下了基础。
22. 玻尔氢原⼦理论的困难不能解释多电⼦原⼦的光谱;不能解释谱线的强度和宽度;玻尔理论的⾓动量 L=nh/2π,与实验结果不符,按量⼦⼒学,⾓动量⼤⼩ L = l (l + 1) h ;不能说明原⼦是如何组成分⼦、构成液体和固体的;在逻辑上也存在⽭盾:把微观粒⼦看成是遵守经典⼒学规律的质点,⼜赋予它们量⼦化的特征。
3第⼆节波粒⼆象性1.经典物理中的波和粒⼦在经典波中有两个结论:要⽆限精确地测准频率,就需要花费⽆限长的时间t v ≥ 1要⽆限精确地测准波长,就必须在⽆限扩展的空间中进⾏观察。
xλ ≥ λ242. 光的波粒⼆象性 2. 光的波粒⼆象性ε = hν相对论质能关系:ε = h ν = mc2光⼦的质量:hν = h m = 2 λc cm = m0 1? v2因为:/c25光⼦的动量:p = mcλh p=数联系在⼀起的。
ε = hν光的波动性(λ)和粒⼦性(p)是通过普朗克常光在传播时显⽰出波动性,在转移能量时显⽰出粒⼦性。
光既具有粒⼦性,⼜具有波动性,即具有波粒⼆象性63.德布罗意假设—微粒的波动性 3.德布罗意假设—微粒的波动性德布罗意关系式德布罗意指出任何物体都伴随以波,不可能将物体的运动和波的传播分拆开来。







第三章一维定态问题3.1)设粒子处在二维无限深势阱中,⎩⎨⎧∞<<<<=其余区域,0,0 ,0),(by a x y x V 求粒子的能量本征值和本征波函数。
如b a = ,能级的简并度如何? 解:能量的本征值和本征函数为m E y x n n 222π =)(2222bn an y x +,2,1, ,sinsin2==y x y x nn n n byn axn abyx ππψ若b a =,则 )(222222y x n nn n ma E yx +=πayn axn ay x nn yx ππψsinsin2=这时,若y x n n =,则能级不简并;若y x n n ≠,则能级一般是二度简并的(有偶然简并情况,如5,10==y x n n 与2,11''==y x n n )3.2)设粒子限制在矩形匣子中运动,即⎩⎨⎧∞<<<<<<=其余区域 ,0,0,0 ,0),,(cz b y a x z y x V 求粒子的能量本征值和本征波函数。
如c b a ==,讨论能级的简并度。
解:能量本征值和本征波函数为)(222222222cn bn an mnn n Ez y x zyx++=π ,,3,2,1,, ,sinsinsin8==z y x z y x n n n czn byn axn abcn n n zy x πππψ当c b a ==时,)(2222222z y x n n n mann n Ezyx++=πayn ayn axn a n n n z y x zy x πππψsinsinsin223⎪⎭⎫⎝⎛=z y x n n n ==时,能级不简并;z y x n n n ,,三者中有二者相等,而第三者不等时,能级一般为三重简并的。
z y x n n n ,,三者皆不相等时,能级一般为6度简并的。
如 ⎩⎨⎧→++=++→++=++)9,6,3()10,5,1(2086161210)11,3,1()9,7,1(10438652222222222223.3)设粒子处在一维无限深方势阱中,⎩⎨⎧><∞<<=ax 0, ,0 ,0),(x ax y x V 证明处于定态)(x n ψ的粒子)61(12)x -(x ,22222πn aa x -==讨论∞→ n 的情况,并于经典力学计算结果相比较。
闽江学院教案课程名称:原子物理课程代码: 21100430授课专业班级: 2010级物理学(师范类)授课教师:翁铭华系别:电子系2012年8 月30 日第三章量子力学导论教学目的和要求:1.了解量子化物质波粒二象性的概念。
2.理解测不准原理;3.掌握波函数及物理意义;4.了解薛定谔方程;了解量子力学问题的几个简例;5.了解氢原子的薛定谔方程;了解量子力学对氢原子的描述。
教学重点和难点:1. 教学重点:波函数及统计解释2.教学难点:波函数及统计解释教学内容:1. 玻尔理论的困难2. 波粒二象性3. 不确定关系4. 波函数及其统计解释5. 薛定谔方程及应用19世纪末的三大发现(1896年发现放射性,1897年发现电子,1900年提出量子化概念)为近代物理学的序幕。
1905年爱因斯坦在解释光电效应时提出光量子概念,1913年玻尔将普朗克-爱因斯坦量子概念用于卢瑟福模型,提出量子态观念,成功地解释了氢光谱。
此外,利用泡利1925年提出的不相容原理和同年乌仑贝克、古兹米特提出的电子自旋假说,可很好地解释元素周期性、塞曼效应的一系列实验事实。
至此形成的量子论称为旧量子论,有严重的缺陷。
在“物质粒子的波粒二象性”思想的基础上,于1925-1928年间由海森堡、玻恩、薛定谔、狄拉克等人建立了量子力学,它与相对论成了近代物理学的两大理论支柱。
量子力学的本质特征在1927年海森堡提出的不确定关系中得到明确的反映,它是微观客体波粒二象性的必然结果。
量子力学的主要内容:1)相关的几个重要实验;2)有别于经典物理的新思想;3)解决具体问题的方法。
§3-1玻尔理论的困难玻尔理论将微观粒子视为经典力学中的质点,把经典力学的规律用于微观粒子,使其理论中有难以解决的内在矛盾,故有重大缺陷。
如:为什么核与电子间的相互作用存在,但处于定态的加速电子不辐射电磁波?电子跃迁时辐射(或吸收)电磁波的根本原因何在?……(薛定谔的非难“糟透的跃迁”:在两能级间跃迁的电子处于什么状态?)玻尔理论在处理实际问题时也“力不从心”,如无法解释氢光谱的强度及精细结构,无法解释简单程度仅次于氢原子的氦光谱,无法说明原子是如何组成分子及构成液体和固体。