当前位置：文档之家 › 第三章 量子力学中的算符12

第三章 量子力学中的算符12

  • 格式：ppt
  • 大小：571.00 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

第三章 力学量的算符表示

第三章 力学量的算符表示


∂ ∂ L y = −ih(cos ϕ − ctg θ sin ϕ ) ∂ϕ ∂θ
∧
∂ L z = −ih ∂ϕ
∧
L = L x+ L y+ L
1 2 ∇ = 2 r
∧2
∧2
∧2
∧2 z
1 ∂ ∂ 1 ∂2 2 = −h [ (sin θ )+ 2 ] 2 sin θ ∂θ ∂θ sin θ ∂ϕ
∂ 2 ∂ 1 ∂ ∂ 1 ∂2 )+ (sin θ )+ (r ∂r ∂r sin θ ∂θ ∂θ sin 2 θ ∂ϕ 2 ˆ 1 ∂ 2 ∂ L2 = 2 (r )− 2 21 r ∂r ∂r h
（连带勒让德微分方程）
d2y dy 2 (1 − x ) 2 − 2 x + λy = 0 dx dx
（m=0, 勒让德微分方程）
[L x , L y ] = L x L y − L y L x = ( y p z − z p y )( z p x − x p z ) − ( z p x − x p z )( y p z − z p y )
∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧
= y pz z px − y pz x pz − z py z px + z py x pz − z px y pz + z px z py + x pz y pz − x pz z py
厄密算符 两个波函数ψ和ϕ，满足下列等式
ˆ ˆ ψ ∗ Fϕdτ = ∫ ( Fψ )∗ϕdτ ∫
ˆ 的算符 F 称为厄密算符
5
厄密算符的本征值为实数
ˆ 若 Fψ = λψ
∗
ˆ ψ Fψdτ = λ ∫ψ ψdτ ∫
第三章-表示力学量算符-习题答案

第三章-表示力学量算符-习题答案

第三章 量子力学中的力学量 1. 证明 厄米算符的平均值都是实数（在任意态）[证] 由厄米算符的定义**ˆˆ()F d F d ψψτψψτ=⎰⎰厄米算符ˆF的平均值 *ˆF Fd ψψτ=⎰ **ˆ[()]F d ψψτ=⎰ ***ˆ[]Fd ψψτ=⎰**ˆ[()]Fd ψψτ=⎰**ˆ[]F d ψψτ=⎰ *F =即厄米算符的平均值都是实数2. 判断下列等式是否正确（1）ˆˆˆHT U =+ （2）H T U =+（3）H E T U ==+[解]：（1）（2）正确 （3）错误因为动能，势能不同时确定，而它们的平均值却是同时确定 。

3. 设()x ψ归一化，{}k ϕ是ˆF的本征函数，且 ()()k kkx c x ψϕ=∑（1）试推导k C 表示式（2）求征力学量F 的()x ψ态平均值2k k kF c F =∑（3）说明2k c 的物理意义。

[解]：（1）给()x ψ左乘*()m x ϕ再对x 积分**()()()()mm k k k x x dx x c x dx ϕϕϕτϕ=⎰⎰*()()k m k kc x x dx ϕϕ=∑⎰因()x ψ是ˆF的本函，所以()x ψ具有正交归一性**()()()()mk m k k k kkx x dx c x x dx c mk c ϕψϕϕδ===∑∑⎰⎰ ()m k = *()()k m c x x dx ϕψ∴=⎰（2）k ϕ是ˆF 的本征函数，设其本征值为kF 则 ˆk k kF F ϕϕ= **ˆˆm k m k k kF F dx F c dx ψψψϕ==∑⎰⎰**()m mk k k kc x F c dx ϕϕ=∑∑⎰**m k kmkx mkc c F dϕϕ=∑⎰*m k k mk mkcc F δ=∑2k k kc F =∑即 2k k kF c F =∑（3）2k c 的物理意义；表示体系处在ψ态，在该态中测量力学量F ，得到本征值k F 的 几率为2k c 。

量子力学第三章算符

量子力学第三章算符

第三章算符与力学量算符3、1 算符概述设某种运算把函数u变为函数v,用算符表示为:(3、1-1)称为算符。

u与v中得变量可能相同,也可能不同。

例如,,,,,,则,x,,,都就是算符。

1.算符得一般运算(1)算符得相等:对于任意函数u,若,则。

(2)算符得相加:对于任意函数u,若,则。

算符得相加满足交换律。

(3)算符得相乘:对于任意函数u,若,则。

算符得相乘一般不满足交换律。

如果,则称与对易。

2.几种特殊算符(1)单位算符对于任意涵数u,若u=u,则称为单位算符。

与1就是等价得。

(2)线性算符对于任意函数u与v,若,则称为反线性算符。

(3)逆算符对于任意函数u,若则称与互为逆算符。

即,。

并非所有得算符都有逆算符,例如把零作为算符时,称之为零算符,零算符就没有逆算符。

对于非齐次线性微分方程:,其中为与函数构成得线性算符,a为常数。

其解u可表示为对应齐次方程得通解u。

与非齐次方程得特解之与,即。

因,所以不存在使。

一般说来,在特解中应允许含有对应齐次方程得通解成分,但如果当a=0时,=0,则中将不含对应齐次方程得通解成分,这时存在使,从而由得:。

从上述分析可知,就是否存在逆算符还与算符所作用得函数有关。

(4)转置算符令,则称与得转置算符,就是一个向左作用得算符。

若算符表示一般函数(或常数),由于函数得左乘等于右乘,所以函数得转置就等于它本身。

定义波函数与得标积为:(3、1-2)与得标积以及与得标积为:若上两式中得与都就是任意波函数,则称上两式中得与为任意标积中得算符。

下面考虑在任意标积中得性质。

波函数与在无限远点也应满足连续性条件:[可都等于零],,所以得:可见在任意标积中,。

(5)转置共轭算符(也称为厄密共轭算符)与厄密算符转置共轭算符通常也就是向左作用得算符,同时算符本身要取共轭。

以标记得转置共轭算符,则若在任意标积中,,则称为厄密算符。

即厄密算符得定义为:或写为(3、1-3)可以证明,位置算符与动量算符都就是厄密算符。

量子力学之算符

量子力学之算符


i
但是坐标算符与其非共轭动量 对易，各动量之间相互对易。
x pˆ pˆ x i
pˆ pˆ pˆ pˆ 0
, x, y, z
量子力学中最基本的 对易关系。
xpˆ y pˆ y x 0
xpˆ z
pˆ z
x
0
pˆ x pˆ y pˆ y pˆ x 0
ypˆ x pˆ x y 0 zpˆ x pˆ xz 0
~ x
x
)
0
由于ψ、φ是 任意波函数,
( ~ x
x
)
0
~ x
x
所以
同理可证:
~ pˆ x pˆ x
可以证明： ( Aˆ Bˆ ) B~ˆ A~ˆ
(11)厄密共轭算符
算符 Ô 之厄密共轭算符 Ô + 定义:
由此可得：:
d *Oˆ d (Oˆ )*
d *Oˆ d (Oˆ )*
pˆ* (i)* i pˆ
（10）转置算符
算 符Uˆ 的 转 置 算 符U~ˆ 定 义 为 ：
d *U~ˆ dUˆ *
式中 和 是两个任意函数。
例1：
~ x
x
证：
dx
*
~ x
利用波函数标准条件: 当|x|→∞ 时ψ,→ 0。
dx
x
*
* |
dx
*
x
dx
*
x
dx
*
(
（2）算符相等
若两个算符 Ô 、Û 对体系的任何波函数 ψ的运算结果都相 同，即Ô ψ= Û ψ，则算符Ô 和算符Û 相等记为Ô = Û 。
（3）算符之和
Hˆ Tˆ Vˆ
表明
Ham ilton算 符Hˆ 等 于
量子力学— —算符

量子力学— —算符


，都是厄米算符。
对于任意量子态
，
。所以，动量算符确实是一个厄米算符。 动量算符确实是一个厄米算符
返回目录
4/52
1.2 （位置算符）本征值与本征函数
假设，位置算符 的本征值为 的本征函数是 。用方程表达， 这方程的一般解为，
其中， 虽然
是常数， 无法归一化：
是狄拉克δ函数。
设定
= 1，我们可以使
满足下述方程：
们立刻再测量可观察量

，得到的答案必定是
可是，假若，我们改为测量可观察量 为
，则量子态不会停留于本征态
的本征态。假若，得到的测量值为其本征值
，则量子态几率地坍缩为本征态

根据不确定性原理， 的不确定性与 与 之间， 与 的不确定性的乘积 之间，也有类似的特性。 ，必定大于或等于 。
返回目录
19/52
返回目录
13/52
3.1 角动量算符 简介
角动量促使在旋转方面的运动得以数量化。在孤立系 统里，如同能量和动量，角动量是守恒的。在量子力 学里，角动量算符的概念是必要的，因为角动量的计 算实现于描述量子系统的波函数，而不是经典地实现 于一点或一刚体。在量子尺寸世界，分析的对象都是 以波函数或量子幅来描述其几率性行为，而不是命定 性(deterministic)行为。
量子力学
算 符
目录
一、位置算符
1.1 厄米算符 1.2 （位置算符）本征值与本征函数 1.3 正则对易关系
七、自旋算符
7.1 概论 7.2 发展史 7.3 自旋量子数
7.3.1 基本粒子的自旋 7.3.2 亚原子粒子的自旋 7.3.3 原子和分子的自旋 7.3.4 自旋与统计
二、动量算符
量子力学中的算符

量子力学中的算符

量子力学中的算符量子力学是描述微观粒子行为的理论，其基本概念之一就是算符。

算符（operator）是量子力学中的基本数学工具，用于描述物理量的测量和演化。

本文将从算符的定义、性质以及在量子力学中的应用等方面进行探讨。

一、算符的定义和性质在量子力学中，算符是描述物理量的数学对象，用于描述系统的状态演化和物理量的测量。

算符作用在量子态上，改变其状态或作用于态矢量的波函数。

1. 算符的基本性质算符具有线性性质，即对于任意的复数a和量子态|ψ⟩、|φ⟩，有：A(a|ψ⟩+ b|φ⟩) = aA|ψ⟩+ bA|φ⟩其中A为算符。

2.算符的厄米性在量子力学中，与每个物理量都有对应的算符。

一个算符是厄米算符，当且仅当它等于其自身的共轭转置，即：A† = A3.算符的本征值与本征态对于算符A，若存在一个常数a和一个非零的量子态|ψ⟩，满足：A|ψ⟩= a|ψ⟩则称a为算符A的本征值（eigenvalue），|ψ⟩为相应的本征态（eigenstate）。

二、算符在量子力学中的应用算符在量子力学中有广泛的应用，下面以几个典型例子来说明其用途。

1.位置算符和动量算符在量子力学中，位置和动量是物理量的基本概念。

对于位置算符X和动量算符P，其定义分别为：X = x，P = -iℏ(d/dx)其中x是位置的算符，ℏ是普朗克常数。

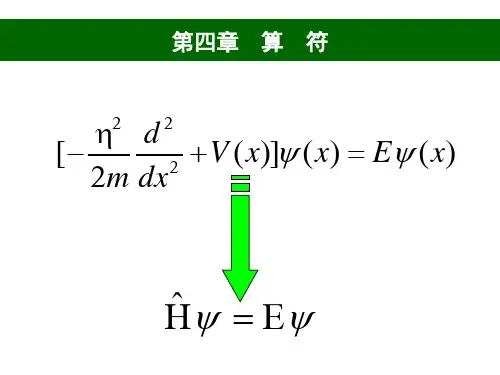
2.哈密顿算符哈密顿算符H在量子力学中描述了体系的能量。

在定态情况下，哈密顿算符作用于波函数后应得到该态的能量值，即：H|ψ⟩= E|ψ⟩其中E为能量的本征值，|ψ⟩为相应的能量本征态。

3.时间演化算符在量子力学中，时间演化算符描述了系统随时间的演化。

设系统在初始时刻t=0时处于量子态|ψ(0)⟩，则该态在后续时刻t的演化由时间演化算符U(t)给出，即：|ψ(t)⟩= U(t)|ψ(0)⟩三、结语算符是量子力学中的重要数学工具，用于描述物理量的测量和演化。

本文介绍了算符的定义、性质以及在量子力学中的应用。

量子力学第三章算符

量子力学第三章算符

第三章 算符和力学量算符3.1 算符概述设某种运算把函数u 变为函数v ，用算符表示为：ˆFuv = （3.1-1） ˆF 称为算符。

u 与v 中的变量可能相同，也可能不同。

例如，11du v dx=，22xu v =3v =，(,)x t ϕ∞-∞，(,)x i p x hx edx C p t -=，则ddx，x dx ∞-∞⎰，x ip x he-⋅都是算符。

1．算符的一般运算（1）算符的相等：对于任意函数u ，若ˆˆFuGu =，则ˆˆG F =。

（2）算符的相加：对于任意函数u ，若ˆˆˆFuGu Mu +=，则ˆˆˆM F G =+。

算符的相加满足交换律。

（3）算符的相乘：对于任意函数u ，若ˆˆˆFFu Mu =，则ˆˆˆM GF =。

算符的相乘一般不满足交换律。

如果ˆˆˆˆFGGF =，则称ˆF 与ˆG 对易。

2．几种特殊算符 （1）单位算符对于任意涵数u ，若ˆIu=u ，则称ˆI 为单位算符。

ˆI 与1是等价的。

（2）线性算符对于任意函数u 与v ，若**1212ˆˆˆ()F C u C v C Fu C Fv +=+，则称ˆF 为反线性算符。

（3）逆算符对于任意函数u ，若ˆˆˆˆFG u G F u u ==则称ˆF 与ˆG 互为逆算符。

即1ˆˆG F -=，111ˆˆˆˆˆˆ,1FG FF F F ---===。

并非所有的算符都有逆算符，例如把零作为算符时，称之为零算符，零算符就没有逆算符。

对于非齐次线性微分方程：ˆ()()Fux af x =，其中ˆF 为ddx与函数构成的线性算符，a 为常数。

其解u 可表示为对应齐次方程的通解u 。

与非齐次方程的特解υ之和，即0u u v =+。

因0ˆ0Fu =，所以不存在1ˆF -使100ˆˆF Fu u -=。

一般说来，在特解υ中应允许含有对应齐次方程的通解成分，但如果当a=0时，υ=0，则υ中将不含对应齐次方程的通解成分，这时存在1ˆF-使11ˆˆˆˆFFv FF v v --==，从而由ˆFvaf =得：1ˆF af υ-=。

量子力学--力学量用算符表示与表象变换 ppt课件

量子力学--力学量用算符表示与表象变换 ppt课件


ppt课件
﹟
4
2、算符的运算性质 （1）算符相等：
若 Aˆ Bˆ
★算符的运算离不开 对波函数的作用
对于任意的波函数都成立
则 Aˆ Bˆ
（特例：若I ，则I 称为单位算符）
（2）算符相加： (Aˆ Bˆ) Aˆ Bˆ
这是算符最基本的运算。
ppt课件
5
交Байду номын сангаас律和结合律：
Aˆ Bˆ Bˆ Aˆ Aˆ (Bˆ Cˆ) (Aˆ Bˆ) Cˆ
用在任意波函数上，看它们是否相等。
若相等，则对易；否则，不对易。
比如将要讨论的位置算符 x 和动量算符 pˆ x 的对易关系。
ppt课件
7
因为对任意波函数ψ ：
xpˆ x
ix
d
dx
而
pˆ x x
i d dx
(x )
i( x d ) i ix d
dx
dx
那么
xpˆ x pˆ x x i
Hˆ pˆ 2 V (r) 2m
2 2 V (r) 2m
其中动量算符 pˆ i，
且
pˆ x
i x
又如前面引进的能量算符
Hˆ i 等 t
ppt课件
2
§3.1 算符的运算规则
1、算符的定义
表示运算的符号叫算符，又叫作用量
如
d， dx
，
, ( )*等
线性算符：
如果算符 Â 满足下列条件
Aˆ(c11 c2 2 ) c1Aˆ 1 c2 Aˆ 2
第三章 力学量用算符表示 与表象变换
前面我们学习了两个量子力学的基本原理
1）微观粒子体系的状态可以用波函数来表示；
2）描述微观粒子运动状态的方程是薛定谔方程；
物理学中的量子力学算符

物理学中的量子力学算符

物理学中的量子力学算符量子力学算符是描述量子体系中物理量的数学符号。

它们起到了连接数学和物理的桥梁作用，在量子力学的研究中扮演着至关重要的角色。

本文将介绍量子力学算符的定义、性质和应用。

一、算符的定义在量子力学中，算符是描述物理量的数学对象。

它们表示了对某一物理量的测量操作，可以通过对量子态作用，得到相应的测量结果。

量子力学中的算符是一个线性操作，它作用在量子态上，将其变换为另一个量子态。

一个算符可以用一个矩阵表示，这个矩阵被称为算符的矩阵表示。

算符的定义可以通过其对量子态的作用来描述。

一个算符作用在一个量子态上，可以得到另一个量子态或者一个实数/复数，表示了对相应物理量的测量结果。

二、算符的性质1. 线性性质：算符是一个线性操作，满足线性组合的性质。

即对于任意两个量子态A和B，以及标量α、β，有F(αA + βB) = αF(A) + βF(B)其中F表示算符。

2. Hermite性质：算符的矩阵表示通常是一个厄米矩阵，即满足Hermitian条件F† = F其中†表示共轭转置。

3. 幺正性质：算符的矩阵表示通常是一个幺正矩阵，即满足Unitary 条件F†F = FF† = I其中I表示单位矩阵。

4. 对易性质：两个算符F和G的对易子为0，即[F, G] = 0，当且仅当F和G的矩阵表示是可交换的。

三、算符的应用1. 算符的本征值和本征态：算符可以在量子体系中寻找本征值和本征态，本征值表示对应物理量的测量结果，本征态表示对应的量子态。

2. 算符的测量：算符作用在量子态上，得到相应物理量的测量结果。

在进行实验测量时，可以通过算符的本征值和本征态来进行计算和预测。

3. 算符的演化：算符可以描述量子体系的演化。

根据量子力学的演化方程，我们可以通过将时间演化算符作用在初始量子态上，得到不同时间的量子态。

4. 算符的代数：算符之间满足代数运算的规律。

通过对算符的代数性质进行研究，可以得到更多有关量子体系的信息和性质。

第三章 量子力学中的力学量

第三章 量子力学中的力学量


1 2πh
eipx/ h
hk E= ≥0 2m
ˆ H p H Lz与 ˆ，ˆ与 ˆ
2 2
k可 续 值 故 是 续 。 连 取 ， E 连 的
能 二 简 。 级 度 并
为啥具有相同的本征态？
（5）坐标算符的本征值和本征函数 ）
ˆ xϕ x′ ( x) = x′ϕ x′ ( x) x′取一切实数 ϕ x′ ( x) = δ ( x − x′)
,
n = 1,2,3L l = 0,1, L n - 1 m = 0,±1 L ± l ，
二、量子力学的基本原理四
在 意 ψ中 ψ = ∑anϕn 任 态 ，
n
测量力学量A，可得到各种可能取值，可能取 值必为某一本征值。
ˆ在 征 谱 取 的 率 | a |2 。 A 本 值 中 A 几 为 n n
2 2 ˆ2 ˆ = Lz = − h ∂ H 2I 2I ∂ϕ2
z
h2 ∂2 − ψ = Eψ 2 2I ∂ϕ
1 imϕ ψm(ϕ) = e 2π m2h2 Em = ≥0 2I
m = 0 ±1 ± 2 L ，， ，
要求： 要求：会求解
(3)求 量 分 px的 征 。 动 x 量ˆ 本 态
∂ −ih ψ = px'ψ ∂x
ˆz = x py − y px = −ih(x ∂ − y ∂ ) ˆ ˆ L ∂y ∂x
1 ∂ ∂2 ∂ 1 ˆ2 L = − h2 sin θ + 2 2 ∂θ sin θ ∂ϕ sin θ ∂θ
从而有
ˆ = ihsin ϕ ∂ +cotθ cosϕ ∂ Lx ∂θ ∂ϕ ˆ = −ihcosϕ ∂ −cotθ sin ϕ ∂ Ly ∂θ ∂ϕ ˆz = −ih ∂ L ∂ϕ
量子力学 算符

量子力学 算符


ˆx ˆ 1 0 ˆx ˆD D
注：对于单纯是作常数乘法的算符，常省略抑扬符。
（5）算符服从乘法结合律
ˆ (B ˆ) (A ˆB ˆ ˆC ˆ )C A
d ˆ ˆ ˆ 3 ˆ ˆ, C , Bx 例如： A dx
ˆ 3x ˆ (B ˆ )] f D ˆC ˆC ˆ (3xf ) 3 f 3xf ˆ, [ A B
量子力学的哈密顿算符：
2 2
px V ( x) 2m
其本征值为体系 能量的可能值
2
d ˆ H V ( x) 2 2m dx
这种经典力学的物理量（如能量，坐标和动量等等） 与量子力学算符之间的对应性是普遍的。这是量子力 学的一个基本假定。即：每一物理量都有一个对应的 量子力学算符。 问题：如何得到物理量F所对应的量子力学算符呢？
第一步：写出F作为笛卡儿坐标和对应动量的函数的经 典力学表示。 第二步：做以下变换：
笛卡儿坐标q代之以该坐标去乘的算符，即：q ˆ q 线动量的每个笛卡儿分量pq代之以算符：
i ˆq p 2 i i q i q q
例:
对应于坐标的算符是乘以坐标：
2 2 d ˆ T ˆ V ˆ H V ( x) 2 2m dx
这与不含时间的薛定谔方程一致。
d [ V ( x)] ( x) E ( x) 2 2m dx
2
2
量子力学算符与体系对应的性质的关系
ˆ 的具有本征值 若i 是 F
a i 的本征函数，则有：
ˆ a F i i i
由此可见，算符的假设和薛定谔方程实际上是一致的。
2
2
量子力学体系的态用包含我们可能了解的关于体系的全 部知识的态函数Ψ(x，t)来描述。Ψ如何给出关于性质F 的知识呢？

量子力学中的量子力学算符

量子力学中的量子力学算符量子力学中的量子力学算符是描述量子系统性质的重要工具。

它们代表了物理量的数学运算符，用于计算和预测系统的态矢量的演化和测量结果。

本文将介绍量子力学算符的基本概念、性质和应用。

1. 算符的定义在量子力学中，算符是表示物理量的数学运算符。

它们作用于态矢量，用于计算物理量的测量结果或表示系统的演化。

量子力学算符通常用大写字母表示，例如位置算符X、动量算符P和能量算符H等。

2. 算符的性质量子力学算符具有多个重要性质，包括线性性、厄米性和厄米算符的本征值问题。

2.1 线性性：量子力学算符是线性的，即对于任意常数a和b，有F(aψ + bφ) = aF(ψ) + bF(φ)，其中F表示任意量子力学算符。

2.2 厄米性：厄米性是量子力学算符的重要性质。

一个算符F的厄米共轭算符F†定义为满足内积关系⟨ψ|F†φ⟩ = ⟨Fψ|φ⟩的算符。

对于厄米算符F，其本征值都是实数。

2.3 厄米算符的本征值问题：对于厄米算符F，存在一组完备正交本征态{φn}，其对应的本征值{fn}都是实数。

即Fφn = fnφn。

这个本征值问题是量子力学中重要的数学工具，可以用于计算物理量的测量结果和态矢量的演化。

3. 常见的量子力学算符量子力学中存在着许多常见的算符，这些算符用于描述各种物理量和系统性质。

3.1 位置算符X：位置算符X表示粒子在空间中的位置。

对于一维情况，位置算符的本征态是位置空间的波函数；对于三维情况，位置算符的本征态是位置空间的波函数。

3.2 动量算符P：动量算符P表示粒子的动量。

对于一维情况，动量算符的本征态是动量空间的波函数；对于三维情况，动量算符的本征态是动量空间的波函数。

3.3 能量算符H：能量算符H表示粒子的能量。

它是量子体系的哈密顿算符，其本征态是能量空间的波函数。

4. 算符的应用量子力学算符在物理学中有广泛的应用。

它们可以用于计算各种物理量的期望值、计算系统的演化和描述量子力学中的各种现象。

第三章力学量用算符表达

性质 II: 两个厄密算符之积一般不是 厄密 算符, 除非二算符对易。
但是坐标算符与其非共轭动量 对易，各动量之间相互对易。
ˆ ˆ x p p x i ˆ ˆ ˆ ˆ p p p p 0
, x, y, z
量子力学中最基本的 对易关系。
ˆ ˆ ˆ ˆ xp y p y x 0 yp x p x y 0 ˆ ˆ ˆ z pz x 0 ypz pz y 0 ˆ xp ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ p x p y p y p x 0 p y pz pz p y 0
Ô(c1ψ1+c2ψ2)= c1Ôψ1+c2Ôψ2
其中c1, c2是任意复常数， ψ1, ψ1是任意两个波函数。 例如：
动量算符 单位算符
ˆ p i ˆ I
是线性算符。
开方算符、取复共轭就不是线性算符。 注意：描写可观测量的力学量算符都是线性算符，这是态叠加原理的反映。
（2）算符相等
例如：体系Hamilton 算符
显然，算符求和满足交换率和结合率。
注意，算符运算没有相减，因为减可用加来代替。 Ô - Û = Ô + （-Û）。 很易证明线性算符之和仍为线性算符。
（4）算符之积
一般来说算符之积不满足 交换律，即 ÔÛ ≠ ÛÔ 这是算符与通常数运算 规则的唯一不同之处。
若Ô (Û ψ ) = (ÔÛ) ψ =Êψ 则ÔÛ = Ê 其中ψ是任意波函数。
ˆ iLz
同理 ˆ ˆ ˆ [ L , L ] iL
y z
x
ˆ ˆ ˆ [ Lz , Lx ] iLy
合记之： ˆ ˆ [ L , L ] i

量子力学中的量子力学力学算符和观测值

量子力学中的量子力学力学算符和观测值量子力学中的量子力学算符和观测值量子力学是描述微观世界中粒子行为的一种物理学理论，它以算符和观测值的概念为核心。

量子力学算符是用来描述物理量的数学表达式，而观测值则是对实际物理量的测量结果。

本文将详细介绍量子力学中的算符和观测值，以及它们之间的关系。

一、量子力学算符1. 算符的定义在量子力学中，算符是用来描述物理量的数学表达式。

算符作用于量子态，能够产生测量的结果。

量子力学中常见的算符有哈密顿算符、动量算符、角动量算符等等，它们分别对应不同的物理量。

2. 算符的性质算符具有以下几个重要的性质：（1）线性性：算符的线性性意味着它可以对两个或多个量子态线性叠加，且叠加后的态所对应的物理量等于对应量子态物理量的线性叠加。

（2）厄米性：算符的厄米性表明其与共轭转置相等，即算符的厄米共轭等于其自身。

（3）幺正性：算符的幺正性表示其逆算符等于其厄米共轭。

3. 算符的代数运算在量子力学中，算符之间可以进行代数运算，常见的运算有相加、相乘和对易等。

（1）相加：对于两个算符A和B，它们可以进行相加运算，即A+ B。

（2）相乘：两个算符A和B的相乘可以有两种方式：A * B和AB。

其中，A * B表示两个算符按照给定的次序先后作用，而AB表示两个算符的乘积。

（3）对易：如果两个算符A和B的乘积AB等于BA，则称它们是可对易的。

二、观测值观测值是通过实际测量得到的物理量的数值。

在量子力学中，观测值与算符之间有着密切的关系。

1. 算符和物理量每个物理量都对应一个算符，这个算符称为该物理量的算符。

当一个算符作用于量子态时，会给出该物理量的一个可能的观测值。

2. 观测和测量在量子力学中，观测是指对量子系统进行实验，通过测量来得到物理量的值。

观测值即为测量结果，它代表了量子系统在对应物理量上的数值。

3. 观测值的统计解释量子力学中，观测值的统计解释是指重复进行同一测量，经过一定次数的实验后，观测值的频率趋向于某个特定值。

第三章 力学量的算符.


若两个算符 Ô、Û 对体系的任何波函数ψ 有： ( Ô + Û) ψ= Ôψ+ Ûψ= Êψ 则Ô + Û = Ê 称为算符之和。
例如：体系Hamilton 算符 算符求和满足交换率和结合率。 注意，算符运算没有相减，因为减可用加来代替。 Ô - Û = Ô + （-Û）。 很易证明线性算符之和仍为线性算符。
f
f
j , j 1,2,, f
ˆ F ˆ F A ji ni nj
f
ˆ A ji F ni
i 1
f
i 1
Fn A ji ni
i 1
f
Fn nj
算符 F 本征值 Fn简并 的本质是当 Fn 确定后 还不能唯一的确定状态， 要想唯一的确定状态还 得寻找另外一个或几个 力学量算符，F 算符与 这些算符对易，其本征 值与 Fn 共同确定状态。
在势场中 V ( r ) 的粒子 H T V
2 ˆ T ˆ V (r ) 2 V (r ) H 2m
问题：算符、动量算符、 Hamilton算符
§3-2
算符的本征值和本征函数
ˆ F F n n n
其中Fn, ψn 分别称为算符 F的本征值和相应的本征态， 上式即是算符 F 的本征方程。求解时，ψ 作为力学量 的本征态或本征函数还要满足物理上对波函数的要求 即波函数的标准条件。
定理I：体系任何状态ψ下，其厄密算符的平
均值必为实数。
证：
F
ˆ d * F
ˆ ) * d ( F
ˆ ]* [ d * F
F*
逆定理：在任何状态下，平均值均为 实数的算符必为厄密算符。
定理II：厄密算符的本征值必为实。

第12讲厄米算符的本征值和本征函数、算符与力学量的关系

令c = 1，得： 令c = i，得：
d
d
1
ˆ d ( F ˆ ) * d * F *F 2 2 1 ˆ 1 ) * 2 d ( F 2 ˆ 1
ˆ d ( F ˆ ) * ] [ d ( F ˆ ) * d * F ˆ ] [ d 1 * F 2 1 2 2 1 2 1
（四）实例
（1）动量本征函数组成正交归一系 （2）线性谐振子能量本征函数组成正交归一系
（3）角动量本征函数组成正交归一系
1. Lz 本征函数
2. L2本征函数
（4）氢原子波函数组成正交归一系
§6 算符与力学量的关系
（一）力学量的可能值
（1） 力学量算符本征函数组成完备系
（2） 力学量的可能值和相应几率
i 1 i 1
Fn nj
因为
j , j 1,2, , f
f2 - f(f+1)/2 = f(f-1)/2 ≥ 0，
算符 F 本征值 Fn简并的本质是： 当 Fn 确定后还不能唯一的确定状 态，要想唯一的确定状态还得寻找 另外一个或几个力学量算符，F 算 符与这些算符两两对易，其本征值 与 Fn 一起共同确定状态。
（2）分立谱、连续谱正交归一表示式
1. 分立谱正 交归一条 件分别为： 3. 正交归一系
n * n d 1 m * n d 0

m
* nd 0
[证毕]

m
* n d mn
2. 连续谱正 交归一条 件表示为：
* d ( )
1. ψ nj是本征值Fn的本征函数。
2. 满足正交归一条件的f个新函数ψnj可以组成。 为此只需证明线性 叠加系数 Aji 的个 数 f 2 大于或等于 正交归一条件方程 个数即可。

量子力学第三章算符

第三章 算符和力学量算符３.1 算符概述设某种运算把函数u 变为函数v ，用算符表示为:ˆFuv =(3.1-1）ˆF 称为算符。

ｕ与v 中的变量可能相同,也可能不同。

例如，11du v dx =,22xu v =3v =，(,)x t ϕ∞-∞,(,)x i p x hx edx C p t -=,则ddx dx ∞-∞⎰，x ip x he-⋅都是算符。

1.算符的一般运算(1)算符的相等：对于任意函数u ，若ˆˆFuGu =,则ˆˆG F =。

(2）算符的相加：对于任意函数u,若ˆˆˆFuGu Mu +=，则ˆˆˆM F G =+。

算符的相加满足交换律。

（3)算符的相乘：对于任意函数u ，若ˆˆˆFFu Mu =，则ˆˆˆM GF =。

算符的相乘一般不满足交换律。

如果ˆˆˆˆFGGF =，则称ˆF 与ˆG 对易。

2.几种特殊算符 （１）单位算符对于任意涵数u,若ˆIｕ=u ，则称ˆI 为单位算符。

ˆI 与１是等价的。

(2)线性算符对于任意函数ｕ与v ，若**1212ˆˆˆ()F C u C v C Fu C Fv +=+,则称ˆF 为反线性算符。

(3）逆算符对于任意函数u ，若ˆˆˆˆFGu GFu u ==则称ˆF 与ˆG 互为逆算符。

即1ˆˆGF -=,111ˆˆˆˆˆˆ,1FG FF F F ---===。

并非所有的算符都有逆算符,例如把零作为算符时，称之为零算符，零算符就没有逆算符。

对于非齐次线性微分方程：ˆ()()Fu x af x =，其中ˆF为ddx与函数构成的线性算符，a 为常数。

其解u 可表示为对应齐次方程的通解u 。

与非齐次方程的特解υ之和，即0u u v =+。

因0ˆ0Fu =，所以不存在1ˆF -使100ˆˆF Fu u -=。

一般说来，在特解υ中应允许含有对应齐次方程的通解成分，但如果当ａ＝０时,υ=0，则υ中将不含对应齐次方程的通解成分,这时存在1ˆF-使11ˆˆˆˆFFv FF v v --==,从而由ˆFvaf =得:1ˆF af υ-=。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(2) 本征问题
ˆ A L2 的本征方程
1 1 2 2 (sin ) 2 Ylm ( , ) 2Ylm ( , ) sin sin 2
ˆ L2Yl ,m ( , ) l l 12 Yl ,m ( , )
（2） 本征能量
能量取下列离散值时，才有满足波函数有限性条件的解
mZ 2es4 Z 2es2 1 En 2 2 2 , n 1,2,3, 2 n 2a0 n
4 2 0 a0 me 2
玻尔第一轨道半径
n称为主量子数
E
电子的能量只与量子数n有关,
es2 • 氢原子的基态能量为 E1 13.6eV 2a0 • 若要使处于基态的氢原子电离，必须外加 13.6eV的能量 • 随量子数n的增加，氢原子能级间隔越来越 小，当n→∞时能级接近连续分布
• 厄米算符在任意状态下的平均值必须是实数 • 力学量观测值必须是实数，要求算符的本征值是实数 • 线性厄米算符的作用就是把态空间中的一个元素变成另一个 元素 • 线性厄米算符的本征函数构成一个正交归一的函数系
量子力学中代表力学量的算符必须是线性厄米算符
—— 量子力学的又一基本概念
第二节
（1） 厄米算符本征函数的正交归一性 (Orthonormality)
波函数为 ( x) 也就是说，此时粒子不处于本征态。 在此状态下，测量粒子的能量 由于波函数是归一化的
1 2 2 9 2 2 5 2 2 1 ) E ( E1 E3 ) ( 2 2ma 2ma 2ma 2
3 轨道角动量算符的本征值和本征函数
第三节
• 若位势与坐标的方向无关，即 V (r ) V (r ) ，则称此位势为 中心力场 • 粒子若在中心力场中运动，角动量是表征体系转动性质的 重要物理量 • 为区别自旋角动量，将其称之为轨道角动量
第三章 量子力学中的力学量

算符
厄米算符的本征函数 动量算符和角动量算符 电子在库仑场中的运动 基本对易关系
重点：厄米算符 平均值 角动量算符 对易关系
第一节
算符
算符 operator
算符是指作用在一个函数上得出另一个函数的运算符号
ˆ Fu v
算符的引入规则
ˆ F
就是一个算符
• 如果量子力学中的力学量F在经典力学中有相应的 力学量，则表示这个力学量的算符由经典表示式 F(r,p)中将动量p换为动量算符得出
Ylm ( , ) Rnl (r ) 的形式不同
同一能量级对应着不同的本征函数 ——库仑场中运动的电子能级是简并的 简并度为

l 0
n 1
n 2 l n 2 (2l 1)
l 0
n 1
电子的能级是n2度简并的
mZ 2es4 例1 对能级 E3 简并度是9，9个不同的波函数(9 2 18 个不同的本征态)有相同的能量

并的，且简并度为 f 2l 1
例题
若粒子处于状态
5 1 1 ( , ) Y21 ( , ) Y20 ( , ) Y31 ( , ) 3 3 3 ˆ ˆ 求：分别测量 L2与Lz 的可能取值与相应的取值概率
解：首先判断波函数是否是归一化的状态 其次计算各种条件下各力学量的可能取值和取值概率
A n n n
（2）当体系处于Â的非本征态 时，力学量A为何值？ •在非本征态中测量力学量的值为一平均值，当体系处于算符Â 的非本征态时，测量力学量A所得为平均值，如果已经归一 化，力学量的平均值为 ˆ
A (r) A (r)d
A
如果尚未归一化，力学量的平均值为
势能
动能
U (r )
总能量 E T U (r )
角动量
Lrp
ˆ r p r (i) ˆ L
算符的本征值和本征函数
• 若一个算符作用在波函数上得出一个常数乘以该 ˆ 波函数 ，如 F f ，则称此方程为该算符的
n n n
本征方程，称此常数fn为算符F的第n个本征值，波
函数为fn相应的本征波函数
简并 degeneration • 当算符Â的某一本征值n的本征函数不止一个， 而是 f 个线性无关的函数n1、 n2、 nf，则称 该本征值 f 度简并。
ˆ A ni n ni
(i 1,2,, f )
线性算符 linear operator
设u1、 u2为任意函数，c1、c2是任意两个复常数，如果
ˆ (r, p) F (r,i) ˆ F ˆ ˆ
经常遇到的力学量所对应的算符
名称 坐标 动量 力学量 Operator 算符
r
p
p T 2m
ˆ rr
ˆ p i ˆ (r ) U (r ) U ˆ p2 2 2 ˆ T 2m 2m ˆ T U (r ) ˆ ˆ H
本征函数
Ylm ( , )
(3)讨论
ˆ L2Yl ,m ( , ) l l 12 Yl ,m ( , )
ˆ LzYlm ( , ) mYlm ( , )
l 0,1,2,3, m 0,1,2,3, l
ˆ ˆ 算符 L2与L 的本征值是量子化的，只能取断续值 z 除了 l 0 的基态外，算符 L2 ˆ 的所有本征值都是简
o
E2 E1 氢原子能级图
（3）能级的简并度
ˆ H nlm (r, , ) En Rnl (r )Ylm ( , )
电子的能级En只与主量子数n有关 对应一个n值， 可以取 0,1,2n-1 共n个 l m又可以取 0,1, 2,… l 共2l+1个 对应一个l 值， • l、m不同，函数 •
ˆ ˆ ˆ A(c1u1 c2 u 2 ) c1 Au1 c2 Au 2 则称Â为线性算符
• x、d/dx是线性算符，而开方运算不是线性算符 • 量子力学中用来表示力学量的算符，都是线性算符 • 是态叠加原理的要求
ˆ A 1 1 设 ˆ A 2 2 也就是假设说是二度简并的 根据态的叠加原理 c1 1 c2 2 ˆ 也是算符Â的本征态，应有 A
(1) 轨道角动量算符定义 ex e y ez
ˆ ˆ L rp x
ˆ Lx y ˆ z z ˆ y p p
(y z ) i z y
ˆ px
y ˆ py
z ˆ pz
ˆ ˆ ˆ Ly zpx xpz
ˆ ˆ ˆ Lz xp y ypx
ˆ ˆ ˆ ˆ L2 L2 L2 L2 x y z
ˆ (r) A (r)d
(r) (r)d
根据本征函数的完全性
(r) cn n (r) n 1 ˆ (r) c A (r) ˆ A n n
用*左乘上式并对全空间积分
m m
n 1
ˆ ˆ (r) A (r)d ( c ) A( cn n )d
例如：l=2时
ˆ L2Y2,m ( , ) 6 2 Y2,m ( , )
m可以取-2,-1,0,1,2;五个值
ˆ L2Y2,2 ( , ) 6 2 Y2,2 ( , ) ˆ L2Y2,0 ( , ) 6 2 Y2,0 ( , ) ˆ L2Y2,2 ( , ) 6 2 Y2,2 ( , )
1 (r) n (r)d mn 0
m
( m n) ( m n)
（2） 完备性(Completeness)
设1 、2、 、n，是某一线性厄米算符的本征函数系，任 何与{n}满足同样边界条件且在同样区间定义的波函数,都 可以按{n}展开，即
B Lz的本征值和本征函数
ˆ L2Y2,1( , ) 6 2 Y2,1( , ) ˆ L2Y2,1( , ) 6 2 Y2,1( , )
• Lz表示体系的轨道角动量在z轴方向的投影
ˆ LzYlm ( , ) mYlm ( , )
本征值
Lz m
l 0,1,2,3, l 称为角量子数，表征角动量的大小 m称为磁量子数 m 0,1,2,3, l
• 本征值为
L2 l (l 1) 2
• 本征函数
Ylm ( , )
Spherical-harmonics
球谐函数，不仅应当在全空间有限，而且是一个单值函数
一个本征值对应2l+1个本征函数，本征值是2l+1度简并的
ˆ 算符L2的本征值为：L2 l (l 1) 2
在态下，相应的取值概率公式为
W（L 6 ）＝ c 21 c 20
2 2 2 2
2 2
W（L l (l 1) ）＝ clm
ml
l
2
ˆ 算符Lz的本征值为：Lz m
W（Lz 0）＝ c 20
2
2 3
W（L 12 ）＝ c31
它们是
l 2
m 0,1,2 322 , 321 , 320 , 321, 322 l 1 m 0,1 311 , 310 , 311 l 0 m 0 300
当Â为线性算符时
ˆ ˆ A A(c1 1 c2 2 ) (c1 1 c2 2 )
1 厄米算符 Hermitian operator
设u、 v为两个任意函数，如果算符Â满足 ˆ ˆ [ Au (r)]v(r)d u (r) Av(r)d


则称Â为厄米算符
2
例：设粒子在一维无限势阱(0,a)中运动，如果描述粒子状态的
1 [ 1 ( x) 3 ( x)] 状态时，粒子的能量？ 2 nx , (0 x a ) 2 / a sin 本征函数为： n ( x) a 0, ( x 0, x a) 解： H ( x) 1 [ H ( x) H ( x)] ˆ ˆ ˆ 1 3 2 1 1 [ E1 1 ( x) E3 3 ( x)] E [ 1 ( x) 3 ( x)] E 2 2