正则表达式的DFA压缩算法_杨毅夫
- 格式:pdf
- 大小:1.02 MB
- 文档页数:7

dfa算法原理
DFA算法全称为DeterministicFiniteAutomaton,即确定有限状态自动机。
该算法是一种基于有限状态机的模式匹配算法,常用于字符串匹配、编译器、正则表达式等领域中。
DFA算法的基本原理是将模式串和文本串视为有限状态自动机的输入,通过状态转换的方式匹配模式串和文本串之间的关系。
具体来说,可以将匹配过程表示为从初始状态开始,经过状态转移,最终到达接受状态的过程。
为了实现这一过程,我们需要对模式串和文本串进行预处理。
首先,将模式串转化为DFA图,确定初始状态和接受状态,并标记每个状态对应的字符。
然后,在匹配文本串时,根据当前状态和下一个字符,进行状态转移,直至到达接受状态,或者匹配失败。
DFA算法的优点在于其匹配效率高、空间复杂度低。
但是,对于一些复杂的模式串,如带有通配符的,DFA算法可能无法实现精确匹配。
总的来说,DFA算法是一种常用的模式匹配算法,具有高效、简便等特点,值得我们深入学习和掌握。
- 1 -。
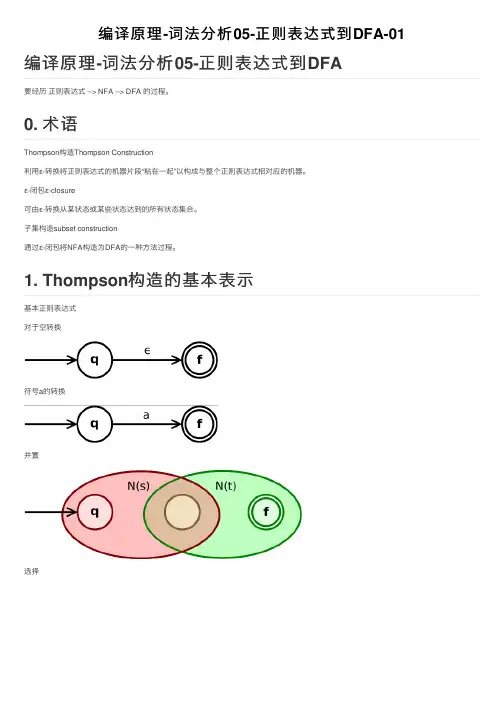
编译原理-词法分析05-正则表达式到DFA-01要经历 正则表达式 --> NFA --> DFA 的过程。
Thompson 构造Thompson Construction
利⽤ε-转换将正则表达式的机器⽚段“粘在⼀起”以构成与整个正则表达式相对应的机器。
ε-闭包ε-closure
可由ε-转换从某状态或某些状态达到的所有状态集合。
⼦集构造subset construction
通过ε-闭包将NFA 构造为DFA 的⼀种⽅法过程。
基本正则表达式
对于空转换
符号a
的转换
并置选择编译原理-词法分析05-正则表达式到DFA 0. 术语
1. Thompson 构造的基本表⽰
重复
(ε|a*b)
2. ⽰例
3. NFA2DFA——⼦集构造算法
input:NFA N
output:DFA D
计算字母表 ∑
计算NFA的开始状态的ε-闭包,作为 D 的初始状态,且未被标记。
while (在 D 中存在未被标记的状态 T)
{
取出T,为 T 加上标记 //出栈
for (在∑中的每个字符a) //遍历字母表
{
states = move (T,a) // 从T经过字母a转换的状态集合
U = ϵ-closure(states) //计算states的闭包
if (U 不在 D 中) {
将 U 加⼊ D 中,且未被标记 //新增⼀个状态,且转为的字符为a
}
T[a]=U //记录转换
}
}
同样可以使⽤表驱动来完成构造过程。
NFA的状态集合DFA上的状态a b c。

正则表达式的DFA算法1正则表达式的定义一个正则表达式RE是符号集合Σ{ε,|,·,某,(,)}上的一个字符串,它可以递归定义如下:空字符ε是正则表达式。
任意字符α∈Σ是正则表达式。
如果RE1和RE2都是正则表达式,则(RE1),(RE1·RE2),(RE1|RE2)和(RE1某)亦是正则表达式。
通常(RE1·RE2)可以简写为RE1RE2。
符号“·”,“某”,“|”称为操作符,可以通过为每个操作符赋予优先级来消除更多的括号。
为了方便起见,这里使用了额外的后缀操作符“+”,它的含义是RE+=RE·RE 某。
其他所使用的操作符如””,字符组,”.”等实际上都可以用上面的方式来表达。
下面定义正则表达式所表达的语言。
如果RE是ε,则L(RE)={ε},即空串。
如果RE是α∈Σ,则L(RE)={α},即包含一个字符的单串。
如果RE是(RE1)这种形式,则L(RE)=L(RE1)。
如果RE是(RE1RE2)这种形式,则L(RE)=L(RE1)L(RE2),其中W1W2可以看成是字符串集w的集合,其中,w=w1w2并且w1∈W1,w2∈W2。
操作符表示字符串的连接。
如果RE是(RE1|RE2)这种形式,则L(RE)=L(RE1)∪L(RE2),是这两种语言的并集,“|”称为并操作符。
如果RE是(RE1某)这种形式,则L(RE)=L(RE)某=∪i≥0L(RE)i,其中L0={ε}并且Li=LLi-1,它表示字符串集合是由0个或者多个RE1表达的字符串连接而成。
“某“称为星操作符。
在文本T中搜索正则表达式RE的问题就是找到文本中所有属于语言L(RE)的字串。
搜索的方法是首先将正则表达式解析成一颗表达式树,然后将表达式树转换成非确定性有限自动机(NFA)。
直接使用NFA进行搜索是可行的,然而NFA算法处理速度通常比较慢,一般的,搜索过程最坏情况时间复杂度是O(mn),但是所需存储空间并不多。

dfa递归构造法DFA递归构造法是一种基于递归的算法,用于将给定的正则表达式转换为等效的DFA。
DFA递归构造法是将一个正则表达式分解为更小的部分,找到每个部分的DFA,然后组合它们以形成整个正则表达式的DFA。
本文将介绍DFA递归构造法的步骤。
步骤1:构建基础状态首先,需要构建正则表达式的基础状态。
将正则表达式中的每个字符作为一个状态,并在其中添加一个转移。
连接起来,形成一个基本的DFA。
这些基础状态将被用于构建更复杂的状态。
例如,一个正则表达式“ab”的基础状态将如下所示:```a -> STATE1InitialState -> STATE2 -> b```其中,InitialState是开始状态,a、b分别表示DFA的输入字符,STATE1和STATE2分别表示两个状态。
步骤2:构建复合状态接下来,需要构建由多个字符组成的复合状态。
例如,""ab"" 表示字符“a”和“b”按顺序出现。
在DFA中,这意味着先从“a”输入的状态开始,在此状态上接收到“b”的输入后进入下一个状态。
为了实现这一点,需要将所有基本状态组合在一起,形成一个新的复合状态。
DFA的每个复合状态都由一个或多个基本状态组成,并且具有一个或多个输入字符的转移。
例如,“ab”可以表示为一个复合状态,如下所示:```a -> STATE1 -> b```其中,STATE1是由基础状态组成的复合状态。
步骤3:构建括号表达式接下来,需要处理括号表达式,它由子表达式、或操作符和括号组成。
需要转换的正则表达式可能包含括号表达式,例如“(a|b)”和“(ab)+”等。
在DFA中,这意味着可以有多个路径到达一个状态。
为了解决这个问题,需要为每个括号表达式构建一个状态机。
这意味着要递归地解析每个括号表达式,然后将结果合并到单个DFA中。
结果是一个DFA,其中每个状态都可以被多个输入字符到达。

dfa转化为正则表达式方法
一。
DFA 这玩意儿,说起来可能让人头大,但咱别怕!把 DFA 转化成正则表达式,其实有窍门。
1.1 先得搞清楚 DFA 是啥。
简单说,就是个状态机,根据输入的字符在不同状态间跳来跳去。
就像走迷宫,不同的路有不同的规则。
1.2 那为啥要转成正则表达式呢?因为正则表达式用起来更方便,更灵活,能解决好多实际问题。
二。
接下来咱说说具体咋转。
2.1 第一步,得仔细观察 DFA 的状态和转换关系。
这就好比摸清敌人的底细,知道每个状态是咋来的,咋走的。
2.2 然后,根据状态之间的关系,找出一些规律和模式。
这可需要点眼力和耐心,别着急,慢慢看。
2.3 比如说,有些状态总是一起出现,或者某些转换总是重复,这都是重要线索。
三。
举个例子给您瞅瞅。
3.1 假设咱有个简单的 DFA,就俩状态,一个起始状态,一个结束状态。
从起始状态输入“a”到结束状态,那正则表达式不就是“a”嘛,多简单!
3.2 再复杂点的,多个状态,多种输入字符,别怕,按照前面说的方法,一步一步来,总能找到规律,写出正则表达式。
把 DFA 转成正则表达式,需要细心、耐心,多练习,熟能生巧。
掌握了这本事,处理好多问题都能事半功倍,轻松搞定!。

正则表达式转DFA一、设计原理1.正则表达式转换为带ε的NFA(Thompson构造法)2.ε-NFA转为DFA3.最小化DFA4.DFA状态转换表判断是否接受输入字符串二、算法描述1.正则表达式转换为NFA(1)建立字母表。
输入的正则表达式由于一般不输入“与”操作符,因此首先给表达式加入 .作为与操作。
再利用逆波兰式的堆栈操作,把操作符与字母分开,便得到了字母表。
(2) Thompson构造法。
首先将构成正则表达式的各个元素分解,对于每一个元素,按照下述规则1和规则2生成NFA。
注意:如果r中记号a出现了多次,那么对于a的每次出现都需要生成一个单独的NFA。
规则1 对于空记号ε,生成下面的NFA。
规则2 对于Σ的字母表中的元素a,生成下面的NFA。
所有字符生成完之后,便根据规则3,把生成的NFA组合在一起。
规则3 令正则表达式s和t的NFA分别为N(s)和N(t)。
a) 对于s|t,按照以下的方式生成NFA N(s|t)。
b) 对于st,按照以下的方式生成NFA N(st)。
c) 对于s*,按照以下的方式生成NFA N(s*)。
d) 对于(s),使用s本身的NFA N(s)。
(3)记录含Epsilon的NFA状态之间转换及输入字母。
由于Epsilon符号不能输出,因此在程序中了利用$代替。
2. ε-NFA转为DFA利用ε-closure规则即闭包规则,把NFA状态划分成集合,而后把每个集合作为DFA的状态。
详细描述:从NFA的状态S开始经过ε到达的状态存储下,然后再把存储结果中的状态有经过ε到达的新状态也存储在一起,这样通过闭包规则就可以这些集合,再把集合作为DFA的状态。
3. 最小化DFA取出DFA状态中的不可达的状态。
4. DFA状态转换表判断是否接受输入字符串利用上次编写的DFA程序中的方法,把状态转换表放入二维数组,再通过读入输入字符串的一个字符状态跳转,假如读完输入串后的结果是到达终态,那么表明该字符串被自动机接受,否则不接受。
dfa算法的工作原理
DFA(确定有限状态自动机)算法是一种用于识别和匹配输
入模式的算法。
它的工作原理可以分为以下几个步骤:
1. 确定有限状态:首先,定义一个有限的状态集合,每个状态代表输入模式的一个状态。
通常有一个初始状态和一个或多个接受状态。
2. 构建状态转换表:针对每个输入符号,从每个状态定义可能的下一个状态。
这些状态转换定义通过一个状态转换表来表示,其中每个表项包含起始状态、输入符号和下一个状态。
3. 执行输入匹配:输入字符串被逐个字符地读入,然后将当前状态根据相应的状态转换表进行转换。
如果在转换结束的过程中达到接受状态,则匹配成功。
4. 匹配失败处理:如果在状态转换过程中没有找到匹配的下一个状态,或者字符串的所有字符已经读取但没有达到接受状态,那么匹配失败。
DFA算法的关键点是其高效的状态转换机制,通过事先构建
状态转换表,可以在O(1)的时间复杂度内进行状态转换和匹配。
这使得DFA算法在处理大量输入数据时具有较高的性能
和效率。
dfa原理
DFA(Deterministic Finite Automaton)是一种有限状态自动机,用于识别正则语言。
它由五个元素组成:一个有限的状态集合、一个有限的输入符号集合、一个转移函数、一个初始状态和一组接受状态。
它的原理是在给定输入的情况下,从初始状态开始,根据输入符号和状态转移函数的规则,自动地向前转移到下一个状态,直到达到接受状态或无法继续转移。
DFA具有确定性,即对于每个状态和输入符号对,只存在一
个唯一的下一个状态。
这使得DFA的行为是可预测和确定的。
DFA还具有有限状态空间,因为状态数量是有限的,所以它
可以在有限的时间内处理任何输入字符串。
DFA的转移函数定义了从一个状态到另一个状态的转移规则。
可以根据当前状态和输入符号来确定下一个状态。
一旦到达某个接受状态,DFA就会停止并接受输入字符串,否则它会继
续转移状态。
DFA可以用来识别正则表达式中的模式。
例如,在文本中搜
索特定的单词或字符串。
它可以较快地进行模式匹配,因为它的状态转移是直接和确定的。
总之,DFA是一种用于识别正则语言的自动机。
它通过从初
始状态开始,根据输入符号和状态转移函数的规则,自动地向前转移状态,直到达到接受状态或无法继续转移。
它的主要特点是确定性和有限状态空间。
正则表达式转dfa例题
正则表达式(Regular Expression)是描述字符串模式的一种方式,而确定有限状态自动机(DFA,Deterministic Finite Automaton)是一种用于识别正则表达式描述的字符串模式的计算机科学概念。
下面我将简要介绍一个例题,说明如何将正则表达式转换为DFA。
假设我们有一个简单的正则表达式,(a|b)abb.
首先,我们需要将正则表达式转换为NFA(Nondeterministic Finite Automaton),然后再将NFA转换为DFA。
1. 将正则表达式转换为NFA:
首先,我们需要将正则表达式转换为后缀表达式,然后根据后缀表达式构建NFA。
这里省略了具体的转换步骤,但需要注意的是,NFA中的状态表示了正则表达式中的每个字符或操作符。
2. 将NFA转换为DFA:
接下来,我们使用子集构造法(Subset Construction)将NFA转换为DFA。
这个过程涉及到状态的转移和状态的合并,最终得到一个等价的DFA。
在这个例题中,我们可以得到一个DFA,它包含了多个状态和状态之间的转移,最终可以用来识别符合正则表达式描述的字符串模式。
需要注意的是,正则表达式的复杂程度和特性会影响到转换的复杂程度,有些正则表达式可能会转换成更简单的DFA,而有些可能会比较复杂。
同时,转换过程中需要考虑一些特殊情况,比如空字符、闭包操作等。
希望这个简要的例题能够帮助你理解如何将正则表达式转换为DFA。
如果你对具体的转换步骤或其他相关内容有更多疑问,欢迎继续提问。
正则表达式-NFA-DFA-化简DFA 原本我也是学习如何将正则表达式⼀步步化到DFA,搜索发现很多不是死板的定义,就是跨度太⼤,所以我决定⽤⼀道例题,看看它是如何转化的,本次以正则表达式:(a|b)*(aa|bb)(a|b)* 为例。
我看到和多⼈会介绍将正则表达式转化为NFA的规则,为了便于理解我也选择简单说⼀下,正则表达式转化为NFA会有基本的⼀个开始,⼀个结束,结束为双圈,其余的都是单圈。
圆圈⾥的是状态,圈到圈的线上代表的⼀个状态到另⼀个状态的转化条件。
对于⼀个识别空字符的NFA便是: 它不需要识别任何字符便可以从开始状态转化为终结状态。
所有从开始状态最从转化为终结状态的线路上的字符串的集合便是这个NFA 和正则表达式所表⽰字符串集合。
简单的对于⼀个终结符a: 假如我们现在有两个NFA,⼀个表⽰识别字符s,记为 N(S); ⼀个识别字符t,记为 N(T)。
那么我们如何表⽰⼀个识别字符串 st 的NFA 呢?它的规则是将两个NFA连接,只保留⼀个初始状态,⼀个终结状态。
如何表⽰识别字符 s 或者字符 t 的NFA呢? 很容易理解,⽆论选择哪条路,都可以从初始状态转化为终结状态,所以这个NFA可以识别 N(S) 或者 N(T) 能够识别的字符串集合。
现在我们继续想⼀下如何识别n个字符 s 呢?我们可以将N(S)的⾸尾相连,这样就会循环⼀次或多次,就可以识别⼀个或者多个字符 s ,那么零个的情况呢?我们可以直接将 N(S) 的前后相连,这样便也可以选择直接跳过 N(S) 了,如下图所⽰: 上⾯便是基本的构建NFA的规则,下⾯给出⼏个基本的例⼦: 对于 a|b: 对于 (a|b)*: 对于(a|b)*c: 其实在⾃⼰做题的时候不需要⼀步步画这么⿇烦的图,上⾯这么多 ‘空’,看着就让⼈头⼤了。
下⾯以(a|b)*(aa|bb)(a|b)* 为例,根据正则表达式画出稍微看着简单的nfa图: 根据的规则是从正则表达式开头开始,遇到 ' * '就先画⼀个圈,前后两个空,根据 ’ * ‘包含的内容在这个圈的周围继续画圈和线。
2009年10月Journal on Communications October 2009 第30卷第10A期通信学报V ol.30No.10A正则表达式的DFA压缩算法杨毅夫1,2,3,刘燕兵1,2,3,刘萍1,3,郭牧怡1,2,3,郭莉1,3(1. 中国科学院计算技术研究所,北京 100190;2. 中国科学院研究生院,北京 100039;3. 信息内容安全技术国家工程实验室,北京 100190)摘要:基于确定有限自动机(DFA)的正则表达式匹配技术通常用于网络流量实时处理、病毒检测等系统中。
随着正则表达式的数量不断增加,DFA的存储空间急剧膨胀。
为此,提出了一种有效的DFA压缩算法——簇分割算法,首先总结了DFA的一个结构特征;然后依据此特征把DFA分割为3个部分分别存入3个矩阵中,由此构造出2个特征明显的矩阵和1个典型的稀疏矩阵;最后分别对3个矩阵进行压缩。
实验表明,簇分割算法在各组数据中均达到了很好的压缩效果,空间压缩率比较稳定。
关键词:字符串匹配;自动机压缩;正则表达式;入侵检测中图分类号:TP302 文献标识码:A 文章编号:1000-436X(2009)10A-0036-07Effective algorithm of compressing regular expressions’ DFAYANG Yi-fu1,2,3, LIU Yan-bing1,2,3, LIU Ping1,3, GUO Mu-yi1,2,3,GUO Li1,3(1. Institute of Computing Technology Chinese Academy of Sciences, Beijing 100190, China;2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China;3. National Engineering Laboratory for Information Security Technologies, Beijing 100190, China)Abstract: Regular expression matching technology based on DFA is often used in network real-time processing and virus detection systems. With the number of regular expressions growing, the storage of DFA expands rapidly. An effective al-gorithm of compressing regular expressions’ DFA was presented, which was called cluster-split algorithm. Firstly, a structural characteristic of DFA was summarized. Secondly, the DFA was divided into three parts based the characteristic.Finally, the three parts was compressed respectively. Experiments show that cluster-split algorithm achieves good effects in all test data, and its space compression rate is relatively stable.Key words: string matching; automaton compression; regular expressions; intrusion detection1引言近年来,正则表达式匹配技术成为计算机安全领域研究的热点问题。
正则表达式广泛应用于入侵检测/入侵防御、病毒检测、协议识别等系统中,如Snort[1]、Bro[2]、L7-filter[3]等。
随着网络带宽和流量的膨胀以及需要处理的正则表达式规模的不断增加,传统的正则表达式匹配技术正面临严峻的挑战。
传统的正则表达式匹配技术主要是基于非确定有限自动机(NFA)实现的,其匹配速度较慢,并且每次匹配都需要逐条扫描每条表达式。
随着表达式规模不断扩大,基于NFA的匹配技术性能急剧下降,已经不能满足应用的需求,因此人们使用匹配速度更快的基于DFA的匹配技术来代替传统的收稿日期:2009-08-08基金项目:国家重点基础研究发展计划(“973”计划)基金资助项目(2007CB311100)Foundation Item: The National Basic Research Program of China (973 Program)(2007CB311100)第10A期杨毅夫等:正则表达式的DFA压缩算法·37·匹配技术。
然而DFA同时带来了另一个问题:DFA 的状态数量有可能指数增加从而导致存储空间急剧增加。
例如正则表达式.*AB.{1024}CD对应的DFA的状态规模高达O(21024)。
目前对正则表达式的研究主要集中在如何压缩DFA的存储空间,以达到用较少存储空间获取较快匹配速度的目的。
针对DFA占用存储空间过大的问题,本文提出了一种DFA的压缩算法——“簇”分割压缩算法。
文章给出了“簇”的定义,并且根据“簇”把DFA 分割成几个部分,然后分别对这些部分进行压缩。
本文第2节介绍DFA压缩的相关工作,第3节详细描述簇分割压缩算法,第4节通过详细的实验分析算法的有效性,第5节是结束语。
2 相关工作正则表达式匹配问题是计算机领域的经典问题,文献[4~6]在正则表达式匹配理论和算法的研究方面卓有成效;随着正则表达式在应用系统中的广泛使用,人们更加关注匹配技术在系统中的实际效果。
在实际的系统中,如何降低DFA的状态规模、减少DFA的存储空间仍是研究的焦点。
Fang Y u在文献[7]中用规则分类和规则改写的方法来化简正则表达式。
文中依据正则表达式转化成确定有限自动机的状态数规模,把正则表达式分为5类,并提出了2条改写规则以DFA的状态规模。
但是经过上述规则改写后的表达式并不与原来的表达式完全等价,只适合于非重叠匹配(non-overlapping match)的情况,因此限制了它的使用范围。
Kumar在文献[8]中提出了D2FA方法来压缩DFA的存储空间。
通过引入默认转移边(default transition)来减少转移边的数目,从而降低自动机的存储空间。
引入默认转移边能极大地减少了确定DFA的转移边,该文的实验表明,该方法平均能够减少95%的转移边。
但是该方法的缺陷是,每处理一个字符可能需要在D2FA中进行多次状态跳转,导致实际的匹配性能不高。
Ficara在文献[9]中提出了δFA方法来压缩DFA 的状态表。
该方法提取子状态和父状态的相同元素来消除状态转换表的冗余。
在状态访问序列中,如果当前状态t要访问的元素next[t, c]与其前一个状态s的对于元素next[s, c]相同,那么可以直接从前一个状态中读取相应的值。
该方法能够取得非常好的压缩效果,但是每次状态转换需要对时间进行更新,因此总的扫描时间是O(n*|Σ|),这是非常费时的。
Smith在文献[10]中提出了XFA方法来解决正则表达式合并过程中出现的状态爆炸问题。
该方法对有限自动机进行扩展,在每个自动机状态上附加计数标记来记录正则表达式中字符的重复次数。
该方法能够比较好地解决DFA的状态爆炸问题,但是有如下2个缺陷:①对每个状态需要更新和检查相关的计数器,影响了匹配速度;②该方法只能对单个字符进行计数,在正则表达式中往往出现一个字符串的多次重复,如(abc){1, 4},XFA无法解决这种计数问题。
陈曙晖等在文献[11]中提出了集合交割的预编码方法(SI-precode)来状态转移表的存储空间。
该方法对于包含大量字符组的正则表达式压缩效果非常明显,但是无法解决一般正则表达式状态表的压缩问题。
张伟等在文献[12]中设计并实现了一种多正则表达式匹配的硬件架构MRM。
该架构将正则表达式分解为普通字符串和限定重复的简单正则表达式,并针对NIDS系统的规则进行了优化,获得了2.8Gbit/s的扫描速度。
但是该方案也只能支持一类特殊的正则表达式规则(分解为普通字符串和限定重复的简单正则表达式),因而限制了其应用范围。
从上面的工作可以看出,现有的正则表达式匹配方法具有如下不足之处:①在已有的对空间进行压缩的方法中,往往只关注压缩比,对匹配性能的分析都是理论层面上的,实际运行效果不佳;②现有的优化方法都是针对一类特殊的正则表达式进行的,无法解决一般正则表达式的匹配问题,其原因在于没有更好地挖掘多正则表达式之间由于正则语义带来的冗余关系和分布特征。
因此需要对多正则表达式做进一步的研究。
3 簇分割压缩算法本节首先引入簇的定义,然后介绍DFA的一个重要特征及压缩思想,接着详细描述整个算法,最后分析算法的状态转移时间复杂度及存储空间复杂度。
整个过程以表达式.*A.{2}CD为例,其对应的DFA和存储矩阵如图1所示。
3.1簇的定义在trie结构中,一个状态的后继状态集合称为一个簇。
初始状态是单独的一个簇。
簇在本质上就是对trie结构的一个划分,因此trie结构中的每个·38· 通 信 学 报 第30卷状态都属于唯一的一个簇。
在DFA 中,按层次进行遍历(宽度优先遍历)可以得到唯一确定的trie 结构,在trie 结构上可以得到唯一确定的簇划分,因此在DFA 中也可以得到唯一确定的簇划分。
图1中右图是DFA 按照层次遍历得到的trie 结构,按照簇的定义,可以知道初始状态{0}是一个簇;0的下一个状态集合是{1},因此{1}也是一个簇;同理,状态集合{2,3}、{4,5}、{6,7}、{8}、{9}都是一个簇。
这些簇不仅是对trie 结构的一个划分,也是对DFA 的一个划分。
3.2 DFA 的特征及压缩算法的主要思想经过大量的实验可以发现DFA 的一个重要特征:每个状态的转移边不是随机分布的,而是比较集中地指向其中的2个簇。
表1列出了L7-Filter 中几条典型规则的转移边分布情况。
把每个状态的转移边按簇进行分类,把指向同一簇最多的转移边放在第1个矩阵T 1中,把指向同一簇第二多的转移边放在第2个矩阵T 2中。
表中第1列是所使用规则的名称,第2、3列是矩阵T 1、T 2中有效元素的比例,第4列是矩阵T 1、T 2有效元素的总比例。