下载文档原格式
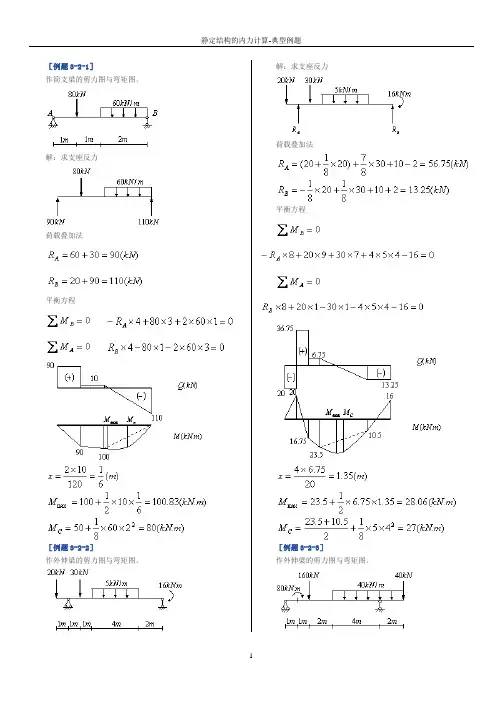
［例题3-2-1］作简支梁的剪力图与弯矩图。
解：求支座反力荷载叠加法平衡方程［例题3-2-2］作外伸梁的剪力图与弯矩图。
解：求支座反力荷载叠加法平衡方程［例题3-2-3］作外伸梁的剪力图与弯矩图。
解：求支座反力荷载叠加法平衡方程［例题3-3-1］作多跨静定梁的内力图。
解：求支座反力荷载叠加法［例题3-3-2］作三跨静定梁的内力图。
解：求支座反力［例题3-3-3］作多跨静定梁的内力图。
解：求支座反力［例题3-4-1］作静定刚架的内力图解：求支座反力［例题3-4-2］作静定刚架的内力图解：求支座反力［例题3-4-3］作静定刚架的内力图解：求支座反力［例题3-4-4］作静定刚架的内力图解：求支座反力［例题3-4-5］作三铰刚架的内力图解：求支座反力［例题3-4-6］作三铰刚架的内力图解：求支座反力??［例题3-4-7］作静定刚架的内力图解：求支座反力［例题3-4-8］作静定刚架的图解：［例题3-4-9］作静定刚架的图解：［例题3-4-10］作静定刚架的图解：［例题3-4-11］作静定刚架的图解：［例题3-4-12］作静定刚架的图解：［例题3-4-13］作静定刚架的图解：［例题3-4-14］作静定刚架的图解：求支座反力?［例题3-4-15］作静定刚架的图解：［例题3-5-1］试绘制三铰拱的内力图。
拱轴方程为解：相应简支梁的反力和内力求支座反力拱轴方程当时?? ? 00053.1301050-3.00-133.5 1 1.5 1.7545157.510513.115.9-132.6 23333.6931510567.541.6-127.0 23333.69315567.5-41.6-71.4 3 4.53,7518.43322.5513.1-21.4-79.9 4640330505-82.5 57.5 3.75-18.43315-25 5.6 2.4-86.2 693-33.69255-557.50-99.1 710.5 1.75-45135-85 5.6-1.8-118.4 8120-53.130-1150-2.9-141.5［例3-5-2］试求对称三铰拱在竖向均布荷载作用下的合理轴线。
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。
l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。
ll21、求图示结构B点的竖向位移，EI = 常数。
