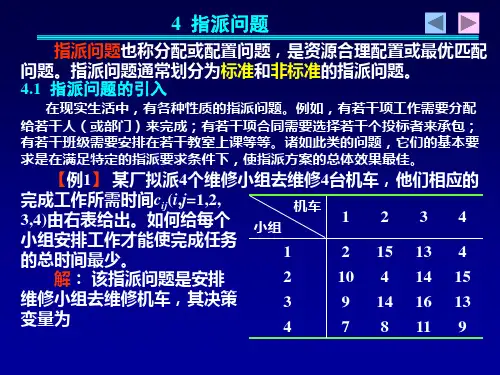
06运筹学教案(整数规划与指派问题)
- 格式:ppt
- 大小:694.00 KB
- 文档页数:53










实验六、用EXCEL 求解整数规划用单纯形法求解线性规划问题,最优解可能是整数,也可能不是整数,但在很多实际问题中,要求全部或部分变量的取值必须是整数,如所求的解是安排上班的人数,按某个方案裁剪钢材的根数,生产设备的台数等等。
对于整数解的线性规划问题,不是用四舍五入或去尾法对线性规划的非整数解加以处理都能解决的,而要用整数规划的方法加以解决,如分枝定界法和割平面算法。
这些算法比单纯形法更为复杂,因此,一般的学习者要想掌握整数规划的数学算法有一定的困难。
然而事实上,由于Excel 的[工具][规划求解]可以求解整数规划问题,所以,对于一个真正有志于运用运筹学方法解决生产经营中问题的管理者来说,算法将不是障碍因素。
一、实验目的1、 掌握如何建立整数线性规划模型,特别是0~1逻辑变量在模型中的应用。
2、 掌握用Excel 求解整数线性规划模型的方法。
3、 掌握如何借助于Excel 对整数线性规划模型进行灵敏度分析,以判断各种可能的变化对最优方案产生的影响。
4、 读懂Excel 求解整数线性规划问题输出的运算结果报告和敏感性报告。
二、 实验内容1、 整数规划问题模型该问题来自于《运筹学基础及应用》(第四版)胡运权主编P126习题4.13,题目如下: 需生产2000件某种产品,该种产品可利用A 、B 、C 、D 设备中的任意一种加工,已知每种设备的生产准备结束费用、生产该产品时的单件成本以及每种设备限定的最大加工数量(件)如表1所示,问企业应该如何安排设备生产该产品才能使得总的生产成本最少,试建立该问题的数学模型并求解。
该产品可以利用四种不同的设备加工,由于采用不同的设备加工需要支付不同的准备结束费用,而如果不采用某种设备加工,是不需要支付使用该设备的准备结束费用的,所以必须借助于逻辑变量来鉴定准备结束费用的支付。
再设,种设备加工的产品数量为利用第设;4,3,2,1=j j x j⎪⎩⎪⎨⎧=>=)种设备生产(即,若不使用第)种设备生产(即若使用第000,1j j i x j x j y 4,3,2,1=j则问题的整数规划模型为:43214321281624207008009801000min x x x x y y y y z +++++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥≤≤≤≤=+++4,3,2,110,01600120010009002000..443322114321j y x y x y x y x y x x x x x t s j j,或2、 [工具][规划求解]命令求解下面我们用Excel 中的[工具][规划求解]对该问题进行求解。