运筹学整数规划补例样本

1 2 3 4 5 6 7 8 9 10 11 J CPM/PERT
B Integer Programming
1234567
K Inventory Models
C Zero One Programming
1234567
L Queueing Theory
D Goal Programming
12345678
H Decision Theory
Q Game Theory
I Network Models
ESC Exit to Dos
123
总目录
例1.(投资问题 )某厂要制订一个产品宣传计划，可利用的广告渠 道有三种：电视、广播、杂志。市场调研的结果如下表所示。该 厂计划用于广告费用不超过 16万元。此外还要求：（ 1）受到广 告影响的妇女至少要有200千人；（2）电视广告费用不超过10万 元；（3）白昼电视至少要订 3个广告，热门时间至少 2个广告； （4）广播和杂志上的广告数都应在5到10之间。该厂如何制订一 个广告计划使受到影响的总人数最多。
每个广告的费用（千元）
电
白昼时间
8
视
热门时间
15
广杂 播志
63
每个广告影响总人数（千人）
40
90
50 2
每个广告影响妇女数（千人）
30
40
20 1
解：设电视白昼时间的广告个数为 x1、电视热门时间的广告个 数为 x2、广播的广告个数为 x3、杂志的广告个数为 x4。
该广告计划模型为：
max z ? 40x1 ? 90x2 ? 50x3 ? 2x4
金属板吨劳动力人月机器设备台月小号容器中号容器大号容器不考虑固定费用每种容器售出一只所得的利润分别为4万元5万元6万元可使用的金属板有500吨劳动力有300人月机器有100台月此外不管每种容器制造的数量是多少都要支付一笔固定的费用

c 1 x 1 c 2 x 2 c n x n ,其 中 c j 0 ,j 1 ,2 , n .
上例中，对所有的 j，cj=1. 如果 cj 表示位置 j 安装 的费 用，那么这些系数就是这些费用值而不再是1.
习题
MobileCo公司拿出1500万美元，最多建造7个发射台来覆盖15个 相邻社区中尽可能多的人口。下表给出了每个发射台可以覆盖 的社区以及建造这个发射台的费用以及社区人口。确定出需要 建设哪几个发射台。
由上例看出，
将其相应的线性规划的最优解“化整”来解原整数线 性规划，虽是最容易想到的，但往往不可行。
化整后不见得是可行解；或虽是可行解，但不一定是 最优解。
因此有必要对整数线性规划的解法进行专门研究。
此类问题为整数线性规划(Integer Linear Programming ， ILP)，整数线性规划是最近几十年来发展起来的规划论 中的一个分支。
有部分变量取小数，这不符合实际，若采用舍入方法，则 x1= x5=1，这意味着5个项目都要选择，显然是不可行解，
对于采用“是否”决策问题，舍入法不可行。
习题
某唱片公司与一位新的歌手签约录制8首歌曲，这8首歌曲 的时间长度分别为8,3,5,5,9,6,7,12分钟，公司希望将所有的 歌曲分配在磁带的两面，使得两面的歌曲时间长度尽量相 同。请建立整数规划模型，求出最优解。
发射台
覆盖社区
1
1，2
2
2，3，5
3
1，7，9，10
4
4，6，8，9
5
6，7，9，11
6
5，7，10，12，14
7
12，13，14，15
各个社区人口数目
建造费用(百万) 3.6 2.3 4.1 3.15 2.8 2.65 3.1

整数规划（Integer Programming，简称IP），是 要求全部或部分决策变量为整数的规划。整数规 划分为线性整数规划和非线性整数规划。本章只 介绍线性整数规划，简称为整数规划。
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题

〈运筹学〉补充例题例题 1.1 某工厂可以生产产品A和产品B两种产品。

生产单位产品A和B所需要的机时、人工工时的数量以及可利用资源总量由下表给出。

这两种产品在市场上是畅销产品。

该工厂经理要制订季度的生产计划，其目标是使工厂的销售额最大。

产品A 产品B 资源总量机器（时） 6 8 120人工（时） 10 5 100产品售价（元） 800 300MAX 800X1 +300X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.2该工厂根据产品A和产品B的销售和竞争对手的策略，调整了两种产品的售价。

产品A和B的价格调整为600元和400元。

假设其它条件不变，请你帮助该工厂经理制订季度的生产计划，其目标仍然是使工厂的销售额最大。

X 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.3由于某些原因，该工厂面临产品原料供应的问题。

因此，工厂要全面考虑各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价等因素。

有关信息在下表中给出。

产品A 产品B 资源总量机器（时） 6 8 120人工（时） 10 5 100原材料(公斤) 11 8 130产品售价（元） 600 400MAX 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 10011X1 +8X2 <= 130X1, X2 >=0例题 1.４随着企业改革的不断深化，该企业的经理的管理思想产生了变化，由原来的追求销售额变为注重销售利润，因此，要考虑资源的成本。

工厂的各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价和各种资源的价格等因素。

有关信息在下表中给出。

产品A 产品B 资源总量资源价格（元／单位）机器（时） 6 8 120 ５人工（时） 10 5 100 20原材料(公斤) 11 8 130 1产品售价（元） 600 400设： J为所用机器资源数量（小时）；R为所用人力资源数量（小时）；L为所用原材料数量（公斤）MAX 600X1 +400X2 -CST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L = 0J <= 120R <= 100L <= 1305J +20R +1L - C = 0x1, x2, J,R,L>=0例题 1.5 学习了管理课程后，该企业的经理明白了产品的成本包括变动成本和固定成本。

案例2： California制造公司问题－ Excel求解
多个决策变量
0-1变量
相依决策
互斥方案
案例2： California制造公司问题－ 灵敏度分析
Capital Spent 100 <=
Capital Available
100
Total Profit ($millions)
10
取整约束
G 12 SUMPRODUCT(UnitProduced,UnitProfit)
6.2 整数规划问题的分类
▪ 纯整数规划问题：
– 所有决策变量均为整数
▪ 混合整数规划问题（MIP）：
B
C
3 NPV ($millions)
LA
4
Warehouse
6
5
6
Factory
8
7
8 Capital Required
9
($millions)
LA
10
Warehouse
5
11
12
Factory
6
13
14
15
Build?
LA
16
Warehouse
0
17
<=
18
Factory
1
19
20
Total NPV ($millions)
原因分析
▪线性规划的可分性假设
–线性规划的决策变量必须允许在满足一定函数 约束与非负约束下取任意实数。
TBA公司的问题由于决策变量只能取整 数，故不满足可分性假设。
整数规划的Excel求解模型－ 案例1
B
3
4
Unit Profit ($millions)

2. 所用原料钢管总根数最少
决策 变量 xi ~按第i 种模式切割的原料钢管根数(i=1,2,…7) 目标1（总余量） Min Z 1 3 x 1 x 2 3 x 3 3 x 4 x 5 x 6 3 x 7
模 式 1 2 3 4 5 6 7 需 求 4米 根数 4 3 2 1 1 0 0 50 6米 根数 0 1 0 2 1 3 0 20 8米 根数 0 0 1 0 1 0 2 15 余 料 3 1 3 3 1 1 3
m in f 0 .1 x1 0 .3 x 2 0 .9 x 3 0 x 4 1 .1 x 5 0 .2 x 6 0 .8 x 7 0 .4 x 8
x8
2 x1 x 2 x 3 x 4 1 0 0 2 x 2 3 x3 3 x5 2 x6 x7 1 0 0 s .t . x1 x 3 3 x 4 2 x 6 3 x 7 4 x 8 1 0 0 x 0, i 1, 2, 3, 4, 5, 6, 7 , 8, x 取 整 i i
8米1根
8米1根
合理切割模式的余料应小于客户需要钢管的最小尺寸
钢管下料问题1
模式 1 2 3 4 5 6 7 4米钢管根数 4 3 2 1 1 0 0
合理切割模式
6米钢管根数 0 1 0 2 1 3 0 8米钢管根数 0 0 1 0 1 0 2 余料(米) 3 1 3 3 1 1 3
为满足客户需要，按照哪些种合理模式，每种模式 切割多少根原料钢管，最为节省？ 两种 标准 1. 原料钢管剩余总余量最小
建立模型：
m ax
f
cx
i i 1
7
i
7 bi x i b i 1 x1 x 2 x 3 2 s .t . x 4 x 5 1 x x 1 7 6 x i 0 或 1, i 1, 2， . . . , 7

B1
A1 A2 A3 A4 年需求 量 2 8 7 4 350
B2
9 3 6 5 400
B3
3 5 1 2 300
B4
4 7 2 5 150
年生产能力
400 600 200 200
工厂A3或A4开工后，每年的生产费用估计分别为 1200万或1500万元。 现要决定应该建设工厂A3还是A4，才能使今后每年的总费用最少。
首先不考虑整数约束，得到线性规划问题（一般称 为松弛问题）。
max Z x1 x 2 14 x1 9 x 2 51 6 x1 3 x 2 1 x , x 0 1 2
用图解法求出最优解为：x1＝3/2, x2 = 10/3，且有Z = 29/6
现求整数解（最优解）：如用 x2 “舍入取整法”可得到4个点即(1， 3) (2，3)(1，4)(2，4)。显然，它 们都不是整数规划的可行解,因而不 3 是最优解。
5
4 24
2
5 13
20
10
解：设X1 , X2 为甲、乙两货物各托运箱数
maxZ = 20 X1 + 10 X2 5X1+4X2 24 2X1+5X2 13 X1 , X2 0
X1 , X2为整数
例4.2 背包问题
背包可装入8单位重量，10单位体积物品 物品 1 2 名称 书 摄像机 重量 5 3 体积 2 1 价值 20 30
变量约束：
x12 x 22 x 32 x 42 1 x13 x 23 x 33 x 43 1 x14 x 24 x 34 x 44 1
xij 0或，、 1 i j 1, 2,3, 4
整数线性规划问题数学模型的一般形式：

* X 2 (6,3.75)T 解为:
f 130
* 1
f 2* 135
B1 的解 X1* (5,4)T 是整数最优解,它当然也是问题 A0 问题
* * 的整数可行解,故 A0 的整数最优解 Z f1 130.
即此时可将 Z 修改为:
Z f1* 130
同时问题 B1 也被查清, 成为“树叶”。
题 A0 的最优目标函数值决不会比它小,故可令 Z =0.
3. 增加约束条件将原问题分枝 当问题 A0 的最优解 X 0* 不满足整数条件时,在 X 0* 中任选一个
不符合整数条件的变量.如本例选 x1 5.6,
显然问题 A0 的
整数最优解只能是 x1 5 或 x1 6 ,而绝不会在5与6之间.
规划.
问题 A1
max Z 20x1 10x2
问题 A2
max Z 20x1 10x2
5 x1 8 x2 60 x1 8 s.t x2 4 x1 5 x1 , x2 0, 取整数
5 x1 8 x2 60 x1 8 s.t x2 4 x1 6 x1 , x2 0, 取整数
用 图 解法求出最优解 x1＝3/2, x2 = 10/3 且有Z = 29/6
x2
3
⑴
⑵
(3/2,10/3)
现求整数解（最优解）： 如用“舍入取整法”可得 到4个点即(1，3) (2， 3)(1，4)(2，4)。显然， 它们都不可能是整数规划 的最优解。
3
x1
按整数规划约束条件，其可行解肯定在线性规划问题 的可行域内且为整数点。故整数规划问题的可行解集 是一个有限集，如图所示。

1. 投资问题 现有总额为b的资金可用于投资，共有n个项目可 供投资者选择，已知项目j所需投资额为aj，投资后可 得利润cj（j ＝ 1，2，…，n），不妨设b，aj，cj 均是 整数，试问为使所得利润最大，应选取那些项目进行 投资？ 1…对项目j投资 先引入0－1变量xj，令 xj＝ 0…否则 n
设每个月从仓库i运往地区j的产品的货物数量为xij，引入0－ 1变量yi= 1表示在Ai设立仓库，否则不设。 设每个月的总花费为z，则上述问题的数学模型为 Min z＝200x11+400x12+500x13+300x21+250x22+450x23 +600x31+400x32+250x33+300x41+150x42+350x43+45000y1+5000 0y2+70000y3+40000y4 s.t. x11+x12+x13≤1000y1 x21+x22+x23≤1000y2 x31+x32+x33≤1000y3 x41+x42+x43≤1000y4 x11+x21+x31+x41≥600 x12+x22+x32+x42≥700 x13+x23+x33+x43≥800 y2-y4≤0 y1+y2+y3+y4≤3
y3+y4 ≤ 1
工厂选址运输问题
设有n个需求点，有m个可供选择的厂址， 每个厂址只能建一个工厂，在i处建厂，生产 能力为Di，单位时间的固定成本为ai，需求点 j的需求量为bj，从厂址i到需求点j的单位运费 为Cij，问应如何选择厂址才能获得经济上的总 花费最小的方案。

5
4
x(0)=(4.81,1.82) Z0=356
3
B 2
1
7x1+20x2=70
C
0 1 2 3 4 5 6 7 8 9 10 x1
x1<=[x1(0)]
12
x1>=[x1(0)]+1
2021/7/26
解：第一步：先不考虑整数约束条件，求解相应的线性 规划问题，得最优解和最优值如下：
x1=4.81, x2=1.82, Z=356 解不满足整数条件。最优值Z=356作为整数规划目标函 数值的上界；用观察法可知x1=0，x2=0是可行解，对应 目标值Z=0作为整数规划目标值的下界，即0 Z* 356
1
2
x6 x7 1
xi 0或1
获利最大的设点方案，第 一个约束条件表示投资总 额限制，之后的三个约束 条件分别表示在东、西和 南区的设点数限制，决策 变量取值0或1。
5
2021/7/26
例3 解决某市消防站的布点问题。该市共有6个区，每 个区都可以建消防站。政府希望设置的消防站最少，但 必须满足在城市任何地区发生火警时，消防车要在15分 钟内赶到现场。据实地测定，各区之间消防车行驶的时 间见下表：
行解, 停止; b) 若有满足整数条件的最优解, 则已得到整数规划问 题的最优解, 停止; c) 若有最优解, 但不满足整数条件, 记此最优值 为原整数规划问题Z*的上界, 然后, 用观察法求出下界. (2)分支、定界直到得到最优解为止
分支：取目标函数值最大的一个支LPs，在LPs的解中任选一不 符合整数条件的变量xj，其值为bj，构造两个约束条件xj≤[bj]和 xj≥[bj]+1。将两个约束条件分别加入问题LPs，得两个后继规划问 题LPs1和LPs2。不考虑整数条件求解这两个后继问题，以每个后 继问题为一分支标明求解结果。

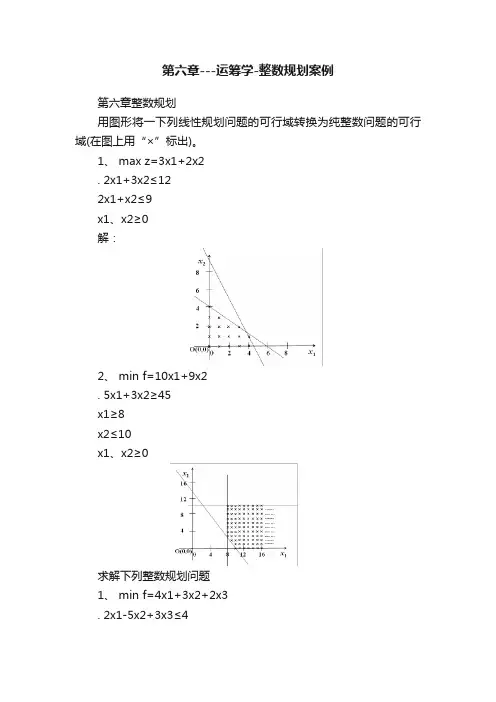
第六章---运筹学-整数规划案例第六章整数规划用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。

1、 max z=3x1+2x2. 2x1+3x2≤122x1+x2≤9x1、x2≥0解：2、 min f=10x1+9x2. 5x1+3x2≥45x1≥8x2≤10x1、x2≥0求解下列整数规划问题1、 min f=4x1+3x2+2x3. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解：最优解（0，0，1），最优值：22、 min f=2x1+5x2+3x3+4x3. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解：此模型没有可行解。

3、max Z=2x1+3x2+5x3+6x4. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解：最优解（0，3，4，3），最优值：474、 min z =8x1 +4 x2+3 x3+5 x4+2 x5＋3 x6＋4 x7＋3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5＋ x6-10 x16≤0x7+ x8＋ x9-20 x17≤0x10+ x11＋ x12-30 x18≤0x13+ x14＋ x15-40 x19≤0x1 + x4+ x7+x10+ x13＝30x2 + x5+ x8+x11+ x14＝20x3 + x6+ x9+x12+ x15＝20x i为非负数（i=1,2…..8）x i为非负整数（i=9,10…..15）x i为为0－1变量（i=16,17…..19）解：最优解（30，0，0，0，0，0，0，0，0，0，0，0，0，20，20，0，0，0，1），最优值：860一餐饮企业准备在全市范围内扩展业务，将从已拟定的14个点中确定8个点建立分店，由于地理位置、环境条件不同，建每个分店所用的费用将有所不同，现拟定的14个店的费用情况如下表：公司办公会决定选择原则如下：（1）B5、B3和B7只能选择一个。

0-1变量的作用
1…方案j被选中 1. xj＝
0…方案j未被选中
n
2. 从n个方案中必须选中一个： x j 1 j 1 n
3. 从n个方案中最多选中m个： x j m j 1
4. 方案i只有在方案j选中时，才可能被选中：
xi x j
5. 方案i与方案j是否选中是同时的： xi x j
解：
令0-1变量为决策变量，即xi＝1表示选中项目i， 否则xi＝0表示项目i未被选中。则模型可以表示为：
max z= 150x1 +210x2 +60x3 +80x4 +180x5
s.t.
210x1 +300x2 +100x3 +130x4 +260x5 ≤600
x1
+x2
+x3
=1
x3
+x4
=1
0y2+70000y3+40000y4
s.t.
x11+x12+x13≤1000y1
x21+x22+x23≤1000y2
x31+x32+x33≤1000y3
x41+x42+x43≤1000y4
x11+x21+x31+x41≥600
x12+x22+x32+x42≥700
x13+x23+x33+x43≥800
y2-y4≤0
y1+y2+y3+y4≤3
y3+y4 ≤ 1
工厂选址运输问题
设有n个需求点，有m个可供选择的厂址， 每个厂址只能建一个工厂，在i处建厂，生产 能力为Di，单位时间的固定成本为ai，需求点 j的需求量为bj，从厂址i到需求点j的单位运费 为Cij，问应如何选择厂址才能获得经济上的总 花费最小的方案。

第四章 整数规划４.1 某工厂生产甲、乙两种设备,已知生产这两种设备需要消耗材料A 、材料B,有关数据如下,问这两种设备各生产多少使工厂利润最大？(只建模不求解）解:设生产甲、乙这两种设备的数量分别为x １、x 2,由于是设备台数,则其变量都要求为整数,建立模型如下:2123max x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,5.45.01432x x x x x x x x４．2 2197max x x z +=⎪⎩⎪⎨⎧≥≤+≤+-且为整数0,35763.212121x x x x x x t s 割平面法求解。

(下表为最优表）线性规划的最优解为：63max ,0,2/7,2/94321=====z x x x x由最终表中得:27221227432=++x x x ﻩ④ 将系数和常数项分解成整数和非负真分式之和，上式化为；2132********+=++x x x移项后得:①②③④①②③即：21221227212212274343-≤--→≥+x x x x 只要把增加的约束条件加到B 问题的最优单纯形表中。

表4-4由ｘ1行得:7327171541=-+x x x 将系数和常数项分解成整数和非负真分数之和:74476715541+=+-+x x x x得到新的约束条件： 74767154-≤--x x747671654-=+--x x x 在的最优单纯形表中加上此约束，用对偶单纯形法求解：则最优解为3,421==x x ，最优目标函数值为z *=55。

4．3 m ａx z =４ｘ1+３x 2+2x ３⎪⎪⎩⎪⎪⎨⎧=≥+≥++≤+-10,,13344352.32132321321或x x x x x x x x x x x t s 隐枚举法解：(１）先用试探的方法找出一个初始可行解,如x 1=ｘ２＝０,x 3＝1。

满足约束条件，选其作为初始可行解，目标函数z 0=2。

5.某企业利用一种设备生产某种试件。

该设备可以在高，低两种不同的负荷下进行生产。

在高负荷下生产的试件产量是投入生产设备数量的10倍，设备年完好率为75%；低负荷下生产的试件产量是投入生产设备数量的8倍，设备年完好率为90%。

现在企业有完好的设备200台，试制定一个5年计划，确定每年投入投入高，低两种负荷下生产的设备数量，使5年内试件的总产量达到最大。

整数规划模型设第i 年投入高负荷下生产的完好的设备数量为i x ，生产的试件数量为10i x ；第i 年投入低负荷下生产的完好的设备数量为i y ，生产的试件数量为8i y 。

模型为：∑∑==+=5151810max i i i i y x z20011=+y x ⌊0.75i x ⌋+⌊0.9i y ⌋-1+i x -1+i y =0i x ,i y 0≥且为整数，（i=1,2,3,4,5）Lingo 程序为：max=10*(x1+x2+x3+x4+x5)+8*(y1+y2+y3+y4+y5);x1+y1=200;z1=@FLOOR( 0.75*x1);u1=@FLOOR(0.9* y1);z1+u1-x2-y2=0;z2=@FLOOR( 0.75*X2);u2=@FLOOR( 0.9*y2);z2+u2-x3-y3=0;z3=@FLOOR( 0.75*X3);u3=@FLOOR( 0.9*y3);z3+u3-x4-y4=0;z4=@FLOOR( 0.75*X4);u4=@FLOOR( 0.9*y4);z4+u4-x5-y5=0;@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5);Lingo 求解结果为：s.t.Objective value: 6362.000Variable ValueX1 200.0000X2 1.000000X3 0.000000X4 119.0000X5 89.00000Y1 0.000000Y2 149.0000Y3 134.0000Y4 1.000000Y5 0.000000由结果可以得知，第1年200台完好的生产设备全部在高负荷下生产；第2年1台完好的生产设备在高负荷下生产，149台完好的生产设备在低负荷下生产；第3年134台完好的生产设备全部在低负荷下生产；第4年119台完好的生产设备在高负荷下生产，1台完好的生产设备在低负荷下生产；第5年89台完好的生产设备全部在高负荷下生产。