哈工大结构力学2009
- 格式:pdf
- 大小:1.57 MB
- 文档页数:7


结构力学张金生绪论§1 . 结构力学的内容和任务一.对象结构分为:杆系结构,板壳结构,实体结构三.内容 结构组成;内力,位移,临界力计算.二.任务 研究结构的刚度,强度,稳定性的 计算原理和计算方法结构:承受并传递荷载的骨架部分确定计算简图的原则: 1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容:1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)半铰结点铰结点刚结点确定计算简图的原则:1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)确定计算简图的原则:1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)4.体系的简化: 空间结构 平面结构确定计算简图的原则:1.能反映实际结构的主要力学特性;2.分析计算尽可能简便§2 . 杆件结构的计算简图计算简图:在结构分析当中用来代替实际结构的计算模型(图形)简化内容: 1.杆件的简化: 杆件 杆件的轴线2.结点的简化: 刚结点 铰结点 半铰结点(组合结点)3.支座的简化: 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座)4.体系的简化: 空间结构 平面结构5.荷载的简化: 集中力、集中力偶、分布荷载§3 . 杆件结构的类型1.梁2.拱3.桁架4.刚架5.组合结构第一章杆件体系的几何组成分析(Geometric construction analysis)§1. 几何组成分析本章假定:所有杆件均为刚体§1-1 基本概念一. 几何不变体系几何可变体系几何可变体系不能作为建筑结构结构必须是几何不变体系本章目的:判定一个体系是否能作为结构结构是如何构造的几何形状不能变化的平面物体几何不变体系的自由度一定等于零几何可变体系的自由度一定大于零§1. 几何组成分析§1-1 基本概念一. 几何不变体系几何可变体系二. 刚片几何形状不能变化的平面物体三. 自由度确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置1. 链杆2. 单铰§1. 几何组成分析§1-1 基本概念一. 几何不变体系 几何可变体系二. 刚片 几何形状不能变化的平面物体 三. 自由度 确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置1. 链杆 2. 单铰 3. 链杆与单铰的关系4. 虚铰3. 链杆与单铰的关系4. 虚铰§1. 几何组成分析2. 单铰 5. 复铰1. 链杆连接N 个刚片的复铰相当于N-1个单铰§1. 几何组成分析§1-1 基本概念一. 几何不变体系 几何可变体系二. 刚片 几何形状不能变化的平面物体 三. 自由度 确定体系位置所需的独立坐标数四. 约束(联系) 能减少自由度的装置五. 计算自由度0632=−×=W 02936=×−×=W 032333=−×−×=W§1. 几何组成分析五. 计算自由度0632=−×=W 08936=×−×=W 032333=−×−×=W 链杆数单铰数刚片数链杆数结点数−×−×=−×=232W W 计算自由度大于零一定可变;若等于零则一定不变吗§1. 几何组成分析五. 计算自由度链杆数单铰数刚片数链杆数结点数−×−×=−×=232W W 计算自由度大于零一定可变;若等于零则一定不变吗六. 多余约束 必要约束计算自由度小于零一定不变吗计算自由度小于零一定有多余约束§1. 几何组成分析§1-1 基本概念一. 几何不变体系几何可变体系二. 刚片三. 自由度四. 约束(联系) 链杆单铰复铰虚铰实铰五. 计算自由度六. 多余约束必要约束P N=构成无多余约束的几何不变体系构成无多余约束的几何不变体系.§1. 几何组成分析§1-2 无多余约束的几何不变体系的组成规则一. 三刚片规则二元体:在一个体系上用两个不共线的链杆连接一个新结点的装置.二. 两刚片规则在一个体系上加减二元体不影响原体系的机动性质.三. 二元体规则§1. 几何组成分析§1-1 基本概念§1-2 无多余约束的几何不变体系的组成规则§1-3 几何组成分析举例例1: 对图示体系作几何组成分析解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束的几何不变体系.§1. 几何组成分析§1-3 几何组成分析举例例2: 对图示体系作几何组成分析解:该体系为无多余约束的几何不变体系.方法1: 若基础与其它部分三杆相连,去掉基础只分析其它部分例3: 对图示体系作几何组成分析解: 该体系为无多余约束的几何不变体系.方法2: 利用规则将小刚片变成大刚片.例4: 对图示体系作几何组成分析解: 该体系为瞬变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.例5:对图示体系作几何组成分析解: 该体系为常变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法4: 去掉二元体.例6:对图示体系作几何组成分析解: 该体系为无多余约束几何不变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.例7: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.解: 该体系为有一个多余约束几何不变体系.练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.方法1: 若基础与其它部分三杆相连,去掉基础只分析其它部分练习: 对图示体系作几何组成分析方法3: 将只有两个铰与其它部分相连的刚片看成链杆.方法2: 利用规则将小刚片变成大刚片.方法5: 从基础部分(几何不变部分)依次添加.方法4: 去掉二元体.几何组成思考题§几何组成分析的假定和目的是什麽?§何谓自由度?系统自由度与几何可变性有何联系?§不变体系有多余联系时,使其变成无多余联系几何不变体系是否唯一?§瞬变体系有何特点?可变体系时如何区分瞬变还是常变?§瞬铰和实际铰有何异同?§无多余联系几何不变体系组成规则各有什麽限制条件?不满足条件时可变性如何?§按组成规则建立结构有哪些组装格式?组装格式和受力分析有无联系?§如何确定计算自由度?§对体系进行组成分析的步骤如何?几何组成作业题§1-1 b c§1-2 a d g h i j k l §交作业时间:本周 5§1. 几何组成分析作业:1-1 (1-1 (b)b)试计算图示体系的计算自由度 解:由结果不能判定其是否能作为结构1321138−=−×−×=W 110222531−=−×−×+×=W 或:§1. 几何组成分析作业:1-1 (c)试计算图示体系的计算自由度解:由结果可判定其不能作为结构131216=−×=W 13240328=−×−×=W 或:§1. 几何组成分析作业:1-2 (a)试分析图示体系的几何组成从上到下依次去掉二元体或从基础开始依次加二元体.几何不变无多余约束§1. 几何组成分析作业:1-2 (d)试分析图示体系的几何组成依次去掉二元体.几何常变体系§1. 几何组成分析作业:1-2 (f)试分析图示体系的几何组成有一个多余约束的几何不变体系§1. 几何组成分析作业:1-2 (h)( i)试分析图示体系的几何组成瞬变体系几何不变无多余约束作业:试分析图示体系的几何组成有一个无穷远铰:四杆不平行不变平行且各自等长常变平行不等长瞬变§1. 几何组成分析作业:1-2 (j)试分析图示体系的几何组成瞬变体系§1. 几何组成分析L)试分析图示体系的几何组成1-2 (L)作业:1-2 (几何不变无多余约束§1. 几何组成分析例:试分析图示体系的几何组成瞬变体系§1. 几何组成分析练习:试分析图示体系的几何组成几何不变无多余约束一个单刚结点相当于三个约束.单刚结点与其它约束的关系:复刚结点:刚片复刚结点相当于练习:试分析图示体系的几何组成无多余约束几何不变体系有两个多余约束的几何不变体系练习:试分析图示体系的几何组成无多余约束几何不变体系无多余约束的几何不变体系。

第一章平面体系的几何组成分析一判断题1.图示体系是几何不变体系。
(×)题1图题2图题3图题4图2.图示体系为几何可变体系。
(×)3.图示体系是几何不变体系。
(×)4.图示体系是几何不变体系。
(√)5.图示体系是几何不变体系。
(×)题5图题6图题19图题20图6.图示体系为几何不变有多余约束。
(×)7.几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)8.两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)9.在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
(√)10.计算自由度 W小于等于零是体系几何不变的充要条件。
( × )11.几何可变体系在任何荷载作用下都不能平衡。
( × )12.三个刚片由三个铰相联的体系一定是静定结构。
( × )13.有多余约束的体系一定是超静定结构。
( ×)14.有些体系为几何可变体系但却有多余约束存在。
(√)15.平面几何不变体系的三个基本组成规则是可以相互沟通的。
(√)16.三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)17.两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
(×)18.若体系计算自由度 W<0,则它一定是几何可变体系。
(×)19.在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
(×)20.图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
(×)21.有多余约束的体系一定是几何不变体系。
(×)22.几何不变体系的计算自由度一定等于零。
(×)23.几何瞬变体系的计算自由度一定等于零。
(×)24.图中链杆 1 和 2 的交点 O可视为虚铰。
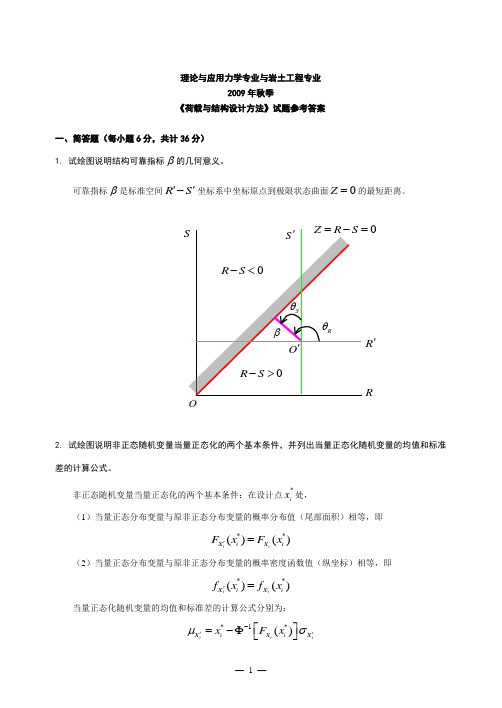
理论与应用力学专业与岩土工程专业2009年秋季《荷载与结构设计方法》试题参考答案一、简答题(每小题6分,共计36分) 1. 试绘图说明结构可靠指标β的几何意义。
可靠指标β是标准空间R S ''-坐标系中坐标原点到极限状态曲面0Z =的最短距离。
2. 试绘图说明非正态随机变量当量正态化的两个基本条件,并列出当量正态化随机变量的均值和标准差的计算公式。
非正态随机变量当量正态化的两个基本条件:在设计点*i x 处,(1)当量正态分布变量与原非正态分布变量的概率分布值(尾部面积)相等,即**()()i i X i X i F x F x '=(2)当量正态分布变量与原非正态分布变量的概率密度函数值(纵坐标)相等,即**()()i i X i X i f x f x '=当量正态化随机变量的均值和标准差的计算公式分别为:*1*()ii i X i X i X x F x μσ-''⎡⎤=-Φ⎣⎦OR 'R{}1**()()i ii X i X X iF x f x ϕσ-'⎡⎤Φ⎣⎦=3. 简述结构构件可靠度设计的实用表达式包括哪些内容,并列出具体表达式。
(1) 承载能力极限状态设计表达式1102()(,,,)iiinG G k Q Q k Q C Q k R k k i S S S R f a γγγγψγ=++≤∑01()(,,,)iiinG G k Q C Q k R k k i S S R f a γγγψγ=+≤∑(2) 正常使用极限状态设计表达式 1) 标准组合设计表达式112[]ii nG k Q k C Q k i S S S f ψ=++≤∑2) 频遇组合设计表达式122[]i ii nG k f Q k q Q k i S S S f ψψ=++≤∑3) 准永久组合设计表达式ii i X i X i '31[]ii nG k q Q k i S S f ψ=+≤∑4. 简述荷载代表值有哪些类型,并说明每种代表值的确定方法。


(完整版)哈⼯⼤结构⼒学题库七章176第七章影响线⼀判断题1. 图⽰梁AB 与A 0B 0,其截⾯C 与C 0弯矩影响线和剪⼒影响线完全相同。
(X )题1图题2图 2.图⽰结构Q E 影响线的AC 段纵标不为零。
(X )3. 图⽰梁K 截⾯的M K 影响线、Q K 影响线形状如图a 、b 所⽰。
4. 图⽰梁的M C 影响线、Q C 影响线形状如图a 、b 所⽰。
5. 图⽰梁的M C 影响线、M B 影响线形状如图a 、b 所⽰。
1776. 图⽰结构M B 影响线的AB 段纵标为零。
7. 图⽰梁跨中C 截⾯弯矩影响线的物理意义是荷载P=1作⽤在截⾯C 的弯矩图形。
(X ) 8. ⽤静⼒法作静定结构某量值的影响线与⽤机动法作该结构同⼀量值的影响线是不等价的。
(X )9. 求某量值影响线⽅程的⽅法,与恒载作⽤下计算该量值的⽅法在原理上是相同的。
(√) 10. 影响线是⽤于解决活载作⽤下结构的计算问题,它不能⽤于恒载作⽤下的计算。
(X ) 11. 移动荷载是指⼤⼩,指向不变,作⽤位置不断变化的荷载,所以不是静⼒荷载。
(X ) 12. ⽤静⼒法作影响线,影响线⽅程中的变量x 代表截⾯位置的横坐标。
(X )13. 表⽰单位移动荷载作⽤下某指定截⾯的内⼒变化规律的图形称为内⼒影响线。
(√) 14. 简⽀梁跨中截⾯弯矩的影响线与跨中有集中⼒P 时的M 图相同。
(X ) 15. 简⽀梁跨中C 截⾯剪⼒影响线在C 截⾯处有突变。
(√) 16. 绝对最⼤弯矩是移动荷载下梁的各截⾯上最⼤的弯矩。
(√) 17. 静定结构及超静定结构的内⼒影响线都是由直线组成。
(X) 18. 图⽰结构Q C 影响线的CD 段为斜直线。
19. 图⽰结构K 断⾯的剪⼒影响线如图b 所⽰。
(√)178题19图20. ⽤机动法作得图a 所⽰Q B 左结构影响线如图b 。
题20图题21图 21. 图⽰结构a 杆的内⼒影响线如图b 所⽰22. 荷载处于某⼀最不利位置时,按梁内各截⾯得弯矩值竖标画出得图形,称为简⽀梁的弯矩包络图。
第五章位移法一判断题1.图a为对称结构,用位移法求解时可取半边结构如图 b 所示。
答:(×)题 1 图2.图示结构,用位移法求解,有三个结点角位移和二个结点线位移未知数。
(×)。
题2图题3图3.以下两个单跨梁左端产生 1 所施加的弯矩相同。
(×)4.用位移法计算刚架,常引入轴向刚度条件,即“受弯直杆在变形后两端距离保持不变”。
此结论是由下述假定导出的:( D)A忽略受弯直杆的轴向变形和剪切变形;B弯曲变形是微小的;C变形后杆件截面仍与变形曲线相垂直;D假定 A 与 B 同时成立。
5.用位移法计算图示结构时,独立的基本未知数数目是 4 。
(×)题 5 图题 6 图6.图示结构用位移法计算时,其基本未知量的数目为 3 个(√)。
7.在位移法典型方程的系数和自由项中,数值范围可为正、负实数的有:( D)A主系数;B主系数和副系数;C主系数和自由项D负系数和自由项。
8.用位移法计算超静定结构时考虑了到的条件是:(A)A物理条件、几何条件、和平衡条件;B平衡条件C平衡条件与物理条件D平衡条件与几何条件9.规定位移法的杆端弯矩正负时,对杆端而言,以顺时针为正,对结点则以逆时针为正,这一规定也适合于杆端剪力的符号规定。
(×)10.图 a 对称结构可简化为图( b)来计算。
(×)题10图题11图11.图示结构用位移法求解时,基本未知量个数是相同的(√)12.图示结构用位移法求解时,只有一个未知数(√)题12图题13 图题14图13. 图示结构横梁无弯曲变形,故其上无弯矩。
(×)14.图a对称结构可简化为图b来计算,EI 均为常数。
(×)15.图示结构用位移法求解的基本未知量数目最少为3。
(√)题15图题16图16.图示结构EI=常数,用位移法求解时有一个基本未知量。
(√)。
17.位移法中固端弯矩是当其基本未知量为零时由外界因数所产生的杆端弯矩(√)18.位移法的典型方程与力法的典型方程一样,都是变形协调方程。
第一章平面体系的几何组成分析一判断题1. 图示体系是几何不变体系。
(×)题1图题2图题3图题4图2. 图示体系为几何可变体系。
(×)3. 图示体系是几何不变体系。
(×)4. 图示体系是几何不变体系。
(√)5. 图示体系是几何不变体系。
(×)题5图题6图题19图题20图6. 图示体系为几何不变有多余约束。
(×)7. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)8. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)9. 在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
(√)10. 计算自由度W小于等于零是体系几何不变的充要条件。
(×)11. 几何可变体系在任何荷载作用下都不能平衡。
(×)12. 三个刚片由三个铰相联的体系一定是静定结构。
(×)13. 有多余约束的体系一定是超静定结构。
(×)14. 有些体系为几何可变体系但却有多余约束存在。
(√)15. 平面几何不变体系的三个基本组成规则是可以相互沟通的。
(√)16. 三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)17. 两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
(×)18. 若体系计算自由度W<0,则它一定是几何可变体系。
(×)19. 在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
(×)20. 图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
(×)21. 有多余约束的体系一定是几何不变体系。
(×)22. 几何不变体系的计算自由度一定等于零。
(×)23. 几何瞬变体系的计算自由度一定等于零。
(×)24. 图中链杆1和2的交点O可视为虚铰。
第三章静定结构的位移计算Displacement of Statically Determinate Structures1. 弹性杆件的变形与变形能计算2. 变形体虚功原理3. 单位荷载法4. 图乘法5. 其他外因引起的位移计算6. 互等定理7. 结论与讨论1 结构位移计算概述一、结构的位移 (Displacement of Structures)x Δy ΔA A ′βF P 线位移,角位移,相对线位移、角位移等统称广义位移线位移角位移DC ΔΔ+相对线位移CD D ΔC ΔαF P γ相对角位移γα +制造误差 δ 等铁路工程技术规范规定: 二、 计算位移的目的引起结构位移的原因(1) 刚度要求如:荷载、温度改变 ΔT 、支座移动 Δc 、在工程上,吊车梁允许的挠度< 1/600 跨度;桥梁在竖向活载下,钢板桥梁和钢桁梁最大挠度 < 1/700 和1/900跨度高层建筑的最大位移< 1/1000 高度。
最大层间位移< 1/800 层高。
(3)理想联结 (Ideal Constraint)。
三、 本章位移计算的假定(2) 超静定、动力和稳定计算(3)施工要求叠加原理适用(principle of superposition)(1) 线弹性 (Linear Elastic),(2) 小变形 (Small Deformation),返首2 变形体虚功原理 (Principle of Virtual Work)一、功(Work)、实功(Real Work)和虚功(Virtual Work)两种状态力状态位移状态F P F P /2F P /2(虚)力状态(虚力状态)(虚位移状态)无关(虚)位移状态q注意:(1)属同一体系;(2)均为可能状态。
即位移应满足变形协调条件;力状态应满足平衡条件。
(3)位移状态与力状态完全无关;一些基本概念:实功:广义力在自身所产生的位移上所作的功功:力×力方向位移之总和广义力:功的表达式中,与广义位移对应的项功:广义力×广义位移之总和虚功:广义力与广义位移无关时所作的功W=F P ×Δ/2W=F P1×Δ11 /2W=F P2×Δ22 /2W=F P1×Δ12or W=F P2×Δ21变力功(1)质点系的虚位移原理具有理想约束的质点系,在某一位置处于平衡的必要和充分条件是:1P F 2N F 1N F 2P F 1m 2m 二、变形杆件的虚功原理Σf i δr i =0→→.对于任何可能的虚位移,作用于质点系的主动力所做虚功之和为零。