最新 基尔霍夫定律叠加原理戴维南定理

叠加原理和戴维南定理叠加原理和戴维南定理，这俩名字听起来是不是有点高大上？但其实它们就像是电路世界里的小道消息，平时没什么人关注，但一旦你掌握了，就能在电路中游刃有余。

想象一下，咱们在电路中就像是在参加一场热闹的派对，每个电流、每个电压都是派对上的嘉宾。

叠加原理就像是邀请你，把不同的嘉宾分开，单独来看看每个人的表现。

你可以先把电路里的各个电源一个个拿出来，看看每个电源带来的电流和电压。

再把这些结果“叠加”在一起，就能看到整个电路的精彩面貌。

说白了，就是把复杂的事简单化，像是把一桌子的菜分成几个小盘子，先尝一口再说。

咱们再聊聊戴维南定理。

这个定理就像是电路的“简化大师”。

想象你在厨房里做菜，原本材料多得不得了，让人眼花缭乱。

可是戴维南定理就好比是一个神奇的调料，让你把这些复杂的材料简化成一个单一的“美味”。

它告诉你，不管电路多复杂，最终你都可以把它变成一个电压源加上一个电阻的组合。

就像是把一场复杂的宴会，变成一个简单的聚餐，只需几道经典菜就能满足大家。

这样你就能轻松计算出电流和电压，不再被复杂的电路搞得头晕脑胀。

说到这里，可能有人会问，这些定理到底有什么用？别着急，咱们慢慢来。

叠加原理就像是让你能分开来看每个电源的“功劳”。

比如，想象一下你的手机充电器，里面可能有好几个电源同时工作。

用叠加原理，你可以把每个电源的贡献都算出来，知道哪一个最给力，哪一个稍微逊色。

这样你就能更好地调整电路，提升整体性能，真是一举多得。

然后，戴维南定理的妙处就更不用说了。

想想看，生活中总是会遇到各种各样的复杂问题。

一道难题让你绞尽脑汁，结果却发现，经过简化，问题变得简单明了。

就像是在追求完美的同时，忽略了简单的快乐。

电路也是如此，很多时候，我们在追求复杂的电路设计时，反而忘记了简单的解决方案。

戴维南定理正好给了我们这个灵感，提醒我们在复杂中寻找简单。

再说说实际应用，叠加原理和戴维南定理在电力工程、电子设计等领域那是相当重要的工具。

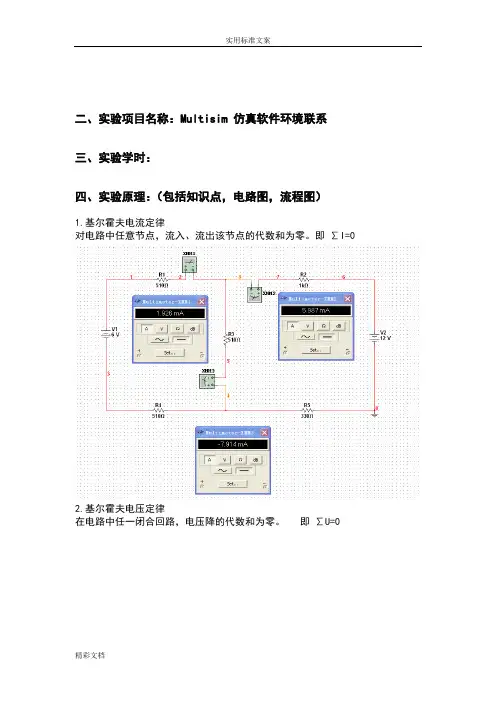
二、实验项目名称：Multisim 仿真软件环境联系三、实验学时：四、实验原理：（包括知识点，电路图，流程图）1.基尔霍夫电流定律对电路中任意节点，流入、流出该节点的代数和为零。

即∑I=02.基尔霍夫电压定律在电路中任一闭合回路，电压降的代数和为零。

即∑U=0(3).叠加原理在线性电路中，有多个电源同时作用时，任一支路的电流或电压都是电路中每个独立电源单独作用时在该支路中所产生的电流或电压的代数和。

某独立源单独作用时，其它独立源均需置零。

（电压源用短路代替，电流源用开路代替。

）4.戴维南定理任何一个线性含源网络，如果仅研究其中一条支路的电压和电流，则可将电路的其余部分看作是一个有源二端网络（或称为含源一端口网络）。

戴维南定理指出：任何一个线性有源网络，总可以用一个电压源与一个电阻的串联来等效代替，此电压源的电动势Us等于这个有源二端网络的开路电压Uoc，其等效内阻R0等于该网络中所有独立源均置零（理想电压源视为短接，理想电流源视为开路）时的等效电阻。

五、实验目的：1.熟悉并掌握Multisim仿真软件的使用2.掌握各种常用电路元器件的逻辑符号3.设计电路并仿真验证KCL、KVL定律和叠加定理、戴维南定理六、实验内容：（介绍自己所选的实验内容）利用Multisim仿真软件，绘制用于验证KCL、KVL定律和叠加定理、戴维南定理的模拟电路模拟电路，并利用Multisim仿真软件获取验证所需的实验数据，并根据实验数据计算出理论值与Multisim仿真电路的模拟值比较，验证KCL、KVL定律和叠加定理、戴维南定理。

七、实验器材（设备、元器件）：计算机；multisim10.0仿真软件八、实验步骤：（编辑调试的过程）(1). 验证基尔霍夫电流定律1. 利用Multisim仿真软件绘制出电路图(四.1)，图中的电流I1、I2、I3的方向已设定，2.加入两直流稳压电源接入电路，令U1=6V，U2=12V。

3. 接入直流数字毫安表分别至三条支路中，测量支路电流。

电学基础戴维南定理与基尔霍夫定律电学基础：戴维南定理与基尔霍夫定律在电学的广袤世界里，戴维南定理和基尔霍夫定律就像是两座坚实的基石，为我们理解和分析电路提供了强大的工具。

让我们一同走进这两个重要的电学概念，揭开它们神秘的面纱。

先来说说戴维南定理。

简单来讲，戴维南定理告诉我们，对于任何一个线性含源二端网络，都可以等效为一个电压源和一个电阻的串联组合。

这个电压源的电压等于该网络的开路电压，而电阻则等于该网络中所有独立电源置零后所得无源网络的等效电阻。

举个例子吧，假如我们有一个复杂的电路，其中包含了各种电阻、电容、电感以及电源。

但是我们只对其中的某一部分感兴趣，这时候戴维南定理就派上用场了。

我们可以把这部分电路从整个大电路中“拎出来”，然后通过测量或者计算得到它的开路电压和等效电阻，这样就把复杂的问题简单化了。

那么，如何去求解这个开路电压和等效电阻呢？对于开路电压，我们可以通过断开感兴趣的部分与电路的连接，然后计算剩余电路两端的电压。

而求等效电阻时，把所有的独立电源置零，也就是把电压源短路，电流源开路，然后求出剩下电阻网络的等效电阻。

再来说说基尔霍夫定律。

基尔霍夫定律包括电流定律（KCL）和电压定律（KVL）。

基尔霍夫电流定律指出，在任何一个节点上，流入节点的电流之和等于流出节点的电流之和。

这就好比是水流进入和流出一个水池，总的水量是不会凭空增加或减少的。

比如说在一个电路节点处，有三条支路，电流分别为 I1、I2 和 I3，流入节点的电流是 I1 和 I2，流出节点的电流是 I3，那么就有 I1 ＋ I2 ＝ I3。

基尔霍夫电压定律则表明，在任何一个闭合回路中，所有元件两端的电压代数和等于零。

想象一下我们沿着一个电路回路走一圈，升高的电压和降低的电压相互抵消，总和为零。

比如说在一个简单的回路中，有电源、电阻和电容，电源提供的电压为 U，电阻上的电压降为U1，电容上的电压降为 U2，那么就有 U U1 U2 ＝ 0。

电学基础戴维南定理与基尔霍夫定律电学基础：戴维南定理与基尔霍夫定律在电学的世界里，戴维南定理和基尔霍夫定律就像是两座坚固的基石，为我们理解和分析电路提供了重要的理论支持。

无论是简单的电路还是复杂的网络，这两个定律都有着广泛的应用，帮助我们解决各种实际问题。

让我们先来聊聊戴维南定理。

想象一下，你面对一个复杂的电路，其中有很多个电阻、电源等等元件，看起来眼花缭乱，让人不知所措。

这时候，戴维南定理就像一把神奇的剪刀，能把复杂的电路剪切成两部分。

一部分是我们需要研究的“目标电路”，另一部分则是可以被等效成一个简单的电源和电阻串联的组合。

这个等效的电源电压被称为戴维南电压，它的值等于原来电路在断开目标电路后的开路电压。

而等效电阻呢，被称为戴维南电阻，它的值等于原来电路中所有电源都置零（电压源短路，电流源开路）后，从断开处看进去的等效电阻。

比如说，我们有一个电路，其中包含了多个电阻和一个电源。

我们想要研究其中某一部分电阻两端的电压和电流。

通过戴维南定理，我们就可以把这部分电阻之外的电路等效成一个简单的电源和电阻串联，这样计算起来就简单多了。

戴维南定理的优点在于它能够将复杂的电路简化，使得分析和计算变得更加容易。

特别是在解决含有多个电源和复杂电阻网络的电路问题时，它的作用尤为明显。

接下来，我们再谈谈基尔霍夫定律。

基尔霍夫定律分为电流定律（KCL）和电压定律（KVL）。

基尔霍夫电流定律（KCL）说的是，在任何一个节点（也就是电路中三条或三条以上支路的连接点）上，流入节点的电流之和等于流出节点的电流之和。

这就好比是水流进入和流出一个节点，进来的水总量必须等于出去的水总量，不然水就会在节点处堆积或者消失，这显然是不符合实际的。

举个例子，如果一个节点上有三条支路，其中两条支路流入节点的电流分别是 2A 和 3A，那么从第三条支路流出的电流必然是 5A，这样才能满足 KCL。

而基尔霍夫电压定律（KVL）则是说，在任何一个闭合回路中，沿回路绕行一周，所有元件的电压代数和等于零。

第六讲 基尔霍夫定律和戴维南定理1 基尔霍夫定律1．1基尔霍夫第一定律对电路中任何一个节点，流出的电流之和等于流入电流之和。

∑∑=出入j i I I或可表达为：汇于节点的各支路电流强度的代数和为零。

∑=±0iI若规定流入电流为正号，则从节点流出的电流强度为负号。

对于有n 个节点的完整回路，可列出n 个方程，实际上只有1-n 个方程是独立的。

1．2基尔霍夫第二定律沿回路环绕一周，电势降落的代数和为零，即()∑∑=±+±0j jiR IE对于给定的回路绕行方向，理想电源，从正极到负极，电势降落为正，反之为负；对电阻及内阻，若沿电流方向则电势降落为正，反之为负。

若复杂电路包括m 个独立回路，则有m 个独立回路方程。

【例1】如图1所示电路中，已知E 1=32V ，E 2=24V ，电源内阻均不计，R 1=5Ω，R 2=6Ω，R 3=54Ω求各支路的电流。

解： 题中电路共有2个节点，故可列出一个节点方程。

而支路3个，只有二个独立的回路，因而能列出两个回路方程。

三个方程恰好满足求解条件。

规定321I I I 、、正方向如图所示，则有0321=-+I I I两个独立回路，有0112221=+-+-R I R I E E033222=++-R I R I E联解方程得：I 1=1A ，I 2=-0.5A ，I 3=0.5A2I ＜0，说明2I 实际电流方向与图中所假定电流方向相反。

2 戴维南定理实际的直流电源可以看作电动势为E ，内阻为零的恒压源与内阻r 的串联，如图2所示，这部分电路被称为电压源。

不论外电阻R 如何，总是提供不变电流的理想电源为恒流源。

实际电源E 、r 对外电阻R 提供电流I 为rR rr E r R E I +⋅=+= 其中E ／r 为电源短路电流0I ，因而实际电源可看作是一定的内阻与恒流源并联的电流源，如图3所示。

实际的电源既可看作电压源，又可看作电流源，电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。

理解电路中的基尔霍夫定律与戴维南定理电路中的基尔霍夫定律与戴维南定理是电路分析中常用的两个重要原理。

通过理解和应用这两个定律，我们可以更好地理解和解决电路中的问题。

基尔霍夫定律是基于电流守恒和电荷守恒原理的。

它由两个部分组成：基尔霍夫第一定律和基尔霍夫第二定律。

基尔霍夫第一定律也称为电流定律，它指出电路中的节点处的所有电流代数和为零。

这个定律是基于电流守恒原理的，即电流在节点处的进出是平衡的。

基尔霍夫第二定律也称为电压定律，它指出沿着任何闭合路径的电压代数和为零。

这个定律是基于电荷守恒原理的，即电荷在闭合回路中是守恒的。

通过应用基尔霍夫定律，我们可以根据电流和电压的关系来解决电路中的问题。

戴维南定理是基于电压和电流之间的线性关系的。

它可以帮助我们计算电路中的电流和电压。

根据戴维南定理，电路中的任何两个节点的电压差等于电流通过这两个节点的电阻的乘积的代数和。

这个定理是基于欧姆定律的推论，即电流与电压之间存在线性关系。

通过应用戴维南定理，我们可以计算电路中的电流和电压分布，从而了解电路的行为和特性。

理解电路中的基尔霍夫定律与戴维南定理对于解决电路问题至关重要。

它们提供了一种分析电路的有效方法，帮助我们理解电路中的各种参数和变量之间的关系。

通过使用这两个定律，我们可以计算电流、电压、功率等电路参数，预测电路的稳定性和性能。

此外，它们还能帮助我们设计和优化电路，提高电路的效率和可靠性。

为了更好地应用基尔霍夫定律与戴维南定理，我们需要有一些基础的电路知识和分析技巧。

首先，我们需要了解基本的电路元件，如电阻、电感和电容等，并熟悉它们的性质和特性。

其次，我们需要了解电路拓扑结构，如串联、并联和混合连接等，并能够分析和计算电路中的参数。

此外，我们还需要学习使用符号和方程表示电路，并掌握解方程的技巧和方法。

在实际应用中，我们可以将基尔霍夫定律和戴维南定理与其他电路分析方法和工具结合起来使用。

例如，我们可以使用模拟电路仿真软件来模拟和验证电路的性能。

叠加定理戴维南定理基尔霍夫定理下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!叠加定理、戴维南定理与基尔霍夫定理：电路分析中的重要工具在电路分析领域，叠加定理、戴维南定理和基尔霍夫定理是至关重要的工具。

实验报告叠加原理和戴维南定理的验证姓名马诗琪班级13教技学号131034 14114叠加原理和戴维南定理的验证一.实验目的：1. 通过实验加深对基尔霍夫定律、叠加原理和戴维南定理的理解。

2. 学会用伏安法测量电阻。

3. 正确使用万用表、电磁式仪表及直流稳压电源。

二.实验原理：1 •基尔霍夫定律:1）•电流定律（KCL人在集中参数电路中，任何时刻，对任一节点，所有各支路电流的代数和恒等于零，即∑∕ = 0o流出节点的支路电流取正号，注入节点的支路电流取负号。

2）•电压定律（KVL）：在集中参数电路中，任何时刻，对任一回路内所有支路或原件电压的代数和恒等于零，在即∑u=0o凡支路电压或原件电压的参考方向与回路绕行方向一致者为正量，反之取负号。

2 •叠加原理在多个独立电源共同作用的线性电路中，任一支路的电流（或电压）等于各个电源独立作用时在该支路所产生的电流（或电压）的代数和。

3.戴维南定理：任一线性有源二端网络对外电路的作用均可用一个等效电压源来代替，其等效电动势EO等于二端网络的开路电压Uo,等效内阻Ro 等于该网络除源（恒压源短路、开流源开路）后的入端电阻。

实验仍釆取用图2-3-1所示电路。

可把ac支路右边以外的电路（含Rs 支路）看成是以a与C为端钮的有源二端网络。

测得a、C两端的开路电压Uab即为该二端网络的等效电动势Eo,内阻可通过以下几种方法测得。

（1）伏安法。

将有源二端网络屮的电源除去，在两端钮上外加一已知电源E,测得电压U和电流I,则U（2）育接测量法。

将有源二端网络中的电压源除去，用万用表的欧姆档直接测量有源二端网络的电阻值即为Ro。

本实验所用此法510测量，图2屮的开关Sl合向右侧，开关S?断开，然后用万能表的欧姆挡侧a、C两端的电阻值即可。

（3）测开路电压和短路电流法。

测量有源二端网络的开路电压UO 和短路电流Is。

则RO=UO∕∣s测试如图2-3-3所示，开关S打开时测得开路电压Uo,闭合时测得短路电流Is。

基尔霍夫叠加定理哎呀，说起基尔霍夫叠加定理，这可真是个让人头疼的玩意儿。

不过，别担心，咱们今天就用大白话聊聊这个听起来高大上的物理定律。

记得那会儿，我还是个电气工程的大学生，第一次听到这个定理的时候，我心想：“这玩意儿能有啥用？”结果，事实证明，这玩意儿在电路分析里头，简直就是个神器。

基尔霍夫叠加定理，简单来说，就是说在一个复杂的电路里头，如果你想要计算某个点的电压或者某个支路的电流，你可以把其他所有的电源都关掉，只留下一个，然后计算这个电源单独作用下的结果。

然后，你再换另一个电源，重复这个过程。

最后，把所有这些结果加起来，就得到了所有电源同时作用的结果。

举个例子吧，想象一下，你面前有一个电路板，上面有好几个电源和电阻。

你想知道某个电阻上的电压是多少。

按照基尔霍夫叠加定理，你可以先假设只有第一个电源在工作，计算出这个电源作用下的电压。

然后，你再假设只有第二个电源在工作，计算出这个电源作用下的电压。

最后，你把这两个电压加起来，就得到了所有电源同时作用下的结果。

这玩意儿的好处就是，它让复杂的电路分析变得简单多了。

你不需要一下子考虑所有的电源和电阻，而是可以一个一个来，就像是在玩拼图一样，一块一块地拼起来。

记得有一次，我在做一个项目，需要计算一个特别复杂的电路板上的电流。

那时候，我真是头大如斗，电路板上的电源和电阻多得数不清。

但是，我想起了基尔霍夫叠加定理，就决定用这个定理来解决问题。

我一个一个地关掉电源，计算电流，然后再加起来。

结果，还真的让我算出来了，而且还挺准确的。

所以，你看，基尔霍夫叠加定理虽然听起来复杂，但其实用起来挺简单的。

它就像是给你一个工具，让你能够把复杂的问题分解成简单的小问题，然后一个一个解决。

这样，即使是最复杂的电路，也能变得容易处理了。

总之，基尔霍夫叠加定理，虽然听起来高大上，但其实它就像是我们日常生活中的瑞士军刀，多功能，实用，而且能解决很多问题。

下次你遇到复杂的电路问题，不妨试试这个定理，说不定会有意想不到的收获呢。

基尔霍夫定律和叠加定理实验总结嘿，伙计们！今天咱们来聊聊那些让人头疼的电路问题——基尔霍夫定律和叠加定理。

这些听起来像是高中物理课上的术语，但你知道吗？其实它们就像是我们日常生活中的小窍门，能让我们在遇到电路难题时游刃有余。

基尔霍夫定律是什么来着？简单来说，它就像是电路中的交通规则，告诉我们电流、电压和功率是如何在电路中流动的。

想象一下，如果电路里的车流量突然增加了，而道路却没变宽，那会发生什么？答案就是：混乱！基尔霍夫定律就像是那个交通警察，确保了电流和电压不会乱跑，而是按照一定的路线安全行驶。

再来说说叠加定理，这就像是我们处理复杂问题时的“分而治之”策略。

想象一下，你面前有一堆需要解决的问题，而每个问题都像是一个独立的小怪兽。

叠加定理就像是一位智慧的魔法师，他告诉你：“不用怕，我来帮你解决！”通过将问题分解成更小的部分，然后分别解决，最后再将这些部分组合起来，就能轻松搞定所有的问题。

那么，如何用这两个定律来解决实际的电路问题呢？让我给你举个例子。

假设你有一个复杂的电路图，里面包含了多个元件，而且它们之间还有相互连接。

这时候，你就可以用基尔霍夫定律来检查电流是否真的按照预期流动。

而当你发现某个元件的电压或电流不符合预期时，叠加定理就能派上用场了。

你可以先独立地分析每个元件，看看是不是哪个环节出了问题，然后再把它们放在一起综合考虑，找到问题的根源。

当然啦，实践是检验真理的唯一标准。

所以，赶紧动手试试吧！把那些电线、电阻、电容和二极管摆弄出来，按照基尔霍夫定律和叠加定理的规则来解决问题。

你会发现，原来学习这些知识不仅能让我们在考试中得高分，还能让我们在日常生活中变得更加聪明能干呢！基尔霍夫定律和叠加定理就像是我们生活中的小助手，帮助我们解决电路问题。

只要我们掌握了它们，就能像侦探一样，一步步揭开电路的秘密，解开生活中的种种谜团。

所以，不要小看了这两个看似简单的定律，它们可是解决复杂问题的好帮手哦！。