当前位置：文档之家 › 第5章 有噪信道编码

第5章 有噪信道编码

  • 格式：ppt
  • 大小：484.00 KB
  • 文档页数：53

下载文档原格式

  / 53

合集下载

有噪信道编码定理

有噪信道编码定理

而编码定理要证明的就是：只要信道速率小于信道容量，总存在一种
编码使误码率任意小。
对理想无噪信道，编码定理需要证明 R = LH (U ) < log D 时，误码任
意小；（平均码长与输入熵的关系）
N
对有噪信道情况，编码定理需要证明 R = LH (U ) < C 时，误码任意
小。（信道速率与信道容量的关系）
z 二元编码误差；
z 多元编码误差，信道编码定理。
¾ 基本要求
z 理解信道编码的目的；理解信道速率的概念；
z 理解最小误差和最大似然两个解码准则，会根据最大似然解码准则 划分输出子集；
z 了解二元编码的误码率上界，会计算 gn ( s) ；
z 了解多元编码的误码率上界，理解编码指数的含义及使用方法，掌 握编码指数的曲线变化，掌握有噪信道编码定理。
121316161213131612yx??????????ppx123111244xxxx????????????????pdiagx12121316141611214161213124181121413161211212418xyyx??????????????????????????????pp1diagyxyxy????ppp2012424信息论与编码有噪信道编码定理14xianjiaotonguniversity52解码准则所以
2012-4-24
《信息论与编码》－－有噪信道编码定理
7
《信息论与编码》--有噪信道编码定理
5.1 信道速率
定义：信道每用一次所需要传递的信息量。
XI’AN JIAOTONG UNIVERSITY
设信道编码器的输入是长为 L 的 K 进制序列，输出是N 位长 D进制序 列。可能的输入有 M = K L 种，输出有 T = DN 种，M < T。

有噪信道编码

有噪信道编码

第7章有噪信道编码本章主要内容：√1.概述√2.最佳判决与译码准则3.信道编码与最佳译码√4.费诺（Fano）不等式√5.有噪信道编码定理6.纠错编码技术简介7.信道编码性能界限§7.1 概述信道编码：就是按一定的规则给信源输出序列增加某些冗余符号，使其变成满足一定数学规律的码序列（或码字），再经信道进行传输。

（提高传输的可靠性）信道译码：就是按与编码器同样的数学规律去掉接收序列中的冗余符号, 恢复信源消息序列。

一般地，所加的冗余符号越多，纠错能力就越强，但传输效率降低。

因此在信道编码中明显体现了传输有效性与可靠性的矛盾。

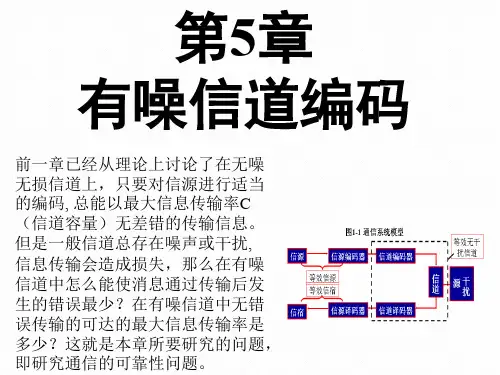
本节主要内容：1. 信道编码的基本概念2. 判决与译码规则3. 译码错误概率7.1.1 信道编码的基本概念简化的通信系统模型如图7.1.1所示。

图7.1.1 简化通信系统模型图信道译码信道编码信道码字（码长为n)等概消息{1,2,……，M}接收序列恢复的消息U Vn Y n X 设信源输出或信道编码器的输入消息集合为U，信道编码器采用分组编码，输出码字为的一个子集，其中每个码符号取自符号集；码字通过离散无记忆信道传输；信道输出或译码器的输入为，其中每个符号取自符号集；译码器输出是被恢复的消息，其集合用V表示。

n X i x X ∈12{,,,}r A a a a = n Y y Y ∈12{,,,}s B b b b =（1）消息产生：由信源发出M 个等概率消息：U ={1，2，…，M}；（2）信道编码：编码器将消息映射成码字，编码函数f ：{1，2，…，M}→C= ，其为码长为n 的码字，码符号集A 的大小为r ；（3）信道传输：为n 维矢量，取自码字集C ，作为n 次扩展信道的输入，，是n 维矢量，为信道输出，；（4）信道译码：译码器根据接收的完成译码功能，译码函数。

12{,,,}M c c c x n C A ∈y n Y ∈y y :{1,2,,}n g Y V M →=⋅⋅⋅信息传送过程衡量信道编码有效性的重要指标就是信息传输速率（也称码率）。

语音编码及信道编码

语音编码及信道编码
第5章 语音编码及信道编码
语音编码及信道编码
第94页，共94页。
第5章 语音编码及信道编码
5.1 概 述
5.1.1 语音编码 语音编码的基本方法可分为波形编码和参量编码两
种。 波形编码是将时域的模拟语音的(电压)波形信号经 过取样、 量化、 编码而形成的数字语音信号。 为了保 证数字语音信号解码后的高保真度， 取样速率应满足奈 奎斯特取样定理， 并且量化分层数要足够大。
第94页，共94页。
第5章 语音编码及信道编码
2) RPE-LTP线性预测解码器 图5 - 10(b)为解码器方框图。 图中粗体箭头表示收 到的编码参数。 RPE参数Mc、Mmaxc和Xmc； 在解码器 中用来重建长时余量信号e′， 以供长时预测滤波器产生 激励信号d′。 短时合成(综合)滤波器将其用来恢复成语 音信号S。 恢复的语音信号S在后处理部分经去加重后成 为解码器最后输出的语音信号S0。
1) RPE-LTP线性预测编码器 图5 - 10(a)示出RPE-LTP线性预测编码器的方框图， 它由预处理、 LPC分析、 短时分析滤波、 长时预测和 规则脉冲激励(RPE)编码 5 个部分组成。 现将其各部分 的功能分述如下。
第94页，共94页。
第5章 语音编码及信道编码
预处理
LP C分 析
2. 规则脉冲激励长期预测编解码器 RPE—LTP线性预测编解码器即是具有长期预测的 规则脉冲激励的线性预测编解码器。 这种RPE-LTP线性 预测编码方式已用于泛欧GSM数字蜂房移动通信系统中， 并作为GSM标准予以公布。 下面分别介绍它的编码器 和解码器。
第94页，共94页。
第5章 语音编码及信道编码
第94页，共94页。
第5章 语音编码及信道编码

信源编码

信源编码

S {S1, S2 ,..., Sq}
编码器
C :{W1,W2 ,...,Wq}
X {x1, x2,..., xr}
wi 称为码字，Li为码字wi 的码元个数，称为码字wi 的码字 长度，简称码长。
第二节 码的分类
1、二元码： 码符号集X={0,1}，如果要将信源通过二元信道传输，必
须将信源编成二元码，这也是最常用的一种码。 2、等长码：
第八章 信源编码
1 引言 2 等长信源编码定理、变长信源编码定理
3 各种编码 4 有噪信道编码定理
5 联合信源信道编码定理
第五章 有噪信道编码
第一节 错误概率与译码规则 第二节 错误概率与编码方法 第三节 有噪信道编码定理 第四节 联合信源信道编码定理 第六节 纠错编码的基本思想 第七节 常用编码方法
l H (S) 2
N log r
则不可能实现无失真编码，当N趋向于无穷大是，译码错 误率接近于1。
第三节 等长信源编码定理
•定理4.3的条件式可写成： l log r NH (S)
左边表示长为 l 的码符号所能载荷的最大信息量， 而右边代表长为N的序列平均携带的信息量。因此， 只要码字传输的信息量大于信源序列携带的信息量， 总可以实现无失真编码 。
信源编码的分类：离散信源编码、连续信源编码和相关信源编 码三类。 离散信源编码：独立信源编码，可做到无失真编码； 连续信源编码：独立信源编码，只能做到限失真信源编码； 相关信源编码：非独立信源编码。
第二节 码的分类
编码器可以看作这样一个系统，它的输入端为原始信
源S，其符号集为S {S1, S2,..., Sq}；而信道所能传输的符号集 为 X {x1, x2,..., xr} 编码器的功能是用符号集X中的元素，将 原始信源的符号 Si 变换为相应的码字符号wi ，所以编码器 输出端的符号集为 C :{W1,W2,...,Wq}

有噪信道编码定理

有噪信道编码定理

错误译码的概率为：P(e | bj ) 1 P(ai | bj ) 1 PF (bj ) | bj
平均错误译码概率为：
PE EP(e | bj ) P(bj ) P(e | bj )
j 1 s
它表示经过译码后平均接收到一个符号所产生 的错误大小，也称平均错误概率。 只要设计译码规则 F (bj ) ai ，使条件错误译码概率
根据最大似然译码准则可选择码函数为 B F (b1) a1 第一列中 P(b1 | a1) 0.5 B : F (b 2) a 3 第二列中 P(b2 | ai ) 0.3(i 1,2,3) F (b3) a 2 第三列中 P(b3 | a 2) 0.5
PE 1 1 (0.2 0.3) (0.3 0.3) (0.2 0.4) 0.567 P ( b | a ) 3 Y , X a 3 1 1 (i ) (0.3 0.2) (0.2 0.3) (0.3 0.4) 0.567 P e 3 X 3
F(yj)=xi (i=1,2,…r; j=1,2,…s)
对于有r个输入，s个输出的信道来说，可以有rs个 不同的译码准则。
【例6.1】有一离散单符号信道，信道矩阵为
0 . 5 0. 3 0. 2 P 0 . 2 0 . 3 0 . 2 0 . 3 0. 3 0. 4
6.1
错误概率和译码规则
我们已经知道错误概率与信道统计特性有关 。信道的统计特性可由信道的传递矩阵来描述 。当确定了输入和输出对应关系后，也就确定 了信道矩阵中哪些是正确传递概率，哪些是错 误传递概率。例如在二元对称信道中，单个符 号的错误传递概率是p，正确传递的概率是 p 1 p

第5章_信源—信道编码定理

第5章_信源—信道编码定理

这种编码方法，可以看成是一种特殊的试验信道
1 P (v j / ui ) 0
d (C )

v j C , v j f (ui ) v j f (ui )
1 N
P (U ) d [ u , f ( u )]
U
1 1 1 [0 1 1 1 0 1 1 1] 3 8 4
要使信源在此二元信道中传输，必须对X进行二元编码：
x1 C1 C2 000 0000
x2 001 0001
x3 010 0010
H (X ) 3
H (X ) 4
x4 011 0011
x5 100 0100
x6 101 0101
对于码 对于码
C1
R1
0 .6 4 6
(比特／信道符号) (比特／信道符号)
第5章
信道—信源编码定理
通用通信系统
其中：编码器包括信源编码和信道编码两个部分； 译码器包括信道译码和信源译码两个部分； 信道为有噪信道。
•信道编码 •给定信道输入符号集AX； •给定信道输出符号集AY； •对每个输入符号x，存在一个非负实数b(x)，为传输x的 代价。 定义n阶容量—代价函数：
信息率为1/3，而平均失真为1/4，根据香农第三定理， 若允许失真D=1/4时，总可以找到一种编码，使信息输出 率达到极限R(1/4)
1 1 R ( ) 1 H ( ) 0 .1 8 9 4 4
信源—信道匹配
• 当信源与信道相连接时，其信息传输率并未 达到最大. • 希望能使信息传输率越大越好，能达到或尽 可能接近于信道容量, 信息传输率接近于信道 容量只有在信源取最佳分布时才能实现。 • 由此可见，当信道确定后，信道的信息传输 率与信源分布是密切相关的。当达到信道容 量时，我们称信源与信道达到匹配，否则认 为信道有剩余。

信息理论与编码课后答案第5章

信息理论与编码课后答案第5章

第5章 有噪信道编码5.1 基本要求通过本章学习，了解信道编码的目的，了解译码规则对错误概率的影响，掌握两种典型的译码规则：最佳译码规则和极大似然译码规则。

掌握信息率与平均差错率的关系，掌握最小汉明距离译码规则，掌握有噪信道编码定理（香农第二定理）的基本思想，了解典型序列的概念，了解定理的证明方法，掌握线性分组码的生成和校验。

5.2 学习要点5.2.1 信道译码函数与平均差错率5.2.1.1 信道译码模型从数学角度讲，信道译码是一个变换或函数，称为译码函数，记为F 。

信道译码模型如图5.1所示。

5.2.1.2 信道译码函数信道译码函数F 是从输出符号集合B 到输入符号集合A 的映射：*()j j F b a A =∈，1,2,...j s =其含义是：将接收符号j b B ∈译为某个输入符号*j a A ∈。

译码函数又称译码规则。

5.2.1.3 平均差错率在信道输出端接收到符号j b 时，按译码规则*()j j F b a A =∈将j b 译为*j a ，若此时信道输入刚好是*j a ，则称为译码正确，否则称为译码错误。

j b 的译码正确概率是后验概率：*(|)()|j j j j P X a Y b P F b b ⎡⎤===⎣⎦ （5.1）j b 的译码错误概率：(|)()|1()|j j j j j P e b P X F b Y b P F b b ⎡⎤⎡⎤=≠==-⎣⎦⎣⎦ （5.2）平均差错率是译码错误概率的统计平均，记为e P ：{}1111()(|)()1()|1(),1()|()s se j j j j j j j ssj j j j j j j P P b P e b P b P F b b P F b b P F b P b F b ====⎡⎤==-⎣⎦⎡⎤⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎣⎦∑∑∑∑ （5.3）5.2.2 两种典型的译码规则两种典型的译码规则是最佳译码规则和极大似然译码规则。

第5章 语音编码、信道编码和交织

第5章 语音编码、信道编码和交织
4
波形编码
3步骤：抽样、量化和编码 步骤：抽样、 步骤
抽样信号
抽样信号 量化信号
011
100
100
011
011
100
100
编码信号
t
5
6
5.1.2 语音信号特征
语音的产生是人的发生器官共同作用的结 简化来讲， 果。简化来讲，是声带和声道共同作用的 结果。由声带产生，经声道发出。 结果。由声带产生，经声道发出。 语音根据声带振动与不振动， 语音根据声带振动与不振动，又可将声音 分为浊音和清音。 分为浊音和清音。 发浊音时，声带紧绷， 发浊音时，声带紧绷，气流冲激声带产生 振荡，激励源是准周期脉冲序列。 振荡，激励源是准周期脉冲序列。 发清音时，生带松弛不振动， 发清音时，生带松弛不振动，气流直接进 入声道，激励源类似于噪声。 入声道，激励源类似于噪声。
23
5.1.6 GSM系统语音编码器 系统语音编码器
1．GSM系统语音编码器性能要求 ． 系统语音编码器性能要求 （1）语音质量 ） 对语音编码最基本的要求就是用户角度测 在可工作的范围内， 试，在可工作的范围内，平均语音质量应 至少不低于900MHz模拟移动系统。 模拟移动系统。 至少不低于 模拟移动系统 语音编码算法应具有很强的适应频谱以及 电平变化的能力。 电平变化的能力。
QCELP（码激励线性预测）是Qualcomm （码激励线性预测） 公司CDMA系统中的语音编码标准 系统中的语音编码标准IS-95。 公司 系统中的语音编码标准 。 QCELP主要是使用码表矢量量化差值信号， 主要是使用码表矢量量化差值信号， 主要是使用码表矢量量化差值信号 然后基于语音的激活程度产生一个可变的 输出数据速率。 输出数据速率。
CELPC应用了矢量量化技术。N个样值构成 应用了矢量量化技术。 个样值构成 应用了矢量量化技术 一个N维矢量的码字 维矢量的码字。 一个 维矢量的码字。若干码字就构成一个 码本。 码本。 发送和接收端拥有同样的码本， 发送和接收端拥有同样的码本，发送端确定 最小失真的码字，将其序号传输给接收端。 最小失真的码字，将其序号传输给接收端。

5有噪信道编码及其定理

5有噪信道编码及其定理

5.1 错误概率和译码规则
通常信道的传递概率P(bj|ai)与输入符号的先验概 率P(ai) 已知，根据贝叶斯定律，有：
P(a
bj )
P(ai
bj )
P(bj
/ a*)P(a*) P(bj )
P(bj / ai )P(ai ) P(bj )
即 P(bj / a*)P(a*) P(bj / ai )P(ai ) 当信源等概分布时，可选择译码函数
X ,Y
Y
Y ,X a
平均正确概率为
s
PE 1 PE P F(bj )bj P(abj )
Y
j 1
5.1 错误概率和译码规则
也可写成： PE P(bj ai )P(ai ) Y ,X a
其中求和符号 Xa表 示对输入符号集A中除 F(b以j ) 外a
的所有元素求和。
上式的平均错误概率是在联合概率矩阵P(ai )P(bj ai )
5.1 错误概率和译码规则
错误：译码输出≠信源输出
产生原因：噪声干扰
研究目的：减少错误，提高可靠性
研究途径：信道的传递矩阵→信道统计特性→错 误概率
为了减少错误，提高通信的可靠性，就必须分析 错误概率与哪些因素有关，有没有办法控制，能 控制到什么程度。
5.1 错误概率和译码规则
我们知道错误概率与信道的统计特性有关， 信道的统计特性由信道的传递矩阵来描述。
第五章 有噪信道编码
我们要尽可能的提高信息传输率，并控制传输误 差。信源编码以提高传输效率作为主要考虑因素， 信道编码以提高传输可靠性作为主要考虑因素。 这一章讨论信道编码的一些基本概念及信道编码 定理
本章介绍了信道编码和译码的基本概念，介绍了 两种常用的译码准则：最大后验概率译码准则和 最大似然译码准则,还介绍了在这两种译码准则 下错误概率的计算方法。还介绍了信道编码定理 及信道编码逆定理，以及信息论中的一个重要不 等式Fnao不等式。

第5章-有噪信道编码

第5章-有噪信道编码

第5章 有噪信道编码
内容提要 本章介绍了信道编码和译码的基 本概念，介绍了两种常用的译码 准则：最大后验概率译码准则和 极大似然译码准则,还介绍了在这 两种译码准则下错误概率的计算 方法。 本章还介绍了信道编码定理以及 信息论中的一个重要不等式Fano 不等式。
5．1 信道编码的基本概念
信源编码以提高传输效率作为主要考虑因素， 信道编码以提高传输可靠性作为主要考虑因素。 这一章讨论信道编码的一些基本概念及信道编码定 理。
y) y)

p(e 000) p(e111)
1 1

1
4 1

3
4 3

44
假设8组输入序列是等概发送的，由于信道的对称性，两
个估值序列也是等概分布的，则每个序列的平均错误概率
为 0.5 p(e 000) 0.5 p(e111) 3
，
误比特率
p1

1 3

3 4

1 4
4 。
判决输出符号集Y = {000,111}
译码规则
F (000， 001， 010， 100) 000

F (011，
101，
110，
111)

111
因为后验概率
（x y ) (000 000)
1 4

（x
y
)

(111111)

1
则出错概率
4

p(e p(e
重复编码的结果使错误概率下降。
书上例题5.2
【例5.3】 逆重复码 离散无记忆二进制对称信道，固有 误码率为p (p<0.5)，信源输出序列为三位二进制数字。

信息论与编码第五章

信息论与编码第五章

r
pE 1 pE s r r 1 s 1 p(ai b j ) log p(ai b j ) log p(ai b j ) log p(aibi ) log (r 1) p(ai | b j ) j 1 i * p ( ai | b j ) j 1 i 1 pE j 1 i * 1 pE j 1 i *
p ( ai b j )

pE (r 1)p(b1 ) p(b2 ) p(bs ) p E p E p E 0 r 1
第二项
s
1 pE 1 pE log 1 p ( ai | b j ) p ( ai | b j )
s
即

j 1 i *
第五章
有噪信道编码
无失真信源编码（无噪离散信道编码）的抗干扰能力很 脆弱，如把信源编码器的输出直接接入信道，必然会因干扰 造成错误，使通信不可靠，为了使通信既有效，又可靠，可 在以缩短平均码长、提高通信有效性为主要目标的信源编码 器的输出与信道的输入之间，对信源编码器输出的最佳码再 进行一次编码，以提高其抗干扰能力，称为信道编码。
1、输入端只有2个消息（符号）且等概出现，则每个消息携
带的信息量是 log M 1 bit / 符号 。 2、简单重复三次后，（三次无记忆扩展信道），入端有 2 3 8 个二进序列，但只选其中两个作为消息，M＝2，每个消 1 息携带的信息量仍为 1bit ，但用三个符号,∴ R bit /符号。
p E min
1 8 1 p(b j | ai ) p 3 p p 2 p p 2 p p 2 p p 2 p p 2 p p 2 p 3 2 j 1 i * 2

第五章有噪信道编码(7)

第五章有噪信道编码(7)

5.5联合信源信道编码定理5.5.1 分两步的思路从香农第一和第二定理可以看出，要做到有效和可靠地传输信息，可以将通信系统设计成二部分的组合，即信源编码和信道编码二部分。

(1) 通过信源编码，用尽可能少的信道符号来表达信源，尽可能减少编码后的数据的剩余度。

(2) 针对信道，对信源编码后的数据独立地设计信道编码，也就是适当增加一些剩余度，使能纠正和克服信道中引起的错误和干扰。

这二部分编码是分别独立考虑的。

分两步编码处理的方法，其信源压缩编码只与信源有关，不依赖于信道；而信道编码只与信道有关，不依赖于信源。

问题：1. 分两步处理的方法是否与一步编码处理一样好呢？2. 分两步处理是否会带来某些损失呢？分析：(1) 无失真信源编码是一一对应的变换，无论编码还是译码都是一一对应的映射，因此无失真信源编码不会带来任何信息损失。

结论：分两步处理不会带来增加信息损失(2) 信源通过两步编码后送入信道，信道输出端接收到的信息会有一些损失(失真)，这是由于信道引起的。

而通过信道编码(又满足)，可使信道引起的损失(或错误)尽可能少（错误概率任意小）。

R C <5.5.2 有效并可靠传输的充要条件证明：在有噪信道中，只要，用两步编码处理方法传输信源信息与一步编码处理方法传输信源信息是一样有效的。

也即，信源通过信道传输，有效和可靠地传输的充要条件是。

H C <H C <首先设信源S ，其符号集。

假设其符号集为有限符号集并随机序列满足渐近等分割性(AEP)。

{}12q s s s =",,,平均错误概率为若接收端，估计值则就造成错误，因此错误概率n n S S ≠ˆ()n nn e P P S S =≠ˆ()()n n n n E S P P S PS S =≠∑ˆ5.5.3 信源－信道编码定理若是有限符号集的随机序列并满足AEP ，又信源S 极限熵，则存在信源信道编码，其。

{}12nn S s s s =",,,H C ∞<0E P →反之，对于任意平稳随机序列，若极限熵，则错误概率远离零，即不可能在信道中以任意小的错误概率发送这随机序列。

第5章 有噪信道编码

第5章 有噪信道编码

按“后验概率最大” 原则定出，又称最大后验 概率译码规则
按“联合概率最大” 原则定出，又称最大联合 概率译码规则
F (b j ) a* A , b j B j F : P(a* , b j P(ai , b j ) , ai A j
9
例5.2 求最佳译码规则
按“转移概率最大” 原则定出，称为极大似 然译码规则。
11
例5.3 极大似然译码规则
已知信道转移矩阵， [ PY | X ] 0.2 0.3 0.5 确定译码规则。 0.5 0.3 0.2 0.3 0.3 0.4
只已知转移概率，无法找出最佳译码规则，只能采用极大似然译码规则。 将转移矩阵各列最大的转移概率标出，如下：
j , b j B j F : * P(a j | b j ) P(ai | b j ) , ai A
P(b j ) P(a* | b j ) P(b j ) P(ai | b j ) j P(a* , b j P (ai , b j ) j
bj的译码错误概率：P(e | b j ) P X F (b j ) | Y b j 1 P F (b j ) | b j 平均差错率Pe : Pe P(b j ) P(e | b j ) P(b j ) 1 P F (b j ) | b j
Pe ( F1 ) 1 P F1 (b j ), b j 1 P(a1 , b1 ) P(a1 , b2 ) 1 (0.32 0.08) 0.6
j 1 s
Pe ( F2 ) 1 P F2 (b j ), b j 1 P(a2 , b1 ) P(a2 , b2 ) 1 (0.06 0.54) 0.4

第五章有噪信道编码(3)

第五章有噪信道编码(3)

（3）则称序列对以示Y n中y间中序列对5.3.2 联合渐近等分割性对于任意小的正数ε≥0，δ≥0，当n 足够大时，则有()()()()()()111n n n P G X P G Y P G XY εεεδδδ≥−≥−≥−(1)定理 5.1(联合渐近等分割性)(2) 联合ε 典型序列对(x,y) 是n次无记忆扩展联合空间中经常出现的高概率序列对。

(3) 这些高概率序列对的出现概率接近相等，并且所有联合典型序列对(x,y) 的概率和趋于1(4) X n是扩展信道的输入概率空间，Y n是扩展信道的输出概率空间，那么典型序列x是输入端高概率出现的序列，典型序列y是输出端高概率出现的序列，而联合典型序列对(x,y) 就是那些信道输入和输出之间密切关联、经常出现的序列对。

5.3.4 定理 5.3随机选择序列对是统计独立的联合典型序列对的概率为()x,y()()()32n I X YnP G XYεε⎡⎤−−⎣⎦⎡⎤∈≤⎣⎦,x,y并对于任意正数δ≥0，当n足够大时有()()()()312n I X YnP G XYεεδ⎡⎤−+⎣⎦⎡⎤∈≥−⎣⎦,x,y(1) 以X n 空间的x 序列为行，以Y n 空间中的y 序列为列，分别将属于ε典型序列的排列在前面，即前面近似2nH (X )行为x 典型序列行，前面近似2nH (Y )列为y 典型序列结论：(2) 阵列左上角是那些属于联合ε典型序列的序列对，用黑点表示序列对()()n G XY ε∈x,y (3) 根据定理5.2可知，阵列左上角中每一列至多有2n [H (X |Y )+2ε]个黑点；左上角中每一行至多只有2n [ H (Y|X ) +2ε ]个黑点(5) 当某一输入典型序列x发送，必定高概率地传送到与它构成联合ε典型序列的那些序列y上。

这种y的个数就是左上角每一行的黑点数，2nH(Y|X)个。

(6) 从编码的角度看，希望选取这样一些典型序列x作为码字，使每行黑点没有对应同一个典型序列y。

信息论与纠错编码有躁信道编码教学课件PPT

信息论与纠错编码有躁信道编码教学课件PPT
通信总希望错误概率最小,由式<5-2>可看出错误概率pe <xk > 〔或者pe <Y > )最小等同于后验概率 〔xk︱y)最大
停发等侯重发 返回重发 选择重发
停发等候重发
停发等候重发方式在两个码组之间有 停顿时间〔T1),使传输效率受到影响,但 由于工作原理简单,在计算机数据通信中 仍得到应用
过程演示
即停等候重发系统中：
TW
发送端 1
发送端在TW时间内送出 一个码组给接收端
接收端 1
接收端进行检验
即停等候重发系统中：
➢实际的信道传输过程中,差错的发生往往不可 避免； ➢错误概率和信道统计特性等相关； ➢选择合适的译码规则能降低差错.
信道编码以及译码
译码器的任务: 受损的信息序列中 尽可能正确地恢复出原信息.
将信道用图5-1所示的模型表示。
u
x
y
X
信道编码器
信道
信道译码器
信道模型
信源输出序列u,经信道编码器编成码字x = f <u> 并输入信道,
错往往要影响到后面一串字----<随参信 道> 差错码元突发开长头度、= 4 以差错码突元发长结度尾= 6,之间1并1 不
纠错码分类
从功能角度讲,差错码分为检错码和纠错码 检错码：用于发现差错 纠错码：能自动纠正差错
纠错码与检错码在理论上没有本质区别,只是应 用场合不同,而侧重的性能参数也不同.
+ 信道编码
+ 提高数字通信可靠性
+ 数字信号在信道的传输过程中,由于实
际信道的传输特性不理想以及存在加性噪
声,在接收端往往会产生误码.
3
有噪信道编码定理〔香农第二定理)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


F (b1 ) a3
F (b2 ) a3 F (b3 ) a3
有 噪 信 道 编 码 定 理
一般我们知道先验概率和传递概率，故由MAP准则得到：
p (a * b j ) p (a i b j ) p (a * b j )
18
p( b j )

p (a i b j ) p( b j )

译码规则：收“0”译“1”，收“1”译“0”，则
9
译错的概率=1/3 译对的概率=2/3
结论：信道总不可避免会搀杂噪声，所以信息在信道传输过 程中，差错是不可避免的。选择合适的译码规则可以弥补信 道的不足。
有 噪 信 道 编 码 定 理
5.1.3 译码（判决）规则
1.单符号译码规则 设信道的输入与输出分别为X和Y，x X , y Y，分别 取自符号集A和B，且 A {a1 , a2 ,, ar } ，B {b1 , b2 ,, bs } 定义译码（判决）规则为 10
译码规则举例
设信道输入X取值为(a1,a2,a3), 信道输出Y取值为 (b1,b2,b3)，转移概率矩阵如下 .5 .3 .2 .2 .3 .5 .3 .3 .4
设计译码规则A为：F(b1)=a1, F(b2)=a2 , F(b3)=a3
11
也可以设计另一个译码规则B：F(b1)=a1, F(b2)=a3 , F(b3)=a2
26
a a *
p( y | x a ) / 3
1/ 2
pE ( B)
a a*
p( y | x a ) / 3
[(1 / 6 1 / 3) (1 / 3 1 / 2) (1 / 6 1 / 2)] / 3
2/3
有 噪 信 道 编 码 定 理
§5.3 费诺(Fano)不等式
信
息
论
第5章. 有噪信道编码
内容提要
本章介绍了信道编码和译码的基本概念，介绍了两种常用的译码
准则：最大后验概率译码准则和极大似然译码准则,还介绍了在这 两种译码准则下错误概率的计算方法。
本章还介绍了信道编码定理以及信息论中的一个重要不等式Fnao
不等式。
有 噪 信 道 编 码 定 理
引言

信道编码的目的：提高传输可靠性。
j 1 j 1
有 噪 信 道 编 码 定 理
举例
b1
b2
b3
a1 0.5 0.3 0.2 P a2 0.2 0.3 0.5 a3 0.3 0.3 0.4
13

b3
F (b1 ) a1 F (b2 ) a2
F (b3 ) a2
b1
b2
a1 1/6 1/10 1/15 [ P(ai b j )] a2 1/15 1/10 1/6 a3 1/10 1/10 2/15
几点说明
1）当输入符号等概时，最大似然准则等价于最大后 验概率准则。 2）该准则可直接从信道传递矩阵中选定译码函数，
21
即收到bj后，译成信道矩阵p中第j列中最大那个元 素所对应的信源符号。
3）该准则本身不再依赖于先验概率p(ai)，但当输入
符号等概时，它使平均错误概率PE最小。 4）当输入符号等概或先验概率未知时，采用此准则。

p(a*)p(b j a *) p(a i )p(b j a i )
有 噪 信 道 编 码 定 理
5.2.2 最大似然译码准则(ML准则)
若输入符号等概，即 p(ai)=1/r 时， 上式变为： 对所有 i, 当
p(b j | a* ) p(b j | ai )
19
则选择译码函数为 F(y)=a*，称此准则为最大似然译 码准则。
的选择有关。
有 噪 信 道 编 码 定 理
举例
例如：二元对称信道中，单个符号的错误传递概率是， 正确的传递概率是1- 。
1-ε
0
0
ε
8
1
ε
1
1-ε

设输入等概，错误传递概率=2/3
有 噪 信 道 编 码 定 理

译码规则：收“0”译“0”，收“1”译“1”，则
译错的概率= 1 / 2 2 / 3 1 / 2 2 / 3 2 / 3 译对的概率=1/3
有 噪 信 道 编 码 定 理
5.1.1 错误概率


为提高可靠性，必须降低传输的错误概率。
通常有两种错误概率的描述：误码率和误字率。

误码率是指传输码元出错概率（对二进制也称误比特率）. 误字率是指码字出错概率。 对同一通信系统，误码率总比误字率低。
7

错误概率既与信道的统计特性有关，也与译码规则
有噪信道编码定理，即香农第二定理，是信道编 码的理论基础。

本章重点介绍通过信道编码通信系统所能达到的 极限性能，不涉及编码技术的具体实现。
2
有 噪 信 道 编 码 定 理
本章主要内容
1. 2. 3. 4. 5.
概述
常用译码准则 费诺(Fano)不等式 序列的最佳译码准则 有噪信道编码定理
3
有 噪 信 道 编 码 定 理
发送序列 还原序列
还原序列
5 编码 传输信道 译码
有 噪 信 道 编 码 定 理
信道译码方式

通常有两类信道译码方式
– 硬判决，即首先进行信道传输符号的判决再进行信道译码 – 软判决，即信道传输符号的判决和信道译码同时完成；
；
6 – 通常，单符号的信道译码指的是信道传输符号的判决。

由于译码算法直接影响系统的传输的错误率，所以要选择使平均 差错率最小的译码算法。
有 噪 信 道 编 码 定 理

思考：若p（a1）=P(a2)=1/4,P(a3)=1/2，仍然用 ML准则，设计F(bj)=ai，并计算PE
23
有 噪 信 道 编 码 定 理
两种准则使用要点

MAP准则
1）由转移概率矩阵的每行分别乘 p(x)，得到联合概率矩阵； 2）对于每一列（相当于 y 固定）找一个最大的概率对应的X 作为译
F ( y1 ) x1 规则A： F ( y ) x 2 2 F ( y ) x 3 3
规则B：
设输入等概，求两种译码规则的错误概率。
有 噪 信 道 编 码 定 理
解：设判决函数为 F ( y ) a*，根据平均错误概率公式得
pE ( A)
[(1 / 6 1 / 3) (1 / 3 1 / 6) (1 / 6 1 / 3)] / 3
有 噪 信 道 编 码 定 理
p E p Emin
1 s P(a i b j ) p(b j a i ) r j1 i * j1 i *
s
20
方法：在信道矩阵中，将每列中最大元素去除， 余下的（r-1）*s项求和后，再乘以1/r，得到p Emin
有 噪 信 道 编 码 定 理
§5.1 概述

信道编码就是按一定的规则给信源输出序列增加 某些冗余符号，使其变成满足一定数学规律的码
序列（或 码字），再经信道进行传输。（具有纠
4

错能力）
信道译码就是按与编码器同样的数学规律去掉接
收序列中的冗余符号，恢复信源消息序列。
有 噪 信 道 编 码 定 理
插 入 冗 余 信 息 抽 出 冗 余 信 息
p 其中， E 为平均错误率。
（5．3．1）
错误概率PE的熵：产生错误概 率的平均不确定性
错误产生后，到底 是哪个符号发送而 造成错误的最大不 确定性
有 噪 信 道 编 码 定 理
物理意义
进行一次判决后，关于X的疑义度可分成两项：
(1) 是否判对，疑义度为H ( PE)
30
(2) 如果判决出错（概率为 PE ）,错在r-1个 符号中的哪一个，其疑义度不会超log (r-1)。
b1
b2
b3
P(a1)=p(a2)=1/4 p(a3)=1/2求译码规则 和 p Emin
a1 0.5 0.3 0.2 P a2 0.2 0.3 0.5 a3 0.3 0.3 0.4
17 由MAP准则

b1
b2
b3
a1 1/8 3/40 1/20 [ P(ai b j )] a2 1/20 3/40 1/8 a3 1/20 3/20 1/5
例题5.2.2
已知信道的转移概率矩阵为
1 / 2 1 / 3 1 / 6 1 / 6 1 / 2 1 / 3 1 / 3 1 / 6 1 / 2
F ( y1 ) x1 F ( y2 ) x3 F ( y ) x 3 2
25
现有两种译码规则：

共有rs种译码规则可供选择（如例子） 选择依据：错误概率最小
有 噪 信 道 编 码 定 理
2．错误概率的计算

假设采用的译码规则为：
F ( y b j ) a* ,
在接收到 b j 的条件下，若实际上发送的是 a * ，则译码正确，反 之就出现差错。则本次译码的正确概率：(a b ) p i j 条件错误率为：

12

平均错误率为： i
a a
P (x a / y b )
i j
*
平均每收到一个符号 所产生错误的大小

PE E[p(e b j )] p(b j ) p(e b j ) p(eb j )
j 1 j 1
s s
s
s
平均正确率为 P 1 P 1 p(b j ) p(e b j ) p(a * b j ) E E