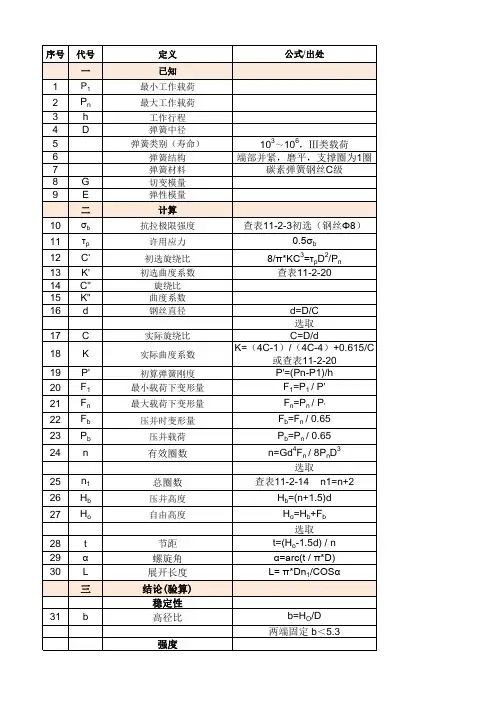
史上最好用机械计算与非标选型—弹簧校核计算合集

弹簧强度校核公式好的，以下是为您生成的文章：咱先来说说弹簧这玩意儿，它在生活里那可是到处都有。

就像我上次去修自行车，师傅换那个刹车弹簧的时候，我就在旁边瞅着。

嘿，就那么个小小的弹簧，作用可大了去啦！要说弹簧强度校核公式，这可是个重要的东西。

就好比你要盖房子，得先知道这房子能承受多大的重量，弹簧也是一样。

咱们常见的弹簧，有压缩弹簧、拉伸弹簧等等。

那怎么判断一个弹簧行不行呢？这就得靠强度校核公式啦。

弹簧强度校核公式里面，涉及到好多参数呢。

比如说弹簧的材料、直径、圈数、工作载荷啥的。

就拿那个自行车刹车弹簧来说，要是它的强度不够，那刹车可就不好使啦，说不定还会出危险。

咱先看看压缩弹簧的强度校核。

这就好比你使劲儿压一个弹簧，得算算它能不能承受住这股压力。

这里面有个切应力的概念，就像是弹簧内部的一股“抵抗力”。

拉伸弹簧也有类似的道理。

你把弹簧拉长，它也得能撑得住才行。

要是随便一拉就断了，那可就麻烦了。

给您举个例子啊，假设咱有一个压缩弹簧，材料是某种钢材，直径是 5 毫米，圈数是 10 圈，工作载荷是 100 牛顿。

通过公式一算，就能知道这个弹簧在这种工作条件下会不会出问题。

在实际应用中，可不能马虎。

有时候一个小弹簧出了差错，可能整个机器就没法正常运转了。

我记得有一次在工厂里，就是因为一个弹簧的强度没校核好，结果一台设备老是出故障，耽误了好多事儿。

而且啊，不同的工作环境对弹簧的要求也不一样。

高温、低温、潮湿，这些条件都可能影响弹簧的性能。

所以在进行强度校核的时候，都得考虑进去。

再比如说，汽车里的减震弹簧。

那要是强度不够，车子开起来就会颠簸得厉害，坐着可不舒服啦。

总之，弹簧强度校核公式虽然看起来有点复杂，但它真的很重要。

咱们得认真对待，不能瞎搞。

就像那个自行车刹车弹簧，小小的一个弹簧，关系到咱们的出行安全呢！希望您通过我的这番讲解，能对弹簧强度校核公式有个更清楚的认识。

可别小看了这小小的弹簧，里面的学问大着呢！。

弹簧参数尺寸及计算公式弹簧是一种用来储存和释放机械能的装置，应用广泛于机械、汽车、电器等领域。

弹簧的参数、尺寸以及计算公式对于设计和选择弹簧十分重要。

1.弹簧的参数：- 预压力（Preload）：弹簧在未加载之前的初始压力。

- 弹性系数（Spring Constant）：弹簧在单位变形下的恢复力。

- 卸载长度（Unloaded Length）：未加载时的弹簧长度。

- 动载荷（Dynamic Load）：弹簧所承受的变动力。

- 疲劳寿命（Fatigue Life）：弹簧能够承受的循环加载次数。

2.弹簧的尺寸：- 线径（Wire Diameter）：弹簧材料的直径，决定着弹簧的承载能力。

- 外径（Outer Diameter）：弹簧的最大直径。

- 内径（Inner Diameter）：弹簧的最小直径。

- 组件高度（Solid Height）：弹簧在最大压缩状态下的高度。

- 活动齿数（Active Coils）：弹簧上具有弹性的齿数。

- 紧齿数（Total Coils）：弹簧上总共的齿数。

3.弹簧的计算公式：-弹性系数（K）的计算公式：K=Gd^4/(8Na^3)其中，G为剪切模量，d为线径，N为齿数，a为活动齿数。

-预压力（P）的计算公式：P=K*δ其中，δ为弹簧的压缩/拉伸变形量。

-力（F）的计算公式：F=K*δ弹簧所受的力正比于弹性系数与变形量之积。

-弹簧的伸长（δ）计算公式：δ=(F*L)/(K*Gd^4)其中，L为弹簧的长度。

-弹簧的疲劳寿命（Nf）计算公式：Nf=(C*S^b)/(F^b)其中，C为常数，S为应力幅值（一般为弹簧的最大变形量）。

以上公式仅为常见的弹簧计算公式，实际应用中可能还需要考虑更多的因素，如安全系数、材料的疲劳强度等。

总结起来，弹簧的参数、尺寸和计算公式对于弹簧的设计和选择至关重要。

具体的参数和尺寸根据实际应用需求和弹簧类型来确定，而计算公式则是根据力学原理和材料特性推导得出的。

7. 离合器膜片弹簧设计7.1 膜片弹簧的结构特点膜片弹簧在结构形状上分为两部分。

在膜片弹簧的大端处为一完整的截锥体，它的形状像一个无底的碟子，和一般机械上用的碟形弹簧类似，故称作碟簧部分，实际起到弹性作用。

其工作原理为：沿轴线方向加载，碟簧受压变平，卸载后又恢复原形。

另一部分是径向开槽部分，像一圈伸出的手指，其作用是作为分离杆，又称分离指。

分离爪与碟簧部分交界处的径向槽较宽，呈长方圆形孔，一方面可以减少分离指根部的应力集中，另一方面又可用来安置销钉固定膜片弹簧。

分离指根部的过渡圆角R ＞4.5。

7.2 膜片弹簧的加载方式和变形由于膜片弹簧采用推式结构，故其正装。

离合器在分离和接合时，膜片弹簧的加载情况不一样，相应的有两种加载方式和变形情况（如图7-1）：图7-1 膜片弹簧在不同工作状态时的变形(a)自由状态 (b)压紧状态 (c)分离状态1．自由状态当离合器盖总成未与飞轮装合以前，膜片弹簧近似处于自由状态，膜片弹簧对压盘无压紧作用。

2．接合状态当离合器盖总成与飞轮装合时，离合器盖前端面向飞轮前端面靠拢。

此时，离合器盖通过支点o 对膜片弹簧施加载荷1P ，膜片弹簧逐渐变形直到离合器盖和飞轮完全贴合为止，此时为接合状态。

同时在压盘处也作用有一载荷1P ，把1P 称作压紧力。

支点o 和压盘接触处之间的高度变化称作大端变形1λ，膜片弹簧分离轴承相对于压盘高度的变化称之为小端变形2λ。

3．分离状态分离轴承以2P 力作用在膜片弹簧的小端，当力达到一定值时，膜片弹簧被压翻。

分离时在膜片弹簧的大端处及小端处将进一步产生附加变形f 1λ和f 2λ。

此时膜片弹簧大端处的变形111b f λλλ=+。

7.3 膜片弹簧的弹性变形特性如前所述，膜片弹簧起弹性作用的部分是其碟簧部分。

碟簧部分的弹性变形特性和螺旋弹簧是不一样的，它是一种非线性的弹簧，其特性和碟簧的原始内截锥高H 及弹簧片厚度h 的比值H/h 有关。

不同的H/h 值可以得到不同的弹性变形特性。

弹簧计算公式弹簧计算公式是用来计算弹簧的弹力的数学公式。

弹簧是一种用来存储和释放能量的弹性元件，广泛应用于各种机械装置和工具中。

根据弹簧的形状和用途，可以分为压簧、拉簧和扭簧。

下面将分别介绍这三种弹簧的弹力计算公式。

1.压簧弹力计算公式压簧是一种用于承受压缩力的弹簧，通常由钢丝绕成螺旋形。

压簧的弹力与其形状、材料的物理性质以及受到的压缩力有关。

压簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为簧系数，x是压簧的变形量。

压簧的弹力与其变形量呈线性关系，即弹簧的弹力与其压缩或拉伸的距离成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

2.拉簧弹力计算公式拉簧是一种用于承受拉力的弹簧，通常由钢丝绕成螺旋形。

拉簧的弹力与其形状、材料的物理性质以及受到的拉力有关。

拉簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为拉簧的刚度系数或簧系数，x是拉簧的变形量。

拉簧的弹力与其变形量呈线性关系，即弹簧的弹力与其拉伸或压缩的长度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

3.扭簧弹力计算公式扭簧是一种用于承受扭转力的弹簧，通常由钢丝绕成螺旋形。

扭簧的弹力与其形状、材料的物理性质以及受到的扭转力矩有关。

扭簧的弹力计算公式如下：T=k*φ其中，T表示弹簧的扭力，k是弹簧的刚度系数或簧系数，φ是弹簧的扭转角度。

扭簧的弹力与其扭转角度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

需要注意的是，以上的公式都是基于线性弹性假设的情况下推导出来的。

实际上，弹簧的变形行为通常是非线性的，因此在计算弹力时需要考虑非线性效应，例如在变形量较大或载荷较高的情况下。

除了弹力的计算公式，还可以根据实际需要计算弹簧的弹性系数、刚度系数、临界长度等参数。

这些参数对于设计和选择弹簧具有重要意义，可以保证弹簧在工作过程中具有足够的弹性和耐力。

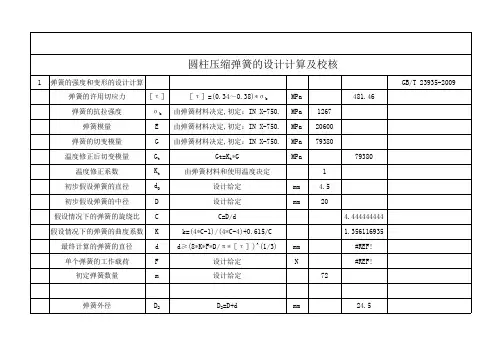
圆柱压缩弹簧的设计计算及校核圆柱压缩弹簧是一种常见的弹簧类型，广泛应用于机械设备中。

它主要由圆柱形的弹簧线圈组成，其功能是在受到外力作用时，通过弹性变形来储存能量，并且在力消失后恢复原状。

在设计和校核圆柱压缩弹簧时，需要考虑以下几个方面：1.弹簧的设计参数：-弹簧的自由长度：即未受压时的长度；-弹簧的线圈直径：即每个线圈的外径；-弹簧的导线直径：即线圈的钢丝直径；-弹簧的线圈数目：即线圈的总数目；-弹簧的材料：如弹簧钢，需要知道其弹性模量和屈服强度等参数。

2.弹簧的计算方法：-圆柱压缩弹簧的刚度计算公式：k=(Gd^4)/(8D^3n)，其中k为弹簧的刚度，G为材料的剪切模量，d为弹簧线圈直径，D为弹簧外径，n为弹簧的线圈数目；-弹簧的最大受力：由于弹簧在使用中可能承受较大的压力，需要计算出最大可承受的受力；-弹簧的最大压缩量：在设计时需要根据使用场景确定弹簧的最大压缩量，以确保其正常工作。

3.弹簧的校核方法：-校核弹簧的刚度：通过比较计算得到的刚度值和要求的刚度范围来判断是否满足要求；-校核弹簧的受力：将最大压力与最大受力进行比较，确保弹簧在工作过程中不会超过其承受范围；-校核弹簧的安全系数：根据设计要求，计算弹簧的安全系数，通常要求安全系数大于1.5以上。

在进行圆柱压缩弹簧的设计和校核时-弹簧的工作条件：根据弹簧的工作条件确定合适的设计参数，包括材料选择、弹簧尺寸等；-弹簧的应力分析：根据受力情况，分析弹簧在工作过程中的应力情况，确保其不会超过材料的屈服强度；-弹簧的设计细节：考虑到弹簧的安装和使用方便性，需要设计合适的弹簧端部形状，以及必要的支撑结构，以确保弹簧的正常工作。

综上所述，圆柱压缩弹簧的设计和校核涉及到弹簧的设计参数、计算方法和校核方法等方面的内容。

在进行设计和校核时，需要综合考虑弹簧的工作条件和要求，以确保弹簧能够正常运行并满足使用需求。

弹簧设计计算公式弹簧是一种经过热处理的金属线，具有弹性变形能力。

在工程设计中，弹簧广泛应用于机械、汽车、电器等领域，用于悬挂、减震、传动等功能。

弹簧设计的核心是确定其几何参数和力学性能，以满足特定的工作要求。

弹簧设计的计算公式包括弹簧刚度、变形、工作力和应力等参数。

以下是一些常用的弹簧设计公式：1.弹簧刚度：弹簧刚度是指单位变形时产生的力的大小。

弹簧刚度可以通过以下公式计算:K=Gd^4/8nD^3其中，K表示弹簧刚度，G表示弹簧材料的剪切模量，d表示弹簧线径，n表示弹簧的有效圈数，D表示弹簧的平均直径。

2.弹簧变形：弹簧的变形可以通过以下公式计算：δ=(F×L)/(K×n)其中，δ表示弹簧的变形，F表示作用在弹簧上的力，L表示弹簧自由长度，K表示弹簧刚度，n表示弹簧的有效圈数。

3.弹簧的工作力：弹簧的工作力可以通过以下公式计算：F=K×δ其中，F表示作用在弹簧上的力，K表示弹簧刚度，δ表示弹簧的变形。

4.弹簧的应力：弹簧的应力可以通过以下公式计算：σ=(8×F×L)/(π×d^3×n)其中，σ表示弹簧的应力，F表示作用在弹簧上的力，L表示弹簧自由长度，d表示弹簧线径，n表示弹簧的有效圈数。

需要注意的是，以上公式适用于简单的弹簧设计，如果涉及复杂的弹簧形状或材料，可能需要使用更复杂的计算方法或有限元分析。

弹簧设计时，需要根据实际工作条件和要求，选择合适的弹簧材料和尺寸，以保证弹簧的功能和安全性。

同时，还需要考虑弹簧的寿命、疲劳强度、预紧力等因素，以确保弹簧在长期使用中的可靠性。

除了上述的计算公式，弹簧设计还需要考虑弹簧的安装方式、表面处理、工艺要求等因素。

综合考虑这些因素，可以进行合理的弹簧设计，满足工程需求。

圆柱压缩弹簧的设计计算及校核设计计算的第一步是选择合适的材料。

常用的弹簧材料包括碳钢、合金钢、不锈钢等。

弹簧材料的选择要考虑到工作环境的要求，如强度、耐腐蚀性等。

在确定材料后，需要计算弹簧的几何参数，包括线径、弹簧圈数、弹簧高度等。

这些参数的确定要考虑到所需的弹簧刚度、预压程度以及空间限制等因素。

设计计算的第二步是根据工作参数确定所需的弹簧刚度。

弹簧刚度是指弹簧在受力下的变形量与受力的比值。

根据力学原理，弹簧的刚度与材料的弹性模量、线径以及弹簧的几何参数有关。

根据所需的刚度值，可以选择合适的线径和弹簧几何参数。

设计计算的第三步是校核计算。

校核计算是对设计计算的验证，用于确认设计的合理性和安全性。

校核计算需要考虑弹簧在工作条件下的各种受力情况，如压缩力、应力分布等。

校核计算可以使用应力分析、变形分析等方法，以确保弹簧的负载能力和寿命符合设计要求。

在校核计算中，需要考虑以下几个关键点：1.弹簧的最大压缩力：根据弹簧的工作要求和所需的刚度，可以计算出弹簧在最大压缩状态下所受到的最大压缩力。

这个力值需要在校核计算中进行验证，以确保弹簧不会超过其负载能力。

2.弹簧的应力分布：弹簧在受力时会出现应力分布，这个分布不是均匀的，而是集中在一些特定的位置。

在校核计算中，需要确定弹簧的应力集中点和应力集中系数，并验证弹簧在这些位置的应力是否符合工程标准。

3.弹簧的变形量：弹簧在受力下会发生变形，变形量与受力的关系可以通过弹簧的刚度和工作负载来计算。

在校核计算中，需要确认弹簧的变形是否满足设计要求，并且在工作过程中不会超过其极限变形范围。

以上是圆柱压缩弹簧设计计算及校核的基本过程和关键点。

在进行设计和校核时，需要充分考虑材料的特性、工作环境的要求以及弹簧的负载能力等因素，以确保设计的合理性和安全性。

最后，还需要进行实际测试和验证，确保设计的弹簧满足工程要求。

弹簧选型计算
1 弹簧的作用
弹簧是机械零件的重要组成部分，它的作用是储存能量、释放能量、平衡和传递力。

由于弹簧受到外部力的影响，它可以调节系统受力的种类和大小，也就是说它的功能范围很广泛。

广泛应用于汽车、机器人、航空航天、机床和设备等领域。

2 弹簧选型
在实际运用中，弹簧种类繁多，而且有多种参数供客户选择，如形状、强度、长度等。

因此，在弹簧选型时，需要考虑到系统的使用条件，选择性能满足应用需求的的弹簧。

根据作用机理，在选择弹簧材料时要求对比较容易变形的材料，确保其具有良好的形变能力。

在弹簧形状上，要根据系统使用要求，选择折弯曲线、屈曲曲线、Spin 螺旋曲线、翻转曲线、止点凸肋曲线等多种选择，进行正确的弹簧选型。

此外，精度、变形范围还要重点考虑和控制，以确保器件具有高精度性能和可靠性。

3 弹簧选型计算
以上是弹簧选型的一些基本原则，但是如何根据实际情况计算选择最优的弹簧，目前还没有完全通用的计算方法。

通常情况下，计算弹簧参数时，可以根据系统的受力、承载量等，采用经典的拉伸、压缩、弯曲实验模型进行，此外，也可以依据市场上已有的技术参数进行模拟计算。

选择完合适的弹簧后，由结构分析和simulation可以
比较准确得到一个完善的弹簧配置方案，从而确保系统具备更高的性能和更稳定的运行。

总之，弹簧参数选择是非常重要的一个环节，它直接影响系统的运行效果，因此在弹簧选择时，应充分考虑材料特性、形状、精度、强度等因素，按照准确的参数进行计算，以便确保最终的弹簧选择结果。

弹簧减震器选型计算公式好的，以下是为您生成的关于“弹簧减震器选型计算公式”的文章：在咱们的日常生活和各种工业场景中，弹簧减震器那可是相当重要的角色。

就比如说，一辆汽车在颠簸的路上行驶，如果没有合适的弹簧减震器，那咱们坐在车里就跟坐过山车似的，颠得七荤八素。

再比如工厂里那些轰轰作响的大型机器，要是没有好的减震器，不仅噪音能把人吵得头疼，机器本身也容易出故障。

要说这弹簧减震器的选型计算公式，那可不是个简单的事儿。

咱先得搞清楚几个关键的参数。

首先是负载重量，这就好比一个人的体重，你得知道机器或者设备有多重，才能选对能承受得住的弹簧减震器。

我之前在一家工厂里就碰到过这么个情况，一台新安装的大型冲压机，本来按照设计选的减震器应该没问题，可安装好一试，那震动还是大得吓人。

一查才发现，厂家在生产的时候给这机器多加了不少部件，结果实际重量比设计的重了好多，之前选的减震器根本就扛不住。

然后是弹簧的刚度。

这刚度就像是弹簧的“脾气”，刚度越大，弹簧越“硬气”，越不容易被压缩；刚度越小，弹簧就越“温柔”，容易被压下去。

比如说，要是给一个轻型设备选了刚度特别大的弹簧，那设备运行的时候就跟被死死摁在地上一样，根本起不到减震的效果，反而可能会让设备受损。

还有个重要的参数就是固有频率。

这固有频率就像是弹簧减震器的“心跳节奏”。

如果设备运行的频率和弹簧减震器的固有频率接近，那就会产生共振，那可就糟糕啦！就像两个人跑步节奏一样的时候，会越跑越带劲，共振会让震动变得超级大。

我记得有一次在一个车间里，一台风机的震动特别厉害，怎么调整都不行，后来一测才发现，风机的运行频率和所选减震器的固有频率太接近了，产生了共振。

那这选型的计算公式到底是啥呢？一般来说，常用的公式是这样的：F = K × X 。

这里的 F 代表弹簧所受的力，K 就是弹簧的刚度，X 是弹簧的变形量。

通过这个公式，再结合上面说的那些参数，就能大致算出需要什么样的弹簧减震器啦。

步骤参数数值备注与图示轴向力Fae(N)(向左为正)400径向力Fre(N)900切向力Fte(N)2200轮节圆d(mm)314距离a(mm)200距离b(mm)320左轴承径向力Fr1(N)1512.62右轴承径向力Fr2(N)875.66200Fa1=Fa2=Fa 轴承类型7000AC左轴承派生轴向力Fd1(N)1028.58右轴承派生轴向力Fd2(N)595.45根据Fae 判断被压紧轴承左侧轴承被压紧左轴承轴向力Fa1(N)995.45右轴承轴向力Fa2(N)595.45轴承型号(查样本)7207C基本额定静载荷C0(N)20000估算e 值(首次取0.45)0.4在左侧填入数值估算左Fd1(N)605.05估算右Fd2(N)350.26根据Fae 判断被压紧轴承右侧轴承被压紧右轴承轴向力Fa2(N)1005.05左轴承轴向力Fa1(N)605.05右轴承Fa2/C00.0503左轴承Fa1/C00.0303右轴承e20.4220左轴承e10.4013右轴承派生轴向力Fd2(N)369.51说明：此模型广泛应用于齿轮或皮带/链传动。

(1)当为直齿轮或皮带/链轮时，轴向力Fae=0；(2)当为齿轮传动时，径向力Fre 为齿轮的重力；当为皮带轮时，Fre 为重力和预紧力的合力；(3)切向力Fte 可以通过转矩T 求得，T=Fte*d/2。

e 平均值=0.4116已知条件轴承径向力两端为7000AC 或7000B 时的轴向力两端为7000C 时的轴向力两端为深沟球轴承时轴向力Fa(N)轴承校核计算合集序：典型轴承模型受力分析Fre Fae Fte a b d 将此值填入再次计算Fae Fae 面朝面安装背靠背安装返回目录左轴承派生轴向力Fd1(N)607.01右轴承轴向力Fa2(N)1007.01左轴承轴向力Fa1(N)607.01轴承型号32206圆锥滚子轴承Y1值 1.6左轴承派生轴向力Fd1(N)472.69右轴承派生轴向力Fd2(N)273.64根据Fae 判断被压紧轴承左侧轴承被压紧左轴承轴向力Fa1(N)673.64右轴承轴向力Fa2(N)273.64步骤参数取值备注径向载荷Fr(N)5500轴向载荷Fa(N)2500转速n(r/min)1250预期计算寿命Lh(h)5000参考表1要求轴承孔径(mm)50轴承型号6310基本额定动载荷Cr(N)62000基本额定静载荷C0(N)38500相对轴向载荷Fa/C00.0649e 值0.2649表2附1自动计算轴径载荷比Fa/Fr0.45对比Fa/Fr 与e Fa/Fr ＞e 径向动载荷系数X 0.56表2轴向动载荷系数Y1.6338表2附1自动计算载荷系数fp1.2表3温度系数ft1表4当量动载荷P(N)8597.30P=fp(XFr+YFa)指数ε3.00所需基本额定动载荷C61997.25C≤Cr 查样本，如表5两端为圆锥滚子轴承时的轴向力已知条件1,按安装尺寸或受力分析初选轴承2,计算当量动载荷P3，校核轴承额定动载荷或深沟球轴承(6系)校核计算轴承额定动载荷Cr 满足要求将以上计算的Fr 和Fa 的较大值带入下方对应表格计算若不合格则重新选择型号ε61060h L n t f P C ⨯⨯=ε⎫⎛⨯Cr f 610计算寿命Ls(h)5000.66Ls≥Lh 步骤参数取值备注径向载荷Fr(N)5500轴向载荷Fa(N)2500转速n(r/min)1250预期计算寿命Lh(h)5000参考表1要求轴承孔径(mm)30确定轴承类型圆锥滚子轴承(3系)轴承型号32206基本额定动载荷Cr(N)52000基本额定静载荷C0(N)60000圆锥滚子轴承e 值0.38圆锥滚子轴承Y1值1.6相对轴向载荷Fa/C00.0417轴径载荷比Fa/Fr0.45系数e0.3800对比Fa/Fr 与e Fa/Fr ＞e 径向动载荷系数X 0.4表2轴向动载荷系数Y1.6000载荷系数fp1.2表3温度系数ft1表4当量动载荷P(N)7440.00P=fp(XFr+YFa)指数ε3.33所需基本额定动载荷C44033.41C≤Cr 计算寿命Ls(h)8703.76Ls≥Lh 步骤参数取值备注查样本，如表57系不用填额定动载荷或使用寿命圆柱滚子轴承(N系)选型计算寿命满足要求，可以使用校核基本额定动载荷C=校核寿命Lh，二者等效，校核其一即可圆锥滚子轴承(3系)或角接触球轴承(7系)校核计算轴承额定动载荷Cr 满足要求寿命满足要求，可以使用校核基本额定动载荷C=校核寿命Lh，二者等效，校核其一即可已知条件1,按安装尺寸或受力分析初选轴承2,计算当量动载荷P3，校核轴承额定动载荷或使用寿命若不合格则重新选择型号ε⎪⎪⎭⎫ ⎝⎛⨯⨯=P Cr t f n Ls 60610ε61060h L n t f P C ⨯⨯=ε⎪⎪⎭⎫ ⎝⎛⨯⨯=P Cr t f n Ls 60610径向载荷Fr(N)5500此处只考虑轴向载荷转速n(r/min)1250预期计算寿命Lh(h)5000参考表1要求轴承孔径(mm)40载荷系数fp1.2表3温度系数ft 1表4当量动载荷P(N)6600.00P=fp*Fr 指数ε3.33所需基本额定动载荷C39061.90初选选择轴承型号N208基本额定动载荷Cr(N)43500基本额定静载荷C0(N)43000计算寿命Ls(h)7157.42Ls≥Lh 步骤参数取值备注径向载荷Fr(N)5500轴向载荷Fa(N)2500转速n(r/min)1250预期计算寿命Lh(h)5000参考表1要求轴承孔径(mm)50轴承型号基本额定动载荷Cr(N)基本额定静载荷C0(N)相对轴向载荷Fa/C0#DIV/0!e 值表2附1自动计算轴径载荷比Fa/Fr0.45对比Fa/Fr 与e Fa/Fr ＞e 径向动载荷系数X 表2轴向动载荷系数Y表2载荷系数fp1.2表3温度系数ft1表4当量动载荷P(N)P=fp(XFr+YFa)已知条件1,按安装尺寸或受力分析初选轴承2,计算当量动载荷P查样本，如表5查样本，如表5寿命满足要求，可以使用其他轴承校核计算已知条件1,计算轴承额定动载荷2,轴承选型3,寿命计算若不合格则重新选择型号ε61060h L n t f P C ⨯⨯=ε⎪⎪⎭⎫ ⎝⎛⨯⨯=P Cr t f n Ls 60610指数ε球轴承 3.00所需基本额定动载荷C 0.00C≤Cr 计算寿命Ls(h)#DIV/0!#DIV/0!文档信息编写：图惜参考：《机械设计——第八版》——蒲良贵、纪名刚《机械设计手册——第五版第三卷》——成大先《NHK轴承综合样本》 2018.9.19说明：1，轴承类型的选择：a 载荷：滚子轴承用于较大载荷，球轴承用于中轻载荷；纯径向载荷一般用深沟球轴承、圆柱棍子轴承、滚针轴承；纯轴向载荷可选用推力轴承(较小的纯轴向载荷可选用推力球球轴承，较大的纯轴向载荷可选用推力滚子轴承)；径向载荷+不大的轴向载荷可选用深沟球、角接触球(70000C\70000AC)、圆锥滚子(α=10~18°)；径向载荷+较大的轴向载荷可选用角接触球(70000AC/70000B)、圆锥滚子(α=27~30°)、向心轴承+推力轴承组合。

弹簧的选型于校核弹簧承载一人和滑板的重量 取人重量为100kg 滑板重量为2kg 一共四根弹簧 所以每根弹簧载荷为229.5N1. 选择弹簧材料及许用应力因为弹簧在一般载荷下工作，可按照第三类弹簧来考虑，选择C 级碳素弹簧钢丝。

初估算弹簧丝直径为d=4mm 。

查机械设计表2-2和表2-3可知[]0.5,1520T B B Mpa τσσ==，于是[]T τ=760Mpa2. 计算弹簧丝直径 d根据给定条件选定 C=10，并根据式0.61541 1.14544C K C C -=+=-3.07d mm == 取离3.07最近的标准值 3.2mm210 3.232D cd mm ==⨯=D=232 3.235.2D d mm +=+=3. 计算弹簧的有效工作圈数n查表 20.2得 G=80000Mpa 并计算弹簧工作圈数为4433280000 3.2708.48824532Gd n FD λ⨯⨯===⨯⨯ 取弹簧n=94验算载荷与变形最小载荷与最大载荷相应的变形量为33min 2min 448820329 5.62580000 3.2F D n Gd λ⨯⨯⨯===⨯ 33max 2max448825032970.3180000 3.2F D n mm Gd λ⨯⨯⨯===⨯ 弹簧的行程为 0max min λλλ=-=64.69mm[]min 1.12 1.12760851.2T Mpa ττ==⨯=22minmin 3.14 3.2851.2298.7988 1.14510d F N KC πτ⨯⨯===⨯⨯ 与之相应的变形量为33lim 2lim 4488298.793298480000 3.2F D n mm Gd λ⨯⨯⨯===⨯5计算弹簧其余几何尺寸 弹簧节距t max 298.79 3.20.2214.629t d mm n λ=++=++= 弹簧螺旋升角2arctan t D απ==,63 弹簧总圈数 029211n n =+=+= 弹簧丝间距 14.62 3.211.3t d δ=-=-= 弹簧的自由长度 00(0.5)911.3(110.5)3.2135.3H n n d mm δ=+-=⨯+-=6.稳定性计算02135.3 4.2 5.332H b D ===< 满足性能要求。