类比探究(一)——平行、直角(讲义及答案)

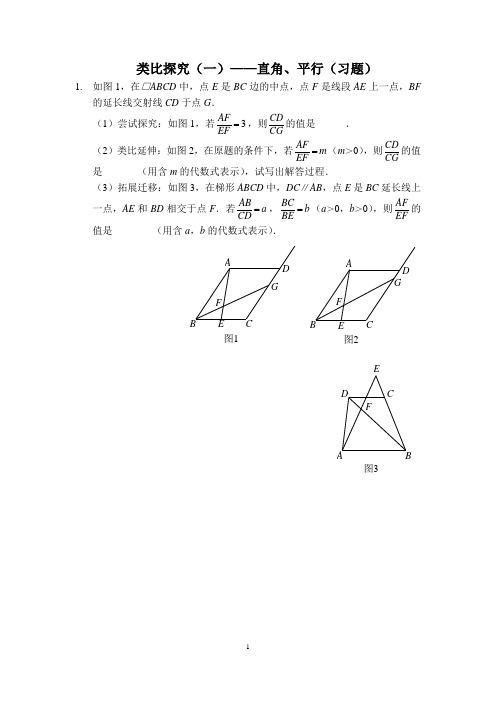
类比探究（一）——直角、平行（习题）1. 如图1，在□ABCD 中，点E 是BC 边的中点，点F 是线段AE 上一点，BF的延长线交射线CD 于点G ．（1）尝试探究：如图1，若3AFEF=，则CD CG 的值是______． （2）类比延伸：如图2，在原题的条件下，若AFm EF=（m ＞0），则CD CG 的值是_______（用含m 的代数式表示），试写出解答过程． （3）拓展迁移：如图3，在梯形ABCD 中，DC ∥AB ，点E 是BC 延长线上一点，AE 和BD 相交于点F ．若AB a CD =，BCb BE=（a ＞0，b ＞0），则AF EF 的值是________（用含a ，b 的代数式表示）．GF DC BA图1GF E DBA图2ADCEFB图32. 如图1，一副直角三角板满足AB =BC ，AC =DE ，∠ABC =∠DEF =90°，∠EDF =30°．【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板DEF 绕点E 旋转，并使边DE 与边AB 交于点P ，边EF 与边BC 交于点Q ．【探究】在旋转过程中，（1）如图2，当1CEEA =时，EP 与EQ 满足怎样的数量关系？并给出证明．（2）如图3，当2CEEA=时，EP 与EQ 满足怎样的数量关系？并给出证明．（3）根据你对（1），（2）的探究结果，试写出当CEm EA=时，EP 与EQ 满足的数量关系式为________________．A (D )C (E )BF图1QPDEFB C A图2Q PDE F B CA图33. 在△ABC 中，已知D 是BC 边的中点，G 是△ABC 的重心，过点G 的直线分别交AB ，AC 于点E ，F ．（1）如图1，当点E 与点B 重合时，AGGD=_______． （2）如图2，当EF ∥BC 时，求证：1=+AFCFAE BE ．（3）如图3，当EF 和BC 不平行，且点E ，F 分别在线段AB ，AC 上时，（2）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由． 提示：①过点A 作AM ∥BC ，交EF 于点M ，直线FE 交BC 于N ；②NB +NC =2ND ．（4）如图4，当点E 在AB 的延长线上或点F 在AC 的延长线上时，（2）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．AB (E )CDFG图1ABCD EF G 图2GFE D CBA图3ABCD EFG图4【参考答案】1. （1）32； （2）2m ；（3）ab ．2. （1）EP =EQ ，证明略；（2）EP =12EQ ，证明略；（3）EP =1mEQ ．3. （1）2；（2）证明略；（3）（2）中的结论仍然成立，证明略； （4）（2）中的结论不成立，理由略．。

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，解决此问题的主要方法是什么？问题2：目前我们所学的结构类比中有两种结构，分别是什么？问题3：如图1，在长方形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，则FG＝CG，请证明．小明发现把AE延长与GC 的延长线交于一点H，证明△AHG是等腰三角形即可证明结论．如图2，将（1）中的长方形ABCD改为平行四边形，其中，AB∥CD，AD∥BC，AB=CD，AD=BC，且其他条件不变，我们可以结合小明的思路，延长AE与GC的延长线交于一点H，此时，证明△AHG是等腰三角形的依据是( )A．△AEG≌△HEG，全等三角形对应边相等B．AF＝HC，FG＝CG，等量加等量和相等C．∠CHE＝∠FAE，等角对等边D．EG⊥AH，三线合一分析题目中的不变特征，画出其线路图.类比探究之结构类比（平行夹中点）（北师版）一、单选题(共6道，每道16分)1.如图1，在长方形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，则FG＝CG，请证明．小明发现把AE延长与GC的延长线交于一点H，证明△AHG是等腰三角形即可证明结论．如图2，将（1）中的长方形ABCD改为四边形，其中，AB∥CD，AD∥BC，AB=CD，AD=BC，且其他条件不变，我们可以结合小明的思路，延长AE与GC的延长线交于一点H，此时，证明△AHG是等腰三角形的依据是( )A.△AEG≌△HEG，全等三角形对应边相等B.AF＝HC，FG＝CG，等量加等量和相等C.∠CHE＝∠FAE，等角对等边D.EG⊥AH，三线合一答案：C解题思路：试题难度：三颗星知识点：类比探究问题2.如图1，在△ABC中，P为BC边的中点，直线a绕顶点A旋转，若B，P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM，PN．要证PM=PN，只需延长MP交CN 于点E，通过说明某对三角形全等就可以证明此结论．此时，证明结论成立的理论基础是( )A.全等三角形的对应边相等B.直角三角形斜边上的中线等于斜边的一半C.等腰三角形等角对等边D.等量代换答案：B解题思路：试题难度：三颗星知识点：类比探究问题3.（上接第2题）若直线a绕点A旋转到图2的位置时，点B，P在直线a的同侧，其他条件不变，要证明PM=PN，类比上题思路，则需要证明的全等三角形是( )A.△APB≌△APEB.△CAN≌△ABMC.△NPB≌△NPED.△MBP≌△ECP答案：D解题思路：试题难度：三颗星知识点：类比探究问题4.如图1，在正方形ABCD的边AB上取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG，CG，易证EG=CG且EG⊥CG．如图2，将△BEF绕点B逆时针旋转90°，如图3，将△BEF绕点B逆时针旋转180°，都可以得到和图1相同的结论.若不想证明三点共线，则最好作什么样的辅助线.( )A.（图1）连接CE；（图2）无需辅助线；（图3）连接CE.B.（图1）延长EG至点H，使GH=EG，连接DH，CE，CH；（图2）延长EG至点H，使GH=EG，连接DH；（图3）延长EG，交AD于点H，连接CE，CH.C.在CD边上取一点H，使CH=BE，连接GH.（适用于图1，图2，图3）D.（图1）延长EG，交AD的延长线于点H，连接CE，CH；（图2）延长EG，交CD的延长线于点H；（图3）延长EG，交AD于点H，连接CE，CH.答案：D解题思路：试题难度：三颗星知识点：类比探究问题5.（上接第4题）在证明过程中，选用什么样的思路，可以类比解决三问.( )①证全等；②再证全等；③等角对等边；④等边对等角；⑤等腰直角三角形的性质.A.①②⑤B.①⑤C.①②③D.①③④答案：A解题思路：试题难度：三颗星知识点：类比探究问题6.（上接第4，5题）类比解决三问的过程中，需要证明三角形全等，那么证全等所依据的判定定理（依次）是( )A.SASB.AASC.SAS，AASD.AAS，SAS答案：D解题思路：试题难度：三颗星知识点：类比探究问题。

类比探究之类比探索（一）一、单选题(共6道，每道16分)1.问题情境：在特殊四边形的复习课上，老师出了这样一道题：如图2，在菱形ABCD中，E，F，G，H分别为AB，BC，CD，DA边上的动点，连接EG，FH相交于点O，若∠HOE=∠D，试探究：EG与FH的数量关系．经过小组讨论后，小聪建议分以下两步进行：（1）特殊情况，探索结论当菱形ABCD是正方形时，如图1，EG与FH有怎样的数量关系呢？小聪想：要求EG与FH的数量关系，就要构造全等三角形或相似三角形，于是，分别过点G，H作GM⊥AB于点M，HN⊥BC于点N，证明△GME≌△HNF，从而得到EG=FH．则判定△GME≌△HNF使用的条件可能是( )A.HLB.ASA或AASC.SASD.AAA答案：B解题思路：试题难度：三颗星知识点：中考数学中的类比探究2.（上接第1题）（2）特例启发，解答题目由此猜想：原题中EG与FH的数量关系是EG=FH，经过思考小聪给出了两种方案：方案一：分别过点G，H作GM⊥AB于点M，HN⊥BC于点N，即可证明结论；方案二：过点G作GM∥AD，交AB于点M，过点H作HN∥AB，交BC于点N，即可证明结论．下列说法正确的是( )A.方案一正确，方案二错误B.方案一错误，方案二正确C.两种方案都正确D.两种方案都错误答案：A解题思路：试题难度：三颗星知识点：全等三角形的判定与性质3.（上接第1，2题）（3）反思提升，拓展延伸课后小聪对本题进行了反思，提出如下猜想：将题目中的菱形ABCD改为平行四边形ABCD，如图3，若AB=a，AD=b，其他条件不变，则EG与FH的数量关系为( )A.EG=FHB.C. D.无法确定答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究4.如图1，在△ABC中，D是BC边上的点（不与点B，C重合），连接AD．问题引入：（1）当D是BC边的中点时，；当D是BC边上任意一点时，．（用图中已有线段表示）A.1:1，BD:CDB.1:2，BD:BCC.2:1，BC:BDD.1:2，CD:BC答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第4题）探索研究：（2）如图2，在△ABC中，O是线段AD上一点（不与点A，D重合），连接OB，OC，则．（用图中已有线段表示）A.OA:CDB.OA:ODC.OD:ADD.OA:AD答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究6.（上接第4，5题）拓展应用（3）如图3，O是线段AD上一点（不与点A，D重合），连接BO并延长，交AC于点F，连接CO并延长，交AB于点E，则的值为( )A.1B.2C.3D.无法确定答案：A解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究。

类比探究（一）——直角、平行（讲义）➢ 课前预习1. 如图，在△ABC 中，AF :FB =2:3，延长BC 至点D ，使得BC =2CD ，则AEEC=_________． 提示：求比例，找相似．利用平行线构造“A 型”或“X 型”相似是我们常用的一种做法．A BEF2. 如图，AB =4，射线BM 和AB 相互垂直，点D 是AB 上的一个动点，点E 在射线BM 上，2BE =DB ，作EF ⊥DE 并截取EF =DE ，连接AF 并延长交射线BM 于点C ．设BE =x ，BC =y ，则y 关于x 的函数解析式是（）A ．124xy x =--B ．21xy x =--C ．31xy x =-- D ．84x y x =-- 提示：斜放置的直角特征，可考虑构造一线三等角，利用相似整合信息．➢ 知识点睛1. 类比探究问题的处理思路（1）根据题干条件，结合_______________先解决第一问． （2）尝试类比解决下一问，探索过程中确定__________． ①如果能类比，根据条件变化，则确定______________．②如果不能类比，分析两问间关系，__________________，并尝试、验证． 注：类比过程中，往往要在不变结构的框架下去思考分析，有时也会进行适当的探索来解决图形变化过程中产生的一些新问题．比如在第3问，会需要根据前2问发现的不变结构去补全图形．➢ 精讲精练1. 现有矩形ABCD 和一个以O 为直角顶点的三角板，移动三角板，使三角板的M FE DC B A两直角边所在直线分别与直线BC ，CD 交于点M ，N ．（1）如图1，当AB =AD 且点O 与点A 重合时，则OM 与ON 的数量关系是________；（2）如图2，当AB =AD 且点O 在矩形的内部（含边界）时，若OM =ON ，请探究点O 在移动过程中可形成什么图形？（3）如图3，当点O 在矩形的对角线BD 上时，若BC =7，CD =283，BO =5，则（1）中的结论是否成立？（4）如图4，在平面直角坐标系中，已知点A (0，，点B (1)，且∠ABC =90°，若点C 到y 轴的距离为4，请直接写出满足题意的点C 的坐标．图1NM (O )D CB A图1 图2图3MOCBA图42. 在△ABC 中，∠ABC =90°．（1）如图1，分别过A ，C 两点作经过点B 的直线的垂线，垂足分别为M ，N ，求证：△ABM ∽△BCN ；（2）如图2，P 是边BC 上一点，∠BAP =∠C ，tan ∠P AC，求tan C 的值；（3）如图3，D 是边CA 延长线上一点，AE =AB ，∠DEB =90°，3sin 5BAC ∠=，25AD AC =，直接写出tan ∠CEB 的值． 图1NB CAMPCB A图2ECB AD图33. 在△ABC 中，∠ABC =90°，ABn BC=，M 是直线BC 上一点，连接AM ．过点B 作BP ⊥AM ，P 为垂足．（1）当n =1时，过点C 作CN ∥AB ，交PB 所在直线于点N ． ①如图1，当M 在CB 的延长线上时，求证：CN =BM ．②如图2，当M 在线段BC 上时，设BN 与AC 的交点为D ，若BC =3BM ，则CD AD=________． （2）连接CP 并延长交AB 于点Q ．①如图3，若n =1，求证：CP BMPQ BQ =； ②如图4，若M 是BC 的中点，直接写出tan ∠BPQ 的值． （用含n 的式子表示）图1NM P CB AD图2N M P CBAQ图3M PCBAQ 图4MPCBA4. 已知：线段OA ⊥OB ，点C 为线段OB 上一点，D 为线段OA 上一点．连接AC ，BD 交于点P ．（1）如图1，当OA =OB ，且C ，D 分别为线段OB ，OA 中点时，则APPC的值为______；（2）如图2，当OA =OB ，C 为线段OB 中点，且13AD AO =时，求APPC的值； （3）如图3，当1AD AO n =（n ＞1），1BC BO m =时，直接写出APPC的值（用m ，n 表示）．图1PO DC BA 图2PODC BA 图3PODCBA5.在等腰三角形ABC中，AB=AC，作CM⊥AB交AB于点M，BN⊥AC交AC于点N．（1）如图1，求证：△BMC≌△CNB；（2）①如图2，若点P为线段CB上一点，且满足PC=2BP，过P作PE∥AB交CM于点E，作PF∥AC交BN于点F，则PFNC=_______，PEBM=_______；②如图2，若点P为线段CB上一动点，过P作PE∥AB交CM于点E，作PF∥AC交BN于点F，求证：PE+PF=BM；（3）如图3，若点P为线段CB的延长线上一动点，类似（2）过P作PE ∥AB交CM的延长线于点E，作PF∥AC交NB的延长线于点F，求证：AM·(PE-PF)=OM·BN．AB OM N图1ABOM N图2PFEPE FAB COMN图3【参考答案】 ➢ 课前预习1. 22. A➢ 知识点睛1. （1）分支条件（2）不变特征；①不变特征；②对比、分析、猜测不变特征➢ 精讲精练1. （1）OM =ON ；（2）形成线段AC ； （3）成立，证明略；（4）(4)或(-4，)． 2. （1）证明略；（2）tan C =5； （3）tan ∠CEB =314．3. （1）①证明略；②13；（2）①证明略；②tan ∠BPQ =1n． 4. （1）2；（2）1AP PC =；（3）1AP m PC n =-． 5. （1）证明略；（2）①13；23；②证明略；（3）证明略．。

类比探究（一）——平行、直角（讲义）知识点1. 类比探究一般会围绕一个不变结构进行考查．常见结构有：平行结构、直角结构、旋转结构、中点结构．2. 类比是解决类比探究问题的主要方法．往往会类比字母、类比辅助线、类比结构、类比思路来解决类比探究问题． 3. 常见结构：①平行结构②直角结构③旋转结构G F EDC BA④中点结构DA BMCABC E MNMA平行夹中点 (类)倍长中线 中位线精讲精练1. 如图，△ABC 中，点E ，P 在边AB 上，且AE =BP ，过点E ，P 作BC 的平行线，分别交AC 于点F ，Q ，记△AEF 的面积为S 1，四边形EFQP 的面积为S 2，四边形PQCB 的面积为S 3． （1）①若EP =2AE ，则EF :PQ :BC =__________； ②求证：EF +PQ =BC ．（2）若S 1+S 3=S 2，求PEAE的值．（3）若S 3-S 1=S 2，直接写出PEAE的值．QPFE CB AFEDCG (B )AAB=ACDBCD'A2. 在△ABC 中，AD 为BC 边上的中线，E 为AD 上一动点，设DE =nEA ，连接CE 并延长交AB 于点F ．（1）如图1，当∠BAC =90°，∠B =30°，DE =EA 时，求FBFA的值； （2）如图2，当△ABC 为锐角三角形，DE =EA 时，求FBFA 的值； （3）如图3，当△ABC 为锐角三角形，DE =nEA 时，求FBFA的值．3. 在正方形ABCD 中，对角线AC 与BD 交于点O ；在Rt △PMN 中，∠MPN =90°． （1）如图1，若点P 与点O 重合且PM ⊥AD ，PN ⊥AB ，分 别交AD ，AB 于点E ，F ，请直接写出PE 与PF 的数量关系． （2）将图1中的Rt △PMN 绕点O 顺时针旋转角度α（0°<α<45°）．①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由． ②如图3，旋转后，若Rt △PMN 的顶点P 在线段OB 上移动（不与点O ，B 重合），当BD =3BP 时，猜想此时PE 与PF 的数量关系，并给出证明． ③当BD =m ·BP 时，请直接写出PE 与PF 的数量关系．（3）在（2）②的条件下，当∠DPM =15°时，连接EF，若正方形的边长为，请直接写出线段EF 的长．图1MN F E O (P )DCBA 图2A BDO (P )E FNM4. 在等腰直角三角形ABC 中，∠BAC =90°，AB =AC ，直线MN 过点A 且MN ∥BC ．以点B 为一锐角顶点作Rt △BDE ，图3PA BDO E FNM图3A D NPECBM ∠BDE =90°，且点D 在直线MN 上（不与点A 重合）．如图1，DE 与AC 交于点P ，易证：BD =DP ． （1）在图2中，DE 与CA 的延长线交于点P ，则BD =DP 是否成立？如果成立，请给予证明；如果不成立，请说明理由．（2）在图3中，DE 与AC 的延长线交于点P ，BD 与DP 是否相等？请直接写出你的结论，无需证明．类比探究（二）——旋转、中点（讲义）知识点1. 若属于类比探究常见结构，调用结构类比解决．若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题． ① 根据题干条件，结合支干条件先解决第一问． ② 类比解决下一问．如果不能，分析条件变化，寻找不变特征、不变结构．③ 结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证． 2. 不变结构既是类比迁移的前提，也是类比迁移过程中发现的结果．① 对比连续两问特征，考虑类比的前提条件是否存在；② 对比特征应用方式，考虑在“相同”的条件下，能否进行“相同”的组合；③ 对比结论，往往先从图上验证上一问结论；或者结合图形以及上一问结论的组合方式猜测新结论．在类比的过程中，也会进行适当的探索来解决图形变化过程中的一些新问题，此时要在不变结构的框架下去思考分析．精讲精练1. 如图1，在Rt △ABC 中，∠ACB =90°，∠A =30°，P 为BC 边上任意一点，Q 为AC 边上一动点，分别以CP ，PQ 为边作等边三角形PCF 和等边三角形PQE ，连接EF ． （1）试探索EF 与AB 的位置关系，并证明．（2）如图2，当点P 为BC 延长线上任意一点时，（1）中的结论是否成立？请说明理由． （3）如图3，在Rt △ABC 中，∠ACB =90°，∠A =m °，P 为BC 延长线上一点，Q 为AC 边上一动点，分别以CP ，PQ 为腰作等腰三角形PCF 和等腰三角形PQE ，使得PC =PF ，PQ =PE ，连接EF ．要使（1）中的结论依然成立，则需要添加怎样的条件？为什么？图1AD NPECBM 图2M BCE PNDA图2QP FCBEA图3QP F CBEA2. 如图1，∠QPN 的顶点P 在正方形ABCD 两条对角线的交点处，∠QPN =α，将∠QPN 绕点P 旋转，旋转过程中∠QPN 的两边分别与正方形ABCD 的边AD 和CD 交于点E 和点F （点F 与点C ，D 不重合）．（1）如图1，当α=90°时，DE ，DF ，AD 之间满足的数量关系是____________；（2）如图2，将图1中的正方形ABCD 改为∠ADC =120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE +DF =12AD ，请给出证明；（3）在（2）的条件下，若旋转过程中∠QPN 的边PQ 与射线AD 交于点E ，其他条件不变，探究在整个运动变化过程中，DE ，DF ，AD 之间满足的数量关系，直接写出结论，不用加以证明．3. 已知直线m ∥n ，点C 是直线m 上一点，点D 是直线n 上一点，CD 与直线m ，n 不垂直，点P 为线段CD 的中点．图1Q P FCBE A图2NQFE P D CB A图1N QPF E DCBA 图3ABCD（1）操作发现：直线l ⊥m ，l ⊥n ，垂足分别为A ，B ，当点A 与点C 重合时（如图1所示），连接PB ，请直接写出线段PA 与PB 的数量关系：____________．（2）猜想证明：在图1的情况下，把直线l 向上平移到如图2的位置，试问（1）中的PA 与PB 的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）延伸探究：在图2的情况下，把直线l 绕点A 旋转，使得∠APB =90°（如图3所示），已知两平行线m ，n 之间的距离为2k ．求证：PA PB k AB ⋅=⋅．图1lmn A (C )BD P 图2PDBCA n m l l m n ACB DP图34. 在Rt △ACB 和Rt △AEF 中，∠ACB =∠AEF =90°，若点P 是BF 的中点，连接PC ，PE ．特殊发现：如图1，若点E ，F 分别落在边AB ，AC 上，则结论：PC =PE 成立（不要求证明）． 问题探究：把图1中的△AEF 绕着点A 顺时针旋转．（1）如图2，若点E 落在边CA 的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由．（2）如图3，若点F 落在边AB 上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．（3）记ACk BC=，当k 为何值时，△CPE 总是等边三角形（请直接写出k 的值，不必说明理由）？图1PFEC BAP A BCEF图2图3PCBAF类比探究（三）——探究应用（讲义）知识点A CB1. 类比探究问题往往会在发现不变结构后，应用不变结构去解决新的问题．此时需要先探索分析新问题，在探索过程中，将新问题与不变结构的特征进行对比，寻求“相同”特征．在“相同”特征基础上，构造不变结构来解决问题．备注：图形不完整时，往往会有多种情形．精讲精练1. 我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1、图2、图3中，AF ，BE 是△ABC 的中线，AF ⊥BE ，垂足为P ，像这样的三角形均为“中垂三角形”．设BC =a ，AC =b ，AB =c ． 特例探索（1）如图1，当∠ABE =45°，c=a =_____，b =_____； 如图2，当∠ABE =30°，c =4时，a =________，b =________．归纳证明（2）请你观察（1）中的计算结果，猜想a 2，b 2，c 2三者之间的关系，用等式表示出来，并利用图3证明你发现的结论．拓展应用（3）如图4，在□ABCD 中，点E ，F 分别是AD ，BC 的中点，BE ⊥AC 于点H ，若AD=AB =3，求AF 的长．CFPECFP ECF BPE图1图2图32. BC D A3. 如图，在等边三角形ABC 中，点D 在直线BC 上，连接AD ，作∠ADN =60°，直线DN 交射线AB 于EFBCD A HF E DCB A图4点E ，过点C 作CF ∥AB 交直线DN 于点F ．（1）当点D 在线段BC 上，∠NDB 为锐角时，如图1，求证：CF +BE =CD ．（提示：过点F 作FM ∥BC 交射线AB 于点M ）（2）当点D 在线段BC 的延长线上，∠NDB 为锐角时，如图2；当点D 在线段CB 的延长线上，∠NDB 为钝角时，如图3，请分别写出线段CF ，BE ，CD 之间的数量关系，不需要证明． （3）在（2）的条件下，若∠ADC=30°，ABC S =△BE =_________，CD =________．图1N MF EDCB A DCABFEN图24. 已知：△ABC 是等腰直角三角形，动点P 在斜边AB 所在的直线上，以PC 为直角边作等腰直角三角形PCQ ，其中∠PCQ =90°．探究并解决下列问题：（1）如图1，若点P 在线段AB 上，且AC=1PA则：①PB =___________，PC =____________； ②猜想：PA 2，PB 2，PQ 2三者之间的数量关系为____________．（2）如图2，若点P 在AB 的延长线上，在（1）中所猜想的结论仍然成立，请你利用图2给出证明过程．（3）若动点P 满足13PA PB =，求PCAC的值． 图1AB PCQ图2QACP B【参考答案】图3ACBD CABFEN图32.（1）证明略（2）2（3）n2+n；n2-n；-n2+n3.（1）证明略（2）BE=CD+CF；CF=BE+CD（3）8；4或84.（1，2；②222PA PB PQ+=（2）证明略（3）42【参考答案】1.（1）EF⊥AB（2）成立（3）∠QPE=∠CPF=∠B2.（1）DE+DF=AD（2）证明略（3）当点E落在AD上时，DE+DF12AD =；当点E落在AD的延长线上时，DF-DE=12 AD3.（1）PA=PB（2）成立，证明略（3）证明略4.（1）成立，证明略（2）成立，证明略（3）k=【参考答案】1.（1）①1:3:4 ②证明略（2）2（32.（1）2（2）2（3）2n3.（1）PE=PF（2）①成立，证明略；②PE=2PF，证明略；③PE=(m-1)PF（3）4.（1）成立，证明略（2）相等。

几何难点突破之类比探究（讲义）一、知识点睛识别类比探究题型特征：1.题目中一般有三问或者更多，每小问的条件和图形相似度很高，因此可以“照搬”第一问的方法；2.每一问的图形或点的位置会有所变化（通常条件从特殊走向一般），但可以在这些变化过程中按照第一问的思路和对应关系找角、找边、找全等．二、精讲精练1. 如图1所示，在△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，且点B 、A 、D 在一条直线上，连接BE 、CD ，M 、N 分别为BE 、CD 的中点．（1）求证：①BE =CD ；②△AMN 是等腰三角形．（2）在图1的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到图2所示的图形．（1）中的两个结论是否仍然成立，若成立，请给予证明；若不成立，请说明理由．图2ME CBNDA图1CBMN ED A2. 已知△ABC 为等边三角形，点D 为直线BC 上一动点（点D 不与B ，C 重合），以AD 为边作菱形ADEF （A 、D 、E 、F 按逆时针排列），使∠DAF ＝60°，连接CF ． （1）如图1，当点D 在边BC 上时，求证：①BD ＝CF ；②AC ＝CF ＋CD ；（2）如图2，当点D 在边BC 的延长线上且其他条件不变时，结论AC ＝CF ＋CD 是否成立？若不成立，请写出AC 、CF 、CD 之间存在的数量关系，并说明理由；（3）如图3，当点D 在边CB 的延长线上且其他条件不变时，探究AC 、CF 、CD 之间存在的数量关系．图1AFECDB图2ABC DFEABCD F3. 如图1，四边形ABCD 是正方形，点E 是边BC 的中点．且90AEF ∠=，且EF 交正方形外角DCG ∠的平分线CF 于点F ．（1）求证：AE =EF ；（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由；（3）如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”是否成立？如果成立，写出证明过程；如果不成立，请说明理由．图1GFE DC B A图2A B CDE FG图3GFE DCBA4.如图1，在△ABC 中，点P 为BC 边的中点，直线a 绕顶点A 旋转，若B 、P 在直线a 的异侧，BM ⊥直线a 于点M ，CN ⊥直线a 于点N ，连接PM 、PN ；（1）求证：PM =PN ；（2）若直线a 绕点A 旋转到图2的位置时，点B 、P 在直线a 的同侧，其它条件不变．此时PM =PN 还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）如图3，若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变．请判断四边形MBCN 的形状及此时PM =PN 还成立吗？图1ABCP aMN图2ABCP aM N图3NMaP CBA5.如图1所示,已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC 、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1.(1)如图2，当点E恰好在直线l上时(此时E1与E重合)，试说明DD1=AB；(2)在图1中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；(3)如图3，当点E在直线l的下方时，请探究三条线段DD1、EE1、AB之间的数量关系.DA BGEFCl D1E1图1GEBACFD1DE1()l图2图3lFGEBACD1DE16. 如图，点P 是正方形ABCD 对角线AC 上一动点，点E 在射线BC 上，且PE ＝PB ，连接PD ，O 为AC 中点． （1）如图1，当点P 在线段AO 上时，试猜想PE 与PD 的数量关系和位置关系，不用说明理由；（2）如图2，当点P 在线段OC 上时，（1）中的猜想还成立吗？请说明理由；（3）如图3，当点P 在AC 的延长线上时，判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．图1BB图2三、课后作业1．已知：如图所示，直线MA∥NB，∠MAB与∠NBA的平分线交于点C，过点C作一条直线l与两条直线MA、NB分别相交于点D、E．（1）如图1所示，当直线l与直线MA垂直时，猜想线段AD、BE、AB之间的数量关系，请直接写出结论，不用证明；（2）如图2所示，当直线l与直线MA不垂直且交点D、E都在AB的同侧时，（1）中的结论是否成立？如果成立，请证明：如果不成立，请说明理由；（3）如图3所示，当直线l与直线MA不垂直且交点D、E在AB的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD、BE、AB之间还存在某种数量关系吗？如果存在，请写出它们之间的数量关系．【几何难点突破之类比探究参考答案】二、精讲精练图1A lCEBDNM图2M NDBElACMNDBEClA图3(1)lCENM1.提示：（1）①证△CAD≌△BAE（SAS）；②证△ACN≌△ABM（SAS）；或证△MEA≌△NDA（SAS）；（2）成立，同（1）可证．2.证明：（1）如图1，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠BAD+∠DAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAC+∠CAF=60°∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BC=BD+DC∴ BC=CF+CD即AC= CF+CD（2）此时AC=CF+CD不成立，CF = AC +CD.理由如下：如图2，在等边△ABC中，AB=AC=BC，∠BAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF∴ ∠BAC+∠CAD=∠DAF+∠CAD∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BD=BC+CD∴ CF= BC+CD即CF = AC +CD（3）CF = CD-AC.理由如下：如图3，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠CAF+∠BAF=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAB+∠BAF=60°∴ ∠DAB+∠BAF =∠CAF+∠BAF∴ ∠DAB=∠F AC∴△ABD≌△ACF（SAS）∴ BD=CF图1AFECDB图2AB C DFE图3AB CDEF∵ BD=CD-CB∴ CF= CD-CB即CF = CD-AC3.提示：（1）在AB上取点M，使得AM=CE，证△AME≌△ECF（ASA）；（2）成立，同（1）可证；（3）成立，在BA的延长线上取点M，使得AM=CE，证△AME≌△ECF（ASA）．4.提示：（1）延长MP交CN于点E，证△BPM≌△CPE（ASA），直角三角形斜边中线等于斜边一半；（2）延长MP交NC的延长线于点E，同（1）可证；（3）四边形MBCN为矩形；成立，同（1）可证．5.提示：（1）△ADD1≌△CAB；（2）AB＝DD1＋EE1，过点C作CM⊥AB于点M，证△ADD1≌△CAM，△EBE1≌△BCM；（3）DD1=AB＋EE1，同（2）可证．6.提示：（1）过P作PM⊥BC于点M，PN⊥DC于点N．证△APB≌△APD（SAS），△PME≌△PND（HL）即可；（2）成立，同（1）可证；（3）作图略；成立，过P分别作BC，DC的垂线，交BE于点M，DC的延长线于点N，同（1）可证．四、课后作业1．解：（1）AD+BE＝AB（2）成立．证明：（方法一）：在AB上截取AG=AD，连接CG．∵ ∠1＝∠2，AC＝AC∴△ADC≌△AGC（SAS）∴∠5＝∠6∵ AM∥BN∴ ∠1+∠2+∠3+∠4=180°图1A lCEBDNM876541C lEDNM∵∠1＝∠2，∠3＝∠4∴ ∠2+∠3=90°∴ ∠ACB＝90°即∠6＋∠7＝90°∵ ∠5+∠6+∠7+∠8=180°∴ ∠5＋∠8＝90°∴∠7＝∠8∵∠3＝∠4，BC＝BC∴△BGC≌△BEC（ASA）∴BG＝BE∴AG+BG＝AD+BE∴AD+BE＝AB（方法二）：过点C作直线FG⊥AM，垂足为点F，交BN于点G．作CH⊥AB，垂足为点H．由（1）得AF+BG=AB∵AM∥BN，∠AFG＝90°∴ ∠BGF＝∠FGE＝90°∵∠1＝∠2，∠3＝∠4∴ CF＝CH，CH＝CG∴ CF＝CG∵ ∠FCD＝∠GCE∴△CFD≌△CGE（ASA）∴DF＝EG∴ AD+BE=AF-DF+GE+BG=AF+BG=AH+BH=AB （方法三）：延长BC，交AM于点F．∵AM∥BN∴∠5＝∠4∵ ∠3＝∠4∴∠5＝∠3HFG1234CAlEBDNM图2方法二51234FCAlEBDNM∴ AF =AB∵ ∠1＝∠2，∴ CF ＝CB∵∠FCD ＝∠BCE∴ △FCD ≌△BCE （ASA ）∴ DF ＝BE∴ AD +BE =AD +DF =AF =AB（3）不成立．存在．当点D 在射线AM 上，点E 在射线BN 的反向延长线上时（如图3（1）），AD -BE =AB当点D 在射线AM 的反向延长线上，点E 在射线BN 上时（如图3（2）），BE -AD =AB图3(2)图3(1)A l C E B D N M MN DBEClA。

学生做题前请先回答以下问题问题1：类比探究问题的处理思路是什么？以下是问题及答案，请对比参考:问题1：类比探究问题的处理思路是什么？答：类比探究问题的处理思路为：（1）类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有：中点结构、直角结构、旋转结构、平行结构．（2）若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．①根据题干条件，结合支干条件先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找不变特征．③结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证．若属于类比探究常见的结构类型，调用结构类比解决．类比探究专题（一）——平行结构一、单选题(共6道，每道16分)1.如图1，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．（1）若BD=CD，CF=2AF，则的值为( )A.2B.C. D.答案：B解题思路：试题难度：三颗星知识点：平行结构2.（上接第1题）（2）如图2，若BD=CD，CF=mAF，则的值为( ) （用含m的代数式表示）A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构3.（上接第1，2题）（3）如图3，将原题改为“过点D的一条直线交AC的延长线于点F，交AB于点E”，若BD=nCD，CF=mAF，则的值为( )（用含m，n的代数式表示）A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构4.已知AD是△ABC的中线，将BC边所在直线绕点D顺时针旋转角，交AB边于点M，交射线AC于点N，设．（1）如图1，满足的函数关系式为( ) A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构5.（上接第4题）（2）如图2，当G是AD上任意一点时（点G不与点A重合），过点G的直线交AB边于点，交AC边于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构6.（上接第4，5题）（3）如图3，当G是AD上任意一点时（点G不与点A重合），过点G 的直线交AB边于点，交AC的延长线于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构。

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合___________________先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找______________．结合所求目标，依据_____________，大胆猜测、尝试、验证问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？以下是问题及答案，请对比参考:问题1：类比探究属于几何综合题，类比（，，）是解决此问题的主要方法，做好类比需要把握变化过程中的．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找．结合所求目标，依据，大胆猜测、尝试、验证答：问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？答：类比探究—平行结构一、单选题(共6道，每道16分)1.现有多个全等直角三角形，先取三个拼成如图1所示的形状，R为DE的中点，BR分别交AC，CD于点P，Q，则BP:PQ:QR等于( )A.3:2:1B.3:2:4C.3:1:2D.2:1:2答案：C解题思路：试题难度：三颗星知识点：类比探究问题2.（上接第1题）若取四个直角三角形拼成如图2所示的形状，S为EF的中点，BS分别交AC，CD，DE于点P，Q，R，则BP:PQ:QR:RS等于( )A.5:1:3:2B.4:1:3:2C.5:1:4:2D.3:1:3:2答案：B解题思路：试题难度：三颗星知识点：类比探究问题3.（上接第1，2题）若取五个直角三角形拼成如图3所示的形状，T为FG的中点，BT分别交AC，CD，DE，EF于点P，Q，R，S，则BP:PQ:QR:RS:ST等于( )A.5:1:4:2:3B.5:1:5:2:3C.4:1:4:2:3D.5:1:4:3:2答案：A解题思路：试题难度：三颗星知识点：类比探究问题4.问题背景：已知在△ABC中，AB边上的动点D由A向B运动(与A，B不重合)，点E与点D同时出发，由点C沿BC的延长线方向运动(E不与C重合)，连接DE交AC于点F，点H是线段AF上一点．（1）初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，则HF，AH，CF之间的数量关系为( )A.HF=AH+CFB.C.HF=2AH+CFD.答案：A解题思路：试题难度：三颗星知识点：全等三角形的判定与性质5.（上接第4题）（2）类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC= 30°，且点D，E的运动速度之比是，则的值为( )A. B.C.2D.答案：C解题思路：试题难度：三颗星知识点：全等三角形的判定与性质6.（上接第4，5题）（3）延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记，且点D，E的运动速度相等，则的值为( )（用含m的代数式表示）A.2B.C.3mD.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究。

几何结构之直角、平行（讲义）>知识点睛1.儿何综合问题的处理思路<1）标注条件，合理转化（2）组合特征，分析结构（3）山因导果，执果索因一般遇到求线段比值的问题时，往往考虑利用相似来解决问题；借助“直角”“平行线”特征可以构造相似三角形.2.（1）直角结构之“斜直角放正"构造一线三等角得到△ADB S ZXBEC构造类"弦图"相似得到HAEBs HBDC构造旋转放缩，得到△ EMDs&NDE[ AB（2）直角结构之“十字模型”特征：①矩形；②BF丄CE 狂 '/< BF AB结论：——=——CE BC 特征：①矩形；② 结论：EF川GH BC特征：①平行四边形；②ZB+ZEGC=180。

応、CF AB结论：一=——DE BC4精讲精练如图，在梯形ABCD 中，AB//CD. 二ZC=90。

，点E 在BC 边上，AB=3. CD=2, BCT.若ZAED=90°,则 CE=如图，已知矩形ABCD 的顶点A, D 分别落在X 轴、 OD=2OA=6. AD:AB=3:i.则点 C 的坐标是（）7） B ・（3, 7） C.如图，将三角板放在矩形ABCD 上，使三角板的一边恰好经 过点B,三角板的直角顶点£落在矩形对角线AC 上，另一y 轴上, A. (2,SC=4,则££=边交CD于点F・若EB ----------如图，直角梯形ABCD中，AD//BC. AB丄BC, AD=3. BC=5, 将腰DC绕点D逆时针方向旋转90。

并缩短，恰好使D气CD, 连接AE,则△*/）£：的面积是4如图，在 RtAABC 中，ZABC=9（r, AB=3. BC=4.将RtMPN 的直角顶点P 放置在AC 上，PM 交AB 于点E, PN交 BC 于点 F,当 PE=2PF 时，AP= ___________ .在矩形ABCD 中，人£丄8£）于点E,点P 是边AD 上一点,PE 丄EC.若 AB=1, BC=2,则 AP 的长为 ________________ .如图，在RtAACB 中，ZACB=90\ AC=BC=3. CD=i. CH 丄BD 于点。