类比探究问题(习题及答案)

➢例题示范类比探究（习题）例1：如图1，在□ABCD 中，点E 是BC 边的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G．（1）尝试探究：如图1，若AF= 3 ，则CD的值是．EF CG（2）类比延伸：如图2，在原题的条件下，若AF=m （m＞EF0），则CD的值是CG解答过程．（用含m 的代数式表示），试写出（3）拓展迁移：如图3，在梯形ABCD 中，DC∥AB，点E是BC 延长线上一点，AE 和BD 相交于点F．若AB=a ，CDBC=b（a＞0，b＞0），则AF的值是（用含a，b 的代BE EF 数式表示）．1【思路分析】根据特征确定问题结构，设计方案解决第一问．问题背景是平行四边形，且已知线段比例关系，考虑通过相似传递比例关系，进而求 CD的值．CG构造相似利用作平行线的方法，即过中点 E 作 EH ∥AB 交 BG于点 H ，可得“A ”字型相似△BEH ∽△BCG ，“X ”型相似△EFH ∽△AFB ，结合 AF= 3 ，可得 CG =2EH ，AB =3EH ，故EFCD = 3 ．CG 2类比第一问思路，解决第二问．分析不变特征，此时平行四边形、中点特征均不变，变化的是 AF ，EF 的比例，照搬第一问思路，过点 E 作 EH ∥AB 交BG 于点 H ，同样可得△BEH ∽△BCG ，△EFH ∽△AFB ，此时 CG =2EH ，AB =mEH ，故 CD = m．CG 2照搬思路解决第三问．虽然此问中图形、中点 E 、比例关系均发生变化，但 DC ∥AB 不变，依然可利用相似来整合条件，可照搬前面思路处理， 依然构造平行．过点 E 作 EH ∥AB 交 BD 的延长线于点 H ，可得△BCD ∽△BEH ，△AFB ∽△EFH ，可得 BC = CD，BE EHAF = AB ，结合 AB = a ， BC = b ，可知 EF EH CD BE AF = AB = a ⋅CD = ab ． EF EH EH212 3➢巩固练习1.如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°．【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板DEF 绕点E 旋转，并使边DE 与边AB 交于点P，边EF 与边BC 交于点Q．【探究】在旋转过程中，（1）如图2，当CE=1时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（2）如图3，当CE= 2 时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（3）根据你对（1），（2）的探究结果，试写出当CE=m时，EAEP 与EQ 满足的数量关系式为．3，=2.如图1，在等边三角形ABC 中，线段AD 为其内角角平分线，过点D 的直线B1C1⊥AC 于C1，交AB 的延长线于B1．（1）请你探究：AC =CD AC1 C1D 是否都成立？AB BD AB1DB1（2）请你继续探究：如图2，若△ABC 为任意三角形，线段AD 为其内角角平分线，请问AC=CD一定成立吗？并证明AB BD你的判断．（3）如图3，在Rt△ABC 中，∠ACB=90°，AC=8，AB=40，3E 为AB 上一点且AE=5，CE 交其内角角平分线AD 于F．试求DF的值．FA43.如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C =90°，∠B =∠E =30°．（1） 操作发现如图 2，固定△ABC ，使△DEC 绕点 C 旋转，当点 D 恰好落在 AB 边上时，填空：①线段 DE 与 AC 的位置关系是 ；②设△BDC 的面积为 S 1，△AEC 的面积为 S 2，则 S 1 与 S 2 的数量关系是．图 1图 2（2） 猜想论证当△DEC 绕点 C 旋转到图 3 所示的位置时，小明猜想（1） 中 S 1 与 S 2 的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中 BC ，CE 边上的高，请你证明小明的猜想．（3） 拓展探究如图 4 ， 已知∠ ABC =60°， 点 D 是其角平分线上一点， BD =CD =4，DE ∥AB 交 BC 于点 E ．若在射线 BA 上存在点 F ， 使 S △DCF =S △BDE ，请直．接．写．出．相应的 BF 的长．5➢思考小结总结类比探究问题中的常见结构①旋转结构始终含有等腰结构（正方形、等腰直角三角形等），并且经过旋转后，能将各条件重新组合应用．②中点结构平行夹中点（类）倍长中线中位线始终含有中点，常考虑利用中点结构补全图形，然后将所证目标放在一个较大的背景下（等腰三角形、直角三角形、等腰直角三角形等）研究．③直角结构始终含有直角，常构造直角与斜直角配合，得到同角的余角相等；再配合构造的其他直角证明相似，所求目标往往和比例关系相关．6④平行结构所求目标为线段间的比例关系，题目中没有相似三角形，往往考虑利用平行线构造相似求解．78 3 3 【参考答案】 ➢ 巩固练习1. （1）EP =EQ ，证明略；（2） EP = 1EQ ，证明略；2 （3） EP = 1EQ ．m2. （1）都成立，证明略； （2）一定成立，证明略；（3） DF = 5 ．FA 83. （1）①DE ∥AC ；②S 1=S 2．（2） 证明略； （3） BF 的长为4 3或 ．38。

学生做题前请先回答以下问题问题1：想一想河南中考数学第22题常考类型有哪些？问题2：想一想河南中考数学第22题答题标准动作有哪些？问题3：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？类比探究与动点问题专项训练（二）一、单选题(共6道，每道16分)1.通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．（1）思路梳理∵AB=AD，∴把△ADF绕点A顺时针旋转90°至△ABG，可使AD与AB重合．∵∠ABC=∠ABG=90°，∴∠EBG=180°，点E，B，G共线．根据___________，易证△AEF≌__________，得EF=BE+DF．（2）类比联想如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E，F分别在BC，CD边上，且∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系___________时，仍有EF=BE+DF．（3）引申拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在BC边上，且∠DAE=45°．猜想BD，DE，EC之间满足的数量关系，并写出推理过程．（建议学生打印做题，并在做完之后对比解题思路中的示范照片）（1）思路梳理∵AB=AD，∴把△ADF绕点A顺时针旋转90°至△ABG，可使AD与AB重合．∵∠ABC=∠ABG=90°，∴∠EBG=180°，点E，B，G共线．根据___________，易证△AEF≌__________，得EF=BE+DF．A.AAS，△AGEB.SAS，△AGEC.SAS，△AEGD.SSS，△AGE答案：C解题思路：见第3题中解析试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）类比联想如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E，F分别在BC，CD边上，且∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系_________时，仍有EF=BE+DF．( )A.∠B=∠DB.∠B+∠D=180°C.∠B-∠D=90°D.∠B=2∠D答案：B解题思路：见第3题中解析试题难度：三颗星知识点：中考数学几何中的类比探究3.（上接第1，2题）（3）引申拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在BC边上，且∠DAE=45°，则BD，DE，EC之间满足的数量关系为( )A.DE=BD+ECB.C. D.答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究4.如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于点E，设．（1）当时，求CE的长；（2）当时，①设，能够得到，求k的值；②连接CF，当的值最大时，求BE的长．（建议学生打印做题，并在做完之后对比解题思路中的示范照片）（1）当α=60°时，EF的长为( )A.5B.C. D.答案：A解题思路：见第6题中解析试题难度：三颗星知识点：中点结构5.（上接第4题）（2）①当时，设，能够得到，则k的值为( )A. B.C. D.3答案：D解题思路：见第6题中解析试题难度：三颗星知识点：中点结构6.（上接第4，5题）（2）②连接CF，当的值最大时，BE的长为( )A. B.C. D.5答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半。

实用文档类比推理题库及标准答案（类比推理部分）1、作家：读者A.售货员：顾客B.主持人：广告C.官员：腐败D.经理：秘书【解答】此题属于专业人员与其面对的对象之间的类比推理题，故正确答案为A。

2、水果：苹果A.香梨：黄梨B.树木：树枝C.经济适用房：奔驰D.山：高山【解答】该题题干中水果与苹果两个词之间是一般和特殊的关系，所以答案为选项D。

选项B的两个词之间的关系是整体与部分的关系。

3、努力：成功A.原告：被告B.耕耘：收获C.城市：福利D.扩招：失业【解答】努力与成功两个词具有因果关系，即只有努力才能成功或者说努力是成功必不可少的原因之一，故正确答案为B。

4、书籍：纸张A.毛笔：宣纸B.橡皮：文具盒C.菜肴：萝卜D.飞机：宇宙飞船【解答】此题属于物品与制作材料的推理关系，故正确答案为C。

5、馒头：食物A.食品：巧克力B.头：身体C.手：食指D.钢铁：金属【解答】此题属于特殊与一般的推理关系，故正确答案为D。

实用文档6、稻谷：大米A.核桃：桃酥B.棉花：棉子C.西瓜：瓜子D.枪：子弹【解答】因为稻谷是大米的惟一来源，而棉花是棉子的惟一来源，故正确答案为B。

7、轮船：海洋A.河流：芦苇B.海洋：鲸鱼C.海鸥：天空D.飞机：海洋【解答】此题属于物体与其运动空间的类比推理题，故正确答案为C。

8、芙蕖：荷花A.兔子：嫦娥B.窑洞：官邸C.伽蓝：寺庙D.映山红：蒲公英【解答】因为芙蕖是荷花的书面别称，而伽蓝是寺庙的书面别称，故正确答案为C。

9、绿豆：豌豆A.家具：灯具B.猴子：树木C.鲨鱼：鲸鱼D.香瓜：西瓜【解答】选项C中的鲸鱼其实不是鱼，而是哺乳动物，故正确答案为D。

10、汽车：运输A.捕鱼：鱼网B.编织：鱼网C.鱼网：编织D.鱼网：捕鱼【解答】此题属于工具与作用的类比推理题，故正确答案为D。

11、医生：患者A.工人：机器B.啄木鸟：病树C.警察：罪犯D.法官：律师答案:B12、紫竹：植物学家A.金属：铸工B.铁锤：石头C.动物：植物D.蝴蝶：昆虫学家答案:D13、老师：学生A.教师：职工B.编辑：读者C.师傅：学徒D.演员：经济人答案:C14、书法：艺术A.抢劫：犯罪B.鲁迅：周树人C.历史：世界史D.权力：金钱答案:A15、森林：树木A.头：身体B.花：菊花C.山脉：山D.身体：身躯答案:C16、工人：机器A.赌球：球员B.无产者：资本家C.农民：土地D.商人：商品答案:C17、教师：教室A.士兵：子弹B.士兵：战斗C.战场：战士D.士兵：军营答案:D18、发奋：成功A.点灯：**B.饮料：可乐C.扶贫：账户D.自满：失败答案:D19、中国：国家A.秦国：战国B.人：动物C.昆仑山：武夷山脉D.生物：植物答案:B20、资本家：工人A.地主：佃户B.教师：学生C.店员：客户D.父亲：儿子答案:A21、跳跃：动作A.男人：女人B.湖南省：长沙市C.青年：妇女D.风俗：习惯答案:D22、周瑜：曹操A.南京：北京B.动作：食物C.汽车：吊车D.官员：群众答案:A23、水壶：开水A.桌子：游戏B.邮箱：信件C.黄梅戏：歌曲D.青蛙：池塘答案:B24、导演：电影A.售货员：货物B.作家：小说C.农民：庄稼D.工人：机器答案:B25、逗号：中止A.拂晓：黎明B.节省：吝啬C.回车：换行D.明星：绯闻答案:C26、射击：手枪A.投掷：石头B.月光：流水C.性格：坚强D.拳击手：攻击答案:A27、鸟：蛋A.老虎：虎仔B.步枪：子弹C.师傅：徒弟D.鱼：卵答案:D28、温度计：气温A.高兴：哀愁B.磅秤：重量C.天才：音乐家D.游泳：运动答案:B29、窑：陶瓷A.蛇：山洞B.商人：金钱C.战争：难民D.烤箱：面包答案:D30、美国：旧金山A.地球：恒星B.黄河：中国C.香港：世贸组织D.中国：淮河答案:D31、南京∶江苏A. 石家庄∶河北B. 渤海∶中国C. 泰州∶江苏D. 秦岭∶淮河答：A题干是省会城市与所属省份关系，选项中符合条件的是A。

天天家教中心数学内部讲义
探究类比归纳（2012/5/26）
27. （2011年青海，27,10分）认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题.
A AA
O
B CO
CDB图11-2 CBDE图11-1O
图11-3
探究1：如图11-1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，∠BOC与∠A 的关系为
探究2：如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A 有怎样的关系？请说明理由.
探究3：如图11-3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）
结论： .
25．（11·南平）（12分）
（1）操作发现：如图1，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．猜想线段GF与GC有何数量关系？并证明你的结论．
（2）类比探究：
如图2，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．
E E
（11·辽阜新）如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE＝EB，连接PD，O为AC中点．
（1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理寒假班暑假班周末班作业班 VIP一对一。

四边形之类比探究（一）（习题）例题示范例1：已知等腰三角形ABC 中，∠ACB =90°，点E 在AC 的延长线上，且∠DEC =45°，M ，N 分别是DE ，AE 的中点，连接MN ，交直线BE 于点F ．当点D 在CB 的延长线上时，如图1所示，易证MF +FN =1BE ．2（1）如图2，当点D 在CB 边上时，上述结论是否成立？若成立，请给出证明；若不成立，请写出你的猜想，并说明理由．（2）当点D 在BC 的延长线上时，如图3所示，请直接写出线段MF ，FN ，BE 之间的数量关系（不需要证明）．1【思路分析】1.里面有多个中点，考虑中位线，先证明易证的思路．连接AD ，由中位线定理可知MN =1AD ，2由题意可证△ACD ≌△BCE ，得到AD =BE ，即MN =1BE ，2所以MF +FN =1BE ．22.照搬易证的思路解决第一问．连接AD ，由中位线定理可知MN =1AD ，2由题意可证△ACD ≌△BCE ，得到AD =BE ，即MN =1BE ，2所以NF -MF =1BE ．23.照搬易证的思路解决第二问．连接AD ，由中位线定理可知MN =1AD ，2由题意可证△ACD ≌△BCE ，得到AD =BE ，即MN =1BE ，2所以MF -NF =1BE ．2【过程书写】证明：（1）不成立，理由如下：连接AD ，在△AED 中，M 是DE 的中点，N 是AE 的中点，∴MN 是中位线∴MN =1AD2在等腰三角形ABC 中，∠ACB =90°∴AC =CB ，∵∠ACB =90°，∠DEC =45°∴CD =CE∴△ACD ≌△BCE （SAS ）∴AD =BE∴MN=1BE 2∴FN-MF=1BE 2（2）MF-FN=1BE 2巩固练习1.已知△ABC是等边三角形，D是直线BC上一动点（不与点B，C重合），以AD为边作菱形ADEF（A，D，E，F按逆时针排列），使∠DAF=60°，连接CF．（1）如图1，当点D在BC边上时，求证：①BD=CF；②AC=CD+CF．（2）如图2，当点D在BC的延长线上时，其他条件不变，结论AC=CD+CF是否仍成立？若成立，请证明；若不成立，请写出AC，CD，CF之间的数量关系，并说明理由．（3）如图3，当点D在CB的延长线上时，其他条件不变，探究AC，CD，CF之间的数量关系．图1图2图32.如图1，C是线段BG上一点，分别以BC，CG为边，向外作正方形BCDA和正方形CGEF，使点D落在线段CF上，M是AE的中点，连接DM，FM．（1）求证：DM=FM，DM⊥FM．（2）如图2，将正方形CGEF绕点C顺时针旋转45°，其他条件不变，探究线段DM，FM之间的关系，并加以证明．（3）如图3，将正方形CGEF绕点C旋转任意角度，其他条件不变，探究线段DM，FM之间的关系，并加以证明．图1图2图33.（1）如图1，△ABC和△BDE都是等腰直角三角形，AB⊥AC，BD⊥DE，点D在AB边上．取CE的中点F，连接AF，DF，猜想AF，DF之间的数量关系和位置关系，并加以证明．（2）将△BDE旋转至如图2所示的位置，使点E在AB的延长线上，点D在CB的延长线上，其他条件不变，判断（1）中AF，DF之间的数量关系和位置关系是否发生变化，并加以证明．图1图2【参考答案】巩固练习1．（1）证明略．提示：证明△ABD≌△ACF，得到BD=CF，进而得到AC=CD+CF．（2）AC=CF-CD，理由略．（3）AC=CD-CF．2．（1）证明略．提示：延长DM，交EF于点H．证明△ADM≌△EHM（ASA），得到AD=EH，DM=HM，进而得到△DFH是等腰直角三角形，所以DM=FM，DM⊥FM．（2）DM=FM，DM⊥FM，证明略．提示：延长DM，交CE于点H，连接DF，HF．证明△ADM≌△EHM（ASA），得到AD=EH，DM=HM，再证明△CDF≌△EHF（SAS），得到DF=HF，∠CFD=∠EFH，进而得到△DFH是等腰直角三角形，则可得证．（3）DM=FM，DM⊥FM，证明略．提示：过点E作EH∥AD，交DM的延长线于点H，连接DF，HF．3．（1）AF=DF，AF⊥DF，证明略．提示：延长DF，交AC于点H．证明△DEF≌△HCF，得到DE=HC，DF=HF，进而得到△ADH是等腰直角三角形，所以AF=DF，AF⊥DF．（2）（1）中AF，DF之间的数量关系和位置关系不发生变化，证明略．提示：过点C作CH∥DE，交DF的延长线于点H，连接AD，AH．。

类比探究（讲义）➢ 知识点睛1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主——“条件类似、图形结构类似、问法类似”．2. 类比探究问题的处理思路（1）根据题干条件，结合分支条件先解决第一问； （2）整体类比上一问，迁移解决下一问．①类比是解决类比探究问题的第一原则，如类比字母、类比辅助线、类比思路；②对比前后条件变化，寻找并利用不变特征，考虑相关几何结构解决问题．类比探究问题中常见几何结构举例旋转结构（手拉手模型）：等线段共端点，考虑旋转，借助全等整合条件．EDC B AEDC B A如图，△ABC 和△ADE 均为等边三角形，则出现了AB =AC ，AD =AE 等线段共端点的结构．连接BD ，CE ，可以证明△ABD ≌△ACE ，△ACE 可看作是由△ABD 绕点A 逆时针旋转60°得到的．➢ 精讲精练1. 如图，在△ABC ，△CDE 中，∠ACB =∠ECD =90°，CA =CB ，CD =CE ，点D在AB 边上．若AD =5，BD =12，则AE =______，DE =_______．EDCA2.如图，在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E在同一条直线上，连接BD，BE．以下五个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=ED2+EC2；⑤BE2=2(AD2+AB2)，其中正确结论的个数是（）A．2 B．3 C．4 D．5A BD E3.如图，在△ABC中，∠BAC=90°，AB=AC，点D是BC上一动点，连接AD，过点A作AE⊥AD，并且始终保持AE=AD，连接CE，AF平分∠DAE交BC 于F．（1）求证：△ABD≌△ACE；（2）若BD=3，CF=4，则DF=_________．EFDBA4.（1）如图1，已知△ABC，以AB，AC为边分别向△ABC外作等边△ABD和等边△ACE，连接BE，CD，求证：BE=CD．（2）如图2，已知△ABC，以AB，AC为边分别向外作正方形ABFD和正方形ACGE，连接BE，CD，猜想BE与CD有什么数量关系？请说明理由．（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，则BE的长为___________．图1DBACE图2CBEADGF图35. 已知△ABC 和△CDE 均为等腰直角三角形，∠ACB =∠DCE =90°，点D 是等腰直角三角形ABC 斜边AB 所在直线上一点（不与点B 重合）．（1）如图1，当点D 在线段AB 上时，直接写出DA 2，DB 2，DE 2三者之间的数量关系：_______________．（2）如图2，当点D 在线段AB 的延长线上时，（1）中的结论仍然成立，请你利用图2给出证明过程． （3）若点D 满足14AD AB ，直接写出DEDB的值：___________．图1EDCB A图2ECAABC备用图6. 在Rt △ABC 中，∠BAC =90°，AB =AC ，在BC 的同侧作任意Rt △DBC ，∠BDC =90°．（1）若CD =2BD ，M 是CD 中点（如图1）， 求证：△ADB ≌△AMC ．（2）若CD <BD （如图2），在BD 边上是否存在一点N ，使得△ADN 是以DN 为斜边的等腰直角三角形？若存在，请在图2中确定点N 的位置，并加以证明；若不存在，请说明理由．小明在解决此题时，是在BD 上截取BN =CD ，连接AN ．你知道小明是怎么解决的吗？请写出过程．（3）当CD =1，BD =4时，则AD 的长为__________．MOD C BA图1ODBA图27.在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．（1）如图1，点E，F分别在AB，AC上，且∠EDF=90°，求证：BE=AF．（2）如图2，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB AN+=．小聪在解决此题时，过点M作AM的垂线，交AB的延长线于点P．你知道小聪是怎么解决的吗？请写出过程．AEB D FC图1ANDB CM图2【参考答案】➢精讲精练1.12，132. C3.（1）略；（2）5，证明略；（3）4.（1）略；（2）BE CD5.（1）222DA DB DE；（2）成立，证明略；（3+=6.（1）略；（2）略；（3）27.（1）略；（2）略。

类比探究综合测试（通用版）试卷简介:测试学生在处理类比探究问题过程中，有没有类比照搬的意识，能否根据题干或者问与问之间的联系，照搬辅助线，照搬思路来解决问题，同时考查学生对于类比探究中中点结构、旋转结构、平行结构这三种特殊结构的处理思路。

一、单选题(共6道，每道16分)1.如图1，△ABC和△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，点D在AB边上．连接EC，取EC的中点F，连接AF，DF．为了证明AF⊥DF，AF=DF，我们只需要延长DF交线段AC于点G，说明AF是等腰直角三角形ADG的中线即可．现将△BDE旋转至如图2所示的位置，使点E在AB的延长线上，点D在CB的延长线上，其他条件不变，类比上面的做法，为了证明AF⊥DF，AF=DF，我们需要作的辅助线是( )A.连接ADB.过点C作CG⊥DF，交DF的延长线于点GC.延长DF交AC的延长于点G，连接ADD.延长DF到G，使DF=FG，连接CG，AD，AG答案：D解题思路：在图1中，给出的辅助线达到的一个效果就是保证F是等腰直角三角形ADG斜边的中点，满足DF=FG．若在图2中达到同样的效果，需要延长DF到G，使DF=FG，这样再连接AD，AG之后才能保证F是等腰直角三角形ADG斜边的中点．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）在试题1图2的证明中，说明△ADG是等腰直角三角形之前，证明AD=AG 需要直接使用到某对三角形全等，则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案：D解题思路：要证明AD=AG，我们需要证明△ABD≌△ACG．根据上一题的分析，如图，延长DF到G，使DF=FG，连接CG，AD，AG，容易证明△DEF≌△GCF，∴CG=ED=BD，∠DEF=∠GCF，∴DE∥CG，∴∠GCD=∠BDE=90°，∴∠GCA=∠DBA=135°．又∵AC=AB，∴△ABD≌△ACG（SAS）．（为了证明AF⊥DF，AF=DF，接下来需要根据得出的条件，说明∠DAG=90°，进而说明AF是等腰直角三角形ADG斜边上的中线）试题难度：三颗星知识点：中考数学几何中的类比探究3.如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF．利用旋转的思想很容易证明DE+BF=EF；如图2，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且．则DE，BF，EF之间的数量关系为( )A. B.C.DE+2BF=EFD.DE+BF=EF答案：D解题思路：在图1中，旋转思想考虑了两个方面，一个是AB=AD，能够实现旋转，一个是，能够将角度放在一起，所以图1中的证明是将△DAE旋转，使得AD 与AB重合，这是一种思想，作辅助线的时候是延长CB到点G，使得BG=DE，最后证明GF=EF．图2中有同样的两个结构：AB=AD，，所以照搬分析图1的思路来研究数量关系．如图，延长CB到点G，使得BG=DE，连接AG．易证△ADE≌△ABG，∴AE=AG，BG=DE，∠DAE=∠BAG，∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF．∵，∴∠GAF=∠EAF．又∵AF=AF，∴△GAF≌△EAF，∴GF=EF，∴EF=GB+BF=DE+BF，即DE，BF，EF满足的数量关系是DE+BF=EF．试题难度：三颗星知识点：类比探究问题4.（上接第3题）如图3，在四边形ABCD中，AB=AD，E，F分别为DC，BC边上的点，且满足，当∠ABC与∠ADC满足( )时，可使得DE+BF=EF．A.∠ABC=∠ADCB.∠ABC+∠ADC=180°C.∠ABC=2∠ADC-180°D.∠ABC+2∠ADC=270°答案：B解题思路：试题3中图1和图2的证明，都是利用旋转的思想来证明DE+BF=EF，从作辅助线开始到结束，整个分析有以下几点：延长CB到点G，使得BG=DE，证明△ABG≌△ADE（SAS），导出∠GAF=∠EAF，进而证明△GAF≌△EAF（SAS），之后导出线段关系．若在图3中用此方法证明，首先延长CB到点G，使得BG=DE，要证明△ABG和△ADE全等，需要保证∠ABG=∠ADE，也就是需要∠ABC+∠ADC=180°，所以需要添加的条件是∠ABC+∠ADC=180°．添加条件之后的证明如下：如图，延长CB到点G，使得BG=DE，连接AG．∵∠ABC+∠ADC=180°，∠ABC+∠ABG=180°，∴∠ABG=∠ADE．又∵AB=AD，BG=DE，∴△ADE≌△ABG，∴AE=AG，BG=DE，∠DAE=∠BAG，∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF．∵，∴∠GAF=∠EAF．又∵AF=AF，∴GF=EF，∴EF=GB+BF=DE+BF．试题难度：三颗星知识点：类比探究问题5.如图，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．若BD=2CD，CF=mAF，则的值是( )A. B.C. D.答案：B解题思路：如图，过点D作DG∥AC，交AB于点G．设CD=a，BD=2a，AF=b，CF=mb．∵△BDG∽△BCA，∴∴，BG=2AG．设AG=c，BG=2c，∴，即∴∴试题难度：三颗星知识点：中考数学几何中的类比探究6.如图，D是△ABC的边BC上一点，过点D的一条直线交AC的延长线于点F，交AB于点E．若BD=aCD，CF=bAF，则的值是( )A. B.C. D.答案：D解题思路：如图，过点D作DG∥AC，交AB于点G．设CD=m，BD=am，AF=n，CF=bn．∵△BDG∽△BCA，∴∴，BG=aAG．设AG=c，BG=ac，∵△EAF∽△EGD，∴，即∴∴．试题难度：三颗星知识点：中考数学几何中的类比探究。

1.A题干是省会城市与所属省份关系，选项中符合条件的是A。

2.A题干是种属关系，锅是种灶具，铜铁是种金属，故答案选A。

3.C题干是作家与其作品的关系，C符合要求。

ABD是作家作品中的人物与作家的关系，与题干不符。

4.B题干是同物异名之间的关系，B符合要求。

AD不具有此性，C是种属关系。

5.D题干中的词成功与失败相对，选项中简单与复杂相对，故答案选D。

6.D题干香蕉是种水果，选项中桌子是种家具，考查的是种属关系，正确答案是D。

7.D 题干是正式称谓与别称的关系，答案选D，A与题干要求相反，B不具有可比性。

8.C题干是文学作品与作品中人物的关系，A与题干要求相反，B是作者与作品关系，D是作品与作者关系，答案选C。

9.A本题考查种属关系，B是部分与整体关系，CD是属种关系，但与题干要求相反。

10. D赫拉克勒斯是古希腊神话中的英雄，阿瑞斯是古希腊神话中的战神，李舜臣是韩鲜民族英雄，李尔王是莎士比亚戏剧中的角色，猪八戒是中国神话中的神，所以应选D。

11. D英国、日本、葡萄牙、西班牙的共同特点是都是君主立宪制国家，都有国王或天皇。

所以选D。

12. A勤奋与成功，生病与住院其中包含直接的因果关系，故答案选A，B 项中革命能引发战争，却不是战争爆发的直接根源，C项鱼网用以捕鱼，D项成绩产生于考试。

13. C题干中稻谷与大米，C项中棉花与棉籽属整体与部分关系，答案选C，ABD与题干内容没有类比性。

14. B本题题干所给两个词语之间是工具和作用的关系。

15. B题干所给出的两个词语之间属于事物和事物的出处关系。

16. D题干所给出的两个词语之间属于事物和事物的出处关系。

17. A本题所给出的两个词语之间属于原因与结果的关系。

18. D本题所给出的两个词语之间属于工具和作用的关系。

19. C本题题干所给出的两个词语之间属于物体与其运动空间的关系。

20. B本题所给出的两个词语之间属于特定环境与专门人员的关系。

21. D题干给出的人物是截然相反的，只有D项符合此条件。

类比探究（讲义）➢知识点睛1.类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主——“条件类似、图形结构类似、问法类似”．2.类比探究问题的处理思路（1）根据题干条件，结合分支条件先解决第一问；（2）整体类比第一问，迁移解决下一问．①类比是解决类比探究问题的第一原则，如类比字母、类比辅助线、类比思路；②对比前后条件变化，寻找并利用不变特征，考虑相关几何结构解决问题．3.类比探究问题中的常见特征举例手拉手模型：两个共顶点且顶角相等的等腰三角形构成，在相对位置变化的过程中，始终存在一对全等三角形．EDAB C条件：AB=AC，AD=AE，∠BAC=∠DAE结论：△ABD≌△ACE➢精讲精练1.如图，在△ABC，△CDE中，∠ACB=∠ECD=90°，CA=CB，CD=CE，点D在AB边上．若AD=5，BD=12，则AE=______，DE=_______．ADEB2. 如图，点D 为等边三角形ABC 内一点，AD =4，BD =3，CD =5．以BD 为一边作等边三角形BDE ，连接CE ． （1）判断△DEC 的形状，并说明理由； （2）求∠ADB 的度数．EDCBA3. 如图，在△ABC ，△ADE 中，∠BAC =∠DAE =90°，AB =AC ，AD =AE ，点C ，D ，E 在同一条直线上，连接BD ，BE ．以下五个结论：①BD =CE ；②BD ⊥CE ；③∠ACE +∠DBC =45°；④BE 2=ED 2+EC 2；⑤BE 2=2(AD 2+AB 2)，其中正确结论的个数是（ ） A ．2B ．3C ．4D ．5ABC DE4. 如图，在△ABC 中，∠BAC =90°，AB =AC ，点D 是BC 上一动点，连接AD ，过点A 作AE ⊥AD ，并且始终保持AE =AD ，连接CE ，AF 平分∠DAE 交BC 于F ． （1）求证：△ABD ≌△ACE ；（2）若BD =3，CF =4，则DF =_________．ECFDBA5. 已知△ABC 和△CDE 均为等腰直角三角形，∠ACB =∠DCE =90°，点D 是等腰直角三角形ABC 斜边AB 所在直线上一点（不与点B 重合）．（1）如图1，当点D在线段AB上时，直接写出DA2，DB2，DE2三者之间的数量关系：_______________．（2）如图2，当点D在线段AB的延长线上时，（1）中的结论仍然成立，请你利用图2给出证明过程．（3）若点D满足14ADAB，直接写出DEDB的值：_________．图1ECBA图2ECAA BC备用图6. 在Rt △ABC 中，∠BAC =90°，AB =AC ，在BC 的同侧作任意Rt △DBC ，∠BDC =90°．（1）若CD =2BD ，M 是CD 中点（如图1）， 求证：△ADB ≌△AMC ．（2）若CD ＜BD （如图2），在BD 边上是否存在一点N ，使得△ADN 是以DN 为斜边的等腰直角三角形？若存在，请在图2中确定点N 的位置，并加以证明；若不存在，请说明理由．（提示：在BD 上截取BN =CD ，连接AN ） （3）当CD =1，BD =4时，则AD 的长为__________．MOD CBA图1OD BA图27.在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．（1）如图1，点E，F分别在AB，AC上，且∠EDF=90°，求证：BE=AF．（2）如图2，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB+ANAM．（提示：过点M作AM的垂线，交AB的延长线于点P）AEB D FC图1ADNMB C图2【参考答案】➢精讲精练1.12，132.（1）△DEC是直角三角形，理由略；（2）∠ADB=150°3. C4.（1）略；（2）55.（1）222DA DB DE；（2）略；（3+=6.（1）略；（2）存在，证明略；（3）27.（1）略；（2）略。

中招考试几何类比探究题集锦（附参考答案）参考答案与试题解析一．解答题（共11小题）1．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ABD≌△ACF；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，请直接写出DE2，BD2，CE2三者之间的等量关系．【解答】解：（1）∵点D关于直线AE的对称点为F，∴EF=DE，AF=AD，∠DAE=∠EAF=α∴∠CAE+∠CAF=α∵∠BAC=2∠DAE=2α．∴∠BAD+∠CAE=∠BAC﹣∠DAE=α，∴∠BAD=∠CAF，在△ABD和△ACF中，第1页（共33页）第2页（共33页）∴△ABD ≌△ACF （SAS ），（2）由（1）知，△ABD ≌△ACF （SAS ），∴CF=BD ，∠ACF=∠B ，∵AB=AC ，∠BAC=2α，α=45°，∴△ABC 是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB +∠ACF=45°+45°=90°，在Rt △CEF 中，由勾股定理得，EF 2=CF 2+CE 2，∴DE 2=BD 2+CE 2，（3）DE 2=BD 2+CE 2；理由：如图，∵∠BAC=2∠DAE=2α．∴∠DAE=α，∵点D 关于直线AE 的对称点为F ，∴EF=DE ，AF=AD ，∠DAE=∠EAF=α∴∠CAF=∠EAF +∠CAE=α+∠CAE∴∠BAD=∠BAC ﹣∠DAC=2α﹣∠DAC=2α﹣（∠DAE ﹣∠CAE ）=2α﹣（α﹣∠CAE）=α+∠CAE∴∠BAD=∠CAF，在△ABD和△ACF中，∴△ABD≌△ACF（SAS），∴CF=BD，∠ACF=∠B，∵AB=AC，∠BAC=2α，α=45°，∴△ABC是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB+∠ACF=45°+45°=90°，在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，∴DE2=BD2+CE2，2．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系（直接写出结果即可）．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第（1）题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF 均为等第3页（共33页）边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．【解答】解：（1）DE=BD+CE．理由如下：如图1，∵BD⊥l，CE⊥l，∴∠BDA=∠AEC=90°又∵∠BAC=90°，∴∠BAD+∠CAE=90°，∠BAD+∠ABD=90°，∴∠CAE=∠ABD在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD；（2）如图2，∵∠BDA=∠AEC=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α，第4页（共33页）∴∠CAE=∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE；（3）DF=EF．理由如下：由（2）知，△ADB≌△CAE，BD=EA，∠DBA=∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°，∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE，∵BF=AF在△DBF和△EAF中，，∴△DBF≌△EAF（SAS），∴DF=EF，∠BFD=∠AFE，第5页（共33页）∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形．∴DF=EF．3．（1）问题发现如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：①∠ACE的度数为60°；②线段AC、CD、CE之间的数量关系为AC=CD+CE．（2）拓展探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC 上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．（3）解决问题如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．第6页（共33页）【解答】解：（1）①∵△ABC和△ADE均为等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=∠B=60°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE=∠B=60°，故答案为：60°；②线段AC、CD、CE之间的数量关系为：AC=CD+CE；理由是：由①得：△BAD≌△CAE，∴BD=CE，∵AC=BC=BD+CD，∴AC=CD+CE；故答案为：AC=CD+CE；（2）∠ACE=45°，AC=CD+CE，理由是：如图2，∵△ABC和△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，∴AB=AC，AD=AE，∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，第7页（共33页）∴△ABD≌△ACE，∴BD=CE，∠ACE=∠B=45°，∵BC=CD+BD，∴BC=CD+CE，∵在等腰直角三角形ABC中，BC=AC，∴AC=CD+CE；（3）如图3，过A作AC的垂线，交CB的延长线于点F，∵∠BAD=∠BCD=90°，AB=AD=2，CD=1，∴BD=2，BC=，∵∠BAD=∠BCD=90°，∴∠BAD+∠BCD=180°，∴A、B、C、D四点共圆，∴∠ADB=∠ACB=45°，∴△ACF是等腰直角三角形，由（2）得：AC=BC+CD，∴AC===．第8页（共33页）4．【探究发现】如图1，△ABC是等边三角形，∠AEF=60°，EF交等边三角形外角平分线CF所在的直线于点F，当点E是BC的中点时，有AE=EF成立；【数学思考】某数学兴趣小组在探究AE、EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（B，C除外）任意一点时（其它条件不变），结论AE=EF仍然成立．假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在备用图1中画出图形，并证明AE=EF．【拓展应用】当点E在线段BC的延长线上时，若CE=BC，在备用图2中画出图形，并运用上述结论求出S△ABC ：S△AEF的值．【解答】证明：第一种情况：点E是线段BC上的任意一点，可作三种辅助线：方法一：如图1，在AB上截取AG，使AG=EC，连接EG，第9页（共33页）∵△ABC是等边三角形，∴AB=BC，∠B=∠ACB=60°．∵AG=EC，∴BG=BE，∴△BEG是等边三角形，∠BGE=60°，∴∠AGE=120°．∵FC是外角的平分线，∠ECF=120°=∠AGE．∵∠AEC是△ABE的外角，∴∠AEC=∠B+∠GAE=60°+∠GAE．∵∠AEC=∠AEF+∠FEC=60°+∠FEC，∴∠GAE=∠FEC．在△AGE和△ECF中，∴△AGE≌△ECF（ASA），∴AE=EF；方法二：在CA上截取CG=CE，连结GE，证明类似方法一；方法三：延长FC到G，使CG=CE，连结EG，易证△CEG是等边三角形，第10页（共33页）∴CE=EG，∠G=∠ACB=60°，∠CEG=∠AEF=60°，∴∠CEG+∠CEF=∠AEF+∠CEF，即∠GEF=∠AEC，∴△GEF≌△CEA，∴AE=EF．第二种情况：点E是线段BC延长线上的任意一点如图2，可作三种辅助线：①在CF上截取CG=CE，连接GE②延长AC到G，使CG=CE，连结EG；③或延长BA到G，使BG=BE，连结EG．第②种添加辅助线的方法证明如下：证明：延长AC到G，使CG=CE，连结EG，易证△CEG为等边三角形，∴∠G=∠ECF=60°，EG=CE，又∠AEG=∠CEG+∠AEC=60°+∠AEC，∠CEF=∠AEF+∠AEC=60°+∠AEC，第11页（共33页）∴∠AEG=∠CEF，∴△AEG≌△FEC，∴AE=EF．第三种情况：点E是线段BC反向延长线上的任意一点如图3，可作三种辅助线：①延长AB到G，使BG=BE，连结EG；②延长CF到G，使CG=CE，连结EG；③在CE上截取CG=CF，连结GF现就第①种添加辅助线的方法证明如下：证明：延长AB到G，使BG=BE，连结EG，易证△BEG为等边三角形，∴∠G=∠ECF=60°，第12页（共33页）∵∠AEB+∠BAE=∠ABC=60°，∠AEB+∠CEF=∠AEF=60°，∴∠BAE=∠CEF，∵AB=BC，BG=BE，∴AB+BG=BC+BE，即AG=CE，∴△AEG≌△EFC，∴AE=EF．拓展应用：如图4：作CH⊥AE于H点，∴∠AHC=90°．由数学思考得AE=EF，又∵∠AEF=60°，∴△AEF是等边三角形，∴△ABC∽△AEF．第13页（共33页）∵CE=BC=AC，△ABC是等边三角形，∴∠CAH=30°，AH=EH．∴CH=AC，AH=AC，AE=AC，∴．∴==．5．问题情境：在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．（1）操作发现：当点O为AC中点时：①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系：AE2+CF2=EF2（无需证明）；②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的结论是否成立．若成立，请证明；若不成立，请说明理由；第14页（共33页）（2）类比延伸：当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若=，请直接写出=．【解答】解：（1）①猜想：AE2+CF2=EF2，连接OB，如图1，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB+∠BOF=∠FOC+∠BOF．∴∠EOB=∠FOC，在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；故答案为：AE2+CF2=EF2；第15页（共33页）②成立．证明：连结OB．如图2，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB=∠FOC．在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；（2）=，如图3，过点O作OM⊥AB于M，ON⊥BC于N．∵∠B=90°，第16页（共33页）∴∠MON=90°，∵∠EOF=90°，∴∠EOM=∠FON．∵∠EMO=∠FNO=90°，∴△OME∽△ONF，∴=，∵△AOM和△OCN为等腰直角三角形，∴△AOM∽△OCN，∴=，∵=，∴=，故答案为．第17页（共33页）第18页（共33页）6．阅读发现：（1）如图①，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，AB=BC=3，BD=BE=1，连结CD ，AE ．易证：△BCD ≌△BAE ．（不需要证明） 提出问题：（2）在（1）的条件下，当BD ∥AE 时，延长CD 交AE 于点F ，如图②，求AF 的长．解决问题：（3）如图③，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，连结CD ，AE ．当∠BAE=45°时，点E 到AB 的距离EF 的长为2，求线段CD的长为 ．【解答】（2）解：如图②中，AB与CF交于点O．由（1）可知：△BCD≌△BAE，∴∠OAF=∠OCB，CD=AE，∵∠AOF=∠COB，∴∠AFO=∠CBO=90°，∴CF⊥AE，∵BD∥AE，∴BD⊥CF，在RT△CDB中，∵∠CDB=90°，BC=3，BD=1，∴CD=AE==2，∵∠BDF=∠DFE=∠DBE=90°，∴四边形EFDB是矩形，∴EF=BD=1，∴AF=AE﹣EF=2﹣1．（3）解：在RT△ABC，RT△EBD中，∵∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，∴AB=BC，BE=BD，∴==，∵∠ABC=∠EBD=90°，∴∠ABE=∠DBC，∴△ABE∽△CBD，∴==，第19页（共33页）第20页（共33页）在RT △AEF 中，∵∠AFE=90°，∠EAF=45°，EF=2，∴AF=EF=2，AE=2，∴=，∴CD=．故答案为．7．如图1，两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现：如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，请猜想（1）中S1与S2的数量关系是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）拓展探究已知∠ABC=60°，BD平分∠ABC，BD=CD，BC=9，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请求相应的BF的长．【解答】解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC=CD，∵∠BAC=90°﹣∠B=90°﹣30°=60°，第21页（共33页）∴△ACD是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE，∴DE∥AC；故答案为：DE∥AC；②∵∠B=30°，∠C=90°，∴CD=AC=AB，∴BD=AD=AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2=×2×2=2；故答案为：S1=S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°﹣90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，，第22页（共33页）∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF1=S△BDE；过点D作DF2⊥BD，∵∠ABC=60°，F1D∥BE，∴∠F2F1D=∠ABC=60°，∵BF1=DF1，∠F1BD=∠ABC=30°，∠F2DB=90°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=×60°=30°，∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°，∠CDF2=360°﹣150°﹣60°=150°，∴∠CDF1=∠CDF2，第23页（共33页）∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=×60°=30°，又∵BD=4，∴BE=×6÷cos30°=3÷=2，∴BF1=2，BF2=BF1+F1F2=2+2=4，故BF的长为2或4．8．问题解决：如图（1），将正方形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN．当时，求的值．类比归纳：第24页（共33页）在图（1）中，若，则的值等于；若，则的值等于；若（n 为整数），则的值等于．（用含n的式子表示）联系拓广：如图（2），将矩形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN，设，则的值等于．（用含m，n的式子表示）【解答】解：（1）方法一：如图（1﹣1），连接BM，EM，BE．由题设，得四边形ABNM和四边形FENM关于直线MN对称．∴MN垂直平分BE，∴BM=EM，BN=EN．∵四边形ABCD是正方形，∴∠A=∠D=∠C=90°，设AB=BC=CD=DA=2．∵，∴CE=DE=1．第25页（共33页）设BN=x，则NE=x，NC=2﹣x．在Rt△CNE中，NE2=CN2+CE2．∴x2=（2﹣x）2+12，解得x=，即BN=．在Rt△ABM和在Rt△DEM中，AM2+AB2=BM2，DM2+DE2=EM2，∴AM2+AB2=DM2+DE2．设AM=y，则DM=2﹣y，∴y2+22=（2﹣y）2+12，解得y=，即AM=（6分）∴．方法二：同方法一，BN=．如图（1﹣2），过点N做NG∥CD，交AD于点G，连接BE．∵AD∥BC，∴四边形GDCN是平行四边形．∴NG=CD=BC．同理，四边形ABNG也是平行四边形．∴AG=BN=∵MN⊥BE，∴∠EBC+∠BNM=90度．∵NG⊥BC，∴∠MNG+∠BNM=90°，第26页（共33页）∴∠EBC=∠MNG．在△BCE与△NGM中，∴△BCE≌△NGM，EC=MG．∵AM=AG﹣MG，AM=﹣1=．∴．（2）如图1，当四边形ABCD为正方形时，连接BE，=，不妨令CD=CB=n，则CE=1，设BN=x，则EN=x，EN2=NC2+CE2，x2=（n﹣x）2+12，x=；作MH⊥BC于H，则MH=BC，又点B，E关于MN对称，则MN⊥BE，∠EBC+∠BNM=90°；而∠NMH+∠BNM=90°，故∠EBC=∠NMH，则△EBC≌△NMH，∴NH=EC=1，AM=BH=BN﹣NH=﹣1=则：==．故当=，则的值等于；若=，则的值等于；第27页（共33页）（3）若四边形ABCD为矩形，连接BE，=，不妨令CD=n，则CE=1；又==，则BC=mn，同样的方法可求得：BN=，BE⊥MN，易证得：△MHN∽△BCE．故=，=，HN=，故AM=BH=BN﹣HN=，故==．故答案为：；；；．第28页（共33页）第29页（共33页）9．阅读理解：如图1，在直角梯形ABCD 中，AB ∥CD ，∠B=90°，点P 在BC 边上，当∠APD=90°时，易证△ABP ∽△PCD ，从而得到BP•PC=AB•CD ，解答下列问题．（1）模型探究：如图2，在四边形ABCD 中，点P 在BC 边上，当∠B=∠C=∠APD 时，结论BP•PC=AB•CD 仍成立吗？试说明理由；（2）拓展应用：如图3，M 为AB 的中点，AE 与BD 交于点C ，∠DME=∠A=∠B=45°且DM 交AC 于F ，ME 交BC 于G ．AB=，AF=3，求FG 的长．【解答】解：（1）∵∠APC=∠APD +∠CPD ，∠APC=∠BAP +∠B （三角形外角定理），∠B=∠APD （已知），∴∠BAP=∠CPD，又∵∠B=∠C，∴△ABP∽△PCD∴=，∴BP•PC=AB•CD；（2）∵∠AFM=∠DME+∠E（三角形外角定理），∠DME=∠A（已知），∴∠AFM=∠A+∠E（等量代换），又∠BMG=∠A+∠E（三角形外角定理），∴∠AFM=∠BMG．∵∠A=∠B，∴△AMF∽△BGM．当∠A=∠B=45°时，∠ACB=180°﹣∠A﹣∠B=90°，即AC⊥BC且AC=BC．∵M为AB的中点，∴AM=BM=，AC=BC=4．又∵△AMF∽△BGM，∴，∴BG===，又∵，CF=4﹣3=1，∴．第30页（共33页）10．基本模型如下图，点B、P、C在同一直线上，若∠B=∠1=∠C=90°，则△ABP∽△PCD成立，（1）模型拓展如图1，点B、P、C在同一直线上，若∠B=∠1=∠C，则△ABP∽△PCD成立吗？为什么？（2）模型应用①如图2，在等腰梯形ABCD中，AD∥BC，AD=1，AB=2，BC=4，在BC上截取BP=AD，作∠APQ=∠B，PQ交CD于点Q，求CQ的长；②如图3，正方形ABCD的边长为1，点P是线段BC上的动点，作∠APQ=90°，PQ交CD于Q，当P在何处时，线段CQ最长？最长是多少？【解答】解：（1）成立，∵∠A=180°﹣（∠B+∠APB），第31页（共33页）∠CPD=180°﹣（∠1+∠APB），∠B=∠1，∴∠A=∠CPD，∵∠B=∠C，∴△ABP∽△PCD；（2）①∵四边形ABCD是等腰梯形，∴∠B=∠C，∵∠B=∠APQ，∴∠B=∠APQ=∠C，由（1）知，△ABP∽△PCD，∴=，∴=，∴CQ=；②设BP=x，CQ=y．∵∠B=∠APQ=90°，∴△ABP∽△PCQ，∴=，即=，∴y=﹣x2+x=﹣（x﹣）2+，第32页（共33页）∴当x=时，y=，最大即当P是BC的中点时，CQ最长，最长为．第33页（共33页）。

学生做题前请先回答以下问题问题1：类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有哪些？问题2：处理类比探究问题时，若属于常见结构，则________．问题3：处理类比探究问题时，若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．此时常见的处理思路是什么？以下是问题及答案，请对比参考:问题1：类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有哪些？答：类比探究中常见的不变结构有：①中点结构，常考虑平行夹中点，构造中位线等；②旋转结构，特征：等线段共点③平行结构，常考虑作平行，造相似④直角结构．常考虑斜直角放正问题2：处理类比探究问题时，若属于常见结构，则．答：调用结构类比解决．问题3：处理类比探究问题时，若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．此时常见的处理思路是什么？答：①根据题干条件，结合支干条件先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找不变特征．③结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证．类比探究专题（五）——探究应用一、单选题(共3道，每道33分)1.如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是_________；②设△BDC的面积为，△AEC的面积为，则与之间的数量关系是_______．( )A.DE=2AC；B.DE⊥AC；C.DE∥AC；D.DE∥AC；答案：C解题思路：试题难度：三颗星知识点：探究应用2.（上接第1题）（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，△BDC的面积与△AEC的面积之间的数量关系是( )A. B. C. D.答案：A解题思路：试题难度：三颗星知识点：探究应用3.（上接第1，2题）（3）拓展探究如图4，已知∠ABC=60°，D是角平分线上一点，BD=CD=4，DE∥AB，交BC于点E．若在射线BA上存在点F，使，则BF的长为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：探究应用。

学生做题前请先回答以下问题问题1：类比探究问题的处理思路是什么？以下是问题及答案，请对比参考:问题1：类比探究问题的处理思路是什么？答：类比探究问题的处理思路为：（1）类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有：中点结构、直角结构、旋转结构、平行结构．（2）若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．①根据题干条件，结合支干条件先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找不变特征．③结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证．若属于类比探究常见的结构类型，调用结构类比解决．类比探究专题（一）——平行结构一、单选题(共6道，每道16分)1.如图1，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．（1）若BD=CD，CF=2AF，则的值为( )A.2B.C. D.答案：B解题思路：试题难度：三颗星知识点：平行结构2.（上接第1题）（2）如图2，若BD=CD，CF=mAF，则的值为( ) （用含m的代数式表示）A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构3.（上接第1，2题）（3）如图3，将原题改为“过点D的一条直线交AC的延长线于点F，交AB于点E”，若BD=nCD，CF=mAF，则的值为( )（用含m，n的代数式表示）A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构4.已知AD是△ABC的中线，将BC边所在直线绕点D顺时针旋转角，交AB边于点M，交射线AC于点N，设．（1）如图1，满足的函数关系式为( ) A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构5.（上接第4题）（2）如图2，当G是AD上任意一点时（点G不与点A重合），过点G的直线交AB边于点，交AC边于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构6.（上接第4，5题）（3）如图3，当G是AD上任意一点时（点G不与点A重合），过点G 的直线交AB边于点，交AC的延长线于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构。

类比考试题及答案一、单项选择题1. 类比推理中，如果“苹果：水果”是正确的类比，那么“铅笔：文具”也是正确的类比。

这是因为：A. 苹果和铅笔都是物品B. 水果和文具都是集合名词C. 苹果是水果的一种，铅笔是文具的一种D. 苹果和铅笔都是可以吃的答案：C2. 在类比推理中，“医生：病人”与“教师：学生”之间的相似性在于：A. 医生和教师都是专业人士B. 病人和学生都是需要帮助的人C. 医生和教师都是服务提供者，病人和学生都是服务接受者D. 医生和教师都需要穿制服，病人和学生都需要穿校服答案：C3. “太阳：地球”与“月亮：地球”之间的类比关系是：A. 太阳和月亮都是地球的卫星B. 太阳和月亮都是地球的光源C. 太阳是地球的恒星，月亮是地球的卫星D. 太阳和月亮都是地球的行星答案：C4. “猫：猫科动物”与“狗：犬科动物”之间的类比关系是：A. 猫和狗都是宠物B. 猫科动物和犬科动物都是哺乳动物C. 猫是猫科动物的一种，狗是犬科动物的一种D. 猫和狗都是食肉动物答案：C5. “汽车：轮胎”与“自行车：轮子”之间的类比关系是：A. 汽车和自行车都是交通工具B. 轮胎和轮子都是圆形的C. 汽车需要轮胎，自行车需要轮子D. 汽车和自行车都是由金属制成的答案：C二、多项选择题6. 下列哪些选项中的类比是正确的？A. “书：知识”与“食物：营养”B. “笔：书写”与“刀：切割”C. “医生：病人”与“教师：学生”D. “太阳：白天”与“月亮：夜晚”答案：A, B, C7. 在类比推理中，以下哪些选项正确地表达了“父亲：儿子”与“祖父：孙子”之间的关系？A. 父亲和祖父都是长辈B. 儿子和孙子都是晚辈C. 父亲和儿子之间有直接的血缘关系，祖父和孙子之间也有直接的血缘关系D. 父亲和祖父都是男性，儿子和孙子都是男性答案：A, B, D8. “图书馆：书籍”与以下哪些选项之间的类比关系是正确的？A. “超市：食品”B. “博物馆：艺术品”C. “学校：学生”D. “医院：医生”答案：A, B9. “春天：播种”与以下哪些选项之间的类比关系是正确的？A. “夏天：收获”B. “秋天：落叶”C. “冬天：滑雪”D. “春天：开花”10. “钥匙：锁”与以下哪些选项之间的类比关系是正确的？A. “密码：账户”B. “遥控器：电视”C. “车票：火车”D. “笔：纸”答案：A, B三、填空题11. 在类比推理中，“鸟：飞行”与“鱼：____”之间的类比关系是正确的。

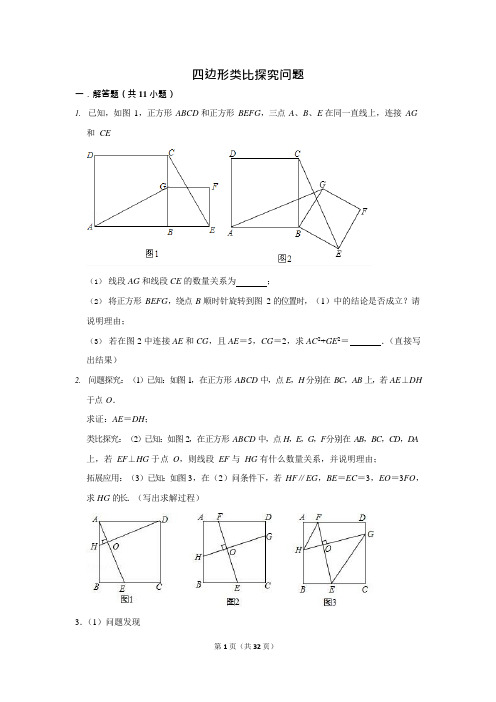
四边形类比探究问题一．解答题（共11 小题）1.已知，如图1，正方形ABCD 和正方形BEFG，三点A、B、E 在同一直线上，连接AG和CE（1）线段AG 和线段CE 的数量关系为；（2）将正方形BEFG，绕点B 顺时针旋转到图2 的位置时，（1）中的结论是否成立？请说明理由；（3）若在图2 中连接AE 和CG，且AE＝5，CG＝2，求AC2+GE2＝．（直接写出结果）2.问题探究：（1）已知：如图1，在正方形ABCD 中，点E，H 分别在BC，AB 上，若AE⊥DH于点O．求证：AE＝DH；类比探究：（2）已知：如图2，在正方形ABCD 中，点H，E，G，F分别在AB，BC，CD，DA 上，若EF⊥HG 于点O，则线段EF 与HG 有什么数量关系，并说明理由；拓展应用：（3）已知：如图3，在（2）问条件下，若HF∥EG，BE＝EC＝3，EO＝3FO，求HG 的长．（写出求解过程）3．（1）问题发现如图1，△ACB 和△DCE 均为等边三角形，点A、D、E 在同一条直线上，连接BE．填空：①∠AEB 的度数为；②线段AD、BE 之间的数量关系为．（2）拓展研究如图2，△ACB 和△DCE 均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E 在同一条直线上，CM 为△DCE 中DE 边上的高，连接BE，请判断∠AEB 的度数及线段CM、AE、BE 之间的数量关系，并说明理由．（3）解决问题如图3，在正方形ABCD 中，CD＝2，若点P 满足PD＝2，且∠BPD＝90°，请直接写出点A 到BP 的距离．4.如图1，点C 在线段AB 上，分别以AC、BC 为边在线段AB 的同侧作正方形ACDE 和正方形BCMN，连结AM、BD．（1）AM 与BD 的关系是：．（2）如果将正方形BCMN 绕点C 顺时针旋转锐角α，其它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．（3）在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求AB2+DM2的值．5.如图①，在▱ABCD 中，点E、F 分别在AD、BC 上，且AE＝CF，连接AF、BE 交于点G，连接CE、DF 交于点H．（1）求证四边形EGFH 为平行四边形．（2）提出问题：在AD、BC 边上是否存在点E、F，使得四边形EGFH 为矩形？小明从特殊到一般探究了问题．【特殊化】如图②，若∠ABC＝90°，AB＝2，BC＝6．在AD、BC 边上是否存在点E、F，使得四边形EGFH 为矩形？若存在，求出此时AE 的长度；若不存在，说明理由．【一般化】如图③，若∠ABC＝60°，AB＝m，BC＝n．在AD、BC 边上是否存在点E、F 使得四边形EGFH 为矩形？根据点E、F 存在（或不存在）的可能情况，写出对应的m、n 满足的条件，存在时直接写出AE 的长度．（用含m、n 的代数式表示）6.问题探究：（1）已知：如图1，在正方形ABCD 中，点E，H 分别在BC，AB 上，若AE⊥DH 于点O，求证：AE＝DH；类比探究：（2）如图2，在正方形ABCD 中，点H，E，G，F分别在AB，BC，CD，DA 上，若EF⊥HG 于点O，探究线段EF 与HG 的数量关系，并说明理由．拓展应用：（3）已知，如图3，在（2）的条件下，若BC＝4，点E 为BC 的中点，DF＝3AF，连结FH，HE，EG，GF．求四边形HEGF 的面积．7.已知AC，EC 分别是四边形ABCD 和EFCG 的对角线，直线AE 与直线BF 交于点H（1）观察猜想如图1，当四边形ABCD 和EFCG 均为正方形时，线段AE 和BF 的数量关系是；∠AHB＝．（2）探究证明如图2，当四边形ABCD 和FFCG 均为矩形，且∠ACB＝∠ECF＝30°时，（1）中的结论是否仍然成立，并说明理由．（3）拓展延伸在（2）的条件下，若BC＝9，FC＝6，将矩形EFCG 绕点C 旋转，在整个旋转过程中，当A、E、F 三点共线时，请直接写出点B 到直线AE 的距离．8.数学学习小组“文化年”最近正在进行几何图形组合问题的研究，认真研读以下三个片段，并回答问题．【片断一】小文说：将一块足够大的等腰直角三角板置于一个正方形中，直角顶点与对角线交点重合，在转动三角板的过程中我发现某些线段之间存在确定的数量关系．如图（1），若三角板两条直角边的外沿分别交正方形的边AB，BC 于点M，N，则①OM+ON ＝MB+NB；②AM+CN＝OD．请你判断他的猜想是否正确？若正确请说明理由；若不正确请说明你认为正确的猜想并证明．【片断】小化说：将角板中个45°角的顶点和正方形的一个顶点重合放置，使得这个角的两条边与正方形的一组邻边有交点．如图（2），若以A 为顶点的45°角的两边分别交正方形的边BC、CD 于点M，N．交对角线BD 于点E、F，我发现：BE2+DE2＝2AE2，只要准确旋转图（2）中的一个三角形就能证明这个结论．请你在图2 中画出图形并写出小化所说的具体的旋转方式：．【片断三】小年说：将三角板的一个45°角放置在正方形的外部，同时角的两边恰好经过正方形两个相邻的顶点．如图（3），设顶点为E 的45°角位于正方形的边AD 上方，这个角的两边分别经过点B、C，连接EA，ED，那么线段EB，EC，ED 也存在确定的数量关系：（EB+ED）2＝2EC2，请你证明这个结论．9．（1）[方法回顾]证明：三角形中位线定理．已知：如图1，在△ABC 中，D、E 分别是AB、AC 的中点．求证：DE∥BC，DE＝BC．证明：如图1，延长DE 到点F，使得EF＝DE，连接CF；请继续完成证明过程：（2）[问题解决]如图2，在矩形ABCD 中，E 为AD 的中点，G、F 分别为AB、CD 边上的点，若AG＝3，DF＝7，∠GEF＝90°，求GF 的长．（3）[思维拓展]如图3，在梯形ABCD 中，AD∥BC，∠A＝90°，∠D＝120°，E 为AD 的中点，G、F 分别为AB、CD 边上的点，若AG＝2，DF＝4，∠GEF＝90°，求GF 的长．10.如图1，图2，△ABC 中，BF，CE 分别为AC，AB 边上的中线，BF⊥CE 于点P．（1）如图1，当BC＝6，∠PCB＝45°时，PE＝，AB＝；（2）如图2，猜想AB2、AC2、BC2 三者之间的数量关系，并给予证明；（3）如图3，▱ABCD 中，点M，N 分别在AD，BC 上，AD＝3AM，BC＝3BN，连接AN，BM，CM，AN 与BM 交于点G，若BM⊥CM 于点M，AB＝4，AD＝3，求AN 的长．11.【探索发现】如图1，△ABC 是等边三角形，点D 为BC 边上一个动点，将△ACD 绕点A 逆时针旋转60°得到△AEF，连接CE．小明在探索这个问题时发现四边形ABCE 是菱形．小明是这样想的：（1）请参考小明的思路写出证明过程；（2）直接写出线段CD，CF，AC 之间的数量关系：；【理解运用】如图2，在△ABC 中，AD⊥BC 于点D．将△ABD 绕点A 逆时针旋转90°得到△AEF，延长FE 与BC 交于点G．（3）判断四边形ADGF 的形状，并说明理由；【拓展迁移】（4）在（3）的前提下，如图3，将△AFE 沿AE 折叠得到△AME，连接MB，若AD＝6，BD＝2，求MB 的长．四边形类比探究问题参考答案与试题解析一．解答题（共11 小题）1.【分析】（1）由正方形的性质得出AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，由SAS证明△ABG≌△CBE，得出对应边相等AG＝CE；（2）由正方形的性质得出AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，证出∠ABG＝∠CBE，由SAS 证明△ABG≌△CBE，得出AG＝CE；（3）连接AC、EG，设AG、CE 交点为H，由由角的互余关系得出∠2+∠BCE＝90°，得出∠ AHC＝90°，得出AG⊥CE；再由勾股定理求出AC2+EG2＝C G2+AE2，求出AC2+EG2，然后由正方形的面积等于对角线平方的一半求解即可．【解答】解：（1）如图1 所示：延长AG 交CE 于H，∵四边形ABCD 和四边形BEFG 是正方形，∴AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，在△ABG 和△CBE 中，∵，∴△ABG≌△CBE（SAS），∴AG＝CE，故答案为：AG＝CE；（2）AG＝CE，且AG⊥CE 仍然成立．理由如下：如图2 所示：∵四边形ABCD 和四边形BEFG 是正方形，∴AB＝CB，BG＝BE，∠ABC＝∠EBG＝90°，∵∠ABG＝∠ABC+∠CBG，∠CBE＝∠EBG+∠CBG，∴∠ABG＝∠CBE，在△ABG 和△CBE 中，∵，∴△ABG≌△CBE（SAS），∴AG＝CE；（3）如图2 所示：连接AC、EG，∵△ABG≌△CBE，∴∠BAG＝∠BCE，∵∠1+∠BAG＝90°，∴∠1+∠BCE＝90°，∵∠1＝∠2，∴∠2+∠BCE＝90°，∴∠AHC＝90°，∴AG⊥CE；在Rt△CGH 中，CG2＝CH2+GH2，在Rt△AEH 中，AE2＝AH2+EH2，∴CG2+AE2＝CH2+GH2+AH2+EH2＝（CH2+AH2）+（GH2+EH2）＝AC2+EG2，∵AE＝5，CG＝2，∴AC2+EG2＝22+52＝29．故答案为：29．【点评】本题是四边形的综合问题，主要考查了正方形的性质、全等三角形的判定与性质、勾股定理；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．2.【分析】（1）由正方形的性质得AB＝DA，∠ABE＝90°＝∠DAH．所以∠HAO+∠OAD＝90°，又知∠ADO+∠OAD＝90°，所以∠HAO＝∠ADO，于是△ABE≌△DAH，可得AE＝DH；（2）EF＝GH．将FE 平移到AM 处，则AM∥EF，AM＝EF，将GH 平移到DN 处，则DN∥ GH，DN＝GH．根据（1）的结论得AM＝DN，所以EF＝GH；（3）易得△AHF∽△CGE，所以，由EC＝3 得AF＝1，过F 作FP⊥BC 于P，根据勾股定理得EF，因为FH∥EG，所以，【解答】解：（1）∵四边形ABCD 是正方形，∴AB＝DA，∠ABE＝90°＝∠DAH．∴∠HAO+∠OAD＝90°．∵AE⊥DH，∴∠ADO+∠OAD＝90°．∴∠HAO＝∠ADO．∴△ABE≌△DAH（ASA），∴AE＝DH．（2）EF＝GH．将FE 平移到AM 处，则AM∥EF，AM＝EF．将GH 平移到DN 处，则DN∥GH，DN＝GH．∵EF⊥GH，∴AM⊥DN，根据（1）的结论得AM＝DN，所以EF＝GH；（3）∵四边形ABCD 是正方形，∴AB∥CD∴∠AHO＝∠CGO∵FH∥EG∴∠FHO＝∠EGO∴∠AHF＝∠CGE∴△AHF∽△CGE∴，∵EC＝3∴AF＝1过 F 作FP⊥BC 于P，根据勾股定理得EF＝，∵根据（2）知EF＝GH，∴GH＝2 ．【点评】本题考查了四边形的综合知识．用到正方形的性质，全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等综合性较强，难度较大．3.【分析】问题发现：（1）①由等边三角形的性质可得AC＝BC，DC＝CE，∠ACB＝∠DCE＝∠CDE＝60°＝∠CED，由“SAS”可证△ACD≌△BCE，可得AD＝BE，∠ADC＝∠CEB＝120°即可求∠AEB 的度数；（2）由全等三角形的性质可得AD＝BE；拓展研究：（2）仿照（1）中的解法可求出∠AEB 的度数，证出AD＝BE；由△DCE 为等腰直角三角形及CM 为△DCE 中DE 边上的高可得CM＝DM＝ME，可得AE＝2CH+BE；解决问题：（3）由题意可得点P 在以D 为圆心，2 为半径的圆上，同时点P 也在以BD 为直径的圆上，即点P 是两圆的交点，分两种情况讨论，由勾股定理可求BP，AH 的长，即可求点A 到BP 的距离．【解答】解：问题发现（1）①∵△ACB 和△DCE 均为等边三角形，∴AC＝BC，DC＝CE，∠ACB＝∠DCE＝∠CDE＝60°＝∠CED∵点A、D、E 在同一条直线上，∴∠ADC＝120°∵∠ACB﹣∠DCB＝∠DCE﹣∠DCB∴∠ACD＝∠BCE，且AC＝BC，DC＝CE∴△ACD≌△BCE（SAS）∴∠ADC＝∠CEB＝120°∴∠ABE＝∠CEB﹣∠CED＝60°②∵△ACD≌△BCE∴AD＝BE故答案为：60°，AD＝BE（2）拓展研究：猜想：①∠AEB＝90°，②AE＝BE+2CM．理由：如图2，∵△ACB 和△DCE 均为等腰直角三角形，∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°．∴∠ACD＝∠BCE．且AC＝BC，CD＝CE∴△ACD≌△BCE（SAS）．∴AD＝BE，∠ADC＝∠BEC．∵△DCE 为等腰直角三角形，∴∠CDE＝∠CED＝45°．∵点A，D，E 在同一直线上，∴∠ADC＝135°．∴∠BEC＝135°．∴∠AEB＝∠BEC﹣∠CED＝90°．∵CD＝CE，CM⊥DE，∴DM＝ME．∵∠DCE＝90°，∴DM＝ME＝CM．∴AE＝AD+DE＝BE+2CM．解决问题：（3）∵点P 满足PD＝2，∴点P 在以D 为圆心，2 为半径的圆上，∵∠BPD＝90°，∴点P 在以BD 为直径的圆上，∴如图，点P 是两圆的交点，若点P 在AD 上方，连接AP，过点A 作AH⊥BP，∵CD＝2＝BC，∠BCD＝90°∴BD＝4，∵∠BPD＝90°∴BP＝＝2∵∠BPD＝90°＝∠BAD∴点A，点B，点D，点P 四点共圆∴∠APB＝∠ADB＝45°，且AH⊥BP∴∠HAP＝∠APH＝45°∴AH＝HP在Rt△AHB 中，AB2＝AH2+BH2，∴8＝AH2+（2 ﹣AH）2，∴AH＝+1（不合题意），或AH＝﹣1若点P 在CD 的右侧，同理可得AH＝+1综上所述：点A 到BP 的距离为：+1 或﹣1【点评】本题是四边形综合题，考查了等边三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质、正方形的性质，勾股定理等知识，熟练运用这些性质进行推理是本题的关键．4.【分析】（1）利用正方形的性质和已知条件证明△AMC≌△DBC，从而求出AM 与BD相等且垂直；（2）如果将正方形BCMN 绕点C 逆时针旋转锐角α，其它不变（1）中所得的结论任然成立，先求出∠ACM＝∠DCB，然后利用“边角边”证明△AMC 和△DBC 全等，再根据全等三角形对应边相等即可得证；（3）根据AM⊥BD，得相交的角为直角，由勾股定理计算可得结论．【解答】解：（1）∵四边形ACDE 和四边形BCMN 都为正方形，∴AC＝DC，∠ACD＝∠BCD＝90°，BC＝CM，在△AMC 和△DBC 中，，∴△AMC≌△DBC（SAS）．∴AM＝BD，∠CAM＝∠CDB，延长AM 交BD 于F，∵∠AMC＝∠DMF，∴∠ACM＝∠DFM＝90°，∴AM⊥BD；故答案为：AM＝BD 且AM⊥BD；（2）如果将正方形BCMN 绕点C 逆时针旋转锐角α，其它不变，（1）中所得的结论仍然成立，理由如下：在正方形ABCE 和正方形BCMN 中，AC＝CD，CM＝BC，∠ACD＝∠MCB＝90°，∵∠ACM＝90°+∠MCD，∠DCB＝90°+∠MCD，∴∠ACM＝∠DCB，在△ACM 和△DCB 中，，∴△AMC≌△DBC（SAS）．∴AM＝BD，∠CAM＝∠CDB，∵∠AFC＝∠DFG，∴∠ACF＝∠DGF＝90°，∴AM⊥BD．（3）如图2，连接AD、BM，∵AC＝4，BC＝2，由勾股定理得：AD2＝42+42＝32，BM2＝22+22＝8，∵AM⊥BD，∴∠AGB＝∠DGM＝∠AGD＝∠BGM＝90°，∴AB2+DM2＝AG2+BG2+DG2+GM2，∵AD2+BM2＝AG2+DG2+BG2+MG2＝32+8＝40，∴AB2+DM2＝40．【点评】本题考查了四边形的综合题、正方形的性质、旋转的性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．5.【分析】（1）由条件可证明四边形AECF 和四边形EDFB 为平行四边形，可得到EH∥GF，GE∥FH，可证明四边形EGFH 为平行四边形；（2）由矩形的性质得出AB＝CD＝2，∠ABC＝∠ADC＝∠BAD＝90°，证出∠ABE＝∠DEC，得出△ABE∽△DEC，得出＝，即可求出AE 的长；（3）作AP⊥AD 于P，CQ⊥AD 于Q，则BP＝CQ，PQ＝BC＝AD，由直角三角形的性质得出AP＝AB＝m，BP＝CQ＝AP＝m，设AE＝x，则PE＝x+m，AQ＝n﹣x﹣m，同（2）得：△BPE∽△EQC，得出＝，得出方程整理得：x2+（m﹣n）x+m2﹣＝0，由判别式△＝n2﹣3m2，当△≥0，即n2﹣3m2≥0 时，方程有解，得出m、n 满足的条件和AE 的长．【解答】（1）证明：∵四边形ABCD 为平行四边形，∴AD∥BC，AD＝BC，∵AE＝CF，∴DE＝BF，∴四边形AECF、四边形EDFB 为平行四边形，∴EH∥GF，GE∥FH，∴四边形EGFH 为平行四边形；（2）解：存在，如图②所示，理由如下：∵四边形ABCD 是矩形，∴AB＝CD＝2，∠ABC＝∠ADC＝∠BAD＝90°，∴∠ABE+∠AEB＝90°，四边形EGFH 为矩形时，∠BEC＝90°，则∠AEB+∠DEC＝90°，∴∠ABE＝∠DEC，∴△ABE∽△DEC，∴＝，即＝，解得：AE＝3±；即在AD、BC 边上存在点E、F，使得四边形EGFH 为矩形，此时AE 的长度为3±；（3）解：存在，如图③所示，理由如下：作AP⊥AD 于P，CQ⊥AD 于Q，则BP＝CQ，PQ＝BC＝AD，∴AP＝DQ，∵AD∥BC，∴∠PAB＝∠ABC＝60°，∴∠ABP＝30°，∴AP＝AB＝m，∴BP＝CQ＝AP＝m，设AE＝x，则PE＝x+m，AQ＝n﹣x﹣m，同（2）得：△BPE∽△EQC，∴＝，即＝，整理得：x2+（m﹣n）x+m2﹣＝0，∵△＝（m﹣n）2﹣4（m2﹣）＝n2﹣3m2，当△≥0，即n2﹣3m2≥0 时，方程有解，即m、n 满足n≥m 时，在AD、BC 边上存在点E、F 使得四边形EGFH 为矩形，此时AE＝．【点评】本题是四边形综合题目，考查了平行四边形的判定和性质、矩形的判定与性质、相似三角形的判定与性质、一元二次方程的解法以及判别式的运用等知识；本题综合性强，证明三角形相似是解决问题的关键．6.【分析】（1）根据正方形的性质得到AB＝DA，∠ABE＝∠DAH＝90°，利用ASA 定理证明△ABE≌△DAH，根据全等三角形的性质得到AE＝DH；（2）过得A 作AM∥EF 交BC 于M，过点D 作DN∥GH 交AB 于N，由（1）的结论证明即可；（3）过点F 作FP⊥BC 于点P，根据勾股定理求出EF，由（2）的结论求出HG，根据四边形的面积公式计算即可．【解答】（1）证明：∵四边形ABCD 是正方形，∴AB＝DA，∠ABE＝∠DAH＝90°，∴∠HAO+∠OAD＝90°，∵AE⊥DH，∴∠ADO+∠OAD＝90°，∴∠HAO＝∠ADO，在△ABE 和△DAH 中，，∴△ABE≌△DAH（ASA），∴AE＝DH；（2）解：EF＝GH．理由：如图2，过得A 作AM∥EF 交BC 于M，则四边形AMEF 为平行四边形，∴AM＝EF，过点D 作DN∥GH 交AB 于N，同理，DN＝GH，∵EF⊥GH，∴AM⊥DN，根据（1）的结论得AM＝DN，所以EF＝GH；（3）解：如图3，过点F 作FP⊥BC 于点P，∵四边形ABCD 是正方形，BC＝4，∴AD＝BC＝AB＝FP＝4，∵E 为BC 的中点，DF＝3AF，∴BE＝2，AF＝1，∴PE＝2﹣1＝1，在Rt△FPE 中，EF＝＝，由（2）得：HG＝EF，∴HG＝，∵EF⊥HG，∴四边形HEGF 的面积＝×EF×GH＝．【点评】本题考查的是正方形的性质、全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．7.【分析】（1）由正方形的性质得出＝＝，∠ACB＝∠ECF＝45°，得出∠ACE＝∠BCF，证出△CAE∽△CBF，得出∠CAE＝∠CBF，＝＝，因此＝，求出∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝45°，再由三角形内角和定理求出∠AHB 的度数即可；（2）不成立；由矩形的性质和已知条件得出＝＝，∠ACE＝∠BCF，得出△CAE ∽△CBF，因此∠CAE＝∠CBF，求出＝＝，∠CAB＝∠CAE+∠EAB＝∠CBF+ ∠EAB＝60°，再由三角形内角和定理即可得出∠AHB 的度数；（3）分两种情况：①如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，由（2）得：∠AFB＝30°，∠AFC＝90°，在Rt△ABC 和Rt△CEF 中，由三角函数求出AC＝6 ，EF＝2，在Rt△ACF 中，由勾股定理求出AF＝6，得出AE＝AF﹣EF＝6﹣2 ，再由（2）的结论＝，求出BF＝3 ﹣3，在Rt△BFM 中，由直角三角形的性质求出BM 即可；②如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，同②得：AE＝6+2，BF＝3+3，由直角三角形的性质求出BM 即可．【解答】解：（1）如图1 所示：∵四边形ABCD 和EFCG 均为正方形，∴＝＝，∠ACB＝∠ECF＝45°，∴∠ACE＝∠BCF，∴△CAE∽△CBF，∴∠CAE＝∠CBF，＝＝，∴＝，∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝45°，∵∠CBA＝90°，∴∠AHB＝180°﹣90°﹣45°＝45°，故答案为：＝，45°；（2）不成立；理由如下：∵四边形ABCD 和EFCG 均为矩形，且∠ACB＝∠ECF＝30°，∴＝＝，∠ACE＝∠BCF，∴△CAE∽△CBF，∴∠CAE＝∠CBF，＝＝，∴∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝60°，∵∠CBA＝90°，∴∠AHB＝180°﹣90°﹣60°＝30°；（3）分两种情况：①如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，由（2）得：∠AFB＝30°，∠AFC＝90°，在Rt△ABC 和Rt△CEF 中，∵∠ACB＝∠ECF＝30°，∴AC＝＝＝6 ，EF＝CF×tan30°＝6×＝2 ，在Rt△ACF 中，AF＝＝＝6 ，∴AE＝AF﹣EF＝6 ﹣2，由（2）得：＝，∴BF＝（6﹣2）＝3﹣3，在△BFM 中，∵∠AFB＝30°，∴BM＝BF＝；②如图3 所示：作BM⊥AE 于M，当A、E、F 三点共线时，同②得：AE＝6+2，BF＝3 +3，则BM＝BF＝；综上所述，当A、E、F 三点共线时，点B 到直线AE 的距离为．【点评】本题是四边形综合题目，考查了正方形的性质、矩形的性质、含30°角的直角三角形的性质、相似三角形的判定与性质、三角函数、勾股定理以及分类讨论等知识；本题综合性强，证明三角形相似是解决问题的关键．8.【分析】【片断一】如图1 中，①错误．结论：OM2+ON2＝BM2+BN2．②正确．只要证明△MOB≌△NOC 即可解决问题；【片断二】如图2 中，将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．理由勾股定理即可证明；【片断三】如图3 中，过点C 作EC 的垂线交EB 延长线于F，构造全等三角形即可解决问题；【解答】解：【片断一】：如图1 中，①错误，②正确；理由：如图1 中，∵四边形ABCD 是正方形，∴AC⊥BD，OB＝OC＝OD＝OA，∠ABO＝∠OCN＝45°，∵∠MON＝∠BOC，∴∠MOB＝∠NOC，∴△MOB≌△NOC，∴BN＝CN，∴AM+CN＝AM+BM＝AB＝OA＝OD，①正确的结论：OM2+ON2＝BM2+BN2．理由：∵OM2+ON2＝MN2，BM2+BN2＝MN2，∴OM2+ON2＝BM2+BN2．【片断二】：如图 2 中，将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．理由：∵AF＝AF，∠GAF＝∠EAF＝45°，AG＝AE，∴△AFG≌△AFE，∴EF＝GF，∵∠ADG＝∠ABE＝∠ADF＝45°，∴∠FDG＝90°，∴GF2＝DF2+DG2，∴EF2＝BE2+DF2．故答案为：将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．【片断三】：如图 3 中，过点C 作EC 的垂线交EB 延长线于F，∵∠ECF＝∠DCB＝90°，∴∠DCE＝∠BCF，∵CD＝CB，CE＝CF，∴△CDE≌△CBF，∴ED＝FB，∴EB+ED＝EB+FB＝EF，又因为EC2+FC2＝EF2，∴（EB+ED）2＝2EC2．【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．9.【分析】（1）用“倍长法”将DE 延长一倍：延长DE 到F，使得EF＝DE，利用“边角边”证明△ADE 和△CEF 全等，根据全等三角形对应边相等可得AD＝CF，然后判断出四边形BCFD 是平行四边形，根据平行四边形的性质可得；（2）先判断出△AEG≌△DEH（ASA），进而判断出EF 垂直平分GH，即可得出结论；（3）如图3，作辅助线构建全等三角形，先求出AG＝HD＝2，进而判断出△PDH 为30 度的直角三角形，再用勾股定理求出HF 即可得出结论．【解答】（1）证明：（1）如图1，延长DE 到点F，使得EF＝DE，连接CF，在△ADE 和△CFE 中，，∴△ADE≌△CFE（SAS），∴∠A＝∠ECF，AD＝CF，∴CF∥AB，又∵AD＝BD，∴CF＝BD，∴四边形BCFD 是平行四边形，∴DE∥BC，DE＝BC．（2）解：如图2，延长GE、FD 交于点H，∵E 为AD 中点，∴EA＝ED，且∠A＝∠EDH＝90°，在△AEG 和△DEH 中，，∴△AEG≌△DEH（ASA），∴AG＝HD＝3，EG＝EH，∵∠GEF＝90°，∴EF 垂直平分GH，∴GF＝HF＝DH+DF＝3+7＝10；（3）解：如图3，过点D 作AB 的平行线交GE 的延长线于点H，过H 作CD 的垂线，垂足为P，连接HF，同（1）可知△AEG≌△DEH，GF＝HF，∴∠A＝∠HDE＝90°，AG＝HD＝2 ，∵∠ADC＝120°，∴∠HDF＝360°﹣90°﹣120°＝150°，∴∠HDP＝30°，∴PH＝DH＝，PD＝3，∴PF＝PD+DF＝3+4＝7，在Rt△HFP 中，∠HPF＝90°，HP＝，PF＝7，∴HF＝＝＝2，∴GF＝2 ．【点评】此题是四边形综合题，主要考查了正方形和直角梯形的性质和判定，全等三角形的判定和性质，等腰直角三角形的性质和判定，勾股定理，解（1）的关键是判断出△ADE ≌△CFE，解（2）的关键是判断出EF 垂直平分GH，解（3）的关键是作出辅助线，是一道比较典型的中考题．10.【分析】（1）证明△BPC 是等腰直角三角形，计算BP＝PC＝6，先根据三角形中线可知：EF是△ABC 的中位线，得EF∥BC，EF＝BC，证明△EPF∽△CPB，列比例式可得PE和AB 的长；（2）设PF＝m，PE＝n，则PB＝2m，PC＝2n，在Rt△PBC，Rt△PBE 和Rt△PCF 中，根据勾股定理列方程后，相加可得结论；（3）本题介绍两种解法：法一：证明△AGM≌△NGB（AAS），得BG 是△ABN 的中线，作辅助线，构建全等三角形和中线，得NF，BG 都为△ABN 的中线，由（2）知，AB2+AN2＝5BN2，代入可得结论；法二：如图4，作BP⊥DA 延长线于点P，CQ⊥AD 于点Q，易知四边形PBCQ 为矩形，设PA＝QD＝x，PB＝CQ＝y，表示PM＝x+，MQ＝2﹣x，证明△PBM∽△QMC，列比例式得方程：y2＝﹣x2+ x+12 ①，根据勾股定理得：AH2＝AB2﹣BH2，y2＝42﹣x2＝16﹣x2②，根据①②得：﹣x2+ x+12＝16﹣x2，解出可得结论．【解答】解：（1）如图1，∵BF⊥CE，∴∠BPC＝90°，∵∠PCB＝45°，∴△BPC 是等腰直角三角形，∵BC＝6 ，∴PC＝BP＝6，∵BF，CE 分别为AC，AB 边上的中线，∴EF 是△ABC 的中位线，∴EF∥BC，EF＝BC，∴△EPF∽△CPB，∴＝，∴，∴EP＝3，由勾股定理得：BE＝＝＝3，∴AB＝2BE＝6 ，故答案为：3，6；（2）猜想：AB2+AC2＝5BC2；证明：∵BF，CE 是△ABC 的中线，∴EF 是△ABC 的中位线，∴EF∥BC，EF＝BC，＝＝，设PF＝m，PE＝n，则PB＝2m，PC＝2n，在Rt△PBC 中，（2m）2+（2n）2＝BC2①在Rt△PBE 中，②在Rt△PCF 中，③由①，②，③得：AB2+AC2＝5BC2；（3）法一：在△AGM 与△NGB 中，，∴△AGM≌△NGB（AAS），∴BG＝MG，AG＝NG，∴BG 是△ABN 的中线，如图3，取AB 的中点F，连接NF，并延长交DA 的延长线于E，同理，△AEF≌△BNF，∴AE＝BN，EM＝2BN＝NC，∵EM∥NC，∴四边ENCM 是平行四边形，∴EN∥CM，∵BM⊥CM，∴EN⊥BM，即BG⊥FN，∵NF，BG 都为△ABN 的中线，由（2）知，AB2+AN2＝5BN2，∵AB＝4，BN＝AD＝，∴42+AN2＝5×，∴AN＝．法二：如图4，作BP⊥DA 延长线于点P，CQ⊥AD 于点Q，在▱ABCD 中，AD＝BC，易知四边形PBCQ 为矩形，∴PQ＝BC，∴PA＝QD，依题意：AM＝BN＝，MD＝2，设PA＝QD＝x，PB＝CQ＝y，∴PM＝x+ ，MQ＝2﹣x，∵BM⊥CM 于点M，∠BMC＝90°，∴∠BMP+∠CMQ＝90°，又∠BMP+∠PBM＝90°，∴∠PBM＝∠CMQ，又∵∠BPM＝∠MQC＝90°，∴△PBM∽△QMC，∴，即，化简得：y2＝﹣x2+ x+12 ①，作AH⊥BC 于点H，则BH＝PA＝x，AH＝y，在Rt△ABH 中，AH2＝AB2﹣BH2，∴y2＝42﹣x2＝16﹣x2②，由①②得：﹣x2+ x+12＝16﹣x2，∴x＝，y2＝，在Rt△AHN 中，AN＝＝＝＝．【点评】本题是四边形的综合题，考查相似三角形的判定和性质、矩形和平行四边形的判定和性质、三角形全等的性质和判定、三角形中线，勾股定理等知识，解题的关键是灵活运用所学知识解决问题，并运用类比的方法解决问题，属于中考常考题型．1.【分析】（1）根据旋转得：△ACE 是等边三角形，可得：AB＝BC＝CE＝AE，则四边形ABCE是菱形；（2）先证明C、F、E 在同一直线上，再证明△BAD≌△CAF（SAS），则∠ADB＝∠AFC，BD ＝CF，可得AC＝CF+CD；（3）先根据∠ADC＝∠DAF＝∠F＝90°，证明得四边形ADGF 是矩形，由邻边相等可得四边形ADGF 是正方形；（4）证明△BAM≌△EAD（SAS），根据BM＝DE 及勾股定理可得结论．【解答】（1）证明：∵△ABC 是等边三角形，∴AB＝BC＝AC，∵△ACD 绕点A 逆时针旋转60°得到△AEF，∴∠CAE＝60°，AC＝AE，∴△ACE 是等边三角形，∴AC＝AE＝CE，∴AB＝BC＝CE＝AE，∴四边形ABCE 是菱形；（2）线段CD，CF，AC 之间的数量关系：CD+CF＝AC，理由是：由旋转得：∠DAF＝60°＝∠BAC，AD＝AF，∴∠BAD＝∠CAF，∵△ABC 是等边三角形，∴AB＝AC，∴△BAD≌△CAF（SAS），∴∠ADB＝∠AFC，BD＝CF，∵∠ADC+∠ADB＝∠AFC+∠AFE＝180°，∴C、F、E 在同一直线上，∴AC＝BC＝BD+CD＝CF+CD，故答案为：CD+CF＝AC；（3）四边形ADGF 是正方形，理由如下：∵Rt△ABD 绕点A 逆时针旋转90°得到△AEF，∴AF＝AD，∠DAF＝90°，∵AD⊥BC，∴∠ADC＝∠DAF＝∠F＝90°，∴四边形ADGF 是矩形，∵AF＝AD，∴四边形ADGF 是正方形；（4）如图3，连接DE，∵四边形ADGF 是正方形，∴DG＝FG＝AD＝AF＝6，∵△ABD 绕点A 逆时针旋转90°，得到△AEF，∴∠BAD＝∠EAF，BD＝EF＝2，∴EG＝FG﹣EF＝6﹣2＝4，∵将△AFE 沿AE 折叠得到△AME，∴∠MAE＝∠FAE，AF＝AM，∴∠BAD＝∠EAM，∴∠BAD+∠DAM＝∠EAM+∠DAM，即∠BAM＝∠DAE，∵AF＝AD，∴AM＝AD，在△BAM 和△EAD 中，∵，∴△BAM≌△EAD（SAS），∴BM＝DE＝＝＝2．【点评】本题属于四边形综合题，主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是熟练掌握等边三角形和全等三角形的性质，依据图形的性质进行计算求解．。

学生做题前请先回答以下问题问题1：类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有哪些？问题2：处理类比探究问题时，若属于常见结构，则________．问题3：处理类比探究问题时，若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．此时常见的处理思路是什么？类比结构构造——类比探究（二）一、单选题(共5道，每道20分)1.阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在BC边上，∠BAD=75°，∠CAD=30°，AD=2，BD=2CD，求AC的长．小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图2）．请回答：∠ACE的度数为_____，AC的长为_____．( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：探究应用2.（上接第1题）参考小腾思考问题的方法，解决问题：如图3，在四边形ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2DE，则BC的长为( )A.6B.C. D.答案：C解题思路：试题难度：三颗星知识点：探究应用3.问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠D=90°．E，F分别是边BC，CD上的点，且∠EAF=60°．求证：EF=BE+DF．关于证明上述结论的辅助线的作法，有如下说法：①延长FD到G，使DG=BE，连接AG；②过点A作AG⊥EF于点G；③将△ABE绕点A逆时针旋转120°得到△ADG（之后证明点G，D，F在同一条直线上）．其中可以证明结论的是( )A.①B.②③C.①③D.①②③答案：C解题思路：试题难度：三颗星知识点：探究应用4.（上接第3题）探索延伸：如图2，在四边形ABCD中，AB=AD，E，F分别是边BC，CD上的点，且，则当∠B和∠D满足什么条件时，EF=BE+DF成立？( )A.∠B=∠DB.∠B+∠D=180°C.∠B=2∠DD.∠B+∠D=120°答案：B解题思路：试题难度：三颗星知识点：探究应用5.（上接第3，4题）实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进．1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，则此时两舰艇之间的距离为( )海里．A. B.210C.300D.条件不够，无法计算答案：B解题思路：试题难度：三颗星知识点：探究应用。