华师大版九年级数学上 第24章 解直角三角形《练闯考》2015年秋章末检测(含答案)

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题，共计45分)1、如图，在正方形中，是等边三角形，，的延长线分别交于点，，连接，，与相交于点.有下列结论：① ；② ；③ ；④.其中正确的个数是（）A.1B.2C.3D.42、如图，一艘船由港沿北偏东65°方向航行至港，然后再沿北偏西40°方向航行至港，港在港北偏东20°方向，则，两港之间的距离为（）.A. B. C. D.3、如图，中，，，，若，则的长为（）A.6B.C.7.5D.104、如图，⊙O直径CD＝5cm，AB是⊙O的弦，AB⊥CD，垂足M，OM：OD＝3：5，则AB 的长是（）A. cmB. cmC. cmD. cm5、等腰三角形两边长分别为4和8，则这个等腰三角形的周长为( )A.16B.18C.20D.16或206、△ABC中，∠B=90°，AC=，tan∠C=，则BC边的长为（）A.2B.2C.D.47、以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边，可以画出三角形的个数为（）A.1个B.2个C.3个D.4个8、如图，小明站在某广场一看台C处，测得广场中心F的俯角为21°，若小明身高CD＝1.7米，BC＝1.9米，BC平行于地面FA，台阶AB的坡度为i＝3：4，坡长AB＝10.5米，则看台底端A点距离广场中心F点的距离约为（）米．（参考数据：sin21°≈0.36，cos21°≈0.93，tan21°≈0.38）A.8.9B.9.7C.10.8D.11.99、如图，在直角坐标系中，四边形 OABC 为菱形，对角线 OB、AC 相交于 D 点，已知 A点的坐标为（10，0），双曲线 y= （ x＞0 ）经过 D 点，交BC 的延长线于 E 点，且OB•AC=120（OB＞AC），有下列四个结论：①双曲线的解析式为y=（x＞0）；②E 点的坐标是（4，6）；③sin∠CO A= ；④EC= ；⑤AC+OB=8 ．其中正确的结论有（）A.4 个B.3 个C.2 个D.1 个10、如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（）A. B. C. D.11、如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE,则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD.其中正确的是（）A.①②③B.①②④C.①③④D.①②③④12、两根木棒分别长5cm、7cm，第三根木棒与这两根木棒首尾依次相接构成三角形．如果第三根木棒的长是偶数（单位：cm），则一共可以构成不同的三角形有（）A.4个B.5个C.8个D.10个13、三角形两条边分别为3和7，则第三边可以为（）A.9B.3C.2D.1014、下列长度的各组线段中可组成三角形的是( )A.1，2，3B.2，3，5C.3，3，6D. ，，15、以长为3cm，5cm，7cm，10cm的四条线段中的三条线段为边可以画出三角形的个数为( )A.1B.2C.3D.4二、填空题(共10题，共计30分)16、如图，直线y=﹣x+4与两坐标轴交A、B两点，点P为线段OA上的动点，连接BP，过点A作AM垂直于直线BP，垂足为M，当点P从点O运动到点A 时，则点M运动路径的长为________．17、如图，在平面直角坐标系中，点A的坐标（﹣2，0），△ABO是直角三角形，∠AOB=60°．现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置，则此时边OB扫过的面积为________．18、如图，水库大坝的横截面是梯形，坝顶AD宽5米，坝高10米，斜坡CD的坡角为45°，斜坡AB的坡度i=1：1.5，那么坝底BC的长度为________米．19、如图，身高1.6米的小丽在阳光下的影长为2米，在同一时刻，一棵大树的影长为8米，则这棵树的高度为________米.20、如图△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC= ，则BC的长为________．21、已知三角形的两边长是3和4，周长是偶数，则这样的三角形的第三边是________．22、如图，当太阳光与地面成角时，直立于地面的玲玲测得自己的影长为1.25m，则玲玲的身高约为________ m．（精确到0. 01m）（参考数据：sin55°≈0.8192，cos55°≈0.5736，tan55°≈1.428）.23、将一张长方形纸片ABCD如图所示折叠，使顶点C落在点，已知，，则折痕DE的长为________（用含a的式子表示）．24、如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上。

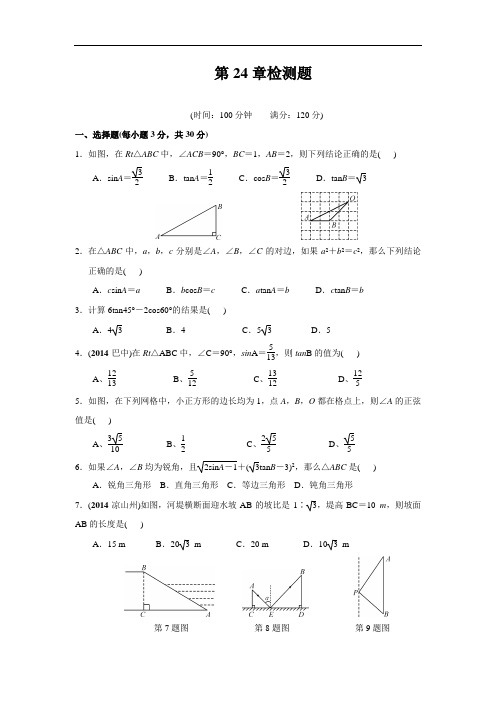
第24章检测题(时间：100分钟 满分：120分)一、选择题(每小题3分，共30分)1．如图，在Rt △ABC 中，∠ACB ＝90°，BC ＝1，AB ＝2，则下列结论正确的是( )A ．sin A ＝32 B ．tan A ＝12 C ．cos B ＝32D ．tan B ＝32．在△ABC 中，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，如果a 2＋b 2＝c 2，那么下列结论正确的是( )A ．c sin A ＝aB ．b cos B ＝cC ．a tan A ＝bD ．c tan B ＝b 3．计算6tan45°－2cos60°的结果是( )A ．4 3B ．4C ．5 3D ．5 4．(2014·巴中)在Rt △ABC 中，∠C ＝90°，sin A ＝513，则tan B 的值为( )A 、1213B 、512C 、1312D 、1255．如图，在下列网格中，小正方形的边长均为1，点A ，B ，O 都在格点上，则∠A 的正弦值是( )A 、3510B 、12C 、255D 、556．如果∠A ，∠B 均为锐角，且2sin A －1＋(3tan B －3)2，那么△ABC 是( )A ．锐角三角形B ．直角三角形C ．等边三角形D ．钝角三角形7．(2014·凉山州)如图，河堤横断面迎水坡AB 的坡比是1∶3，堤高BC ＝10 m ，则坡面AB 的长度是( )A ．15 mB ．20 3 mC ．20 mD ．10 3 m第7题图 第8题图 第9题图8．如图，CD 是平面镜，光线从A 点射出，经CD 上点E 反射后照射到B 点，若入射角为α，AC ⊥CD ，BD ⊥CD ，垂足分别为C ，D ，且AC ＝3，BD ＝6，CD ＝11，则tan α的值为( )A 、113B 、311C 、911D 、1199．(2014·绵阳)如图，一艘海轮位于灯塔P 的北偏东30°方向，距离灯塔80海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东45°方向上的B 处，这时，海轮所在的B 处与灯塔P 的距离为( )A ．40 2 海里B ．40 3 海里C ．80海里D ．40 6 海里10．如图，在两建筑物之间有一旗杆，高15米，从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点，且俯角α为60°，又从A 点测得D 点的俯角β为30°，若旗杆底点G 为BC 的中点，则矮建筑物的高CD 为( )A ．20米B ．10 3 米C ．15 3 米D ．5 6 米 二、填空题(每小题3分，共24分)11．(2014·锦州)计算：tan 45°－13(3－1)0＝____．12．如图，在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD ＝2，AC ＝3，则sinA 的值是____．13．如图，某山坡的坡面AB ＝200米，坡角∠BAC ＝30°，则该山坡的高BC 的长为____米．第12题图 第13题图 第14题图14．如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE ＝6 cm ，sinA ＝35，则菱形ABCD 的面积是____cm 2、15．将一副三角尺如图所示叠放在一起，则BEEC的值是____．16．如图，△ABC 的顶点A ，C 的坐标分别是(0，4)，(3，0)，且∠ACB ＝90°，∠B ＝30°，则顶点B 的坐标是_____________．第15题图 第16题图 第18题图17．△ABC 中，AB ＝4，BC ＝3，∠BAC ＝30°，则△ABC 的面积为． 18．(2014·宁波)为解决停车难的问题，在如图一段长56米的路段开辟停车位，每个车位是长5 米，宽2、2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出____个这样的停车位．(2≈1、4)三、解答题(共66分) 19．(8分)计算：(1)(－2)2＋|－3|＋2sin 60°－12； (2)6tan 230°－3cos 30°－2sin 45°、20．(8分)(2014·重庆)如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sinC 的值．21．(8分)如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上(其中A，B，C在同一平面上)．求这个标志性建筑物底部A到岸边BC的最短距离．22．(10分)(2014·乐山)如图，在梯形ABCD中，AD∥BC，∠ADC＝90°，∠B＝30°，CE⊥AB，垂足为点E，若AD＝1，AB＝23，求CE的长．23、(10分)如图，一堤坝的坡角∠ABC＝62°，坡面长度AB＝25米(图为横截面)，为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB＝50°，则此时应将坝底向外拓宽多少米？(结果保留到0、01米；参考数据：sin62°≈0、88，cos62°≈0、47，tan50°≈1、20)24．(10分)(2014·泰州)图①，②分别是某型号跑步机的实物图与示意图，已知踏板CD 长为1、6 m，CD与地面DE的夹角∠CDE为12°，支架AC长为0、8 m，∠ACD为80°，求跑步机手柄的一端A的高度h、(精确到0、1 m；参考数据：sin12°＝cos78°≈0、21，sin68°＝cos22°≈0、93，tan68°≈2、48)25．(12分)如图，已知斜坡AB长602米，坡角(即∠BAC)为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE、(1)若修建的斜坡BE的坡比为3∶1，求休闲平台DE的长是多少米？(2)一座建筑物GH距离A点33米远(即AG＝33米)，小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°，点B，C，A，G，H在同一个平面内，点C，A，G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？参考答案一、选择题(每小题3分，共30分)1．如图，在Rt △ABC 中，∠ACB ＝90°，BC ＝1，AB ＝2，则下列结论正确的是( D )A ．sin A ＝32 B ．tan A ＝12 C ．cos B ＝32D ．tan B ＝32．在△ABC 中，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，如果a 2＋b 2＝c 2，那么下列结论正确的是( A )A ．c sin A ＝aB ．b cos B ＝cC ．a tan A ＝bD ．c tan B ＝b 3．计算6tan45°－2cos60°的结果是( D )A ．4 3B ．4C ．5 3D ．5 4．(2014·巴中)在Rt △ABC 中，∠C ＝90°，sin A ＝513，则tan B 的值为( D )A 、1213B 、512C 、1312D 、1255．如图，在下列网格中，小正方形的边长均为1，点A ，B ，O 都在格点上，则∠A 的正弦值是( D )A 、3510B 、12C 、255D 、556．如果∠A ，∠B 均为锐角，且2sin A －1＋(3tan B －3)2，那么△ABC 是( B )A ．锐角三角形B ．直角三角形C ．等边三角形D ．钝角三角形7．(2014·凉山州)如图，河堤横断面迎水坡AB 的坡比是1∶3，堤高BC ＝10 m ，则坡面AB 的长度是( C )A ．15 mB ．20 3 mC ．20 mD ．10 3 m第7题图 第8题图 第9题图8．如图，CD 是平面镜，光线从A 点射出，经CD 上点E 反射后照射到B 点，若入射角为α，AC ⊥CD ，BD ⊥CD ，垂足分别为C ，D ，且AC ＝3，BD ＝6，CD ＝11，则tan α的值为( D )A 、113B 、311C 、911D 、1199．(2014·绵阳)如图，一艘海轮位于灯塔P 的北偏东30°方向，距离灯塔80海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东45°方向上的B 处，这时，海轮所在的B 处与灯塔P 的距离为( A )A ．40 2 海里B ．40 3 海里C ．80海里D ．40 6 海里10．如图，在两建筑物之间有一旗杆，高15米，从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点，且俯角α为60°，又从A 点测得D 点的俯角β为30°，若旗杆底点G 为BC 的中点，则矮建筑物的高CD 为( A )A ．20米B ．10 3 米C ．15 3 米D ．5 6 米 二、填空题(每小题3分，共24分)11．(2014·锦州)计算：tan 45°－13(3－1)0＝__23__．12．如图，在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD ＝2，AC ＝3，则sinA 的值是4． 13．如图，某山坡的坡面AB ＝200米，坡角∠BAC ＝30°，则该山坡的高BC 的长为__100__米．第12题图 第13题图 第14题图14．如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE ＝6 cm ，sinA ＝35，则菱形ABCD 的面积是__60__cm 2、15．将一副三角尺如图所示叠放在一起，则BE EC 的值是3．16．如图，△ABC 的顶点A ，C 的坐标分别是(0，4)，(3，0)，且∠ACB ＝90°，∠B ＝30°，则顶点B 的坐标是．第15题图 第16题图 第18题图17．△ABC 中，AB ＝4，BC ＝3，∠BAC ＝30°，则△ABC 的面积为． 18．(2014·宁波)为解决停车难的问题，在如图一段长56米的路段开辟停车位，每个车位是长5 米，宽2、2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出__17__个这样的停车位．(2≈1、4)点拨：如图，BC ＝2、2×sin 45°≈1、54，CE ＝5×sin 45°≈3、5，BE ＝BC ＋CE ≈5、04，EF ＝2、2÷sin 45°≈3、14，(56－5、04)÷3、14＋1≈16＋1＝17(个)，故这个路段最多可以划出17个这样的停车位 三、解答题(共66分) 19．(8分)计算：(1)(－2)2＋|－3|＋2sin 60°－12； 解：4(2)6tan 230°－3cos 30°－2sin 45°、 解：12－220．(8分)(2014·重庆)如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sinC 的值．解：121321．(8分)如图，湖中的小岛上有一标志性建筑物，其底部为A ，某人在岸边的B 处测得A 在B 的北偏东30°的方向上，然后沿岸边直行4公里到达C 处，再次测得A 在C 的北偏西45°的方向上(其中A ，B ，C 在同一平面上)．求这个标志性建筑物底部A 到岸边BC 的最短距离．解：过A 作AD ⊥BC 于点D ，则AD 的长度就是A 到岸边BC 的最短距离．在Rt △ACD 中，∠ACD ＝45°，设AD ＝x ，则CD ＝AD ＝x ，在Rt △ABD 中，∠ABD ＝60°，BD ＝xtan60°＝33x ，又BC ＝4，即BD ＋CD ＝4，所以33x ＋x ＝4，解得x ＝6－23，则这个标志性建筑物底部A 到岸边BC 的最短距离为(6－23)公里22．(10分)(2014·乐山)如图，在梯形ABCD 中，AD ∥BC ，∠ADC ＝90°，∠B ＝30°，CE ⊥AB ，垂足为点E ，若AD ＝1，AB ＝23，求CE 的长．解：过点A 作AH ⊥BC 于点H ，则AD ＝HC ＝1，在△ABH 中，BH ＝AB ·cos 30°＝3，∴BC ＝BH ＋BC ＝4，∵CE ⊥AB ，∴CE ＝BC ·sin 30°＝223、(10分)如图，一堤坝的坡角∠ABC ＝62°，坡面长度AB ＝25米(图为横截面)，为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB ＝50°，则此时应将坝底向外拓宽多少米？(结果保留到0、01米；参考数据：sin 62°≈0、88，cos 62°≈0、47，tan 50°≈1、20)解：过A 点作AE ⊥CD 于点E ，在Rt △ABE 中，AE ＝AB ·sin 62°≈22，BE ＝AB ·cos 62°≈11、75，在Rt △ADE 中，DE ＝AE tan50°≈18、33，∴DB ＝DC －BE ≈6、58，故此时应将坝底向外拓宽大约6、58米24．(10分)(2014·泰州)图①，②分别是某型号跑步机的实物图与示意图，已知踏板CD 长为1、6 m ，CD 与地面DE 的夹角∠CDE 为12°，支架AC 长为0、8 m ，∠ACD 为80°，求跑步机手柄的一端A 的高度h 、(精确到0、1 m ；参考数据：sin 12°＝cos 78°≈0、21，sin 68°＝cos 22°≈0、93，tan 68°≈2、48)解：过C 点作FG ⊥AB 于点F ，交DE 于点G 、∵CD 与地面DE 的夹角∠CDE 为12°，∠ACD 为80°，∴∠ACF ＝90°＋12°－80°＝22°，∴∠CAF ＝68°，在Rt △ACF 中，CF ＝AC ·sin ∠CAF ≈0、744，在Rt △CDG 中，CG ＝CD ·sin ∠CDE ≈0、336，∴FG ＝FC ＋CG ≈1、1，故跑步机手柄的一端A 的高度约为1、1 m25．(12分)如图，已知斜坡AB 长602米，坡角(即∠BAC )为45°，BC ⊥AC ，现计划在斜坡中点D 处挖去部分斜坡，修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE 、(1)若修建的斜坡BE 的坡比为3∶1，求休闲平台DE 的长是多少米？(2)一座建筑物GH 距离A 点33米远(即AG ＝33米)，小亮在D 点测得建筑物顶部H 的仰角(即∠HDM )为30°，点B ，C ，A ，G ，H 在同一个平面内，点C ，A ，G 在同一条直线上，且HG ⊥CG ，问建筑物GH 高为多少米？解：(1)∵FM ∥CG ，∴∠BDF ＝∠BAC ＝45°，∵斜坡AB 长602，D 是AB 的中点，∴BD ＝302，∴DF ＝BD ·cos ∠BDF ＝30，BF ＝DF ＝30，∵斜坡BE 的坡比为3∶1，∴BF EF ＝31，∴EF ＝103，∴DE ＝DF －EF ＝30－103，即休闲平台DE 的长是(30－103)米 (2)设GH ＝x 米，则MH ＝GH －GM ＝x －30，DM ＝AG ＋AP ＝33＋30＝63，在Rt △DMH 中，tan 30°＝MH DM ，即x －3063＝33，解得x ＝30＋213，则建筑物GH 的高为(30＋213)米。

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题，共计45分)1、下列各组长度的线段能构成三角形的是（）A.1,2,4B.4,5,9C.4,6,8D.5,5,112、如图，在2×2正方形网格中，以格点为顶点的△ABC的面积等于，则sin∠CAB=（）A. B. C. D.3、如图，已知菱形ABCD，DF1BC交AC于点，交C于点F，若tan∠BDF= ，AB=30，则CE的长是（）A. B. C. D.4、在△ABC中，AB=6，AC=8，则BC边上中线AD的取值范围为（）（提示：可以构造平行四边形）A.2＜AD＜14B.1＜AD＜7C.6＜AD＜8D.12＜AD＜165、在Rt△ABC中，∠C=90°，∠B=30°，斜边AB的长为2，则AC长为（）A.4B.2C.1D.6、如图，矩形ABCD的对角线AC、BD相交于点O，AB：BC＝2：1，且BE∥AC，CE∥DB，连接DE，则tan∠EDC＝（）A. B. C. D.7、如图，小颖身高为160cm，在阳光下影长AB=240cm，当她走到距离墙角（点D）150cm处时，她的部分影子投射到墙上，则投射在墙上的影子DE的长度为（）A.50B.60C.70D.808、将下列长度的三根木棒首尾顺次连接，能组成直角三角形的一组是（）A.2、4、6B.4、6、8C.8、10、12D.6、8、109、如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形顶点上，则tan∠ACB的值为（）A. B. C. D.310、如图（1）所示，E为矩形ABCD的边AD上一点，动点P，Q同时从点B出发，点P沿折线BE﹣ED﹣DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5；② ；③当0＜t≤5时，；④当秒时，△ABE∽△QBP；其中正确的结论是（）A.①②③B.②③C.①③④D.②④11、在下面四根木棒中，选一根能与长为4cm，9cm的两根木棒首尾依次相接钉成一个三角形的是（）A.4cmB.5cmC.9cmD.13cm12、下列是无理数的是（）A. B. C.0.202002000… D.13、已知三角形两边长分别为2和9，第三边的长为二次方程x2-14x+48=0的一根，则这个三角形的周长为( )A.11B.17C.17或19D.1914、在△ABC中，∠C=90°，cosA=， AC=6，则AB的长度为（）A.8B.10C.12D.1415、如图，⊙O的直径AB=2，点C在⊙O上，弦AC=1，则∠D的度数是（）A.30°B.60°C.45°D.75°二、填空题(共10题，共计30分)16、如图，在△ABC中，AB=AC=5，BC=8．若∠BPC= ∠BAC，则tan∠BPC=________．17、如图，在Rt△ABC中，∠ACB=90°，，CM是斜边AB的中线，将△ACM沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A=________.18、点P是菱形ABCD的对角线AC上的一个动点，已知AB=1，∠ADC=120°, 点M，N分别是AB，BC边上的中点，则△MPN的周长最小值是________.19、一个直角三角形斜边上的高与中线分别是5㎝和6㎝，则它的面积是________ .20、等腰三角形的两边长为3 和，那么它的周长为________．21、如图，已知，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE.点P，C，E在一条直线上，，M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时，点M、N之间的距离最短为________.22、在扇形纸片AOB中，∠AOB=90°，OA=4，将扇形纸片AOB按如图所示折叠，使对折后点A与点O重合，折痕为DE，则的长度为________．23、如图，Rt△ACB中，∠ACB=90°，AC=2BC=4，点P为AB边中点，点D为AC 边上不与端点重合的一动点，将△ADP沿着直线PD折叠得△PDE，若DE⊥AB，则AD的长度为________。

第24章 解直角三角形检测题（本检测题满分:120分，时间：120分钟）一、选择题（每小题2分，共24分） 1.计算:tan 45° + Sin 30° =（ ）2. 在直角三角形ABC 中，已知ZC = 9O% ZA = 40o, BC = 3,则AC = （） A. 3sin 40oB. 3sin 50oC. 3taιι 40oD. 3tail 50°3. （2013 <江温州中考）如图，在ZMBC 中，ZC=903AB = 5,3C = 3,则Sin A 的値是（）c∙l4•如图•四边形個S 是梯形，AD//BC. Ci 是Z 万C 的平分线，且ABLAa ZIg1, Q6,则 tan B≡（ ） 5.如图.Rt △遊中，ΛB = 9,BC = 6,ZB = 90o,将△磁折叠，使月点与庞的中点Q 重合. 折痕为MV,则线段Ey 的长为（）7.已知AD//BC^ AB 丄AP ，点E,点尸分别在射线初，射线兀上，若点E 与点B 关于AC 对称，点E 与点F 关于对称，AC 与3D 相交于点G •则（） A. 1+ tan ZADB = V∑C. ZAEB+22? = ZDEFA-2C. 一l + √3 2β∙iA. 2y 3B. 2vr2c∙τ第3題图C.4D. 56.在△/!恭中, 若三边 BU CA,曲满足 BC ： CA ： AB=5 : 12 : 13,则 COS 庆（12 13 D.Z13B. 2BC = 5CF D. 4cosZAGB = >∕62第5题图B第8题图第9题图8•河堤横断面如图所示，堤高於6 m,迎水坡曲的坡比为1 : v J,则曲的长为（A. 12 InB. 4√3 mC. 5√3 mD. 6√3 m9•如图∙ 一个小球由地而沿着坡度/=1：2的坡面向上前进了 10 m,此时小球距离地面的髙 度为（ ）•310.如图，在菱形ABCD 中，DE 丄ΛB ∙ cosA = - , BE=2,贝IJtanZDBE 的值是（）第17题图16. 已知等腰三角形的腰长为2,腰上的A. 5 mB. 2A /5 mA. 1B-2 c∙T11.已知直角三角形两直角边长之和为7,而积为6,则斜边长为（A. 5B- √37C. 712•如图•已知：45o<ZJ<90o,则下列各式成立的是（ ）A. Sin A=COS AB. Sin A>cos AC. Sin Λ>tan A->填空题（每小题3分，共18分）D. Sin A<cos A13•比较大小：8cos 31° _______ 届.（填“>—二”或 “V”）14. 如图，在△月氏中，Z 血¢30° , AB^Aa 肋是證边上的中线，Z M 决丄ZBAC 9CE 交朋于点E …交AD 于点氏若Be=‰则前的长 2 为 ___________ ・ 15. 如图，小兰想测量南塔的髙度，她在A 处仰望塔顶，测得仰角为 30° ,再往塔的方向前进50 m 至B 处，测得仰角为60° ,那么塔髙约为 ____________ 血（小兰身髙忽略不计，≈ 1.732）第Iel 题)高为1,则它的底角等于 ___________ ・17.图①是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的宜角三角形围成的，^AC =6, SC = 5,将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图②所示的“数学风车”，则这个风车的外围周长是 ________________________________ •18•在Rt△遊中，ZC二90° , AB^2BG现给出下列结论：①Sin A=—:②COS 5=1 ：③tan A=—:④tan 5=75 ,2 2 3苴中正确的结论是 ____________ •（只需填上正确结论的序号）三、解答题（共78分）19 （8分）计算下列各题:ω√2(2cos45β-s in60β)+^; (2) (-2)° -3tan30β+1√3 - 24 I21.（10分）如图.在一笔直的海岸线2上有乩万两个观测站，月在万的正东方向，AB-2 （单位：加）・有一艘小船在点P处，从E测得小船在北偏西60°的方向，从万测得小船在北偏东45°的方向・（1）求点P到海岸线』的距离：（2）小船从点尸处沿射线汕的方向航行一段时间后，到达点Q处，此时，从万测得小船在北偏西15°的方向•求点Q与点万之间的距离.（上述2小题的结果都保留根号）22.（10分）如图，为了测量某建筑物切的髙度，先在地面上用测角仪自月处测得建筑物顶部的仰角是30° ,然后在水平地而上向建筑物前进了 IoOllb此时自万处测得建筑物顶部的仰角是45°・已知测角仪的高度是1. 5 m,请你计算出该建筑物的髙度•（取√323.（8 分）如图，在梯形ABCD中，AD//BC. AB = CD = AD. BDLCD.（1）求SinZDBC的值：（2）若BC长度为4 cm,求梯形ABCD的而积.24.（10分）如图，在一次数学课外实践活动中，小文在点Q处测得树的顶端川的仰角为37° ,Q20 m,求树的高度月3（参考数据：Sin 37 ≈0.60, COS 37 ≈0.80, tan 37 ≈0.75 ）25.（10分）如图，在小山的东侧A处有一热气球，以每分钟30 m的速度沿着仰角为60。

第24章《解直角三角形》单元测试参考答案一．选择题（每小题3分，共24分）1答案：D．解：由α为锐角，且sinα=，得cosα===，tanα===，故选：D．2．答案：D．解：在直角△OAC中，OC=2，AC=3，则OA===，则sin∠AOB===．故选D．3．答案：A．解：在Rt△BDC中，BF=CF，∴DF=BC，Rt△ABC中，AE=CE，∴BE=AC，∵BC＜AC，∴BE＞DF，故选：A．4．答案：D．解：A、==3，是无理数；B、4π是无理数；C、sin45°=是无理数；D、==2，是有理数；故选D．5．答案：C．解：∵sin∠CAB===，∴∠CAB=45°．∵==，∴∠C′AB′=60°．∴∠CAC′=60°﹣45°=15°，鱼竿转过的角度是15°．故选：C．6．答案：C．解：作ME⊥OB于E，∵MD⊥OB，∠OMD=75°，∴∠MOD=15°，∵OM平分∠AOB，∴∠AOB=2∠MOD=30°，∵MC∥OB，∴∠ECM=∠AOB=30°，∴EM=MC=4，∵OM平分∠AOB，MD⊥OB，ME⊥OB，∴MD=ME=4，故选：C．7．答案：B．解：连接AH，CH，∵在四边形ABCD中，∠BCD=∠BAD=90°，H是BD的中点，∴AH=CH=BD．∵点G时AC的中点，∴HG是线段AC的垂直平分线，∴∠EGH=90°．∵∠BEC=80°，∴∠GEH=∠BEC=80°，∴∠GHE=90°﹣80°=10°．故选B．8．答案：C．解：如图：过点M作MN⊥AC于点N，根据题意得：∠MAN=60°﹣30°=30°，∠BCM=75°，∠DCA=60°，∴∠MCN=180°﹣75°﹣60°=45°，设MN=x米，在Rt△AMN中，AN==x（米），在Rt△CMN中，CN==x（米），∵AC=1000米，∴x+x=1000，解得：x=500（﹣1），∴AN=x≈634（米）．故选C．二．填空题（每小题3分，共24分）9．答案：55°．解：∵sinα=cos35°，∴α=90°﹣35°=55°，故答案为55°．10．答案：．解：∵A（﹣1，3），∴OA=，∴角α的余弦值为=；故答案为：．11．答案：0°＜∠A＜45°．解：∵∠A是Rt△ABC的一个内角，∴∠A＜90°，∵sinA＜，∴0°＜∠A＜45°．12．答案：．解：∵AD、BE分别是△ABC中BC、AC边上的高，∴∠BDA=∠ADC=90°，∴∠CBE=∠DAC，∵∠ADC=90°，AD=4，AC=6，∴CD=，∴sin，∴sin∠EBC=，故答案为：．13．答案：．解：令α=45°，β=30°，则sin15°=×﹣×，=．故答案为：．14．答案：1﹣．解：∵30°＜α＜β＜90°，∴cosβ＜cosα，cosβ＜．∴原式=|cosβ﹣cosα|+cosβ﹣+1﹣cosα=﹣cosβ+cosα+cosβ﹣+1﹣cosα=1﹣．故答案为：1﹣．15．答案：150a.解：如图，作BA边的高CD，设与BA的延长线交于点D，∵∠BAC=150°，∴∠DAC=30°，∵CD⊥BD，AC=30m，∴CD=15m，∵AB=20m，∴S△ABC=AB×CD=×20×15=150m2，∵每平方米售价a元，∴购买这种草皮的价格为150a 元．故答案为：150a．16．答案：．解：如图，延长AD交地面于E，过D作DF⊥CE于F．∵∠DCF=45°，∠A=60°，CD=4m，∴CF=DF=m，EF=DFtan60°=（m）．∵，∴（m）．三．解答题（８个小题，共72分）17. 解：（1）原式=4×﹣×+×=1+3；（2）原式=•+（）2﹣+2×=+﹣+=1+．18. 解：（1）如图，过点A作AD⊥BC于D，在Rt△ABD中，AB=10，sinB==，∴=，∴AD=6，在Rt△ACD中，由勾股定理得CD2=AC2﹣AD2，∴CD2=（2）2﹣62=16，∴CD=4，∴tanC===；（2）在Rt△ABD中，AB=10，AD=6，∴由勾股定理得BD=8，由（1）得CD=4，∴BC=BD+CD=12．19. 解：∵点E是Rt△ABC，Rt△ACD斜边AC的中点，∴BE=DE=AC=CE，DE⊥AC，∴∠ACB=∠EBC，∠BDE=∠EBD，又∵∠ACB=30°，∴∠AEB=∠EBC+∠ECB=30°+30°=60°∴∠BED=∠BEA+∠DEA=60°+90°=150°∴∠BDE=（180°﹣∠BED）=（180°﹣150°）=15°．20. 解：如图，PQ⊥AB于点C．∵在Rt△QBC中，QC：BC=5：12，∴设QC=5x米，BC=12x米，∵BQ=13米，∴（5x）2+（12x）2=132，∴x=±1（负值舍去），∴QC=5米，BC=12米．∵AB=8米，∴AC=AB+BC=20米．∵tanα=0.75，∴=0.75，即=0.75，∴PC=15．∴PQ=PC﹣QC=15﹣5=10米．答：香樟树PQ的高度为10米．21.解：如图，作BE⊥l于点E，DF⊥l于点F．根据题意，得BE=24mm，DF=48mm．在Rt△ABE中，sin，∴mm在Rt△ADF中，cos，∴mm．∴矩形ABCD的周长=2（40+60）=200mm．22．解：（1）作AD⊥OC，易知台风中心O与A市的最近距离为AD的长度，∵由题意得：∠DOA=45°，OA=60km，∴AD=DO=60÷=60km，∵60＞50，∴A市不会受到此台风的影响；（2）作BG⊥OC于G，∵由题意得：∠BOC=30°，OB=80km，∴BG=OB=40km，∵40＜50，∴会受到影响，如图：BE=BF=50km，由题意知，台风从E点开始影响B城市到F点影响结束，∴EG==30km，∴EF=2EG=60km，∵风速为40km/h，∴60÷40=1.5小时，∴影响时间约为1.5小时．23. 解：过点N作NF⊥AE于点F，则四边形NDEF为矩形，ND=EF，设BF=x米，在Rt△BMF中，∵∠BMF=30°，∴MF=BF=x，∵MN=10米，∴NF=x﹣10，∵∠ANF=45°，∴AF=NF=x﹣10，∴x﹣10+1.7=18.7，解得：x=9，则AB=AF﹣BF=17﹣9．即广告屏幕AB的长度为（17﹣9）米．24．解：（1）△A1A2B2是等边三角形，理由如下：连结A1B2．∵甲船以每小时30海里的速度向正北方向航行，航行20分钟到达A2，∴A1A2=30×=10，又∵A2B2=10，∠A1A2B2=60°，∴△A1A2B2是等边三角形；（2）如图，∵B1N∥A1A2，∴∠A1B1N=180°﹣∠B1A1A2=180°﹣105°=75°，∴∠A1B1B2=75°﹣15°=60°．∵△A1A2B2是等边三角形，∴∠A2A1B2=60°，A1B2=A1A2=10，∴∠B1A1B2=105°﹣60°=45°．在△B1A1B2中，∵A1B2=10，∠B1A1B2=105°﹣60°=45°，∠A2A1B2=60°，由阅读材料可知，=，解得B1B2==，所以乙船每小时航行：÷=20海里．。

九年级数学上册第24章解直角三角形检测卷华东师大版有答案第24章检测题(时间：100分钟满分：120分)一、精心选一选(每小题3分，共30分)1．如图，在平面直角坐标系中，直线OA过点(2，1)，则tanα的值是( C )A.55B.5C.12 D．2,第1题图) ,第2题图) ,第3题图) ,第4题图)2．河堤横断面如图所示，堤高BC＝5米，迎水坡AB的坡比为1∶3(坡比是坡面的铅直高度BC与水平宽度AC之比)，则AC的长是( A ) A．53米 B．102米 C．15米 D．10米3．如图，正方形ABCD中，对角线AC，BD交于点O，点M，N分别为OB，OC的中点，则cos∠OMN的值为( B )A.12B.22C.32 D．14．如图，在矩形ABCD中，DE⊥AC于E，设∠ADE＝α，且cosα＝35，AB＝4，则AC的长为( C )A．3 B.165 C.203 D.1635．如图，在四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，BC＝2，CD＝3，则AB＝( D )A．4 B．5 C．23 D.833,第5题图) ,第9题图) ,第10题图)6．在△ABC中，若sinA＝32，tanB＝1，则这个三角形是( A ) A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形7．式子2cos30°－tan45°－（1－tan60°）2的值是( B )A．23－2 B．0 C．23 D．28．李红同学遇到了这样一道题：3tan(α＋20°)＝1，你认为锐角α的度数应是( D )A．40° B．30° C．20° D．10°9．为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图图形，其中AB⊥BE，EF⊥BE，AF交BE于D，C在BD上．有四位同学分别测量出以下四组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B间距离的有( C )A．1组 B．2组 C．3组 D．4组10．如图，某人在大楼30米高(即PH＝30米)的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡角i为1∶3，点P，H，B，C，A在同一个平面上，点H，B，C 在同一条直线上，且PH⊥HC.则A，B两点间的距离是( B )A．15米 B．203米 C．202米 D．103米二、细心填一填(每小题3分，共24分)11．若α为锐角，cosα＝35，则sinα＝__45__，tanα＝__43__．12．在Rt△ABC中，∠C＝90°，tanA＝512，△ABC的周长为18，则S△ABC＝__545__．13．在△ABC中，若|2cosA－1|＋(3－tanB)2＝0，则∠C＝__60°__．14．如图，在顶角为30°的等腰三角形ABC中，AB＝AC，若过点C作CD⊥AB于点D，则∠BCD＝15°，根据图形计算tan15°＝__2－3__．,第14题图) ,第15题图) ,第16题图) ,第17题图) 15．(2017•仙桃)为加强防汛工作，某市对一拦水坝进行加固．如图，加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB＝12米，背水坡面CD＝123米，∠B＝60°，加固后拦水坝的横断面为梯形ABED，tanE＝3133，则CE的长为__8__米．16．如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC.若BD＝8，AC＝6，∠BOC＝120°，则四边形ABCD的面积为__123__．(结果保留根号)17．如图，在Rt△ABC中，∠C＝90°，AC＝3，tanA＝43.点D，E分别是边BC，AC上的点，且∠EDC＝∠A.将△ABC沿DE所在直线对折，若点C恰好落在边AB上，则DE的长为__12548__．18．(2017•舟山)如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C＝1，tan∠BA2C＝13，tan∠BA3C＝17，计算tan∠BA4C＝__113__，…按此规律，写出tan∠BAnC＝__1n2－n＋1__(用含n的代数式表示)．三、用心做一做(共66分)19．(10分)解下列各题：(1)先化简，再求代数式(1x＋x＋1x)÷x＋2x2＋x的值，其中x＝3cos30°＋12；解：原式＝x＋1，当x＝2时，原式＝3(2)已知α是锐角，且sin(α＋15°)＝32.计算8－4cosα－(π－3.14)0＋tanα＋(13)－1的值．解：α＝45°，原式＝320．(8分)解下列各题：(1)已知∠A，∠B，∠C是锐角三角形ABC的三个内角，且满足(2sinA －3)2＋tanB－1＝0，求∠C的度数；解：75°(2)(原创题)已知tanα的值是方程x2－x－2＝0的一个根，求式子3sinα－cosα2cosα＋sinα的值．解：∵方程的根为x1＝2，x2＝－1.又∵tanα＞0，∴tanα＝2，∴原式＝3tanα－12＋tanα＝3×2－12＋2＝5421．(10分)如图，在△ABC中，AD是BC上的高，tanB＝cos∠DAC.(1)求证：AC＝BD；(2)若sinC＝1213，BC＝12，求AD的长．解：(1)∵AD是BC上的高，∴AD⊥BC，∴∠ADB＝90°，∠ADC＝90°，在Rt△ABD和Rt△ADC中，∵tanB＝ADBD，cos∠DAC＝ADAC，又tanB ＝cos∠DAC，∴ADBD＝ADAC，∴AC＝BD (2)在Rt△ADC中，sinC＝1213，故可设AD＝12k，AC＝13k，∴CD＝AC2－AD2＝5k.∵BC＝BD＋CD，AC＝BD，∴BC＝13k＋5k＝18k，∴18k＝12，∴k＝23，∴AD＝12k ＝12×23＝822．(8分)(2017•绍兴)如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°，教学楼底部B 的俯角为20°，量得实验楼与教学楼之间的距离AB＝30 m.(1)求∠BCD的度数；(2)求教学楼的高BD.(结果精确到0.1 m，参考数据：tan20°≈0.36，tan18°≈0.32)解：(1)过点C作CE⊥BD，则有∠DCE＝18°，∠BCE＝20°，∴∠BCD ＝∠DCE＋∠BCE＝18°＋20°＝38°(2)由题意得：CE＝AB＝30 m，在Rt△CBE中，BE＝CE•tan20°≈10.80(m)，在Rt△CDE中，DE＝CE •tan18°≈9.60(m)，∴教学楼的高BD＝BE＋DE＝10.80＋9.60≈20.4(m)，则教学楼的高约为20.4 m23．(8分)(2017•南京)如图，港口B位于港口A的南偏东37°方向，灯塔C恰好在AB的中点处．一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行5 km到达E处，测得灯塔C 在北偏东45°方向上，这时，E处距离港口A有多远？(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)解：过C作CH⊥AD于H.设CH＝x km，在Rt△ACH中，∠A＝37°，∵tan37°＝CHAH，∴AH＝CHtan37°＝xtan37°，在Rt△CEH中，∵∠CEH＝45°，∴CH＝HD. ∵CH⊥AD，BD⊥AD，∴CH∥BD，∴AHHD＝ACCB. ∵AC＝CB，∴AH＝HD，∴xtan37°＝x＋5，∴x＝5•tan37°1－tan37°≈15，∴AE＝AH＋HE＝15tan37°＋15≈35(km)，∴E处距离港口A有35 km24．(10分)(2017•内江)如图，某人为了测量小山顶上的塔ED的高，他在山下的点A处测得塔尖点D的仰角为45°，再沿AC方向前进60 m到达山脚点B，测得塔尖点D的仰角为60°，塔底点E的仰角为30°，求塔ED的高度．(结果保留根号)解：由题知，∠DBC＝60°，∠EBC＝30°，∴∠DBE＝∠DBC－∠EBC ＝60°－30°＝30°.又∵∠BCD＝90°，∴∠BDC＝90°－∠DBC＝90°－60°＝30°.∴∠DBE＝∠BDE.∴BE＝DE.设EC＝x m．则DE＝BE＝2EC＝2x m，DC＝EC＋DE＝x＋2x＝3x m，BC＝BE2－EC2＝（2x）2－x2＝3x，由题知，∠DAC＝45°，∠DCA＝90°，AB＝60，∴△ACD 为等腰直角三角形，∴AC＝DC.∴3x＋60＝3x，解得：x＝30＋103，2x＝60＋203.答：塔高约为(60＋23) m25．(12分)(2017•资阳)如图，光明中学一教学楼顶上竖有一块高为AB的宣传牌，点E和点D分别是教学楼底部和外墙上的一点(A，B，D，E在同一直线上)，小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°，同时测得教学楼外墙外点D的仰角为30°，从点C沿坡度为1∶3的斜坡向上走到点F时，DF正好与水平线CE平行．(1)求点F到直线CE的距离(结果保留根号)；(2)若在点F处测得宣传牌顶部A的仰角为45°，求出宣传牌AB的高度(结果精确到0.01)．(注：sin67°≈0.92，tan67°≈2.36，2≈1.41，3≈1.73)解：(1)过点F作FH⊥CE于H.∵FH∥DE，DF∥HE，∠FHE＝90°，∴四边形FHED是矩形，则FH＝DE，在Rt△CDE中，DE＝CE•tan∠DCE ＝9×tan30°＝33(米)，∴FH＝DE＝33(米)．答：点F到CE的距离为33米(2)∵CF的坡度为1∶3，∴在Rt△FCH中，CH＝3FH＝9(米)，∴EH＝DF＝18(米)，在Rt△BCE中，BE＝CE•tan∠BCE＝9×tan67°≈21.24(米)，∴AB＝AD＋DE－BE＝18＋33－21.24≈1.95(米)．答：宣传牌AB的高度约为1.95米。

华师大版九年级数学上册期末专题：第24章解直角三角形单元检测试卷一、单选题（共10题；共30分）1.在△ABC中，∠C=90°，BC=3，AC=4，则sinA的值是（）A. B. C. D.2.一个三角形的两边长分别是3和7，且第三边长为整数，这样的三角形周长最大的值为（）A. 15B. 16C. 18D. 193.为测量某河的宽度，小军在河对岸选定一个目标点A，再在他所在的这一侧选点B，C，D，使得AB⊥BC，CD⊥BC，然后找出AD与BC的交点E．如图所示，若测得BE=90m，EC=45m，CD=60m，则这条河的宽AB等于（）A. 120mB. 67.5mC. 40mD. 30m4.等腰三角形的周长为20cm，腰长为x cm，底边长为y cm，则底边长与腰长之间的函数关系式为（）A. y=20﹣x（0＜x＜10）B. y=20﹣x（10＜x＜20）C. y=20﹣2x（10＜x＜20）D. y=20﹣2x（5＜x＜10）5.一段拦水坝横断面如图所示，迎水坡AB的坡度为i=1：，坝高BC=6m，则坡面AB的长度（）A. 12mB. 18mC. 6D. 126.汶川地震后，抢险队派一架直升飞机去A、B两个村庄抢险，飞机在距地面450米上空的P点，测得A村的俯角为30°，B村的俯角为60°（如图）则A，B两个村庄间的距离是（）米．A. 300B. 900C. 300D. 3007.如图，小明晚上由路灯A下的点B处走到点C处时，测得自身影子CD的长为1米，他继续往前走3米到达点E处（即CE=3米），测得自己影子EF的长为2米，已知小明的身高是1.5米，那么路灯A的高度AB是（）A. 4.5米B. 6米C. 7.2米D. 8米8.一个三角形的两边长为2和6，第三边为偶数，则这个三角形的周长为（）A. 10B. 12C. 14D. 169.如图，斜面AC的坡度（CD与AD的比）为1：2，AC=3 米，坡顶有旗杆BC，旗杆顶端B点与A点有一条彩带相连．若AB=10米，则旗杆BC的高度为（）A. 5米B. 6米C. 8米D. （3+ ）米10.如图，在□ABCD中，AB∶AD=3∶2，∠ADB=60°，那么cosＡ的值等于（）A. B. C. D.二、填空题（共10题；共33分）11.小凡沿着坡角为30°的坡面向下走了2米，那么他下降________米．12.已知一个等腰三角形的两边长分别为3和6，则该等腰三角形的周长是________．13.如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=30°，AC=1，则BB′的长为________．14.如图,在直角坐标系中,P是第二象限的点,其坐标是(x,8),且OP与x轴的负半轴的夹角α的正切值是 ,则x=________,cosα=________.15.在Rt△ABC中，∠C=90°，如果AC=4，sinB=，那么AB=________16.高4 m的旗杆在水平地面上的影子长6 m，此时测得附近一个建筑物的影长24 m，则该建筑物的高是________m.17.tan________ °=0.7667．18.如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于________．19.如图，将两块直角三角形的一条直角边重合叠放，已知AC=BC= +1，∠D=60°，则两条斜边的交点E到直角边BC的距离是________．20.已知当x1=a，x2=b，x3=c时，二次函数y= x2+mx对应的函数值分别为y1，y2，y3，若正整数a，b，c恰好是一个三角形的三边长，且当a＜b＜c时，都有y1＜y2＜y3，则实数m的取值范围是________．三、解答题（共8题；共57分）21.如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？22.小宇想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°．若直线AB与EF之间的距离为60米，求A、B 两点的距离．23.如图，为了测量出楼房AC的高度，从距离楼底C处60 米的点D（点D与楼底C在同一水平上）出发，沿斜面坡度为i=l：的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53 °，求楼房AC的高度（参考数据：sin53 °= , cos53 °= , tan53 °= ，≈1.732，结果精确到0.1米）24.如图，平台AB高为12m，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD 的高度（=1.7）．25.“蘑菇石”是我国著名的自然保护区梵净山的标志，小明从山脚B点先乘坐缆车到达观景平台DE观景，然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点，“蘑菇石”A点到水平面BC的垂直距离为1890m．如图，DE∥BC，BD=1800m，∠DBC=80°，求斜坡AE的长度．（结果精确到0.1m，可参考数据sin29°≈0.4848，sin80°≈0.9848，cos29°≈0.8746，cos80°≈0.1736）26.在一次数学活动课上，老师带领同学们去测量一座古塔CD的高度．他们首先从A处安置测倾器，测得塔顶C的仰角∠CFE=21°，然后往塔的方向前进50米到达B处，此时测得仰角∠CGE=37°，已知测倾器高1.5米，请你根据以上数据计算出古塔CD的高度．（参考数据：sin37°≈ ，tan37°≈ ，sin21°≈ ，tan21°≈ ）27.在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE＝CG，BF＝DH，连结EF、FG、GH、HE．（1）求证：四边形EFGH为平行四边形；（2）若矩形ABCD是边长为1的正方形，且∠FEB＝45°，tan∠AEH＝2，求AE的长．28.如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．答案解析部分一、单选题1.【答案】B【考点】锐角三角函数的定义【解析】【解答】解：在△ABC中，∠C=90°，∵AC=4，BC=3，∴AB= =5．∴sinA= ，故答案为：B．【分析】先根据勾股定理算出AB，再根据正切定义得出结论。

九年级数学上学期：第24章检测题(时间：100分钟 满分：120分)一、选择题(每小题3分，共30分)1．在平面直角坐标系内有一点P(3，4)，若OP 与x 轴正半轴的夹角为α，下列结论正确的是( A )A ．tan α＝43B ．tan α＝45C ．sin α＝35D ．cos α＝542．(三明中考)如图，在Rt △ABC 中，斜边AB 的长为m ，∠A ＝35°，则直角边BC 的长是( A )A ．m sin35°B ．m cos35° C.m sin35° D.mcos35° ,第2题图) ,第5题图),第7题图)3．计算6tan 45°－2cos 60°的结果是( D )A ．4 3B ．4C ．5 3D ．54．在Rt △ABC 中，∠C ＝90°，sin A ＝513，则tan B 的值为( D ) A.1213 B.512 C.1312 D.1255．如图，网格中的小正方形的边长均为1，点A ，B ，O 都在格点上，则∠A 的正弦值是( D )A.3510B.12C.255D.556．如果∠A，∠B 均为锐角，且2sin A －1＋(3tan B －3)2＝0，那么△ABC 是( B )A ．锐角三角形B ．直角三角形C ．等边三角形D ．钝角三角形 7．如图，河堤横断面迎水坡AB 的坡比是1∶3，堤高BC ＝10 m ，则坡面AB 的长度是( C )A ．15 mB ．20 3 mC ．20 mD ．10 3 m8．如图，CD 是平面镜，光线从A 点射出，经CD 上点E 反射后照射到B 点，若入射角为α，AC ⊥CD ，BD ⊥CD ，垂足分别为C ，D ，且AC ＝3，BD ＝6，CD ＝11，则tan α的值为( D )A.113B.311C.911D.119,第8题图) ,第9题图),第10题图)9．江津四面山是国家5A 级风景区，里面有一个景点被誉为亚洲第一岩——土地神岩，土地神岩壁画高度从石岩F 处开始一直竖直到山顶E 处，为了测量土地神岩上壁画的高度，小明从山脚A 处，沿坡度i ＝0.75的斜坡上行65米到达C 处，在C 处测得山顶E 处仰角为26.5°，再往正前方水平走15米到达D 处，在D 处测得壁画底端F 处的俯角为42°，壁画底端F 处距离山脚B 处的距离是12米，A ，B ，C ，D ，E ，F 在同一平面内，A ，B 在同一水平线上，EB ⊥AB ，根据小明的测量数据，则壁画的高度EF 为(精确到0.1米，参考数据：sin 26.5°≈0.45，cos 26.5°≈0.9，tan 26.5°≈0.5，sin 42°≈0.67，cos 42°≈0.74，tan 42°≈0.9)(A)A ．49.5米B ．68.7米C ．69.7米D ．70.2米10．如图，从点A 处观测一山坡上的电线杆PQ ，测得电线杆顶端P 的仰角是45°，向前走6 m 到达B 点，测得电线杆顶端P 和底端Q 的仰角分别是60°和30°，则该电线杆PQ 的高度(A) A ．6＋2 3 B ．6＋ 3 C ．10－ 3 D ．8＋ 3二、填空题(每小题3分，共24分)11．计算：tan 45°－13(3－1)0＝__23__． 12．如图，某山坡的坡面AB ＝200米，坡角∠BAC＝30°，则该山坡的高BC 的长为__100__米．13．如图，∠B ＝∠C，DE ⊥BC 于E ，EF ⊥AB 于F ，∠ADE 等于140°，∠FED ＝__50°__．,第12题图) ,第13题图),第14题图)14．如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE ＝6 cm ，sin A ＝35，则菱形ABCD 的面积是__60__cm 2.15．将一副三角尺按如图所示叠放在一起，则BE EC 的值是__33__． 16．如图，△ABC 的顶点A ，C 的坐标分别是(0，4)，(3，0)，且∠ACB＝90°，∠B ＝30°，则顶点B 的坐标是__(3＋43，33)__．,第15题图) ,第16题图),第18题图)17．在△ABC 中，AB ＝4，BC ＝3，∠BAC ＝30°，则△ABC 的面积为__23＋5或23－5__．18．为解决停车难的问题，在如图一段长56米的路段开辟停车位，每个车位是长5 米，宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出__17__个这样的停车位．(2≈1.4)三、解答题(共66分)19．(8分)计算：(1)(－12)0＋(13)－1·23－|tan 45°－3|； (2)24sin 45°＋cos 230°－12·tan 60°＋2sin 60°.解：2＋3 解：1＋53620．(8分)如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sin C 的值．解：121321．(8分)(2018·岳阳)图1是某小区入口实景图，图2是该小区入口抽象成的平面示意图．已知入口BC 宽3.9米，门卫室外墙AB 上的O 点处装有一盏路灯，点O 与地面BC 的距离为3.3米，灯臂OM 长为1.2米(灯罩长度忽略不计)，∠AOM ＝60°.(1)求点M 到地面的距离；(2)某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏CD 保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由．(参考数据：3≈1.73，结果精确到0.01米)解：(1)如图，过M 作MN⊥AB 于N ，交BA 的延长线于N ，在Rt △OMN 中，∠NOM ＝60°，OM＝1.2，∴∠M＝30°，∴ON＝12OM＝0.6，∴NB＝ON＋OB＝3.3＋0.6＝3.9，即点M到地面的距离是3.9米．(2)取CE＝0.65，EH＝2.55，∴HB＝3.9－2.55－0.65＝0.7，过H作GH⊥BC，交OM于G，过O作OP⊥GH于P.∵∠GOP＝30°，∴tan30°＝GPOP＝33，∴GP＝33OP＝1.73×0.73≈0.404，∴GH＝3.3＋0.404＝3.704≈3.70＞3.5，∴货车能安全通过．22．(10分)(2018·铁岭)如图，某地质公园中有两座相邻小山．游客需从左侧小山山脚E处乘坐竖直观光电梯上行100米到达山顶C处，然后既可以沿水平观光桥步行到景点P 处，也可以通过滑行索道到达景点Q处，在山顶C处观测坡底A的俯角为75°，观测Q处的俯角为30°，已知右侧小山的坡角为30°.(图中的点C，E，A，B，P，Q均在同一平面内，点A，Q，P在同一直线上)(1)求∠CAP的度数及CP的长度；(2)求P，Q两点之间的距离．(结果保留根号)解：(1)∵PC∥AB，∴∠APC＝∠PAB＝30°，∴∠CAP＝180°－75°－30°＝75°，∴∠CAP＝∠PCA，∴PC＝AP，过P作PF⊥AB于F，则PF＝CE＝100，∴PA＝2PF＝200米，∴PC＝PA＝200米．(2)∵∠PCQ＝∠QPC＝30°，∴CQ＝PQ.过Q作QH⊥PC于H，∴PH＝12PC＝100，∴PQ＝PHcos30°＝20033米．答：P，Q两点之间的距离是20033米．23．(8分)(2018·镇江)如图，校园内有两幢高度相同的教学楼AB，CD，大楼的底部B，D在同一平面上，两幢楼之间的距离BD长为24米，小明在点E(B，E，D在一条直线上)处测得教学楼AB顶部的仰角为45°，然后沿EB方向前进8米到达点G处，测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F，H距离地面的高度均为1.6米，求教学楼AB的高度．(精确到0.1米，参考值：2≈1.41，3≈1.73)解：延长HF交CD于点N，延长FH交AB于点M，如右图所示，由题意可得，MB＝HG＝FE＝ND＝1.6 m，HF＝GE＝8 m，MF＝BE，HN＝GD，MN＝BD＝24 m，设AM＝x m，则CN＝x m，在Rt△AFM中，MF＝AMtan45°＝x1＝x，在Rt△CNH中，HN＝CNtan30°＝x33＝3x，∴HF＝MF＋HN－MN＝x＋3x－24，即8＝x＋3x－24，解得x≈11.7，∴AB＝11.7＋1.6＝13.3 m，答：教学楼AB的高度AB长13.3 m.24.(12分)为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度，一天，我两艘海监船刚好在我某岛东西海岸线上的A ，B 两处巡逻，同时发现一艘不明国籍的船只停在C 处海域．如图所示，AB ＝60(6＋2)海里，在B 处测得C 在北偏东45°的方向上，A 处测得C 在北偏西30°的方向上，在海岸线AB 上有一灯塔D ，测得AD ＝120(6－2)海里．(1)分别求出A 与C 及B 与C 的距离AC ，BC ；(结果保留根号)(2)已知在灯塔D 周围100海里范围内有暗礁群，我在A 处海监船沿AC 前往C 处盘查，途中有无触礁的危险？(参考数据：2≈1.41，3≈1.73，6≈2.45)解：(1)过点C 作CE⊥AB 于点E ，可得∠CBD ＝45°，∠CAD ＝60°，设CE ＝x ，在Rt△CAE 中，AE ＝CE·tan30°＝33x ，在Rt △BCE 中，BE ＝CE ＝x ，∵AB ＝60(6＋2)海里，∴x ＋33x ＝60(6＋2)，解得x ＝606，则AC ＝233x ＝1202，BC ＝2x ＝1203，答：A 与C 的距离为1202海里，B 与C 的距离为1203海里．(2)过点D 作DF⊥AC 于点F ，在△AD F 中，∵AD ＝120(6－2)，∠CAD ＝60°，∴DF ＝ADsin60°＝1802－606≈106.8＞100，故海监船沿AC 前往C 处盘查，无触礁的危险．25．(12分)如图，已知斜坡AB 长602米，坡角(即∠BAC)为45°，BC ⊥AC ，现计划在斜坡中点D 处挖去部分斜坡，修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE.(1)若修建的斜坡BE 的坡比为3∶1，求休闲平台DE 的长是多少米？(2)一座建筑物GH 距离A 点33米远(即AG ＝33米)，小亮在D 点测得建筑物顶部H 的仰角(即∠HDM)为30°，点B ，C ，A ，G ，H 在同一个平面内，点C ，A ，G 在同一条直线上，且HG⊥CG，问建筑物GH 高为多少米？解：(1)∵FM∥CG ，∴∠BDF ＝∠BAC ＝45°.∵斜坡AB 长602，D 是AB 的中点，∴BD ＝30 2.在△BDF 中，DF ＝BD ·cos ∠BDF ＝30，BF ＝DF ＝30.∵斜坡BE 的坡比为3∶1，∴BF EF ＝31，∴EF ＝103，∴DE ＝DF －EF ＝30－103，即休闲平台DE 的长是(30－103)米． (2)设GH ＝x 米，则MH ＝GH －GM ＝x －30，DM ＝AG ＋AP ＝33＋30＝63.在Rt △DMH 中，tan30°＝MH DM ，即x －3063＝33，解得x ＝30＋213，则建筑物GH 的高为(30＋213)米．。

第24章 解直角三角形检测题知己知彼，百战不殆。

《孙子兵法·谋攻》 樱落学校 曾泽平（本检测题满分:120分，时间：120分钟） 一、选择题（每小题2分，共24分） 1.计算：错误!未找到引用源。

A.错误!未找到引用源。

B.232+ C.23D.231+ 2.在直角三角形ABC 中，已知90C ∠=︒，40A ∠=︒，3BC =，则AC =( ) A.3sin 40︒ B.3sin 50︒ C.3tan 40︒ D.3tan 50︒ 3.（2013·浙江温州中考）如图，在ABC △中，90,5,3,∠C AB BC =︒==则sin A 的值是（ ）A.34B.34 C.35 D.454.如图，四边形ABCD 是梯形，AD ∥BC ，CA 是∠BCD 的平分线，且AB ⊥AC ，AB =4，AD =6，则tan B =( ) A.2错误!未找到引用源。

B.2错误!未找到引用源。

C.错误!未找到引用源。

D.错误!未找到引用源。

5.如图，Rt △ABC 中，9,6,AB BC B ==∠=9°，将△ABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，则线段BN 的长为（ ） A.53B.52C.4D.56.在△ABC 中，若三边BC ，CA ，AB 满足 BC ∶CA ∶AB =5∶12∶13，则cos B =错误!未找到引用源。

（ ）A.125 B.512 C.135 D.13127.已知AD BC ∥，AB AD ⊥，点E ,点F 分在射线AD ，射线BC 上，若点E 与点B 关于AC 对称，点E 与点F 关于BD 对，AC 与BD 相交于点G ，则（ ） A.1tan 2ADB +∠= B.25BC CF = C.22AEB DEF ∠+︒=∠ D.4cos 6AGB ∠=第7题图8.河堤横断面如图所示，堤高BC =6 m ，迎水坡AB 的坡比为1∶错误!未找到引用源。

第24章知识升华一、知识脉络：二、典例分析：例1 在Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，CD ⊥AB 于点D ，求∠BCD 的四个三角函数值．【分析】求∠BCD 的四个三角函数值，关键要弄清其定义，由于∠BCD 是在Rt △BCD 中的一个内角，根据定义，仅一边BC 是已知的，此时有两条路可走，一是设法求出BD 和CD ，二是把∠BCD 转化成∠A ，显然走第二条路较方便，因为在Rt △ABC 中，三边均可得出，利用三角函数定义即可求出答案．【解】 在Rt △ABC 中，∵ ∠ACB ＝90°∴∠BCD ＋∠ACD ＝90°，∵CD ⊥AB ，∴∠ACD ＋∠A ＝90°，∴∠BCD ＝∠A ．在Rt △ABC 中，由勾股定理得，AB ＝22AC BC ＝10，∴sin ∠BCD =sinA =BC AB =45 ，cos ∠BCD =cosA =AC AB =35 ，tan ∠BCD =tanA =BC AC =43 ，cot ∠BCD =cotA =AC BC =34．【说明】本题主要是要学生了解三角函数定义，把握其本质，应强调转化的思想，即本题中角的转换．例2 如图，在电线杆上的C 处引拉线CE 、CF 固定电线杆，拉线CE 和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪离AB为1.5米，求拉线CE的长．（结果保留根号）【分析】求CE的长，此时就要借助于另一个直角三角形，故过点A作AG⊥CD，垂足为G，在Rt△ACG中，可求出CG，从而求得CD，在Rt△CED中，即可求出CE的长．【解】过点A作AG⊥CD，垂足为点G，在Rt△ACG中，∵∠CAG＝30°，BD＝6，∴tan30°=CGAG，∴CG=6×33=2 3 ，∴CD=2 3 +1.5，在Rt△CED中，sin60°=CDEC，∴EC=CDsin60°=23+1.53=4+ 3 ．答：拉线CE的长为4+ 3 米．【说明】在直角三角形的实际应用中，利用两个直角三角形的公共边或边长之间的关系，往往是解决这类问题的关键，在复习过程中应加以引导和总结．例3 如图，某县为了加固长90米，高5米，坝顶宽为4米的迎水坡和背水坡，它们是坡度均为1∶0.5，橫断面是梯形的防洪大坝，现要使大坝顺势加高1米，求⑴坡角的度数；⑵完成该大坝的加固工作需要多少立方米的土？【分析】大坝需要的土方＝橫断面面积×坝长；所以问题就转化为求梯形ADNM的面积，在此问题中，主要抓住坡度不变，即MA与AB的坡度均为1∶0.5．【解】⑴∵i=tanB，即tanB=10.5=2，∴∠B=63.43°．⑵过点M、N分别作ME⊥AD，NF⊥AD，垂足分别为E、F．由题意可知：ME＝NF＝5，∴MEAE＝10.5，∴AE＝DF＝2.5，∵AD=4，∴MN=EF=1.5，∴S梯形ADNM＝12(1.5+4)×1＝2.75．∴需要土方为2.75×90=247.5 (m3) ．【说明】本题的关键在于抓住前后坡比不变来解决问题，坡度＝垂直高度水平距离 ＝坡角的正切值．例4 某风景区的湖心岛有一凉亭A ，其正东方向有一棵大树B ，小明想测量A 、B 之间的距离，他从湖边的C 处测得A 在北偏西45°方向上，测得B 在北偏东32°方向上，且量得B 、C 间距离为100米，根据上述测量结果，请你帮小明计算A 、B 之间的距离．（结果精确到1米，参考数据：sin 32°≈0.5299，cos 32°≈0.8480，tan s 32°≈0.6249，cot 32°≈1.600）【分析】本题涉及到方位角的问题，要解出AB 的长，只要去解Rt △ADC 和Rt △BDC 即可． 【解】过点C 作CD ⊥AB ，垂足为D ．由题知：∠α=45°，∠β=32°．在Rt △BDC 中，sin 32°=BD BC ，∴BD ＝100sin 32°≈52.99．cos 32°=CDBC，∴CD =100 cos 32°≈84.80．在Rt △ADC 中，∵∠ACD =45°，∴AD =DC =84.80． ∴AB =AD +BD ≈138米．答：AB 间距离约为138米．【说明】本题中涉及到方位角的问题，画图是本题的难点，找到两个直角三角形的公共边是解题的关键，在复习中应及时进行归纳、总结由两个直角三角形构成的各种情形．例5 在某海滨城市O 附近海面有一股台风，据监测，当前台风中心位于该城市的东偏南70°方向200千米的海面P 处，并以20千米/ 时的速度向西偏北25°的PQ 的方向移动，台风侵袭范围是一个圆形区域，当前半径为60千米，且圆的半径以10千米/ 时速度不断扩张．(1)当台风中心移动4小时时，受台风侵袭的圆形区域半径增大到 千米；又台风中心移动t 小时时，受台风侵袭的圆形区域半径增大到 千米．(2)当台风中心移动到与城市O 距离最近时，这股台风是否侵袭这座海滨城市？请说明理由(参考数据2 1.41≈，3 1.73≈)．【分析】先要计算出OH 和PH 的长，即可求得台风中心移动时间，而后求出台风侵袭的圆形区域半径，此圆半径与OH 比较即可．【解】⑴100； (6010)t +．⑵作OH ⊥PQ 于点H ，可算得1002141OH =（千米），设经过t 小时时，台风中心从P 移动到H ，则201002PH t ==，算得52t =（小时），此时，受台风侵袭地区的圆的半径为：601052130.5+⨯≈（千米）＜141（千米）．∴城市O 不会受到侵袭．【说明】本题是在新的情境下涉及到方位角的解直角三角形问题，对于此类问题常常要构造直角三角形，利用三角函数知识来解决．第24章测试题设计一、选择题：1、某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（ ） A ．8米B ．83米C ．833米 D ．433米 2、如图，ABC △中BC 边上的高为1h ，DEF △中DE 边上的高为2h ，下列结论正确的是（ ） A ．12h h >B ．12h h <C ．12h h =D ．无法确定3、已知在ABC △中，90C ∠=，设sinB n =，当B ∠是最小的内角时，n 的取值范围是 A ．202n <<B ．102n << C ．303n << D ．302n << 4、如图，矩形ABCD 中，AB ＞AD ，AB =a ，AN 平分∠DAB ，DM ⊥AN 于点M ，CN ⊥AN 于点N ．则DM +CN 的值为（用含a 的代数式表示）( )A ．aB ．a 54C ．a 22D ． a 23 5、已知α为锐角，则m =sinα+cosα的值（ ） A ．m ＞1B ．m =1C ．m ＜1D ．m ≥16、如果方程2430x x -+=的两个根分别是Rt△ABC 的两条边，△ABC 最小的角为A ，那么tan A 的值为（ ）． A、34或13B 、24C 、13D 、13或247、已知α为锐角，且cos （90°－α）＝3，则α的度数为（ ） A ．30° B ．60° C ．45° D ．75° 8、如图，在Rt △ABC 中，∠C =90°， AM 是BC 边上的中线，53sin =∠CAM ，则B ∠tan 的值为( )．A 、32 B 、34 C 、12D 、139、在△ABC 中，AB =8，∠ABC =30°，AC =5，那么BC 的长等于（ ）A 、43B 、43+3C 、43－3D 、43+3或43－3 10、如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m（即小颖的眼睛距地面的距离），那么这棵树高是（ ） A ．（5332+）m B ．（3532+）m C ． 53m D ．4m二、填空题：11、如图所示，小华同学在距离某建筑物6米的点A 处测得广告牌B 点．C 点的仰角分别为52°和35°，则广告牌的高度BC 为_____________米(精确到0.1米)．(sin35°≈0.57，cos35°≈0.82，tan35°≈0.70；sin52°≈0.79，cos52°≈0.62，tan52°≈1.28)12、长为4m 的梯子搭在墙上与地面成45°角，作业时调整为60°角（如图所示），则梯子的顶端沿墙面升高了 m ．13、如图，在Rt △ABC 中，∠ACB=90°，∠A ＜∠B ，沿△ABC 的中线CM 将△CMA 折叠，使点A 落在点D 处，若CD 恰好与MB 垂直，则tanA 的值为 ．14、某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为52米，则这个坡面的坡度为_________.15、如图，是一张宽m 的矩形台球桌ABCD ，一球从点M （点M 在长边CD 上）出发沿虚线MN 射向边BC ，然后反弹到边AB 上的P 点. 如果MC n =，CMN α∠=.那么P 点与B 点的距离为 .16、如图所示，某河堤的横断面是梯形ABCD ，BC AD ∥，迎水坡AB 长13米，且12tan 5BAE ∠=，则河堤的高BE 为 米．17、如图，小明同学在东西方向的环海路A 处，测得海中灯塔P 在北偏东60°方向上，在A 处东500米的B 处，测得海中灯塔P 在北偏东30°方向上，则灯塔P 到环海路的距离PC ＝ 米（用根号表示）．18、水管的外部需要包扎，包扎时用带子缠绕在管道外部.若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD 时的∠ABC ，其中AB 为管道侧面母线的一部分）.若带子宽度为1，水管直径为2，则α的余弦值为 .19、如图，在Rt △ABC 中，∠CAB =90°，AD 是∠CAB 的平分线，tan B =21，则CD ∶DB = .20、若等腰梯形ABCD 的上、下底之和为4，并且两条对角线所夹锐角为60，则该等腰梯形的面积为 （结果保留根号的形式）． 三、解答题：21、计算：（1）1sin 60cos302⋅-； （233602cos 458-+；22、一种千斤顶利用了四边形的不稳定性. 如图，其基本形状是一个菱形，中间通过螺杆连接，转动手柄可改变ADC ∠的大小（菱形的边长不变），从而改变千斤顶的高度（即A 、C 之间的距离）.若AB=40cm ，当ADC ∠从60︒变为120︒时，千斤顶升高了多少？2 1.414,3 1.732，结果保留整数）23、某大草原上有一条笔直的公路，在紧靠公路相距40千米的A、B两地，分别有甲、乙两个医疗站，如图，在A地北偏东45°、B地北偏西60°方向上有一牧民区C.一天，甲医疗队接到牧民区的求救电话，立刻设计了两种救助方案，方案I：从A地开车沿公路到离牧民区C最近的D 处，再开车穿越草地沿DC方向到牧民区C.方案II：从A地开车穿越草地沿AC方向到牧民区C.已知汽车在公路上行驶的速度是在草地上行驶速度的3倍.（1）求牧民区到公路的最短距离CD.（2）你认为甲医疗队设计的两种救助方案，哪一种方案比较合理？并说明理由.（结果精确到0.1，参考数据：3取1.73，2取1.41）24、如图，小唐同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时，在AQ 延长线上B处的小宋同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.（1）已知旗杆高为10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求A、B之间的距离；（2）此时，在A处背向旗杆又测得风筝的仰角为75°，若绳子在空中视为一条线段，求绳子AC 约为多少？（结果可保留根号）25、某大学计划为新生配备如图（1）所示的折叠椅．图（2）是折叠椅撑开后的侧面示意图，其中椅腿AB 和CD 的长相等，O 是它们的中点．为使折叠椅既舒适又牢固，厂家将撑开后的折叠椅高度设计为32cm ，∠DOB ＝100°，那么椅腿的长AB 和篷布面的宽AD 各应设计为多少cm ？（结果精确到0.1cm ）26、路边的路灯的灯柱BC 垂直于地面，灯杆BA 的长为2米，灯杆与灯柱BC 成120°角，锥形灯罩的轴线AD 与灯杆AB 垂直，且灯罩轴线AD 正好通过道路里面的中心线（D 在中心线上），已知C 点与D 点之间的距离为12米，求灯柱BC 的高（结果保留根号）27、如图，家住江北广场的小李经西湖桥到教育局上班，路线为A →B →C →D ．因西湖桥维修封桥，他只能改道经临津门渡口乘船上班，路线为A →F →E →D ．已知BC EF ∥，BF CE ∥，AB BF ⊥，CD DE ⊥，200AB =米，100BC =米，37AFB ∠=°，53DCE ∠=°．请你计算小李上班的路程因改道增加了多少？（结果保留整数）温馨提示：sin370.60cos370.80tan370.75︒°≈，≈，°≈．28、如图，在小山的西侧A 处有一热气球，以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空，40分钟后到达C 处，这时热气球上的人发现，在A 处的正东方向有一处着火点B ，十分钟后，在D 处测得着火点B 的俯角为15°，求热气球升空点A 与着火点B 的距离.（结果保留根号，参考数据：(42615sin -=︒，42615cos +=︒，3215tan -=︒，3215cot +=︒）.参考答案：一、选择题： 1、C 2、C 3、A 4、C 5、A 6、D 7、B 8、A 9、D 10、A二、填空题：11、3.512、2(32)- 13、33 14、1:215、tan tan m n αα-⋅ 16、1217、325018、π21 19、1∶2 20、43或433 三、解答题：21、（1）14；（2）2.5 22、解: 连结AC ，与BD 相交于点O ，四边形ABCD 是菱形，AC BD ，ADB =CDB ，AC =2AO ， 当ADC =60时，△ADC 是等边三角形，AC =AD =AB =40 . 当ADC =120时，ADO =60，AO =AD sinADO =40×32=203，AC =403 ，因此增加的高度为40340=400.73229（cm ）23、解：（1）设CD 为x 千米，由题意得，∠CBD=30°，∠CAD=45°，∴AD=CD=x.在Rt △BCD 中，tan30°=BDx ，所以BD=3x. ∵AD ＋DB=AB=40，∴x ＋3x=40.解得 x ≈14.7，所以，牧民区到公路的最短距离CD 为14.7千米.（2）设汽车在草地上行驶的速度为v ，则在公路上行驶的速度为3v ，在Rt △ADC 中，∠CAD=45°，∴AC=2CD ，方案I 用的时间t 1=v CD v CD AD v CD v AD 34333=+=+；方案II 用的时间t 2=v CD v AC 2=； 所以t 1－t 2=v CD v CD 342-=vCD 3)423(-.因为32－4>0，所以t 1－t 2>0.所以方案I 用的时间少，方案I 比较合理.24、解：(1) 在Rt△BPQ 中，PQ =10米，∠B =30°，则BQ =cot30°×PQ ＝103，又在Rt△APQ 中，∠PAB =45°，则AQ =cot45°×PQ =10， 即：AB =(103+10)(米)；(2) 过A 作AE ⊥BC 于E ，在Rt△ABE 中，∠B =30°，AB =103+10，∴ AE =sin30°×AB =12（103+10）=53+5，∵∠CAD =75°，∠B =30°，∴ ∠C =45°，在Rt△CAE 中，sin45°＝AE AC，∴AC =2（53+5）=(56+52)(米)25、解：连接AC ，BD ， ∵OA=OB=OC=OB ，∴四边形ACBD 为矩形∵∠DOB=100º， ∴∠ABC=50º，由已知得AC=32，在Rt △ABC 中，sin∠ABC=AB AC，∴AB=ABC AC ∠sin =︒50sin 32≈41.8（cm ），tan∠ABC=BC AC ，∴BC=ABC AC ∠tan =︒50tan 32≈26.9（cm ），∴AD=BC =26.9 （cm ）答：椅腿AB 的长为41.8cm ，篷布面的宽AD 为26.9cm .26、解：设灯柱BC 的长为h 米，过点A 作AD ⊥CD 于点H ，过B 作BE ⊥AH 于点E ，∴四边形BCHE 为矩形，∵∠ABC ＝120°，∴∠ABE ＝30°，又∵∠BAD ＝∠BCD ＝90°，∴∠ADC ＝60°，在Rt △AEB 中，∴AE ＝AB sin30°＝1，BE ＝AB cos303∴CH 3，又CD ＝12，∴DH ＝123，在Rt △AHD 中，tan ∠ADH ＝AH HD 3123=-h ＝3－4（米），∴灯柱BC 的高为（34）米．27、解：在Rt ABF △中， 37200333sin 37AB AFB AB AF ∠===°，，≈，°267tan 37AB BF =≈°， BC EF BF CE ∴∥，∥，四边形BCEF 为平行四边形．267CE BF ∴==，100BC EF ==．在Rt CDE △中，53DCE ∠=°，CD DE ⊥，37CED ∴∠=°，cos37214DE CE =≈·°，sin37160CD CE =︒≈·，∴ 增加的路程∴ =()()AF EF DE AB BC DC ++-++(333100214)++≈-(200100160)187++=（米）．28、解：由题意可知，AD ＝(40＋10)×30＝1500（米）过点D 作DH ⊥BA ，交BA 延长线于点H. 在Rt △DAH 中，DH ＝AD ·sin60°＝1500×23＝7503（米）.AH ＝AD ·cos60°＝1500×21＝750（米）.在Rt △DBH 中， BH ＝DH ·cos15°＝7503×(2＋3)＝（15003＋2250）（米），∴BA ＝BH －AH ＝15003＋2250－750＝1500（3＋1）（米）.答：热气球升空点A 与着火点B 的距离为1500（3＋1）（米）。