暑期重点学校提升密卷(重点学校密卷)总复习 统计与概率 统计

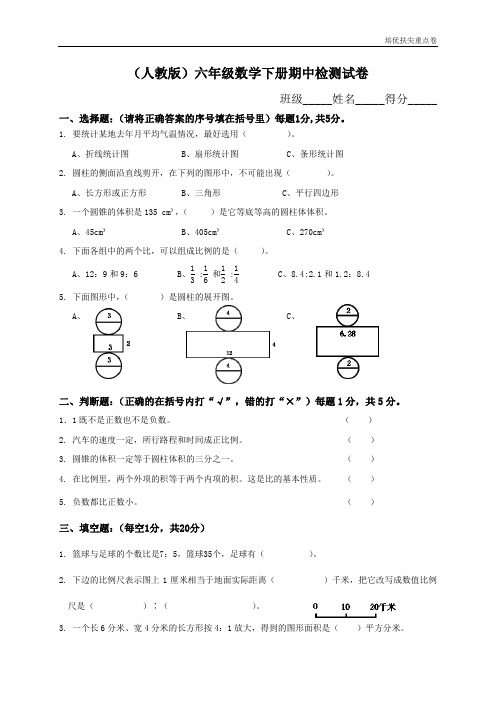
培优扶尖重点卷（人教版）六年级数学下册期中检测试卷班级_____姓名_____得分_____一、选择题：（请将正确答案的序号填在括号里）每题1分,共5分。

1. 要统计某地去年月平均气温情况，最好选用（ ）。

A 、折线统计图B 、扇形统计图C 、条形统计图2. 圆柱的侧面沿直线剪开，在下列的图形中，不可能出现（ ）。

A 、长方形或正方形B 、三角形C 、平行四边形3. 一个圆锥的体积是135 cm ³，（ ）是它等底等高的圆柱体体积。

A 、45cm ³B 、405cm ³C 、270cm ³4. 下面各组中的两个比，可以组成比例的是（ ）。

A 、12：9和9：6B 、13 :16 和12 :14C 、8.4:2.1和1.2：8.4 5. 下面图形中，（ ）是圆柱的展开图。

A 、B 、C 、二、判断题：（正确的在括号内打“√”，错的打“×”）每题1分，共5分。

1．1既不是正数也不是负数。

（ ）2. 汽车的速度一定，所行路程和时间成正比例。

（ ）3. 圆锥的体积一定等于圆柱体积的三分之一。

（ ）4. 在比例里，两个外项的积等于两个内项的积。

这是比的基本性质。

（ ）5. 负数都比正数小。

（ ）三、填空题：（每空1分，共20分）1. 篮球与足球的个数比是7：5，篮球35个，足球有（ ）。

2. 下边的比例尺表示图上1厘米相当于地面实际距离（ ）千米，把它改写成数值比例尺是（ ）∶（ ）。

3. 一个长6分米、宽4分米的长方形按4：1放大，得到的图形面积是（ ）平方分米。

高三数学总复习知识点强化提升训练78---统计与概率1．(2019·河北九校第二次联考)已知某种植物种子每粒成功发芽的概率都为13，某植物研究所分三个小组分别独立进行该种子的发芽试验，每次试验种一粒种子，每次试验结果相互独立．假定某次试验种子发芽则称该次试验是成功的，如果种子没有发芽，则称该次试验是失败的．(1)第一小组做了四次试验，求该小组恰有两次失败的概率；(2)第二小组做了四次试验，设试验成功与失败的次数的差的绝对值为X ，求X 的分布列及数学期望；(3)第三小组进行试验，到成功了四次为止，在第四次成功之前共有三次失败的前提下，求恰有两次连续失败的概率．[解] (1)该小组恰有两次失败的概率P ＝C 24⎝ ⎛⎭⎪⎫232⎝ ⎛⎭⎪⎫134－2＝2481＝827. (2)由题意可知X 的取值集合为{0,2,4}，则P (X ＝0)＝C 24⎝ ⎛⎭⎪⎫132⎝ ⎛⎭⎪⎫234－2＝2481＝827，P (X ＝2)＝C 14⎝ ⎛⎭⎪⎫131⎝ ⎛⎭⎪⎫234－1＋C 34⎝ ⎛⎭⎪⎫133⎝ ⎛⎭⎪⎫234－3＝32＋881＝4081， P (X ＝4)＝C 04⎝ ⎛⎭⎪⎫234＋C 44⎝ ⎛⎭⎪⎫134＝16＋181＝1781. 故X 的分布列为X 0 2 4 P82740811781E (X )＝0×827＋2×4081＋4×1781＝14881，即所求数学期望为14881.(3)由题意可知，在第四次成功之前共有三次失败，共有C 36＝20(个)基本事件，而满足恰有两次连续失败的基本事件共有A 24＝12(个)，从而由古典概型可得所求概率P ＝1220＝35.2．(2019·湘东五校联考)已知具有相关关系的两个变量x ，y 之间的几组数据如下表所示：x 2 4 6 8 10 y3671012(1)请根据上表数据在图中绘制散点图；(2)请根据上表提供的数据，求出y 关于x 的线性回归方程y ^＝b ^x ＋a ^，并估计当x ＝20时y 的值；(3)将表格中的数据看作5个点的坐标，则从这5个点中随机抽取3个点，记落在直线2x －y ＝4＝0右下方的点的个数为ξ，求ξ的分布列及数学期望．参考公式：b ^＝∑i ＝1nx i y i －n x － y－∑i ＝1nx 2i －n x －2，a ^＝y －－b ^x －. [解] (1)散点图如图所示．(2)依题意得，x －＝15×(2＋4＋6＋8＋10)＝6， y －＝15×(3＋6＋7＋10＋12)＝7.6，∑i ＝15x 2i ＝4＋16＋36＋64＋100＝220，∑i ＝15x i y i ＝6＋24＋42＋80＋120＝272，b ^＝∑i ＝15x i y i －5x － y－∑i ＝15x 2i －5x －2＝272－5×6×7.6220－5×62＝1.1，所以a ^＝7.6－1.1×6＝1，所以线性回归方程为y^＝1.1x＋1，故当x＝20时，y^＝23.(3)可以判断，落在直线2x－y－4＝0右下方的点的坐标满足2x－y－4>0，所以符合条件的点的坐标为(6,7)，(8,10)，(10,12)，故ξ的所有可能取值为1,2,3.P(ξ＝1)＝C22C13C35＝310，P(ξ＝2)＝C12C23C35＝610＝35，P(ξ＝3)＝C33C35＝110，故ξ的分布列为E(ξ)＝1×310＋2×35＋3×110＝95.3．(2019·武汉调研)中共十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的要求，带领广大农村地区人民群众脱贫奔小康．经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加．为了更好地制订2019年关于加快提升农民年收入，力争早日脱贫的工作计划，该地扶贫办统计了2018年50位农民的年收入(单位：千元)并制成如下频率分布直方图：(1)根据频率分布直方图，估计50位农民的年平均收入x －(单位：千元)(同一组数据用该组数据区间的中点值表示)；(2)根据频率分布直方图，可以认为该贫困地区农民年收入X 服从正态分布N (μ，σ2)，其中μ近似为年平均收入x －，σ2近似为样本方差s 2，经计算得s 2＝6.92.利用该正态分布，解决下列问题：(ⅰ)在2019年脱贫攻坚工作中，若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？(ⅱ)为了调研“精准扶贫，不落一人”的落实情况，扶贫办随机走访了1000位农民．若每个农民的年收入相互独立，问：这1000位农民中年收入不少于12.14千元的人数最有可能是多少？附：参考数据与公式6.92≈2.63，若X ～N (μ，σ2)，则 ①P (μ－σ<X ≤μ＋σ)≈0.6827； ②P (μ－2σ<X ≤μ＋2σ)≈0.9545； ③P (μ－3σ<X ≤μ＋3σ)≈0.9973.[解] (1)x －＝12×0.04＋14×0.12＋16×0.28＋18×0.36＋20×0.10＋22×0.06＋24×0.04＝17.40(千元)．(2)由题意，知X～N(17.40,6.92)．(ⅰ)P(X>μ－σ)≈12＋0.68272≈0.8414，μ－σ≈17.40－2.63＝14.77，即最低年收入大约为14.77千元．(ⅱ)由P(X≥12.14)＝P(X≥μ－2σ)≈0.5＋0.95452≈0.9773，得每个农民的年收入不少于12.14千元的事件的概率为0.9773，记这1000位农民中年收入不少于12.14千元的人数为ξ，则ξ～B(1000，p)，其中p＝0.9773.于是恰好有k位农民的年收入不少于12.14千元的事件的概率是P(ξ＝k)＝C k1000p k(1－p)1000－k，从而由P(ξ＝k)P(ξ＝k－1)＝(1001－k)pk×(1－p)>1，得k<1001p，而1001p＝978.2773，所以，当0≤k≤978时，P(ξ＝k－1)<P(ξ＝k)，当979≤k≤1000时，P(ξ＝k－1)>P(ξ＝k)，由此可知，在所走访的1000位农民中，年收入不少于12.14千元的人数最有可能是978.4．(2019·全国卷Ⅰ)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得－1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得－1分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.(1)求X的分布列；(2)若甲药、乙药在试验开始时都赋予4分，p i(i＝0,1，…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0＝0，p8＝1，p i＝ap i－1＋bp i＋cp i(i＝1,2，…，7)，其中a＝P(X＝－1)，b＝P(X＝0)，c＝P(X＝1)．假设α＝0.5，β＝0.8. ＋1(ⅰ)证明：{p i＋1－p i}(i＝0,1,2，…，7)为等比数列；(ⅱ)求p4，并根据p4的值解释这种试验方案的合理性．[解](1)X的所有可能取值为－1,0,1.P(X＝－1)＝(1－α)β，P(X＝0)＝αβ＋(1－α)(1－β)，P(X＝1)＝α(1－β)．所以X的分布列为(2)(ⅰ)证明：由(1)得a＝0.4，b＝0.5，c＝0.1.因此p i ＝0.4p i －1＋0.5p i ＋0.1p i ＋1，故0.1(p i ＋1－p i )＝0.4(p i －p i －1)，即p i ＋1－p i ＝4(p i －p i －1)．又因为p 1－p 0＝p 1≠0，所以{pi ＋1－p i }(i ＝0,1,2，…，7)为公比为4，首项为p 1的等比数列．(ⅱ)由(ⅰ)可得p 8＝p 8－p 7＋p 7－p 6＋…＋p 1－p 0＋p 0 ＝(p 8－p 7)＋(p 7－p 6)＋…＋(p 1－p 0) ＝48－13p 1.由于p 8＝1，故p 1＝348－1，所以p 4＝(p 4－p 3)＋(p 3－p 2)＋(p 2－p 1)＋(p 1－p 0)＝44－13p 1＝1257.p 4表示最终认为甲药更有效的概率．由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8时，认为甲药更有效的概率为p 4＝1257≈0.0039，此时得出错误结论的概率非常小，说明这种试验方案合理．。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年新疆哈密市高中数学人教B 版 必修二统计与概率专项提升(2)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）1. 随机掷两枚质地均匀的骰子，它们向上的点数之和不大于6的概率记为，点数之和大于6的概率记为，点数之和为奇数的概率记为 ，则（ ）A.B. C. D.＞＜= ，的大小不确定2. 如图是南阳市某中学在会操比赛中七位评委为甲、乙两班打出的分数的茎叶图（其中m 为数字0﹣9中的一个），去掉一个最高分和一个最低分后，甲、乙两个班级的平均分分别为 ， ，则一定有（ ）A. B. C. D. 15030060012003. 某工厂从一批产品中抽取一个容量为的样本，根据样本数据分成，， ，， 五组，得到频率分布直方图如图所示．若样本数据落在 内的个数是66，则 （ ）A. B. C. D. 4. 为了提升全民身体素质，学校十分重视学生体育锻炼.某校篮球运动员投篮练习，若他第1球投进则后一球投进的概率为，若他前一球投不进则后一球投进的概率为 .若他第1球投进的概率为 ，则他第2球投进的概率为（ ）A. B. C. D.15. 已知一组数据共10个数（10不全相等），方差为，增加一个数后得到一组新数据，新数据的平均数不变，方差为，则（）A. B. C. D.6. 关于圆周率，数学发展史上出现过许多有创意的求法，如著名的普丰实验和查理斯实验.受其启发，我们也可以通过设计下面的实验来估计的值：先请120名同学每人随机写下一个都小于1的正实数对，再统计其中能与1构成钝角三角形三边的数对的个数m，最后根据统计个数m估计的值.如果统计结果是，那么可以估计的值为（）A. B. C. D.13506759004507. 采用分层随机抽样的方法抽取一个容量为45的样本，高二年级被抽取15人，高二年级共有300人，则这个学校共有高中学生的人数为（）A. B. C. D.-2103360210168. 若是一组数据的方差，则的展开式的常数项为（）A. B. C. D.①简单随机抽样，②系统抽样，③分层抽样①分层抽样，②系统抽样，③简单随机抽样①系统抽样，②简单随机抽样，③分层抽样①简单随机抽样，②分层抽样，③系统抽样9. 完成下列抽样调查，较为合理的抽样方法依次是（）①从30件产品中抽取3件进行检查．②某校高中三个年级共有2460人，其中高一890人、高二820人、高三810人，为了了解学生对数学的建议，拟抽取一个容量为300的样本；③某剧场有28排，每排有32个座位，在一次报告中恰好坐满了听众，报告结束后，为了了解听众意见，需要请28名听众进行座谈．A. B.C. D.1820222410. 青少年近视问题已经成为我国面临的重要社会问题.现用分层随机抽样的方法调查某校学生的视力情况，该校三个年级的学生人数如下表：年级高一高二高三人数550500450已知在抽取的样本中，高二年级有20人，那么该样本中高三年级的人数为（）A. B. C. D.5，325，191，324，3511. 设样本数据x1， x2， …，x20的均值和方差分别为1和8，若y i=2x i+3（i=1，2，…，20），则y1， y2， …，y20的均值和方差分别是（）A. B. C. D.12.23090216某班有34位同学，座位号记为01，02，…34，用如图的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号．选取方法是从随机数表第一行的第6列和第7列数字开始，由左到右依次选取两个数字，则选出来的第4个志愿者的座号是（ ）A. B. C. D. 13. 设甲乘汽车､火车前往目的地的概率分别为0.6､0.4，汽车和火车正点达到目的地的概率分别为0.9，0.8，则甲正点到达目的地的概率为 .14. 在甲，乙，丙三个地区爆发了流感，这三个地区分别有8%，6%，4%的人患了流感.若这三个地区的人口数的比为5：3：2，现从这三个地区中任意选取一个人，这个人患流感的概率是 .15. 一袋中有红、黄、蓝三种颜色的小球各一个，每次从中取出一个，记下颜色后放回，当三种颜色的球全部取出时停止取球，则恰好取5次球时停止取球的概率为 ．16. 随着社会的发展与进步，人们更加愿意奉献自己的力量，积极参与各项志愿活动．某地单位甲有10名志愿者（其中8名男志愿者，2名女志愿者），单位乙有15名志愿者（其中9名男志愿者，6名女志愿者）．若从单位甲任选2名志愿者参加某项活动，则恰是一男一女志愿者的概率为 ；若从两单位任选一个单位，然后从中随机选1名志愿者参加某项活动，则该志愿者为男志愿者的概率为 （以上两空用数字作答）．17. 2021年某省约有28万理科考生参加高考，除去成绩在630分及以上的8145人与成绩在430分以下的103600人，还有约16.81万理科考生的成绩集中在内，其成绩的频率分布如下表所示：分数段频率0.230.250.240.180.10(1) 请估计该次高考理科考生成绩在内的平均分（同一组中的数据用该组区间的中点值代表）；(2) 若在分数段和的考生中采用分层抽样的方法抽取7名考生进行电话访问，再从被电话访问的7名考生中随机抽取3名考生进行问卷调查，求进行问卷调查的3名考生中至少有2名分数不低于550分的概率．18. 为了响应政府“节能减排”的号召，某知名品牌汽车厂家决定生产一款纯电动汽车.生产前，厂家进行了人们对纯电动汽车接受程度的调查.在20~60岁的人群中随机抽取了100人，调查数据的频率分布直方图和接受纯电动汽车的人数与年龄的统计结果如图所示：年龄接受的人数146152817附： (1) 由以上统计数据填列联表，并判断能否在犯错误的概率不超过0.05的前提下，认为以44岁为分界点的不同年龄人群对纯电动汽车的接受程度有差异？44岁以下44岁及44岁以上总计接受不接受总计(2) 若以44岁为分界点，从不接受“纯电动汽车”的人群中，按分层抽样的方法抽取8人调查不接受“纯电动汽车”的原因，现从这8人中随机抽取2人.记抽到44岁以下的人数为 ，求随机变量 的分布列及数学期望.0.1000.0500.0100.0012.7063.8416.63510.82819. 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动．（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？（Ⅱ）设抽出的7名同学分别用A ，B ，C ，D ，E ，F ，G 表示，现从中随机抽取2名同学承担敬老院的卫生工作．（i ）试用所给字母列举出所有可能的抽取结果；（ii ）设M 为事件“抽取的2名同学来自同一年级”，求事件M 发生的概率．20. 某校要组织知识竞赛，先外别在高一、高二年级内进行对抗预赛，然后高一、高二每个年级再派出预赛积分最高的一个队参加学校组织的决赛，高一预赛积分最高的是甲队，积分为8分，高二预赛积分最高的是乙队，积分为6分．决赛规则：甲、乙两队均要回答2道A 组题和2道B 组题，A 组题答对一题计1分，B 组题答对一题计2分，每题答错均不计分，每队四道题答完后，积分高的获得冠军，若每队四道题答完后积分相同，则预赛成绩计入总分，总分高的获得冠军．假设甲队答对A 组每题的概率均为 ， 答对B组每题的概率均为 ， 乙队答对A ，B 两组每题的概率均为 ．(1) 求乙队决赛答对题数X 的概率分布列；(2) 求甲队答对3题，乙队至少答对2题，且甲队获得冠军的概率．21. 袋中装着标有数字1、2、3、4、5的小球各2个，从袋中任取3个小球，每个小球被取出的可能性都相等，用ξ表示取出的3个小球上的最大数字，求：(1) 取出的3个小球上的数字互不相同的概率；(2) 随机变量ξ的概率分布列和数学期望．答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)18.(1)(2)19.(1)(2)(1)(2)。

选题表：将试题题号按照知识点填到下表基础中档稍难1.（填知识点）抽样方法、用频率估计总体，茎叶图、直方图、正态分布1、2、5、6、13、14 16、172.（填知识点）线性回归方程与独立性检验思想3、4、13、10 12、183.（填知识点）古典概型和几何概型以及概率分布列的综合运用7、8、9、14、11、15、19、20 21、22说明：试题选择回归基础，典型试题，体现了新课改的思想，侧重于能力的运用,需要用心来体会和掌握实质。

一、选择题(本大题共12小题，每小题5分，共60分．)1、采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[]1,450的人做问卷A,编号落入区间[]451,750的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为（）A．7 B．9 C．10 D．152 ．从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则（）A．x x<甲乙,m甲>m乙B．x x<甲乙,m甲<m乙C ．x x >甲乙,m 甲>m 乙D ．x x >甲乙,m 甲<m 乙4、样本(x 1,x 2,x n )的平均数为x,样本(y 1,y 2,,y n )的平均数为()y x y ≠.若样本(x 1,x 2,x n ,y 1,y 2,,y n )的平均数(1)z ax a y =+-,其中0<α<12,则n,m 的大小关系为（ ） A ．n<m B ．n>mC ．n=mD ．不能确定4、 [答案]A【解析】由统计学知识,可得1212,n m x x x nx y y y my +++=+++=,()()()12121n m x x x y y y m n z m n x y αα⎡⎤+++++++=+=++-⎣⎦.()()()1m n x m n y αα=+++-,7、在长为12cm 的线段AB 上任取一点 C ．现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm 2的概率为 （ ）A ．16 B ．13C ．23D ．457、 【答案】C【解析】设线段AC 的长为x cm,则线段CB 的长为(12x -)cm,那么矩形的面积为(12)x x -cm 2,由(12)32x x -<,解得48x x <>或.又012x <<,所以该矩形面积小于32cm 2的概率为23,故选C 8、如图,在圆心角为直角的扇形OAB 中,分别以OA ,OB 为直径作两个半圆. 在扇形OAB 内随机取一点,则此点取自阴影部分的概率是 （ ）11、设不等式组0202xy≤≤⎧⎨≤≤⎩表示的平面区域为D．在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是（）2524232221x x x x x ++++=,所以12ξξD D <,选A.二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上) 13 ．某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为____________.三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分) 某校100位学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:[)50,60、[)60,70、[)70,80、[)80,90、[]90,100.(Ⅰ)求图中a 的值;(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分; (Ⅲ)若这100名学生的语文成绩某些分数段的人数(x )与数学成绩相应分数段的人数(y )之比如下表所示,求数学成绩在[)50,90之外的人数.●分数段●[)50,60●[)60,70●[)70,80●[)80,90●:x y●1:1●2:1●3:4●4:518. （本试题12分）电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.列联表,并据此资料你是否认为“体育迷”与性别(Ⅰ)根据已知条件完成下面的22有关?非体育迷体育迷合计男女合计(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.19．(本小题满分12分)为征求个人所得税法修改建议，某机构对当地居民的月收入调查10000人，并根据所得数据画了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在 [1000，1500））。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年江西省高中数学人教B 版 必修二统计与概率专项提升(6)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）两次都从甲箱取球时“成功”的概率最大两次都从乙箱取球时“成功”的概率最大先从甲箱取球再从乙箱取球时“成功”的概率最大先从乙箱取球再从甲箱取球时“成功"”的概率最大1. 已知甲箱有2个红球和2个白球，乙箱有3个红球和3个白球，现任选1个箱子并从中任取1个球，记下球的颜色后将球放入另1个箱子内，再任选1个箱子并任取1个球，若两次取出的球的颜色相同为“成功”，则（ ）A. B. C. D. 100辆200辆300辆400辆2.某路段检查站监控录像显示，在某时段内，有1000辆汽车通过该站，现在随机抽取其中的200辆汽车进行车速分析，分析的结果表示为如右图的频率分布直方图，则估计在这一时段内通过该站的汽车中速度不小于90km/h 的约有A. B. C. D. 15、17、1815、16、1914、17、1915、16、203. 某校为了解学生的学习情况，采用分层抽样的方法从高一600人、高二680人、高三720人中抽取50人进行问卷调查，则高一、高二、高三抽取的人数分别是（ ）A. B. C. D.4. 若，其中，则等于（ ）A. B. C. D.5.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中有一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率是（ ）A. B. C. D.325312.5316.673106. 将某新电动车的续航里程数统计如下图所示，则该款电动车的续航里程数的中位数约为（）A. B. C. D. 7. 在普通高中新课程改革中，某地实施“3+1+2”选课方案．该方案中“2”指的是从政治，地理，化学，生物4门学科中任选2门，假设每门学科被选中的可能性相等，那么政治和地理至少有一门被选中的概率是（ ）A.B.C.D.8. 先后抛掷两枚骰子，骰子朝上的点数分别记为，，则满足的概率为（ ）A.B.C.D.405060709. 某校为了解高三学生身体素质情况，从某项体育测试成绩中随机抽取个学生成绩进行分析，得到成绩频率分布直方图（如图所示），已知成绩在的学生人数为8，则的值为（）A. B. C. D. 直方图中x 的值为0.00410. 耀华中学全体学生参加了主题为“致敬建党百年，传承耀华力量”的知识竞赛，随机抽取了400名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示，下列说法正确的是（）A.在被抽取的学生中，成绩在区间的学生数为30人估计全校学生的平均成绩为84分估计全校学生成绩的样本数据的80%分位数约为93分B. C. D. 频率分布直方图中a 的值为0.06估计全部销售员工销售额的中位数为15估计全部销售员工中销售额在区间内有6人估计全部销售员工销售额的第76百分位数为1711. 某品牌家电公司从其全部200名销件员工中随机抽出50名调查销售情况，销售额都在区间（单位：百万元）内，将其分成5组： ， 并整理得到如下的频率分布直方图，下列说法正确的是（ ）A. B. C. D. 12. 某省新高考改革方案推行“”模式，要求学生在语数外3门全国统考科目之外，在历史和物理2门科目中必选且只选1门，再从化学、生物、地理、思想政治4门科目中任选2门．某学生各门功课均比较优异，因此决定按方案要求任意选择，则该生选考物理、生物和政治这3门科目的概率为（ ）A.B.C.D.13. 某校从高一新生中随机抽取了一个容量为20的身高样本，数据从小到大排序如下（单位：）：152，155，158，164，164，165，165，165，166，167，168，168，169，170，170，170，171，x ，176，178，若样本数据的85百分位数是173，则x 的值为 ．14. 小明在抛掷图钉时，在200次至300次抛掷中钉尖触地的频率约在35%~35.4%之间，那么再抛掷100次，钉尖触地次数的取值范围是 .15. 从4男2女六名志愿者中任选三名参加某次公益活动，则选出的三名志愿者中既有男志愿者又有女志愿者的概率是 （结果用数值表示）16. 关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的浦丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请120名同学，没人随机写下一个都小于1的正实数对（x ，y ）；再统计两数能与1构成钝角三角形三边的数对（x ，y ）的个数m ；最后再根据统计数m 估计π的值．假如统计结果是m=34，那么可以估计π≈ （用分数表示）．17. 在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由3个人依次出场解密，每人限定时间是1分钟内，否则派下一个人.3个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲100次的测试记录，绘制了如下的频率分布直方图.(1) 若甲解密成功所需时间的中位数为47，求a、b的值，并求出甲在1分钟内解密成功的频率；(2) 在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为，其中表示第个出场选手解密成功的概率，并且定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立.①求该团队挑战成功的概率；②该团队以从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人员数目X的分布列与数学期望.18. 为了解某校高三毕业生报考体育专业学生的体重（单位：千克）情况，将他们的体重数据整理后得到如下频率分布直方图，已知图中从左至右前3个小组的频率之比为1：2：3，其中第2小组的频数为12.（Ⅰ）求该校报考体育专业学生的总人数；（Ⅱ）已知A，是该校报考体育专业的两名学生，A的体重小于55千克，的体重不小于70千克，现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名，然后再从这6人中抽取体重小于55千克学生1人，体重不小于70千克的学生2人组成3人训练组，求A不在训练组且在训练组的概率.19. 某市某街道办为了绿植街道两边的绿化带，购进了1000株树苗．这批树苗最矮2米，最高2.5米，桉树苗高度绘制成如图频率分布直方图（如图）．(1) 试估计这批树苗高度的众数，中位数；(2) 现按分层抽样方法．从高度在的树苗中任取6株树苗．从这6株树苗中任选3株，求3株树苗中至少有一株树苗高度在的概率．20. 第31届世界大学生夏季运动会（简称大运会）将于2023年7月28日在四川成都开幕，这是中国西部城市第一次举办世界性综合运动会.为普及大运会相关知识，营造良好的赛事氛围，某学校举行“大运会百科知识”答题活动，并随机抽取了20名学生，他们的答题得分（满分100分）的频率分布直方图如图所示.(1) 求频率分布直方图中的值及这20名学生得分的80%分位数；(2) 若从样本中任选2名得分在内的学生，求这2人中恰有1人的得分在内的概率21. 某中学为研究学生的身体素质与体育锻炼时间的关系，对该校200名高三学生平均每天体育锻炼时间进行调查，如表：（平均每天锻炼的时间单位：分钟）平均每天锻炼的时间/分钟总人数203644504010将学生日均体育锻炼时间在的学生评价为“锻炼达标”.(1) 请根据上述表格中的统计数据填写下面的列联表；锻炼不达标锻炼达标合计男女20110合计并通过计算判断，是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关？(2) 在“锻炼达标”的学生中，按男女用分层抽样方法抽出5人，进行体育锻炼体会交流，再从这5人中选出2人作重点发言，求作重点发言的2人中，至少1人是女生的概率.参考公式：，其中 .临界值表0.100.050.0250.0102.7063.841 5.024 6.635答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)18.19.(1)(2)20.(1)(2)21.(1)(2)。

2024年苏教版六年级下册数学暑假必刷专题：统计与概率一、单选题1．三（2）班的同学在玩摸球游戏。

现在箱里有3个红球和4个黄球。

下面说法正确的是（）A．一定能摸到黄球B．一定能摸到红球C．摸到红球的可能性13D．摸到红球的可能性是372．旋转转盘的指针，如果指针箭头停在合数的位置，就能得到奖品。

玲玲第一次旋转的结果如图，她得奖了。

如果再旋转一次，这次她（）A．一定能得奖B．得奖的可能性小C．得奖的可能性大D．不可能得奖3．为了说明苹果中各种营养成分所占的百分比，应绘制（）A．条形统计图B．折线统计图C．扇形统计图D．复式条形统计4．小红在一次期末考试中，语文和数学两科的平均分是a分，这两科的平均分比英语高9分，小红这三科的平均分是（）分。

A．a﹣2B．a﹣3C．a﹣4D．a﹣65．《龟兔赛跑》的意思是乌龟和兔子赛跑，兔子开始远超乌龟，就在路边睡了一觉，乌龟一直向前爬并获得了胜利。

能正确反映这个故事情节的图象是（）A．B．C．D．二、填空题6．要表示一位病人一天的体温变化情况，用统计图比较合适。

7．口袋里有7个红球和6个白球，从中任意摸出1个球。

那么摸出球的可能性大。

8．国家提出了全面加强劳动教育的意见，实验小学响应国家要求，开辟了劳动实践基地，六年级的菜园里栽种了4种不同的蔬菜各种蔬菜的种植面积分布如图，其中土豆的种植面积是100平方米，番茄的种植面积占%，青菜的种植面积是平方米。

9．春节到了，百货商场搞促销活动。

凡购物满500元者皆可参加抽奖活动：盒子里有大小、质量相同的红球100个，黄球10个，蓝球5个。

你认为商场会规定抽到球的为一等奖，抽到球的为三等奖。

请你简要说下理由。

10．气象站在某一天的1时、7时、13时、19时，测得气温分别是﹣2℃、3℃、12℃、7℃，那么这一天的平均温度是℃。

11．一个盒子里放有4个红球与5个黄球（这些球除了颜色，大小、轻重都相同），从中任意摸一个球，摸到红球的可能性是；要使摸到红球的可能性是13，可以放个绿球。

【快乐假期】2011年八年级数学暑假培优提高作业4统计与概率学生姓名 家长签字 【学习目标】了解简单的统计与概率知识，能够运用统计与概率解释生活中的现象和解决问题，培养实事求是的作风和意识，体会估计思想在生活中的运用。

【基础探究】1、将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出，出现的数字分别为a b c 、、，则a b c 、、正好是直角三角形三边长的概率是（ ） A ．1216B ．172C ．112D ．1362、为了防控输入性甲型H1N1流感，某市医院成立隔离治疗发热流涕病人防控小组，决定从内科5位骨干医师中（含有甲）抽调3人组成，则甲一定抽调到防控小组的概率是（ ） A ．35B ．25C ．45D ．153、在一个不透明的布袋中装有红色、白色玻璃球共40个，除颜色外其他完全相同．小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15％左右，则口袋中红色球可能有（ ） A ．4个B ．6个C ．34个D ．36个4、某校为了了解七年级学生的身高情况（单位：cm ，精确到1cm ），抽查了部分学生，将所得数据处理后分成七组（每组只含最低值，不含最高值），并制成下列两个图表（部分）：根据以上信息可知，样本的中位数落在A ．第二组B ．第三组C ．第四组D ．第五组5、 “只要人人都献出一点爱，世界将变成美好的人间”．在今年的慈善一日捐活动中，济南市某中学八年级三班50名学生自发组织献爱心捐款活动．班长将捐款情况进行了统计，并绘制成了统计图．根据右图提供的信息，捐款金额．．的众数和中位数分别是（ ） A ．20、20 B ．30、20 C ．30、30 D ．20、306、近几年来，国民经济和社会发展取得了新的成就，农村经济快速发展，农民收入不断提高．下图统计的是某地区2004年—2008年农村居民人均年纯收入．根据图中信息，下列判断：①与上一年相比，2006年的人均年纯收入增加的数量高于2005年人均年纯收入增加的数量；②与上一年相比，2007年人均年纯收入的增长率为35873255100%3255-⨯；③若按2008年人均年纯收入的增长率计算，2009年人均年纯收入将达到41403587414013587-⎛⎫⨯+ ⎪⎝⎭元．其中正确的是（ ）A ．只有①②B ．只有②③C 7、在3 □ 2 □（－2）的两个空格□中，任意填上“+ 8、在一个不透明的布袋中装有2个白球和n 摸到黄球的概率是45，则n =__________． 9均有一次转动转盘的机会(如图，转盘被分为8个全等的小扇形时，该顾客获一等奖；当指针最终指向2或5时，该顾客获二等奖(当天发放一、二等奖奖品共600份，那么据此估计参与此次活动的顾客为______人次．10、在科学课外活动中，小明同学在相同的条件下做了某种作物种子发芽的实验，结果如下表所示：由此估计这种作物种子发芽率约为 （精确到0.01）．11、某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费．某顾客刚好消费200元．（1）该顾客至少可得到 元购物券，至多可得到 元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．12、小明和小亮是一对双胞胎，他们的爸爸买了两套不同品牌的运动服送给他们，小明和小亮都想先挑选．于是小明设计了如下游戏来决定谁先挑选．游戏规则是：在一个不透明的袋子里装有除数字以外其它均相同的4个小球，上面分别标有数字1、2、3、4．一人先从袋中随机摸出一个小球，另一人再从袋中剩下的3个小球中随机摸出一个小球．若摸出的两个小球上的数字和为奇数，则小明先挑选；否则小亮先挑选．（1）用树状图或列表法求出小明先挑选的概率；（2）你认为这个游戏公平吗？请说明理由．13、某航班约有a 名乘客.在一次飞行中飞机失事的概率p =5×10-5.一家保险公司要为乘客保险，许诺飞机一旦失事，向每位乘客赔偿50万元人民币.平均来说，保险公司应如何收取保费呢？ 【综合探究】)14、某校数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数，满分为100分)作了统计分析，绘制成如下频数、频率分布表和频数分布直方图． 请你根据图表提供的信息解答下列问题： (1) 频数、频率分布表中a = ，b = ；(2)补全频数分布直方图；(3)数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了93分的小华被选上的概率是多少？15、全国实施“限塑令”于今年6月1日满一年，某报三名记者当日分别在武汉三大商业集团门口，同时采用问卷调查的方式，随机调查了一定数量的顾客，在“限塑令”实施前后使用购物袋的情况．下面是这三名记者根据汇总的数据绘制的统计图．请你根据以上信息解答下列问题（1）图1中从左到右各长方形的高度之比为2∶8∶8∶3∶3∶1，又知此次调查中使用4个和5个塑料购物袋的顾客一共24人，问这三名记者一共调查了多少人？（2）“限塑令”实施前，如果每天约有6000人到该三大商场购物，根据记者所调查的一定数量顾客平均一次购物使用塑料购物袋的平均数，估计这三大商业集团每天需要为顾客提供多少个塑料购物袋？（3）据武汉晚报报道，自去年6月1日到去年12月底，三大商业集团下属所有门店，塑料袋的使用量与上一年同期相比，从12927万个下降到3355万个，降幅为 （精确到百分之一）．这一结果与图2中的收费塑料购物袋 %比较，你能得出什么结论，谈谈你的感想．16、某校九年级学生共900人，为了解这个年级学生的体能，从中随机抽取部分学生进行1min 的跳绳测试，并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理，下图是这四名同学提供的部分信息：甲：将全体测试数据分成6组绘成直方图（如图）； 乙：跳绳次数不少于105次的同学占94％吧。

盐城中学高二数学暑假作业（20）-----统计与概率姓名 学号 班级一、填空题：1．为了了解参加运动会的2000名运动员的年龄情况，从中抽取100名运动员，就这个问题，下列说法中正确的有 ．①2000名运动员是总体；②每个运动员是个体；③所抽取的100名运动员是一个样本；④样本容量为100；⑤每个运动员被抽到的概率相等．2．某地区有小学150所，中学75所，大学25所. 现采用分层抽样的方法从这些学校中抽取30所学校对学生进行视力调查，应从小学中抽取_________所学校，中学中抽取________所学校． 3．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1,2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间[]1,450的人做问卷A ，编号落入区间[]451,750的人做问卷B ，其余的人做问卷C .则抽到的人中，做问卷B 的人数为 ．4．从装有５只红球、５只白球的袋中任意取出３只球，有事件：① “取出２只红球和１只白球”与“取出１只红球和２只白球”；② “取出２只红球和１只白球”与“取出３只红球”；③ “取出３只红球”与“取出３只球中至少有１只白球”；④ “取出３只红球”与“取出３只白球”．其中是对立事件的有 ．5．有一段长为11米的木棍，现要剪成两段，每段不小于3米的概率是 ．6. 某老师从星期一到星期五收到信件数分别是10，6，8，5，6，则该组数据的方差2s = ．7. 从1，2，3，4，5中任取2个不同的数，事件A=“取到的2个数之和为偶数”，事件B=“取到的2个数均为偶数”，则P （B ︱A ）= ．8．从1，2，3，4这四个数中一次随机取两个数，则其中一个数是另一个的两倍的概率为 ．9．甲、乙两人下棋，甲获胜的概率为0.3，两人下成和棋的概率为0.5，那么甲不输的概率是 ．10. 甲、乙两人玩数字游戏，先由甲心中任想一个数字记为a ，再由乙猜甲刚才想的数字，把乙想的数字记为b ，且a,b {1,2,3,4,5,6}∈，若a b 1-≤，则称“甲乙心有灵犀”，现任意找两个人玩这个游戏，得出他们“心有灵犀”的概率为 ．11．有5本不同的书，其中语文书2本，数学书2本，物理书1本．若将其随机的并排摆放到书架的同一层上，则同一科目的书都不相邻的概率 ．12．小波通过做游戏的方式来确定周末活动，他随机地往单位圆内投掷一点，若此点到圆心的距离大于12，则周末去看电影；若此点到圆心的距离小于14，则去打篮球；否则，在家看书，15．从某中学高三年级参加期中考试的1000名学生中，用系统抽样法抽取了一个容量为200的总成绩的样本，分数段及各分数段人数如下(满分800分)：分数段 300～400 400～500 500～600 600～700 700～800 人数2030804030(1)中所占的比例；(4)估计分数在600分以上的总体中占的比例．16．某队员射击一次，命中7～10环的概率如下表所示：命中环数 10环 9环 8环 7环 概率0.320.280.180.12(1)射中9环或10环的概率；(2)至少命中8环的概率；(3)命中不足8环的概率．17．设关于x 的一元二次方程22x 2ax b 0++=．(1)若a 是从0,1,2,3四个数中任取的一个数，b 是从0,1,2三个数中任取的一个数，求上述方程有实根的概率；(2)若a 是从区间[0,3]中任取的一个数，b 是从区间[0,2]中任取的一个数，求上述方程有实根的概率．18. 某居民小区有两个相互独立的安全防范系统（简称系统）A 和B ，系统A 和B 在任意时刻发生故障的概率分别为110和p ．（1）若在任意时刻至少有一个系统不发生故障的概率为4950，求p 的值；（2）设系统A 在3次相互独立的检测中不发生故障的次数为随机变量ξ，求ξ的概率分布列及数学期望E ξ．。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年江西省高中数学人教B 版 必修二统计与概率专项提升(3)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）1. 已知a ∈{0，1，2}，b ∈{﹣1，1，3，5}，则函数f （x ）=ax 2﹣2bx 在区间（1，+∞）上为增函数的概率是（ ）A.B.C.D.0.320.560.440.682. 甲、乙两人各进行1次射击，如果两人击中目标的概率分别为0.8和0.4，则其中恰有1人击中目标的概率是( )A. B. C. D. 众数为2平均数为2.5方差为1.6标准差为43. 给定一组数据5，5，4，3，3，3，2，2，2，1，则这组数据（ ）A. B. C. D. 0.630.70.90.5674. 下图展现给我们的是唐代著名诗人杜牧写的《清明》，这首诗不仅意境极好，而且还准确地描述出了清明时节的天气状况，那就是“雨纷纷”，即天气多阴雨．某地区气象监测资料表明，清明节当天下雨的概率是0.9，连续两天下雨的概率是0.63，若该地某年清明节当天下雨，则随后一天也下雨的概率是（ ）A. B. C. D. 5. 甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a ，再由乙猜甲刚才所想的数字，把乙猜的数字记为b ，其中， 则“a ＝b”的概率为（ ）A. B. C.D.总体是240名学生个体是每一个学生样本是40名学生样本量是406. 为了了解全校240名高一学生的身高情况，从中抽取40名学生进行测量，下列说法正确的是（ ）A. B. C. D. 甲的极差是29甲的中位数是25乙的众数是21甲的平均数比乙的大7. 关于茎叶图的说法，结论错误的一个是（ ）A. B. C. D. 202530408. 某次娱乐节目中有 三个方阵，其人数之比为 ，现用分层抽样方法抽出一个容量为 的样本，方阵 被抽出人数为12人，则此样本容量 为（ ）A. B. C. D. 01239. 已知事件A 与事件B 发生的概率分别为、 ， 有下列命题：①若A 为必然事件，则； ②若A 与B 互斥，则；③若A 与B 互斥，则.其中真命题有（ ）个A. B. C. D. 100人60人80人20人10. 某大学中文系共有本科生5000人，其中一、二、三、四年级的学生比为5：4：3：1，要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本，则应抽二年级的学生（ ）A. B. C. D. 012311. 给出下列结论：⑴若 在第四象限，则 角的终边在第三或第四象限；⑵正切函数在定义域内是单调递增函数；⑶正方体的边长与体积成正相关；⑷抛一枚均匀的硬币4次，则出现正面的次数多于反面次数的概率为 ．其中正确结论的个数是（ ）A. B. C. D. 0.180.210.390.4212. 甲、乙两队进行篮球决赛，采取五场三胜制（当一队赢得三场胜利时，该队获胜，比赛结束）.根据前期比赛成绩，甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队不超过 场即获胜的概率是（ ）A. B. C. D. 阅卷人得分二、填空题（共4题，共20分）13. 甲乙两人组队参加答题大赛，比赛共两轮，每轮比赛甲、乙两人各答一题，已知甲答对每个题的概率为 ，乙答对每个题的概率为，甲、乙在答题这件事上互不影响，则比赛结束时，甲、乙两人共答对三个题的概率为．14. 在一次反恐演习中，我方三架武装直升机分别从不同方位对同一目标发动攻击（各发射一枚导弹），由于天气原因，三枚导弹命中目标的概率分别为0.9，0.9，0.8，若至少有两枚导弹命中目标方可将其摧毁，则目标被摧毁的概率为．15. 在如图所示一组数据的茎叶图中，有一个数字被污染后模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为 .16. “双十一”是指每年的11月11日，以一些电子商务为代表，在全国范围内兴起的大型购物促销狂欢日.某商家在去年的“双十一”中开展促销活动：凡购物满5888元的顾客会随机获得A，B，C三种赠品中的一件，现恰有3名顾客的购物金额满5888元.设随机变量X表示获得赠品完全相同的顾客人数，则， .17.某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[8 0，90），[90，100]．（1）求图中a的值；（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，9 0）之外的人数．分数段[50，60）[60，70）[70，80）[80，90）x：y1：12：13：44：518. 从某校高一年级1000名学生中随机抽取100名测量身高，测量后发现被抽取的学生身高全部介于155厘米到195厘米之间，将测量结果分为八组：第一组[155，160），第二组[160，165），…，第八组[190，195），得到频率分布直方图如图所示．（Ⅰ）计算第三组的样本数；并估计该校高一年级1000名学生中身高在170厘米以下的人数；（Ⅱ）估计被随机抽取的这100名学生身高的中位数、平均数．19. 甲、乙、丙三台机床同时生产一种零件，在10天中，甲乙机床每天生产的次品数如下表所示：第1天第2天第3天第4天第5天第6天第7天第8天第9天第10天甲010*******乙2411021101(1) 分别计算这两组数据的平均数和方差；(2) 已知丙机床这10天生产次品数的平均数为1.4，方差为1.41．以平均数和方差为依据，若要从这三台机床中淘汰一台，你应该怎么选择？这三台机床你认为哪台性能最好？20. 某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．(1) 求出第4组的频率，并补全频率分布直方图；(2) 根据样本频率分布直方图估计样本的中位数与平均数；(3) 如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？21. 某射击队派出甲、乙两人参加某项射击比赛，比赛规则如下：开始时先在距目标50米射击，命中则停止射击；第一次没有命中，可以进行第二次射击，但目标为100米；第二次没有命中，还可以进行第三次射击，此时目标在150米处；若第三次没命中则停止射击，比赛结束．已知甲在50米，100米，150米处击中目标的概率分别为，，，乙在50米，100米，150米处击中目标的概率分别为，，．(1) 求甲，乙两人中恰有一人命中目标的概率；(2) 若比赛规定，命中目标得2分，没有命中目标得0分，求该射击队得分X（X为甲，乙得分之和）的分布列和数学期望．答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.(1)(2)20.(1)(2)(3)21.(1)(2)。