《第四章几何图形初步》练习题：角的比较与运算(一)

角【课后作业】一、P120随堂练习1。

难易度：★★★关键词：角答案：（1)135°，135°，45°,（2）两个钝角相等，以钝角和锐角的和是180°。

【举一反三】典例:如图,小于平角的角有（）思路导引：首先理解平角的定义，然后找出小于平角的角的个数．主要考查角的比较与运算这一知识点。

标准答案：小于平角的角有∠BAC、∠BCA、∠DAC、∠ACD、∠BAD、∠BCD、∠B、∠D共8个角。

尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

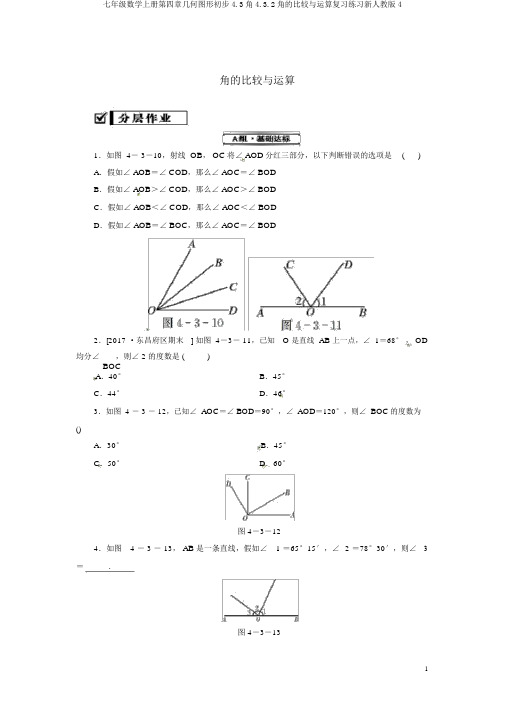
角的比较与运算1．如图 4－ 3－10，射线OB，OC将∠AOD分红三部分，以下判断错误的选项是() A．假如∠AOB＝∠COD，那么∠AOC＝∠BODB．假如∠AOB＞∠COD，那么∠AOC＞∠BODC．假如∠AOB＜∠COD，那么∠AOC＜∠BODD．假如∠AOB＝∠BOC，那么∠AOC＝∠BOD2．[2017 ·东昌府区期末] 如图 4－3－ 11，已知O 是直线 AB 上一点，∠1＝68°， OD 均分∠，则∠ 2 的度数是 ()BOCA．40°B．45°C．44°D．46°3．如图 4 － 3 － 12，已知∠AOC＝∠BOD＝90°，∠AOD＝120°，则∠BOC的度数为()A．30°B．45°C．50°D．60°图 4－3－124．如图 4 － 3 － 13，AB是一条直线，假如∠ 1 ＝65°15′，∠ 2 ＝78°30′，则∠3＝.图 4－3－135． [ 2017·海港区月考] 如图 4－3 － 14，点O在直线AB上，OD是∠AOC的均分线，OE 是∠ COB的均分线，则∠ DOE＝.图 4－3－146．如图 4－ 3－ 15，直线AB，CD订交于点O，OE均分∠AO D. 若∠BOD＝100°，则∠AOE ＝.图 4－3－157．计算：(1)27 °26′＋ 53°48′；(2 )90 °－ 79°18′6″；(3)18 °13′× 5；(4)178 °53′÷ 5( 精准到1′) ．8．如图 4－ 3－ 16，已知OD均分∠ AOB，射线 OC在∠ AOD内，∠ BOC＝2∠ AOC，∠ AOB ＝114°. 求∠COD的度数．图 4－3－ 169． (1) 如图 4－ 3－ 17，∠AOB＝90°，∠BOC＝30°，OM均分∠AOC，ON均分∠BOC，求∠MON的度数．(2) 若第 (1) 题中∠＝α，其余条件不变，求∠的度数；AOB MON(3) 若第 (1) 题中∠BOC＝β( β为锐角 ) ，其余条件不变，求∠MON的度数；(4)从以上结果中你能看出什么规律？图 4－3－17参照答案4． 3.2角的比较与运算【分层作业】1． D 2.C 3.D 4.36 °15′ 5.90 ° 6.40 °7．(1)81 °14′(2)10 °41′54″ (3)91°5′ (4)35 °47 ′8．∠COD＝19°.α1 9． (1) ∠MON＝45°. (2) ∠MON＝2 .(3)∠ MON＝45°.(4) ∠MON＝2∠AOB，∠MON 的大小与∠ BOC的大小没关．。

4.6.2角的比较和运算1.如图,∠1=∠2,∠3=∠4,则下列结论正确的个数是( )①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.A.4B.3C.2D.12.如图,OC是∠AOB的平分线,OD平分∠AOC,若∠COD=25°,则∠AOB的度数为 ( )A.100°B.80°C.70°D.60°3.如图所示,将一张长方形纸的一角斜折过去,使顶点A落在A'处,BC为折痕,如果BD为∠ABE的平分线,则∠CBD= ( )A.80°B.90°C.100°D.70°4.如图,O为直线AB上一点,OD平分∠AOC,OE平分∠BOC,则∠DOE=_______°;若∠AOD=30°,则∠DOC=_______°,∠COE=_______°,∠BOE=_______°,∠BOD=_______°.5.已知∠AOB=60°,OC是∠AOB的一条三等分线,则∠AOC=________.6.若∠A=20°18',∠B=20.25°,则∠A________∠B(填“>”“<”或“=”).7.比较两个角的大小,有以下两种方法(规则):①用量角器度量两个角的大小,用度数表示,则度数大的角大;②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.对于如图给定的∠ABC与∠DEF,用以上两种方法分别比较它们的大小.注:构造图形时,作示意图(草图)即可.8.如图,BD平分∠ABC,BE分∠ABC为2∶5两部分,∠DBE=21°,求∠ABC的度数.9. (1)如图所示,已知∠AOB是直角,∠BOC=30°.OM平分∠AOC,ON平分∠BOC,求∠MON的度数.(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.(4)你从(1)(2)(3)的结果中能发现什么规律?参考答案：1.【解析】因为∠1=∠2,所以AE平分∠DAF,故③正确.又因为∠3=∠4,所以∠1+∠3=∠2+∠4,即∠BAE=∠CAE,所以AE平分∠BAC.故⑤正确.【答案】C2.【解析】因为OC是∠AOB的平分线,所以∠AOC=∠COB.因为OD是∠AOC的平分线,所以∠AOD=∠COD.因为∠COD=25°,所以∠AOC=2∠COD=50°,所以∠AOB=2∠AOC=100°.【答案】A3.【解析】因为将顶点A折叠落在A'处,所以∠ABC=∠A'BC,又因为BD为∠ABE的平分线,所以∠ABD=∠DBE,因为∠ABC+∠A'BC+∠ABD+∠DBE=180°,所以∠CBD=90°.【答案】B4.【解析】因为OD平分∠AOC,OE平分∠BOC,所以∠AOD=∠COD,∠COE=∠BOE.又因为∠AOD+∠COD+∠COE+∠BOE=180°,所以∠DOE=90°;因为∠AOD=30°,所以∠COD=∠AOD=30°,所以∠COE=60°,∠BOE=60°,∠BOD=150°.【答案】90 30 60 60 1505.【解析】因为OC是∠AOB的三等分线,所以∠AOC=∠AOB或∠BOC=∠AOB,所以∠AOC=20°或∠BOC=20°,所以∠AOC=20°或40°.【答案】20°或40°6.【解析】因为18×()°=0.3°,所以∠A=20°18'=20.3°>20.25°,所以∠A>∠B.【答案】>7.解：①用量角器度量∠ABC=50°,∠DEF=70°,即∠DEF>∠ABC.②如图:把∠ABC放在∠DEF上,使顶点B和E重合,边EF和BC重合,边ED和BA在EF的同侧,从图形可以看出∠DEF包含∠ABC,即∠DEF>∠ABC.8.解：因为BD平分∠ABC,所以∠ABD=∠CBD,因为BE分∠ABC为2∶5两部分,设∠ABE=2x°,则∠EBC=5x°,∠ABC=7x°,所以∠ABD=3.5x°.因为∠DBE=21°,所以3.5x-2x=21,解得x=14,所以∠ABC=14°×7=98°.9.解：(1)∠MON=∠COM-∠CON=∠AOC-∠BOC=×120°-×30°=45°.(2)∠MON=∠COM-∠CON=∠AOC-∠BOC=(α+30°)-×30°=α.(3)∠MON=∠COM-∠CON=∠AOC-∠BOC=(90°+β)-β=45°.(4)∠MON的大小等于∠AOB的一半,而与∠BOC的大小无关.。

人教版七年级数学上册 第四章 几何图形初步4.3.2 角的比较与运算 课后练习一、选择题1．已知α=76°5′，β=76.5°，则α与β的大小关系是（ ）A ．α＞βB ．α=βC ．α＜βD ．以上都不对2．如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=211∠BOD ． A ．1个 B ．2个 C ．3个 D ．4个3．如图所示,OC 是∠AOB 的平分线,OD 是∠BOC 的平分线,那么下列各式正确的是( )A ．∠COD=12∠AOB B ．∠AOD=23∠AOB C ．∠BOD=13∠AOB D ．∠BOC=23∠AOD 4．如图，已知OA ⊥OB ，OC ⊥OD ，∠BOA ∶∠AOD ＝3∶4，则∠BOD 的度数为( )A ．120°B ．125°C ．150°D ．157.5°5．将一副直角三角尺按如图所示的不同方式摆放,则图中α∠与β∠相等的是( )A ．B ．C ．D ． 6．已知三条不同的射线OA 、OB 、OC 有下列条件：①∠AOC=∠BOC ②∠AOB=2∠AOC ③∠AOC+∠COB=∠AOB ④∠BOC=12∠AOB ，其中能确定OC 平分∠AOB 的有（ ） A ．4个B ．3个C ．2个D ．1个 7．射线OC 在AOB ∠内部，下列条件不能说明OC 是AOB ∠的平分线的是（ ）A ．12AOC AOB ∠=∠ B ．1BOC AOB 2∠=∠ C ．AOC BOC AOB ∠+∠=∠ D ．AOC BOC ∠=∠8．在∠AOB 的内部任取一点C ，作射线OC ，则一定有（ ）A ．∠AOC =∠BOCB ．∠BOC >∠AOC C ．∠AOC >∠BOCD ．∠AOB >∠AOC9．如图，AOB ∠，以OB 为边作BOC ∠，使2BOC AOB ∠=∠，那么下列说法正确的是（ ）A ． 3AOC AOB ∠=∠B ．AOB AOC ∠=∠或3AOC AOB ∠=∠ C ．AOC BOC ∠>∠D ． AOC AOB ∠=∠10．已知∠AOB ＝20°，∠AOC ＝4∠AOB ，OD 平分∠AOB ，OM 平分∠AOC ，则∠MOD 的度数是（ ） A ．20°或50°B ．20°或60°C ．30°或50°D ．30°或60°二、填空题11．如图，在OB 边上取一点C ，过C 作直线MN 交OA 于D ，图中所有角（平角除外有_______个，其中∠BCN 和_______∠BCM 或∠DCO 构成平角．12．如图，A ，O ，B 三点在一条直线上，OM 是∠AOC 的平分线，ON 是∠BOC 的平分线．若∠1：∠2＝1：2，则∠1＝_______°．13．如图所示，∠AOB 是平角，∠AOC=30°，∠BOD=60°，OM ，ON 分别是∠AOC ，∠BOD 的平分线，∠MON 等于_____度．14．如图，直线AB 、CD 相交于点O ，OE 平分∠BOD ，∠BOE=36°．求∠AOC 的度数．15．如图所示，OC 是AOE ∠的平分线，OB 是AOC ∠的平分线，OD 是COE ∠的平分线，那么AOD ∠=∠_______．三、解答题16．已知OC 是AOB ∠内部的一条射线，M ，N 分别为OA ，OC 上的点，线段OM ，ON 同时分别以30/s ︒，10/s ︒的速度绕点O 逆时针转动，设转动时间为s t ．（1）如图（1），若120AOB ∠=︒，OM ，ON 逆时针转动到OM '，ON '处．①若OM ，ON 的转动时间t 为2，则BON COM ''∠+∠=________；②若OM '平分AOC ∠，ON '平分BOC ∠，求M ON ''∠的值．（2）如图（2），若4AOB BOC ∠=∠，当OM ，ON 分别在AOC ∠，BOC ∠内部转动时，请猜想COM ∠与BON ∠的数量关系，并说明理由．17．如图，已知150AOB ∠=，将一个直角三角形纸片(90D ∠=)的一个顶点放在点O 处，现将三角形纸片绕点O 任意转动，OM 平分斜边OC 与OA 的夹角，ON 平分BOD ∠.（1）将三角形纸片绕点O 转动(三角形纸片始终保持在AOB ∠的内部)，若30COD ∠=，则MON ∠=_______；（2）将三角形纸片绕点O 转动(三角形纸片始终保持在AOB ∠的内部)，若射线OD 恰好平分MON ∠，若8MON COD ∠=∠，求COD ∠的度数;（3）将三角形纸片绕点O 从OC 与OA 重合位置逆时针转到OD 与OA 重合的位置，猜想在转动过程中COD ∠和MON ∠的数量关系？并说明理由.18．一个问题解决往往经历发现猜想——探索归纳——问题解决的过程，下面结合一道几何题来体验一下.（发现猜想）（1）如图①，已知∠AOB ＝70°，∠AOD ＝100°，OC 为∠BOD 的角平分线，则∠AOC 的度数为 ；.（探索归纳）（2）如图①，∠AOB ＝m ，∠AOD ＝n ，OC 为∠BOD 的角平分线. 猜想∠AOC 的度数（用含m 、n 的代数式表示），并说明理由.（问题解决）（3）如图②，若∠AOB ＝20°，∠AOC ＝90°，∠AOD ＝120°.若射线OB 绕点O 以每秒20°逆时针旋转，射线OC 绕点O 以每秒10°顺时针旋转，射线OD 绕点O 每秒30°顺时针旋转，三条射线同时旋转，当一条射线与直线OA 重合时，三条射线同时停止运动. 运动几秒时，其中一条射线是另外两条射线夹角的角平分线？19．如图，已知90AOB ∠=︒，AOC ∠为锐角，OD 平分AOC ∠，OE 平分BOC ∠.（1）求DOE ∠的度数；（2）当AOB m ∠=°时，求DOE ∠的度数.20．点A ，O ，B 依次在直线MN 上，如图1，现将射线OA 绕点O 顺时针方向以每秒10°的速度旋转，同时射线OB 绕着点O 按逆时针方向以每秒15°的速度旋转，直线MN 保持不动，如图2，设旋转时间为t 秒（t≤12）．（1）在旋转过程中，当t=2时，求∠AOB 的度数．（2）在旋转过程中，当∠AOB=105°时，求t 的值．（3）在旋转过程中，当OA 或OB 是某一个角（小于180°）的角平分线时，求t 的值．21．如图，∠EOD ＝70°，射线OC ，OB 分别是∠AOE ，∠AOD 的平分线． (1)若∠AOB ＝20°，求∠BOC 的度数；(2)若∠AOB ＝α，求∠BOC 的度数；(3)若以OB 为钟表上的时针，OC 为分针，再过多长时间由B ，O ，C 三点构成的三角形的面积第一次达到最大值？22．如图，直线CD 与EF 相交于点O .60COE ∠=︒，将一直角三角尺AOB 的直角顶点与点O 重合.OA 平分COE ∠.(1)求BOD ∠的度数.(2)将三角尺AOB 以每秒3º的速度绕点O 顺时针旋转.同时直线EF 也以每秒9º的速度绕点O 顺时针旋转，设运动时间为t s(040t ≤≤).①当t 为何值时，直线EF 平分AOB ∠?②若直线EF 平分BOD ∠，直接写出t 的值.23．如图，已知AOB 是一条直线，OC 是∠AOD 的平分线，OE 是∠BOD 的平分线.（1）若∠AOE=140°，求∠AOC 的度数；。

4.6 2. 角的比较和运算一、选择题1．借助一副三角尺，你能画出下面哪个度数的角( )A．65° B．75° C．85° D．95°2．如图K－44－1，∠AOD－∠AOC＝( )图K－44－1A．∠AOC B．∠BOCC．∠BOD D．∠COD3．如图K－44－2，若∠AOC＝∠BOD，则∠AOD与∠BOC的关系是 ( )图K－44－2A．∠AOD>∠BOC B．∠AOD<∠BOCC．∠AOD＝∠BOC D．无法确定4．已知∠A＝20°18′，∠B＝20°15′30″，∠C＝20.25°，则( )A．∠A>∠B>∠CB．∠B>∠A>∠CC．∠A>∠C>∠BD．∠C>∠A>∠B5．如图K－44－3，OC是∠AOB的平分线．若∠AOC＝75°，则∠AOB的度数为( )图K－44－3A．145° B．150° C．155° D．160°6. 如图K－44－4，直线AB，CD相交于点O，射线OM平分∠AOC.若∠BOD＝76°，则∠BOM等于( )图K－44－4A. 38° B．104°C．142° D．144°7．在放大镜下去观察一个角，正确的说法是( )A．角的度数扩大了B．角的度数缩小了C．角的度数没有变化D．以上都不对8．如图K－44－5，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC等于( )图K－44－5A．30° B．40°C．50° D．60°9．如图K－44－6，OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOB＝50°，∠COE＝60°，那么下列结论错误的是( )图K－44－6A．∠AOE＝110° B．∠BOD＝80°C．∠BOC＝50° D．∠DOE＝30°10．已知∠AOB＝70°，以O为端点作射线OC，使∠AOC＝42°，则∠BOC的度数为( ) A．28° B．112°C．28°或112° D．68°二、填空题11．如图K－44－7，∠PBC________∠ABC.(填“＞”“＜”或“＝”)图K－44－712．如图K－44－8，∠1，∠2，∠3构成一个平角，若∠1＝64°25′，∠2＝74°35′，则∠3＝________．图K－44－813．如图K－44－9，∠AOB＝90°，∠BOC＝42°，OD平分∠AOC，则∠AOD的度数为________．图K－44－914．如图K－44－10所示，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝20°，则∠AOB＝________°.图K－44－10三、解答题15．尺规作图：(不写作法，但要保留作图痕迹)已知：∠α和∠β.图K－44－11求作：∠AOB，使∠AOB＝∠α－∠β.16．如图K－44－12所示，∠AOC和∠BOD都是直角．若∠DOC＝18°，求∠AOB的度数．图K－44－1217．如图K－44－13，已知轮船A在灯塔P的北偏东30°的方向上，轮船B在灯塔P的南偏东70°的方向上．(1) 求从灯塔P看两轮船的视角(即∠APB)的度数；(2) 若轮船C在∠APB的平分线上，则轮船C在灯塔P的什么方位？图K－44－1318．如图K－44－14所示，OE平分∠BOC，OD平分∠AOC，∠BOE＝20°，∠AOD＝40°，求∠DOE 的度数.链接听课例3归纳总结图K－44－141．B 2.D3．C 4．A 5.B 6.C 7.C 8．A 9．A 10．C 11．＜ 12．41° 13．24° 14 12015．解：如图所示，∠AOB 即为所求．16．解：因为∠BOD＝∠DOC＋∠COB＝90°， ∠AOC ＝∠AOB＋∠COB＝90°， 所以∠AOB＝∠DOC＝18°.17．解：(1)由题意知，∠1＝30°，∠2＝70°，则∠APB＝180°－∠1－∠2＝180°－30°－70°＝80°，所以从灯塔P 看两轮船的视角为80°.(2)由(1)知，∠APB ＝80°， 因为点C 在∠APB 的平分线上， 所以∠APC＝∠BPC，则∠APC＝12∠APB＝12×80°＝40°，所以∠1＋∠APC＝30°＋40°＝70°.即轮船C 在灯塔P 的北偏东70°的方向上．18解：由OE 平分∠BOC，得∠EOC＝∠BOE＝20°.由OD 平分∠AOC，得∠COD＝∠AOD＝40°，所以∠DOE ＝20°＋40°＝60°.。

4.3.2 角的比较与运算一．选择题（共12小题）1．（2018•香洲区模拟）如图所示，已知∠AOC=∠BOD=70°，∠BOC=30°，则∠AOD的度数为（）A．100°B．110°C．130°D．140°2．（2017•夏津县一模）如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB=（）A．90° B．120°C．160°D．180°3．（2017•广东模拟）一副三角板如图所示放置，则∠AOB等于（）A．120°B．90° C．105°D．60°4．（2017•大兴区一模）如图是我们常用的一副三角板．用一副三角板可以拼出的角度是（）A．70° B．135°C．140°D．55°5．（2017秋•榆树市期末）如图，OC⊥AB，OE为∠COB的角平分线，∠AOE的度数为（）A．130°B．125°C．135°D．145°6．（2017秋•揭西县期末）如图，已知∠COB=2∠AOC，OD平分∠AOB，且∠COD=20°，则∠AOB=（）A．40° B．60° C．120°D．135°7．（2017秋•秦淮区期末）如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（）A．45° B．45°+∠AOC C．60°﹣∠AOC D．不能计算8．（2017秋•南京期末）用一副三角尺，不能画出的角是（）A．15° B．75° C．165°D．145°9．（2017秋•凉州区期末）如图，∠AOC和∠DOB都是直角，如果∠AOB=150°，那么∠DOC=（）A．30° B．40° C．50° D．60°（2017秋•定安县期末）如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°，10．则∠COE=（）A．65° B．70° C．75° D．80°11．（2017秋•五莲县期末）下列说法正确的个数是（）（1）连接两点之间的线段叫两点间的距离；（2）木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；（3）若AB=2CB，则点C是AB的中点；（4）若∠A=20°18′．∠B=20°28″，∠C=20.25°，则有∠A＞∠C＞∠B．A．1个B．2个C．3个D．4个12．（2017秋•长兴县期末）如图，∠AOB是直角，∠COD也是直角，若∠AOC=α，则∠BOD 等于（）A．90°+αB．90°﹣α C．180°+α D．180°﹣α二．填空题（共8小题）13．（2018•昆明）如图，过直线AB上一点O作射线OC，∠BOC=29°18′，则∠AOC的度数为．14．（2018•凉山州）已知两个角的和是67°56′，差是12°40′，则这两个角的度数分别是．15．（2017秋•甘井子区期末）如图，O是直线AB上的一点，OC是∠AOB的平分线，∠COD=36°24′，则∠BOD的度数是．16．（2016•湘潭一模）如图，点O在直线AB上，射线OC平分∠DOB，若∠COB=35°，则∠AOD= °．17．（2017秋•建昌县期末）如图，点O是直线AB上的点，在AB同侧画射线OC、OD，且OD 平分∠AOC，若∠BOC=57°，则∠AOD= °′．18．（2017秋•黄梅县期末）设∠A=18°18′，∠B=18.18°，则∠A ∠B（填“＞“或”＜“或”=“）19．（2017秋•椒江区期末）已知：∠AOC=146°，OD为∠AOC的平分线，∠AOB=90°，∠BOD 的度数．20．（2017秋•武清区期末）如图，点O在直线AB上，射线OD平分∠AOC，若∠AOD=20°，则∠COB的度数为度．三．解答题（共4小题）21．（2017秋•厦门期末）按要求作答：（1）画图，使得∠AOC﹣∠BOC=∠AOB；（2）在（1）中，若∠AOC=80°，∠BOC比2∠AOB少10°，求∠AOB的度数．22．（2017秋•费县期末）如图，已知∠AOC=∠BOD=70°，∠BOC=31°，求∠AOD的度数．23．（2017秋•定陶区期末）如图，已知OE是∠AOC的角平分线，OD是∠BOC的角平分线．（1）若∠AOC=120°，∠BOC=30°，求∠DOE的度数；（2）若∠AOB=90°，∠BOC=α，求∠DOE的度数．24．（2017秋•重庆期末）填空，完成下列说理过程如图，点A，O，B在同一条直线上，OD，OE分别平分∠AOC和∠BOC．（1）求∠DOE的度数；（2）如果∠COD=65°，求∠AOE的度数．2018年暑假七年级数学一日一练： 4.3.2 角的比较与运算参考答案与试题解析一．选择题（共12小题）1．【解答】解：∵∠AOC=70°，∠BOC=30°，∴∠AOB=40°；同理可得，∠COD=40°．∴∠AOD=∠AOB+∠BOC+∠COD=40°+30°+40°=110°，故选：B．2．【解答】解：设∠AOD=a，∠AOC=90°+a，∠BOD=90°﹣a，所以∠AOC+∠BOD=90°+a+90°﹣a=180°．故选：D．3．【解答】解：根据三角板的度数可得：∠2=45°，∠1=60°，∠AOB=∠1+∠2=45°+60°=105°，故选：C．4．【解答】解：A、不能拼出70°的角，故此选项错误；B、可以利用90°和45°的角拼出135°的角，故此选项正确；C、不能拼出140°的角，故此选项错误；D、不能拼出55°的角，故此选项错误；故选：B．5．【解答】解：∵OC⊥AB，∴∠COB=∠AOC=90°，∵OE为∠COB的角平分线，∴∠COE=45°，∴∠AOE=∠AOC+∠COE=90°+45°=135°；故选：C．6．【解答】解：设∠AOC=x，则∠BOC=2x，则∠AOD=1.5x．∵∠AOD﹣∠AOC=∠COD，∴1.5x﹣x=20°，解得：x=40°．∴∠AOB=3x=120°．故选：C．7．【解答】解：∵OM平分∠BOC，ON平分∠AOC，∴∠MOC=∠BOC，∠NOC=∠AOC，∴∠MON=∠MOC﹣∠NOC=（∠BOC﹣∠AOC），=（∠BOA+∠AOC﹣∠AOC），=∠BOA，=45°．故选：A．8．【解答】解：145°不能够被15整除，所以不能画出145°的角．故选：D．9．【解答】解：∠DOC=90°+90°﹣∠AOB=180°﹣150°=30°．故选A．10．【解答】解：∵OD平分∠AOC，∠AOC=50°，∴∠COD=∠AOD=∠AOC=×50°=25°，∴∠COE=∠DOE﹣∠COD=90°﹣25°=65°．故选：A．11．【解答】解：（1）连接两点之间的线段的长度叫两点间的距离，错误；（2）木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点确定一条直线，错误；（3）当C在线段AB上，且AB=2CB时，点C是AB的中点，当C不在线段AB上时，则不是中点，故命题错误；（4）若∠A=20°18′．∠B=20°28″，∠C=20.25°，则有∠A＞∠C＞∠B，正确；故选：A．12．【解答】解：根据∠AOB是直角，∠COD也是直角，若∠AOC=α，那么∠BOC=90°﹣α，∴∠BOD=∠BOC+∠COD=90°﹣α+90°，=180°﹣α．故选：D．二．填空题（共8小题）13．【解答】解：∵∠BOC=29°18′，∴∠AOC的度数为：180°﹣29°18′=150°42′．故答案为：150°42′．14．【解答】解：设这两个角的度数为x、y，则，解得：x=40°18′，y=27°38′，故答案为：40°18′、27°38′．15．【解答】解：∵O是直线AB上的一点，OC是∠AOB的平分线，∴∠BOC=90°．∴∠BOD=∠BOC﹣∠COD=90°﹣36°24′=53°36′．故答案为：53°36′．16．【解答】解：∵射线OC平分∠DOB．∴∠BOD=2∠BOC，∵∠COB=35°，∴∠DOB=70°，∴∠AOD=180°﹣70°=110°，故答案是：110．17．【解答】解：∠AOC=180°﹣∠BOC=123°．∵OD平分∠AOC，∴∠AOD=×123°=61.5°=61°30′．故答案为：61；30．18．【解答】解：因为∠A=18°18′=18.3°，18.3°＞18.18°，故答案为：＞19．【解答】解：∵∠AOC=146°，OD为∠AOC的平分线，∴∠AOD=∠AOC=×146°=73°，OB在∠AOC内部时，如图1，∠BOD=∠AOB﹣∠AOD=90°﹣73°=17°，OB在∠AOC外部时，如图2，∠BOD=∠AOD+∠AOB=73°+90°=163°，所以，∠BOD的度数是17°或163°．故答案为：17°或163°．20．【解答】解：∵OD平分∠AOC，∴∠AOC=2∠AOD=40°，∴∠COB=180°﹣∠COA=140°，故答案为：140．三．解答题（共4小题）21．【解答】解：（1）如图所示，（2）设∠AOB=x°，则∠BOC=（2x+10）°，∵∠AOB+∠BOC=∠AOC，∴x+2x﹣10=80∴3x=90∴x=30∴∠AOB=30°22．【解答】解：∵∠AOC=70°，∠BOC=31°，∴∠AOB=∠AOC﹣∠BOC=70°﹣31°=39°．又∵∠BOD=70°，∴∠AOD=∠AOB+∠BOD=39°+70°=109°．23．（1）∵OE是∠AOC的角平分线，OD是∠BOC的角平分线，∠AOC=120°，∠BOC=30°，【解答】解：∴∠EOC=60°，∠DOC=15°，∴∠DOE=∠EOC﹣∠DOC=60°﹣15°=45°；（2））∵OE是∠AOC的角平分线，OD是∠BOC的角平分线，∠AOB=90°，∠BOC=α，∴∠EOC=（90°﹣α），∠DOC=α，∴∠DOE=∠EOC﹣∠DOC=（90°﹣α）﹣α=45°．24．【解答】解：（1）如图，∵OD是∠AOC的平分线，∴∠COD=∠AOC．∵OE是∠BOC的平分线，∴∠COE=∠BOC．所以∠DOE=∠COD+∠COE=（∠AOC+∠BOC）=∠AOB=90°．（2）由（1）可知：∠BOE=∠COE=90°﹣∠COD=25°．所以∠AOE=180°﹣∠BOE=155°．。

第四章几何图形4．3 角4.3.2 角的比较与运算【知识点1】角的比较(1)度量法：用量角器量出角的度数，然后比较它们的大小．(2)叠合法：把两个角的顶点和一边分别重合，另一边放在重合边的同旁，通过另一边的位置关系比较大小，如图所示，比较∠ABC和∠DEF的大小．图1 图2 图3①如图1所示，EF落在∠ABC的内部，那么∠DEF小于∠ABC，记作∠DEF<∠ABC；②如图2所示，EF落在∠ABC的外部，那么∠ABC小于∠DEF，记∠ABC<∠DEF；③如图3所示，EF和BC重合，那么∠ABC等于∠DEF，记作∠ABC＝∠DEF.【典例1】若∠A＝20°18′，∠B＝20°15″，∠C＝20.25°，则有 ( ) A．∠A＞∠B＞∠C B．∠B＞∠A＞∠CC．∠A＞∠C＞∠B D．∠C＞∠A＞∠B分析：∵∠A＝20°18′，∠B＝20°15″，∴∠A＞∠B．∵∠C＝20.25°＝20°15′，∴∠A＞∠C，∠C＞∠B，∴∠A＞∠C＞∠B．答案：C【知识点2】角的和与差如图所示，∠AOC是∠AOB和∠BOC的和，记作∠AOC＝∠AOB＋∠BOC；∠AOB是∠AOC与∠BOC的差，记作∠AOB＝∠AOC－∠BOC．类似地，∠BOC＝∠AOC－∠AOB．【典例2】如图，点B、O、D在同一直线上，若∠1＝15°，∠2＝105°，则∠AOC的度数是 ( )A．75° B．90° C．105° D．125°分析：∵∠2＝105°，∴∠BOC ＝180°－∠2＝75°，∴∠AOC ＝∠1＋∠BOC ＝15°＋75°＝90°. 答案：B【知识点3】 角平分线(1)定义：从一个角的顶点出发，把这个角分成两个相等的角的射线叫做这个角的平分线．如右图，若∠AOB ＝∠BOC ，则OB 是∠AOC 的平分线．(2)性质：如上图所示，OB 是∠AOC 的平分线，那么∠AOB ＝∠BOC ＝12∠AOC ．(3)类似地，可以得到角的三等分线．如图，OB 、OC 是∠AOD 的三等分线，那么∠AOB ＝∠BOC ＝∠COD ＝13∠AOD ． 注意：角平分线是一条射线，角的平分线的定义也是判断一条射线是角的平分线的一种方法．【典例3】已知，如图，∠AOC ＝80°，∠BOC ＝50°，OD 平分∠BOC ，则∠AOD 是( )A ．85°B ．100°C ．105°D ．115°答案：C1．下列关于角平分线的说法中，正确的是 ( )A ．平分角的一条线段B ．平分角的一条直线C ．经过角的顶点且把这个角分成相等的两个角的一条线段D ．经过角的顶点且把这个角分成相等的两个角的一条射线2．如果∠1和∠2的顶点和一条边都重合，另一条边都在公共边的同旁，且∠1<∠2，那么∠2的另一边落在∠1的 ( )A ．另一边上B ．内部C ．外部D ．以上都不对3．【2017·湖北随州中考】如图，用尺规作图作∠AOC ＝∠AOB 的第一步是以点O 为圆心，以任意长为半径画弧①，分别交OA 、OB 于点E 、F ，那么第二步的作图痕迹②的作法是 ( )A ．以点F 为圆心，OE 长为半径画弧B ．以点F 为圆心，EF 长为半径画弧C ．以点E 为圆心，OE 长为半径画弧D ．以点E 为圆心，EF 长为半径画弧4．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC＝100°，则∠BOD的度数是 ( )A．20° B．40°C．50° D．80°5．已知∠AOB＝70°，以点O为端点作射线OC，使∠AOC＝42°，则∠BOC的度数为( ) A．28° B．112°C．28°或112°D．68°6．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC＋∠DOB＝ ( )A．90°B．120°C．160° D．1807．两个角度数之比为7∶3，它们度数之差为72°，这两个角度数之和为 ( ) A．120° B．144° C．180°D．360°8．在钟表上，1点30分时，时针与分针所成的角是 ( )A．135° B．165° C．150°D．120°9．如图，OC是∠AOB内的一条射线，若∠AOC＝12_________，则OC平分∠AOB；若OC是∠AOB的平分线，则________＝2∠AOC．9题 10题 11题 12题10．如图所示，射线OC平分∠DOB，OB平分∠AOC，下列结论中：①∠DOC＝∠BOC＝∠AOB；②∠BOD＝∠AOB；③∠BOD＝2∠AOB；④∠AOB＝2∠COD．其中正确的是________.(只填序号)11．如图所示，OM平分∠AOC，ON平分∠BOC，则∠MON＝__________.12．将一张长方形纸片折叠成如图所示的形状，则∠ABC的度数为__________. 13．计算：(1)34°34′＋21°51′；(2)180°－52°31′；(3)25°36′12″×4；(4)10°9′24″÷6.14．如图，∠AOB＝120°，∠BOD＝90°，OC平分∠BOD，求∠AOC的度数．15．如图，OC是∠AOD的平分线，OE是∠BOD的平分线．(1)如果∠AOB＝130°，求∠COE的度数；(2)在(1)条件下，如果∠COD＝20°，求∠BOE的度数．。