07-08高等数学试题(A)解答

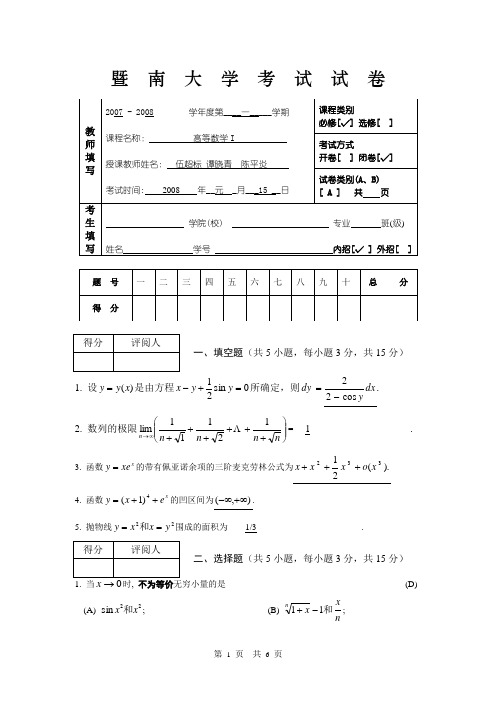
暨 南 大 学 考 试 试 卷一、填空题（共5小题，每小题3分，共15分）1. 设)(x y y =是由方程0sin 21=+-y y x 所确定，则=dy dx ycos 22-. 2. 数列的极限⎪⎪⎭⎫⎝⎛++++++∞→n n n n n 12111lim = __1____________________. 3. 函数xxe y =的带有佩亚诺余项的三阶麦克劳林公式为).(21332x o x x x +++4. 函数xe x y ++=4)1(的凹区间为),(+∞-∞.5. 抛物线22y x x y ==和围成的面积为____1/3________________________.二、选择题（共5小题，每小题3分，共15分）1. 当时, 不为等价无穷小量的是 (D) (A) 22sin x x 和; (B)nx x n和11-+;(C) x x 和)1ln(+; (D) 2cos 1x x 和-.2.设]1,0[上0)(">x f ,则)1()0()0()1(),1('),0('f f f f f f --或几个数的大小顺序为(B)(A) );0()1()0(')1('f f f f ->> (B) );0(')0()1()1('f f f f >-> (C) );0(')1(')0()1(•f f f f >>- (D) ).0(')1()0()1('f f f f >-> 3. 以下函数有可去间断点的是 (B )(A) ⎩⎨⎧>-≤-=;0,3,0,1)(x x x x x f (B) ;39)(2--=x x x f(C) ⎪⎩⎪⎨⎧=≠=;0,0,0,1sin )(x x xx f (D) .|sin |)(x x x f = 4. 摆线⎩⎨⎧-=-=)cos 1(),sin (θθθa y a x 的一摆)20(πθ≤≤的长度为 (D)(A) a 2; (B) a 4; (C) a 6; (D) a 8.5. 函数],[)(b a x f 在区间上连续是],[)(b a x f 在可积的 (A) (A) 充分条件; (B) 必要条件;(D) 即不是充分条件也不是必要条件.三、计算题（共7小题，每小题7分，共49分）1. 求定积分⎰210arcsin xdx ;解: 原式⎰--=21022101|arcsin dx xx x x ----------------------------------4⎰--+=21022)1(112112x d x π----------------------------------5 2102112x -+=π--------------------------------------------6.12312-+=π----------------------------------------------7 2. 求极限3sin 1tan 1limx xx x +-+→;解: 原式)sin 1tan 1()sin 1(tan 1lim3x x x x x x ++++-+=→-------------------------------------------------230sin tan lim21x xx x -=→ )21~cos 1,~sin ,0(cos )cos 1(sin lim 21230x x x x x xx x x x -→-=→时当 --------5.4121lim 21320=⋅=→x x x x -----------------------------------------------------------------73. 设)(x y y =由参数方程⎪⎩⎪⎨⎧==te y t e x ttsin ,cos 所确定，求22dx y d ; 解:)sin (cos t t e dt dx t -=, )cos (sin t t e dtdyt +=,-------------------------------------2,s in c o s c o s s in t t t t dtdx dt dy dx dy -+==-------------------------------------------------------4dx dtt t t t dt d dx dy dx d dx y d ⋅-+==)sin cos cos sin ()(22------------------------------------------------6 )sin (cos 1)sin (cos )cos (sin )cos (sin 222t t e t t t t t t t -⋅-++-=.)s i n (c o s 23t t e t -=--------------------------------------------------------------------74. 求不定积分⎰+x x xdxcos sin cos ;解: 原式⎰+-++=dx x x x x x x cos sin )sin (cos )sin (cos 21-------------- -- ----------------------3⎰⎰+++=x x x x d dx cos sin )cos (sin 2121----------------------------------------------------5C x x x +++=|cos sin |ln 2121.---------------------------------------------------75. 求极限2020222)1(limxdte t x x tx ⎰-→+;解: 原式22222)1(limxdt e t ex t x x ⎰+=-→------------- ---------------------------------------222022)1(limx dt e t x t x ⎰+=→-----------------------------------------------------------4xxe x x x 22)1(lim 440⋅+=→------------------------------------------------------------61)1(lim 440=+=→x x e x .-------------------------------------------------------------76. 求过点)0,23(与曲线21xy =相切的直线方程; 解: 设切点为)1,(20x x , 32'xy -=, 所以切线方程为-----------------------------1 )(21032x x x x y --=-.-----------------------4因)0,23(过切线, 所以)23(210032x x x --=-.-----------------------6 解得.10=x 因此切线方程为 .032=-+x y --------------------------------------7 7. 讨论瑕积分⎰10q x dx(q >0)的收敛性，如果收敛则计算其值.解: 对任意)1,0(∈ε,⎪⎪⎩⎪⎪⎨⎧≠--=-=-==--⎰.1),1(1111,1,ln |ln 11111q q x q q x x dx q q q εεεεε------------------------------------------3因此⎪⎩⎪⎨⎧≥∞+<-=⎰+→.1,,1,11lim10q q q x dx qεε--------------------------------------------------------------------6即1≥q 发散,当1<q 时收敛,其值为q-11.----------------------------------------------------------7四、应用题（共2小题，每小题8分，共16分）h m, 底面半径为r m , 桶内盛满了某种液体. 试问要把桶内的液体全部吸出需要作多少功? 已知这种液体的密度为ρ.解: 建立如图所示的坐标. 在任一小区间 上的一薄液体的 O的重力为dx r g 2ρπ(KN)----------------------------------3这薄层液体吸出桶外所做的功(功元素)为 xdx r g dW 2ρπ=----------------------------5所求的功为 hh x r g xdx r g W 02202|21ρπρπ==⎰2221h r g ρπ=(KN).---------------------8 2. 要做一个容积为V 的圆柱形罐头筒, 怎样设计才能使所用的材料最省? 解: 设底面半径为r , 则高为2r Vπ,表面积为 .0,2222222>+=⋅+=r r Vr rV r r S ππππ------------------------------------3令022'2=-=rV r S π得3πV r =,--------------------------------------------------------------------------5 又0|)42(|'333>+===πππV r Vr r V S , 因此当3πV r =时S 取最--------------------------------------7 即当底面半径为3πV,高为3πV时所用的材料最少.--------------------------------------------------8五、证明题（共1小题，每小题5分，共5分）1. 设)(x f 在区间],[b a 上连续,且0)(>x f ,⎰⎰∈+=x bx ab a x t f dtdt t f x F ],[,)()()(. 证明: (1) 2)('≥x F ; (2) 方程0)(=x F 在),(b a 内有且仅有一个根.证明: (1) .2)(1)(2)(1)()('=⋅≥+=x f x f x f x f x F ---------------------------------------------2 (2) )(x F 在],[b a 上连续, 且]d ,[x x x +0)()()()()()()(<-===⋅⎰⎰⎰⎰b a b a baa bdt t f t f dt •dt t f t f dt x F b F a F ,因此由介值定理)(x F 在),(b a 至少有一根, ----------------------------------------------------------4 又0)('>x F , 所以)(x F 在],[b a 上单调增, 因此)(x F 在),(b a 是只有一根.----------------5。

华东交通大学2007—2008学年第一学期考试卷承诺：我将严格遵守考场纪律，知道考试违纪、作弊的严重性，还知道请他人代考或代他人考者将被开除学籍和因作弊受到记过及以上处分将不授予学士学位，愿承担由此引起的一切后果。

专业 班级 学号 学生签名：试卷编号： （A ）卷《高等数学Ⅰ(A)》 课程 (工科本科07级) 课程类别：必 闭卷（√） 考试时间：2008.1.14题号 一 二 三四 五 总分 1 2 3 4 5 6 7 1 2分值 10 15 77777779 98阅卷人 (全名)考生注意事项：1、本试卷共 6 页，总分 100 分，考试时间 120 分钟。

2、考试结束后，考生不得将试卷、答题纸和草稿纸带出考场。

一、填空题(每题2分，共10分)_____sin 1sin12lim=→xx x x 极限、_________ cos sin 2='+=y x x x y 则，设、__________)2)(1(12 32的水平渐近线为曲线、-+-+=x x x x y_________ 42围成平面图形面积为及直线由曲线、x y x y == ______5的通解为微分方程、x yy =' 二、选择题(每题 3分，共15分)D. 1 C. 2 B. 3 A.)B ()23()1()( 12第一类间断点的个数为函数、+--=x x x x x x f0 D. 4!1 C. 5!1 B. 6!1 A.)D ()1(124)( 2)16(515=+-+=f x x x x f ，则设、得分 评阅人得分 评阅人x x cos 02=y cx y =C x y +=ln ln 或61dxx f x f dx x f x f dx x f dx x f a a x f aaaaa⎰⎰⎰⎰---+=-- 0)]()([ D. )]()([ C. )(2B. 0 A.)C ()( ] [)( 3则上连续，，在设函数、arctan 1D. arctan 1 C. arctan 1B. arctan 1 A.)A ()1(1422C x x C x x C x x C x x dx x x+++-++-+--=+⎰不定积分、 0D. 4 C. 2 B. A.)B (1 5 2πππ=+⎰∞+∞-dx e e xx反常积分、三、解答题(每题 7分，共49分).)( 1322limxdte exttx ⎰-→-求极限、2322limx e e x x x -→-=原式xxe xex x x 62222lim-→+=32322lim=+=-→x x x e e.? 11 0 2说明理由等价无穷小是否为与无穷小时，当、x x x x --+→xx x x --+→11limΘ)11(2lim 0x x x xx -++=→1112lim=-++=→xx x.11 0 为等价无穷小与时，当x x x x --+→∴ 得分 评阅人评阅人. )( 333dy x y y e y xy x 求，确定隐函数设方程、==++ 033 22='+'++y y y x y x x 求导得：两边对2233 y x yx y ++-='⇒dxyx y x dx y dy 2233++-='=⇒033 22=+++dy y xdy ydx dx x 或两边取微分得：dxyx y x dy 2233++-=⇒的凹凸区间及拐点求曲线、x x y ln 42= x x x x x x x y +=⋅+='ln 21ln 2 2Θ 3ln 2112ln 2 +=+⋅+=''∴x x x x y 23 0-==''e x y 得：令0 002323>''><''<<--y ex y ex 时当，时当) [23∞+-，故凹区间为e ] 0(23-e ，凸区间为 )23(323ee --，拐点为得分 评阅人评阅人dxx x ⎰+)1ln( 5求不定积分、2)1ln(21dxx ⎰+=原式 )1ln(212)1ln(22+-+=⎰x d x x xdxx x x x ⎰+-+=1212)1ln(22dxx x x x ⎰++--+=)111(212)1ln(2Cx x x x x ++-+-+=2)1ln(242)1ln(22)1()1ln(212-+=⎰x d x 或原式)1ln()1(212)1ln()1(22+--+-=⎰x d x x x dxx x x ⎰--+-=)1(212)1ln()1(2Cxx x x ++-+-=242)1ln()1(22⎰-22221 6dxx x求定积分、tdt dx t x cos sin ==则，令⎰⎰==4240 2sin cos cos sin ππtdttdt tt原式⎰-=422cos 1πdt t40)42sin 2(πt t -=418-=π得分 评阅人得分 评阅人的通解求微分方程、x e y y y =+'-''2 7012 2=+-r r 特征方程为1 21==⇒r rx e x C C Y y y y )(0221+==+'-''⇒的通解为x e ax y 2*1==解为特征方程重根，设特λ 12 *=a y 代入原方程得把x ex y a 221* 21=⇒=⇒xx ex C C e x y )(21212++=⇒原方程通解为四、综合题(每题 9分，共18分)的通解求微分方程、xxe y x y ='-''1 1则，令 )(x p y =' xxe p x p =-'1)(111C exe e p dxx xdxx+⎰⎰=⇒---⎰）1(C dx e x x +=⎰)(1C e x x+= )(1C e x y x +='⇒⎰+=dxC e x y x )(1通解212x C xde x +=⎰2212C x Ce xe x x ++-=得分 评阅人得分 评阅人周所得旋转体的体积轴旋转一绕求轴围成平面图形为及该切线与曲线的切线，经过坐标原点作曲线、 .ln ln 2y D D x x y x y == 则，，设切点坐标为 )ln (00x x)(1ln 000x x x x y -=-切线方程为)0(1ln 0 000x x x -=-由切线过原点得：)1 ( 0，即切点为，e e x =⇒ e xy =⇒切线方程为dyey dy e V y 2112)()(⎰⎰-=⇒ππ所求体积为 或13)(212⋅-=⎰e dy e V y ππ103210232ye ey ππ-=210232eey ππ-=262ππ-=e262ππ-=e五、证明题(8分).0)()(201 ) ( 0)()() ( ] [)(='+∈==ξξξf f b a b f a f b a b a x f 使得，，存在证明：，内可导且，在上连续，，在设)()(201x f e x F x=令 内可导，在上连续，，在则) ( ] [)(b a b a x F 0)()(==b F a F 且0)( ) (='∈⇒ξξF b a 使，，存在 )()(201)(201201x f e x f e x F x x '+='又0)()(201 201201='+ξξξξf e f e 故0)()(201 0201='+≠ξξξf f e 得由得分 评阅人得分 评阅人。

2007-2008学年第一学期2007级电气、电子、工程管理、机制、教技、土木工程、计算机、农机、网络工程、物理专业高等数学Ⅰ 试卷A 参考答案一、填空题(填对每空得2分，填错或不填每空得0分，计20分) 1．982442424++++x x x x ．2．3-e．3． 3 ． 4． 3 ． 5． （ 0 ，-1 ）． 6．21．7．0144=++y x ．8．51．9． 0 ． 10．14．二、选择题（选对每题得2分，不选、选错或多选每题得0分，计10分） 1．（ D ） 2．（ B ） 3．（ C ） 4．（ A ） 5．（ B ）三、计算题（每小题5分，计20分）1．解： xx x x x x x x sin )sin 21(1lim sin 2cos 1lim 200--=-→→…………………………2分xx xx sin sin 2lim 20→= …………………………………3分 x xx sin 2lim0→=..........................................4分 2=． (5)分2．解：应用洛必达法则得xxx xtd t t x xx 2arctan limarctan lim20-=∞-→∞-→⎰………………………3分x x a r c t a nlim 21∞-→-= ………………………4分 4)2(21ππ=-⨯-=. ………………………5分3．解： ⎰dx xx2sin ⎰-=x xd cot ……………………………………1分 ⎰+-=xdx x x cot cot ， …………………………2分 ⎰+-=dx x x x x sin cos cot ……………………………3分 ⎰+-=x d x x x s i n s i n1c o t ………………………4分c x x x ++-=|s i n |ln cot ．………………………5分4．解： ⎰-+1021xx dx ⎰+=20cos sin cos sin πtt tdt tx ……………………………1分⎰++=202)cos (sin )cos (sin cos πt t dt t t t (2)分⎰+++=202sin 112cos 2sin 21πdttt t……………………3分⎰⎪⎭⎫ ⎝⎛++=202sin 12cos 121πdt t t ………………………4分 4)2sin 1ln(212120ππ=⎥⎦⎤⎢⎣⎡++=t t ．………………5分四、解答题（每小题5分，计20分） 1．解：)sin ()cos 1(t t ad t ad dxdy --= (1)分ttcos 1sin -=． …………………………………………2分)sin (cos 1sin 22t t ad t t d dxy d -⎪⎭⎫ ⎝⎛-= ………………………………………3分)cos 1()cos 1(sin )cos 1(cos 22t a t t t t ----=……………………………4分23)cos 1(1)cos 1(1cos t a t a t --=--=． …………………5分 2．解： 方程两边同时微分得)()(y x e d xy d += ………………………1分即 )(dy dx e xdy ydx y x +=++ ……………………3分 整理得 ydx dx e dy e xdy y x y x -=-++， …………………4分 从而得 dx ex yedy yx yx ++--=．……………………………5分3．解：令u e x=可得u x ln =，代入已知式得 ……………………………1分 u u f ln )(='， c u u u udu +-=⎰ln ln …………………2分 从而有 0ln )(c u u u u f +-= ……………………………………3分 由0)1(=f 得 10=c ……………………………………………4分 因此 1ln )(+-=x x x x f ． ……………………………………5分4．解：设所求平面的法线向量为0),,(≠=C B A n ，两个已知平面的法线向量分别为)4,2,1(,)2,5,3(21-=-=n n， ……………………………………1分则有n n n n⊥⊥21, 即有 ⎩⎨⎧=+-=-+0420253C B A C B A ………………………2分得 A C A B 1611,87-=-=，0≠A ……………………………………3分 所以所求平面的方程为 0)3(161187)2(=+---z A Ay x A ，………4分整理得所求平面的方程为 065111416=---z y x ． …………………5分五、证明题（6分×2题＝12分） 1．证明：由题设有hx f h x f x f h )()(lim)(0000-+='→，所以…………………1分hx f h x f x f h x f hh x f h x f h h )]()5([)()3(lim)5()3(lim 00000000----+=--+→→……………2分⎥⎦⎤⎢⎣⎡----+=→h x f h x f h x f h x f h )()5()()3(lim 00000…………3分hx f h x f h x f h x f h h 5)()5(lim53)()3(lim3000000---+-+=→→……5分)(8)(5)(3000x f x f x f '='+'=． (6)分2．证：设x x x x f -++=)1ln()1()(，则0)0(=f ，………………………1分 又 )1l n ()(x x f +='． ……………………………………………2分 当0>x 时， 0)(>'x f ，函数单调增加， ……………………3分当01<<-x 时， 0)(<'x f ，函数单调减少．………………………4分 从而，当01≠<-x 时有0)(>x f ，且0)0(=f ， ………………………5分因此，当1->x 时，x x x ≥++)1ln()1(． ……………………………6分六、综合应用题（6分×3题＝18分）解：由⎩⎨⎧=+-=022y x x y 得两曲线交点为)4,2(),1,1(-， …………………1分1．图形面积为 ⎰--+=212)2(dx x x A …………………………3分 29312212132=⎥⎦⎤⎢⎣⎡-+=-x x x ， …………………6分2．图形绕x 轴旋转一周所得旋转体的体积为⎰--+=21222])()2[(dx x x V x π……………………………9分 57251)2(312153ππ=⎥⎦⎤⎢⎣⎡-+=-x x ……………………12分3．曲线2x y =交y 轴于点)0,0(，直线02=+-y x 与y 交于点)2,0( ……………………………13分图形绕y 轴旋转一周所得旋转体的体积为⎰⎰--=4422)2(dy y ydy V y ππ， (15)分 316)2(32423402πππ=--=y y ； ………………………18分。

高等数学（一）、（二）（上）试题（A ）评分标准与分工一、 填空题（每小题4分, 共24分）1．e . 2． =a －１. 3．)4ln 2,2(+ .4．０ . 5． x e x C C y )(21+=）. 6.21=ξ注：该题评分原则是 非对即错二、选择题 (每小题4分, 共20分) D C BB C 三、（5分）解: 30sin tan sin limx x x x -→30tan sin lim xxx x -=→ x x x x x sin cos 1cos lim 30-=→22021lim xx x -=→21-= -------------------------------- 5分注：该题评分原则 体现方法3分、结果正确2分；主要有以下几种方法 1）洛必达法则、2）等价无穷小替换、3）其他 四、（8分）解: 212)111(22tt t tdtdxdt dy dx dt dt dy dx dy =++-==⋅=； ------------- 4分t t dt dx t dt d dx dy dx d dx y d 412222+=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=……. ------------- 4分 五、（8分）1）⎰-+x x e e dx ⎰+=xxede 21-------------------------------- 4分 C e x+=arctan -------------------------------- 4分2）. 解: ⎰⎰⎰⎰+=+=ππππ002200222]2cos [2122cos 1cos xdx x dx x dx x x xdx x ………2分 （第一个积分1分；第二个积分3分）⎰⎰⎰-==ππππ22122122122sin 0|2sin 2sin 2cos xdx x x x d x xdx x ………3分=⎰⎰=-=ππππ0022121212cos 0|2cos 2cos xdx x x x xd4361ππ+=∴原式 ……………………………………3分 注：本题主要考察学生对分部积分的内容的掌握情况。

浙江理工大学2007~2008学年第二学期高等数学A 期终试题（A ）卷班级 学号 姓名 一、 选择题（每小题4分，满分28分）1、函数2222),(y x y x y x f +-= 在点)1,1(处的全微分)1,1(df 为 （ ）(A) 0 (B) dy dx + (C) dx 4 (D) dy dx -2 ２、设L 是从A (1,0)到B (-1,2)的直线段，则()Lx y ds +⎰＝ （ ）(B)(C) 2 (D) 03、方程234sin 2y y x '''+=+的特解为 （ ）(A)1(cos 2sin 2);2y x x =-+ (B) 31cos 222y x x =- (C)31sin 222y x x =- (D)311cos 2sin 2.222y x x x =--4、设)(x f 在),0(+∞上有连续的导数，点A )2,1(，B )8,2(在曲线22x y =上。

L为由A 到B 的任一曲线，则=++-⎰dy x xy f x dx x y f x y xy L])(1[)](22[22223（ ）。

(A) 20， (B) 30， (C) 35， (D) 40。

5、 设b 为大于1的自然数，对幂级数∑∞=1n bnnx a，有a a a nn n =+∞→1l i m，（1,0≠>a a ），则其收敛半径=R （ ）。

(A) a ， (B) a1， (C)ba ， (D)ba1。

6、下列级数收敛的是 （ ）(A) ∑∞=1sin n n π； （B ）∑∞=1100!n n n ； （C ）∑∞=+12)11ln(n n ； （D ）∑∞=+-12)11(21)1(n n n nn ． 7、已知曲线)(x f y =过原点，且在原点处的法线垂直于直线)(,13x y y x y ==-是微分方程02=-'-''y y y 的解，则=)(x y （ ）（A ）x xe e--2 （B ）x x e e 2-- （C ）x x e e 2-- （D ）x x e e --2二、填空题（每小题4分，满分20分）1、设函数22(,)22f x y x ax xy y =+++在点(1,1)-取得极值, 则常数a = 。

2007-2008年第一学期※※※※※※高等数学（180学时）试题A 卷※※※※※※一．试解下列各题（每小题7分，共56分） 1．计算.3lim ⎪⎭⎫ ⎝⎛--+∞→n n n n n解：=⎪⎭⎫ ⎝⎛--+∞→n n n n n 3lim nn n n n n -++∞→34lim.224111314lim==-++=∞→nn n 2．计算().1cos 1ln lim0--+→x xx x解：()=--+→1cos 1ln lim0x x x x xx x sin 111lim 0--+→().1cos 11lim 20=-+-=→x xx 3．计算.arctan ⎰xdx x解：.arctan ⎰xdx x ⎰⎪⎪⎭⎫ ⎝⎛=2arctan 2x xd ⎰+-=dx x x x x 222121arctan .2⎰⎰++-=dx x dx x x 22112121arctan .2.arctan 2121arctan .22c x x x x ++-= 4．计算.14⎰+dx xx解：令x t =，即.2t x =则.2tdt dx =dt t t dx x x⎰⎰+=+20240121()dt tt t t ⎰++--+=2021112 dt t ⎰=202⎰⎰++-20201122dt t dt =.3ln 21ln 222.2|||20|20202=++-=t t t 5．计算.0⎰+∞-dx xe x解：=⎰+∞-0dx xe x ()⎥⎦⎤⎢⎣⎡--=-⎰⎰+∞-∞=-+∞-000|dx e xe e xd x x x .1|00=-==+∞-+∞-⎰x x e dx e6．设曲线方程为⎩⎨⎧==.2cos ,sin t y t x 求此曲线在点4π=t 处的切线方程.解：t dt dy 2sin 2-=，.cos t dt dx =故.sin 4cos 2sin 2t ttdt dx dtdydx dy -=-== 所以，.22|0-===t dx dy k 切， 又，0=t 时，.0,22==y x ， 所以，切点为⎪⎪⎭⎫ ⎝⎛0,22，因此切线方程为：⎪⎪⎭⎫⎝⎛--=-22220x y . 7．已知⎰⎰=yx t tdt dt e 022cos ，求.dxdy解：⎰⎰=yx t tdt dt e 022cos 两边关于x 求导得：x x dxdye y 2.cos .22= 所以 ..cos 222y e x x dxdy-= 8．设,11x xy +-=求().n y 解：()().112111.21121-+=-+=++-=-x xx x y ()()212.1-+-='x y ； ()()()312.2.1-+--=''x y ；……… 归纳可得()()()()()()()111!.1.212.2.1+---+-=+---=n nn n x n x n y二．（15分）已知函数()(),123-=x x x f 求（1）函数()x f 的单调增加、单调减少区间，极大、极小值； （2）函数图形的凸性区间、拐点、渐进线. 解： ()()+∞∞-=,11, D ； 1.因为()()32lim lim1x x x f x x →∞→∞==∞-，所以无水平渐进线；（具体地讲()()32lim lim1x x x f x x →-∞→-∞==-∞-；()()32lim lim1x x x f x x →+∞→+∞==+∞-.）；因为函数在1=x 处无定义，且()()3211lim lim1x x x f x x →→==+∞-，故有垂直渐进线1=x ；因为()()22lim lim 1,1x x f x x a x x →∞→∞===-，()()()32222lim lim lim 211x x x x x x b f x ax x x x →∞→∞→∞⎡⎤-=-=-==⎡⎤⎢⎥⎣⎦--⎢⎥⎣⎦均存在， 所以，有斜渐进线2+=x y . 2．令()()()2123300, 3.1x x f x x x x -'==⇒==-；3．令()()4600.1xf x x x ''==⇒=-可得下表：（)0,∞- 0 ()1,0 1 ()3,1 3 ()+∞,3()f x ' + 0 + 不存在 — 0 + ()f x '' — 0 + 不存在 + + + ()x f 升 拐点 升 间断 降 升 三．（10分）设()x g 是[]2,1上的连续函数，()().1dt t g x f x⎰= （1）证明在()2,1内可导. （2）证明()x f 在1=x 处右连续. 解：（1）任取点()2,1∈x ，()()()().11dt t g dt t g x f x x f f xxx ⎰⎰-=-∆==∆∆+ ①其中 ()()()dt t g dt t g dt t g xx xxxx ⎰⎰⎰∆+∆++=11故 ()dt t g f x x x⎰∆+=∆（积分中值定理）()x g ∆=.ξ（ξ介于x 与x x ∆+之间）②所以 x f x ∆∆→∆0lim（因为②）()xxg x ∆∆=→.limξξ()().lim x g g x ==→ξξ 因此 ()x f 在()2,1内可导，且()()..x g x f =' （2）记()()=-∆+=∆11f x f f ()()x g dt t g x∆=-⎰∆+.011ξ （ξ介于1与x ∆+1之间）则 f x ∆+→∆0lim ()0.lim `=∆=+→x g ξξ，故()x f 在1=x 处右连续. 四．（10分）（1）设平面图形A 由抛物线2x y =，直线8=x 及x 轴所围成，求平面图形A 绕x 轴旋转一周所形成的立体积.（2）在抛物线2x y =求一点，使得过此点所作切线与直线8=x 及x 轴所围图形面积最大. 解：（1）()..58558052802|πππ===⎰x dx xV（2）任取抛物线2x y =上一点()2,t t ，则抛物线2x y =在点()2,t t 处切线方程为 ()t x t t y L -=-2:2 即 .22t tx y -=设由L 与直线8=x 及x 轴所围图形面积为()()216.2821t t t t S -⎪⎭⎫ ⎝⎛-=()80<<t 令 ()()()0216281621212=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-+--='t t t t t S ，得驻点 316=t 或.16=t （舍） 又因为 ()()40321-=''t t S ，012316<-=⎪⎭⎫ ⎝⎛''S ，所以当316=t 时，()t S 取到极大值，所求之点为.9256,316⎪⎭⎫⎝⎛五．（9分）当0≥x 时，对在[]b ,0上应用拉格朗日中值定理，有()()()b f f b f .0ξ'=-. ()b ,0∈ξ.对于函数()x x f arcsin = ，求.lim 0bb ξ→证明：对()x x f arcsin =在[]b ,0上应用拉格朗日中值定理，有 ()0.110arcsin arcsin 2--=-b b ξ，().,0b ∈ξ所以22arcsin 1⎪⎭⎫⎝⎛-=b b ξ因此 ()⎥⎦⎤⎢⎣⎡-=→→220220arcsin 11lim lim b b b b b ξ()22220)(arcsin arcsin lim b b b b b -=→（等价） ()422)(arcsin arcsin lim b b b b -=→（令)arcsin b t =4220sin lim ttt t -=→ （洛必达）3042sin 2lim t t t t -=→（洛必达）()20122cos 12lim t t t -=→（等价）().3112221.2lim 220==→tt t 故 .31lim=→bb ξ。

华东政法大学2007-2008学年第一学期期末考试商学院07级各专业《高等数学》A 卷参考答案一、填空题（每题2分，共20分）(1) e(2) 0(3) -2(4) 0(5) 3(6) C x F +-)(c o s(7) xdy x dx yxy y ln 1+- (8) ⎰⎰ee y dx y xf dy ),(10(9 ) 1/2 (10) 222-。

二、单项选择题（在每小题的四个备选答案中选出一个正确答案，每小题2分，共20分）(1) C (2) B (3) D (4) A (5) A (6) B (7) C （8）A （9）C （10）A三、计算题（每小题6分，共30分）1、解：x x xf x x dt t tf x x x x F 2)(0)(00lim lim )(lim 20→→→=⎰= （3分）2/)(lim 0x f x →= 02/)0(==f （5分）所以当0=x 时，F （x ）在x=0处连续。

（6分）2、解：)111111(1lim )21111(lim 1nn n n n n n n n +++++=++++∞→∞→ n n i n i n 111lim 1∑=∞→+= （2分） ⎰+=1011dx x （4分）2ln |)1ln(10=+=x （6分）3、解：323552x x y -= 0)'52(332351310'＝令x x x x y -=-=，所以x=1是函数的稳定点。

X=0是函数的不可导的点，这两点是可能的极值点。

在0)('),0,(>-∞x f ,0)('),1,0(<x f ,0)('),,1(>∞x f所以函数的单调区间增区间为)0,(-∞),1(∞，单调递减区间为)1,0(在点x=0处，函数取得极大值0； 在点x=1处，函数取得极小值－3。

（3分）)12()'(''3239101310+==--x x y x x 令,0''=y 则x=-1/2，则在0)(''),,(21<--∞x y ，0)(''),,(21>+∞-x y ，因此，函数在区间),(21--∞内凸，在),(21+∞-内凹。

中国矿业大学徐海学院2007－2008学年第二学期《高等数学》试卷（A ）卷考试时间：120分钟 考试方式：闭卷班级： 姓名： 学号： 序号：考生注意：本试卷共10页，四大题，草稿纸附两张，不得在草稿纸上答题。

一、填空题（每小题3分，共15分）1. 微分方程xy y 2='的通解是____________________________。

2.二元函数)ln(y x x z +=的定义域为_____________________________________。

3.设xyxe z =，则=∂∂xz_____________________________________。

4.过点（1，2，－1）且垂直于平面0423=+-+z y x 的直线方程是___________________________________________。

5. 曲线t x =，2t y =，3t z =在1-=t 处的法平面方程为___________________________________________。

二、选择题（每小题3分，共15分）1. 设二重积分的积分区域D 是222a y x ≤+（0>a ），则⎰⎰=+Ddxdy y x )2(23（ ）。

A. 0B. 2πa C. 2π2a D. 22.曲线⎩⎨⎧==052y x z 绕x 轴旋转所形成的旋转面方程是（ ）。

A. 2225y x z +±= B. 2225y x z +=C. x z y 522=+D. 225x z =3.对于级数]1)1([31p n p n n n -∞=∑+-，下列结论正确的是（ ）。

A. 当0>p 时，级数收敛B. 当1>p 时，级数收敛C. 当20<<p 时，级数绝对收敛D. 当21<<p 时，级数绝对收敛 4.函数2)(x e x f -=展开成x 的幂级数是（ ）。