【K12教育学习资料】[学习]江苏省扬州市高邮市车逻镇2018届中考数学一轮复习 第38课时 用轴对

第8课时 一元二次方程学习目标1. 理解一元二次方程的概念。

能根据具体问题的实际意义，检验方程的解是否合理。

2. 理解配方法，能用配方法、公式法、因式分解法解数字系数的一元二次方程。

3. 会用一元二次方程根的判别式判别方程根的情况。

4. *了解一元二次方程的根与系数的关系。

学习重点一元二次方程的解法及根的判别式判别方程根的情况。

学习难点一元二次方程解法的解法。

学习过程一．知识梳理1. 只含有 ,并且 的方程叫做一元二次方程。

2.一元二次方程的一般形式是 ，二次项系数是 ，一次项系数是 ，常数项是 。

3.一元二次方程的解法（1）直接开平方法：形如()2(0)x p a a +=≥的方程的根为 .（2）配方法：解方程的基本步骤：①化1:②移项:③配方④开平方 ⑤求解.（3）公式法：一般形式的一元二次方程: )0(02≠=++a c bx ax ；当240b ac -≥时， x = .（4）因式分解法:如果一元二次方程可以化为12()()0(0)a x x x x a --=≠，那么方程的解为 .4.一元二次方程: )0(02≠=++a c bx ax 根的情况是：当240b ac -≥时，方程 ；当042=-ac b 时，方程 ；当042<-ac b 时，方程 ；*5.方程)0(02≠=++a c bx ax 的两个根是1x 、2x ，则11x x +=______，12x x =______6. ①如果某种产品原来的数量是a ，平均增长率是x ，那么连续增长了2次后的数量是b ,那么列出的方程是 _______________ ；②如果某种产品原来的数量是a ，平均下降率是x ，那么连续下降了2次后的数量是b , 那么列出的方程是_____ _ .7.在商品销售问题中，常用的相等关系有：（1）利润= — ； (2)利润率= ；(3)总利润=销售数量× 。

二、典型例题1.一元二次方程的概念（1）（2015•高邮期末） 下列关于x 的方程中，一定是一元二次方程的是（ ）A ．230ax x +=B ．222(3)x x -=+C ．2350x x+-= D ．210x -= （2）（2015•毕节市）关于x 的方程2430x x +=﹣与121x x a =-+有一个解相同，则a = ． 2.一元二次方程的解法（1）已知()()22222340a b a b +-+-=，则22a b +的值为 。

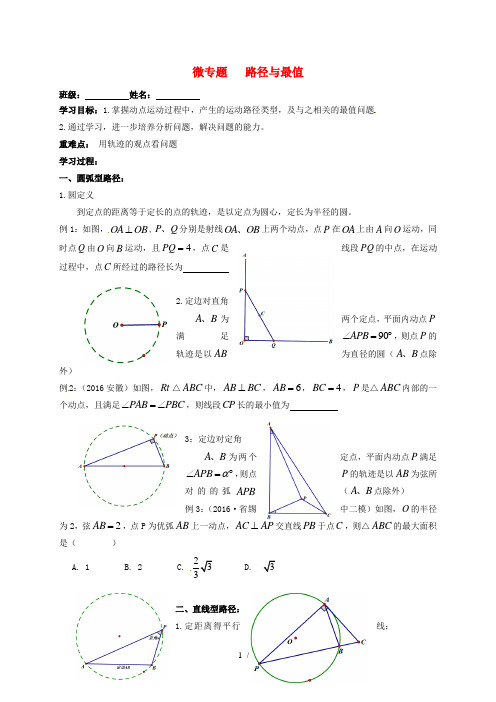
微专题 路径与最值班级： 姓名：学习目标：1.掌握动点运动过程中，产生的运动路径类型，及与之相关的最值问题 2.通过学习，进一步培养分析问题，解决问题的能力。

重难点： 用轨迹的观点看问题 学习过程： 一、圆弧型路径： 1.圆定义到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆。

例1：如图，OA OB ⊥,P Q 、分别是射线OA OB 、上两个动点，点P 在OA 上由A 向O 运动，同时点Q 由O 向B 运动，且4PQ =，点C 是线段PQ 的中点，在运动过程中，点C 所经过的路径长为2.定边对直角两个定点，平面内动点PA B 、为90APB ∠=︒，则点P 的满足迹是以AB 为直径的圆（A B 、点除外）轨例2：（2016安徽）如图，Rt △ABC 中，AB BC ⊥，6AB =，4BC =，P 是△ABC 内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为3：定边对定角定点，平面内动点P 满足A B 、为两个P 的轨迹是以AB 为弦所APB α∠=︒，则点对的的弧APB （A B 、点除外） 中二模）如图，O 的半径例3：（2016·省锡为2，弦2AB =，点P 为优弧AB 上一动点，AC AP ⊥交直线PB 于点C ，则△ABC 的最大面积是（ ）A. 1B. 2C.二、直线型路径： 1.定距离得平行线：到定直线l的距离等于定长d 的志向的点的轨迹，是平行于直线l ，并且到直线l 的距等于定长d 的两条直线。

例4：如图，在△ABC 中，8BC =,M 是边BC 上一动点，连接AM ，取AM 的中点P ，当点M从点B 运动到点C ，则动点P 的路径长为2.定夹角得直线： 直线l 与定点A ，已知若直线BA 与直线l 的夹角α不变，则动点B 始终在定直线AB上，即：点A 的运动轨迹为直线型。

例5：如图，正方形ABCD 的边长为2，动点E 从点A 出发，沿边AD 向终点D 运动，以DE 为边作正方形DEFG （点D E F G 、、、按顺时针方向排列）．求出整个运动过程中，点F 经过的路径长．3：解析法：建立直角坐标系，用函数知识来解决问题。

a 第16课时 解直角三角形 班级： 姓名：学习目标：1.能利用直角三角形的边边关系、边角关系解直角三角形。

2.能结合仰角、俯角、坡度等知识，运用锐角三角函数解决与直角三角形有关的实际问题 重难点：运用锐角三角函数解决与直角三角形有关的实际问题学习过程一．知识梳理直角三角形的边角关系1.在Rt ABC 中，90C A B C ∠︒∠∠∠＝，，，的对边分别为.a b c ，，(1)三边之间的关系： ；(2)两个锐角之间的关系： ；(3)边角之间的关系： sinA ＝ ，cosA ＝ ，tanA ＝ ，2.解直角三角形的应用（1）仰角、俯角：如图①，在测量时，视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角．（2）坡度(坡比)、坡角：如图②，坡面的高度h 和 的比叫做坡度(或坡比)，即=t a n =i h lα，坡面与水平面的夹角α叫做坡角．二、典型例题1.三角函数的实际应用 （1）（2017山东滨州）如图，在△ABC 中，30AC BC ABC ⊥∠︒，＝，点D 是CB 延长线上的一点，且BD BA ＝，则tan DAC ∠的值为（ ）A ．2B． C ．3 D ．（2）（2017包头）如图，在矩形ABCD 中，点E 是CD 的中点，点F 是BC 上一点，且2FC BF =，连接AE ，EF ．若23AB AD ==，，则cos AEF ∠的值是 ．（3）（中考指要例2）（2016梧州）如图，四边形ABCD 是一片水田，某村民小组需计算其面积，测得如下数据：906054200300A ABD CBD AB m BC m ∠=︒∠=︒∠=︒==，，，，． 请你计算出这片水田的面积． （参考数据：540.809540.58854 1.376 1.732sin cos tan ︒≈︒≈︒≈≈，，，）2.解直角三角形的应用（1）（2017益阳）如图，电线杆CD 的高度为h ，两根拉线AC 与BC 相互垂直，CAB ∠=α，则拉线BC 的长度为（ ）（A D B 、、在同一条直线上）A ．sin h αB ．cos h αC ．tan h αD ．cos h α⋅（2）（2017山西）如图所示，飞机在一定高度上沿水平直线飞行，先在点A 处测得正前方小岛C 的俯角为30°，面向小岛方向继续飞行10km 到达B 处，发现小岛在其正后方，此时测得小岛的俯角αAC DB为45°，如果小岛高度忽略不计，求飞机飞行的高度（结果保留根号）．（3）（中考指要例1）（2016贺州）如图，是某市一座人行天桥的示意图，天桥离地面的高BC 是10米，坡面10米处有一建筑物HQ ，为了方便使行人推车过天桥，市政府部门决定降低坡度，使新坡面DC 的倾斜角30BDC ∠=︒，若新坡面下D 处与建筑物之间需留下至少3米宽的人行道，问该建筑物是否需要拆除（计算最后结果保留一位小数）．）三、中考预测（2017淮安）A B ，两地被大山阻隔，若要从A 地到B 地，只能沿着如图所示的公路先从A 地到C 地，再由C 地到B 地．现计划开凿隧道A B ，两地直线贯通，经测量得：304520CAB CBA AC km ∠=︒∠=︒=，，，求隧道开通后与隧道开通前相比，从A 地到B 地的路程将缩短多少？（结果精确到0.1km 1.414 1.732）四、反思总结1.本节课你复习了哪些内容？2.通过本节课的学习，你还有哪些困难？五、达标检测1.（2017泰州）小明沿着坡度i =50m ，则小明沿垂直方向升高了 m ．2.（2014•孝感）如图，在ABCD 中，对角线AC BD 、相交成的锐角为α，若AC a BD b ==，，则ABCD 的面积是（ ）A ．1sin 2ab a B ．sin ab a C ．1cos 2ab a D ．cos ab a3.（2017黑龙江）ABC 中，12,B=30AB AC =°，则ABC 的面积是4.（中考指要第8题）（2016上海）如图，在Rt ABC 中，903ACB AC BC ∠=︒==，，点D 在边AC 上，且2AD CD DE AB =⊥，，垂足为点E ，联结CE ，求：（1）线段BE 的长；（2）ECB ∠的余切值．5.（中考指要第9题）（2017乌鲁木齐）一艘渔船位于港口A 的北偏东60°方向，距离港口20海里B 处，它沿北偏西37°方向航行至C 处突然出现故障，在C 处等待救援，B C ，之间的距离为10海里，救援船从港口A 出发20分钟到达C 处，求救援的艇的航行速度．（370.6370.8 1.732sin cos ︒≈︒≈≈，，结果取整数）。

第26课时与圆有关的概念及性质姓名学号班级学习目标1.理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等弧的概念．2.探索并掌握垂径定理及其推论．3.探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论．4. 知道三角形的外心，并能画任意三角形的外接圆．学习重难点：利用圆周角与圆心角及其所对弧的关系学习过程一．知识梳理(1)圆的基本概念：在同一平面内，线段OA绕它固定的一个端点形成的图形叫做圆，叫做圆心，叫做半径．圆上任意两点间的叫做圆弧；在同圆或等圆中，能够的弧叫做等弧．(2) 圆的有关性质：①对称性：圆是中心对称图形，是它的对称中心；圆也是轴对称图形，都是它的对称轴．②圆心角、弧、弦之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别 .③垂径定理：垂直于弦的直径弦，并且平分弦所对的两条弧．推论：平分弦(不是直径)的直径于弦，并且平分这条弦所对的两条弧．⑶圆心角和圆周角：①圆心角：顶点在的角叫做圆心角；圆心角的度数它所对的弧的度数．圆周角：顶点在圆上，两边都与圆的角叫做圆周角．②圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角，都等于这条弧所对的圆心角的．推论：半圆(或直径)所对的圆周角是，90°的圆周角所对的弦是．⑷确定圆的条件：①不在的三个点可以确定一个圆．②三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆．外接圆的圆心叫做三角形的.⑸圆的内接四边形：圆的内接四边形的对角 .二、典型例题1.垂直定理及其推论，问题1.(2017·呼和浩特)如图，CD为O的直径，弦AB CD垂足为M ，若12AB ＝，58OM MD ∶＝∶，则 O 的周长为 ( )A. 26πB. 13πC.965π2.圆心角的应用问题2 (2016·兰州)如图，在 O 中，C 是 AB 的中点，50A ∠︒＝，则BOC ∠的度数为 ( ) A. 40︒ B. 45︒ C.50︒ D. 60︒ 3.圆周角定理及其推论问题3、点O 是△ABC 的外心，若80BOC ∠=︒，求BAC ∠的度数．4.圆内接四边形问题4、(2017·广东)如图，四边形ABCD 内接于 O ，DA DC ＝，50CBE ∠︒＝，则DAC ∠的度数为( )A. 130︒B. 100︒C. 65︒D. 50︒问题5、如图，将O 沿弦AB 折叠，圆弧恰好经过圆心O ，点P 是优弧AMB 上一点，求APB ∠．5.圆的性质与其他知识的综合应用问题6、（中考指要例3）如图，AB 是O 的直径，弦CD AB ⊥与点E ，点P 在O 上，1C ∠=∠，（1）求证：CB ∥PD ；（2）若335BC sin P =∠=，，求O 的直径．问题7、 (2017·六盘水)如图，MN 是O 的直径，4MN ＝，点A 在O 上，30AMN ∠︒＝，B为弧AN 的中点，P 是直径MN 上一动点．(1) 利用尺规作图，确定当PA PB ＋最小时点P 的位置(不写作法，但要保留作图痕迹)；(2) 求PA PB ＋的最小值．三、中考预测.如图，AB 是O 的直径，点D 是圆上一动点，连接.BD(1)若30CDB ∠=︒，则ABC ∠=_______(2)若BD ABC ∠平分，CD BC =，图中相等的线段有__________，相等的弧(不包括半圆)有_______,ABC ∠=_____。

第27课时 与圆有关的位置关系班级： 姓名：学习目标: 1. 探索并了解点与圆的位置关系，了解直线与圆的位置关系及三角形内切圆的概念，会判断图形的位置关系．2. 掌握切线的概念，探索切线与过切点的半径的关系，会用三角尺过圆上一点画圆的切线．3. 探索并证明切线长定理，会利用它进行证明和相关计算重难点：灵活运用切线的性质定理和判定定理进行相关计算和证明． 学习过程 一．知识梳理1.点与圆的位置关系：如果设圆的半径为r ，点到圆心的距离为d ，那么： ①d r < ⇔点在 ． ②d r ＝ ⇔点在 ． ③d r > ⇔点在 ．2.直线与圆的位置关系：如果⊙O 的半径为r ，圆心O 到直线l 的距离为d ，那么： ①d r < ⇔ 直线l 与圆 ． ②d r ＝ ⇔ 直线l 与圆 ． ③d r > ⇔ 直线l 与圆 ．3.与圆有 公共点的直线叫做圆的切线，唯一的公共点叫做 ． 切线的判定定理：经过半径的外端并且 于这条半径的直线是圆的切线． 性质定理：圆的切线垂直于经过 的半径．4.在经过圆外一点的圆的切线上，这点和切点之间 的长，叫做这点到圆的切线长．切线长定理：从圆外一点引圆的两条切线，它们的切线长 ，圆心和这一点的连线 两条切线的夹角．5.与三角形各边 的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的 ，这个三角形叫做圆的 三角形． 、典型例题 1.点与圆的位置关系（2017宁夏）如图，点A B C ，，均在6×6的正方形网格格点上，过A B C ，，三点的外接圆除经过A B C ，，三点外还能经过的格点数为 ． 2.切线的性质与判定（1）（2017自贡）AB 是⊙O 的直径，PA 切⊙O 于点A ，PO 交⊙O 于点C ; 连接BC ,若P 40∠=,则B ∠等于 （ ）A.20°B.25°C. 30°D.40°（2）（中考指要例1）（2017南充）如图，在Rt △ABC 中，90ACB ∠=︒，以AC 为直径作⊙O 交AB 于点D ，E 为BC 的中点，连接DE 并延长交AC 的延长线于点F ．①求证：DE 是⊙O 的切线；②若24CF DF ==，，求⊙O 直径的长．（3）（中考指要例3）（2015青海）如图，在△ABC 中，60B ∠=︒，⊙O 是△ABC 的外接圆，过点A 作⊙O 的切线，交CO 的延长线于点M ，CM 交⊙O 于点D ． ①求证：AM AC =； ②若3AC =，求MC 的长．P3.切线长定理与内切圆（1）(2016·荆州)如图，过⊙O 外一点P 引⊙O 的两条切线PA PB ，，切点分别是A B ，，OP 交⊙O 于点C ，D 是优弧上不与点A C ，重合的一个动点，连接AD CD ，.若80APB ∠︒＝，则 ADC ∠的度数是( )A.15°B. 20°C. 25°D. 30°（2）(2017·武汉)已知一个等腰三角形三角形的底边长为10，腰长为分别13，则其内切圆的半径为 三、中考预测（2017东营）如图，在△ABC 中，AB AC =，以AB 为直径的⊙O 交BC 于点D ，过点D 作⊙O 的切线DE ，交AC 于点E ，AC 的反向延长线交⊙O 于点F ． （1）求证：DE AC ⊥；（2）若8DE EA +=，⊙O 的半径为10，求AF 的长度．四、反思总结1.本节课你复习了哪些内容？第6题图F B2.通过本节课的学习，你还有哪些困难？五、达标检测1、（2015•湘西州）⊙O 的半径为5cm ，点A 到圆心O 的距离3OA cm =，则点A 与圆O 的位置关系为（ ） A ．点A 在圆上 B ． 点A 在圆内C ． 点A 在圆外D ． 无法确定2、（2016嘉兴）如图，中，534AB BC AC ===，，，以点C 为圆心的圆与AB 相切，则⊙C的半径为（ ） A. 2.3B.2.4C.2.5D.2.63、（2016南京）如图，在矩形ABCD 中，45AB AD ==，，AD AB BC 、、分别与⊙O 相切于E F G 、、三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为()A. 133B.92C.D.4、（2016鄂州）如图，在△ABC 中，AB AC =，AE 是BAC ∠的平分线，ABC ∠的平分线 BM 交AE 于点M ，点O 在AB 上，以点O 为圆心，OB 的长为半径的圆经过点M ，交BC 于点G ，交 AB 于点F ．（1）求证：AE 为⊙O 的切线．（2）当812BC AC ==，时，求⊙O 的半径． （3）在（2）的条件下，求线段BG 的长．5、（中考指要例2）（2015温州）如图，AB 是半圆O 的直径，CD AB ⊥于点C ，交半圆于点E ，DF 切半圆于点F 。

第14课时 二次函数(3)姓名 班级 学号学习目标：1.通过二次函数的性质解决实际问题2.会解二次函数与几何图形的综合题学习重难点：会解二次函数与几何图形的综合题学习过程： 一、知识梳理（1）二次函数常用来解决最优化问题，这类问题实际上就是求函数的最大（小）值；（2）二次函数的应用包括以下方面：分析和表示不同背景下实际问题中变量之间的二次函数关系；运用二次函数的知识解决实际问题中的最大（小）值．二、典型例题例1 某商品每天的销售利润y （元）与销售单价x （元）之间满足：275y ax bx =+﹣．其图象如图所示．（1）销售单价为多少元时，该商品每天的销售利润最大？最大利润为多少元？（2）销售单价在什么范围时，该商品每天的销售利润不低于16元？例2近年来，“宝胜”集团根据市场变化情况，采用灵活多样的营销策略，产值、利税逐年大幅度增长．第六销售公司2004年销售某型号电缆线达数万米，这得益于他们较好地把握了电缆售价与销售数量之间的关系．经市场调研，他们发现：这种电缆线一天的销量y （米）与售价x （元/米）之间存在着如图所示的一次函数关系，且4070x ≤≤．(1) 根据图象，求y 与x 之间的函数解析式；(2) 设该销售公司一天销售这种型号电缆线的收入为w 元．① 试用含x 的代数式表示w ；② 试问当售价定为每米多少元时，该销售公司一天销售该型号电缆的收入最高？最高是多少元？（中考指要例1）某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A B 、两组，采用不同工艺做降温对比实验，设降温开始后经过x min 时，A 、B 两组材料的温度分别为A B A B y y y y ℃、℃，、与x 的函数关系式分别为21604A B y kx b y x m =+=+，（﹣）（部分图象如图所示），当40x =时，两组材料的温度相同．（1）分别求A B y y 、关于x 的函数关系式；（2）当A 组材料的温度降至120℃时，B 组材料的温度是多少？（3）在040x <<的什么时刻，两组材料温差最大？（中考指要例3）（2015•来宾）在矩形ABCD 中，AB a AD b ==，，点M 为BC 边上一动点（点M 与点B C 、不重合），连接AM ，过点M 作MN AM ⊥，垂足为M ，MN 交CD CD 或的延长线于点N ．（1）求证：△CMN ∽△BAM ；（2）设BM x CN y ==，，求y 关于x 的函数解析式．当x 取何值时，y 有最大值，并求出y 的最大值；（3）当点M 在BC 上运动时，求使得下列两个条件都成立的b 的取值范围：①点N 始终在线段CD 上，②点M 在某一位置时，点N 恰好与点D 重合．三、中考预测如图, 已知抛物线212y x bx c =++与y 轴相交于C ，与x 轴相交于A B 、，点A 的坐标为20（，），点C 的坐标为01-（，）.（1）求抛物线的解析式；（2）点E 是线段AC 上一动点，过点E 作DE x ⊥轴于点D ，连结DC ，当△DCE 的面积最大时，求点D 的坐标；（3）在直线BC 上是否存在一点P ，使△ACP 为等腰三角形，若存在，求点P 的坐标，若不存在，说明理由.四、反思总结1、本课复习了哪些内容？2、你还有什么困惑？五、达标检测1．如图，点A B ，的坐标分别为()(2555)，和，，抛物线2()y a x m n ＝－＋的顶点在线段AB 上运动(抛物线随顶点一起平移)，与x 轴交于C D ，两点(C 在D 的左侧)，点C 的横坐标最小值为－3，则点D 的横坐标最大值为( )．3A ．－ 1B ． 8C ． 10D ．2.飞机着陆后滑行的距离s (单位：米)与滑行的时间t (单位：秒)之间的函数关系式是260 1.5s t t =－．飞机着陆后滑行 秒才能停下来，此时飞机滑行了__________米．3.某种商品每件的进价是20元，在一段时间内如果以每件x 元销售，可以卖出100x -（）件，为了使得最大利润，那么该商品的定价是 .4.某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件。