二阶高通巴特沃兹滤波器

二阶无限增益多路反馈巴特沃斯带通滤波器摘要：一、巴特沃斯带通滤波器简介1.滤波器原理2.应用场景二、二阶无限增益多路反馈滤波器设计1.结构特点2.设计方法三、反馈网络构建与分析1.反馈网络拓扑结构2.稳定性分析四、滤波器性能仿真与测试1.仿真软件介绍2.性能指标五、应用实例1.信号处理领域2.通信系统中的应用正文：一、巴特沃斯带通滤波器简介1.滤波器原理巴特沃斯带通滤波器是一种以巴特沃斯函数为传递函数的滤波器，具有频率响应平坦、群延迟均匀的优点。

它能在特定的频率范围内，让信号通过，而阻隔其他频率的信号。

2.应用场景巴特沃斯带通滤波器广泛应用于信号处理、通信系统、音频处理等领域，如滤波、降噪、信号分离等。

二、二阶无限增益多路反馈滤波器设计1.结构特点二阶无限增益多路反馈巴特沃斯带通滤波器，其主要特点是具有多个反馈路径，从而提高滤波器的性能。

这种滤波器的反馈网络由多个运放和电阻、电容组成，形成多路反馈结构。

2.设计方法设计二阶无限增益多路反馈滤波器时，首先需确定滤波器的通带频率、阻带频率和截止频率。

然后，根据这些参数，选取合适的巴特沃斯函数作为滤波器的传递函数，并根据反馈网络的拓扑结构设计电阻、电容的值。

最后，通过仿真软件对滤波器的性能进行仿真和测试。

三、反馈网络构建与分析1.反馈网络拓扑结构二阶无限增益多路反馈滤波器的反馈网络主要包括多个运放、电阻和电容。

根据巴特沃斯函数的特性，设计合适的反馈网络拓扑结构，使滤波器在通带内具有较好的频率响应和群延迟特性。

2.稳定性分析分析滤波器的稳定性，主要看其反馈网络是否产生自激振荡。

通过调整反馈网络的参数，避免不稳定现象的发生，确保滤波器在工作过程中稳定可靠。

四、滤波器性能仿真与测试1.仿真软件介绍使用专业的仿真软件（如Multisim、ADS等），对二阶无限增益多路反馈滤波器进行性能仿真。

这些软件能实时显示出滤波器的频率响应、群延迟等性能指标，便于设计师对滤波器进行优化。

电子线路设计作业语音滤波器的设计学生姓名：X X 学生学号：XXXXXXXXXXX一、前言从上世纪二十年代至六十年代，电滤波器主要由无源元件R、L、C构成，称为无源滤波器。

为了提高无源滤波器的质量，要求所用的电感元件具有较高的品质因数Q，但同时又要求有一定的电感量，这就必然增加电感元件的体积，重量与成本。

为了解决这一矛盾，五十年代有人提出用由电阻、电容与晶体管组成的有源网络替代电感元件，由此产生了用有源元件和无源元件(一般是R和C)共同组成的电滤波器，称为有源滤波器。

六十年代末由分立元件组成的有源滤波器得到应用。

有源滤波器一般由集成运放与RC网络构成，它具有体积小、性能稳定等优点，同时，由于集成运放的增益和输入阻抗都很高，输出阻抗很低，故有源滤波器还兼有放大与缓冲作用。

利用有源滤波器可以突出有用频率的信号，衰减无用频率的信号，抑制干扰和噪声，以达到提高信噪比或选频的目的，因而有源滤波器被广泛应用于通信、测量及控制技术中的小信号处理。

若将低通滤波器和高通滤波器串联，并使低通滤波器的通带截止频率f p2大于高通滤波器的通带截止频率f p1，则频率在f p1<f<f p2范围内的信号能通过，其余频率的信号不能通过，因而构成了带通滤波器。

设计要求1.该语音滤波器的截止频率Hz f H 3000=，Hz f L 300=，10=V A ；2.阻带衰减速率为1040dB -倍频程。

二、设计原理由于是要设计一个带通滤波器，那么可以将一级二阶低通滤波器与一级二阶高通滤波器级联。

1.二阶低通滤波器的传输函数与性能参数：①传输函数为：()222c cc V s Q s A s A ωωω++=其中：V A ——电压增益，c ω——截止角频率，Q ——品质因数 ②性能参数如表1.1所示：表1.1 二阶低通滤波器（巴特沃斯响应）设计表2.二阶低通滤波器的传输函数与性能参数：①传输函数为：()222c cV s Q s s A s A ωω++=其中：V A ——电压增益，c ω——截止角频率，Q ——品质因数 ②性能参数如表1.2所示：表1.2 二阶高通滤波器（巴特沃斯响应）设计表三、设计工具计算机一台，Multisim软件四、设计内容与步骤1.一级二阶低通滤波器的设计：①由表1.1得到二阶压控电压源低通滤波器的电路，如图1.1所示；图1.1 二阶压控电压源低通滤波器电路 ②由Cf K H 100=得Hz f H 3000=，1=K 时，取nF C 33=； ③从表1.1得10=V A 时，电容nF C C 6621==；电阻Ω=K R 462.01，Ω=K R 742.22，Ω=K R 560.33，Ω=K R 038.324；④将③中得到的电容1C ；电阻1R ，2R ，3R ，4R 的数据分别带入图1.1二阶压控电压源低通滤波器电路中；得到一级截止频率为Hz f H 3000=的二阶低通滤波器，如图1.2所示。

滤波电路设计去除噪声和干扰的方法与技巧在电子器件和电路设计中，噪声和干扰是普遍存在的问题，它们给数据传输和信号处理带来了不利的影响。

为了解决这一问题，滤波电路被广泛应用于各种电子设备中，以去除噪声和干扰。

本文将介绍滤波电路设计中去除噪声和干扰的一些常用方法与技巧。

一、低通滤波器低通滤波器是一种能够通过只允许低频信号通过而去除高频信号的滤波器。

在滤波电路设计中，低通滤波器常常用来去除高频噪声和干扰。

其中，常用的低通滤波器包括RC低通滤波器和二阶巴特沃斯低通滤波器等。

1. RC低通滤波器RC低通滤波器是最简单的一种低通滤波器，它由一个电阻和一个电容组成。

在设计RC低通滤波器时，可以通过调整电阻和电容的数值来滤除不同频率的噪声和干扰。

一般情况下，较大的电阻和电容值会使得滤波器的截止频率较低，从而去除更高频的噪声和干扰。

2. 二阶巴特沃斯低通滤波器二阶巴特沃斯低通滤波器是一种常用的滤波器设计，它能够提供更陡峭的滚降斜率和更好的抑制高频噪声和干扰的能力。

在设计二阶巴特沃斯低通滤波器时，可以根据需要选择合适的电容和电感数值，并通过合理的电路布局和滤波器阻抗匹配来提高滤波效果。

二、高通滤波器高通滤波器是一种能够通过只允许高频信号通过而去除低频信号的滤波器。

在滤波电路设计中，高通滤波器常常用来去除低频噪声和干扰。

常见的高通滤波器有RC高通滤波器和二阶巴特沃斯高通滤波器等。

1. RC高通滤波器RC高通滤波器与RC低通滤波器相似，只是传输的频率范围相反。

在RC高通滤波器中，较小的电阻和电容值会使得滤波器的截止频率较高，从而去除更低频的噪声和干扰。

因此，在滤波电路设计时，可以根据需要选择合适的数值以满足去除低频噪声和干扰的要求。

2. 二阶巴特沃斯高通滤波器与二阶巴特沃斯低通滤波器类似，二阶巴特沃斯高通滤波器也能够提供更陡峭的滚降斜率和更好的抑制低频噪声和干扰的能力。

通过合理的设计和电路参数的选择，二阶巴特沃斯高通滤波器能够满足更高要求的高频信号滤波。

二阶巴特沃斯滤波器的分析与实现电路首先，我们需要了解二阶巴特沃斯滤波器的传输函数。

传输函数描述了输入信号与输出信号之间的关系。

二阶巴特沃斯滤波器的传输函数可以写成如下的形式：H(s)=K/(s^2+(ω0/Q)s+ω0^2)其中，s是复频率变量，ω0是滤波器的中心频率，Q是滤波器的品质因数，K是增益系数。

为了实现二阶巴特沃斯滤波器，我们可以使用运算放大器和电容、电阻组成的电路。

具体电路如下所示：其中，R1、R2、C1、C2为电阻和电容元件，OPAMP为运算放大器。

根据传输函数的形式，我们可以将电路分解为三个部分：1.第一个部分是一个非反馈的增益电路，由R1和C1组成。

它起到了对输入信号进行增益的作用，增益大小与R1和C1的取值有关。

2.第二个部分是一个双端口的带通滤波器，由R2、C2和OPAMP组成。

它的作用是滤除输入信号中低频和高频成分，只保留中心频率附近的成分。

中心频率由R2和C2的取值决定。

3.第三个部分是一个反馈网络，由R2和C2组成。

它起到了对输出信号进行反馈的作用，使得滤波器的传输函数满足巴特沃斯滤波器的形式。

根据传输函数的形式，我们可以得到R1、R2、C1、C2的取值公式如下：R1=Q/(K*ω0*C1)R2=1/(K*ω0^2*C2)C1=1/(Q*ω0*R1)C2=1/(K*ω0^2*R2)其中，K可以根据实际需求进行调整，选取适当的增益值。

Q和ω0由滤波器的需求决定，分别代表品质因数和中心频率。

总结起来，二阶巴特沃斯滤波器的分析与实现包括以下几个步骤：1.确定滤波器的中心频率和品质因数，根据传输函数的形式计算出R1、R2、C1、C2的取值。

2.选取合适的电阻和电容元件，连接电路。

3.根据实际需求选择适当的增益值K。

4.搭建电路，并进行测试和调试，确保滤波器的性能符合要求。

二阶巴特沃斯滤波器电路设计
二阶巴特沃斯滤波器可以通过使用电容器和电感器来实现。

下面是一个常见的二阶巴特沃斯低通滤波器的电路设计：
1. 选择合适的电容和电感。

根据要求的截止频率和阻带衰减率选择合适的电容和电感。

截止频率是滤波器开始衰减的频率，阻带衰减率是滤波器在截止频率之上的衰减量。

2. 设计RC网络。

使用一个电阻和一个电容构建一个RC网络。

这个网络是滤
波器的一部分，用于控制截止频率。

3. 设计RL网络。

使用一个电阻和一个电感构建一个RL网络。

这个网络也是
滤波器的一部分，用于增加滤波器的阻带衰减率。

4. 连接RC和RL网络。

将RC网络和RL网络连接起来，形成一个二阶巴特沃斯低
通滤波器。

5. 使用操作放大器。

如果需要，可以使用操作放大器来增强滤波器的增益和带宽。

6. 测试及调整。

连接信号源和输出设备，对滤波器进行测试，并根据需要调
整电路参数。

需要注意的是，这只是一个基本的二阶巴特沃斯滤波器电路设计步骤的概述。

具体的设计取决于所需的截止频率、阻带衰减率和其他特定需求。

二阶巴特沃斯滤波器的作用二阶巴特沃斯滤波器是一种常用的滤波器，可以用于信号处理、音频处理、图像处理等领域。

它的主要作用是根据设定的频率范围，滤除或放大特定的频率成分，从而实现对信号的处理和改善。

巴特沃斯滤波器是一种无失真的滤波器，其特点是在通带内具有较为平坦的幅频响应和较小的相位延迟。

二阶巴特沃斯滤波器是巴特沃斯滤波器的一种特殊形式，其具有更为陡峭的滚降斜率和更窄的过渡带宽度。

二阶巴特沃斯滤波器的作用主要体现在以下几个方面：1. 频率选择性二阶巴特沃斯滤波器可以根据设定的参数对信号进行频率选择性的处理。

通过调整滤波器的截止频率，可以选择性地滤除或放大特定频率范围内的信号成分。

这在音频处理中尤为常见，比如在音响系统中，可以使用二阶巴特沃斯滤波器来滤除杂音和不需要的频率分量，从而提高音质和音响效果。

2. 信号增强二阶巴特沃斯滤波器可以通过调整增益参数来放大特定频率范围内的信号成分。

在某些应用场景中，需要对某些特定频率的信号进行增强，比如在语音增强、图像增强等领域。

通过使用二阶巴特沃斯滤波器，可以选择性地放大指定频率范围内的信号，从而达到对信号的增强效果。

3. 陷波效应除了滤波作用外，二阶巴特沃斯滤波器还可以实现陷波效应。

陷波是指对指定的频率进行抑制的效果。

在某些应用场景中，需要对某些频率进行抑制，比如在音频系统中抑制某些共振频率，或者在通信系统中抑制干扰频率。

二阶巴特沃斯滤波器可以通过设定适当的参数实现陷波效应，从而抑制指定频率的信号成分。

4. 相位校正滤波器在信号处理中不仅会引入幅度变化，还会引起相位变化。

二阶巴特沃斯滤波器具有较小的相位延迟，可以对信号的相位进行校正。

在某些应用场景中，比如音频系统中，相位校正对于保持信号的时域特性和相位一致性非常重要。

总的来说，二阶巴特沃斯滤波器作为一种常用的滤波器，在信号处理和改善中发挥着重要的作用。

它可以实现频率选择性、信号增强、陷波效应和相位校正等功能。

在实际应用中，根据具体的需求和信号特点，可以通过调整滤波器的参数来实现对信号的精确处理和改善，从而满足不同领域的需求。

输入电容值与分频点C1（μF）f（HZ）R1(Ω）R2(Ω）C2（μF）C1（μF） F μF）f(HZ)0.04722021767.80321767.80260.02350.047220#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!使用方法： 为了不破坏表格中的计算公式设置了保护工作表，只有C1,F竖据，双击任意一个C1,F竖列下的单元格，在弹出的密码框中输入1234。

即可输入你想设定点。

在前两竖列中输入一组合适的参数值后就会在后面单元格中返回一组自动计算的结果注意：该表格的计算公式是针对，Q值位0.707的巴特沃斯二阶滤波器，其带内增益为上各方面性能综合来看最合适的滤波器。

其它Q值或者带内增益不为1的滤波器并不适用。

输入电容值与分频点巴特沃斯二阶有源滤波器自动计算表二阶低通滤波器的计算返回结果二阶高通滤注意：不同分频点的电容C1都有一个合理的取值区间，在下面表格中找。

一共可以样便于比较选择哪一组阻容值在合适的区间内，哪一组你更具备合适的器件。

比如在低通C1为0.047微，分频点220赫兹，计算结果中C1恰好是接近0.047微发，R1、R2恰好接近220值电阻值的东西遍地都是，而且电容值也在合理的区间内。

以下是不同的分频点电容C1合适的取值范围R1(Ω）R2(Ω）C2（μF）10883.921767.802620.047#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!0#DIV/0!#DIV/0!01,F竖列下的单元格可以输入数4。

二阶巴特沃斯滤波器的分析与实现电路Hessen was revised in January 2021巴特沃斯滤波器的分析与实现巴特沃斯滤波器网上没有提供现成的电路和具体参数，此处本文给出几种类型的巴特沃斯滤波器，并给出了参数计算分析。

1、巴特沃斯低通滤波器的定义：巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, n = 滤波器的阶数ωc=截止频率 =振幅下降为 -3分贝时的频率ωp= 通频带边缘频率1/(1 + ε2) = |H(ω)|2在通频带边缘的数值.2、巴特沃斯滤波器的实现一些常见资料的滤波器的错误有些资料上给出的二阶巴特沃斯滤波器电路图为：图中红线部分为放大电路，其实滤波器为2阶RC滤波器。

其传递函数为：H（s）=11+s(R1C1+R1C2+R2C2)+s2R1R2C1C2下面证明此滤波器不可能为二阶巴特沃斯滤波器：滤波器幅频传递函数为：|H(jw)|=|11+jw(R1C1+R1C2+R2C2)−w2R1C1R2C2|=11+w4(R1R2C1C2)2+w2((R1C1+R1C2+R2C2)2−2R1R2C1C2)若滤波器是巴特沃斯滤波器，则((R1C1+R1C2+R2C2)2−2R1R2C1C2要为0 。

因为(R1C1+R1C2+R2C2)2−2R1R2C1C2始终大于零（R1R2C1C2不取零值，C1或C2为零时为1阶RC滤波器，此时为巴特沃斯滤波器），所以不论R1R2C1C2取何值，都不是二阶巴特沃斯滤波器二阶巴特沃斯滤波器的实现方法本文列举了2种2阶巴特沃斯滤波器的实现方法，并给出了滤波器是巴特沃斯滤波器的参数。

以下详述：方法1：RC压控电压源滤波器传递函数为：H（s）=11+s(R1C1+R1C2+R2C2-A*R1C1)+s2R1R2C1C2（A为放大倍数）下面证明此滤波器在一定情况下可成为为二阶巴特沃斯滤波器：情况1：滤波器幅频传递函数为：|H(jw)|=|A1+jw(R1C1+R1C2+R2C2−A∗R1C1)−w R1C1R2C2|=A若滤波器是巴特沃斯滤波器，则((R1C1+R1C2+R2C2−A∗R1C1)2−2R1R2C1C2要为0 。

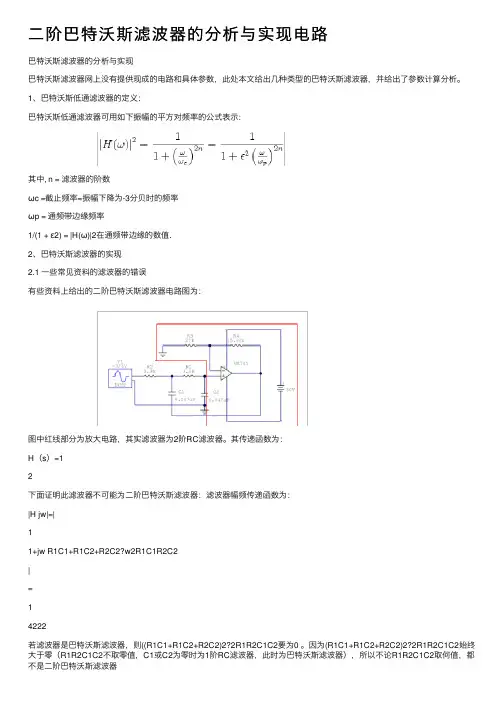
⼆阶巴特沃斯滤波器的分析与实现电路巴特沃斯滤波器的分析与实现巴特沃斯滤波器⽹上没有提供现成的电路和具体参数，此处本⽂给出⼏种类型的巴特沃斯滤波器，并给出了参数计算分析。

1、巴特沃斯低通滤波器的定义：巴特沃斯低通滤波器可⽤如下振幅的平⽅对频率的公式表⽰:其中, n = 滤波器的阶数ωc =截⽌频率=振幅下降为-3分贝时的频率ωp = 通频带边缘频率1/(1 + ε2) = |H(ω)|2在通频带边缘的数值.2、巴特沃斯滤波器的实现2.1 ⼀些常见资料的滤波器的错误有些资料上给出的⼆阶巴特沃斯滤波器电路图为：图中红线部分为放⼤电路，其实滤波器为2阶RC滤波器。

其传递函数为：H（s）=12下⾯证明此滤波器不可能为⼆阶巴特沃斯滤波器：滤波器幅频传递函数为：|H jw|=|11+jw R1C1+R1C2+R2C2?w2R1C1R2C2|=14222若滤波器是巴特沃斯滤波器，则((R1C1+R1C2+R2C2)2?2R1R2C1C2要为0 。

因为(R1C1+R1C2+R2C2)2?2R1R2C1C2始终⼤于零（R1R2C1C2不取零值，C1或C2为零时为1阶RC滤波器，此时为巴特沃斯滤波器），所以不论R1R2C1C2取何值，都不是⼆阶巴特沃斯滤波器2.2 ⼆阶巴特沃斯滤波器的实现⽅法本⽂列举了2种2阶巴特沃斯滤波器的实现⽅法，并给出了滤波器是巴特沃斯滤波器的参数。

以下详述：⽅法1：RC压控电压源滤波器传递函数为：H（s）=11+s R1C1+R1C2+R2C2-A*R1C1+s2R1R2C1C2（A为放⼤倍数）下⾯证明此滤波器在⼀定情况下可成为为⼆阶巴特沃斯滤波器：情况1：滤波器幅频传递函数为：|H jw|=|A2|=A4222若滤波器是巴特沃斯滤波器，则((R1C1+R1C2+R2C2?A?R1C1)2?2R1R2C1C2要为0 。

令A=（3-20.5）C1=C2 R1=R2则|H jw|=21+w4(RC)4符合巴特沃斯滤波器⽅程，但是有⼀个（3-20.5）的放⼤倍数。

二阶巴特沃斯滤波器公式在信号处理和电子工程领域，滤波器是一种常见的工具，用于去除信号中的噪声和干扰，以便更好地提取有用的信息。

而二阶巴特沃斯滤波器则是一种常用的滤波器类型，其公式和原理值得我们深入了解。

1. 巴特沃斯滤波器的概念巴特沃斯滤波器是一种基于极点和零点的滤波器，其设计目的是在通带内尽可能平坦地传递信号，而在截止频率以上或以下尽可能削弱信号。

巴特沃斯滤波器的特点是具有平滑的通带和陡峭的阻带，因此在信号处理中被广泛应用。

2. 二阶巴特沃斯滤波器的公式二阶巴特沃斯滤波器是一种二阶滤波器，其公式可以表示为： H(s) = K / ((s^2 + s(Q/ω) + 1) (s^2 + s(Q/ω) + 1)) 其中，s是复变量，K是增益，ω是截止频率，Q是品质因数。

品质因数Q是一个重要的参数，它决定了滤波器的阻带衰减速度。

品质因数越大，阻带衰减越快。

3. 二阶巴特沃斯滤波器的原理二阶巴特沃斯滤波器的原理是基于巴特沃斯滤波器的原理，其本质是将一阶巴特沃斯滤波器级联起来，从而形成一个二阶滤波器。

在二阶巴特沃斯滤波器中，信号经过两个一阶滤波器的级联，从而实现更陡峭的阻带衰减和更平坦的通带响应。

4. 二阶巴特沃斯滤波器的应用二阶巴特沃斯滤波器广泛应用于信号处理、音频处理、图像处理等领域。

在音频处理中，二阶巴特沃斯滤波器可以用于去除噪声和杂音，从而提高音频质量。

在图像处理中，二阶巴特沃斯滤波器可以用于去除图像中的噪点和伪影，从而提高图像清晰度。

5. 总结二阶巴特沃斯滤波器是一种常用的滤波器类型，其公式和原理对于信号处理和电子工程的研究非常重要。

通过了解二阶巴特沃斯滤波器的原理和应用，我们可以更好地理解信号处理和滤波器技术的相关知识，从而更好地应用于实际工程中。

butterworth滤波器阶数Butterworth滤波器是一种常见的模拟滤波器，由英国数学家S. Butterworth在20世纪30年代开发。

它可以应用于信号处理中，常常被用来消除不需要的信号成分，使得滤波后的信号更加适合特定的应用。

Butterworth滤波器的阶数是指滤波器所具有的极点和零点的数量。

根据阶数的不同，可以将Butterworth滤波器分为一阶、二阶、三阶、四阶以及更高阶的滤波器，不同阶数的滤波器具有不同的频率特性和幅频响应。

下面我们将对Butterworth滤波器的阶数进行详细的阐述。

一阶Butterworth滤波器：一阶Butterworth滤波器由一个极点和一个零点组成。

它的幅频响应不是完全的理想低通滤波器，但在0dB时有一点峰值。

一阶滤波器有一个非常简单的形式，因此易于设计和实现。

然而，它的滤波效果并不是最好的。

二阶Butterworth滤波器：二阶Butterworth滤波器由两个极点和两个零点组成。

它具有更好的滤波效果和频率特性，同时也更加复杂。

二阶滤波器是一种比较常见的滤波器，它可以用于各种信号处理应用，例如声音处理和图像处理等。

三阶Butterworth滤波器：三阶Butterworth滤波器比二阶滤波器更加复杂，由三个极点和三个零点组成。

它的滤波效果更好，频率特性也更加平缓。

三阶滤波器通常在需要更加精确滤波时使用，例如高分辨率的数码音频处理。

四阶Butterworth滤波器：四阶Butterworth滤波器具有更加平滑的频率特性和更好的滤波效果。

它由四个极点和四个零点组成，是一种比较复杂的滤波器。

四阶滤波器可以用于处理许多需要高精度滤波的应用，例如声音合成和数字信号处理等。

总结：Butterworth滤波器的阶数越高，滤波效果越好，频率特性越平滑。

不同阶数的滤波器适用于不同的应用场合，需要根据具体应用进行选择。

但需要注意的是，随着阶数的增加，滤波器也变得更加复杂，难以设计和实现。

二阶带通滤波器引言滤波器是信号处理中常用的工具，它可以通过改变信号的频谱来实现信号的处理和分析。

在滤波器的分类中，二阶带通滤波器是一种常见且有实际应用的滤波器。

本文将介绍二阶带通滤波器的基本概念、设计方法以及其在信号处理中的应用。

一、二阶带通滤波器的基本概念1.1 二阶滤波器的定义二阶滤波器指的是滤波器的阶数为2的滤波器。

阶数表示滤波器对信号的响应能力，阶数越高，滤波器对信号的处理能力越强。

1.2 带通滤波器的定义带通滤波器是指在一定频率范围内放行信号，而将其他频率范围内的信号抑制掉的滤波器。

带通滤波器通常由一个低通滤波器和一个高通滤波器级联而成。

1.3 二阶带通滤波器的特性二阶带通滤波器具有以下特性：•适用于音频和语音处理等应用；•可以选择滤波器的中心频率、带宽和衰减等参数；•可以实现有源或无源滤波器，适应不同的系统需求；•具有较好的相位响应和幅频特性。

二、二阶带通滤波器的设计二阶带通滤波器的设计过程包括确定滤波器的频率响应和参数。

2.1 选择滤波器类型常见的二阶带通滤波器类型有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。

不同的滤波器类型具有不同的特性，选择适合应用场景的滤波器类型是设计过程的第一步。

2.2 确定中心频率和带宽根据需要滤波的信号频率范围，确定带通滤波器的中心频率和带宽。

中心频率是指带通滤波器放行信号的中心频率，带宽是指带通滤波器放行信号的频率范围。

2.3 设计滤波器响应根据选择的滤波器类型和中心频率、带宽的要求，设计带通滤波器的频率响应。

常用的设计方法有频域法和时域法等。

2.4 参数调整和优化根据设计的频率响应，对滤波器的参数进行调整和优化，以满足实际应用的需求。

三、二阶带通滤波器的应用二阶带通滤波器在信号处理中具有广泛的应用。

以下是二阶带通滤波器的一些典型应用：3.1 音频处理在音频处理中，二阶带通滤波器可应用于语音增强、音频均衡和音效处理等环节。

通过控制滤波器的中心频率和带宽等参数，可以选择性地增强或抑制特定频率的音频信号。

二阶巴特沃斯滤波器系数二阶巴特沃斯滤波器是一种常用于信号处理的滤波器，其特点是具有平滑的频率响应和较高的滚降率。

在设计二阶巴特沃斯滤波器时，关键是确定滤波器的截止频率以及系数的计算方法。

截止频率是指滤波器开始起作用的频率，其决定了滤波器对信号频率的抑制程度。

对于二阶巴特沃斯滤波器，截止频率可以通过将原始信号的频率除以采样频率来计算。

根据巴特沃斯滤波器的特性，截止频率越高，滤波器对高频信号的抑制效果越明显。

具体计算巴特沃斯滤波器的系数有两种方法：标准形式和带通形式。

标准形式适用于低通和高通滤波器的设计，而带通形式适用于带通和带阻滤波器的设计。

对于标准形式巴特沃斯滤波器，系数的计算可以通过双极二阶巴特沃斯低通滤波器的系数公式来进行。

该公式包括了两个极点和一个零点的计算，其中极点是截止频率处的复数根，零点则为原点。

通过计算得到极点和零点后，可以求得巴特沃斯滤波器的系数，并将其应用于信号的滤波过程中。

对于带通形式巴特沃斯滤波器，系数的计算方法相对较复杂。

首先需要将带通滤波器转化为低通滤波器，然后再根据低通滤波器的系数计算方法来计算带通形式巴特沃斯滤波器的系数。

具体的计算方法包括将带通滤波器的中心频率归一化到1，然后计算归一化低通滤波器的系数，并通过带通到低通的频率变换来求得带通形式巴特沃斯滤波器的系数。

通过合理选择截止频率和正确计算巴特沃斯滤波器的系数，我们可以实现对信号的滤波和频率选择。

巴特沃斯滤波器的特点使其在音频处理、图像处理、通信等领域得到广泛应用。

熟练掌握二阶巴特沃斯滤波器的系数计算方法，对于互联网技术介绍和技术应用的文章撰写非常重要。

二阶无限增益多路反馈巴特沃斯带通滤波器巴特沃斯滤波器是一种常用的滤波器类型，其特点是在通带内具有平坦的幅频响应，并具有较快的衰减斜率。

在信号处理和通信系统中广泛应用。

二阶无限增益多路反馈巴特沃斯带通滤波器是一种特殊的巴特沃斯滤波器，具有更高的阶数和更好的性能。

巴特沃斯滤波器的设计是基于巴特沃斯函数，该函数是一种理想低通滤波器的幅频响应曲线。

通过对巴特沃斯函数进行变换和级联，可以得到不同阶数的巴特沃斯滤波器。

在带通滤波器中，巴特沃斯滤波器可以通过对低通滤波器进行频率变换得到。

二阶无限增益多路反馈巴特沃斯带通滤波器是一种特殊的巴特沃斯滤波器，它具有无穷多个级联的二阶滤波器，每个二阶滤波器都具有无限增益。

这意味着在通带内，滤波器的增益不随频率变化而变化，而在截止频率处，滤波器的增益会发生跳变，从而形成带通滤波器的特性。

二阶无限增益多路反馈巴特沃斯带通滤波器的设计是基于级联二阶滤波器的原理。

每个二阶滤波器由一个电容和两个电阻组成，通过调整电容和电阻的数值，可以改变滤波器的截止频率和增益。

在级联的过程中，每个二阶滤波器的输出被反馈到输入，从而形成了无限增益的特性。

二阶无限增益多路反馈巴特沃斯带通滤波器具有很多优点。

首先，它具有平坦的幅频响应，在通带内的增益基本保持不变。

其次，它具有较快的衰减斜率，可以有效地抑制不需要的频率分量。

此外，由于采用了无限增益的设计，滤波器的增益不会受到电路增益的限制，可以实现更高的增益。

然而，二阶无限增益多路反馈巴特沃斯带通滤波器也存在一些限制。

首先，由于采用了无限增益的设计，滤波器在通带内的增益会发生跳变，这可能会导致一些非线性失真。

其次，滤波器的阶数越高，电路复杂度越高，对元器件的要求也越高，对于一些特定应用而言可能会存在一定的挑战。

二阶无限增益多路反馈巴特沃斯带通滤波器是一种特殊的巴特沃斯滤波器，具有无穷多个级联的二阶滤波器和无限增益的特性。

它在信号处理和通信系统中具有重要的应用价值，可以实现平坦的幅频响应和较快的衰减斜率。

巴特沃斯二阶带通滤波器simulink实现巴特沃斯二阶带通滤波器的设计和实现在信号处理领域中是非常常见的。

本文将一步一步地回答如何使用Simulink工具来实现巴特沃斯二阶带通滤波器。

第一步：理解巴特沃斯二阶带通滤波器的原理巴特沃斯二阶带通滤波器是一种常用的滤波器类型，可以通过选择适当的截止频率来过滤出特定频率范围内的信号。

它的传递函数表达式为：H(s) = K/[(s^2 + s/Q + 1)]其中，K是增益系数，s是复频域变量，Q是品质因数。

巴特沃斯二阶带通滤波器的特点是通过选择合适的Q值和截止频率来实现带通滤波的效果。

第二步：创建Simulink模型打开MATLAB软件并启动Simulink工具。

然后，创建一个新模型。

第三步：添加输入信号源在模型中添加一个信号源，用于提供待滤波的输入信号。

可以选择Sin波形作为输入信号。

在Simulink库浏览器中，找到"Sources"文件夹，在其中选择"Sine Wave"模块并拖动到模型中。

第四步：添加巴特沃斯二阶带通滤波器在模型中添加一个巴特沃斯二阶带通滤波器。

在Simulink库浏览器中，找到"Continuous"文件夹，在其中选择"Transfer Fcn"模块并拖动到模型中。

双击该模块，打开其参数设置窗口。

在参数设置窗口中，将传递函数的表达式输入框中的表达式设置为H(s) =K/[(s^2 + s/Q + 1)]。

设置增益系数K和品质因数Q的值。

这些值可以根据实际需求进行调整。

第五步：连接信号源和滤波器将信号源模块的输出端口连接到巴特沃斯二阶带通滤波器的输入端口。

在模型中拖动一个连接线，从信号源的输出端口连接到滤波器的输入端口。

第六步：添加输出显示在模型中添加一个显示模块，用于显示滤波器输出的信号。

在Simulink库浏览器中，找到"Sinks"文件夹，在其中选择"Scope"模块并拖动到模型中。

二阶带通滤波器二阶带通滤波器（Second Order Bandpass Filter）概述：二阶带通滤波器是一种常用的电子滤波器，用于从信号中提取特定频率范围的信号。

它具有一定的带宽，在该带宽范围内的信号将会被放大，而在带外的信号将会被抑制。

这种滤波器常用于音频处理、通信系统、地震测量等领域。

工作原理：二阶带通滤波器由一个一阶低通滤波器和一个一阶高通滤波器串联而成。

这两个滤波器的输出经过级联后形成一个带通滤波器。

一阶低通滤波器通过允许低频信号通过并抑制高频信号来实现对频率的限制，而一阶高通滤波器则相反。

当两者级联时，就可以实现对指定频率范围内的信号进行放大。

参数设计：设计二阶带通滤波器时，需要确定一些重要参数，包括中心频率、带宽、阻带衰减、通带增益等。

中心频率指的是要通过的信号的频率，在这个频率附近的信号将会被放大。

带宽是指在中心频率附近的一定范围内的频率，该范围内的信号将被放大。

阻带衰减是指在带外频率范围内的信号被滤波器抑制的程度。

通带增益是指在通过的频率范围内，信号在滤波器输出上的放大倍数。

滤波器类型：二阶带通滤波器有多种类型，包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。

它们有着不同的频率响应特性和阻带衰减性能。

选择适合的滤波器类型取决于应用的具体要求，例如需要更好的通带纹波特性还是更高的阻带衰减。

性能评估：二阶带通滤波器的性能可以通过多种指标来评估，如通带纹波、阻带衰减、相移等。

通带纹波描述了在通带范围内信号增益的不均匀性，通常以分贝为单位来表示。

阻带衰减是指在带外范围内信号被滤波器抑制的程度，也是以分贝为单位来表示。

相移是指信号在滤波器中传输过程中的延迟，通常以角度来表示。

应用领域：二阶带通滤波器在许多领域都有广泛的应用。

在音频处理中，它可以用来消除低频噪声或强化音频信号的特定频段。

在通信系统中，它可以用来滤除噪声或选择特定频率的信号。

在地震测量中，它可以用来提取地震信号的特定频带，以进行地震活动监测。

二阶巴特沃斯滤波器的分析与实现电路一、二阶巴特沃斯滤波器的分析1.二阶巴特沃斯滤波器的传递函数H(s)=K/(s^2+s/Q+1)其中，s是复频率变量，K是增益系数，Q是品质因数。

2.二阶巴特沃斯滤波器的频率响应-通带增益：在通带上的频率响应为平坦的，即各个频率上的增益相同，达到最大的增益，同时增益是线性的。

-阻带增益：在阻带上的频率响应有较大的衰减，一般以-20dB/10倍数进行衰减。

-边缘频率：通带和阻带的分界点被称为边缘频率，可以用截止频率表示。

3.品质因数Q的影响品质因数Q是二阶巴特沃斯滤波器一个重要的参数，它决定了滤波器的响应特性。

-当Q值较大时，滤波器具有较窄的通带和深的阻带，对于截止频率的变化较为敏感。

-当Q值较小时，滤波器具有较宽的通带和浅的阻带，对于截止频率的变化不敏感。

4.构建二阶巴特沃斯滤波器的实现电路构建二阶巴特沃斯滤波器的实现电路有多种方式，其中比较常见的方式是使用运算放大器和电容、电感等元件构成。

二、二阶巴特沃斯滤波器的实现电路1.无源滤波器无源滤波器是利用电容、电感等被动元件构成的滤波器，可以直接用于振荡电路中的滤波。

-RC二阶无源巴特沃斯低通滤波器电路由两个电阻R和两个电容C构成，电容负载在两个分立性电阻之间。

-RL二阶无源巴特沃斯带通滤波器电路由两个电阻R和两个电感L构成，电感负载在两个分立性电阻之间。

2.有源滤波器有源滤波器是利用运算放大器（OP-AMP）和电容、电感等被动元件组成的滤波器，可以增加放大倍数和频率范围。

- Sallen-Key二阶有源巴特沃斯低通滤波器电路由一个运算放大器、两个电阻R1和R2，两个电容C1和C2构成。

- Sallen-Key二阶有源巴特沃斯带通滤波器电路由一个运算放大器、两个电阻R1和R2，两个电容C1和C2构成。

以上是两种常见的二阶巴特沃斯滤波器的实现电路示例，实际构建时还需根据具体的需求进行参数调整和电路优化。

总之，二阶巴特沃斯滤波器是一种常见而有效的模拟滤波器，可以用于对信号进行滤波处理。