下载文档原格式
第一章第一章 抽象群概论§1 什么是群什么是群？？群公理不同元素的集合不同元素的集合，，赋予一定的合成规则赋予一定的合成规则（（称为群称为群““乘法乘法””—— 加、乘、对易子等对易子等）。
）。
满足下列满足下列条件条件（（群公理群公理））： （1）封闭性 i g 和G g j ∈，则G g g g k j i ∈=⋅； （2）结合律 )()(k j i k j i g g g g g g ⋅⋅=⋅⋅；（3）存在唯一的单位元素e （或E ）G ∈ ，对任一元素j g 有j j j e g g e g ⋅=⋅=； （4）对每一元素有逆元对每一元素有逆元，，对i g 有 1−i g ，使e g g ii =⋅−1。
阶 —— 群元的个数群元的个数：：阶有限为有限群阶有限为有限群；；阶无穷为无限群阶无穷为无限群。
无限群又分无限离散和无限连续无限群又分无限离散和无限连续。
注：1. 乘法不可对易乘法不可对易，，即i j j i g g g g ⋅≠⋅。
若可对易若可对易，，则称为阿贝尔称为阿贝尔（（Abel ）群。
2. 若G c b a ∈,,，则G 中包含p l k c b a ,,（其中p l k ,,为整数为整数））。
例1．复数1，i ，-1，-i 组成四阶群组成四阶群。
四阶循环群 —— 由一个元素由一个元素，，i （或-i ）出发出发，，由它及其幂由它及其幂次次生成整个群G ，称为循环群称为循环群。
循环群必是阿贝尔群环群必是阿贝尔群。
n 阶循环群可表为{23,,...n a a a a e =}。
例2．所有实数组合所有实数组合，，加法运算下成群加法运算下成群。
全体正实数在乘法运算下成连续群全体正实数在乘法运算下成连续群。
例3．定轴转动定轴转动：：Π<Θ≤20，)2(SO 无限连续群无限连续群。
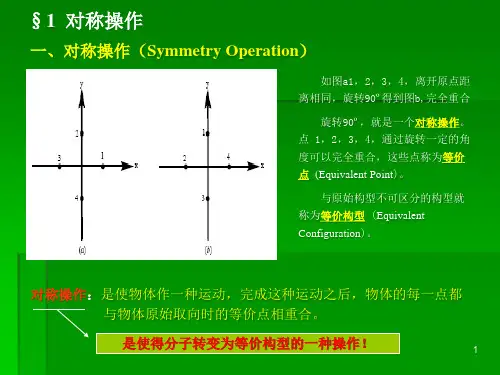
特例 —— 转角为m 倍nπϑ2=构成n 阶群n C ；定点转动定点转动（（三维空间转动三维空间转动））：),,(γβαR ，)3(SO 群。
第二章 群 论 §1 群的定义群论是代数学中内容最丰富的分支之一，它是近世代数的基础。
在所有只含一个代数运算的代数系统中，最重要的一个研究对象就是群。
本节只是依照教材作一些一般性地介绍，为扩大知识面，这里引入 “半群”和“幺半群”基本概念。
说明：群的代数运算“ ”习惯上称为乘法（群也称为乘法群），b a 简记成ab 。
一 单位元与逆元定义1 设},{ A 是一个代数系统，如果A 中存在一个特殊的元素e ，具有性质：A a ∈∀都有a ae ea ==，那么称e 为A 的关于“ ”的单位元(幺元)。
结论1若},{ A 中有单位元，那么单位元一定是唯一的。
证明 设21,e e 都是A 的单位元，2211e e e e ==⇒。
定义2设},{ A 是一个代数系统，如果A 中存在一个特殊的元素L e ，具有性质：A a ∈∀都有a a e L =，那么称L e 为A 的关于“ ”的左单位元(左幺元)。
如果A 中存在一个特殊的元素R e ，具有性质：A a ∈∀都有a ae R =，那么称R e 为A 的关于“ ”的右单位元(右幺元)。
结论2若},{ A 中有左单位元L e 和右单位元R e ，则R L e e =，且就是},{ A 的单位元。
证明 R R L L e e e e ==。
例1 },{},{},,{+++R ，Z N 的单位元是0，},{},{},,{⋅⋅⋅R ，Z N 的单位元是1。
例2 )(R M n 是n 阶实矩阵的全体，“+”和“.”是矩阵加法与乘法，})({+，R M n 的单位元是n 阶零矩阵n O ，})({⋅，R M n 的单位元是n 阶单位阵n I 。
例3 A 是一个非空集合，)(A P 是A 的幂集，即A 的所有子集的集合。
}),({ A P 的单位元是Φ，}),({ A P 的单位元是A 。
例4 }{-Z ，，}{-R ，中无单位元，但有右单位元0。
