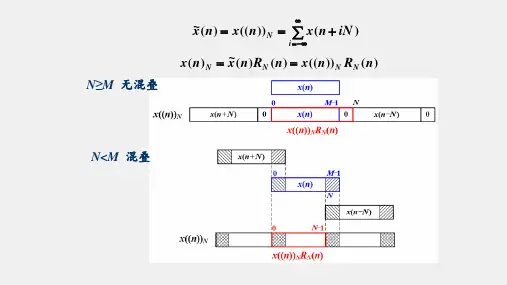
(2) 补零到L点长 x(m)L、 h((m))LRL(m) (3) 将h((m))LRL(m)翻褶为h((−m))LRL(m) (4) h((−m))LRL(m)与x(m)对应位相乘相加得 yc(0)
(5) 循环右移到h((n−m))LRL(m),与x(m)相乘相加得 yc(n)
例3-6 x(n)= {1, 2, 3},0 n 2;h(n)= {1, 2, 2, 1},0n3。
翻褶 翻褶循环右移1位
§3.2.2 有限长复序列共轭的DFT
DFT[ x*( N n)]N X *(k), 0 k N 1
DFT[ x*(n)]N X *( N k), 0 k N 1
证明:
X*(N
k)
N 1
x(n)W
n0
(N N
k
)n
*
N 1
x(n)W
n0
N
kn
n 4 3 2 1 0 1 2 3 4 5
y(n4) 1 4 9 11 8 3
y(n)
1 4 9 11 8 3
yc1(n)
9 7 9 11
3. 循环卷积定理 x(n)长度M,h(n)长度N,L max(M, N) yc(n) = x(n) L h(n),Yc(k) = X(k)H(k) DFT[x1(n)x2(n)]L = X1(k) L X2(k)/L 0nL1,0kL1
N 4,
X (k)4
1 e j2k 1 e jk 2
4, 0,
k0 1k 3
4 (k),
0 k 3
N 8,
X (k)8
1 e jk 1 e jk 4
,
0
k
7
N 16,
X (k )16
1 e jk 1 e jk