当前位置：文档之家 › 第三讲 正态分布及其应用

第三讲 正态分布及其应用

  • 格式：ppt
  • 大小：1.06 MB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

正态分布与应用

正态分布与应用

正态分布
© 2023 maxiaofeng
正态分布的性质是什么
正态分布的突出性质：
➢ 分布围绕平均值对称：一半的值低于平均值，一半高于平均值。
➢ 分布可以用两个值来描述：平均值和标准差。
➢ 平均值是位置参数，而标准差是刻度参数。
➢ 平均值确定曲线峰值的中心位置，增加均值使曲线向右移动，而减小均值使曲
要首先得到 z 值，z 值告诉我们 1380 与平均值相差多少个标准差。
公式
=
−μ

计算
=
1380−1150
150
当 z 为 1.53 时， 为 0.937，这是 SAT 分数为 1380
或更低的概率，要获得阴影区域的概率(面积)，需要从整体中
减去 0.937：
S（x > 1380） = 1 – 0.937 = 0.063
即在=μ这条直线左右两边的面积各为0.5，即S(＜μ)=S(＞μ)=0.5；
⑤当＜μ时，曲线上升(增函数)；当＞μ时，曲线下降(减函数)，并且
当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近;
⑥当σ一定时，曲线随着μ的变化而沿x轴平移；
⑦当μ一定时，曲线的形状由σ确定，σ越小，曲线越尖削，表示总体的分布越集中；σ越大，曲线越平阔，
线向左移动。
➢ 标准差拉伸或挤压曲线。小的标准差导致窄曲线，而大的标准差导致宽曲线。
正态分布
© 2023 maxiaofeng
正态分布的特点
➢
➢
➢
➢
➢
➢
➢
➢
➢
①曲线位于轴上方，与轴不相交；
②曲线是单峰的，它关于直线x=μ对称；
③曲线在=u处达到峰值；

正态分布的概念及应用

正态分布的概念及应用
正态分布的概念及应用
• 正态分布的简介 • 正态分布的性质 • 正态分布的应用场景 • 正态分布在数据分析中的应用 • 正态分布在机器学习中的应用 • 正态分布与其他统计分布的关系
01
正态分布的简介
正态分布的定义
01
正态分布是一种连续概率分布， 描述了许多自然现象的概率分布 形态，其概率密度函数呈钟形曲 线，且具有对称性。
贝叶斯推断
正态分布在贝叶斯推断中发挥了重要作用。通过贝叶斯定理，我们可以根据先 验知识和数据更新对未知参数的估计，而正态分布可以作为先验知识的分布形 式。
核方法和支持向量机
核方法
在支持向量机（SVM）等核方法中，正态分布作为核函数的一 种形式，用于将输入空间映射到高维特征空间，从而使得线性 不可分的数据变得线性可分。
在时间序列分析中，正态分布可用于描述时间序列数据的分布特征， 并建立预测模型。
05
正态分布在机器学习中的应用
概率模型和贝叶斯推断
概率模型
正态分布是一种常用的概率分布，在贝叶斯推断中，我们常常假设某些参数服 从正态分布，以便进行统计推断。例如，在朴素贝叶斯分类器中，特征的概率 分布被假设为正态分布。
考试成绩和测试评分
考试成绩和各种测试评分也经常呈现正态分布，因为大多数人的得分集中在平均分附近， 而高分和低分的人数较少。
气温、降雨量等气候数据
气温、降雨量等自然现象数据也可以用正态分布来描述，因为它们通常遵循类似的统计规 律。
科学研究和技术开发
01 02
实验结果和测量数据
在科学实验和测量中，很多数据呈现正态分布，如放射性衰变的半衰期、 化学反应速率等。这些数据反映了物质内部微观粒子的随机运动和相互 作用。
正态分布在统计学中的地位

课件3：§7.5　正态分布

课件3：§7.5　正态分布

( B) A．95.45%
B．99.73%
C．4.55%
D．0.27%
【解析】由 X～N(－2，14)，知 μ＝－2，σ＝21，
∴P(－3.5<X≤－0.5)＝P(－2－3×0.5<X≤－2＋3×0.5)
＝0.997 3.
3．已知正态分布总体的数据落在区间(－3，－1)内的概率 和落在区间(3,5)内的概率相等，那么这个正态总体的均值 为________． 【解析】区间(－3，－1)和区间(3,5)关于直线 x＝1 对称， 所以均值 μ 为 1. 【答案】1
课堂检测
1．下列函数可以作为正态分布密度函数的是 ( A )
A．f(x)＝
( x1)2
1e 2 2π
B．f(x)＝σ
1
( xu)2
e 2 2
2π
C．f(x)＝
1
e
(
x u )2 2 2
2πσ
D．f(x)＝21π
e
(
xu 2π
)2
2．若 X～N(－2，41)，则 X 落在(－3.5，－0.5]内的概率是
归纳领悟 1．在正态分布 X～N(μ，σ2)中，μ 就是随机变量 X 的均值，σ2 就是随机变量 X 的方差，它们分别反映 X 取值的平均大小和 稳定程度． 2．正态密度曲线的性质 (1)曲线位于 x 轴上方，与 x 轴不相交； (2)曲线是单峰的，它关于直线 x＝μ 对称；
(3)曲线在
x＝μ
处达到峰值 σ
课堂小结 1.知识清单： (1)正态曲线及其特点. (2)正态分布. (3)正态分布的应用，3σ原则. 2.方法归纳：转化化归、数形结合. 3.常见误区：概率区间转化不等价.
本节内容结束 更多精彩内容请登录：

正态分布及其应用

正态分布及其应用

Part
04
正态分布在金融领域的应用
资产收益率的正态分布假设
资产收益率的正态分布假设
在金融领域中，正态分布被广泛用于描述资产收益率的概率分布。这一假设基于大量历史 数据的统计分析，认为资产收益率的分布近似于正态分布。
中心极限定理
中心极限定理是正态分布假设的理论基础，它表明无论总体分布是什么，当样本量足够大 时，样本均值近似服从正态分布。
生物医学研究
在生物医学研究中，许多生理指 标和疾病发生概率的分布并不服 从正态分布，而是呈现出偏态分 布或泊松分布等其他类型。
正态分布在大数据时代的发展
01 02
机器学习算法的改进
随着机器学习算法的不断改进，正态分布在大数据时代的 应用场景将得到进一步拓展。例如，深度学习算法可以处 理大规模、高维度的数据集，并能够自动提取特征，从而 减少对正态分布假设的依赖。
参数估计
在正态分布假设下，可以使用历史数据估计资产的预期收益率和风险波动率等参数，为投 资决策提供依据。
VaR（风险价值）的计算
VaR（风险价值）定义
VaR是指在一定置信水平下，某 一金融资产或投资组合在未来特 定时间段内的最大可能损失。
VaR计算方法
基于正态分布假设，可以使用历 史模拟法、蒙特卡洛模拟法等计 算VaR。这些方法通过模拟资产 价格的随机变动，计算出在给定 置信水平下的潜在损失。
无法处理复杂数据
正态分布在处理具有复杂结构或非线性关系的数据时可能表现不佳， 无法准确描述数据的分布特性。
非正态分布的适用场景
金融领域
自然语言处理
在金融领域中，许多金融变量的 分布并不服从正态分布，而是呈 现出尖峰厚尾的特点。例如，股 票收益率、波动率等金融时间序 列数据的分布往往具有这些特征。

正态分布和其应用

正态分布和其应用
限和上限，即双侧界值；有些指标如
肺活量一般只以过低为异常，血铅以
过高为异常，只需要拟定下限或上限， 即单侧界值。
根据资料旳分布类型有下列两种计 算医学参照值范围旳常用措施。
➢正态近似法 合用于服从正态分布或近 似正态分布旳资料
➢双侧1 参照值范围
x u 2s➢单侧 1 源自照值范围x u s 或 x u s
或称 变换u 。
u x
• 实际应用中，经u 变换后，就可把 求解任意一种正态分布曲线下面积旳问 题，转化成原则正态分布曲线下相应旳 面积问题。附表1给出了原则正态分布 曲线下从 到 u旳面积，根据正态分布 旳对称性，我们能够求出任何一种区间 内原则正态分布曲线下旳面积，也就是
u 落在任何一种区间内旳概率。
1
2
exp(
(X )2 2 2
)
其中参数为均值， 为原则差，由此
决定旳正态分布记作 N (, 2 ) 。
正态分布概率密度曲线示意图
➢ 三．特征
➢ 正态分布是单峰曲线，形状呈钟型，中间高，两
端低，以 X 为对称轴，左右完全对称。
➢ 在 X 处，f ( X ) 取得最大值。
➢ 有两个参数：位置参数 和变异度参数 。 一定， 越大，数据越分散，曲线越平坦； 一
➢百分位数法 合用于偏态分布资料、分 布型未知旳资料以及分布末端有不拟定 值旳资料。
➢双侧95%参照值范围
P2.5 ~ P97.5
➢单侧95%参照值范围
P5 或 P95
• 根据正态 分布旳对称性知，外侧尾部面 积 u 2.21 与外侧尾部面积 u 2.21 相同，查附表1，得相应旳概率为0.0136， 体重在50kg以上旳12岁小朋友占1.36%。
第三节 医学参照值范围旳制定

医学统计3-正态分布及其应用

医学统计3-正态分布及其应用

频数
27 169 167
94 81 42 28 14
4 3 1 630
累积频数
27 196 363 457 538 580 608 622 626 629 630
-
累积频率(%)
4.3 31.1 57.6 72.5 85.4 92.1 96.5 98.7 99.4 99.8 100.0
-
PX
LX
求出在4 ×1012/L~5.5 ×1012/L范围内所占的比 例
即求P(4.0≤X≤5.5)
(5.5 4.78 ) ( 4 4.78 ) (1.89) (2.05)
0.38
0.38
[1 (1.89)] (2.05) 0.9504
例3-2 上节课的例题中已计算出101名正常成年 女子的血清总胆固醇均数为4.03mmol/L，标准 差为0.659mmol/L。试估计该单位：正常成年女 子血清总胆固醇在4.00mmol/L以下者占正常女 子总人数的百分比；在4.00~5.00mmol/L之间者 占正常女子总人数的百分比；在5.00mmol/L以 上者占正常女子总人数的百分比。
样本含量一般要较大，如n>120。
（二）对选定的参照样本进行准确的测定
为保证原始数据可靠，要严格控制检测误差， 包括分析仪器的灵敏度、试剂的纯度、操作技术及 标准的掌握等，同时必须对测量条件做出统一的规 定和说明，如临床化验参考值范围的制定，应对收 集样本时的环境和生理条件（温度、季节、体育活 动强度、饮食、妊娠等），收集、转运和储藏样品 的方法及时间有明确的规定。
f (z)
1
z2
e 2 , z
2
即将X~N(μ,σ2)的正态分布转化为z~ N(0,12)的标准 正态分布，z称为标准正态变量，其分布函数为

03 正态分布及其应用

03 正态分布及其应用

正态分布法：适于正态分布资料。对数正态分
布的资料取对数后可用正态分布法。
•
百分位数法：适于偏态分布资料或不知道分布 类型的资料。所需样本含量较大。
表1. 正常值范围的界值
正态分布法 ％ 90 百分位数法
双侧单 侧Fra bibliotek下限上限
双 侧
P5～P95
单 侧
下限 上限
P10 P90
X 1.64 S X 1.28 S X 1.28 S
二、正态曲线下面积的 分布规律
正态曲线下面积的意义：正态曲线下一
定区间内的面积代表变量值落在该区间 的概率。整个曲线下的面积为1，代表总 概率为1。
曲线下面积的求法：定积分法和标准正
态分布法
三、标准正态分布

标准正态分布：指均数为0，标准差为1的 正态分布。常称u分布或z分布。 标准正态分布与正态分布的转换公式：

Z
X

即若X服从正态分布N（μ，σ），则Z就 服从均数为0，标准差为1的正态分布。
标准正态分布
（Standardized normal distribution）
Φ(z)
z
0
例：某地100名一年级男大学生的平均
身高为166.2cm，标准差为5.2cm，现 欲估计该地身高低于160cm、身高介 于165～175cm范围的男大学生人数。 由于本例是一个大样本，故可用 样本均数和样本标准差作为总体均数 和标准差的估计。作标准化变换：
正态分布曲线下的面积
四、正态分布的应用

正态分布的判断和检验：
经验法 正态性检验

估计正态分布资料的频数分布
医学参考值（正常值）的制定（后）

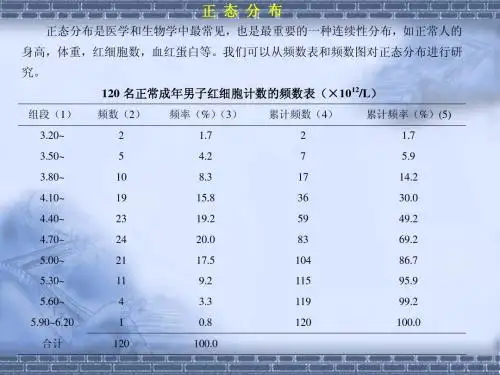
第三章 正态分布及其应用

第三章 正态分布及其应用

二、标准正态分布
正态分布是一个分布族，对应于不同的参数 和 会产生不同位置、不同形状的正态 分布，为了应用方便，我们将正态分布转化成标准正态分布。
u x
f (X )
1
(x )
2

2
e
2
2
, X

ห้องสมุดไป่ตู้
(u )
1 2
u
2
e
2
, u
由频数分布表可知尿汞值呈偏态分布，且尿汞值仅 以过高为异常（单侧） ，所以采用百分位数法计算 上侧界值即求第 95 百分位数 P95。 公式： P
X
L
i fx
(n x%
8 .0 11

fL )
PX 4 0 .0
( 2 8 2 9 5 % 2 6 3 ) 4 3 .6 ( / L )
正 态 分 布
正态分布是医学和生物学中最常见，也是最重要的一种连续性分布，如正常人的 身高，体重，红细胞数，血红蛋白等。我们可以从频数表和频数图对正态分布进行研 究。 120 名正常成年男子红细胞计数的频数表（×1012/L）
组段（1） 3.20~ 3.50~ 3.80~ 4.10~ 4.40~ 4.70~ 5.00~ 5.30~ 5.60~ 5.90~6.20 合计 频数（2） 2 5 10 19 23 24 21 11 4 1 120 频率（%） （3） 1.7 4.2 8.3 15.8 19.2 20.0 17.5 9.2 3.3 0.8 100.0 累计频数（4） 2 7 17 36 59 83 104 115 119 120 累计频率（%）(5) 1.7 5.9 14.2 30.0 49.2 69.2 86.7 95.9 99.2 100.0

第三章-统计学正态分布及其应用(医学统计学)-幻灯片

第三章-统计学正态分布及其应用(医学统计学)-幻灯片
-1.96
68.27%
+1.0 95.00% 2.5%
+1.96
二、标准正态分布表 附表Ⅰ
Φ(u)
－∞ －3 －2
－1
0
＋1 ＋2 ＋3 ＋ ∞
查表确定标准正态分布曲线下的面积时 必须注意：
（1）当μ，σ和X已知时，先按u变 换公式求得u值，再用u值查表；
ux
当μ，σ和X未知时，用样本均数 和样本标准差S代替求u值。
Ф(u2)- Ф(u1) = 0.2643 - 0.1251
=0.1392=13.92%
即身高界于116.5-119.0cm范围内 的7岁男童比例为13.92%，其人数 为110×13.92%=15（人）。
第三节 正态分布的应用
一、估计频数分布 二、制定参考值范围 三、质量控制 四、统计处理方法的基础
u1=
＝ － 1.15
4.72
119.0－121.95
u2=
＝ － 0.63
4.72
例3.3 已知 X=121.95cm, S=4.72cm 欲估计身高界于116.5-119.0cm范
围内的7岁男童比例及人数。
求该面积
-1.15 -0.63
Ф(u1) =Ф(-1.15)=0.1251
Ф(u2) =Ф(-0.63)=0.2643
1、正态分布法
(1)适用范围：（近似）正态分布或对数正态分布 资料
x (2)计算公式： ±uS x 双侧： 95％ ±1.96S
x 99％ ±2.58S x 单侧： 上限 95％ ＋1.645S
x 99％ ＋2.326S x 下限 95％ －1.645S
x 99％ －2.326S
2、百分位数法 (1)适用范围： a.偏态分布资料 b.分布不清资料 c.开口资料

正态分布及其应用

正态分布及其应用

正态分布及其应用
正态分布（也被称为高斯分布）是概率统计学中常见的一种连续型概率分布。

正态分布的概率密度函数具有钟形曲线的特征，它由两个参数决定：均值μ和方差σ²。

正态分布在许多实际问题中具有广泛的应用。

以下是一些常见的应用：
1. 自然科学研究：正态分布被广泛用于描述许多自然现象，如测量误差、实验数据分布等。

2. 金融领域：正态分布被用于描述许多金融指标的变动，如股票价格、债券收益率等。

投资者可以利用正态分布进行风险管理和投资决策。

3. 质量控制：正态分布被应用于质量控制，例如在制造业中检测产品的质量是否合格。

4. 医学研究：正态分布经常用于研究人群的生理指标或疾病的发病率，如身高、体重、血压等。

5. 教育测量：正态分布可应用于评估学生的考试成绩、能力水平等。

6. 数据分析：正态分布常用于数据分析和拟合，在假设检验、参数估计和统计推断等方面被广泛使用。

总之，正态分布在许多领域中都有广泛的应用，特别是在统计学和概率论中被广泛研究和应用。

第三讲正态分布及其应用要点

第三讲正态分布及其应用要点

第三讲正态分布及其应用要点正态分布是概率统计学中最重要的概率分布之一，也是最常见的连续型概率分布之一、在应用中，正态分布常常被用来描述随机实验中连续型随机变量的分布规律。

下面我将介绍正态分布的定义、性质及其在实际应用中的一些要点。

正态分布是指在数学上由期望值μ和方差σ²完全确定的一簇曲线以及它们之上的概率分布。

其定义为：f(x) = (1/√(2πσ²)) * exp(-((x-μ)² / (2σ²)))其中，f(x)表示随机变量X的概率密度函数，μ和σ²分别为正态分布的期望值和方差。

由于正态分布的特殊性质，它具有以下几个重要的性质：1.对称性：正态分布呈镜像对称分布，其曲线关于期望值μ对称。

2.峰度：正态分布的峰度是常数3，意味着正态分布的数据相对于均值较为集中，尖峭。

3.概率密度函数的特点：正态分布的概率密度函数图像呈钟形曲线，大部分数据集中在均值附近，随着离均值的距离增大，概率密度逐渐减小。

正态分布在实际应用中具有广泛的应用，几乎在所有领域都能找到其身影。

以下是正态分布在实际应用中的一些要点：1.统计推断：许多统计推断方法都是基于正态分布的假设进行的，例如参数估计、假设检验和置信区间估计等。

因此，正态分布在统计学中扮演了重要的角色。

2.风险管理：正态分布广泛应用于金融领域的风险管理。

例如，根据股票价格的正态分布特征，可以进行股价的波动性分析和期权定价等。

3.质量控制：正态分布在质量控制中被广泛应用。

例如，生产线上的产品尺寸、重量等属性往往符合正态分布，通过正态分布的参数估计和概率分布计算，可以对生产过程进行控制和优化。

4.教育评估：在教育领域中，正态分布被用来评估学生的成绩分布。

例如，常用的标准化考试（如SAT、高考）成绩可以通过正态分布来进行阈值的设定和学生的成绩排名。

5.自然科学研究：正态分布在自然科学研究中也有广泛应用。

例如，物理学中的测量误差、生态学中的种群分布、生物学中的生物体测量等往往服从正态分布。

[课件]第三章 正态分布及其应用PPT

[课件]第三章 正态分布及其应用PPT
第三章 正态分布及 其应用
第 一 节
正态分布的概l Distribution)
(一)、正态分布的概念
f ( X ) 1.2
1 0.8 0.6 0.4 0.2 0 3.8 4.2 4.6 5.0 5.4 5.8 X
图3-1 某地成年男子红细胞数的分布逐渐接近正态分布示意图
… … … … … … … … … … … … … … … … … … … … …
-4
-3
-2
-1
01
1
2 2
2
3
3 4
3
5
6
7
1

图3-3 三种不同均数的正态分布
1
2
3
-5
-4
-3
-2
1
-1
0
1
2

2
3
3
4
5
图3-4 三种不同标准差的正态分布
5、正态曲线下的面积分布有一定的规律: ⑴. 无论μ与σ取何值, 正态曲线与横轴所 夹的面积恒等于1 (100%); ⑵. 正态曲线下的面积有一定的分布规律.
f ( X ) 1.2
1 0.8 0.6 0.4 0.2 0 3.8 4.2 4.6 5 5.4 5.8 X
f (X )1.2 1 0.8 0.6 0.4 0.2 0 3.6 4 4.4 4.8 5.2 5.6 6 X
25 20
人 数
15 10 5 0 110 112 114 116 118 120 122 124 126 128 130 132 134 136
( u )
X u
u ~ N(0,1 )
1 e ， u 2
2 u 2

第三章第3节正态分布及其应用

第三章第3节正态分布及其应用

双侧界值：x 1.96s
95 单侧上界：x 1.645s%源自单侧下界：x 1.645s
双侧界值：x 2.58s
99 单侧上界：x 2.335s % 单侧下界：x 2.335s
2．对数正态分布法
适用于对数正态或近似正态分布资料
95% 99%
双侧界值：lg 1(x lg x 1.96s lg x) 单侧上界：lg 1(x lg x 1.645s lg x) 单侧下界：lg 1(x lg x 1.645s lg x)
第三节 正态分布和医学参考值范围
一、正态分布（normal distribution）
（一）.概念： 以均数为中心，左右两侧基本对称，靠近均数 两侧频数较多，离均数越远，频数越少，形成一个 中间多，两侧逐渐减少基本对称的分布，称为正态 分布。
a
b
c
图8-2 频数分布逐渐接近正态分布示意图
其概率密度函数为：
小结
x • 1.集中趋势指标： G M P50 • 2.离散趋势指标：R Q S 2 S cv
• 3.正态分布和医学参考值范围
如一般以 4.0109 / L～10作.0为10人9 W/ LBC总数
的参考值范围。参考值范围在诊断方面可用于 划分正常与异常。
制定方法：
1.首先从正常人总体中抽取足量样本 正常人是 指排除了影响所研究指标的疾病和有关因素的同质 人群。
2.根据指标的实际用途确定单侧或双侧界值：若 某种指标的过高或过低均属异常，需要确定正常值 范围的上限和下限（双侧），如某指标过高为异常， 则确定上限，在某指标过低为异常则确下限（单 侧）。
u2

e
2
－∞＜u ＜+∞
（8.13）

正态分布及其应用课件

正态分布及其应用课件
市成年男性的血红细胞计数在3.5×1012个/升以 下者，估计约占1.92％。
表3.1 100名12岁男童血红细胞计数的实际分布与理论分布的比较
血红细胞计数 (1012个/升) 实际分布
X us X 1.00s X 1.96s X 2.58s
人数
百分数(％)
理论分布(%)
4.13～5.31
正态分布的重要性
医学上某些指标服从或近似服从正态分布； 很多统计方法是建立在正态分布基础上的； 很多其他分布的极限为正态分布。
(a )
(b )
( c)
(d )
图3.1 直方图逐渐接近一条光滑曲线
正态分布图形
.4
f (x)
.3
.2
.1
0
x
正态分布的数学形式
f (X ) 1 e
( X ) 2 2 2

2
为总体均数，为总体标准差 π为圆周率，e为自然对数的底
X为变量，代表横轴的数值，f(X)为纵轴数值。
正态分布的表示
用N（μ，σ2）表示均数为μ ，标准差为σ的正态
分布，可写作：
X~ N（μ，σ2）
例如： X ～ N（120，8.22）
X ～ N（5，32）
正态分布曲线的三个特点 集中性 对称性 均匀变动性
S(-, )=0.5 -3)=0.1587 -2 -1 )=0.0013 )=0.0228
S(-, +1 +3 +2 )=1 )=0.8413 )=0.9987 )=0.9772
-3 -2 -

+ +2 +3
-4
-3
-2
-1
0
1

3.计量资料统计(2)正态分布

3.计量资料统计(2)正态分布

. 例3.2 已知某市120名男孩身高的均数 为 143.1cm ，标准差为 5.67cm ，试估计该 市12岁男孩身高的95%正常值范围。 将已知条件代入公式： X ª 1.96S 即 143.10 －1.96¬5.67 143.10 ＋1.96¬5.67 得 131.99~154.21cm 即该市12岁男孩身高的95%正常值范围 是131.99 ~ 154.21cm。
例 3.1 前例2.1中，某市1982年110名7 岁男童的身高，已知均数 =119.6cm，标 准差=4.72cm。 试（1）估计该地7岁男童身高在110cm 以下者占该地7岁男童总数的百分数。 （2）分别求 X 1S ， X 1.96S ， X 2.58S 范围内 7岁男童人数占该组儿童总数的实际百分 数（频率），并与理论频率比较。
这种资料在临床中很常见，称为正 态分布。用N（μ、σ2）表示。
正态分布 的特征
1、正态曲线在横轴上方，均数处最高。 2、正态分布以均数为中心，左右对称。 3、正态分布有两个参数： 均数μ是位置参数
标准差σ是变异度参数。
4、正态曲线下面积有一定的分布规律。
标准正态分布
当μ = 0，σ = 1时为标准正态分布， 为了应用方便可通过下列公式进行变 量变换，将原点在任何位置的正态分 布变换为标准正态分布，式中的 u 称 为标准正态变量或标准正态离差。 u = (X – μ) /σ
第三章 正态分布及其应用Leabharlann 第一节 正态分布的 概念和特征
正态分布的概念
正态分布(normal distribution)，又称高斯 分布，是医学和生物界最常见的分布。
该分布是以均数为中心，低于均数的频数与高于 均数的频数大致相等，越接近均数，频数越多，离 均数越远，频数逐渐减少，形成以均数为中心两侧 基本对称的钟型分布。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正态分布及其应用
一、正态分布的概念和特征
（一）、正态分布的概念和图形
频
数
f（x）
5岁女孩身高的直方图
身高x（cm）
频 数 f（x）
5岁女孩身高的直方图
身高X（cm）
频数
组段 a b
频 数 f（x）
5岁女孩身高的频数分布曲线
身高x（cm）
f(X)
m
X
正态分布以均数为中心，左右两侧对称， 靠近均数两侧的频数较多，而距均数两侧较远
（二）、正态分布的特征
正态分布曲线的密度函数：
( X m )2 1 f (X ) exp , X 2 2 2 ＝3.14159， exp 是以2.72818为底的自然对数指数 X ~ N ( m , 2 ), m为X的总体均数，为总体标准差 f ( X )称为概率密度函数（probabilit y density function ） 以f ( X )为纵坐标，X为横坐标，绘制的曲线就是 正态曲线（normal curve ）
处，频数逐渐减少，形成的钟形分布。
正态分布
正态分布是应用最 广泛的一种连续型分布. 德莫佛最早发现了二项概 率的一个近似公式，这一公式 被认为是正态分布的首次露面.
德莫佛
正态分布在十九世纪前叶由 高斯加以推广，所以通常称为高 斯分布.
高斯
正态分布（normal distribution）也 叫高斯分布（Gaussian distribution）， 是最常见、最重要的一种连续型分布。 因为医学卫生领域中，有许多变量为连 续的随机变量，并呈现正态分布。如，身高 、体重，血压。
例2.21 某地调查正常成年男子120人的第一秒肺 通气量，得均数＝ 4.2L, 标准差 s=0.7L ，试估 计该地成年男子第一秒肺通气量的 95%参考值 范围。 因肺第一秒通气量过低为异常，故按单侧 估计95%界值。 下限为：x – 1.64s=4.2-1.64 ×0.7 =3.05（L） 故该地成年男子第一秒肺通气量的95%参 考值范围为不低于3.05Lຫໍສະໝຸດ 分析三条正态曲线的共同特征：
①均数处最高 （一个最高点） ②左右对称（一个对称轴x=µ ）
观察以上三条正态曲线，归纳出正态曲线的性质
①曲线在 x轴的上方，与x轴不相交． 确定． 越大，曲线越“矮 当 m 一定时，曲线的形状由
越小，曲线越“瘦高”，表 胖”，表示总体的分布越分散； ②曲线关于直线 x m对称，且在 x m 时位于最高点. 示总 ③当时 x m ，曲线上升；当时 x m ，曲线下降．并且当 体的分布越集中．
曲线向左、右两边无限延伸时，以 x轴为渐近线，向它无限靠 µ 为正态曲线的位置参数 近．
0.6 0.5
曲线2 曲线1
0.4 0.3 0.2 0.1 0.0
0 1 2 3 4 5 6
曲线3
三条不同μ和σ的正态分布曲线
当σ相同时,正态分布曲线的位置由μ来决定.
σ为正态曲线的形态参数
③正态分布有两个参数，一个正态分布 可以表示为N(µ,σ2)
解：第一步，将该分布进行标准正态变换，以样本均数和 标准差代替总体均数和标准差，进行U变换。
U1=(104.0-110.15)/5.86 =-1.05 , U2=(108.0-110.15)/5.86 =-0.37
第二步，查附表1得： Ф (u1)=0.1469 ,Ф (u2)=0.3557
D=0.3557-0.1469=0.2088
步骤： 1. 2. 3. 4. 5. 6.
异常
从“正常人”总体中抽样：明确研究总体 统一测定方法以控制系统误差。 判断是否需要分组（如性别、年龄）确定。 根据专业知识决定单侧还是双侧。 确定绝大多数的比例;最常用95% 选择适合的计算方法
正常
正常
异常
正常 异常
异常
单侧下限
单侧上限
双侧下限
双侧上限
1．正态分布法估计参考值范围公式为：
例题2.18：已知u1=-1.2，u2=1.6，
求标准正态曲线下（-1.2，1.6）范围内的面 积。
请同学们不看书，自己试做一下。 题目有什么不同，如何解决？
例题2.19：已知120名5岁女孩身高X=110.15， S=5.86，现欲估计该市城区某年身高界于 104.0~108.0cm范围内的5岁女孩所占比例和人 数。
f=120×0.2088=25(人)
三、正态分布的应用
正态分布是一种重要的分布，它是许多统计处理 方法的基础。对于服从正态分布或近似正态分布或对 数正态分布的资料，都可以借助于正态分布的规律来 解决问题。其在医药卫生领域的应用有以下方面：
（一）估计频数分布
（二）制定医学参考值范围 （三）质量控制 （四）作为许多统计方法的基础
（一）估计频数分布
例题2.20 某项研究显示，某地婴儿出生体重均数 为3100g，标准差为300g，试估计该地当年出生低体 重儿（≤2500g）所占比例。 解：已知婴儿出生体重服从正态分布。记做变 量X， 则当X ≤2500时，其对应于标准正态分布的u
值为：
u
X m

2500 3100 2.00 300
例题2.17：已知u1=-1.76，u2=-0.25，
求标准正态曲线下（-1.76，-0.25）范围内 的面积。 解：查附表1，得； Φ(u1)=0.0392,同理，Φ(u2)=0.4013, 则(-1.76,-0.25)范围内的面积为 D= Φ(u2)-Φ(u1)=0.4013-0.0392=0.3621
2. 百分位数法 用于描述偏态分布资料 。
确定尿铅的95%参考值范围，因为尿铅以 过高为异常，应计算P95 白细胞数的95％参考值范围，因为白细胞数 无论过高或过低均属异常，则分别计算P2.5 和P97.5。这是双侧95％参考值范围；
一般正态分布为一个分布族:N(m,2) ；标准 正态分布只有一个 N(0,1) ；这样简化了便
于应用 。
曲线下面积
0.5
f(X)
0.4
-∞
u 0.3
0.2 0.1 0.0
(u )
2
4
1
u

e
u 2
2
du
-4
-3
-2
-1
0 X
1
2
3
附表1（P261） 就是根据此公式 和图形制定的
2 ( 2 )
1 X F(X ) e 2
( X m ) 2
dX
正态曲线下面积
标准正态曲线下面积分布规律
正态曲线下面积分布规律
正态分布 μ±σ μ±1.96σ μ±2.58σ
面积或概率 68.27% 95.00% 99.00%
标准正态分布的意义
标准正态曲线下面积分布有规律，统计 学家将曲线下所有的U值对应的的面积全部计 算出来，并做成一个表，叫“标准正态分布 表”，供查用。见P261附表1。 借助于“标准正态分布表”，任何正态 分布都可以进行正态变换，计算出曲线任意 两个变量值之间的面积。
查表得：Φ (-2.00)=0.0228=2.28%,即该地当 年低体重出生儿的比例为2.28%
（二）制订医学参考值范围
定义：指包括绝大多数正常人的人体形态、功能 和代谢等各种生理生化指标的波动范围，也可以 看作是常数，又称“正常值”
制订方法有两种： 1、正态分布法：适合正态或近似正 态分布的资料 2、百分位数法：适合偏态分布资料
X us
如制定95％参考值范围，双侧界值 u=1.96，单侧界值u=1.645。 双侧界值：x1.96s 单侧上界：x+1.645s 单侧下界：x-1.645s
[ 例 2.21] 某地调查正常成年男子 200 人的红细胞 数近似正态分布，得均数＝ 5.526 （ 10 12 /L ） , 标准差s=0.38（1012/L），试估计该地成年男 子红细胞数的95%参考值范围。 因红细胞数过多或过少均为异常，故按双 侧估计95%界值。 下限为：x - 1.96s=5.526-1.96 ×0.38 =5.452 (1012/L) 上限为：x + 1.96s=5.526+1.96×0.38 =5.600(1012/L) 故该地成年男子红细胞数的95%参考值范围 （5.452—5.600）1012/L
④正态曲线下面的面积分布有一定规律
二、标准正态分布
经标准正态变量u变换：一般正态分布 N ( m , )被变为 X m 标准正态分布 N (0,1); 即令u
2

u2 1 f (u ) exp , 2 2 X
f(X)
a
m
X
σ
标准正态分布 (standard normal distribution) 的两个参数为：μ=0,σ=1 记为 N(0,1)