二次根式全章复习

二次根式小结与复习【主要内容】本单元是在学习了平方根和算术平方根的意义的基础上，引入一个符号“”．主要内容有：（1）二次根式的有关概念，如：二次根式定义、最简二次根式、•同类二次根式等；（2）二次根式的性质；（3）二次根式的运算，如：二次根式的乘除法、二次根式的加减法等．【要点归纳】1. 二次根式的定义：形如的式子叫二次根式，其中叫被开方数，只有当是一个非负数时，才有意义．2. 二次根式的性质：①②③④3. 二次根式的运算二次根式的运算主要是研究二次根式的乘除和加减．（1）二次根式的加减：需要先把二次根式化简，然后把被开方数相同的二次根式（即同类二次根式）的系数相加减，被开方数不变。

注意：对于二次根式的加减，关键是合并同类二次根式，通常是先化成最简二次根式，再把同类二次根式合并．但在化简二次根式时，二次根式的被开方数应不含分母，不含能开得尽的因数．（2）二次根式的乘法：（3）二次根式的除法：注意：乘、除法的运算法则要灵活运用，在实际运算中经常从等式的右边变形至等式的左边，同时还要考虑字母的取值范围，最后把运算结果化成最简二次根式．（4）二次根式的混合运算：先乘方（或开方），再乘除，最后加减，有括号的先算括号里面的；能利用运算律或乘法公式进行运算的，可适当改变运算顺序进行简便运算．注意：进行根式运算时，要正确运用运算法则和乘法公式，分析题目特点，掌握方法与技巧，以便使运算过程简便．二次根式运算结果应尽可能化简．另外，根式的分数必须写成假分数或真分数，不能写成带分数．例如不能写成．【难点指导】1、如果是二次根式，则一定有；当时，必有；2、当时，表示的算术平方根，因此有；反过来，也可以将一个非负数写成的形式；3、表示的算术平方根，因此有，可以是任意实数；4、区别和的不同：中的可以取任意实数，中的只能是一个非负数，否则无意义．5、简化二次根式的被开方数，主要有两个途径：（1）因式的内移：因式内移时，若，则将负号留在根号外．即：．（2）因式外移时，若被开数中字母取值范围未指明时，则要进行讨论．即：6、二次根式的比较：（1）若，则有；（2）若，则有．说明：一般情况下，可将根号外的因式都移到根号里面去以后再比较大小．二次根式强化训练与复习巩固自测试题1．化简：______；_________．2．当______时，．3．等式成立的条件是______．4．当，化简_______．5．比较与的大小：_______．6．分母有理化：（1）__________；（2）__________；（3）__________．7．已知，，，那么________．8．计算_________．9．如果，那么的值为___________．10．若有意义，则的取值范围是___________．1．下式中不是二次根式的为（）A．；B．；C．；D．2．计算得（）3．若，则化简等于（）4．化简的结果是（）5．计算的结果是（）6．化简的结果是（）7．把式子中根号外的移到根号内，得（）A．B．C．D．8．等式成立的条件是（）9．的值为（）10．若代数式有意义，则的取值范围是（）（1）（2）（3）（4）（5）（6）（7）（8）（9）（10）求值题：1．已知：，求的值．2．已知，求的值。

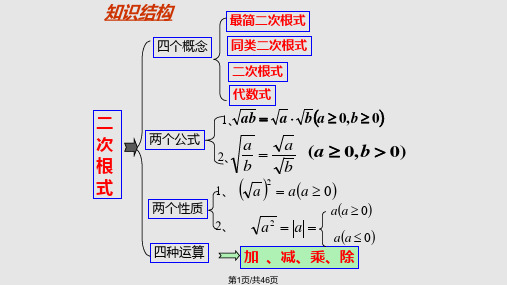
二次根式全章复习巩固知识点一：二次根式的相关概念和性质 1. 二次根式形如(0)a a ≥的式子叫做二次根式，如13,,0.02,02等式子，都叫做二次根式. 2.二次根式的性质 （1）； （2）；（3）.要点诠释：（1） 一个非负数a 可以写成它的算术平方根的平方的形式，即a 2)a =（0a ≥），如2221122););)33x x ===（0x ≥）.（2）2a a 的取值范围可以是任意实数，即不论a 2a . （32a a ，再根据绝对值的意义来进行化简.（42a 2)a 的异同2a a 可以取任何实数，而2a 中的a 必须取非负数；2a a ，2)a =a （0a ≥）.相同点：被开方数都是非负数，当a 2.3. 最简二次根式（1）被开方数是整数或整式；（2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式，叫做最简二次根式.. 要点诠释：最简二次根式有两个要求：（1）被开方数不含分母；（2）被开方数中每个因式的指数都小于根指数2. 4.同类二次根式几个二次根式化成最简二次根式后，被开方数相同，这几个二次根式就叫同类二次根式.要点诠释：判断是否是同类二次根式，一定要化简到最简二次根式后，看被开方数是否相同，再判断.. 知识点二：二次根式的运算 1. 乘除法（1）乘除法法则：类型法则逆用法则二次根式的乘法0,0)a b =≥≥积的算术平方根化简公式：0,0)a b =≥≥二次根式的除法0,0)a b≥>商的算术平方根化简公式：0,0)a b =≥>2.加减法将二次根式化为最简二次根式后，将同类二次根式的系数相加减，被开方数和根指数不变，即合并同类二次根式. 要点诠释：二次根式相加减时，要先将各个二次根式化成最简二次根式，再找出同类二次根式，最后合并同类二次根式.(13=+-=【例题训练】类型一、二次根式的概念与性质1． 当________在实数范围内有意义.2x =-成立的条件是 .=成立的条件是 .2．当0≤x <11x -的结果是__________.【变式】已知﹣=2，则+的值为_____________．3.下列二次根式中属于最简二次根式的是（ ）. A. 14 B. 48 C. abD. 44a + 类型二、二次根式的运算 4．下列计算正确的是（ ） A ．﹣= B ．3×2=6C ．（2）2=16D ．=1【变式】计算：48(54453)8335.化简20102011(32)(32)⋅.6.已知2231,12x x x x=-+求.【变式】已知a b +=-3, ab =1,求ab b a +的值.。

清单05二次根式全章复习（3个考点梳理+10种题型+10类型）考点一二次根式的相关概念二次根式的概念：一般地，我们把形如（≥0）的式子叫做二次根式，“”称为二次根号，二次根号下的数叫做被开方数．二次根式有意义的条件：当a≧0时，即被开方数大于或等于0，二次根式有意义.最简二次根式：开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．最简二次根式必须同时满足以下两个条件：①开方数所含因数是整数，因式是整式（分母中不应含有根号）；②不含能开得尽方的因数或因式的二次根式，即被开方数的因数或因式的指数都为1.同类二次根式的概念：二次根式化成最简二次根式后，若被开方数相同，则这几个二次根式就是同类二次根式.【考试题型1】二次根式有意义的条件1．（20-21九年级上·吉林长春·在实数范围内有意义的条件是．x的值．2．（2023·浙江杭州·1．（22-23七年级下·广东汕头·m的最小值是（）A．2B．3C．8D．11∴12m -是完全平方数，当120m -=时，即12m =，当121m -=时，即11m =，当124m -=时，即8m =，当129m -=时，即3m =，综上所述，自然数m 的值可以是3、8、11、12，所以m 的最小值是3，故答案选：B ．【点睛】本题考查了二次根式的化简及自然数的定义，掌握二次根式的化简法则及自然数是指大于等于0的整数是解答本题的关键．2．（22-23八年级下·福建莆田·开学考试）若实数a ，b 4b +，则a b -=．3．（20-21七年级下·广东广州·期中）若()230a -+=，则a b -的立方根是．【点睛】本题考查平方、二次根式的非负性以及求立方根，得到30a -=，50b +=是解题的关键．4．（20-21八年级上·四川达州·期中）已知a ，b 0b =（1）a=_______，b=______（2）把a ，b 的值代下以下方程并求解关于x 的方程()221a xb a ++=-1．（23-24八年级上·上海青浦·）ABC D2．（23-24八年级上·山东滨州·期末）下列各式化成最简二次根式正确的是（）A=B =C =D 10=（）A ．2个B ．3个C ．4个D ．5个4．（22-23八年级下·海南省直辖县级单位·是同类二次根式，则=a ．【答案】5-【分析】本题考查了同类二次根式的定义，熟练掌握同类二次根式的定义是解答本题的关键，化成最简二1．（23-24九年级上·四川宜宾·a 的值可能是（）A ．16B ．0C ．2D ．任意实数2．（22-23九年级上·四川遂宁·是同类二次根式，则m 的值为（）A ．4m =B ．3m =C ．5m =D ．6m =3．（22-23八年级下·山东泰安·是最简二次根式，则m，n的值为（）A．0，1-B．1-，0C．1，1-D．0，04．（21-22八年级下·江西赣州·期中）若考点二二次根式的性质与化简二次根式的化简方法：1）利用二次根式的基本性质进行化简；2）利用积的算术平方根的性质和商的算术平方根的性质进行化简．a =•（≥0，≥0）（≥0，＞0）化简二次根式的步骤：1）把被开方数分解因式；2）利用积的算术平方根的性质，把各因式（或因数）积的算术平方根化为每个因式（或因数）的算术平方根的积；3）化简后的二次根式中的被开方数中每一个因数（或因式）的指数都小于根指数2．【考试题型5】利用二次根式的性质化简【类型一】数形结合法1．（22-23八年级下·四川绵阳·阶段练习）已知实数a ，b ，c 在数轴上的位置如图所示，化简2a b b c --+．【答案】a-【分析】本题考查了数轴的定义、二次根式的运算、绝对值运算．观察数轴可得0c b a <<<，从而得到0,0,0a b c a b c ->-<+<，再根据二次根式的运算、绝对值运算计算即可．【详解】解：观察数轴得：0c b a <<<，2．（23-24八年级上·重庆万州·阶段练习）已知实数x 、y 、z 在数轴上的对应点如图所示：(1)若5x =-，y =x 对应的点与z 对应的点恰好关于y 对应的点对称，求z 的值．(2)2+3．（23-24八年级上·湖北襄阳·开学考试）已知实数x ，y ，z 在数轴上的对应点如图所示，试化简：．【类型二】估值法方法简介：先运用二次根式的运算法则化简，再将最后的化简结果化成根式再确定取值范围.1．（2023·重庆·(最接近的整数是（）A ．7B ．8C ．9D ．10A ．5m <-B ．54m -<<-C ．43m -<<-D ．3m >-3．（23-24九年级上·四川宜宾·阶段练习）若a ，则a 的值所在的范围为（）A ．2a ≥B ．2a >C ．12a <<D ．01a <<【类型三】公式法方法简介：根据题目已知条件，通过变形、凑元等方法，凑成可用乘法公式，快速求解.1．（23-24九年级上·河南周口·阶段练习）已知2M=，2N，则M与N的关系为（）A．相等B．绝对值相等C．互为相反数D．互为倒数2．（23-24八年级上·云南文山·阶段练习）计算题：；(2)【类型四】换元法方法简介：根据已知条件，利用未知变量替换有规律表达式，寻找规律，快速求解.1．（19-20八年级上·福建泉州·期中）若ab＝1，我们称a与b1与1互为倒数：方法一：∵)22111211+-=-=-=1+1互为倒数．()2211111211⋅--====--111互为倒数．(1)互为倒数；(2)若()21x x -=，求21x x ⎛⎫- ⎪⎝⎭的值；(3)利用“换元法”求((101022⨯的值．＝1．【点睛】本题考查了二次根式的混合运算，在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质是，选择合适的解题途径，往往能事半功倍．【类型五】拆项法【类型六】整体代入法方法简介：由已知条件，通过加减乘除运算，得到与求解表达式相关的表达数值，整体代入.1．（23-24八年级下·云南昭通·期中）已知x =2(8x x -+的值．2．（23-24八年级下·海南省直辖县级单位·期中）已知33a b ==-求下列各式的值：(1)a b +和ab ；(2)22a ab b ++．22(1)223x xy y ++(2)x y y x +【类型七】因式分解法【类型八】配方法1．（23-24八年级下·北京·期中）阅读材料：材料一：数学上有一种根号内又带根号的数，它们能通过完全平方式及二次根式的性质化去一层（或多层）1===-．材料二：配方法是初中数学思想方法中的一种重要的解题方法，配方法的最终目的就是配成完全平方式，利用完全平方式来解决问题，它的应用非常广泛，在解方程、化简根式、因式分解等方面都经常用到．如：(2222311x x x++=+++=+，(20x+≥，(211x∴+≥，即231x++≥．23x∴++的最小值为1．阅读上述材料解决下面问题：_______=______；(2)求211x++的最值；(3)2-2．阅读材料：材料一:数学上有一种根号内又带根号的数，它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,1材料二：配方法是初中数学思想方法中的一种重要的解题方法，配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题，它的应用非常广泛，在解方程、化简根式、因式分解等方面都经常用到．如：2222321(x 1x x x ++=+++=+∵2(0x ≥，∴2(11x ++≥，即231x ++≥∴23x ++的最小值为1阅读上述材料解决下面问题：（1=，=；（2）求211x ++的最值；（3）已知x =221(41)54x y xy -++-的最值．【类型九】辅元法【类型十】先判断后化解解题的关键．【考试题型6】分母有理化1．（新疆维吾尔自治区克孜勒苏柯尔克孜自治州2023-2024学年八年级下学期4月期中考试数学试题）在进样的式子，这样的式子我们可以将其进一步化简：行二次根式化简时，我们有时会碰上如1==；====．以上这种化简的方法叫做分母有理化，通过观察请利用分母有理化解答下列问题：(1)利用你观察到的规律，化简L(2)2．（23-24八年级下·山东济宁·期中）【阅读材料】（材料一）细心观察图形，认真分析各式，总结其中蕴含的规律．22212OA =+=，112S =（1S 是12RtA A O △的面积）；22313OA =+=，22S =（2S 是23Rt A A O △的面积）；22414OA =+=，32S =（3S 是34Rt A A O △的面积）；．==【问题解决】利用你总结的规律，解答下面的问题：(1)填空：100S =_________，11OA =_________；(2)求11111S S S S S S S S S S +++++++++的值．3．（23-24七年级下·上海嘉定·期中）阅读下列解题过程：1⨯-()()221⨯===-请回答下列问题：(1)=______()2n≥．(2)利用上面所提供的解法，请化简：+(3)模仿上面所提供的解法，试一试化简：+考点三二次根式的运算乘法法则:两个二次根式相乘，把被开方数相乘，根指数不变.即：a =•（≥0，≥0）.除法法则：=加减法法则：先把各个二次根式化为最简二次根式后，再将被开方数相同的二次根式合并.【口诀】一化、二找、三合并.分母有理化：通过分子和分母同乘以分母的有理化因式，将分母中的根号去掉的过程.【分母有理化方法】==2）分母为多项式时，分母的有理化因式是与分母相乘构成平方差的另一部分.==混合运算顺序：先乘方、再乘除，最后加减，有括号的先算括号里的(或先去掉括号)．【考试题型7】二次根式的乘除运算1．（2024·陕西西安·三模）计算：)()02252π---2．（23-24八年级下·安徽铜陵·00)b ⎛÷⨯>> ，3．（23-24八年级下·全国·课后作业）计算：(1)÷；()0,0x y ⎫÷>>⎪⎪⎭．1．（23-24八年级下·吉林松原·期中）计算：((-．2．（23-24八年级下·广东阳江·期中）已知b=-，求22a=+，11a b+的值．3．（23-24八年级下·北京海淀·这个数叫做黄金分割数，著名数学家华罗庚优选法中就应用了黄金分割数．设a=b=(1)直接写出a b+和ab的值：a b+=______，ab=______；(2)求1111sa b=+的值．2．（23-24九年级下·山东烟台·期中）计算：(2)3．（23-24八年级下·辽宁营口·期中）（1）先化简，再求值：111a a -⎛⎫-÷⎪--⎝⎭，其中，2a =．1．（23-24八年级下·浙江金华·的计算，将分母转化为有理数，这就是“分母有理化()22==；()()2232++====+--．类似地，将分子转化为有理数，就称为“分子有理化21===()222111+-==．根据上述知识，请你解答下列问题：(1)(2)的大小，并说明理由．2．（23-24八年级下·福建福州·期中）如图，正方形A，B的面积分别为25cm和27cm，现将正方形A的边长分别增加2cm和3cm得到矩形甲；将正方形B的边长都增加2cm得到一个新的正方形乙，请通过计算比较甲、乙两个图形的面积的大小．【答案】矩形甲的面积小于矩形乙的面积．【分析】此题考查了二次根式混合运算的应用，根据题意表示出矩形甲和乙的面积，然后相减得到3．（23-24八年级下·江苏扬州·阶段练习）观察下列等式：1==-；==；==；……像)221-=()0a a =≥，)()1110b b -=-≥，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式．11，与-答下列问题：(1)化简：(2)=___________（n为正整数）．(3)计算：)1+ =___________；(4)已知a==b试比较a、b的大小，则a___________b．（填“<”“>”或“=”）1．（23-24八年级下·甘肃庆阳·期中）高空抛物极其危险，是我们必须杜绝的行为．据研究，高空抛出的物体下落的时间t（单位：s）和高度h（单位：m）近似满足t=（不考虑风速的影响）．(1)从30m高处抛下的物体落地所需的时间1t=s；从60m高处抛下的物体落地所需的时间2t=s(2)2t是1t的多少倍？(3)若从高空抛下的物体经过4s落地，则该物体下落的高度是多少？2．（23-24八年级下·江西宜春·阶段练习）有一块长方形木板，木工师傅采用如图所示的方式，在木板上截出面积分别为218dm 和232dm 的两块正方形木板．(1)截出的两块正方形木板的边长分别为______dm ，______dm ；(2)求剩余木板的面积；(3)如果木工师傅想从剩余的木板中截出长为1.5dm 、宽为1.2dm 的长方形木条，最多能截出______个这样的木条． 1.414≈）3．（23-24八年级下·广东东莞·期中）小乐是一个善于思考的学生，学习完“二次根式”和“勾股定理”后，他发现可以有多种方法求三角形的面积，以下是他的数学笔记，请认真阅读并完成任务，的面积；(1)请根据思路1的公式，求ABC(2)请你结合思路2，在如图所示的网格中（正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点），完成下列任务，，要求三个顶点都在格点上；①画出ABC面积的计算过程．②结合图形，写出ABC②过点A 作AD CB ⊥∴4．（23-24八年级下·广西南宁·期中）安全问题，时刻警醒．高空坠物严重威胁着人们的“头顶安全”，即便是常见小物件，一旦高空落下，也威力惊人，而且用时很短，常常避让不及．经过查阅相关资料，小南同学得到高空坠物下落的时间t （单位：s ）和高度h （单位：m ）近似满足公式t 10N /kg g ≈）(1)求从45m 高空抛物到落地的时间；(2)已知高空拋物动能（单位：J ）10=（单位：N /kg ）⨯物体质量（单位:kg ）⨯高度（单位：m ），某质量为0.2kg 的玩具在高空被抛出后经过4s 后落在地上，根据以上信息，小南判断这个玩具产生的动能会伤害到楼下的行人，请通过计算说明小南的判断是否正确．（注：伤害无防护人体只需要65J 的动能）5．（23-24八年级下·安徽铜陵·期中）铜陵市各小区都有“禁止高空抛物”的宣传标语，高空抛物极其危险，是我们必须杜绝的行为．据研究，从高度为h（单位：m）的高空抛出的物体下落的时间t（单位：s）和高度h（单位：m）近似满足公式t=（不考虑风速的影响）．(1)从50m高空抛出的物体从抛出到落地所需时间1t，从100m高空抛出的物体从抛出到落地所需时间2t，那么2t是1t的多少倍？(2)从足够高的高空抛出物体，经过1.5s，所抛物体下落的高度是多少？6．（23-24八年级下·湖北孝感·期中）学习完《二次根式》后，聪聪发现了下面这类有趣味的试题，请你根据他的探索过程，解答下列问题：(1)具体运算，发现规律：131711122236=+==+=⨯⨯11313412=+=⨯，…计算：=(2)观察归纳，写出结论=（1n ≥且n 为正整数）(3)灵活运用，提升能力请利用你所发现的规律，。

二次根式复习【知识回忆】1. 二次根式： 式子 a 〔 a ≥ 0〕叫做二次根式。

2. 最简二次根式： 必定同时满足以下条件：⑴被开方数中 不含开方开的尽的因数或因式 ； ⑵被开方数中 不含分母 ； ⑶分母中 不含根式 。

3. 同类二次根式：二次根式化成最简二次根式后，假设被开方数相同，那么这几个二次根式就是同类二次根式。

4. 二次根式的性质：〔1〕〔2〔 a ≥ 0〕；〔2〕a 〕 = a 2aa 5. 二次根式的运算： ⑴二次根式的加减运算：先把二次根式化成最简二次根式，尔后合并同类二次根式即可。

⑵二次根式的乘除运算：a 〔 a ＞0〕0 〔 a =0〕；a 〔 a ＜ 0〕① ab =a ?b 〔 a ≥ 0,b ≥ 0〕；②aaba 0,b 0b【例题讲解】例 1 计算：〔1〕 (3)2 ；〔2〕 (2 ) 2 ； 〔3〕 ( a b )2〔a+b ≥ 0〕3解析：依照二次根式的性质可直接获取结论。

例 2 计算：⑴6·15⑵ 1 ·24⑶ a 3 · ab 〔 a ≥ 0，b ≥ 0〕2解析：本例先利用二次根式的乘法法那么计算， 再利用积的算术平方根的意义进行化简得出计算结果。

例 3计算：〔1〕32+23－22+3〔 2〕12 +18 － 8 －32〔 3〕40 －1 +10510【基础训练】1．化简：〔 1〕72____ ；〔2〕252242___ __；〔3〕612 18 ____；〔4〕75x3 y2 (x0, y0) ____；〔5〕204_______ 。

2.(08 ，安徽 ) 化简42=_________。

3. 〔 08，武汉〕计算 4 的结果是Ａ .2Ｂ．± 2Ｃ． -2Ｄ． 44. 化简：〔1〕〔 08，泰安〕9 的结果是；〔 2〕〔 08，南京〕12 3 的结果是；〔3〕(08 ，宁夏 ) 528 =；〔 4〕〔 08，黄冈〕 5 x -2x =_____ _；5．〔 08，重庆〕计算82的结果是A、 6B、 6C、 2D、 26．〔 08，广州〕 3 的倒数是。

⼆次根式总复习总复习（⼀）⼆次根式知识点：1.⼆次根式的有关概念：（1）形如的式⼦叫做⼆次根式. （即⼀个的算术平⽅根叫做⼆次根式⼆次根式有意义的条件:被开⽅数⼤于或等于零（2）代数式：⽤基本的运算符号（包括加、减、乘、除、乘⽅、平⽅）把数或表⽰数的字母连接起来的式⼦叫做代数式。

（3）最间⼆次根式：满⾜下列两个条件的⼆次根式，叫做最简⼆次根式：①被开⽅数不含分母；②被开⽅数中不含能开得尽⽅的因数或因式；(4）同类⼆次根式：⼏个⼆次根式化成最简⼆次根式后，如果被开⽅数相同，那么这⼏个⼆次根式叫做同类⼆次根式。

2.⼆次根式的性质：（1）双重⾮负性3.⼆次根式的运算：⼆次根式乘法法则⼆次根式除法法则⼆次根式的加减： (⼀化，⼆找，三合并 )（1）将每个⼆次根式化为最简⼆次根式；（2）找出其中的同类⼆次根式；（3）合并同类⼆次根式。

0()a a ≥ ≥0 2(2))(0)a a (= ≥ a =2(3) (4)(0,0)ab a b = ≥ ≥(5)(00)a a b b = ≥> (0,0)a b a b ?= ≥≥ (0,0)a a b b= ≥>Ps:类似于合并同类项，关键是把同类⼆次根式合并。

⼆次根式的混合运算：原来学习的运算律（结合律、交换律、分配律）仍然适⽤填空题：1、n 24是整数，则正整数n 的最⼩值是（）A.4B.5C.6D.72、下列各式中，不是⼆次根式的是（） A.45 B.π-3 C.22+a D.213、若使⼆次根式 21+-x x 在实数范围内有意义，则x 的取值范围是（）A ．x ≥-2B ．x ＞-2C ．x>-2 且x ≠1D ．x ≤-24、(1)若 2)(11y x x x +=---，则x-y 的值为（）A ．-1B ．1C ．2D ．3(2)若实数a 、b 满⾜11122+-+-=a a a b ，则a+b 的值是（） 5、（1）已知a 为实数，那么 2a -等于（）A ．aB ．-aC ．-1D ．0（2）若 a a -=-1)1(2，则a 的取值范围是（）A ．a ＞1B ．a ≥1C ．a ＜1D ．a ≤1(3)若)3(692a a a --=+-，则a 的取值范围是（）A.a>3B.a<3C.a ≥3D.a ≤3（4）如果代数式ab 1+a 有意义，则直⾓坐标系中点A （a ，b ）的位置（）A ．第⼀象限B ．第⼆象限C ．第三象限D ．第四象限6、（1）已知a ＜0，那么| 2a -2a|可化简为（）A ．-a B.a C.-3a D.3a（2）如果表⽰a ，b 两个实数的点在数轴上的位置如图所⽰，那么化简|a-b|+ 2)(b a +的结果等于（） A.-2b B.2b C.-2a D.2a7、下列根式中3,8,,2,543a x b a a ，最简⼆次根式的个数是（）A.4B.3C.2D.18、下列各式中正确的是（）A ．2-2=-4B ．（33）2=35 C. 1)12)(12(=-+ D ．x 8÷x 4=x 29、（1）若)6(6-=-?x x x x ，则（）A ．x ≥6B ．x ≥0C ．0≤x ≤6D ．x 为⼀切实数（2）1a 3-a 13-=--a a 成⽴的条件是（） A.a ≠1 B.a ≥3且a ≠1 C.a ＞1 D.a ≥3 10、已知实数a 满⾜|2008-a|+=a ，那么a-20082的值是（）A.2009B.2008C.2007D.200911、化简20092009)23()23(+-的结果是（） A.-1 B.23- C.23+ D.23--12、(1)把)2(12---的根号外的（-2）移到根号内的结果是（）(2)把b b 1-的根号外的因式移到根号内的结果是（）A.b -B.b --C.bD.b -13、（1）下列各组⼆次根式中，属于同类⼆次根式的为（）A ．和B ．和C ．和D ．和（2）（填空）如果最简⼆次根式83-a 和a 217-同类⼆次根式，则a=（）（3）如果最简根式63-a 与4+a 是同类⼆次根式，那么使x a 24-有意义的x 的取值范围是（）A ．x ≤10B ．x ≥10C ．x ＜10D ．x ＞1014、下列计算正确的是（） A.228=- B. 14931227=-=- C.()()15252=+- D.23226=- 简答题：1、（1）先化简，在求值：21244422--++++--x x x x x x x 其中x=2-2（2）（x-1-）÷，其中x=3-2、(1)若1＜x ＜4，则|x ?5|+2)1(-x 的值为？(2)若3，ｍ，5为三⾓形三边，化简：-3、已知：实数a ，b 在数轴上的位置如图所⽰，化简：4、计算题：12323-24-27314)3218)(1223(33)154276485(2)3352()3352(122?+-÷+--+）、、、、 5、 )3()23(235a b b a b a b ÷-?（其中a>0 ,b>0）5、找规律：;23231;12)12)(12(12121-=+-=-+-=+...,34341-=+=+=+9910019101)1(（2）从计算结果找出规律：（3）利⽤此规律计算：()12006200520061...341231121+??? ??++++++++的值。