直线与圆的方程(必修2)_学业水平复习
- 格式:ppt
- 大小:626.50 KB
- 文档页数:18

直线与圆的方程的应用【学习目标】1.能利用直线与圆的方程解决有关的几何问题; 2.能利用直线与圆的方程解决有关的实际问题;3.进一步体会、感悟坐标法在解决有关问题时的作用. 【要点梳理】要点一、用直线与圆的方程解决实际问题的步骤 1.从实际问题中提炼几何图形;2.建立直角坐标系,用坐标和方程表示问题中的几何元素,将平面问题转化为代数问题; 3.通过代数运算,解决代数问题; 4.将结果“翻译”成几何结论并作答.要点二、用坐标方法解决几何问题的“三步曲”用坐标法解决几何问题时,先用坐标和方程表示相应的几何元素:点、直线、圆;然后对坐标和方程进行代数运算;最后再把代数运算结果“翻译”成相应的几何结论.这就是用坐标法解决平面几何问题的“三步曲”.第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中涉及的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论. 要点诠释:坐标法的实质就是借助于点的坐标,运用解析工具(即有关公式)将平面图形的若干性质翻译成若干数量关系.在这里,代数是工具、是方法,这是笛卡儿解析几何的精髓所在.要点三、用坐标法解决几何问题时应注意以下几点1.建立直角坐标系时不能随便,应在利于解题的原则下建立适当的直角坐标系; 2.在实际问题中,有些量具有一定的条件,转化成代数问题时要注意范围; 3.最后要把代数结果转化成几何结论. 【典型例题】类型一:直线与圆的方程的实际应用例1. 如图是某圆拱桥的一孔圆拱的示意图.该圆拱跨度AB=20m ,拱高OP=4m ,在建造时每隔4m 需要用一个支柱支撑,求支柱22A P 的长度(精确到0.01m ).【答案】3.86m【解析】建立坐标系如图所示.圆心的坐标是(0,b),圆的半径是r,那么圆的方程是:222+-=()x y b r因为P(0,4)、B(10,0)都在圆上,所以22222204100()()b r b r⎧+-=⎨+-=⎩ 解得105=-.b ,22145=.r.所以圆的方程为222105145++=(.).x y把22-(,)P y 代入圆的方程得2222105145-++=()(.).y ,所以386≈.y ,即支柱的高度约为3.86m.举一反三:【变式1】某市气象台测得今年第三号台风中心在其正东300 km 处,以40 km/h 的速度向西偏北30°方向移动.据测定,距台风中心250 km 的圆形区域内部都将受到台风影响,请你推算该市受台风影响的起始时间与持续时间.(精确到分钟) 【答案】90 10 h. 【解析】利用坐标法来求解.如图,不妨先建立直角坐标系xOy ,其中圆A 的半径为250 km ,过B(300,0)作倾斜角为150°的直线交圆于点C 、D ,则该市受台风影响的起始与终结时间分别为C 开始至D 结束,然后利用圆的有关知识进行求解.以该市所在位置A 为原点,正东方向为x 轴的正方向建立直角坐标系,开始时台风中心在B(300,0)处,台风中心沿倾斜角为150°方向的直线移动,其轨迹方程为y=33-(x-300)(x ≤300). 该市受台风影响时,台风中心在圆x 2+y 2=2502内,设射线与圆交于C 、D ,则CA=AD=250,∴台风中心到达C 点时,开始影响该市,中心移至D 点时,影响结束,作AH ⊥CD 于H ,则 AH=AB ·sin30°=150,HB=3150,CH=HD=22AH AC -=200,∴BC=3150-200,则该市受台风影响的起始时间t 1=402003150-≈1.5(h),即约90分钟后台风影响该市,台风影响的持续时间t 2=40200200+=10(h),即台风对该市的影响持续时间为10 h.【总结升华】应用问题首先要搞清题意,最好是画图分析,运用坐标法求解,首先要建立适当的坐标系,设出点的坐标.还要搞清里面叙述的术语的含义.构造圆的方程进行解题(如求函数的最值问题)时,必须充分联想其几何意义,也就是由数思形.如方程y=1+21x -表示以(0,1)为圆心,1为半径的上半圆,xy表示原点与曲线f(x ,y)=0上动点连线的斜率. 类型二:直线与圆的方程在平面几何中的应用例2.如图,在圆O 上任取C 点为圆心,作一圆与圆O 的直径AB 相切于D ,圆C 与圆D 交于E 、F ,求证:EF 平分CD .证明:令圆O 方程为x 2+y 2=1. ①EF 与CD 相交于H ,令C (x 1,y 1),则可得圆C 的方程 (x -x 1)+(y -y 1)2=y 12,即x 2+y 2-2x 1x -2y 1y+x 12=0. ② ①-②得2x 1x+2y 1y -1-x 12=0. ③③式就是直线EF 的方程,设CD 的中点为H ',其坐标为11,2y x ⎛⎫ ⎪⎝⎭, 将H '代入③式,得222222211111111122121102y x y x x y x x y +⋅--=+--=+-=. 即H '在EF 上,∴EF 平分CD .【总结升华】 利用直线与方程解决平面几何问题时,要充分利用圆的方程、直线和圆的位置关系、圆与圆的位置关系等有关知识,正确使用坐标方法,使实际问题转化为代数问题,然后通过代数运算解决代数问题,最后解释代数运算结果的实际含义.举一反三:【变式1】平面内动点P 满足到定点,A B 的距离之比为2=||||PA PB ,请问动点P 的轨迹是什么图形?【答案】22331030+-+=x y x【解析】不妨设2=||AB ,以线段AB 为x 轴,其中垂线为y 轴建立直角坐标系,那么A (-1,0),B(1,0).设P (x,y ).2=,化简得到22331030+-+=x y x 表示一个圆.类型三:直线与圆的方程在代数中的应用例3.已知圆22()()1x a y b -+-=与直线1l :3x ―4y ―1=0和2l :4x +3y +1=0都有公共点,求2b a -的取值范围.【思路点拨】圆22()()1x a y b -+-=与二直线1l :3x ―4y ―1=0和2l :4x +3y +1=0都有公共点,可得圆心C 到直线的距离小于等于半径,即可求2ba -的取值范围. 【答案】143[,]234-【解析】∵圆:22()()1x a y b -+-=,圆心为C (a ,b ),半径为1. ∵直线1l :3x ―4y ―1=0和圆:22()()1x a y b -+-=有公共点,∴圆心C 到直线的距离:|341|15a b --≤,即34603440a b a b --≤⎧⎨-+≥⎩① ∵直线2l :4x +3y +1=0和圆:22()()1x a y b -+-=有公共点, ∴圆心C 到直线的距离:|431|15a b ++≤,即43404360a b a b +-≤⎧⎨-+≥⎩② ∴作出①②不等式组表示的平面区域如图:∴由34404340a b a b -+=⎧⎨+-=⎩ 得428(,)2525B ,A (2,0).∴由2ba -的几何意义可得,最大值为34AC k =,最小值为281425423225ABk -==--, ∴2ba -的取值范围为143[,]234-.举一反三:【变式1】设函数()f x a =和4()13g x x =+,已知当x ∈[-4,0]时,恒有()()f x g x ≤,求实数a 的取值范围. 【答案】(],5-∞-【解析】因为()()f x g x ≤,所以413a x +,即413x a ≤+-,分别画出y =和413y x a =+-的草图,利用数形结合法,当直线413y x a =+-与半圆y =相切时a 取到最大值,由圆心到直线的距离为2,求出5a =-,即得答案. 类型四:直线与圆的方程的综合应用例4.(2018春 辽宁庄河市期中)已知圆C的圆心在坐标原点,且与直线1:0l x y --=相切. (1)求圆C 的方程;(2)求直线l 2:4x -3y +5=0被圆C 所截得的弦AB 的长;(3)过点G (1,3)作两条与圆C 相切的直线,切点分别为M ,N ,求直线MN 的方程. 【思路点拨】(1)设出圆的方程,由直线和圆相切的条件,求得半径,即可得到圆的方程; (2)求出圆心到直线的距离,运用直线和圆相交的弦长公式,即可得到;(3)判断出C ,M ,N ,G 四点共圆,求出圆的方程,再与圆C 方程相减,即可得到相交弦方程. 【答案】(1)x 2+y 2=4;(2)(3)x +3y ―4=0 【解析】(1)设圆的方程为:x 2+y 2=r 2, 由于圆C与直线1:0l x y --=相切,则2d r ===, 则有圆C :x 2+y 2=4;(2)圆收到直线l 2:4x -3y +5=的距离为1d ==,则被圆C 所截得的弦AB 的长为=;(3)过点G (1,3)作两条与圆C 相切的直线,切点分别为M ,N , 由CM ⊥MG ,CN ⊥NG ,则四点C ,M ,G ,N 共圆,且以PC 为直径,则方程为22213()()222x y -+-=,① 又圆C :x 2+y 2=4,②由于MN 为两圆的公共弦, 则①-②,可得,x +3y ―4=0.【总结升华】解决直线与圆的综合问题,一方面,我们要注意运用解析几何的基本思想方法(即几何问题代数化),把它转化为代数问题,通过代数的计算,使问题得到解决;另一方面由于直线与圆和平面几何联系得十分紧密(其中直线与三角形、四边形紧密相连),因此我们要充分挖掘几何图形中所隐含的条件(性质),利用几何知识使问题得到较简捷的解决.举一反三:【变式1】若圆C :22420x y x y m +-++=与y 轴交于A ,B 两点,且∠ACB =90°,求实数m 的值.【思路点拨】由圆C :22420x y x y m +-++=与y 轴交于A ,B 两点,且∠ACB =90°,知圆心C (2,―1),过点C 作y 轴的垂线交y 轴于点D ,在等腰直角三角形BCD 中,CD =BD =2,由此能求出实数m .【答案】―3【解析】∵圆C :22420x y x y m +-++=, ∴ 22(2)(1)5x y m -++=-,圆心C (2,―1),因为∠ACB =90°,过点C 作y 轴的垂线交y 轴于点D , 在等腰直角三角形BCD 中,CD =BD =2, ∴ 2544m CB -==+, 解得m =―3.【巩固练习】1.直线()()110a x b y +++=与圆222x y +=的位置关系是( )A .相切B .相离C .相切或相交D .相切或相离2.圆C 1:x 2+y 2+4x-4y+7=0与圆C 2:x 2+y 2-4x-10y+13=0的公切线有( ) A .1条 B .2条 C .3条 D .4条3.与圆x 2+(y-2)2=1相切,且在两轴上截距相等的直线有( ) A .2条 B .3条 C .4条 D .6条4.直线ax+by=c 与圆x 2+y 2=1相切,且a 、b 、c 均不为零,则以|a|、|b|、|c|为长度的线段能构成( ) A .不等边锐角三角形 B .等腰锐角三角形 C .直角三角形 D .钝角三角形 5.(2017春 河北衡水期末)若圆2O :22(3)(3)4x y -++=关于直线l :ax +4y ―6=0对称,则直线l 的斜率是( )A .6B .23 C .32- D .23- 6.直线2x -y=0与圆C :(x -2)2+(y+1)2=9交于A 、B 两点,则△ABC (C 为圆心)的面积等于( ).A .B .C .D .7.圆(x -4)2+(y -4)2=4与直线y=kx 的交点为P 、Q ,原点为O ,则|OP|·|OQ|的值为( ).A .B .28C .32D .由k 确定8.点P 是直线2x+y+10=0上的动点,直线PA 、PB 分别与圆x 2+y 2=4相切于A 、B 两点,则四边形PAOB(O 为坐标原点)的面积的最小值等于( ). A .24 B .16 C .8 D .4 9.(2018 山西太原二模)已知过点P (2,2)的直线与圆(x ―1)2+y 2=5相切,且与直线ax ―y +1=0垂直,则a =________.10.过原点的直线与圆x 2+y 2-2x -4y+4=0相交所得弦的长为2,则该直线的方程为________. 11.设圆22450x y x +--=的弦AB 的中点为(3,1)P ,则直线AB 的方程是 .12.若过定点M (―1,0)且斜率为k 的直线与圆22(2)9x y ++=在第一象限内的部分有交点,则k 的取值范围是 .13.(2017春 江苏宿迁期末)已知圆D 的半径为1,圆C 的方程是22(2)(1)4x y -++=,若圆D 与圆C 相切于点(4,―1),求圆D 的标准方程. 14.(2018春 黑龙江肇东市期末)已知圆C :x 2+y 2=4和直线l :3x +4y +12=0,点P 是圆C 上的一动点,直线与坐标轴的交点分别为点A 、B ,(1)求与圆C 相切且平行直线l 的直线方程; (2)求△P AB 面积的最大值.15.有弱、强两个喇叭在O 、A 两处,若它们的强度之比为1∶4,且相距60 m ,问在什么位置听到两个喇叭传来的声音强度是相等的?【答案与解析】1.【答案】C直线过定点()1,1--.又()()22112-+-=,∴点在圆上,过圆上一点的直线与圆的位置关系有两种相切或相交.2. 【答案】C【解析】两圆公切线的条数取决于两圆的位置关系,相离:4条;外切:3条;相交:2条;内切:1条;内含:0条.C 1:(x+2)2+(y-2)2=1,C 2:(x-2)2+(y-5)2=16,C 1C 2=5=r 1+r 2,故两圆外切,公切线共3条. 3. 【答案】C【解析】此题主要考查圆的切线及直线的截距的概念.过原点的有2条;斜率为-1的有2条. 4. 【答案】C【解析】由圆心到直线的距离为圆的半径1,得22||b a c +=1,两边平方得a 2+b 2=c 2.5.【答案】C【分析】由题意可知直线通过圆的圆心,求出圆心坐标代入直线方程,即可得到a 的值,然后求出直线的斜率.【解析】圆2O :22(3)(3)4x y -++=关于直线l :ax +4y ―6=0对称,则直线通过圆心(3,―3),故3a ―12―6=0,∴a =6, ∴直线l 的斜率32k =-, 故选:C . 6.【答案】A【解析】 ∵圆心到直线的距离d ==,∴||4AB ==,∴142ABC S ∆=⨯= 7.【答案】B【解析】 由平面几何知识可知|OP|·|OQ|等于过O 点圆的切线长的平方. 8.【答案】C【解析】 ∵四边形PAOB 的面积12||||2S PA OA =⨯⨯==OP 垂直直线2x+y+10=0时,其面积S 最小. 9.【答案】2【解析】因为点P (2,2)满足圆(x ―1)2+y 2=5的方程,所以P 在圆上,又过点P (2,2)的直线与圆(x ―1)2+y 2=5相切,且与直线ax ―y +1=0垂直, 所以切点与圆心连线与直线ax ―y +1=0平行,所以直线ax ―y +1=0的斜率为:20221a -==-. 故答案为:2. 10.【答案】2x ―y=0 【解析】 设所求直线方程为y=kx ,即kx ―y=0.由于直线kx ―y=0被圆截得的弦长等于2,圆的半径是1,0=,即圆心位于直线kx ―y=0上,于是有k ―2=0,即k=2,因此所求直线方程为2x ―y=0. 11.【答案】40x y +-= 【解析】12.【答案】.【分析】化简圆的方程求出圆与y 正半轴的交点,画出图象,即可推出过定点M (―1,0)斜率为k 的直线的范围.【解析】圆22(2)9x y ++=与y 正半轴交于,因为过定点M (―1,0),且斜率为k 的直线与圆22(2)9x y ++=在第一象限内的部分有交点,如图,∴ MA MB k k k <<,∴0<k k 的取值范围是.故答案为:.13.【答案】22(5)(1)1x y -++=或22(3)(1)1x y -++=.【分析】分两圆外切、内切两种情况,分别求得圆心的坐标,可得要求的圆的方程. 【解析】圆22(2)(1)4x y -++=的圆心为C (2,―1),半径为2,设所求的圆心坐标为(a ,b ),切点为A (4,―1)且半径为1(1123=+=,② 由①②得a =5,b =―1,即此时圆心为M (5,―1),(2211=-=,③ 由①③得a =3,b =―1,即此时圆心为N (3,―1),故要求的圆的方程为22(5)(1)1x y -++=或22(3)(1)1x y -++=.【点评】主题主要两圆相切的性质,求圆的标准方程,求出圆心的坐标,是解题的关键,注意要分内切和外切两种情况. 14.【答案】(1)3x +4y ±10=0;(2)11 【解析】(1)设所求直线方程为3x +4y +a =0,由题意得:圆心(0,0)到直线的距离d =r ,即||25a =, 解得:a =±10,则所求直线方程为3x +4y ±10=0;(2)当直线与AB 平行,且与圆相切时,△P AB 面积的最大值,此时直线方程为3x +4y -10=0, ∵点C 到直线AB 的距离12||5CN =,CM =2, ∴1222||255MN =+=, ∵A (-4,0),B (0,3),即OA =4,OB =3,∴|AB |=5,即△P AB 面积最大值为12251125⨯⨯=. 15.【答案】P 点的轨迹是以(-20,0)为圆心,40为半径长的圆周,也就是在此圆周上听到的声音强度相等【解析】以OA 为x 轴,O 为坐标原点建立如图所示的直角坐标系.设在P (x ,y )处听到O 、A 两处的喇叭声音强度相等.由物理学知22||1||4OP PA =,即22221(60)4x y x y +=-+,整理得(x+20)2+y 2=402. 故P 点的轨迹是以(-20,0)为圆心,40为半径长的圆周,也就是在此圆周上听到的声音强度相等.。

第四章直线与圆的方程复习三维目标1.能建构本章的知识框架;2. 掌握直线与圆知识的综合应用;3. 通过圆的几何性质的运用,体会代数问题与几何问题的联系,及数形结合思想.___________________________________________________________________________目标三导学做思1问题1. 完成本章知识结构.(1)圆的方程是什么?(2)点与圆的位置关系判断方法为?【思考】①圆外一点B,圆上一动点P,讨论PB的最值为?. ②圆内一点A,圆上一动点P,讨论PA的最值?(3)直线与圆的位置关系的判断方法?【思考】①直线l与圆C相切意味着什么?②关于切线的常见题型有哪些?③直线与圆相交时的弦长公式为?(4)圆与圆的位置关系判断方法为?【思考】 两圆公共弦所在直线方程为?(5)对称问题、最值问题、求轨迹方程等问题的解决方法为?。
【学做思2】1.根据下列条件求圆的方程:(1)圆心在直线035:1=-y x l 上,并且圆与直线0106:2=--y x l 相切于点P (4,-1);(2)圆过点P (-2,4),Q (3,-1)并且在x 轴上截得的弦长等于6;(3)求与圆522=+y x 外切于点)2,1(-P ,且半径为52的圆的方程.【思考】求圆的方程要注意什么?*2.已知圆A :x 2+y 2-2x -2y -2=0.(1)若直线l :ax +by -4=0平分圆A 的周长,求原点O 到直线l 的距离的最大值;(2)若圆B 平分圆A 的周长,圆心B 在直线y =2x 上,求符合条件且半径最小的圆B 的方程.达标检测1. 已知点(03)P ,及圆C :082822=---+y x y x ,过P 的最短弦所在的直线方程为( ) A 、x +2y +3=0 B 、x -2y +3=0 C 、2x -y +3=0 D 、2x +y -3=02. 在空间直角坐标系中,点P ,过点P 作平面xOy 的垂线PQ ,则Q 的坐标为( )A.(0 B.(0 C.(10 D. 3.当点P 在圆x 2+y 2=1上变动时,它与定点Q (3,0)连线段PQ 中点的轨迹方程是( )A .(x +3)2+y 2=4B .(x -3)2+y 2=1 C .(2x -3)2+4y 2=1D .(2x +3)2+4y 2=14. 已知三角形的三个顶点(214)A -,,,(326)B -,,,(502)C ,,.则(1)过A 点的中线长为 ;(2)过B 点的中线长为 ;(3)过C 点的中线长为 .*5. 已知圆C : x 2+(y -2)2=5,直线l :mx -y +1=0.(1)求证:对m ∈R ,直线l 与圆C 总有两个不同交点;(2)若圆C 与直线l 相交于A ,B 两点,求弦AB 的中点M 的轨迹方程.。

直线与圆的方程综合复习(含答案)一. 选择题1.已知点A(1,. 3),B(-1,33),则直线AB 的倾斜角是( C ) A 3B 6C 23D 562.已知过点A(-2,m)和B (m,4)的直线与直线2x+y-1=0平行,则m 的值为( C ) A 0 B 2 C -8 D 103.若直线L 1:ax+2y+6=0与直线L 2:x+(a-1)y+(2a -1)=0平行但不重合,则a 等于( D ) A -1或2 B23C 2D -1 4.若点A (2,-3)是直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的公共点,则相异两点(a 1,b 1)和(a 2,b 2)所确定的直线方程是( A ) A.2x-3y+1=0 B.3x-2y+1=0 C.2x-3y-1=0 D.3x-2y-1=0 5.直线xcos θ+y-1=0 (θ∈R )的倾斜角的范围是 ( D )A.[)π,0B.⎪⎭⎫⎢⎣⎡ππ43,4C.⎥⎦⎤⎢⎣⎡-4,4ππD.⎪⎭⎫⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ,434,06.“m= 12”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2y)-3=0相互垂直”的( B )A 充分必要条件B 充分而不必要条件C 必要而不充分条件D 既不充分也不必要条件 7.已知A(7,-4)关于直线L 的对称点为B (-5,6),则直线L 的方程为(B ) A 5x+6y-11=0 B 6x-5y-1=0 C 6x+5y-11=0 D 5x-6y+1=0 8.已知直线1l 的方向向量a=(1,3),直线2l 的方向向量b=(-1,k).若直线2l 经过点(0,5)且1l 2l ,则直线2l 的方程为( B )A x+3y-5=0B x+3y-15=0C x-3y+5=0D x-3y+15=0 9. 过坐标原点且与圆2x +2y -4x+2y+52=0相切的直线方程为( A )A y=-3x 或y= 13xB y=3x 或y= -13xC y=-3x 或y= -13xD y=3x 或y= 13x 10.直线x+y=1与圆2x +2y -2ay=0(a>0)没有公共点,则a 的取值范围是(A )22222211.圆2x +2y -4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( C )A 36B 18C 62D 5212.以直线:y=kx-k 经过的定点为P 为圆心且过坐标原点的圆的方程为(D ), A 2x +2y +2x=0 B 2x +2y +x=0 C 2x +2y -x=0 D 2x +2y -2x-013.已知两定点A(-2,0),B(1,0),如果定点P 满足PA=2PB,则定点P 的轨迹所 包围的面积等于( B )A B 4 C 8 D 914.若直线3x+y+a=0过圆2x +2y +2x-4y=0的圆心,则a 的值为( B )A 1B -1C 3D -315.若直线2ax-by+2=0 (a >0,b >0)始终平分圆x 2+y 2+2x-4y+1=0的周长,则ba11+的最小值是( C ) A.41B.2C.4D.2116.若直线y=k(x-2)+4与曲线y=1+24x -有两个不同的交点,则k的取值范围是 ( A )A.⎥⎦⎤ ⎝⎛43,125 B.⎪⎭⎫⎝⎛+∞,125 C.⎥⎦⎤⎝⎛43,21D.⎪⎭⎫⎝⎛125,017.设两圆1C ,2C 都和两坐标轴相切,且过点(4,1),则两圆心的距离 ︱1C 2C ︱等于( C )A 4B 42C 8D 8218.能够使得圆x 2+y 2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c 的一个值为 ( C ) A.2B.5C.3D.3519.若直线by ax +=1与圆x 2+y 2=1有公共点,则( D )A.a 2+b 2≤1B.a 2+b 2≥1C.2211ba +≤1 D.2211ba +≥120.已知A (-3,8)和B (2,2),在x 轴上有一点M ,使得|AM|+|BM|为最短,那么点M 的坐标为( B ) A.(-1,0)B.(1,0)C.⎪⎭⎫ ⎝⎛0522,D. ⎪⎭⎫⎝⎛522,021.直线y=kx+3与圆2(3)x +2(2)y =4相交于M 、N 两点,若︱MN ︱≥23,则k 的取值范围是( A )A [-34,0] B [-∞,-34] [0,∞) C [-33,33] D [-23,0] 22.(广东理科2)已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则AB 的元素个数为(C )A .0B .1C .2D .323.(江西理科9)若曲线02221=-+x y x C :与曲线 0)(2=--m mx y y C :有四个不同的交点,则实数m 的取值范围是 ( B ) A. )33,33(-B. )33,0()0,33( -C. ]33,33[-D. ),33()33,(+∞--∞ 答案:B 曲线0222=-+x y x 表示以()0,1为圆心,以1为半径的圆,曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-,0=y 与圆有两个交点,故0=--m mx y 也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应3333=-=m m 和,由图可知,m 的取值范围应是)33,0()0,33( -二.填空题24.已知圆C 经过)3,1(),1,5(B A 两点,圆心在X 轴上,则C 的方程为10)2(22=+-y x ___________。

必修2第四章直线和圆复习一圆的标准方程学习目标:回顾确定圆的几何要素,在平面直角坐标系中,掌握圆的标准方程;能用待定系数法、几何法求圆的标准方程.知识要点:1. 圆的标准方程:方程222()()(0)x a y b r r -+-=>表示圆心为A (a ,b ),半径长为r 的圆.2. 求圆的标准方程的常用方法:(1)几何法:根据题意,求出圆心坐标与半径,然后写出标准方程; (2)待定系数法:先根据条件列出关于a 、b 、r 的方程组,然后解出a 、b 、r ,再代入标准方程. 例题精讲:【例1】过点(1,1)A -、(1,1)B -且圆心在直线x +y -2=0上的圆的方程是( ).A.(x -3)2+(y +1)2=4B.(x +3)2+(y -1)2=4C.(x -1)2+(y -1)2=4D.(x +1)2+(y +1)2=4解:由圆心在直线x +y -2=0上可以得到A 、C 满足条件, 再把A 点坐标(1,-1)代入圆方程. A 不满足条件. 所以,选C.另解:设圆心C 的坐标为(a ,b ),半径为r , 因为圆心C 在直线x +y -2=0上, ∴b =2-a .由|CA |=|CB |,得(a -1)2+(b +1)2=(a +1)2+(b -1)2,解得a =1,b =1. 因此,所求圆的方程为(x -1)2+(y -1)2=4. 选C.【例2】求下列各圆的方程:(1)过点(2,0)A -,圆心(3,2)-;(2)圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4),(0,2)A B -- 解:(1)设所求圆的方程为222(3)(2)x y r -++=. 则222(23)(02)r --++=, 解得229r =. ∴ 圆的方程为22(3)(2)29x y -++=. (2)圆心在线段AB 的垂直平分线3y =-上,代入直线270x y --=得2x =,圆心为(2,3)-,半径r =∴ 圆C 的方程为22(2)(3)5x y -++=.【例3】一个圆经过点(5,0)A 与(2,1)B -,圆心在直线3100x y --=上,求此圆的方程.解:设圆心(,)P a b ,则3100a b --=⎧= 解得13a b =⎧⎨=-⎩.圆的半径5r ===. ∴ 圆的标准方程为22(1)(3)25x y -++=.另解:线段AB 的中点'5201(,)22P -+,即'31(,)22P . 直线AB 的斜率101257k -==---. 所以弦AB 的垂直平分线的方程为137(22y x -=-,即7100x y --=.解方程组31007100x y y --=⎧⎨--=⎩,得13x y =⎧⎨=-⎩, 即圆心(1,3)P -.圆的半径5r ===. ∴ 圆的标准方程为22(1)(3)25x y -++=.点评:两种解法,都是先求出圆心与半径,第一种解法用设圆心坐标后列方程而求,第二种解法用两条直线的交点求圆心. 由上可得,解法关键都是如何求圆心与半径.二圆的一般方程学习目标:回顾确定圆的几何要素,在平面直角坐标系中,掌握圆的一般方程;能用待定系数法求圆的一般方程.知识要点:1. 圆的一般方程:方程220x y Dx Ey F ++++= (2240D E F +->)表示圆心是(,22D E--,半径长的圆. 2. 轨迹方程是指点动点M 的坐标(,)x y 满足的关系式.例题精讲:【例1】求过三点A (2,2)、B (5,3)、C (3,-1)的圆的方程. 解:设所求圆的方程为220x y Dx Ey F ++++=. 则442202595309130D E F D E F D E F ++++=⎧⎪++++=⎨⎪++-+=⎩, 解得8212D E F =-⎧⎪=-⎨⎪=⎩. ∴ 圆的方程为2282120x y x y +--+=.【例2】设方程222422(3)2(14)16790x y m x m y m m +-++-+-+=,若该方程表示一个圆,求m 的取值范围及圆心的轨迹方程.解:配方得[]222(3)(14)16x m y m m ⎡⎤-++--=+⎣⎦,该方程表示圆,则有160m +>,得1(,)6m ∈-+∞,此时圆心的轨迹方程为2314x m y m=+⎧⎨=-⎩,消去m ,得24(3)1y x =--, 由1(,)6m ∈-+∞得x =m +317(,)6∈+∞. ∴所求的轨迹方程是24(3)1y x =--,17(,)6x ∈+∞ 【例3】已知线段AB 的端点B 的坐标是(4,3),端点A 在圆22(1)4x y ++=上运动,求线段AB 的中点轨迹方程. (教材P 133 例5 另解)(利用中点坐标公式可更简单)解:设圆22(1)4x y ++=的圆心为P (-1,0),半径长为2,线段AB 中点为M(x , y ).取PB 中点N ,其坐标为(142-+,032+),即N (32,32).∵ M 、N 为AB 、PB 的中点, ∴ MN ∥P A 且MN =12P A =1. ∴ 动点M 的轨迹为以N 为圆心,半径长为1的圆. 所求轨迹方程为:2233()(122x y -+-=.点评:此解为定义法,利用中位线这一几何性质,将所求动点的轨迹转化为到定点的距离等于定长,即圆的定义. 解法关键是连接PB ,取PB 的中点N ,得到MN 的长度为定值. 教材中的解法是通过设动点的坐标,然后找出相关的几何条件,得到动点坐标所满足等式即所求轨迹方程.【例4】求经过(4,2),(1,3)A B -两点,且在两坐标轴上的四个截距之和为4的圆的方程.解:设所求圆的方程为220x y Dx Ey F ++++=. 当0x =时,20y Ey F ++=,则122E y y +=-; 当0y =时,20x Dx F ++=,则122D x x +=-. 则1644201930((422D E F D E F D E ⎧⎪++++=⎪+-++=⎨⎪⎪-+-=⎩, 解得352D E F =-⎧⎪=-⎨⎪=⎩. ∴ 圆的方程为223520x y x y +--+=.点评:用待定系数法的一般步骤是“设(设含待定系数的方程)→列(利用条件列出系数所满足的方程组)→求(解方程组)→写(写出所求方程)”. 当已知圆上三点或两点时,选用圆的一般方程形式较为简单. 当易知圆心和半径时,选用圆的标准方程形式易求解.三 直线与圆的位置关系学习目标:能根据给定直线、圆的方程,判断直线与圆的位置关系;能用直线和圆的方程解决一些简单的问题.知识要点:1. 直线与圆的位置关系及其判定: 方法一:方程组思想,由直线与圆的方程组成的方程组,消去x 或(y ),化为一元二次方程,由判别式符号进行判别;方法二:利用圆心(,a b )到直线0Ax By C ++=的距离d =,比较d 与r 的大小.(1)相交d r ⇔<⇔ 0∆>;(2)相切d r ⇔=⇔0∆=;(3)相离d r ⇔>⇔0∆<.2. 直线与圆的相切研究,是高考考查的重要内容. 同时,我们要熟记直线与圆的各种方程、几何性质,也要掌握一些常用公式,例如点线距离公式d =例题精讲:【例1】若直线(1+a )x +y +1=0与圆x 2+y 2-2x =0相切,则a 的值为 . 解:将圆x 2+y 2-2x =0的方程化为标准式:(x -1)2+y 2=1, 其圆心为(1,0),半径为1,由直线(1+a )x +y +1=0与该圆相切,则圆心到直线的距离1d ==, ∴ a =-1. 【例2】求直线:220l x y --=被圆22:(3)9C x y -+=所截得的弦长.解:由题意,列出方程组22220(3)9x y x y --=⎧⎨-+=⎩,消y 得251440x x -+=,得12145x x +=,1245x x =. 设直线220x y --=与圆22(3)9x y -+=交于点11(,)A x y ,22(,)B x y ,则21|||AB x x =-==.另解:圆心C 的坐标是(3,0),半径长3r =. 圆心到直线220x y --=的距离d =所以,直线220x y --=被圆22(3)9x y -+=截得的弦长是==. 【例3】若经过点(1,0)P -的直线与圆224230x y x y ++-+=相切,则此直线在y 轴上的截距是 .解:圆的标准方程为22(2)(1)2x y ++-=,则圆心(2,1)C -,半径r 设过点(1,0)P -的直线方程为(1)y k x =+,即0kx y k -+=.∴ 圆心到切线的距离d r ==1k =.∴ 直线方程为1y x =+,在y 轴上的截距是1.点评:研究直线和圆的相切,简捷的方法是利用公式d r ==,还可以由方程组只有一个实根进行解答. 选择恰当的方法,是我们解题的一种能力.【例4】设圆上的点A (2,3)关于直线x +2y =0的对称点仍在这个圆上,且与直线x -y +1=0相交的弦长为求圆的方程.解:设A 关于直线x +2y =0的对称点为A ’. 由已知得AA ’为圆的弦,得到AA ’的对称轴x +2y =0过圆心. 设圆心P (-2a ,a ),半径为r , 则r =|P A |=(-2a -2)2+(a -3)2.又弦长,圆心到弦AA ’的距离为d∴ 22(31)22a R -=+, 即4(a +1)2+(a -3)2=2+2(31)2a -, 解得a =-7或a =-3.当a =-3时,r a =-7时,r ∴ 所求圆方程为(x -6)2+(y +3)2=52或(x -14)2+(y +7)2=244.点评:在解答与圆的弦长相关的一些问题时,常用勾股定理,得到圆心到弦的距离d 、半径r 、半弦长的一个勾股式. 这种方法与方程组的思想求解弦长问题相比,计算过程较为简单. 四圆与圆的位置关系学习目标:能根据给定圆的方程,判断圆与圆的位置关系. 掌握坐标法的思想,用解方程组判别位置关系或求交点坐标.知识要点:两圆的位置关系及其判定: 设两圆圆心分别为12,O O ,半径分别为12,r r ,则:(1)两圆相交121212||||r r O O r r ⇔-<<+;(2)两圆外切1212||O O r r ⇔=+; (3)两圆内切1212||||O O r r ⇔=-;例题精讲:【例1】已知圆1C :22660x y x +--=①,圆2C :22460x y y +--=② (1)试判断两圆的位置关系;(2)求公共弦所在的直线方程.解:(1)∵圆1C 的圆心为(3,0),半径为1r =2C 的圆心为(0,2),半径为2r =又12||C C =12||r r -<12||C C <12r r +,∴圆1C 与2C 相交.(2)由①-②,得公共弦所在的直线方程为320x y -=.【例2】求经过两圆22640x y x ++-=和226280x y y ++-=的交点,并且圆心在直线40x y --=上的圆的方程.解:设所求圆的方程为22628x y y ++-22(64)0x y x λ+++-=,即22(1)(1)662840x y x y λλλλ+++++--=,则所求圆的圆心为33(,)11λλλ--++.∵圆心在直线40x y --=上, ∴334011λλλ-+-=++,解得17λ=-.∴ 所求圆的方程为2x +27320y x y -+-=【例3】已知圆C 与圆22(1)1x y -+=关于直线y x =-对称,则圆C 的方程为 A.22(1)1x y ++= B.221x y += C.22(1)1x y ++= D.22(1)1x y +-= 解:已知圆的半径1r =,圆心(1,0),圆心(1,0)关于直线y x =-的对称点为(0,1)-, 则圆C 的方程为22(1)1x y ++=. 选C.点评:圆关于直线的对称图形仍然是圆,半径不变,圆心关于直线对称. 我们要掌握一些常见对称问题的解答思路,例如点关于直线的对称,曲线关于直线的对称,曲线关于点的对称等,解答理论基础有中点坐标公式、垂直时斜率乘积为-1、代入法、转化思想.同时,我们也要掌握一些简单对称,如点(,)a b 关于直线y x =的对称点为(,)b a .【例4】求圆2240x y +-=与圆2244120x y x y +-+-=的公共弦的长.解:由题意,列出方程组22224044120x y x y x y ⎧+-=⎪⎨+-+-=⎪⎩,消去二次项,得2y x =+. 把2y x =+代入2220x y x y +-+=,得220x x +=,解得122,0x x =-=,于是120,2y y ==,两圆的交点坐标是(2,0)A -,(0,2)B,所以,公共弦长||AB =. 另解:由题意,列出方程组 22224044120x y x y x y ⎧+-=⎪⎨+-+-=⎪⎩,消去二次项,得2y x =+,它即公共弦所在直线的方程. 圆2240x y +-=的圆心到直线20x y -+=的距离为d =所以,两圆的公共线长为==点评:为何两圆的方程消去二次项后,即为公共弦所在直线的方程,我们易由曲线系的知识可得. 比较方程思想与几何方法求解两圆的公共弦长,几何方法更为简捷. 先求公共弦所在直线,再求一圆心到直线的距离,通过公式.五直线与圆的方程的应用【例1】实数,x y 满足222410x y x y ++-+=, 求下列各式的最大值和最小值:(1)y;(2)2x y -. 解:原方程为22(1)(2)4x y ++-=,表示以(1,2)P -为圆心,2为半径的圆. (1)设4yk x =-,几何意义是:圆上点(,)M x y 与点(4,0)Q 连线的斜率. 由图可知当直线MQ 是圆的切线时,k 取最大值与最小值。
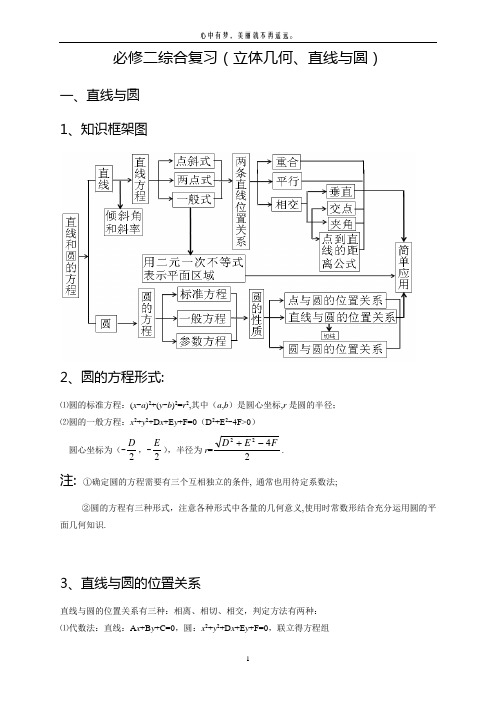
必修二综合复习(立体几何、直线与圆)一、直线与圆 1、知识框架图2、圆的方程形式:⑴圆的标准方程:(x -a )2+(y -b )2=r 2,其中(a ,b )是圆心坐标,r 是圆的半径; ⑵圆的一般方程:x 2+y 2+D x +E y +F=0(D 2+E 2-4F>0) 圆心坐标为(-2D ,-2E ),半径为r =2422FE D-+.注: ①确定圆的方程需要有三个互相独立的条件, 通常也用待定系数法;②圆的方程有三种形式,注意各种形式中各量的几何意义,使用时常数形结合充分运用圆的平面几何知识.3、直线与圆的位置关系直线与圆的位置关系有三种:相离、相切、相交,判定方法有两种: ⑴代数法:直线:A x +B y +C=0,圆:x 2+y 2+D x +E y +F=0,联立得方程组2200Ax By C x y Dx Ey F ++=⎧⎨++++=⎩−−−→消元一元二次方程24b ac =-−−−→判别式△000>⇔⎧⎪=⇔⎨⎪<⇔⎩△相交△相切△相离(2)几何法:直线:A x +B y +C=0,圆:(x -a )2+(y -b )2=r 2,圆心(a ,b )到直线的距离为d=22||Aa Bb C A B+++,则d r d r d r >⇔⎧⎪=⇔⎨⎪<⇔⎩相离相切相交4、圆和圆的位置关系:设两圆圆心分别为O 1、O 2,半径分别为r 1,r 2,|O 1O 2|为圆心距,则两圆位置关系如下: ①|O 1O 2|>r 1+r 2⇔两圆外离; ②|O 1O 2|=r 1+r 2⇔两圆外切; ③| r 1-r 2|<|O 1O 2|< r 1+r 2⇔两圆相交; ④| O 1O 2 |=| r 1-r 2|⇔两圆内切; ⑤0<| O 1O 2|<| r 1-r 2|⇔两圆内含。
注:直线和圆位置关系及圆和圆位置关系常借助于平面几何知识。

直线与圆的方程综合复习(含答案)一. 选择题1.已知点A(1,. 3),B(-1,33),则直线AB 的倾斜角是( C ) A 3B 6C 23D 562.已知过点A(-2,m)和B (m,4)的直线与直线2x+y-1=0平行,则m 的值为( C ) A 0 B 2 C -8 D 103.若直线L 1:ax+2y+6=0与直线L 2:x+(a-1)y+(2a -1)=0平行但不重合,则a 等于( D )A -1或2B 23C 2D -14.若点A (2,-3)是直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的公共点,则相异两点 (a 1,b 1)和(a 2,b 2)所确定的直线方程是( A ) A.2x-3y+1=0 B.3x-2y+1=0 C.2x-3y-1=0 D.3x-2y-1=05.直线xcos θ+y-1=0 (θ∈R )的倾斜角的范围是 ( D )A.[)π,0B.⎪⎭⎫⎢⎣⎡ππ43,4C.⎥⎦⎤⎢⎣⎡-4,4ππD.⎪⎭⎫⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ,434,06.“m=12”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2y)-3=0相互垂直”的( B )A 充分必要条件B 充分而不必要条件C 必要而不充分条件D 既不充分也不必要条件7.已知A(7,-4)关于直线L 的对称点为B (-5,6),则直线L 的方程为(B ) A 5x+6y-11=0 B 6x-5y-1=0 C 6x+5y-11=0 D 5x-6y+1=0 8.已知直线1l 的方向向量a=(1,3),直线2l 的方向向量b=(-1,k).若直线2l 经过点(0,5)且1l 2l ,则直线2l 的方程为( B )A x+3y-5=0B x+3y-15=0C x-3y+5=0D x-3y+15=0 9. 过坐标原点且与圆2x +2y -4x+2y+52=0相切的直线方程为( A )A y=-3x 或y= 13xB y=3x 或y= -13xC y=-3x 或y= -13xD y=3x 或y= 13x10.直线x+y=1与圆2x +2y -2ay=0(a>0)没有公共点,则a 的取值范围是(A )A (02-1,)B (2-1, 2+1)C (-2-1, 2-1)D (0, 2+1) 11.圆2x +2y -4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( C )A 36B 18C 62D 5212.以直线:y=kx-k 经过的定点为P 为圆心且过坐标原点的圆的方程为(D ), A 2x +2y +2x=0 B 2x +2y +x=0 C 2x +2y -x=0 D 2x +2y -2x-013.已知两定点A(-2,0),B(1,0),如果定点P 满足PA=2PB,则定点P 的轨迹所 包围的面积等于( B )A B 4 C 8 D 914.若直线3x+y+a=0过圆2x +2y +2x-4y=0的圆心,则a 的值为( B )A 1B -1C 3D -315.若直线2ax-by+2=0 (a >0,b >0)始终平分圆x 2+y 2+2x-4y+1=0的周长,则ba11+的最小值是( C )A.41B.2C.4D.2116.若直线y=k(x-2)+4与曲线y=1+24x -有两个不同的交点,则k 的取值范围是 ( A )A.⎥⎦⎤⎝⎛43,125 B.⎪⎭⎫⎝⎛+∞,125 C.⎥⎦⎤⎝⎛43,21D.⎪⎭⎫⎝⎛125,17.设两圆1C ,2C 都和两坐标轴相切,且过点(4,1),则两圆心的距离 ︱1C 2C ︱等于( C )A 4B 42C 8D 8218.能够使得圆x 2+y 2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c的一个值为 ( C ) A.2B.5C.3D.3519.若直线by ax +=1与圆x 2+y 2=1有公共点,则( D )A.a 2+b 2≤1B.a 2+b 2≥1C.2211ba +≤1 D.2211ba +≥120.已知A (-3,8)和B (2,2),在x 轴上有一点M ,使得|AM|+|BM|为最短,那么点M 的坐标为( B ) A.(-1,0)B.(1,0)C.⎪⎭⎫⎝⎛0522,D. ⎪⎭⎫⎝⎛522,021.直线y=kx+3与圆2(3)x+2(2)y =4相交于M 、N 两点,若︱MN ︱≥23,则k 的取值范围是( A )A [-34,0] B [-∞,-34] [0,∞) C [-33,33] D [-23,0] 22.(广东理科2)已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则AB 的元素个数为(C )A .0B .1C .2D .3 23.(江西理科9)若曲线02221=-+x y x C :与曲线 0)(2=--m mx y y C :有四个不同的交点,则实数m 的取值范围是 ( B ) A. )33,33(-B. )33,0()0,33( -C. ]33,33[-D. ),33()33,(+∞--∞ 答案:B 曲线0222=-+x y x 表示以()0,1为圆心,以1为半径的圆,曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-,0=y 与圆有两个交点,故0=--m mx y 也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应3333=-=m m 和,由图可知,m 的取值范围应是)33,0()0,33( -二.填空题24.已知圆C 经过)3,1(),1,5(B A 两点,圆心在X 轴上,则C 的方程为10)2(22=+-y x ___________。
直线与圆的方程复习题知识汇总(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(直线与圆的方程复习题知识汇总(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为直线与圆的方程复习题知识汇总(word版可编辑修改)的全部内容。
直线与圆的方程知识汇总知识一:直线与圆的位置关系1、已知直线0323=-+y x 和圆422=+y x ,则此直线与已知圆的位置关系是__________。
2、若直线m x y +=与曲线24x y -=有且只有一个公共点,则实数m 的取值范围是_________。
知识二:圆与圆的位置关系3、两圆221:2220Cx y x y +++-=,222:4210C x y x y +--+=的公切线有且仅有( )A .1条B .2条C .3条D .4条4、若圆042222=-+-+m mx y x 与圆08442222=-+-++m my x y x 相切,则实数m 的取值集合是 。
知识三:圆的切线问题5、过点P (-1,6)且与圆4)2()3(22=-++y x 相切的直线方程是________________.6、已知直线0125=++a y x 与圆0222=+-y x x 相切,则a 的值为 。
知识四:圆的弦长问题7、求直线063:=--y x l 被圆042:22=--+y x y x C 截得的弦AB 的长__________.8、设直线03=+-y ax 与圆4)2()1(22=-+-y x 相交于A 、B 两点,且弦AB 的长为32,则=a 。
知识五:圆的方程问题9、求经过点A(2,-1),和直线1=+y x 相切,且圆心在直线x y 2-=上的圆的方程.10、圆0322222=++-++a a ay ax y x 的圆心在( )A .第一象限B .第二象限C .第三象限D .第四象限知识六:综合问题11、圆0104422=---+y x y x 上的点到直线014=-+y x 的最大距离与最小距离的差是( )A 。
《直线和圆的方程》复习一、直线的方程1、倾斜角:范围 ,若x l //轴或与x 轴重合时, 。
2、斜率: k=α与k 的关系:α=0⇔k =0<α<2k π⇔> α=2k π⇔22k ππ<<⇔<已知L 上两点P 1(x 1,y 1)P 2(x 2,y 2)⇒k=当1x =2x 时,α= ,κ 。
3、截距: 特别:曲线过原点⇔横纵截距都为0。
几种特殊位置的直线 ①x 轴: ②y 轴:③平行于x 轴:④平行于y 轴: ⑤过原点:②任何一个关于x 、y 的二元一次方程都表示一条直线。
5、直线系:(1)共点直线系方程:p 0(x 0,y 0)为定值,k 为参数(1) (2) 特别:y=kx+b ,表示过(0、b )的直线系(不含y 轴) (2)平行直线系:①y=kx+b ,k 为定值,b 为参数。
②与Ax+By+C=0 平行的直线系 ③与Ax+By+C=0垂直的直线系 (3)过L 1 :A 1x+B 1y+C 1=0,L 2: A 2X+B 2Y+C 2=0交点的直线系 (不含2l ) 6、三点共线的判定:①AC BC AB =+,② ,③写出过其中两点的方程,再验证第三点在直线上。
二、两直线的位置关系:2、距离:①点到直线距离:已知点p 0(x 0,y 0),L :AX+BY+C=0d=②两行平线间距离:L 1=AX+BY+C 1=0 L 2:AX+BY+C 2=0⇒ d=(与AX+BY+C=0平行且距离为d 的直线方程为Ax+By+C ±022=+B A d 与AX+BY+C 1=0和AX+BY+C 2=0平行且距离相等的直线方程是:0221=+++C C BY AX )3、对称:(1)点关于点对称:p(x 1,y 1)关于M (x 0,y 0)的对称)2,2(1010Y Y X X P --' (2)点关于线的对称:设p(a(3)求点P (X 0、Y 0)关于L :如图:(思路1)设P 点关于L 的对称点为P 0(x 0,y 0) 则 Kpp 0﹡K L =-1P, P 0中点满足L 方程解出P 0(x 0,y 0)(思路2)写出过P ⊥L 的垂线方程,先求垂足,然后用中点坐标公式求出P 0(x 0,y 0)的坐标。
圆的标准方程【知识梳理】1.圆的标准方程(1)圆的定义:平面内到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径.(2)确定圆的要素是圆心和半径,如图所示.(3)圆的标准方程:圆心为A (a ,b ),半径长为r 的圆的标准方程是(x -a )2+(y -b )2=r 2. 当a =b =0时,方程为x 2+y 2=r 2,表示以原点为圆心、半径为r 的圆.2.点与圆的位置关系圆的标准方程为(x -a )2+(y -b )2=r 2,圆心A (a ,b ),半径为r .设所给点为M (x 0,y 0),则题型一、求圆的标准方程【例1】 过点A (1,-1),B (-1,1)且圆心在直线x +y -2=0上的圆的方程是( )A .(x -3)2+(y +1)2=4B .(x +3)2+(y -1)2=4C .(x -1)2+(y -1)2=4D .(x +1)2+(y +1)2=4[解析] 法一:设所求圆的标准方程为(x -a )2+(y -b )2=r 2,由已知条件知⎩⎪⎨⎪⎧ (1-a )2+(-1-b )2=r 2,(-1-a )2+(1-b )2=r 2,a +b -2=0,解此方程组,得⎩⎪⎨⎪⎧ a =1,b =1,r 2=4.故所求圆的标准方程为(x -1)2+(y -1)2=4.法二:设点C 为圆心,∵点C 在直线x +y -2=0上,∴可设点C 的坐标为(a,2-a ).又∵该圆经过A ,B 两点,∴|CA |=|CB |. ∴(a -1)2+(2-a +1)2 =(a +1)2+(2-a -1)2,解得a =1.∴圆心坐标为C (1,1),半径长r =|CA |=2.故所求圆的标准方程为(x -1)2+(y -1)2=4.法三:由已知可得线段AB 的中点坐标为(0,0),k AB =1-(-1)-1-1=-1,所以弦AB 的垂直平分线的斜率为k =1,所以AB 的垂直平分线的方程为y -0=1·(x -0),即y =x .则圆心是直线y =x 与x +y -2=0的交点,由⎩⎪⎨⎪⎧ y =x ,x +y -2=0,得⎩⎪⎨⎪⎧x =1,y =1, 即圆心为(1,1),圆的半径为(1-1)2+[1-(-1)]2=2,故所求圆的标准方程为(x -1)2+(y -1)2=4.[答案] C【类题通法】确定圆的标准方程就是设法确定圆心C (a ,b )及半径r ,其求解的方法:一是待定系数法,如解法一,建立关于a ,b ,r 的方程组,进而求得圆的方程;二是借助圆的几何性质直接求得圆心坐标和半径,如解法二、三.一般地,在解决有关圆的问题时,有时利用圆的几何性质作转化较为简捷.【对点训练】1.求下列圆的标准方程:(1)圆心是(4,-1),且过点(5,2);(2)圆心在y 轴上,半径长为5,且过点(3,-4);(3)求过两点C (-1,1)和D (1,3),圆心在x 轴上的圆的标准方程.解:(1)圆的半径长r = (5-4)2+(2+1)2=10,故圆的标准方程为(x -4)2+(y +1)2=10.(2)设圆心为C (0,b ),则(3-0)2+(-4-b )2=52,解得b =0或b =-8,则圆心为(0,0)或(0,-8).又∵半径r =5,∴圆的标准方程为x 2+y 2=25或x 2+(y +8)2=25.(3)直线CD 的斜率k CD =3-11+1=1,线段CD 中点E 的坐标为(0,2),故线段CD 的垂直平分线的方程为y -2=-x ,即y =-x +2,令y =0,得x =2,即圆心为(2,0).由两点间的距离公式,得r = (2-1)2+(0-3)2=10.所以所求圆的标准方程为(x -2)2+y 2=10.题型二、点与圆的位置关系【例2】 如图,已知两点P 1(4,9)和P 2(6,3).(1)求以P 1P 2为直径的圆的方程;(2)试判断点M (6,9),N (3,3),Q (5,3)是在圆上,在圆内,还是在圆外.[解] (1)设圆心C (a ,b ),半径长为r ,则由C 为P 1P 2的中点,得a=4+62=5,b =9+32=6.又由两点间的距离公式得r =|CP 1|= (4-5)2+(9-6)2=10,故所求圆的方程为(x -5)2+(y -6)2=10.(2)由(1)知,圆心C (5,6),则分别计算点到圆心的距离:|CM |= (6-5)2+(9-6)2=10;|CN |= (3-5)2+(3-6)2=13>10;|CQ |= (5-5)2+(3-6)2=3<10.因此,点M 在圆上,点N 在圆外,点Q 在圆内.【类题通法】1.判断点与圆的位置关系的方法(1)只需计算该点与圆的圆心距离,与半径作比较即可;(2)把点的坐标代入圆的标准方程,判断式子两边的符号,并作出判断.2.灵活运用若已知点与圆的位置关系,也可利用以上两种方法列出不等式或方程,求解参数范围.【对点训练】2.点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围是()A.-1<a<1B.0<a<1C.a>1或a>-1 D.a=±1解析:选A由于点(1,1)在圆(x-a)2+(y+a)2=4的内部,所以(1-a)2+(1+a)2<4,a2<1,所以-1<a<1.【练习反馈】1.圆(x-1)2+(y+3)2=1的圆心坐标是()A.(1,3)B.(-1,3)C.(1,-3) D.(-1,-3)答案:C2.点P(m,5)与圆x2+y2=24的位置关系是()A.在圆外B.在圆内C.在圆上D.不确定解析:选A∵m2+25>24,∴点P在圆外.3.若点P(-1,3)在圆x2+y2=m2上,则实数m=________.解析:∵P点在圆x2+y2=m2上,∴(-1)2+(3)2=4=m2,∴m=±2.答案:±24.经过原点,圆心在x轴的负半轴上,半径为2的圆的方程是________.解析:圆心是(-2,0),半径是2,所以圆的方程是(x+2)2+y2=4.答案:(x+2)2+y2=45.求以A(2,2),B(5,3),C(3,-1)为顶点的三角形的外接圆的方程.解:设所求圆的方程是(x-a)2+(y-b)2=r2.将点A(2,2),B(5,3),C(3,-1)代入上式得⎩⎪⎨⎪⎧ (2-a )2+(2-b )2=r 2,(5-a )2+(3-b )2=r 2,(3-a )2+(-1-b )2=r 2,解此方程组,得⎩⎪⎨⎪⎧ a =4,b =1,r 2=5. 所以,△ABC 的外接圆方程是(x -4)2+(y -1)2=5.。
第12课 直线与圆、圆与圆的问题 复习目标1. 理解直线与圆、圆与圆的位置关系;2. 掌握直线与圆的方程的简单应用;知识归纳1、直线与圆的位置关系有三种:(1)直线与圆______⇔有两个公共点;(2)直线与圆______⇔有一个公共点;(3)直线与圆______⇔没有公共点。
2、直线与圆的位置关系直线l :Ax+By+C=0与圆(r>0)的位置关系的判定方法(1)几何法 圆心C(a,b)到直线l :Ax+By+C=0的距离=d ________________, 若______⇔直线与圆相交;若______⇔直线与圆相切;若______⇔直线与圆相离。
(2)代数法 由直线与圆的方程联立得方程组,消元后得到的一元二次方程的判别式为∆,则:若_______⇔直线与圆相交;若_______⇔直线与圆相切;若_______⇔直线与圆相离。
3、直线被圆所截得的弦长公式如右图,222||2||d r BC AB -==(垂径分弦定理)。
3、圆与圆的位置关系(1)圆与圆的位置关系有相离、相交、外切、内切、内含五种情况。
(2)设两圆)0()()(1212121>=-+-r r b y a x 与)0()()(2222222>=-+-r r b y a x 的圆心距d O O =||21,则:____________________⇔相离;____________________⇔外切;____________________⇔相交;____________________⇔内切;____________________⇔内含。
基础训练1、两圆229x y +=和228690x y x y +-++=的位置关系是( )A .相离B .相交C .内切D .外切2、若直线2=-y x 被圆4)(22=+-y a x 所截得的弦长为22,则实数a 的值为A .1-或3B .1或3C .2-或6D .0或43、若直线1=+by ax 与圆122=+y x 相交,则点),(b a P 的位置是( )A 、在圆上B 、在圆外C 、在圆内D 、都有可能4、过点)6,1(-P 且与圆4)2()3(22=-++y x 相切的直线方程是___________________;A CB O d r5、已知圆C 的方程为03222=--+y y x ,过点(1,2)P -的直线l 与圆C 交于,A B 两点,若使AB 最小,则直线l 的方程是________________。