2016年05月01日4--4高中数学组卷 (1)

高中数学组卷高中数学组卷一．选择题（共12小题）1．（2016•山东模拟）已知集合，则集合A的真子集的个数为（）A．3 B．4 C．1 D．22．（2014•郴州三模）设函数，且函数f（x）为偶函数，则g（﹣2）=（）A．6 B．﹣6 C．2 D．﹣23．（2016•江门模拟）若复数z=（a2+2a﹣3）+（a+3）i为纯虚数（i为虚数单位），则实数a的值是（）A．﹣3 B．﹣3或1 C．3或﹣1 D．14．（2016•江西校级一模）如图是一个无盖器皿的三视图，正视图、侧视图和俯视图中的正方形边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是（）A．π+24 B．π+20 C．2π+24 D．2π+205．（2016•南昌校级二模）执行如图所示的程序框图，如果输入的t=50，则输出的n=（）A．5 B．6 C．7 D．86．（2016•绵阳模拟）直线x﹣y﹣3=0的倾斜角是（）A．30°B．60°C．120°D．150°7．（2016•贵州校级模拟）已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（）A．﹣2 B．﹣4 C．﹣6 D．﹣88．（2016•新余校级一模）已知{a n}是等差数列，a10=17，其前10项的和S10=80，则其公差d=（）A．2 B．﹣2 C．﹣1 D．19．（2016•福州模拟）若实数x，y满足不等式组目标函数t=x﹣2y的最大值为2，则实数a的值是（）A．﹣2 B．0 C．1 D．210．（2016•莱芜一模）已知直线ax+by=1经过点（1，2），则2a+4b的最小值为（）A．B．2C．4 D．411．（2016•延安校级二模）已知椭圆的标准方程为，则椭圆的焦点坐标为（）A．B．C．（0，3），（0，﹣3）D．（3，0），（﹣3，0）12．（2016•郴州一模）函数y=的图象大致是（）A．B．C．D．二．填空题（共4小题）13．（2016•台州一模）已知角α的终边落在直线y=﹣2x上，则tanα=，=．14．（2016•揭阳一模）已知=（1，﹣2），+=（0，2），则||=．15．（2016•嘉兴二模）计算：sin15°=；=．16．（2015•龙岩模拟）为了判断高中二年级学生是否喜欢足球运动与性别的关系，现随机抽取50名学生，得到2×2列联表：喜欢不喜欢总计男15 10 25女 5 20 25总计20 30 50附表：P（K2≥k0）0.010 0.005 0.001k0 6.635 7.879 10.828（参考公式k2=，（n=a+b+c+d）则有以上的把握认为“喜欢足球与性别有关”．三．解答题（共7小题）17．（2016•郴州二模）已知向量=（sinx，），=（cosx，﹣1），（Ⅰ）当∥时，求tan2x的值；（Ⅱ）求函数f（x）=（+）•在[﹣，0]上的值域．18．（2016•渭南一模）在△ABC中，角A，B，C的对应边分别是a，b，c满足b2+c2=bc+a2．（Ⅰ）求角A的大小；（Ⅱ）已知等差数列{a n}的公差不为零，若a1cosA=1，且a2，a4，a8成等比数列，求{}的前n项和S n．19．（2016•黔东南州模拟）移动公司在国庆期间推出4G套餐，对国庆节当日办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元．国庆节当天参与活动的人数统计结果如图所示，现将频率视为概率．（1）求某人获得优惠金额不低于300元的概率；（2）若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选出两人，求这两人获得相等优惠金额的概率．20．（2016•常州一模）在平面直角坐标系xOy中，设椭圆（a＞b＞0）的离心率是e，定义直线y=为椭圆的“类准线”，已知椭圆C的“类准线”方程为y=，长轴长为4．（1）求椭圆C的方程；（2）点P在椭圆C的“类准线”上（但不在y轴上），过点P作圆O：x2+y2=3的切线l，过点O且垂直于OP的直线l交于点A，问点A是否在椭圆C上？证明你的结论．21．（2016•佛山模拟）设a∈R，函数f（x）=lnx﹣ax．（Ⅰ）讨论函数f（x）的单调区间和极值；（Ⅱ）已知x1=（e为自然对数的底数）和x2是函数f（x）的两个不同的零点，求a的值并证明：x2＞．22．（2016•蚌埠一模）如图，已知AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．（I）求证：AC⊥平面BCE；（II）求三棱锥E﹣BCF的体积．23．（2016•安康二模）已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合．直线l的参数方程是（t为参数），曲线C的极坐标方程为ρ=sin（）．（1）求曲线C的直角坐标方程；（2）设直线l与曲线C相交于M、N两点，求M、N两点间的距离．参考答案与试题解析一．选择题（共12小题）1．（2016•山东模拟）已知集合，则集合A的真子集的个数为（）A．3 B．4 C．1 D．2【解答】解：∵集合={2}，∴集合A的真子集只有一个为∅．故选：C．2．（2014•郴州三模）设函数，且函数f（x）为偶函数，则g（﹣2）=（）A．6 B．﹣6 C．2 D．﹣2【解答】解：∵为偶函数，令h（x）=x+x2则g（﹣2）=h（2）=6故选A3．（2016•江门模拟）若复数z=（a2+2a﹣3）+（a+3）i为纯虚数（i为虚数单位），则实数a的值是（）A．﹣3 B．﹣3或1 C．3或﹣1 D．1【解答】解：∵复数z=（a2+2a﹣3）+（a+3）i为纯虚数，∴，解得a=1，故选D．4．（2016•江西校级一模）如图是一个无盖器皿的三视图，正视图、侧视图和俯视图中的正方形边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是（）A．π+24 B．π+20 C．2π+24 D．2π+20【解答】解：该器皿的表面积可分为两部分：去掉一个圆的正方体的表面积s1和半球的表面积s2，s1=6×2×2﹣π×12=24﹣π，s2==2π，故s=s1+s2=π+24故选：A．5．（2016•南昌校级二模）执行如图所示的程序框图，如果输入的t=50，则输出的n=（）A．5 B．6 C．7 D．8【解答】解：第一次运行后s=2，a=3，n=1；第二次运行后s=5，a=5，n=2；第三次运行后s=10，a=9，n=3；第四次运行后s=19，a=17，n=4；第五次运行后s=36，a=33，n=5；第六次运行后s=69，a=65，n=6；此时不满足s＜t，输出n=6，故选：B．6．（2016•绵阳模拟）直线x﹣y﹣3=0的倾斜角是（）A．30°B．60°C．120°D．150°【解答】解：设直线的倾斜角为θ，θ∈[0，180°）．∴tanθ=．∴θ=60°．故选：B．7．（2016•贵州校级模拟）已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（）A．﹣2 B．﹣4 C．﹣6 D．﹣8【解答】解：圆x2+y2+2x﹣2y+a=0 即（x+1）2+（y﹣1）2=2﹣a，故弦心距d==．再由弦长公式可得2﹣a=2+4，∴a=﹣4，故选：B．8．（2016•新余校级一模）已知{a n}是等差数列，a10=17，其前10项的和S10=80，则其公差d=（）A．2 B．﹣2 C．﹣1 D．1【解答】解：设{a n}等差数列的公差为d，则由题意可得a10=a1+9d=17，S10=10a1+d=80，联立可解得d=2故选：A9．（2016•福州模拟）若实数x，y满足不等式组目标函数t=x﹣2y的最大值为2，则实数a的值是（）A．﹣2 B．0 C．1 D．2【解答】解：画出约束条件表示的可行域由⇒A（2，0）是最优解，直线x+2y﹣a=0，过点A（2，0），所以a=2，故选D10．（2016•莱芜一模）已知直线ax+by=1经过点（1，2），则2a+4b的最小值为（）A．B．2C．4 D．4【解答】解：∵直线ax+by=1经过点（1，2），∴a+2b=1．则2a+4b≥==2，当且仅当时取等号．故选：B．11．（2016•延安校级二模）已知椭圆的标准方程为，则椭圆的焦点坐标为（）A．B．C．（0，3），（0，﹣3）D．（3，0），（﹣3，0）【解答】解：由椭圆的标准方程，得a2=10，b2=1，∴c2=a2﹣b2=10﹣1=9，则c=3，∴椭圆的焦点坐标为（3，0），（﹣3，0）．故选：D．12．（2016•郴州一模）函数y=的图象大致是（）A．B．C．D．【解答】解：f（﹣x）==﹣f（x），故函数为奇函数，图象应关于原点对称，排除BC，∵（x﹣sinx）′=1﹣cosx≥0，∴当x＞0时，函数x﹣sinx单调递增，故单调递减，D不符合，A符合，故选：A二．填空题（共4小题）13．（2016•台州一模）已知角α的终边落在直线y=﹣2x上，则tanα=﹣2，=．【解答】解：角α终边在直线y=﹣2x上，在直线y=2x上取一个点A（1，﹣2），则OA=，所以：sinα=﹣，cosα=．所以：tanα=﹣2，所以：=sin2α===﹣．故答案为：﹣2，．14．（2016•揭阳一模）已知=（1，﹣2），+=（0，2），则||=．【解答】解：因为=（1，﹣2），+=（0，2），所以=（﹣1，4），所以；故答案为：15．（2016•嘉兴二模）计算：sin15°=；=．【解答】解：sin15°=sin（45°﹣30°）=sin45°cos30°﹣cos45°sin30°=﹣=；==tan60°=，故答案为：；．16．（2015•龙岩模拟）为了判断高中二年级学生是否喜欢足球运动与性别的关系，现随机抽取50名学生，得到2×2列联表：喜欢不喜欢总计男15 10 25女 5 20 25总计20 30 50附表：P（K2≥k0）0.010 0.005 0.001k0 6.635 7.879 10.828（参考公式k2=，（n=a+b+c+d）则有99.5%以上的把握认为“喜欢足球与性别有关”．【解答】解：∵根据表中数据，得到k2的观测值≈8.333＞7.879，由于P（k2≥7.879）≈0.005，∴有99.5%以上的把握认为“喜欢足球与性别有关”．故答案为：99.5%．三．解答题（共7小题）17．（2016•郴州二模）已知向量=（sinx，），=（cosx，﹣1），（Ⅰ）当∥时，求tan2x的值；（Ⅱ）求函数f（x）=（+）•在[﹣，0]上的值域．【解答】解：（Ⅰ）∵∥，=（sinx，），=（cosx，﹣1），∴sinx•（﹣1）﹣•cosx=0，即sinx+cosx=0，得sinx=﹣cosx，由此可得tanx==﹣，∴tan2x==；（Ⅱ）∵=（sinx，），=（cosx，﹣1），∴•=sinxcosx﹣，=cos2x+（﹣1）2=cos2x+1，f（x）=（+）•=•+=sinxcosx﹣+cos2x+1=sin2x+（1+cos2x）﹣=sin（2x+），∵x∈[﹣，0]，可得2x+∈[﹣，]，∴sin（2x+）∈[﹣，1]，f（x）=sin（2x+）∈[﹣，]．即函数f（x）=（+）•在[﹣，0]上的值域为[﹣，]．18．（2016•渭南一模）在△ABC中，角A，B，C的对应边分别是a，b，c满足b2+c2=bc+a2．（Ⅰ）求角A的大小；（Ⅱ）已知等差数列{a n}的公差不为零，若a1cosA=1，且a2，a4，a8成等比数列，求{}的前n项和S n．【解答】解：（Ⅰ）∵b2+c2﹣a2=bc，∴=，∴cosA=，∵A∈（0，π），∴A=．（Ⅱ）设{a n}的公差为d，∵a1cosA=1，且a2，a4，a8成等比数列，∴a1==2，且=a2•a8，∴（a1+3d）2=（a1+d）（a1+7d），且d≠0，解得d=2，∴a n=2n，∴==，∴S n=（1﹣）+（）+（）+…+（）=1﹣=．19．【解答】解（1）设事件A=“某人获得优惠金额不低于300元”，则．（2）设事件B=“从这6人中选出两人，他们获得相等优惠金额”，由题意按分层抽样方式选出的6人中，获得优惠200元的1人，获得优惠500元的3人，获得优惠300元的2人，分别记为a1，b1，b2，b3，c1，c2，从中选出两人的所有基本事件如下：a1b1，a1b2，a1b3，a1c1，a1c2，b1b2，b1b3，b1c1，b1c2，b2b3，b2c1，b2c2，b3c1，b3c2，c1c2，共15个．其中使得事件B成立的为b1b2，b1b3，b2b3，c1c2，共4个则．20．【解答】解：（1）由题意得：==2，2a=4，又a2=b2+c2，联立以上可得：a2=4，b2=3，c2=1．∴椭圆C的方程为+y2=1；（2）如图，由（1）可知，椭圆的类准线方程为y=±2，不妨取y=2，设P（x0，2）（x0≠0），则k OP=，∴过原点且与OP垂直的直线方程为y=﹣x，当x0=时，过P点的圆的切线方程为x=，过原点且与OP垂直的直线方程为y=﹣x，联立，解得：A（，﹣），代入椭圆方程成立；同理可得，当x0=﹣时，点A在椭圆上；当x0≠±时，联立，解得A1（，﹣），A2（﹣，），PA1所在直线方程为（2+x0）x﹣（x0﹣6）y﹣x02﹣12=0．此时原点O到该直线的距离d==，∴说明A点在椭圆C上；同理说明另一种情况的A也在椭圆C上．综上可得，点A在椭圆C上．21．【解答】解：（Ⅰ）函数f（x）的定义域为（0，+∞）．求导数，得f′（x）=﹣a=．①若a≤0，则f′（x）＞0，f（x）是（0，+∞）上的增函数，无极值；②若a＞0，令f′（x）=0，得x=．当x∈（0，）时，f′（x）＞0，f（x）是增函数；当x∈（，+∞）时，f′（x）＜0，f（x）是减函数．∴当x=时，f（x）有极大值，极大值为f（）=ln﹣1=﹣lna﹣1．综上所述，当a≤0时，f（x）的递增区间为（0，+∞），无极值；当a＞0时，f（x）的递增区间为（0，），递减区间为（，+∞），极大值为﹣lna﹣1（Ⅱ）∵x1=是函数f（x）的零点，∴f （）=0，即﹣a=0，解得a==．∴f（x）=lnx﹣x．∵f（）=﹣＞0，f（）=﹣＜0，∴f（）•f（）＜0．由（Ⅰ）知，函数f（x）在（2，+∞）上单调递减，∴函数f（x）在区间（，）上有唯一零点，因此x2＞．22．【解答】（I）证明：过C作CM⊥AB，垂足为M，∵AD⊥DC，∴四边形ADCM为矩形，∴AM=MB=2，∵AD=2，AB=4，∴AC=2，CM=2，BC=2∴AB2=AC2+BC2，即AC⊥BC，∵AF⊥平面ABCD，AF∥BE，∴EB⊥平面ABCD，∵AC⊂平面ABCD，∴AC⊥EB，∵EB∩BC=B，∴AC⊥平面BCE；（II）解：∵AF⊥平面ABCD，∴AF⊥CM，∴CM⊥AB，AB∩AF=A，∴CM⊥平面ABEF，∴V E﹣BCF=V C﹣BEF===．23．【解答】解：（1）将曲线C的极坐标方程化为ρ=sin（）=cosθ+sinθ两边都乘以ρ，得ρ2=ρcosθ+ρsinθ因为x=ρcosθ，y=ρsinθ，ρ2=x2+y 2代入上式，得方求曲线C的直角坐标方程为：x2+y2﹣x﹣y=0（2）直线l的参数方程是（t为参数），消去参数t得普通方程：4x﹣3y+1=0，将圆C的极坐标方程化为普通方程为：x2+y2﹣x﹣y=0，所以（）为圆心，半径等于所以，圆心C到直线l的距离d=所以直线l被圆C截得的弦长为：|MN|=2 =．即M、N两点间的距离为．。

高中数学组卷复习一．选择题（共12小题）1．（2016•南昌校级二模）设A={x∈Z||x|≤2}，B={y|y=x2+1，x∈A}，则B的元素个数是（）A．5 B．4 C．3 D．22．（2016•石嘴山校级一模）下列函数中，既是偶函数，又在（0，+∞）上是单调减函数的是（）A．y=B．y=cosx C．y=ln|x+1| D．y=﹣2|x|3．（2016•石嘴山校级二模）下列函数中，既是奇函数又在（﹣∞+∞）上单调递增的是（）A．y=﹣B．y=sinx C．y=x D．y=ln|x|4．（2016•河南一模）f（x）=则f[f（）]=（）A．﹣2 B．﹣3 C．9 D．5．（2016•日照一模）将函数y=sin（2x﹣）图象向左平移个单位，所得函数图象的一条对称轴的方程是（）A．x=B．x=C．x=D．x=﹣6．（2016•大连一模）已知向量=（2，﹣1），=（0，1），则|+2|=（）A．2 B．C．2 D．47．（2016•河南模拟）已知tan（α﹣）=，则的值为（）A．B．2 C．2D．﹣28．（2016•大连一模）在△ABC中，a，b，c分别是角A，B，C的对边，且满足acosA=bcosB，那么△ABC的形状一定是（）A．等腰三角形B．直角三角形C．等腰或直角三角形 D．等腰直角三角形9．（2016•北海一模）等差数列{a n}中，a4+a8=10，a10=6，则公差d等于（）A．B．C．2 D．﹣10．（2016•合肥二模）若a，b都是正数，则的最小值为（）A．7 B．8 C．9 D．1011．（2016•湖南二模）执行如图所示的程序框图，输出的k值是（）A．4 B．5 C．6 D．712．（2016•福建模拟）已知x与y之间的一组数据，则y与x的线性回归方程=x+必过点（）x 0 1 2 3y 1 3 5 7A．（2，2）B．（1，2）C．（1.5，4）D．（1.5，0）二．填空题（共4小题）13．（2016•四川模拟）log212﹣log23=．14．（2016•赣州模拟）已知向量，的夹角为60°，||=1，|2﹣|=，则||=．15．（2016•平度市一模）如果实数x，y满足条件那么2x﹣y的最大值为．16．（2016•佛山模拟）已知正项等比数列{a n}的前n项和为S n，若S3=3，S9﹣S6=12，则S6=．三．解答题（共10小题）17．（2016•郴州二模）已知函数f（x）=sin2x﹣cos2x﹣，x∈R．（1）求函数f（x）的最小正周期及单调递增区间；（2）设△ABC的内角A，B，C的对边分别为a，b，c，且c=，f（C）=0，sinB=2sinA，求△ABC的面积S．18．（2016•朔州模拟）已知数列{a n}为等差数列，数列{b n}满足b n=a n+n，若b2，b5，b11成等比数列，且b3=a6．（1）求a n，b n；（2）求数列{}的前n项和S n．19．（2016•红桥区一模）要将两种大小不同的较大块儿钢板，裁成A，B，C三种规格的小钢板，每张较大块儿钢板可同时裁成的三种规格小钢板的块数如下表：A规格B规格C规格第一种钢板 21 1第二种钢板 13 1第一种钢板面积为1m2，第二种钢板面积为2m2，今分别需要A规格小钢板15块，B规格小钢板27块，C规格小钢板13块．（1）设需裁第一种钢板x张，第二种钢板y张，用x，y列出符合题意的数学关系式，并在给出的平面直角坐标系中画出相应的平面区域；（2）在满足需求的条件下，问各裁这两种钢板多少张，所用钢板面积最小？20．（2016•白山一模）某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．（Ⅰ）求直方图中x的值；（Ⅱ）求续驶里程在[200，300]的车辆数；（Ⅲ）若从续驶里程在[200，300]的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为[200，250）的概率．21．（2016春•东台市校级月考）已知函数f（x）=log2．（1）求函数f（x）的定义域A；（2）设集合B={x|（x﹣a）（x﹣a﹣2）＜0}，若A∩B=B，求实数a的取值范围．22．（2015秋•青海校级期末）计算：（1）（π）0+2﹣2×（2）（2）2log510+log50.25．23．（2015秋•铅山县校级期末）若x1和x2分别是一元二次方程x2+4x﹣3=0的两个根，求：（1）|x1﹣x2|的值；（2）+的值；（3）x12+x22的值．24．（2015秋•赤峰期末）（1）计算：（2）+（lg5）0+（）；（2）解方程：log3（6x﹣9）=3．25．（2015秋•宜昌校级期末）计算：（Ⅰ）（Ⅱ）．26．（2015秋•株洲校级期末）已知函数f（x）=lg（1+x）﹣lg（1﹣x），（1）求函数f（x）的定义域；（2）判断函数f（x）的奇偶性；（3）求不等式f（x）＞0的解集．参考答案与试题解析一．选择题（共12小题）1．（2016•南昌校级二模）设A={x∈Z||x|≤2}，B={y|y=x2+1，x∈A}，则B的元素个数是（）A．5 B．4 C．3 D．2【解答】解：A={x∈Z||x|≤2}={﹣2，﹣1，0，1，2}，B={y|y=x2+1，x∈A}={5，2，1}B的元素个数是3故选C．2．（2016•石嘴山校级一模）下列函数中，既是偶函数，又在（0，+∞）上是单调减函数的是（）A．y=B．y=cosx C．y=ln|x+1| D．y=﹣2|x|【解答】解：对于A，为幂函数，定义域为[0，+∞），不关于原点对称，则不具奇偶性，则A不满足；对于B，为余弦函数，为偶函数，在（2kπ，2kπ+π）（k∈Z）上递减，则B不满足；对于C，定义域为{x|x≠﹣1}不关于原点对称，则不具奇偶性，则C不满足；对于D，定义域为R，f（﹣x）=﹣2|﹣x|=f（x），为偶函数，x＞0时，y=﹣2x递减，则D满足．故选D．3．（2016•石嘴山校级二模）下列函数中，既是奇函数又在（﹣∞+∞）上单调递增的是（）A．y=﹣B．y=sinx C．y=x D．y=ln|x|【解答】解：y=﹣在（﹣∞，0），（0，+∞）上单调递增，但在定义域内不单调，故排除A；y=sinx在每个区间（2kπ﹣，2kπ+）（k∈Z）上单调递增，但在定义域内不单调，故排除B；令f（x）=，其定义域为R，且f（﹣x）==﹣=﹣f（x），所以f（x）为奇函数，又f′（x）=3x2≥0，所以f（x）在R上单调递增，故选：C．4．（2016•河南一模）f（x）=则f[f（）]=（）A．﹣2 B．﹣3 C．9 D．【解答】解：∵f（x）=，∴==﹣2．∴f[f（）]=f（﹣2）==9．故选：C．5．（2016•日照一模）将函数y=sin（2x﹣）图象向左平移个单位，所得函数图象的一条对称轴的方程是（）A．x=B．x=C．x=D．x=﹣【解答】解：将函数y=sin（2x﹣）图象向左平移个单位，所得函数图象对应的解析式为y=sin[2（x+）﹣]=sin （2x+）．令2x+=kπ+，k∈z，求得x=+，故函数的一条对称轴的方程是x=，故选：A．6．（2016•大连一模）已知向量=（2，﹣1），=（0，1），则|+2|=（）A．2 B．C．2 D．4【解答】解：向量=（2，﹣1），=（0，1），则|+2|=|（2，1）|=．故选：B．7．（2016•河南模拟）已知tan（α﹣）=，则的值为（）A．B．2 C．2D．﹣2【解答】解：由tan（α﹣）==，得tanα=3．则=．故选：B．8．（2016•大连一模）在△ABC中，a，b，c分别是角A，B，C的对边，且满足acosA=bcosB，那么△ABC的形状一定是（）A．等腰三角形B．直角三角形C．等腰或直角三角形 D．等腰直角三角形【解答】解：根据正弦定理可知∵bcosB=acosA，∴sinBcosB=sinAcosA∴sin2A=sin2B∴A=B，或2A+2B=180°即A+B=90°，即有△ABC为等腰或直角三角形．故选C．9．（2016•北海一模）等差数列{a n}中，a4+a8=10，a10=6，则公差d等于（）A．B．C．2 D．﹣【解答】解：在等差数列{a n}中，由a4+a8=10，得2a6=10，a6=5．又a10=6，则．故选：A．10．（2016•合肥二模）若a，b都是正数，则的最小值为（）A．7 B．8 C．9 D．10【解答】解：∵a，b都是正数，则=5++≥5+2=9，当且仅当b=2a＞0时取等号．故选：C．11．（2016•湖南二模）执行如图所示的程序框图，输出的k值是（）A．4 B．5 C．6 D．7【解答】解：第一次循环：n=3×5+1=16，k=0+1=1，继续循环；第二次循环：n==8，k=1+1=2，继续循环；第三次循环：n==4，k=2+1=3，继续循环；第四次循环：n==2，k=3+1=4，继续循环；第五次循环：n==1，k=4+1=5，结束循环．输出k=5．故选B．12．（2016•福建模拟）已知x与y之间的一组数据，则y与x的线性回归方程=x+必过点（）x 0 1 2 3y 1 3 5 7A．（2，2）B．（1，2）C．（1.5，4）D．（1.5，0）【解答】解：回归方程必过点（，），∵==，==4，∴回归方程过点（1.5，4）．故选：C二．填空题（共4小题）13．（2016•四川模拟）log212﹣log23=2．【解答】解：log212﹣log23==log24=2．故答案为：2．14．（2016•赣州模拟）已知向量，的夹角为60°，||=1，|2﹣|=，则||=1．【解答】解：∵向量，的夹角为60°，||=1，|2﹣|=，∴|2﹣|2==3，解得：=1．故答案为：115．（2016•平度市一模）如果实数x，y满足条件那么2x﹣y的最大值为1．【解答】解：先根据约束条件画出可行域，当直线2x﹣y=t过点A（0，﹣1）时，t最大是1，故答案为：1．16．（2016•佛山模拟）已知正项等比数列{a n}的前n项和为S n，若S3=3，S9﹣S6=12，则S6=9．【解答】解：∵正项等比数列{a n}的前n项和为S n，∴S3，S6﹣S3，S9﹣S6成等比数列即（S6﹣S3）2=S3•（S9﹣S6），∴（S6﹣3）2=3×12解得S6=9或﹣3（正项等比数列可知﹣3舍去），故答案为：9三．解答题（共10小题）17．（2016•郴州二模）已知函数f（x）=sin2x﹣cos2x﹣，x∈R．（1）求函数f（x）的最小正周期及单调递增区间；（2）设△ABC的内角A，B，C的对边分别为a，b，c，且c=，f（C）=0，sinB=2sinA，求△ABC的面积S．【解答】解：（1）∵f（x）=sin2x﹣cos2x﹣=sin2x﹣=sin（2x﹣）﹣1，…（3分）∴最小正周期T=，．由2k，k∈Z 得k，k∈Z，∴f（x）的最小正周期为π，单调递增区间为[k，k]（k∈Z）．…（6分）（2）f（C）=sin（2C﹣）﹣1=0，则sin（2C﹣）=1，∵0＜C＜π，∴0＜2C＜2π，∴﹣，∴2C﹣=，∴C=，…（8分）∵sinB=2sinA，由正弦定理，得，①由余弦定理，得c2=a2+b2﹣2abcos，即a2+b2﹣ab=3，②由①②解得a=1，b=2．∴S△ABC==．…（12分）18．（2016•朔州模拟）已知数列{a n}为等差数列，数列{b n}满足b n=a n+n，若b2，b5，b11成等比数列，且b3=a6．（1）求a n，b n；（2）求数列{}的前n项和S n．【解答】解：（1）设数列{a n}的公差为d，则a n=a1+（n﹣1）d，b n=a1+（n﹣1）d+n，∵b2，b5，b11成等比数列，且b3=a6．∴，解得．于是a n=n+2，b n=2n+2．（2）==．∴S n=++…+==．19．（2016•红桥区一模）要将两种大小不同的较大块儿钢板，裁成A，B，C三种规格的小钢板，每张较大块儿钢板可同时裁成的三种规格小钢板的块数如下表：A规格B规格C规格第一种钢板 21 1第二种钢板 13 1第一种钢板面积为1m2，第二种钢板面积为2m2，今分别需要A规格小钢板15块，B规格小钢板27块，C规格小钢板13块．（1）设需裁第一种钢板x张，第二种钢板y张，用x，y列出符合题意的数学关系式，并在给出的平面直角坐标系中画出相应的平面区域；（2）在满足需求的条件下，问各裁这两种钢板多少张，所用钢板面积最小？【解答】解：（1）设需截第一种钢板x张，第二种钢板y张，所用钢板数为z，则有，作出可行域（如图），，（2）设所用钢板的面积是zm2，目标函数为z=x+2y，∴y=﹣x+z，由得M（6，7），结合图象得z的最小值是6+2×7=20，故在满足需求的条件下，裁第一种钢板6张，第二种钢板7张，所用钢板面积最小．20．（2016•白山一模）某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．（Ⅰ）求直方图中x的值；（Ⅱ）求续驶里程在[200，300]的车辆数；（Ⅲ）若从续驶里程在[200，300]的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为[200，250）的概率．【解答】解：（Ⅰ）由直方图可得：（0.002+0.005+0.008+x+0.002）×50=1，∴x=0.003；（Ⅱ）由题意可知，续驶里程在[200，300]的车辆数为：20×（0.003×50+0.002×50）=5；（Ⅲ）由（Ⅱ）及题意可知，续驶里程在[200，250）的车辆数为3，续驶里程在[250，300]的车辆数为2，从这5辆中随机抽取2辆车，共有=10种抽法；其中恰有一辆汽车的续驶里程为[200，250）抽法有•=6种，∴恰有一辆车的续驶里程为[200，250）的概率为=．21．（2016春•东台市校级月考）已知函数f（x）=log2．（1）求函数f（x）的定义域A；（2）设集合B={x|（x﹣a）（x﹣a﹣2）＜0}，若A∩B=B，求实数a的取值范围．【解答】解：（1）由题意={x|x＞1或x＜﹣1}，即A=（﹣∞，﹣1）∪（1，+∞）…（6分）（2）B={x|（x﹣a）（x﹣a﹣2）＜0}=（a，a+2）．因为A∩B=B，所以B⊆A，进而a+2≤﹣1或a≥1，故a≤﹣3或a≥1…（8分）22．（2015秋•青海校级期末）计算：（1）（π）0+2﹣2×（2）（2）2log510+log50.25．【解答】解：（1）原式=1+×（）=1+×=；…（5分）（2）原式=log5100+log50.25=log525=2．…（10分）23．（2015秋•铅山县校级期末）若x1和x2分别是一元二次方程x2+4x﹣3=0的两个根，求：（1）|x1﹣x2|的值；（2）+的值；（3）x12+x22的值．【解答】解：（1）∵x1和x2分别是一元二次方程x2+4x﹣3=0的两个根，∴x1+x2=﹣4，x1x2=﹣3，∴（x1﹣x2）2=（x1+x2）2﹣4x1x2=16+12=28，∴|x1﹣x2|=．（2）+===．（3）x12+x22=（x1+x2）2﹣2x1x2=16+6=22．24．（2015秋•赤峰期末）（1）计算：（2）+（lg5）0+（）；（2）解方程：log3（6x﹣9）=3．【解答】解：（1）=（）+（lg5）0+[（）3]=+1+=4．（2）由方程log3（6x﹣9）=3得6x﹣9=33=27，∴6x=36=62，∴x=2．经检验，x=2是原方程的解．∴原方程的解为x=2．25．（2015秋•宜昌校级期末）计算：（Ⅰ）（Ⅱ）．【解答】解：（Ⅰ）原式=，（Ⅱ）原式=．26．（2015秋•株洲校级期末）已知函数f（x）=lg（1+x）﹣lg（1﹣x），（1）求函数f（x）的定义域；（2）判断函数f（x）的奇偶性；（3）求不等式f（x）＞0的解集．【解答】解：（1）由函数有意义得，解得﹣1＜x＜1．∴f（x）的定义域是（﹣1，1）．（2）∵f（﹣x）=lg（1﹣x）﹣lg（1+x）=﹣f（x），∴f（x）是奇函数．（3）∵f（x）＞0，∴lg（1+x）＞lg（1﹣x），∴，解得0＜x＜1．∴不等式f（x）＞0的解集是（0，1）．。

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合，π2π{|sin ,(,]}63B y y x x ==?,则()A B R I ð=A.1(2,](1,4)2--U B.1(2,]4)2--U C.{-1,2,3} D.{-1,1,2,3}【命题意图】本题主要考查函数的定义域、值域及集合运算，考查运算求解能力，是基础题. 【答案】C2. 已知复数z 的共轭复数z 在复平面内对应的点的坐标为（2，-1），则复数i1+z的虚部为 （ ） A.1- B.21-C.23-D.23 【命题意图】本题主要考查复数的概念及复数的运算，考查运算求解能力，是基础题. 【答案】B【解析】由题知z =i 2-，所以i 2+=z ，所以i 1+z =i 1i 2++= )i 1)(i 1()i 1)(i 2(-+-+=i 2123-，故其虚部为21-,选B.3 下列函数既是奇函数又在（-1,1）上是增函数的是 （ ）A.πcos()2y x =+ B.x y 2-= C.xx y +-=22ln D.x x y --=22 【命题意图】本题主要考查函数的奇偶性与单调性，考查运用数学基础知识解决问题的能力，是基础题. 【答案】D【解析】πcos()2y x =+=x sin -是奇函数，但在（-1,1）上是减函数，故A 不符合题意； xy 2-=是奇函数，但在（-1,1）上不是单调函数，故B 不符合题意；xxy +-=22ln=)2ln()2ln(x x +--是奇函数，但在（-1,1）上是减函数，故C 不符合题意；x x y --=22是奇函数，且在（-1,1）上是增函数，故D 符合题意，选D.4. 《九章算术》有这样一个问题：今有男子善走，日增等里，九日走一千二百六十里，第一日、第四日、第七日所走之和为三百九十里，问第八日所走里数为 （ ） A ．150 B ．160 C ．170 D ．180 【命题意图】本题主要考查等差数列的通项公式与前n 项和公式，是基础题. 【答案】C5. 执行如图所示的程序框图，输入p ＝10，则输出的A 为 （ ）A ．－12B ．10C ．16D ．32 【命题意图】本题主要考查程序框图，考查运算求解能力，是基础题. 【答案】C【解析】第1次执行循环体：102+-=n S S =0-2+10=8>A =0，是，A =S =8，n =1≥p =10，否，n n 2==2，第2次执行循环体：102+-=n S S =8-4+10=14>A =8，是，A =S =14，n=2≥p=10，否，n n 2==4， 第3次执行循环体：102+-=n S S =14-8+10=16>A =14，是，A =S =16，n =4≥p =10，否， n n 2==8， 第4次执行循环体：102+-=n S S =16-16+10=10>A =16，否，n =8≥p =10，否， n n 2==16， 第5次执行循环体：102+-=n S S =10-32+10=-12>A =16，否，n =16≥p =10，是，输出A =16，故选C.6. 某空间几何体的三视图如图所示，则该几何体的体积为 （ ）A.128B.3128 C.364 D.332【命题意图】本题主要考查简单几何体的三视图及其体积的计算，考查空间想象能力、运算求解能力，是基础题. 【答案】C7. 已知函数)(x f =)sin(ϕω+x A )π||,0,0(<>>ϕωA 的图象向右平移6π个单位得到)(x g 的部分图象如图所示，则)cos(ϕω+=x A y 的单调增区间为( )A.]3ππ,π65π[--k k ，Z k ∈ B.]6π,π31π[π+-k k ，Z k ∈C. ]12ππ,π127π[--k k ，Z k ∈ D.]125ππ,π121π[+-k k ，Z k ∈ 【命题意图】本题主要考查三角函数的图象变换、三角函数的图象与性质，考查运算求解能力，是基础题. 【答案】A【解析】由题知)(x g =])6(sin[ϕπω+-x A =)6sin(ϕωπω+-x A ，由五点作图法知，⎪⎪⎩⎪⎪⎨⎧=+-⨯=+-⨯π6π3π2π6π12πϕωωϕωω，解得2=ω，3π2=ϕ，2=A ，所以)32π2cos(2+=x y ，令π23π22ππ2k x k ≤+≤-，Z k ∈，解得365ππππ-<≤-k x k ，Z k ∈，所以)cos(ϕω+=x A y 的单调增区间为]3,65[ππππ--k k ，Z k ∈，故选A. 8. 已知1A 、2A 与1F 、2F 分别为双曲线22221x y a b-=（00a b >>，）的左、右顶点与左、右焦点，P 是双曲线右支上任意一点，则以线段1PF 和12A A 为直径的两圆一定 （ ） A ．相交B.相切C.相离D.以上都可能【命题意图】本题主要考查双曲线的定义及两圆的位置关系的判定，考查运算求解能力，是基础题. 【答案】B9.如图所示，在△DEF 中，M 在线段DF 上，DE =3，DM =EM =2，sin F =35,则边EF 的长为（ ） A.4916C.154【命题意图】本题主要考查利用正、余弦定理解三角形，考查运算求解能力，是基础题. 【答案】D10. 已知函数()f x =ln 2b a x x x ++（,a b R ∈）的两个极值点分别在区间（12，1）和（1,2）内，则z a b =+的最大值为 （ ） A.-10 B.-7 C. -4 D.4【命题意图】本题主要考查函数的极值及简单线性规划的解法，考查转化与化归思想、运算求解能力，是中档题. 【答案】C【解析】易知函数()f x 的定义域为（0，+∞），()f x '=22a bx x -+=222x ax b x +-，由题知22x ax b +-=0的两解分别在区间（12，1）和（1,2）内，设()g x =22x ax b +-，则111()0222(1)20(2)820g a b g a b g a b ⎧=+->⎪⎪=+-<⎨⎪=+->⎪⎩，即21020280a b a b a b -+>⎧⎪-+<⎨⎪-+>⎩，作出可行域如图中阴影部分所示，作出直线0l ： 0a b +=，平移直线0l ，当直线z a b =+过点A 时，z 取得最大值，由21020a b a b -+=⎧⎨-+=⎩解得A (-3,-1)，z max =-3-1=-4，故选C.11.在三棱锥BCD A -中，△ABC 与△BCD 都是边长为6的正三角形，平面ABC ⊥平面BCD ，则该三棱锥的外接球的体积为 （ ） A.π155 B.π60 C.π1560 D.π1520 【命题意图】本题主要考查球的截面性质及球的体积计算，考查空间想象能力、运算求解能力、逻辑推理能力，是难题..【答案】D12. 已知函数)(x f =ax ax x +-2ln 恰有两个零点，则实数a 的取值范围为 （ ）A.（-∞，0）B.（0，+∞）C.（0,1）∪（1，+∞）D.（-∞，0）∪{1}【命题意图】本题主要考查函数零点、利用导数研究函数的图象与性质等综合问题，考查转化与化归思想、数形结合思想和运算求解能力，是难题. 【答案】C【解析】函数)(x f 的定义域为（0，+∞），由题知方程 ax ax x +-2ln =0，即方程)1(ln -=x a xx恰有两解，设x x x g ln )(=，则)(x g '=2ln 1xx-，当e 0<<x 时，)(x g '＞0，当e >x 时，)(x g '＜0，所以)(x g 在（0,e ）上是增函数，在（e ，+∞）上是减函数，且0)1(=g ，当e >x 时，)(x g ＞0，1)1(='g ，作出函数)(x g y =与函数)1(-=x a y 的图象如下图所示，由图可知，函数)(x g y =的图象与函数)1(-=x a y 的图象恰有2个交点的充要条件为10<<a 或1>a ，故选C.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知二项式n xx )3(2-的展开式的各项系数和为64，则展开式中含3x 的项的系数为 .【命题意图】本题主要考查二项式定理及其展开式的通项公式的应用，考查运算求解能力，是基础题. 【答案】540-14. 在△ABC 中，AB=3，AC=2，∠BAC=60°，M 是BC 的中点，N 在线段AM 上，且BN ⊥AM ，则向量在向量上的投影为 .【命题意图】本题主要考查向量的线性运算及向量数量积的应用，考查运算求解能力，是基础题. 【答案】3827【解析】以A 为原点、AB 所在直线为x 轴建立直角坐标系，则A （0,0），B （3,0），C （1，3），所以)23,2(M ，设λ==)23,2(λλ，∴-==)23,32(λλ-，因为BN AM ⊥，所以AM BN ×uuu r uuu r =0232332(2=⨯+-λλ），解得1924=λ，所以)19312,199(-=，所以BN AC ×uuu r uuu r =193123199⨯+-=1927，所以向量BN 在向量AC 上的投影为||BN AC AC ×uuu r uuu ruuu r =3827. 15. 已知P 是抛物线x y 42=上一点，F 是该抛物线的焦点，则以PF 为直径且过（0,2）的圆的标准方程为 .【命题意图】本题主要考查抛物线的定义、圆的标准方程，考查运算求解能力，是基础题.【答案】22223939()(()(2424x y x y -+=-+-=或 【解析】设),4(020y y P ，由题知)0,1(F ，由抛物线的定义知，圆的直径为||PF =4120y +，圆心为)2,821(020y y +，由题知20220)02()2821(-+-+y y = )41(2120y +，解得220±=y ，所以圆心为)2,23(±，半径为23，所以所求圆的标准方程为49)2()23(22=±+-y x . 16.已知函数)(x f =))(1(22b ax x x ++-的图象关于直线3=x 对称，则函数)(x f 的值域为 .【命题意图】本题主要考查函数的对称性、函数的值域，考查转化与化归思想、数形结合思想、运算求解能力，是难题.【答案】[-36,+∞）三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （本小题满分12分）已知数列{n a }的前n 项和为n S ，且满足*2()n n S a n n =+?N .（Ⅰ）求数列{n a }的通项公式；（Ⅱ）若n b =n na ，求数列{n b }的前n 项和n T .【命题意图】本题主要考查等比数列的概念、构造法求数列通项公式、错位相减法求和等，考查转化与化归思想、运算求解能力，是基础题.【解析】（Ⅰ）当n =1时，12111+==a S a ，解得11-=a ， 当2≥n 时，n a =1--n n S S =)12(21-+-+-n a n a n n ， 即121-=-n n a a ，………………2分 即)1(211-=--n n a a ，∵0211≠-=-a ，∴01≠-n a ，∴{1-n a }是首项为-2，公比为2的等比数列，………………4分 ∴1-n a =n2-，∴12+-=n n a . ………………6分 （Ⅱ）由（Ⅰ）知n b =n n n +⨯-2， ∴231212223232nn T n n =-?-?-?--?L=n n n ++++⨯++⨯+⨯+⨯- 21223222132）（，………………8分 设n n n M 223222132⨯++⨯+⨯+⨯= ，则13222)1(22212+⨯+-++⨯+⨯=n n n n n M ，两式相减得13222222+⨯-++++=-n nn n M =1221)21(2+⨯---n n n =22)1(1--+n n ， ∴n M =22)1(1+-+n n ，………………10分∵2)1(321+=++++n n n ， ∴n T =22)1(2)1(1-++-+n n n n . .………………12分 18.（本小题满分12分）中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”，为了了解人们对“延迟退休年龄政策”的态度，责成人社部进行调研，人社部从网上年龄在15~65的人群中随机调查50人，调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下：（Ⅰ）由以上统计数据填下面2´2列联表，并问是否有90％的把握认为以45岁为分界点对“延迟退休年龄政策”的支持度有差异；（Ⅱ）若从年龄在[45，55），[55，65]的被调查人中各随机选取两人进行调查，记选中的4人中支持“延迟退休”人数为ξ，求随机变量ξ的分布列及数学期望． 参考数据：【命题意图】本题主要考查总体估计、独立性检验、离散型随机变量的分布列与期望，考查阅读理解能力、运算求解能力，是基础题.(Ⅱ)由频率分布直方图知，被调查的50人中年龄在[45,55)和年龄在[55,65]的人数都为0.01×10×50=5，其中年龄在[45,55)和年龄在[55,65]支持“延迟退休”的人数分别为2，1，故ξ的所有可能取值为0, 1,2,3, ………………………6分22342255C C 9(0),C C 50P ξ=== ()11221234342255C C C C C 1C C P ξ+===2512， ()22111242342255C C C C C 2C C P ξ+===103， 142255C (3)C C P ξ===251，……………………10分所以的分布列是所以的期望值是012350251025E ξ=⨯+⨯+⨯+⨯=56. ………………………12分 19.（本小题满分12分）如图，在直角三角形ABC 中，∠BAC =60°，点F 在斜边AB 上，且AB=4AF ，D ，E 是平面ABC 同一侧的两点，AD ⊥平面ABC ，BE ⊥平面ABC ，AD =3，AC =BE =4. (Ⅰ)求证：平面CDF ⊥平面CEF ；(Ⅱ)若点M 是线段CB 的中点，求EM 与平面CEF 所成角的正弦值.ξξ【命题意图】本题主要考查空间线线垂直、线面垂直、面面垂直的判定与性质及线面角的计算，考查空间想象能力、运算求解能力，是中档题.(Ⅱ)以C 为坐标原点，建立如图所示的空间直角坐标系xyz C -，则)0,0,0(C ，)0,34,0(B ，)4,34,0(E ，)0,3,3(F ，)0,32,0(M ，∴=)4,34,0(，=)0,3,3(，=(0,4)--， ┄┄┄7分设平面CEF 的法向量为m =),,(z y x ，则4030CEz CFx ìï?+=ïíï?+=ïïîuur uu u rm m ，取x =1，则3-=y ，z =3，∴平面CEF 的一个法向量为m =（1，3-，3）， ┄┄┄9分 设直线ME 与平面CEF 所成的角为θ，则θsin =||||||EM EM ××uuu ruuu rm m91919， ┄┄┄11分 ∴直线ME 与平面12分20. （本小题满分12分）已知1F 、2F 分别是椭圆E ：)0(12222>>=+b a by a x 的左、右焦点，M 是椭圆E上一点，线段M F 1的中点为N ，△O NF 1（O 为坐标原点）的周长为3，过右焦点2F 与x 轴垂直的直线与椭圆E 在第一象限交于点C，23||2=C F .(Ⅰ)求椭圆E 的标准方程；(Ⅱ)过1F 作直线l 交椭圆E 于B A ,两点，)0,5(-P ，以PB PA ,为邻边作平行四边形PAQB ，求四边形PAQB 面积的取值范围.【命题意图】本题主要考查椭圆的定义、几何性质及直线与椭圆的位置关系，考查运算求解能力、逻辑思维能力，是难题.21. （本小题满分12分）已知函数2()x xf x x x e=+-（其中e 2.71828=L ）. (Ⅰ)求)(x f 在))1(,1(f 处的切线方程；(Ⅱ)若函数2()ln[()]g x f x x x b =-+-的两个零点为12,x x ，证明：1()g x '+2()g x '12()2x x g +'>. 【命题意图】本题主要考查常见函数的导数、导数的运算法则、导数的综合应用，考查运算求解能力、转化与化归思想，是难题. 【解析】(Ⅰ)由题意得1()+21e x x f x x -'=-，e1)1(=f ， ∴)(x f 在))1(,1(f 处的切线斜率为1)1(='f ， ∴)(x f 在))1(,1(f 处的切线方程为1e1-=-x y ，即01e e e =+--y x . ……………4分 (Ⅱ)由题意知函数()ln g x x x b =--，所以1()1g x x'=-， 因为12,x x 是函数()g x 的两个零点，所以1122ln ln x b x x b x +=⎧⎨+=⎩，相减得2211ln xx x x -=请考生在第22，23，24题中任选一题作答，如果多做，则按所做的第一题计分．22．（本小题满分10分）选修4—1：几何证明选讲如图，点P是△ABC的外接圆O在C点的切线与直线AB的交点．（Ⅰ）若∠ACB＝∠APC，证明：BC⊥PC；2，PC＝4，求CD的长．（Ⅱ）若D是圆O上一点，∠BPC=∠DAC，AC=2，AB=2【命题意图】本题主要考查三角形相似的判定与性质、弦切角定理、切割线定理等平面几何知识，考查推理论证能力，是容易题.【证明】（Ⅰ）由弦切角定理知，∠ABC=∠ACP，∵∠ACB＝∠APC，∴△ACB∽△APC，∴∠BAC=∠CAP，∵∠BAC+∠CAP=180°，∴∠BAC=∠CAP =90°，∴BC 是圆O 的直径，又PC 是圆O 的的切线，∴BC ⊥PC . ┄┄┄5分 （Ⅱ）由切割线定理知，PB PA PC ⨯=2，即)22(42+=PA PA ， 即016222=-+PA PA ，解得22=PA （负值舍去），由弦切角定理及同弧所对的圆周角相等知，∠ACP =∠ABC =∠CDA ， ∵∠BPC =∠DAC ，∴△CAD ∽△APC ，∴CD AC AC AP =，∴22)2(22==AP AC CD =22. ┄┄┄10分23. （本小题满分10分）选修4—4 ：坐标系与参数方程在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知曲线C ：2sin 4cos ρθθ-=0，直线l 过点M (0,4)且斜率为-2.（Ⅰ）将曲线C 的极坐标方程化为直角坐标方程，写出直线l 的标准参数方程； （Ⅱ）若直线l 与曲线C 交于A 、B 两点，求||AB 的值.【命题意图】本题主要考查参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化、直线参数方程的应用，是基础题.（Ⅱ）由（Ⅰ）知直线l的标准参数方程为xy⎧=⎪⎪⎨⎪=⎪⎩(t为参数），代入24y x=整理得2200t++=，┄┄6分设BA,点对应的参数分别为1t，2t，则20,552121=-=+t ttt，┄┄8分则||AB=||21tt-.┄┄10分24. （本小题满分10分）选修4—1：不等式选讲(Ⅰ) 若a,b,均为正数，且1a b+=.证明：11(1)(1)9a b++≥；(Ⅱ)若不等式2|||3|≥--+axx的解集为}1|{≥xx，求实数a的值.【命题意图】本题主要考查简单不等式的证明、基本不等式的应用、含绝对值不等式的解法，考查运算求解能力，是基础题.：。

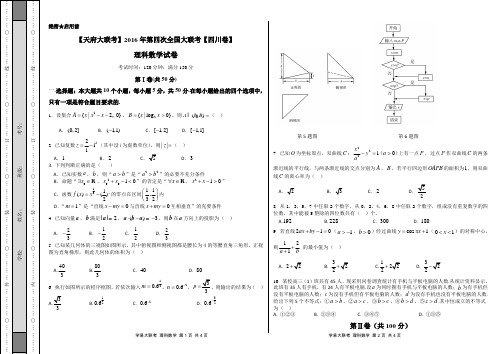
学易大联考 理科数学 第1页 共4页 学易大联考 理科数学 第2页 共4页绝密★启用前【天府大联考】2016年第四次全国大联考【四川卷】理科数学试卷考试时间：120分钟；满分150分第Ⅰ卷(共50分)一.选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合2{|20}A x x x =--…，2{|log 0}B x x =>，则()R A B = ð（ ） A ．(0,2] B ．(1,1)- C ．[1,2]- D ．[1,1]-2. 已知复数52i iz =-（其中设i 为虚数单位），则||z =（ ） A ．1B ．2CD ．33. 下列判断正确的是（ ）A ．已知实数a ，b ，则“a b >”是“22a b >”的必要不充分条件B ．命题“0R x ∃∈，20010x x +-<”的否定是“R x ∀∈，210x x +->”C ．函数131()(2x f x x =-的零点在区间11,32⎛⎫⎪⎝⎭内D ．“1m =”是“直线0x my -=与直线0x my +=互相垂直”的充要条件4. 已知向量a ，b 满足|a |=2，()-⋅a b a =3-，则b 在a 方向上的投影为（ ） A ．23-B ．12-C．12 D ．235.已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积为（ ）A.403B.803C. 40D. 806. 执行如图所示的程序框图，若依次输入120.6m =，20.6n -=，p =，则输出的结果为（ ）A.3B.120.6C. 20.6- D. 320.6-ABC ．2D 8. 从1，3，5，7中任取2个数字，从0，2，4，6，8中任取2个数字，组成没有重复数字的四位数，其中能被5整除的四位数共有（ ）个. A.192 B.228 C. 300 D. 180 9. 若直线210ax by +-=（1a >-，0b >）经过曲线cos 1y x =π+（01x <<）的对称中心，则121a b++ 的最小值为（ ） A. 2B.32+ C.12+ D.3210. 某校高三（1）班共有45人，现采用问卷调查统计有手机与平板电脑的人数.从统计资料显示，此班有35人有手机，有24人有平板电脑.设a 为同时拥有手机与平板电脑的人数；b 为有手机但没有平板电脑的人数；c 为没有手机但有平板电脑的人数；d 为没有手机也没有平板电脑的人数.给出下列5个不等式：①a b >，②a c >，③b c >，④b d >，⑤c d >.其中恒成立的不等式为（ ） A. ①②③ B. ②③④ C. ③④⑤ D. ①③⑤第Ⅱ卷（共100分）学易大联考 理科数学 第3页 共4页 学易大联考 理科数学 第4页 共4页二、填空题（每题5分，满分25分，将答案填在答题纸上）11.二项式12nx x ⎛⎫-⎪⎝⎭的展开式中各项系数之和为164，则展开式中的常数项为___________． 12.设变量x ，y 满足约束条件1023030x y x y x y -+⎧⎪--⎨⎪+-⎩………，则目标函数23z x y =+的最大值为 __ .13. 某地区发生爆炸事故后，为了尽快缓解该地区地下水的污染状况，环保部门采取了一系列的措施，其中包括投放化学制剂A.现投放化学制剂A ，30天后，地下水中氰化物的浓度N （单位：3g /m ）与投放化学制剂A 的强度m （kg /天）之间的关系为e lg 2km N -=⋅.若要使30天后，氰化物的浓度变为2lg 233g /m ，需要投放化学制剂A 的强度为100kg /天，则要使30天后，氰化物的浓度变为16lg 2813g /m ，需要投放化学制剂A 的强度为_______kg /天.14.如图，在正四棱锥P ABCD -中，4AB =，高h =点M 是侧棱PC 的中点，则异面直线BM 与AC 所成角的余弦值为________.15. 已知()f x 是定义在[],a b 上的函数，如果存在常数0M >，对区间[],a b 的任意划分：011n n a x x x x b -=<<<<=L ，和式11()()ni i i f x f x M -=-≤∑恒成立，则称()f x 为[],a b 上的“绝对差有界函数”.现有下列四个命题：① 函数()sin cos f x x x =+在,02π⎡⎤-⎢⎥⎣⎦上是“绝对差有界函数”； ② 函数0,0,()cos ,01,2x f x x x x π=⎧⎪=⎨<≤⎪⎩不是[]0,1上的“绝对差有界函数”； ③ 若函数()f x 满足：“存在常数0k >，对任意的1x ，2x [],a b ∈，有1212()()f x f x k x x-≤-成立”，则()f x 为[],a b 上的“绝对差有界函数”； ④ 若函数()f x ，()g x 都是[],a b 上的绝对差有界函数，则()()f x g x +也是[],a b 上的“绝对差有界函数”.其中所有正确命题的序号是______________.（写出所有正确命题的序号）三、解答题 （本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．）16.（本小题满分12分）已知ABC ∆的三个内角A ，B ，C 的对边分别为a ，b ，c ，且2B A =． （1）求证：3sin 3sin 4sin C A A =-；（2）求cb a-的取值范围． 17.（本小题满分12分）设X 为随机变量，从侧面均是等边三角形的正四棱锥的8条棱中任选两条，X 为这两条棱所成的角. （1）求概率()2P X π=；（2）求X 的分布列和数学期望EX . 18.（本小题满分12分）如图，在三棱台DEF ABC -中，底面ABC 是以AB 为斜边的直角三角形，FC ⊥底面ABC ，2AB DE =，G ，H 分别为AC ，BC 的中点.（1）求证： 平面ABED ∥平面GHF ； （2）若12BC CF AB ==，求二面角A DE F --的余弦值. 19.（本小题满分12分）设数列{}n a 的前n 项和为n S ，且11a =，12n n na S +=，N n *∈. （1）求数列{}n a 的通项公式； （2）若21n nnb a a =+，记数列{}n b 的前n 项和为n T ，求证：323231692322126n n n n n n n T n n ++-++-+剟20.（本小题满分13分）在平面直角坐标系xOy 中，圆224x y +=上的一点00(,)P x y (0x ，00y>)处的切线l 分别交x 轴，y 轴于点A ，B ，以A ，B 为顶点且以O 为中心的椭圆记作Γ，直线OP 交椭圆Γ与M ，N 两点.（1）若椭圆Γ的离心率为3P 的坐标；（2）证明四边形AMBN 的面积S >21. （本小题满分14分）已知函数2()e e x f x ax x =+-，其中R a ∈，e 2.71828= 是自然对数的底数.(1) 若曲线()y f x =在点()1,(1)f 处的切线平行于x 轴，求函数()f x 的单调区间；(2) 试确定a 的取值范围，使得曲线()y f x =上存在唯一的点P ，曲线在P 点处的切线与曲线只有一个公共点P .。

【学易大联考】2016年第四次全国大联考统考【新课标Ⅲ卷】理科数学试卷第I 卷（共60分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数12z =-，则21z z +在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 【答案】D【命题意图】本题考查复数的基本运算及其几何意义，意在考查学生的基本运算能力和对基础知识的掌握程度.2．设全集U R =,集合{}2|760A x x x =--≥, {}|lg(2)(4)B x y x x ==+-,则()U B A = ð（ ） A ．[4,6) B ．]9,4( C ．[1,2] D ．[2,1]- 【答案】D【命题意图】本题主要考查集合的基本运算，涉及一元二次不等式的求解、对数函数定义域的求法,意在考查学生的基本运算能力.【解析】由2760(1)(7)071x x x x x --≥⇒-+≤⇒-≤≤，即{}|71A x x =-≤≤，又由(2)(4)02x x x +->⇒<-或4x >，即{|2B x x =<-或4}x >, 从而U B ð{}|24x x =-≤≤,故()U B A = ð{}|21x x -≤≤，选D ．3．在6与316中间插入n 个数，组成各项和为18916的等比数列，则此数列的项数为（ ） A ．8 B ．7 C ．6 D ．5【答案】C【命题意图】本题考查等比数列的通项公式及前n 项和公式的应用，意在考查学生的计算能力和对基本公式的熟练应用能力.4．已知圆C ：)0(4)2()(22<=-+-a y a x 及直线03:=+-y x l ，若直线l 被圆C 截得的弦长为32，则a 的值为（ ）A ．12--B ．2-C ．13--D ．3-【答案】A【命题意图】本题主要考查直线与圆的位置关系，可利用半径、半弦长及弦心距三者之间的关系进行求解，意在考查数形结合思想的应用.【解析】由于圆C 的半径为2，弦长为32，因此，弦心距为1)3(222=-=d ，即圆心到直线的距离为12|32|=+-a ，解得21±-=a ，又因为0<a ，所以=a 12--，选A5．执行如图所示的程序框图，若输入的2,2a n ==，则输出的q 的值为（ ） A ．24 B ． 25 C ．26 D ． 27 【答案】A【命题意图】本题考查程序框图的阅读、理解与应用，意在考查学生的识图、读图能力.【解析】运行程序，依次可得：0,0,1,2,p q i i ===≤成立；2,2,20,2p q a i ====，2,i 成立≤；22,24,200,3p q a i ====，2,i 不成立≤，跳出循环体，此时输出24q =.选A ．6．已知角ϕ的终边经过点P （-4，3），函数f （x ）=sin(ωx +ϕ)（ω＞0）的图象的相邻两条对称轴之间的距离等于π2，则f (π4)的值为（ ） A ．35 B ．45 C ．35- D ．45-【答案】D【命题意图】本题主要考查三角函数的定义，三角函数的图象与性质，诱导公式等，意在考查学生的运算求解能力和对基础知识的综合运用能力.【解析】由题意得，53sin =ϕ，4cos 5φ=-，由函数)(x f 的图象的相邻两条对称轴之间的距离等于π2，可得函数)(x f 的周期π2π2T =?，又2πT ω=，所以2=ω，所以ππ4()sin()cos 425f φφ=+==-.选D ．7．设12F F 、是椭圆22221x y a b+=的两个焦点，P 是椭圆上的点，1:2||:||21=PF PF ，且12PF F △为直角三角形，则椭圆的离心率为（ ）A 或B 或CD 或 【答案】C【命题意图】本题考查椭圆方程中基本量之间的关系，意在考查学生的转化变形能力和对分类讨论思想的熟练应用能力.8．△ABC 中，点D 在BC 上，∠A ＝60°，若1()4||||AB AC AD k AC AB AB AC λ=+=+，且4AB =，则AD 的长为（ ）A B ． C ． D ． 【答案】C【命题意图】本题考查单位向量的应用，向量共线的性质，向量的加法等基础知识与基本技能的应用，意在考查学生的转化与化归能力及对一些常用结论的熟知程度. 【解析】由于点D 在BC 上，即D 、B 、C 三点共线，所以13144λλ+=⇒=. 由3344||||AB k k AB AB AB =⇒=，又4AB =，即4AB = ，所以3k =. 所以3()||||AB ACAD AB AC =+， 所以222||9[()2()()()]=||||||||AB AB AC ACAD AB AB AC AC =+⋅+2291+211cos 60+127（）⨯⨯⨯⨯= ||AD ⇒=.9．已知一几何体的三视图如图所示，其中，正视图与侧视图完全一样，根据图中的数据，该几何体的表面积为（ ）A B ． C ．4 D ．6【答案】B【命题意图】本题考查三视图与直观图的转化，几何体的表面积，意在考查学生将三视图转化为直观图的转化能力、计算能力及空间想象能力.10．若n xx )3(3+的展开式中存在常数项，则正整数n 的最小值及相应的常数项分别为（ ）A ．6,280B ．6,270C ．5,280D ．5,270 【答案】D【命题意图】本题考查二项式定理的应用，意在考查学生的计算能力及对公式的理解和掌握程度.【解析】由二项展开式的通项公式得3561C C 3n rr n rr r rr nn T x --+=⋅=⋅⋅，令0653=-r n ，即r n 53=，因为*n ÎN ，所以最小的正整数5=n ，此时3=r ，所以相应的常数项为335C 3270?.选D ．11．已知数列{}n a 的前n 项和为n S ，若112a =且21()(1)n n n a n a a n n -=---，则下列四个结论：①1n n a a +>； ②(1)2n n n S ->； ③{}n n a -是增数列； ④{}(1)n n a +是等差数列，其中正确的个数为（ ）A ．1B ．2C ．3D ．4 【答案】C【命题意图】本题主要考查数列的基本运算，数列中的有关概念，意在考查学生综合分析问题、解决问题的能力.【解析】将21()(1)n n n a n a a n n -=---的两边同除以(1)n n -，得1(1)11n n n a na n n -+-=-，又1211a=，所以数列(1)n n a n +⎧⎫⎨⎬⎩⎭是以1为首项，1为公差的等差数列. 所以2(1)1n n n a n n a n n +=⇒=+， 因为2221(1)31021(2)(1)n n n n n n a a n n n n ++++-=-=>++++，所以1n n a a +>，①正确； 因为221111n n n a n n n -=>=-++，所以[0(1)](1)22n n n n n S +-->=，②正确；由22111n n n n na n a n n n n =⇒-=-=+++，所以易得数列{}n n a -为增数列，③正确； 由22(1)1n n n a n a n n =⇒+=+，显然{}(1)n n a +不是等差数列，故④不正确.综上可知，选C ．12．设函数()f x =若曲线e 1e 1sin 22y x -+=+上存在点00(,)x y 使得00(())f f y y =成立，则实数a 的取值范围为（ ）A ． 2[0,e e 1]-+ B ． 2[0,e e 1]+- C ． 2[0,e e 1]-- D ． 2[0,e e 1]++ 【答案】C【命题意图】本题主要考查函数与导数的综合问题，意在考查学生的转化与化归能力、运算求解能力以及利用所学知识综合分析问题、解决问题的能力.第Ⅱ卷（非选择题 共90分）二、填空题（每小题5分，满分20分.将答案填在答题纸上）13. 定义在R 上的函数()f x 满足22,0()(1)(2),0x x x f x f x f x x ⎧-≤=⎨--->⎩，则(2016)f 的值为 .【答案】1-【命题意图】本题考查分段函数求值，函数的周期性等知识，意在考查学生对递推式子和函数周期性的应用能力，以及对抽象函数的理解程度.【解析】当0x >时，由)2()1()(---=x f x f x f ，得(+1)()(1)f x f x f x =--，两式相加得(+1)(2)f x f x =--，所以(+3)()f x f x =-，所以()(+6)f x f x =，故20(2016)(6336)(0)021f f f =⨯==-=-.14．已知乒乓球队的10名队员中有3名主力队员，现要派5名参加比赛，3名主力队员一定参加且安排在第一、三、五位置，其余7名队员中选2名安排在第二、四位置，则不同的出场安排有 种. 【答案】252【命题意图】本题主要考查排列、组合的应用，意在考查学生的阅读理解能力和分析问题、解决问题的能力.【解析】先安排3名主力队员在第一、三、五位置，有33A 种方法，再从7名队员中选2名放在第二、四位置上，有27A 种方法，所以不同的出场安排有3237A A 252=种.15．若,x y 满足不等式组⎪⎩⎪⎨⎧≤-≤+≤1222y x y x xy ，则32z x y =+的最大值为 .【答案】72【命题意图】本题考查线性规划的基本应用，意在考查学生的作图能力和数形结合思想.16． 已知双曲线()222210,0x y a b a b-=>>的半焦距为c ，过右焦点且斜率为1的直线与双曲线的右支交于两点，若抛物线24y cx =2（e 为双曲线的离心率），则e 的值为 .【解析】由题意，得抛物线的准线为x c =-，它正好经过双曲线的左焦点，所以准线被双曲线截得的弦长为22b a ，所以222b a =，即2b a =，所以e ==，整理，得422990e e -+=，解得e =或e =1的直线与双曲线的右支交于两点，所以2b a =<1，所以e =． 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）17．（本小题满分12分）在ABC △中，角,,A B C 所对的边分别为c b a ,,，且ABC △的面积S 满足2()()S c a b c a b =-++-.（1）求cos C ；（2）若2c =，2cos b a C =，求边长b .【命题意图】本题考查余弦定理、三角形的面积公式等，意在考查学生的灵活变形能力和对基本公式的掌握程度.18．（本小题满分12分）如图，90BCD?o ，⊥==AB CD BC ,1平面BCD ，60ADB ?o ，F E ,分别是AD AC ,上的动点，且AE AFAC AD=. （1）若平面BEF 与平面BCD 的交线为l ，求证：//EF l ；（2）当平面⊥BEF 平面ACD 时，求平面BEF 与平面BCD 所成的二面角的余弦值.【命题意图】本题考查线面平行、垂直的判定定理与性质定理，空间向量求解二面角等，意在考查学生的空间想象能力和对基本定理的掌握程度.【解析】（1）由CD EF ADAFAC AE //⇒=， ……………（2分） 又EF ⊄平面BCD ，CD ⊂平面BCD ,所以EF ∥平面BCD , 又EF ⊂平面BEF ，且平面BCD 平面BEF l =,故EF l ∥. ……………（4分）（2）因为AB ^平面BCD ，所以AB DC ^，又BC DC ⊥，所以⊥DC 平面ABC ， 所以DC BE ^，又EF CD ∥，所以EF BE ⊥.若平面⊥BEF 平面ACD ，则⊥BE 平面ACD ，所以BE AC ^，由1==CD BC 且90BCD ?o 2=⇒BD ，又60ADB?o ，所以6=AB . ……………（6分）以B 为坐标原点，,BD BA 所在的直线分别为,y z 轴，以过点B 且垂直于BD 的直线为x 轴建立空间直角坐标系，则(0,0,0),A B C ，设(,,)E a a b ，则(,,),(,,BE a a b AC AE a a b ===-,由,aBE ACAC AEb可得∥⎧+-==⎪⎧⋅=⎪⎪⇒⎨⎨⎪⎪⎩==⎪⎩，即E所以可得F，所以BE BF，==……………（8分）设平面BEF的一个法向量为(,,)x y z=m，则0000x yBE zBF zy z+=⎧⋅=++=⎪⇒⇒⎨⋅=+=⎪⎪⎩⎩=mm，取z=，得1,1x y=-=-，所以(1,1,=--m，……………（10分）易知平面BCD的一个法向量为(0,0,1)=n，设平面BEF与平面BCD所成的二面角为θ，则cosθ==，结合图形可知平面BEF与平面BCD.……………（12分）19．（本小题满分12分）某班n名同学的数学小测验成绩的频率分布直方图如图所示，其中,,a b c成等差数列，且分数在[90,100]的有6人.（1）求n的值；（2）若分数在[40,50)的人数是分数在[50,60)的人数的13，现从不及格的人中任意选取3人进行谈话，记分数在50分以下的人数为X ，求X 的分布列和数学期望.【命题意图】本题考查频率分布直方图的应用，离散型随机变量的分布列和数学期望的求解，意在考查整体运算的基本思想，以及学生的阅读理解能力、运算求解能力.（2）由（1）及题意可得0.020.00510.0153a c a c a c +=⎧=⎧⎪⇒⎨⎨==⎩⎪⎩， ……………（6分） 所以分数在[40,50)的有0.0051060=3⨯⨯（人），分数在[50,60)的有0.0151060=9⨯⨯（人），即不及格的有12人.现从中任选3人，记分数在50分以下的人数为X ，则X 的所有可能取值分别为：0,1,2,3，30219393331212C C C C 2127(0),(1),C 55C 55P X P X ======12039393331212C C C C 271(2),(3)C 220C 220P X P X ======.所以，X 的分布列如下表：………………（10分）故X 的数学期为21272713012355552202204EX =⨯+⨯+⨯+⨯=. ……………（12分） 20．（本小题满分12分）已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F 、，上、下顶点分别是12,B B C 、是12B F 的中点，且11122B F B F ⋅= ，112CF B F ⊥.（1）求椭圆的标准方程；（2）点,M N 是椭圆上的两个动点，过,M N 两点的切线交于点P ，当0PM PN ⋅=时，求点P 的轨迹方程.【命题意图】本题考查椭圆的标准方程及简单的几何性质，直线与椭圆的位置关系等，意在考查学生的基本运算能力及对常用技巧的灵活应用能力.（2）设点()00,y x P ，①当PM x ⊥轴或PM x ∥轴时，对应PN x ∥轴或PN x ⊥轴，可知点(P ±或点(2,P ±. ……………（6分）②当PM 与x 轴不垂直且不平行时，设直线PM 的斜率为k ，则0k ≠，且直线PN 的斜率为1k-，所以直线PM 的方程为00()y y k x x -=-，与22143x y +=联立,得00222220000()(34)8()4()120143y y k x x k x k y kx x y kx x y -=-⎧⎪⇒++-+--=⎨+=⎪⎩，因为直线与椭圆相切，所以=∆0，即222200004()(34)[()3]0k y kx k y kx --+--=，即2220000(4)230x k x y k y --+-=，所以k 是方程2220000(4)230x x x y x y --+-=的一个根， ……………（9分） 同理1k-是方程2220000(4)230x x x y x y --+-=的另一个根，2220002031()74y k x y k x -⋅-=⇒+=-，其中02x ≠±，所以点P 的轨迹方程为227x y +=（2x ≠±），因为点(P ±或点(2,P ±均满足上式.综上可知，点P 的轨迹方程为227x y +=． ……………（12分） 21．（本小题满分12分）已知函数22()(1)ln(1)f x m x n x =+-+.（1）若函数21()()2g x f x nx =-在区间[2,4]上单调递增，且,m n 均为正数，求mn 的取值范围；（2）若函数()f x 的图象在点(0,(0))f 处的切线方程为2(1)y n x n =-+，设2()h x x x b =++，若函数()()f x h x ≥在区间]2,0[上恒成立，求实数b 的取值范围.【命题意图】本题考查导数在函数中的应用，恒成立问题的转化与求解等，意在考查学生的转化与化归能力、运算求解能力以及利用所学知识综合分析问题、解决问题的能力.【解析】（1）由题意可知222211()()=(1)ln(1)22g x f x nx m x n x nx =-+-+-，则2()2(1)1ng x m x nx x'=+--+， 因为函数21()()2g x f x nx =-在区间[2,4]上单调递增，所以()0g x '≥恒成立， …………（2分） 即221112(1)01(1)2(1)2n m m x nx x n x x +--≥⇒≥-++++在区间[2,4]上恒成立，即max 2111[](1)2(1)2m n x x ≥-+++. 由11124513x x ≤≤⇒≤≤+，令1=1t x +， 则221111111=()(1)2(1)22253t t t x x -+-+≤≤++的最大值为49. 故m n 的取值范围为4[,)9+∞. ……………（5分）即实数b 的取值范围为(,22ln 2]-∞-. .……………（12分）请考生在第（22）、（23）、（24）三题中任选一题作答.注意：只能做所选定的题目.如果多做，则按所做第一个题目计分.22．（本小题满分10分）选修4-1：几何证明选讲如图，直线ΡQ 与O 相切于点A ，AB 是O 的弦，PAB ∠的平分线AC 交O 于点C ，连接CB 并延长与直线PQ 相交于点Q ，若6AQ =，5AC =．（1）求证：22QC QA BC QC -=⋅； （2）求弦AB 的长．【命题意图】本题主要考查切割线定理，弦切角定理，相似三角形的证明等，意在考查学生的识图能力、运算能力、逻辑推理能力以及对基本定理的掌握程度.【解析】（1）因为PQ 与O 相切于点A ，所以由切割线定理可得： 22()=QA QB QC QC BC QC QC BC QC =⋅=-⋅-⋅，所以22QC QA BC QC -=⋅． …………（5分） （2）因为PQ 与O 相切于点A ，所以PAC CBA ∠=∠．因为PAC BAC ∠=∠，所以BAC CBA ∠=∠，所以5AC BC ==，又6AQ =，22QC QA BC QC -=⋅，所以9QC =（负值不合题意，舍去）．由QAB ACQ ∠=∠，AQB CQA ∠=∠易知QAB QCA △∽△，所以AB QAAC QC=，即659AB =，所以103AB =，即弦AB 的长为103． ………………（10分）23．（本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系中，以坐标原点为极点，x 轴非负半轴为极轴建立极坐标系．已知直线l 与椭圆C 的极坐标方程分别为cos 2sin 0θθ+=，2224cos 4sin ρθθ=+.（1）求直线与椭圆的直角坐标方程；（2）若点Q 是椭圆C 上的动点，求点Q 到直线l 的距离的最大值.【命题意图】本题主要考查极坐标方程与直角坐标方程的互化，普通方程与参数方程的互化，点到直线的距离的最大值问题等，意在考查学生的转化与化归能力、运算求解能力. 【解析】（1）由cos 2sin 0cos 2sin 020x y θθρθρθ+=⇒+=⇒+=，即直线l 的直角坐标方程为20x y +=. .……………（2分） 又由2222222224cos 4sin 444cos 4sin x y ρρθρθθθ=⇒+=⇒+=+ 22+=14x y ⇒，即椭圆C 的直角坐标方程为22+=14x y . .……………（4分）24．（本小题满分10分）选修4-5：不等式选讲已知不等式|21||1|2x x --+<的解集为{|}x a x b <<.（1）求,a b 的值；（2）已知x y z >>，求证：存在实数k ，使32()4()a b kx y y z x z-+≥---恒成立，并求k 的最大值. 【命题意图】本题主要考查绝对值不等式的求解，不等式恒成立问题等，意在考查学生的化归与转化能力.【解析】（1）（i ）当1x <-时，不等式可转化为(21)[(1)]2x x ----+<，得0x >，此时无解； （ii ）当112x -≤≤时，不等式可转化为(21)(1)2x x ---+<，得23x >-，此时，不等式的解集为：2132x -<≤； （iii ）当12x >时，不等式可转化为21(1)2x x --+<，得4x <，此时，不等式的解集为：142x <<. 由（i ）、（ii ）、（iii ）得不等式的解集为2{|4}3x x -<<，比较即得2,43a b =-=. .……………（5分）：。

2016年福建省普通高中毕业班质量检查理科数学试题答案及评分参考 2016.4评分说明：1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分．（1）B （2）C （3）D （4）A （5）B （6）C（7）B （8）C （9）D （10）D （11）A （12）B二、填空题：本大题考查基础知识和基本运算．每小题5分，满分20分．（13）0.3 （14）3- （15）5- （16）263三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．（17）本小题主要考查正弦定理、余弦定理、三角形面积公式及三角恒等变换等基础知识，考查运算求解能力，考查化归与转化思想、函数与方程思想等．满分12分．解法一：（Ⅰ）因为BCD S △即1sin 2BC BD B ⋅⋅= ···················· 2分 又因为3B π=,1BD =，所以4BC = ． ················································· 3分 在△BDC 中,由余弦定理得，2222cos CD BC BD BC BD B =+-⋅⋅, ··········· 5分即21161241132CD =+-⨯⨯⨯=，解得CD = ······························ 6分 （Ⅱ）在△ACD 中，DA DC =，可设A DCA θ∠=∠=，则ADC θ=π-2∠，又AC =sin 2sin AC CD θθ=， ······································ 7分所以CD =． ·········································································· 8分 在△BDC 中, 22,23BDC BCD θθπ∠=∠=-，由正弦定理得，sin sin CD BD B BCD =∠，即12cos 2sin sin(2)33θθ=ππ-， ··········· 10分 化简得2cos sin(2)3θθπ=-， 于是2sin()sin(2)23θθππ-=-． ························································ 11分 因为02θπ<<，所以220,222333θθπππππ<-<-<-<， 所以2223θθππ-=-或2+2=23θθππ--π, 解得==618θθππ或，故=618DCA DCA ππ∠∠=或． ······························ 12分 解法二：（Ⅰ）同解法一．（Ⅱ）因为DA DC =，所以A DCA ∠=∠．取AC 中点E ，连结DE ， 所以DE AC ⊥． ··············································································· 7分设DCA A θ∠=∠=，因为AC =EA EC ==在Rt △CDE中，cos 2cos CE CD DCA θ==∠． ····································· 8分 以下同解法一．（18）本小题主要考查空间直线与直线、直线与平面的位置关系及直线与平面所成的角等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．满分12分． 解法一：（Ⅰ）连结1AB ，在1ABB △中，111,2,60AB BB ABB ==∠=，由余弦定理得，22211112cos 3AB AB BB AB BB ABB =+-⋅⋅∠=，∴1AB =，…………………………………………1分∴22211BB AB AB =+，∴1AB AB ⊥．………………………………………2分又∵ABC △为等腰直角三角形，且AB AC =，∴AC AB ⊥，又∵1AC AB A =，1B∴AB ⊥平面1AB C ． ········································································· 4分又∵1B C ⊂平面1AB C ，∴AB ⊥1B C ． ················································································· 5分（Ⅱ）∵111,2AB AB AC BC ====， ∴22211B C AB AC =+，∴1AB AC ⊥． ················································ 6分如图，以A 为原点，以1,,AB AC AB 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，······································································································ 7分则()(()()1000,0,100010A B B C ，，0，，，，，， ∴()()11,0,3,1,1,0BB BC =-=-．···················································· 8分设平面1BCB 的法向量(),,x y z =n ，由10,0,BB BC ⎧⋅=⎪⎨⋅=⎪⎩n n 得0,0,x x y ⎧-+=⎪⎨-+=⎪⎩令1z =，得x y ==∴平面1BCB 的一个法向量为)=n ． ……………………9分∵()((1110,1,0AC AC CC AC BB =+=+=+-=-， ……………………………………………………………………………10分∴111cos ,||||AC AC AC ⋅<>===n n n ，….……………11分 ∴1AC 与平面1BCB 所成角的正弦值为35． ······································ 12分 解法二：（Ⅰ）同解法一．（Ⅱ）过点A 作AH ⊥平面1BCB ，垂足为H ，连结1HC ，则1AC H ∠为1AC 与平面1BCB 所成的角． ············································· 6分由（Ⅰ） 知，1AB AB ⊥，1AB ，1AB AC ==，12B C =， ∴22211AB AC B C +=，∴1AB AC ⊥，又∵AB AC A =，∴1AB ⊥平面ABC ， ············································ 7分∴1111113326B ABC ABC V S AB AB AC AB -=⋅=⨯⨯⨯⨯=△． ······················· 8分1取BC 中点P ，连结1PB ，∵112BB B C ==，∴1PB BC ⊥．又在Rt ABC △中，1AB AC ==，∴BC =BP =∴12PB ===，∴1112B BC S BC B P =⨯=△． ···························································· 9分 ∵11A BCB B ABC V V --=，∴113BCB S AH ⋅=△，即13AH =7AH =． ············ 10分 ∵1AB ⊥平面ABC ，BC ⊂平面ABC ，∴1AB BC ⊥，三棱柱111ABC A B C -中，11//BC B C ，112B C BC ==，∴111AB B C ⊥，∴1AC == ···································· 11分在1Rt AHC △中，11sin AH AC H AC ∠===， 所以1AC 与平面1BCB所成的角的正弦值为35． ································ 12分 （19）本小题主要考查古典概型、随机变量的分布列及数学期望等基础知识，考查运算求解能力、数据处理能力、应用意识，考查分类与整合思想、必然与或然思想、化归与转化思想．满分12分． 解：（Ⅰ） 记“抽取的两天送餐单数都大于40”为事件M ， 则220210019()495C P M C ==． ···································································· 4分 （Ⅱ）（ⅰ）设乙公司送餐员送餐单数为a ，则当38a =时，384152X =⨯=；当39a =时，394156X =⨯=；当40a =时，404160X =⨯=；当41a =时，40416166X =⨯+⨯=；当42a =时，40426172X =⨯+⨯=．所以X 的所有可能取值为152,156,160,166,172． ······································· 6分1故X 的分布列为：······································································································ 8分11121()1521561601661721621055510E X =⨯+⨯+⨯+⨯+⨯=所以． ······ 9分 （ⅱ）依题意， 甲公司送餐员日平均送餐单数为380.2390.4400.2410.1420.139.5⨯+⨯+⨯+⨯+⨯=． ············· 10分 所以甲公司送餐员日平均工资为70239.5149+⨯=元． ·························· 11分 由（ⅰ）得乙公司送餐员日平均工资为162元．因为149162<，故推荐小明去乙公司应聘． ········································· 12分（20）本小题考查圆与抛物线的标准方程及几何性质、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查数形结合思想、函数与方程思想、分类与整合思想等．满分12分．解法一：(Ⅰ)将2p x =代入22y px =，得y p =±，所以2STp =， ·················· 1分 又因为90SPT ∠=，所以△SPT 是等腰直角三角形， 所以SF PF =，即32p p =-， 解得2p =，所以抛物线2:4E y x =，…………………………………………3分 此时圆P =所以圆P 的方程为()2238x y -+=． ···························································· 4分(Ⅱ)设()()()001122,,,,,M x y A x y B x y ，依题意()220038x y -+=，即2200061y x x =-+-． ··········································· 5分（ⅰ）当直线l 斜率不存在时，()3M ±， ①当3x =+24y x =，得()2y =±．不妨设()()32,32A B ++-， 则1,1,1,AF BF AF BF k k k k ==-=-即AF BF ⊥．②当3x =-AF BF ⊥．………………….6分 （ⅱ）当直线l 斜率存在时，因为直线l 与抛物线E 交于,A B 两点，所以直线l 斜率不为零，01x ≠且00y ≠． 因为l MF ⊥，所以1l MF k k =-，所以01l x k y -=，…………………………………………………..7分直线()00001:x l y x x y y -=-+． 由()200004,1y x x y x x y y ⎧=⎪-⎨=-+⎪⎩得，2220000004444011y x y x y y x x +--+=-- ， ················ 8分 即200004204011y x y y x x --+=--，所以001212004204,11y x y y y y x x -+==--， ············· 9分 所以()()121211FA FB x x y y ⋅=--+=2212121144y y y y ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭······················· 10分 ()()()222221212121212123111641642y y y y y y y y y y y y ++=-++=-++()()()22000220005143061111x y x x x x --=-++---()()()()()2220000020514165111x y x x x x --+-+--=- ()2200020244441x x y x ---=-()()220002046101x y x x -+-+==-，所以AF BF ⊥． ··················································································· 12分 解法二：(Ⅰ)同解法一．(Ⅱ)设()00,M x y ，依题意()220038x y -+=，即2200061y x x =-+-， （*） ······ 5分设()22121212,,,44y y A y B y y y ⎛⎫⎛⎫≠ ⎪ ⎪⎝⎭⎝⎭，则()222100211,,,4y y FM x y AB y y ⎛⎫-=-=- ⎪⎝⎭， 2212010020,,,44y y MA x y y MB x y y ⎛⎫⎛⎫=--=-- ⎪ ⎪⎝⎭⎝⎭， ········································ 6分由于FM AB ⊥，//MA MB ，所以()()()()22210021221202001010,40.44y y x y y y y y x y y x y y ⎧--+-=⎪⎪⎨⎛⎫⎛⎫⎪-----= ⎪ ⎪⎪⎝⎭⎝⎭⎩ ································ 7分 注意到12y y ≠，()()()()()1200120120140,140.2y y x y y y y y y x +-+=⎧⎪⎨-++=⎪⎩ ························ 8分 由（1）知，若01x =，则00y =，此时不满足（*），故010x -≠，从而（1），（2）可化为001212004204,11y x y y y y x x -+==--． ······················ 9分 以下同解法一.（21）本小题主要考查导数的几何意义、导数及其应用、不等式等基础知识，考查推理论证能力、运算求解能力、创新意识等，考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等．满分12分．解法一：（Ⅰ）因为()()111f x a x x '=->-+，()e 1x g x '=-， ···························· 2分 依题意，()()00f g ''=，解得1a =，························································ 3分 所以()111f x x '=-+1xx =+，当10x -<<时，()0f x '<；当0x >时，()0f x '>． 故()f x 的单调递减区间为()1,0-， 单调递增区间为()0,+∞． ···················· 5分 （Ⅱ）由（Ⅰ）知，当0x =时，()f x 取得最小值0．所以()0f x ≥，即()ln 1x x +≥，从而e 1x x +≥． 设()()()()()e ln 111,x F x g x kf x k x k x =-=++-+- 则()()()e 11111x k kF x k x k x x '=+-+++-+++≥，····································· 6分 （ⅰ）当1k =时，因为0x ≥，所以()11201F x x x '++-+≥≥（当且仅当0x =时等号成立）， 此时()F x 在[)0,+∞上单调递增，从而()()00F x F =≥，即()()g x kf x ≥． ······ 7分 （ⅱ）当1k <时，由于()0f x ≥，所以()()f x kf x ≥． ································ 8分 由（ⅰ）知()()0g x f x -≥，所以()()()g x f x kf x ≥≥，故()0F x ≥，即()()g x kf x ≥． ······································································································ 9分（ⅲ）当1k >时， 令()()e 11x kh x k x =+-++，则()()2e 1x k h x x '=-+，显然()h x '在[)0,+∞上单调递增，又())1010,110h k h ''=-<=->，所以()h x '在()1上存在唯一零点0x ， ··········································· 10分 当()00,x x ∈时，()0,h x '<所以()h x 在[)00,x 上单调递减， 从而()()00h x h <=，即()0,F x '<所以()F x 在[)00,x 上单调递减，从而当()00,x x ∈时，()()00F x F <=，即()()g x kf x <，不合题意． ········· 11分 综上， 实数k 的取值范围为(],1-∞． ··················································· 12分 解法二：（Ⅰ）同解法一．（Ⅱ）由（Ⅰ）知，当0x =时，()f x 取得最小值0．所以()0f x ≥，即()ln 1x x +≥，从而e 1x x +≥． 设()()()()()e ln 111,x F x g x kf x k x k x =-=++-+- 则()()()e 11111x k k F x k x k x x '=+-+++-+++≥()11xx k x =+-+， ··············· 6分 （ⅰ）当1k ≤时，()0F x '≥在[)0,+∞恒成立，所以()F x 在[)0,+∞单调递增． 所以()()00F x F =≥，即()()g x kf x ≥． ·················································· 9分 （ⅱ）当1k >时，由（Ⅰ）知，当1x >-时，e1xx +≥（当且仅当0x =时等号成立），所以当01x <<时，e1xx ->-+，1e 1x x<-． 所以1()e 1(1)e 111xx kx F x k x x '=---=--++ 1111kx x x <---+11x kxx x =--+()211()11k k x x k x -+-+=-． ··············· 10分于是当101k x k -<<+时，()0,F x '<所以()F x 在10,1k k -⎡⎫⎪⎢+⎣⎭上单调递减.故当101k x k -<<+时，()(0)0F x F <=，即()()g x kf x <，不合题意． ······ 11分 综上， 实数k 的取值范围为(],1-∞． ··················································· 12分 解法三：（Ⅰ）同解法一．（Ⅱ）（ⅰ）当0k ≤时，由（Ⅰ）知，当0x =时，()f x 取得最小值0． 所以()0f x ≥，即()ln 1x x +≥，从而e 1x x +≥，即()0g x ≥．所以()0kf x ≤，()0g x ≥，()()g x kf x ≥． ················································ 6分 （ⅱ）当0k >时，设()()()()()e ln 111,x F x g x kf x k x k x =-=++-+-则()()e 11x kF x k x '=+-++， 令()()h x F x '=，则()()2=e 1x kh x x '-+．显然()h x '在[)0,+∞上单调递增． ·························································· 7分 ①当01k <≤时，()()'010h x h k '=-≥≥，所以()h x 在[)0,+∞上单调递增，()()00h x h =≥； 故()0F x '≥，所以()F x 在[)0,+∞上单调递增，()()00F x F =≥，即()()g x kf x ≥． ······································································································ 9分 ②当1k >时，由于())1'010,'110h k h =-<=->，所以()h x '在()1上存在唯一零点0x ， ··········································· 10分 当()00,x x ∈时，()0,h x '< ()h x 单调递减，从而()()00h x h <=，即()0,F x '<()F x 在[)00,x 上单调递减，从而当()00,x x ∈时，()()00F x F <=，即()()g x kf x <，不合题意． ········· 11分 综上， 实数k 的取值范围为(],1-∞． ··················································· 12分请考生在第（22），（23），（24）题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清题号．（22）选修41-：几何证明选讲本小题主要考查圆周角定理、相似三角形的判定与性质、切割线定理等基础知识，考查推理论证能力、运算求解能力等，考查化归与转化思想等．满分10分．解法一：（Ⅰ）连结DE ，因为,,,D C E G 四点共圆，则ADE ACG ∠=∠． ······· 2分 又因为,AD BE 为△ABC 的两条中线， 所以点,D E 分别是,BC AC 的中点，故DEAB ． ············································ 3分 所以BAD ADE ∠=∠， ················································································ 4分 从而BAD ACG ∠=∠． ················································································ 5分 （Ⅱ）因为G 为AD 与BE 的交点，故G 为△ABC 的重心，延长CG 交AB 于F ，则F 为AB 的中点，且2CG GF =． ······························································· 6分 在△AFC 与△GFA 中，因为FAG FCA ∠=∠，AFG CFA ∠=∠，FABCDEG所以△AFG ∽△CFA ， ······································································ 7分 所以FA FGFC FA=，即2FA FG FC =⋅．………………………………………………………9分 因为12FA AB =，12FG GC =，32FC GC =，所以221344AB GC =，即AB =，又1GC =，所以AB =． ········································································ 10分 解法二：（Ⅰ）同解法一． ····································································· 5分 (Ⅱ) 由(Ⅰ) 知，BAD ACG ∠=∠，因为,,,D C E G 四点共圆，所以ADB CEG ∠=∠， ········································· 6分所以ABD △∽CGE △，所以AB ADCG CE=， ……………………………………………7分 由割线定理，AG AD AE AC ⋅=⋅， ······························································ 9分又因为,AD BE 是ABC △的中线，所以G 是ABC △的重心， 所以23AG AD =,又=2=2AC AE EC ，所以222=23AD EC ，所以AD CE =所以AB CG=1CG =，所以AB = ····································· 10分 （23）选修44-；坐标系与参数方程本小题考查直线的极坐标方程和参数方程、椭圆的参数方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想等． 满分10分．解法一：（Ⅰ）由3cos ,sin x y αα=⎧⎨=⎩消去参数α，得2219x y +=， 即C 的普通方程为2219x y +=． ······························································ 2分由sin 4ρθ⎛π⎫-= ⎪⎝⎭，得sin cos 2ρθρθ-=，………（＊） ···················· 3分 将cos ,sin x y ρθρθ=⎧⎨=⎩代入（＊），化简得2y x =+，········································· 4分所以直线l 的倾斜角为4π． ···································································· 5分。

绝密★启用前【学易大联考】2016年第四次全国大联考【江苏版】数学试卷考试时间：理150分钟，文120分钟第Ⅰ卷 必做题部分一、填空题：本大题共14个小题，每小题5分，共计70分，请把答案直接填写在答题卡相应的位置．．．．．．．．上． 1．已知全集U {1,2,3,4},=集合{1,2},{2,4}A B ==，则集合()U A B U ð等于_______. 2. 已知复数z满足(1i)i z -=（i 是虚数单位），则z 的模为_______.3. 已知一组数据：8,10,,12,11a 的方差为2，那么相对应的另一组数据：17,21,21,25,23a +的方差为_______.4. 运行如图所示的伪代码，其运行后输出的结果为____.5. 袋中有形状、大小都相同的五只球，其中2只红球，3只白球，从中一次随机摸出2只球，则至少有1只白球的概 率为_______.6. 已知sin 2cosαα+，那么tan 2α的值为_______.7. 已知正三棱柱的各条棱长均为1，圆锥侧面展开图为半径为2的半圆，那么这个正三棱柱与圆锥的体积比是_______.8. 在ABD ∆中，13112,,343AB AD AE AD BC BD BE AC ====⋅= ，，则BAD ∠的值为_______.9. 已知等比数列{}n a 的前n 项和为n S ，满足243n n S S +=+，且30S <，则 2a 的值为_______. 10. 已知正数,,a b c 满足42250a b c -+=，则lg lg 2lg a c b +-的最大值为_______.11.设F 为双曲线22221(0,0)x y a b a b-=>>的右焦点，过点F 作双曲线一条渐近线的垂线，垂足为A ，垂线交另一条渐近线于B 点，若向量BF 与FA同向，且3AB OA OB =+，则双曲线的离心率为_______.12. 在平面直角坐标系xOy 中，圆221x y +=交x 轴于,A B 两点，且点A 在点B 左边，若直线0x m +=上存在点P ，使得2PA PB =，则m 的取值范围为_______.13.扇形AOB 中，弦1AB =，C 为劣弧 AB 上的动点，AB 与OC 交于点P ，则OP BP ⋅的最小值是_______.14.已知函数(),()()()(),()()f x f xg xh x g x f x g x ≤⎧=⎨>⎩， 31(),()ln 4f x x ax g x x =++=-，若()0h x =在(0,)+∞上有三个不同的实数根，则实数a 的取值范围为_______.二、解答题：本大题共6小题，计90 分。

高一5月月考数学试题分值： 100分 时间： 100分钟一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．与－457°角终边相同角的集合是( )A ．{α|α＝k ·360°＋457°，k ∈Z}B ．{α|α＝k ·360°＋97°，k ∈Z}C ．{α|α＝k ·360°＋263°，k ∈Z}D ．{α|α＝k ·360°－263°，k ∈Z}2．已知扇形的圆心角为23π弧度，半径为2，则扇形的面积是 ( ) A ．83π B ．43 C ．2π D ．43π 3．若sin α＝－513，且α为第四象限角，则tan α 的值等于 ( ) A ．125 B ． －512 C ． 512 D ．－1254．已知sin α－cos α＝2，α∈(0，π)，则tan α＝ ( )A ．－1B ．－22 C.22D ．1 5． 若0cos sin 3=+αα，则αα2sin cos 12+值为 （ ） A.310 B. 35 C. 2- D. 32 6．设A 是第三象限角，且⎪⎪⎪⎪⎪⎪sin A 2＝－sin A 2，则A 2是 ( ) A ．第一象限角B ．第四象限角C ．第三象限角D ．第二象限角 7. 已知3π=+B A ，则3tan tan 3tan tan -++B A B A 的值等于 ( )A. 32-B. 32C. 0D. 31-8．下列四式中不能．．化简为PQ 的是 A. ()BQ PA AB ++ B. ()()QC BA PC AB -++ C. CQ QP QC +- D. BQ AB PA -+9．设D 为△ABC 所在平面内一点，BC →＝3CD →，则( )A ．AD →＝－13AB →＋43AC → 3.AD →＝13AB →－43AC → C.AD →＝43AB →＋13AC → D.AD →＝43AB →－13AC → 10．已知A ，B ，C 是△ABC 的三个内角，设f (B )＝4sin B ·cos 2⎝ ⎛⎭⎪⎫π4－B 2＋cos 2B ， 若f (B )－m <2恒成立，则实数m 的取值范围是 ( )A ．m <1B ．m >－3C ．m <3D ．m >1二、填空题（本题共5小题，每小题4分，共20分)11．有一两岸平行的河流，水速为1，小船的速度为2，为使所走路程最短，小船应朝与水速成________角的方向行驶．12．求值 ︒︒︒︒80cos 60cos 40cos 20cos =_________13．已知sin α＝12＋cos α，且α∈（0，2π），则cos 2αsin ⎝ ⎛⎭⎪⎫α－π4的值为________． 14．给出下列命题：(1)f (x )＝－2cos(72π－2x )是奇函数； (2)若α，β都是第一象限角，且α＞β，则tan α＞tan β；(3)x ＝－38π是函数y ＝3sin(2x －34π)的图像的一条对称轴； (4)已知函数f (x )＝3sin 2π2x ＋1，使f (x ＋c )＝f (x )对任意x ∈R 都成立的正整数c 的 最小值是2.其中正确命题的序号是________．15．设α，β，γ∈（0，2π），且sin α＋sin γ＝sin β，cos β＋cos γ＝cos α，则β－α=________三．解答题（共40分）16.(本小题满分10分)（1）求值：2cos 10°－sin 20°sin 70°（2）已知α∈⎝ ⎛⎭⎪⎫0，π2，β∈⎝ ⎛⎭⎪⎫π2，π且sin(α＋β)＝3365，cos β＝－513.求sin α； 17．(本小题满分10分)设两个非零向量e 1和e 2不共线．(1)如果AB →＝e 1－e 2，BC →＝3e 1＋2e 2，CD →＝－8e 1－2e 2，求证：A 、C 、D 三点共线； （2）如果AB →＝e 1＋e 2，BC →＝2e 1－3e 2，CD →＝2e 1－ke 2，且A 、C 、D 三点共线，求k 的值．18．(本小题满分10分)已知函数f (x )＝2sin x cos x ＋2cos 2x .(1)求函数f (x )的单调递增区间；(2)将函数y ＝f (x )的图像向右平移π4个单位后，得到函数y ＝g (x )的图像，求方程g (x )＝1在x ∈[0，π]上的解集．19．(本小题满分10分) 如图，矩形ABCD 的长AD ＝23，宽AB ＝1，A ，D 两点分别在x ，y 轴的正半轴上移动，B ，C 两点在第一象限，求OB 2的最大值．高一年级数学答案一：选择题(每小题 4 分，共 40分)1-5 CDBAA 6-10 BCDAD二 填空题(每小题 4 分，共 20 分)11．135° 12．116 13．－14214．（1）（3）（4） 15． π3三 解答题（共40分）16．（10分）（1）原式＝2cos (30°－20°)－sin 20°sin 70°＝3cos 20°＋sin 20°－sin 20°sin 70°＝3cos 20°sin 70°＝ 3.（2）(1)∵β∈⎝ ⎛⎭⎪⎫π2，π，cos β＝－513， ∴sin β＝1213.又∵0<α<π2，π2<β<π， ∴π2<α＋β<3π2，又sin(α＋β)＝3365，∴cos(α＋β)＝－1－sin 2(α＋β)＝－ 1－⎝ ⎛⎭⎪⎫33652＝－5665，∴sin α＝sin[(α＋β)－β]＝sin(α＋β)cos β－cos(α＋β)sin β＝3365·⎝ ⎛⎭⎪⎫－513－⎝ ⎛⎭⎪⎫－5665·1213＝35.17．（10分）（1）证明∵AB →＝e 1－e 2，BC →＝3e 1＋2e 2，CD →＝－8e 1－2e 2，∴AC →＝AB →＋BC →＝e 1－e 2＋3e 1＋2e 2＝4e 1＋e 2＝12-（－8e 1－2e 2) ＝12-CD →．∴AC →与CD →共线．又∵AC →与CD →有公共点C ，∴A 、C 、D 三点共线．（2） AC →＝AB →＋BC →＝（e 1＋e 2)＋（2e 1－3e 2) ＝3e 1－2e 2，∵A 、C 、D 三点共线，∴AC →与CD →共线．从而存在实数λ使得AC →＝λCD →即3e 1－2e 2＝λ(2e 1－ke 2)．由平面向量的基本定理得⎩⎨⎧ 3＝2λ，－2＝－λk .解之，得⎩⎪⎨⎪⎧ λ＝32，k ＝43.∴k 的值为43. 18．（10分）(1)f (x )＝2sin(2x ＋π4)＋1，由2k π－π2≤2x ＋π4≤2k π＋π2(k ∈Z)得：k π－3π8≤x ≤k π＋π8， ∴f (x )的单调递增区间是[k π－3π8，k π＋π8](k ∈Z)． (2)由已知，g (x )＝2sin(2x －π4)＋1，由g (x )＝1，得2sin(2x －π4)＝0， ∴x ＝k π2＋π8(k ∈Z)，∵x ∈[0，π]，∴x ＝π8或5π8，∴方程的解集为{π8，5π8}．19.（10分）过点B 作BH ⊥OA ，垂足为H .设∠OAD ＝θ⎝ ⎛⎭⎪⎫0<θ<π2，则∠BAH ＝π2－θ，OA ＝ 23cos θ，BH ＝sin ⎝ ⎛⎭⎪⎫π2－θ＝cos θ， AH ＝cos ⎝ ⎛⎭⎪⎫π2－θ＝sin θ，所以B (23cos θ＋sin θ，cos θ)，OB 2＝(23cos θ＋sin θ)2＋cos 2θ＝7＋6cos 2θ＋23sin 2θ＝7＋43sin ⎝ ⎛⎭⎪⎫2θ＋π3. 由0<θ<π2，知π3<2θ＋π3<4π3， 所以当θ＝π12时，OB 2取得最大值7＋4 3.。

扬州中学2016届高三数学5月四模试卷（附答案）江苏省扬州中学高三模拟考试数学试题2016.5.20一、填空题：(共14题，总分70分)1．已知集合，，则等于▲．2．已知虚数满足，则▲．3．对一批产品的长度（单位：毫米）进行抽样检测，样本容量为400，右图为检测结果的频率分布直方图．根据产品标准，单件产品长度在区间[25，30)的为一等品，在区间[20，25)和[30，35)的为二等品，其余均为三等品．则样本中三等品的件数为▲．4.在平面直角坐标系xOy中，“双曲线的标准方程为”是“双曲线的渐近线方程为”成立的▲条件．(填“充要”、“充分非必要”、“必要非充分”、“非充分非必要”中的一种)5.下图是一个算法流程图，则输出的的值是▲。

6．如果实数满足线性约束条件，则的最小值等于▲．7.为强化安全意识，某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练，则选择的2天恰好为连续2天的概率是▲．8．设，，为三条不同的直线，给出如下两个命题：①若，，则；②若，，则．试类比以上某个命题，写出一个正确的命题：设，，为三个不同的平面，▲．9若数列满足（为常数），则称数列为等比和数列，k称为公比和．已知数列是以3为公比和的等比和数列，其中，则▲．10．函数的所有零点之和为▲．11．已知，，则的值为▲．12．如果将直线：向左平移1个单位，再向下平移2个单位，所得直线与圆：相切，则实数的值构成的集合为▲．13．已知点为△的重心，且，，则的值为▲．14．若幂函数(a)及其导函数在区间(0，)上的单调性一致(同为增函数或同为减函数)，则实数a的取值范围是▲．二、解答题：本大题共6小题，共90分.解答时应写出必要的文字说明、证明过程或演算步骤．15.(本小题满分14分)在△ABC中，角A，B，C的对边分别为a，b，c.已知bc＝233，A＋3C＝π.(1)求cosC的值；(2)求sinB的值；(3)若b＝33，求△ABC的面积．16.(本小题满分14分)如图，四边形AA1C1C为矩形，四边形CC1B1B为菱形，且平面CC1B1B⊥平面AA1C1C，D、E分别为A1B1、C1C的中点．求证：(1)BC1⊥平面AB1C；(2)DE∥平面AB1C.17.(本小题满分14分)如图，某水域的两直线型岸边l1，l2成定角120o，在该水域中位于该角角平分线上且与顶点A相距1公里的D 处有一固定桩．现某渔民准备经过该固定桩安装一直线型隔离网BC（B，C分别在l1和l2上），围出三角形ABC 养殖区，且AB和AC都不超过5公里．设AB＝x公里，AC ＝y公里．（1）将y表示成x的函数，并求其定义域；（2）该渔民至少可以围出多少平方公里的养殖区？18．（本题满分16分）定义：如果一个菱形的四个顶点均在一个椭圆上，那么该菱形叫做这个椭圆的内接菱形，且该菱形的对角线的交点为这个椭圆的中心．如图，在平面直角坐标系中，设椭圆的所有内接菱形构成的集合为．（1）求中菱形的最小的面积；（2）是否存在定圆与中的菱形都相切?若存在，求出定圆的方程；若不存在，说明理由；（3）当菱形的一边经过椭圆的右焦点时，求这条边所在的直线的方程．19．（本题满分16分）设函数，的定义域均为，且是奇函数，是偶函数，其中为自然对数的底数.（1）求，的表达式；（2）设，，，证明：.20.己知数列是公差不为零的等差数列，数列是等比数列．（1）若（n∈N*），求证：为等比数列；（2）设（n∈N*），其中是公差为2的整数项数列，，若，且当时，是递减数列，求数列的通项公式；（3）若数列使得是等比数列，数列的前项和为，且数列满足：对任意，N*,或者恒成立或者存在正常数，使恒成立，求证：数列为等差数列．附加题1.（本小题满分10分）已知矩阵（1）求；（2）满足AX=二阶矩阵X2.（本小题满分10分）在平面直角坐标系中，曲线的参数方程为为参数），且曲线上的点对应的参数，以O为极点，x轴的正半轴为极轴建立极坐标系．（1）求曲线的普通方程；（2）若是曲线上的两点，求的值．3、（本小题满分10分）某公司有10万元资金用于投资，如果投资甲项目，根据市场分析知道：一年后可能获利10%，可能损失10%，可能不赔不赚，这三种情况发生的概率分别为12，14，14；如果投资乙项目，一年后可能获利20%，也可能损失20%，这两种情况发生的概率分别为α和β(α＋β＝1)．(1)如果把10万元投资甲项目，用X表示投资收益(收益＝回收资金－投资资金)，求X的概率分布列及数学期望E(X)；(2)若10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益，求α的取值范围．4．（本小题满分10分）设为虚数单位，为正整数．（1）证明：；（2）结合等式“”证明：．江苏省扬州中学高三数学五月质量检测参考答案一、填空题：(共14题，总分70分)1．已知集合，，则等于▲．1．2．已知虚数满足，则▲．2．3．对一批产品的长度（单位：毫米）进行抽样检测，样本容量为400，右图为检测结果的频率分布直方图．根据产品标准，单件产品长度在区间[25，30)的为一等品，在区间[20，25)和[30，35)的为二等品，其余均为三等品．则样本中三等品的件数为▲．3.【答案】1004.在平面直角坐标系xOy中，“双曲线的标准方程为”是“双曲线的渐近线方程为”成立的▲条件．(填“充要”、“充分非必要”、“必要非充分”、“非充分非必要”中的一种)4.【答案】充分非必要5.下图是一个算法流程图，则输出的的值是5.596．如果实数满足线性约束条件，则的最小值等于．6.7.为强化安全意识，某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练，则选择的2天恰好为连续2天的概率是．[来源:学#科#网Z#X#X#K]7.8．设，，为三条不同的直线，给出如下两个命题：①若，，则；②若，，则．试类比以上某个命题，写出一个正确的命题：设，，为三个不同的平面，▲．8.若，，则9若数列满足（为常数），则称数列为等比和数列，k称为公比和．已知数列是以3为公比和的等比和数列，其中，则．9.10．函数的所有零点之和为．10.答案：8方程即，令，，这两个函数的图象都关于点对称，在区间内共有8个零点，从左往右记为，则，故所有零点和为8．11．已知，，则的值为▲．11.【解析】．12．如果将直线：向左平移1个单位，再向下平移2个单位，所得直线与圆：相切，则实数的值构成的集合为▲．12.易得直线：，即，圆：的圆心到直线：的距离，解得或．13．如图，点为△的重心，且，，则的值为▲．13.以AB的中点M为坐标原点，AB为x轴建立平面直角坐标系，则，，设，则，因为OAOB，所以，从而，化简得，，所以．14．若幂函数(a)及其导函数在区间(0，)上的单调性一致(同为增函数或同为减函数)，则实数a的取值范围是▲．14．【答案】【解析】易得，，当时，，；当时，，；当时，，；当时，，；当时，，，综上得，．二、解答题：本大题共6小题，共90分.解答时应写出必要的文字说明、证明过程或演算步骤．15.(本小题满分14分)在△ABC中，角A，B，C的对边分别为a，b，c.已知c(b)＝3(3)，A＋3C＝π.(1)求cosC的值；(2)求sinB的值；(3)若b＝3，求△ABC的面积．15.解：(1)因为A＋B＋C＝π，A＋3C＝π，所以B＝2C.(2分)又由正弦定理，得sinB(b)＝sinC(c)，c(b)＝sinC(sinB)，3(3)＝sinC(2sinCcosC)，化简，得cosC＝3(3).(5分)(2)因为C∈(0，π)，所以sinC＝＝3(1)＝3(6).所以sinB＝sin2C＝2sinCcosC＝2×3(6)×3(3)＝3(2).(8分)(3)因为B＝2C，所以cosB＝cos2C＝2cos2C－1＝2×3(1)－1＝－3(1).(10分)因为A＋B＋C＝π，所以sinA＝sin(B＋C)＝sinBcosC＋cosBsinC＝3(2)×3(3)＋3(1)×3(6)＝9(6).(12分)因为c(b)＝3(3)，b＝3，所以c＝2(9).所以△ABC的面积S＝2(1)bcsinA＝2(1)×3×2(9)×9(6)＝4(2).(14分)16.(本小题满分14分)如图，四边形AA1C1C为矩形，四边形CC1B1B为菱形，且平面CC1B1B⊥平面AA1C1C，D、E分别为A1B1、C1C的中点．求证：(1)BC1⊥平面AB1C；(2)DE∥平面AB1C.16.证明：(1)∵四边形AA1C1C为矩形，∴AC⊥C1C.(1分) 又平面CC1B1B⊥平面AA1C1C，平面CC1B1B∩平面AA1C1C ＝CC1，∴AC⊥平面CC1B1B.(3分)∵C1B平面CC1B1B,∴AC⊥C1B.(4分)又四边形CC1B1B为菱形，∴B1C⊥BC1.(5分)∵B1C∩AC＝C，AC平面AB1C,B1C平面AB1C，∴BC1⊥平面AB1C.(7分)(2)取AA1的中点F，连结DF，EF.∵四边形AA1C1C为矩形，E，F分别为C1C，AA1的中点，∴EF∥AC.又平面AB1C，AC平面AB1C，∴EF∥平面AB1C.(9分)∵D，F分别为边A1B1，AA1的中点，∴DF∥AB1.又DF平面AB1C，AB1平面AB1C，∴DF∥平面AB1C.∵EF∩DF＝F，EF平面DEF，DF平面DEF，∴平面DEF∥平面AB1C.(12分)∵DE平面DEF,∴DE∥平面AB1C.(14分)17.(本小题满分14分)如图，某水域的两直线型岸边l1，l2成定角120o，在该水域中位于该角角平分线上且与顶点A相距1公里的D 处有一固定桩．现某渔民准备经过该固定桩安装一直线型隔离网BC（B，C分别在l1和l2上），围出三角形ABC 养殖区，且AB和AC都不超过5公里．设AB＝x公里，AC ＝y公里．（1）将y表示成x的函数，并求其定义域；（2）该渔民至少可以围出多少平方公里的养殖区？试题解析：解：(1)由SΔABD＋SΔACD＝SΔABC得xsin60&ordm;＋ysin60&ordm;＝xysin120&ordm;……………2分所以x+y=xy，所以y＝……………4分又0＜y≤5，0＜x≤5，所以≤x≤5所以定义域为{x|≤x≤5}………………6分18．（本题满分16分）定义：如果一个菱形的四个顶点均在一个椭圆上，那么该菱形叫做这个椭圆的内接菱形，且该菱形的对角线的交点为这个椭圆的中心．如图，在平面直角坐标系中，设椭圆的所有内接菱形构成的集合为．（1）求中菱形的最小的面积；（2）是否存在定圆与中的菱形都相切?若存在，求出定圆的方程；若不存在，说明理由；（3）当菱形的一边经过椭圆的右焦点时，求这条边所在的直线的方程．18.解：（1）如图，设，，当菱形的对角线在坐标轴上时，其面积为；当菱形的对角线不在坐标轴上时，设直线的方程为：，①则直线的方程为：，又椭圆，②由①②得，，，从而，同理可得，，（3分）所以菱形的面积为(当且仅当时等号成立),综上得，菱形的最小面积为；（6分）（2）存在定圆与中菱形的都相切，设原点到菱形任一边的距离为，下证：，证明：由(1)知，当菱形的对角线在坐标轴上时，，当菱形的对角线不在坐标轴上时，，即得，综上，存在定圆与中的菱形都相切；（12分）（3）设直线的方程为，即，则点到直线的距离为，解得，所以直线的方程为．（16分）19．（本题满分16分）设函数，的定义域均为，且是奇函数，是偶函数，其中为自然对数的底数.（1）求，的表达式；（2）设，，，证明：.解：（1）由得，，因为是奇函数，是偶函数，所以，从而，(4分)（2）当时，，所以，.(6分)由（1）得，，，(8分)当时，，，设函数，(10分)则，(12分)若，，则，故为上增函数，所以，若，，则，故为上减函数，所以，综上知，.（16分）20.己知数列是公差不为零的等差数列，数列是等比数列．（1）若（n∈N*），求证：为等比数列；（2）设（n∈N*），其中是公差为2的整数项数列，，若，且当时，是递减数列，求数列的通项公式；（3）若数列使得是等比数列，数列的前项和为，且数列满足：对任意，N*,或者恒成立或者存在正常数，使恒成立，求证：数列为等差数列．（1）证明：，设公差为且，公比为，=常数，为等比数列………3分（2）由题意得：对恒成立且对恒成立，…5分对恒成立…………7分对恒成立………………9分而或或.………………10分（3）证明：设不妨设，，即.………………13分若，满足，若，则对任给正数M，则取内的正整数时，，与矛盾.若，则对任给正数T=，则取内的正整数时=，与矛盾.，而是等差数列，设公差为，为定值，为等差数列.………………16分附加题答案1.已知矩阵（1）求；（2）满足AX=二阶矩阵X1.解：(1)………4分(2)………10分2.在平面直角坐标系中，曲线的参数方程为为参数），且曲线上的点对应的参数，以O为极点，x轴的正半轴为极轴建立极坐标系．（1）求曲线的普通方程；（2）若是曲线上的两点，求的值．(1)(2)3、某公司有10万元资金用于投资，如果投资甲项目，根据市场分析知道：一年后可能获利10%，可能损失10%，可能不赔不赚，这三种情况发生的概率分别为2(1)，4(1)，4(1)；如果投资乙项目，一年后可能获利20%，也可能损失20%，这两种情况发生的概率分别为α和β(α＋β＝1)．(1)如果把10万元投资甲项目，用X表示投资收益(收益＝回收资金－投资资金)，求X的概率分布列及数学期望E(X)；(2)若10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益，求α的取值范围．3.解：(1)依题意，X的可能取值为1，0，－1，(2分) X的分布列为X10－1P2(1)4(1)4(1)(4分)E(X)＝1×2(1)－1×4(1)＝4(1).(5分)(2)设Y表示10万元投资乙项目的收益，则Y的分布列为Y2－2Pαβ(8分)E(Y)＝2α－2β＝4α－2，依题意要求4α－2≥4(1)，∴16(9)≤α≤1.(10分)23．（本小题满分10分）设为虚数单位，为正整数．（1）证明：；（2）结合等式“”证明：．证明：（1）①当时，，即证；②假设当时，成立，则当时，，故命题对时也成立，由①②得，；（5分）（2）由（1）知，，其实部为；，其实部为，根据两个复数相等，其实部也相等可得：．（10分）。