刘鸿文《材料力学》(第5版)课后习题(交变应力)【圣才出品】
- 格式:pdf
- 大小:1.48 MB
- 文档页数:20


第8章 组合变形一、解答题1.矩形截面梁如图8-1(a )所示。
已知:q =2kN /m ,P 0=240kN ,P 1=160kN ,P 2=4kN ,b =12cm,l =2m ,h =16cm 。
求梁内的最大拉应力和压应力以及危险截面上中性轴的位置。
图8-1解:梁的固定端为危险截面,其上的内力为危险截面上M y 和M z所引起的应力的正、负号如图8-1(b )所示。
从图中可以看出,最大拉应力发生在第一象限的角点A ,最大压应力发生在第四象限的角点B 。
对于危险截面,N <0、M y >0、M z >0;而矩形截面的惯性半径的平方所以,中性轴n -n 在z 轴和y 轴的截距分别为2.简易摇臂吊车如图8-2(a )所示,吊重F =8 kN ,梁由两根槽钢组成,许用应力[σ]=120 MPa 。
试按正应力强度条件选择槽钢的型号。
图8-2解:梁AB 的受力简图如图8-2(b )所示,由平衡方程∑M A =0,得F (2.5+1.5)-F C sin30°×2.5=0F C =25.6 kN力F Cr 在x ,y 方向的分量分别为F xC =F C cos30°=22.2kNF Cy =F C sin30°=12.8 kNAB 梁受轴力F Cr ,横向力F 及F Cy作用发生压缩与弯曲组合变形,其轴力图和弯矩图如图8-2(c)所示,危险截面是C 截面。
C 截面的压缩应力和最大弯曲正应力分别为压缩和弯曲的组合应力为有两个未知参数,可先不考虑轴力的影响,按弯曲应力选取即得W z ≥10×1044 mm 3每根槽钢w'z ≥5×104mm 3,查型钢表,选取12.6槽钢,其W'z =6.2×104mm 3,A =1569 mm 2。
根据压缩和弯曲的组合应力进行校核强度满足,选定12.6槽钢。
3.偏心拉伸杆,弹性模为E ,尺寸、受力如图8-3所示,试求:(1)最大拉应力和最大压应力的位置和数值;(2)AB 长度的改变量。


第11章 交变应力一、选择题1.在对称循环的交变应力作用下,构件的疲劳强度条件为:;若按非对称循环的构件的疲劳强度条件进行了疲劳强度校核,则()。
A .是偏于安全的B .是偏于不安全的C .是等价的,即非对称循环的构件的疲劳强度条式也可以用来校核对称循环下的构件疲劳强度D .不能说明问题,必须按对称循环情况重新校核【答案】C2.一交变应力的应力变化曲线如图11-1所示,则其平均应力σm ,应力幅σa 和循环特性r 为( )。
A .σm =-20 MPa ,σa =30 MPa ,γ=-5B .σm =-20 MPa ,σa =30 MPa ,51-=γC .σm =30 MPa ,σa =-20 MPa ,γ=5D .σm =30 MPa ,σa =-20 MPa ,51=γ【答案】A【解析】从图可知,σmax =10 MPa ,σmin =-50 MPa ,则有因此答案选A。
图11-1 图11-23.如图11-2所示,在σa-σm坐标系中(σa为交变应力的幅度,σm为平均应力),C1,C2两点均位于一条过原点0的直线上,设C1,C2两点对应的两个应力的循环特征为r1,r2,最大应力分别为σmax1,σmax2,则()。
A.γ1=γ2,σmax1>σmax2B.γ1=γ2,σmax1<σmax2C.γ1=γ2,σmax1>σmax2D.γ1=γ2,σmax1<σmax2【答案】A【解析】在射线OC1上,有σa+σm=σmax则C1,C2的循环特征相同,且C2的最大应力比C1的大。
因此答案选A。
4.在对称循环的交变应力作用下,构件的持久极限为()。
A.B.C.D.【答案】B5.图11-3所示为传动轴在匀速运行中,危险截面危险点处,弯曲正应力的循环rσ和扭转切应力的循环特征rτ分别为()。
图11-3A.rσ=-1,rτ=1B.rσ=1,rτ=-1C.rσ=rτ=-1D.rσ=rτ=1【答案】A6.有效应力集中因数Kσ和尺寸因数εσ的数值范围分别为()。

第11章交变应力11.1本章要点详解本章要点■交变应力与疲劳失效■交变应力的循环特征、应力幅和平均应力■持久极限及其影响因素■提高构件疲劳强度的措施重难点导学一、交变应力与疲劳失效(1)交变应力:随时间做周期性变化的应力。
(2)疲劳失效:构件在名义应力低于强度极限,甚至低于屈服极限的情况下,突然发生断裂。
在交变应力作用下,虽然应力低于屈服极限,但长期反复之后,构件也会突然断裂。
即使是塑性较好的材料,断裂前也无明显的塑性变形。
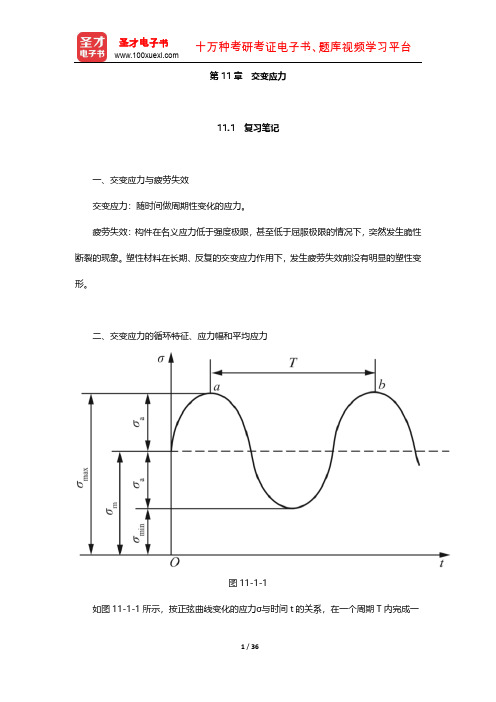
二、交变应力的循环特征、应力幅和平均应力图11-1如图11-1所示,按正弦曲线变化的应力σ与时间t 的关系,在一个周期T 内完成一个应力循环,该交变应力的最大应力和最小应力分别记作σmax 和σmin ,则该交变应力有①循环特征(应力比)②应力幅③平均应力对于max σ与min σ大小相等,符号相反的应力循环称为对称循环;对于min 0σ=(或max 0σ=)的循环称为脉动循环。
三、持久极限及影响持久极限的因素1.持久极限持久极限即疲劳极限,是交变应力作用下的强度指标,一般由试验测得。
即只要应力不超过疲劳极限,则应力循环次数N 可无限增长,即试样可经历无数次循环而不发生疲劳。
2.影响持久极限的因素(1)构件外形的影响。
构件外形的突然变化可能会引起应力集中,使构件的持久极限显著降低。
(2)构件尺寸的影响。
随着试样横截面尺寸的增大,会引起持久极限相应的降低。
(3)构件表面质量的影响。
表面质量对持久极限有显著的影响,且构件的强化或机械处理都将提高构件的持久极限。
除上述三种因素外,构件的工作环境,如温度、介质等也会影响持久极限数值。
四、提高构件疲劳强度的措施(1)减轻应力集中。
在设计构件外形时,要避免出现方形或带有尖角的孔和槽;在尺寸截面突然改变处要采用较大的过渡圆角。
(2)降低表面粗糙度。
构件表面的粗糙度对疲劳强度影响很大,高强度钢对表面粗糙度更为敏感,在使用过程中避免构件表面受到机械损伤。
第7章 应力和应变分析强度理论一、填空题图7-1所示单元体的最大切应力为( )MPa 。
[西安交通大学2005研]图7-1【答案】50 MPa【解析】根据图7-1所示单元体和主应力的符号规定可知,该单元体的主应力为:MPa ,MPa ,MPa801=σ202==τσ203-=-=τσ三向应力状态下的最大切应力:二、选择题1.关于杆件受力的正确的论述是( )。
[北京科技大学2010研]A .圆轴扭转时,材料内仅有剪应力作用而没有正应力作用B .圆轴弯曲时,材料内仅有正应力作用而没有剪应力作用C .圆轴拉伸时,材料内仅有正应力作用而没有剪应力作用D .圆轴扭转时,材料内既可能有剪应力作用也可能有正应力作用【答案】D论是扭转、弯曲还是拉伸,材料内都即可能有剪应力作用也可能有正应力作用。
2.低碳钢构件中危险点应力状态如图7-2所示,材料的许用应力为[σ],则强度条件应满足( )。
[北京科技大学2010研]图7-2【答案】B【解析】根据主应力的符号规定知,危险点的三个主应力大小分别为:123,,στσσστ===-又构件材料为低碳钢,采用第三强度理论,强度条件为,综合结果为[]13σσσ-≤。
[]2τσ≤3.单元体应力状态如图7-3所示,其主应力之间关系为()。
[华南理工大学2010研]图7-3123B.σ1≥0,σ2=0,σ3≤0,|σ1|≥|σ3|C.σ3≤σ2≤0;σ1=0D.σ1≥0,σ2=0,σ3≤0,|σ1|≤|σ3|【答案】D【解析】由单元体应力状态图可看出,根据主应力计算公式可0,0,0x xy y στσ<>=得:max,min22x y x σσσσ+==±分析可见,。
123130,0,0,σσσσσ≥=≤≤4.已知斜截面应力公式:22cos sin 2sin cos x y xy θσσθσθτθθ=+-()()22sin cos cos sin x y xy θτσσθθτθθ=-+-一个平面等边三角形单元体如图7-4所示,截面应力如图7-4,则单元体的最大切应力为( )。
第11章 交变应力
11.1 火车轮轴受力情况如图11-1所示。
α=500 mm ,l =1 435 mm ,轮轴中段直径d =15 cm 。
若F =50 kN ,试求轮轴中段截面边缘上任一点的最大应力σ
max ,最小应力
σmin ,循环特征r ,并作出σ-t
曲线。
图11-1 图
11-2解:分析可知,轮轴中间段受纯弯曲作用,梁中间段任意截面的弯矩值为:任一截面边缘顶部各点有拉应力:
任一截面边缘底部各点有压应力:
故循环特征:
曲线如图11-2所示。
11.2 柴油发动机连杆大头螺钉在工作时受到最大拉力F max =58.3 kN ,最小拉力F min =55.8 kN 。
螺纹处内径d =11.5 mm 。
试求其平均应力σm ,应力幅σa ,循环特征r ,并作出σ-t 曲线。
解:
根据题意,最大应力:
最小应力:
则平均应力:
应力幅:
循环特征:
曲线如图11-3所示。
图11-3
11.3 某阀门弹簧如图11-4所示。
当阀门关闭时,最小工作载荷F min =200 N ;当阀门顶开时,最大工作载荷=500 N 。
设簧丝的直径d =5 mm ,弹簧外径D 1=36 max F mm ,试求平均应力,应力幅
,循环特征r ,并作出
τ-t 曲线。
m τa τ
图11-4 图11-5
解:根据题意,弹簧的平均直径:则旋绕比:,曲度系数:
最大切应力:
最小切应力:
则平均应力:
应力幅:
循环特征:
曲线如图11-5所示。
11.4 阶梯轴如图11-6所示。
材料为铬镍合金钢,σb =920 MPa ,σ-1=420 MPa ,τ-1=250 MPa 。
轴的尺寸:d =40 mm ,
D =50 mm ,R =5 mm 。
求弯曲和扭转时的有效应力集中因数和尺寸因数。
图11-6
解:根据题意,可得:
①查教材图11-8(c ),,插值得弯曲时的有效应力集中因数MPa b 920=σ;查教材表11.1,由,得弯曲时尺寸因数。
55.1=αK mm d 40=77.0=σε②查教材图11-8(c ),,插值得扭转时的有效应力集中因数MPa b 920=σ;查教材表11.1,得扭转时的尺寸因数。
1.26K τ=81.0=τε
11.5 货车轮轴两端载荷F =110 kN ,材料为车轴钢,σb =500 MPa ,σ-1=240
MPa 。
规定安全因数n =1.5。
试校核1-1和2-2截面的强度。
图11-8解:(1)校核1-1截面该截面的弯矩:
则该截面最大正应力:
根据题意,1-1截面:185.0108
20,23.1108133====
d R d D
由此查表得弯曲时的有效应力集中系数:
,尺寸系数:,查表插值得表面质量因数:。
则工作安全因数为:
故该截面强度满足要求。
(2)校核2-2截面弯矩:
则该截面最大正应力:
根据题意,2-2截面:3.013340,098.1133146====d R d D 由此查表得弯曲时的有效应力集中系数:,尺寸系数:,查表插 1.15K
σ=0.68σε=值得表面质量因数:。
则工作安全因数为:
故该截面强度满足要求。
11.6 在坐标系中,标出与图11-9所示应力循环对应的点,并求出自原点m
a σσ-出发并通过这些点的射线与轴的夹角α。
m σ图11-9
解:(a )已知
则应力幅:
,平均应力:故斜率:
,解得a 1=90°。
(b )已知
则应力幅:
平均应力:
故斜率:,解得a 2=63.4°。
(c )已知
则应力幅:
,平均应力:
故斜率:,解得a 3=45°。
(d )已知
则应力幅:
平均应力:
故斜率:
解得a 4=33.7°。
对应点如图11-10所示。
图11-10。