抽象函数小专题

专题8 抽象函数一、单选题1．函数()f x 是R 上的增函数，点()0,1A −，()3,1B 是其图象上的两点，则()11f x +<的解集为（ ） A ．()[),14,−∞−+∞ B ．()[) ,12,−∞−+∞ C ．1,2D ．()1,42．已知函数()f x 在定义域R 上单调，且(0,)x ∈+∞时均有(()2)1f f x x +=，则(2)f −的值为（ ） A ．3B ．1C ．0D ．1−3．单调增函数()f x 对任意,x y R ∈满足()()()f x y f x f y +=+，若()()33920x x xf k f ⋅+−−<恒成立，则k 的取值范围是（ ）A ．()1− B ．()1−∞C ．(1⎤⎦D ．)1,⎡+∞⎣4．定义在R 上的奇函数()f x 满足()()2f x f x −=，当(]0,1x ∈，()2log f x x x =−，则20212f ⎛⎫= ⎪⎝⎭（ ）A ．32B ．12C ．12−D ．32−5．已知定义在R 上的函数()f x 满足()()()f x y f x f y −=−，且当0x <时，()0f x >，则关于x 的不等式()()()()2222f mx f m f m x f x +>+（其中0m << ）A ．2x m x m ⎧⎫<<⎨⎬⎩⎭B ．{|x x m <或2}x m > C ．2x x m m ⎧⎫<<⎨⎬⎩⎭D ．{|x x m >或2}x m<6．已知函数()f x 是R 上的偶函数，且()f x 的图象关于点()1,0对称，当[]0,1x ∈时，()22xf x =−，则()()()()0122020f f f f ++++的值为（ ）A ．2−B ．1−C ．0D ．17．已知奇函数()f x 的定义域为R ，若()2f x +为偶函数，且()11f −=−，则()()20172016f f += A ．2−B ．1−C ．0D ．18．已知函数()f x 是定义在R 上的奇函数，当0x >时，()2f x x x =+，则不等式()()ln 1f x f <−的解集为（ ） A ．()0,e B ．1,e ⎛⎫−∞ ⎪⎝⎭C ．(10,e ⎛⎫⎪⎝⎭D ．1,e⎛⎫+∞ ⎪⎝⎭二、多选题9．已知函数()f x 满足x R ∀∈，有()(6)f x f x =−，且(2)(2)f x f x +=−，当[1,1]x ∈−时，)()lnf x x =，则下列说法正确的是（ ）A ．(2021)0f =B ．(2020,2022)x ∈时，()f x 单调递增C ．()f x 关于点(1010,0)对称D ．(1,11)x ∈−时，方程()sin 2f x x π⎛⎫=⎪⎝⎭的所有根的和为30 10．已知()f x 是定义在R 上的偶函数，()()11f x f x −=−+，且当[]0,1x ∈时，()22f x x x =+−，则下列说法正确的是（ ）A ．()f x 是以4为周期的周期函数B ．()()201820212f f +=−C ．函数()2log 1y x =+的图象与函数()f x 的图象有且仅有3个交点D ．当[]3,4x ∈时，()2918f x x x =−+11．已知函数()f x 的定义域为R ，且在R 上可导，其导函数记为()f x '.下列命题正确的有（ ） A ．若函数()f x 是奇函数，则()f x '是偶函数 B ．若函数()'f x 是偶函数，则()f x 是奇函数 C ．若函数()f x 是周期函数，则()f x '也是周期函数 D ．若函数()f x '是周期函数，则()f x 也是周期函数12．已知函数()y f x =是R 上的奇函数，对于任意x ∈R ，都有(4)()(2)f x f x f +=+成立，当[)0,2x ∈时，()21=−x f x ，给出下列结论，其中正确的是（ ）A ．(2)0f =B ．点(4,0)是函数()y f x =的图象的一个对称中心C ．函数()y f x =在[6,2]−−上单调递增D ．函数()y f x =在[6,6]−上有3个零点 三、填空题13．写出一个满足()()2f x f x =−的奇函数()f x =______.14．已知函数()f x 是R 上的奇函数，且()y f x =的图象关于1x =对称，当[0,1]x ∈时，()21x f x =−，计算(0)(1)(2)(3)(2021)f f f f f +++++＝________．15．函数()f x 为定义在R 上的奇函数，且满足()(2)f x f x =−，若(1)3f =，则(1)(2)(50)f f f +++=__________．16．设()f x 是定义在R 上的函数，且()()2f x f x =+，在区间[)1,1−上，(),102,015x a x f x x x +−≤<⎧⎪=⎨−≤<⎪⎩，其中a ∈R .若5922f f ⎛⎫⎛⎫−= ⎪ ⎪⎝⎭⎝⎭，则()5f a 的值是________.四、解答题17．已知定义在R 上的函数()f x ，()g x 满足： ①()01f =；②任意的x ，R y ∈，()()()()()f x y f x f y g x g y −=−.（1）求()()22f xg x −的值；（2）判断并证明函数()f x 的奇偶性.18．已知函数()f x 满足对,x y R ∀∈，都有()()()f x y f x f y +=+，且(1)2f =． （1）求(0)f 与(2)f −的值；（2）写出一个符合题设条件的函数()f x 的解析式（不需说明理由），并利用该解析式解关于x 的不等式(21)1()1f x f x +≥−．19．如果存在一个非零常数T ，使得对定义域中的任意的x ，总有f x Tf x 成立，则称()f x 为周期函数且周期为T .已知()f x 是定义在R 上的奇函数，且()y f x =的图象关于直线x a =（0a ≠，为常数）对称，证明：()f x 是周期函数.20．已知函数()()y f x x =∈R ．（1）若()f x 满足(1)y f x =+为R 上奇函数且(1)=−y f x 为R 上偶函数，求(3)(5)f f −+的值；（2）若函数()()y g x x =∈R 满足1(3)2g x +=x ∈R 恒成立，函数()()()h x f x g x =+，求证：函数()h x 是周期函数，并写出()h x 的一个正周期；（3）对于函数()y f x =，()()y k x x =∈R ，若(())()f k x f x =对x ∈R 恒成立，则称函数()y f x =是“广义周期函数”， ()k x 是其一个广义周期，若二次函数2()(0)f x ax bx c a =++≠的广义周期为()k x （()k x x =不恒成立），试利用广义周期函数定义证明：对任意的12,x x ∈R ，12x x ≠，()()12f x f x =成立的充要条件是12b x x a+=−．参考答案1．C【解析】解法一：因为()f x 是R 上的增函数，()0,1A −，()3,1B 是其图象上的两点，所以函数()f x 的草图如图所示.由图象得，()()11111013f x f x x +<⇔−<+<⇔<+<，即12x −<<.解法二：因为()f x 是R 上的增函数，()0,1A −，()3,1B 是其图象上的两点，所以当03x ≤≤时，()11f x −≤≤.又已知()11f x +<，即()111f x −<+<， 所以013x <+<，解得12x −<<. 故选：C2．A【解析】根据题意，函数()f x 在定义域R 上单调，且(0,)x ∈+∞时均有(()2)1f f x x +=， 则()2f x x +为常数，设()2f x x t +=，则()2f x x t =−+，则有()21f t t t =−+=，解可得1t =−，则()21f x x =−−，故(2)413f −=−=； 故选：A. 3．B【解析】因为()()()f x y f x f y +=+，所以()()3392(3392)0x x x x x xf k f f k ⋅+−−=⋅+−−<又对任意,x y R ∈满足()()()f x y f x f y +=+， 所以(0)(0)(0)f f f =+， 解得(0)0f =，由()f x 为R 上单调增函数可得33920x x x k ⋅+−−<，令30x t =>，即2(1)20k t t +−−<恒成立， 即21k t t+<+，而2t t +≥，当且仅当2t t=，即t =所以1k +<1k <， 故选：B 4．D【解析】因为()f x 满足()()2f x f x −=，所以()f x 的图像关于x=1对称. 又()f x 为定义在R 上的奇函数，所以()()()22f x f x f x =−=−−， 所以()()()42f x f x f x +=−+=， 所以()f x 为周期函数，且周期T =4. 所以2021552524222f f f ⎛⎫⎛⎫⎛⎫=⨯+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，而25511132log 222222f f f⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=−=−=−−− ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭， 所以20212f ⎛⎫= ⎪⎝⎭32−.故选：D 5．A【解析】任取12x x <，由已知得()120f x x −>，即()()120f x f x −>，所以函数()f x 单调递减．由()()()()2222f mx f m f m x f x +>+可得()()()()2222f mx f x f m x f m −>−，即()22f mx x f −>()22m x m −，所以2222mx x m x m −<−，即()22220mx m x m −++<，即()()20mx x m −−<，又因为0m << 所以2m m>，此时原不等式解集为2x m x m ⎧⎫<<⎨⎬⎩⎭．故选：A 6．D【解析】因为()f x 是R 上的偶函数，所以()()f x f x −=， 又()f x 的图象关于点()1,0对称，则()(2)f x f x =−−，所以()(2)f x f x −=−−，则()(2)f x f x =−+，得(4)(2)()f x f x f x +=−+=， 即(4)()f x f x +=−，所以()f x 是周期函数，且周期4T =，由[]0,1x ∈时，()22xf x =−，则(0)1,(1)0f f ==，(2)(0)1f f =−=−，(3)(3)(1)0f f f =−==，则(0)(1)(2)(3)0f f f f +++=， 则()()()()0122020f f f f ++++(0)5050(0)1f f =+⨯==故选：D 7．D【解析】奇函数()f x 的定义域为R ，若(2)f x +为偶函数， (0)0f ∴=，且(2)(2)(2)f x f x f x −+=+=−−，则(4)()f x f x +=−，则(8)(4)()f x f x f x +=−+=， 则函数()f x 的周期是8，且函数关于2x =对称， 则(2017)(25281)f f f =⨯+=（1）(1)(1)1f =−−=−−=，(2016)(2528)(0)0f f f =⨯==，则(2017)(2016)011f f +=+=， 故选D ． 8．C【解析】因为当0x >时，()2f x x x =+，且函数()f x 是定义在R 上的奇函数，所以0x <时，()()()()22f x f x x x x x ⎡⎤=−−=−−+−=−+⎣⎦， 所以()22,0,0x x x f x x x x ⎧−+<=⎨+>⎩，作出函数图象：所以函数()f x 是()+−∞∞，上的单调递增， 又因为不等式()()ln 1f x f <−，所以ln 10x x <−⎧⎨>⎩，即10x e <<，故选：C. 9．CD【解析】由题设知：2221()ln(1)lnln(1)()1f x x x x x f x x x−=++==−+−=−+−，故()f x 在[1,1]x ∈−上为奇函数且单调递减，又(2)(4)(2)f x f x f x +=−=−，即关于21x k =+、(2,0)k ，k Z ∈对称，且最小周期为4， A ：(2021)(50541)(1)ln(21)0f f f =⨯+==−≠，错误；B ：(2020,2022)x ∈等价于(0,2)x ∈，由上易知：(0,1)上递减，(1,2)上递增，故()f x 不单调，错误；C ：由上知：()f x 关于(2,0)k 对称且k Z ∈，所以()f x 关于(1010,0)对称，正确；D ：由题意，只需确定()f x 与sin 2xy π=在(1,11)x ∈−的交点，判断交点横坐标的对称情况即可求和，如下图示，∴共有6个交点且关于5x =对称，则16253410x x x x x x +=+=+=， ∴所有根的和为30，正确. 故选：CD 10．ACD【解析】对于A 选项，由已知条件可得()()()()1113f x f x f x f x +=−−=−−=−， 所以，函数()f x 是以4为周期的周期函数，A 选项正确；对于B 选项，()()()2018202f f f ==−=，()()202110f f ==，则()()201820212f f +=，B 选项错误；对于C 选项，作出函数()2log 1y x =+与函数()f x 的图象如下图所示：当[]0,1x ∈时，()[]221922,024f x x x x ⎛−=+⎫−=−∈− ⎪⎝⎭，结合图象可知，()22f x −≤≤.当3x >时，()2log 12x +>，即函数()2log 1y x =+与函数()f x 在()3,+∞上的图象无交点， 由图可知，函数()2log 1y x =+与函数()f x 的图象有3个交点，C 选项正确； 对于D 选项，当[]3,4x ∈时，[]41,0x −∈−，则[]40,1x −∈，所以，()()()()()2244442918f x f x f x x x x x =−=−=−+−−=−+，D 选项正确. 故选：ACD. 11．AC【解析】解：由导数的定义：()()()=lim x f x x f x f x x ∆→+∆−∆'选项A ：()()()()()()00=lim=lim=x x f x x f x f x f x x f x f x xx∆→∆→−+∆−−−−∆∆∆''−，即()f x '是偶函数，故A 正确；选项B ：如()sin 1f x x =+不是奇函数，而()cos f x x '=为偶函数；故B 错误， 选项C ：()()()()()()00=lim=limx x f x T x f x T f x x f x f x T f x xx∆→∆→++∆−++∆−=∆∆''+即()f x '也是周期函数，故C 正确；选项D ：如()sin f x x x =+不是周期函数，但()1cos f x x '=+是周期函数；故D 错误， 故选：AC. 12．AB【解析】在(4)()(2)f x f x f +=+中，令2x =−，得(2)0f −=，又函数()y f x =是R 上的奇函数，所以(2)(2)0f f =−=，(4)()f x f x +=，故()y f x =是一个周期为4的奇函数，因(0,0)是()f x 的对称中心，所以(4,0)也是函数()y f x =的图象的一个对称中心，故A 、B 正确；作出函数()f x 的部分图象如图所示，易知函数()y f x =在[6,2]−−上不具单调性，故C 不正确；函数()y f x =在[6,6]−上有7个零点，故D 不正确. 故选：AB 13．πsin2x （答案不唯一） 【解析】取()sin2f x x π=，下面为证明过程：显然，其定义域为R ； 由()sin sin ()22f x x x f x ππ⎛⎫⎛⎫−=−=−=− ⎪ ⎪⎝⎭⎝⎭，故()sin 2f x x π=为奇函数；又()(2)sin 2sin sin ()222f x x x x f x ππππ⎡⎤⎛⎫−=−=−== ⎪⎢⎥⎣⎦⎝⎭.故答案为：sin 2x π（答案不唯一）.14．1【解析】由题意，()()f x f x −=−且(2)()f x f x −=，∴()(2)()(2)(2)f x f x f x f x f x −=+=−=−−=−，即()(4)f x f x =+， ∴()f x 是周期为4的函数.令10x −≤<，则01x <−≤，而[0,1]x ∈时()21x f x =−，∴1()()(21)12xxf x f x −=−−=−−=−， ∴(0)(2)0,(1)1,(3)(1)1f f f f f ====−=−，即(0)(1)(2)(3)0f f f f +++=， 而(0)(1)(2)(3)(2021)505[(0)(1)(2)(3)]f f f f f f f f f +++++=⨯+++(5054)f +⨯(50541)f +⨯+(0)(1)1f f =+=.故答案为：115．3【解析】()(2)f x f x =−，(2)()f x f x ∴+=−，又()f x 为奇函数，(2)()(),(4)(2)()f x f x f x f x f x f x ∴+=−=−+=−+=()f x ∴是周期为4的周期函数，()f x 是定义在R 上的奇函数，(0)0,(4)(0)0f f f ∴=∴==，(2)(0)0,(3)(1)(1)3f f f f f ===−=−=−(1)(2)(3)(4)0f f f f ∴+++=，()()()()()12...50012123f f f f f ∴+++=⨯++=.故答案为：3．16．25− 【解析】因为()()2f x f x =+， 所以511222f f a ⎛⎫⎛⎫−=−=−+ ⎪ ⎪⎝⎭⎝⎭，9112210f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，所以11210a −+=，解得35a =， 所以()()()25315f a f f ==−=−. 故答案为：25− 17．（1）1；（2）偶函数，证明见解析.【解析】（1）依题意，()()()()()()22f x g x f x f x g x g x −=−()()01f x x f =−==.（2）由（1）知()()22001f g −=，∴()()220010g f =−=，即()00g =，∴()()()()()()()000f x f x f f x g g x f x −=−=−=，又因为()f x 的定义域为R ，所以函数()f x 为偶函数.18．（1）(0)0f =，(2)4f −=−；（2）31(,](,)22−∞−+∞（答案不唯一）. 【解析】（1）由()()()f x y f x f y +=+，令0x y ==，得(0)2(0)f f =，所以(0)0f =，令1,1x y ==−，得(0)(1)(1)f f f =+−，因为(1)2f =，所以(1)2f −=−，令1x y ==−，得(2)(1)(1)4f f f −=−+−=−，（2）答案不唯一，例如：()2f x x =满足条件.由(21)1()1f x f x +≥−，得2(21)2(21)23110212121x x x x x x +++≥⇔−=≥−−−， 解得：32x ≤−或12x >， 故解集为31(,](,)22−∞−+∞ 19．证明见解析【解析】∵()f x 是定义在R 上的奇函数，∴()()f x f x −=−，∵()y f x =的图象关于直线x a =（0a ≠，为常数）对称，所以()()f a x f a x +=−，∴(2)[()][()]()()f a x f a a x f a a x f x f x +=++=−+=−=−.从而(4)(2)()f a x f a x f x +=−+=.∴()f x 是周期函数，且周期为4a .20．（1）0；（2）证明见解析，正周期为24；（3）证明见解析．【解析】（1）因为()f x 满足(1)y f x =+为R 上奇函数，所以(1)(1)f x f x −=−+，所以()(2)0f x f x −++=，又因为()f x 满足(1)=−y f x 为R 上偶函数，所以(1)(1)f x f x −−=−，所以()(2)f x f x −=−，所以有(2)(2)0f x f x −++=，所以(2)(2)f x f x +=−−，所以(4)()f x f x +=−，所以(8)(4)()f x f x f x +=−+=，所以()f x 的一个周期为8，所以(3)(5)2(5)f f f −+=，在()(2)0f x f x −++=中令1x =−，得(1)(1)0f f +=，所以(1)0f =，在(4)()f x f x +=−中令1x =，得(5)(1)f f −=，所以(5)(1)0f f =−=，所以(3)(5)0f f −+=；（2）因为11(3)22g x +=≥，所以1(6)2g x +=12=因为[]11(3)1(3)122g x g x ⎡⎡+−+=+−⎢⎢⎣⎣ 21()()4g x g x =−+ 21()2g x ⎡⎤=−⎢⎥⎣⎦，所以111(6)()222g x g x +==+−()g x =，所以函数()g x 的一个周期为6，因为()()()h x f x g x =+，所以(24)(83)(64)()()()h x f x g x f x g x h x +=+⨯++⨯=+=，所以()h x 是周期函数，一个正周期为24；（3）充分性：当12b x x a +=−时，12b x x a=−−， 此时()()221222222b b b f x f x a x b x c ax bx c f x a a a ⎛⎫⎛⎫⎛⎫=−−=−−+−−+=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 所以充分性满足；必要性：因为二次函数2()(0)f x ax bx c a =++≠的广义周期为()k x ，所以(())()f k x f x =，所以22(())()a k x bk x c ax bx c ++=++，所以22()[()]0a k x x b k x x ⎡⎤−+−=⎣⎦，又因为()k x x =不恒成立，所以[()]0a k x x b ++=，所以()b k x x a =−−，又因为()()12f x f x =，且()()()11f k x f x =，所以()()()21f k x f x =，因为12x x ≠，所以1212()b b k x x x x a a +=−−+≠−， 所以()12k x x =，即12b x x a −−=，也即12b x x a +=−， 所以必要性满足．所以：对任意的12,x x ∈R ，12x x ≠，()()12f x f x =成立的充要条件是12b x x a +=−．。

抽象函数1.定义：没有给出具体解析式的函数叫做抽象函数，抽象函数问题可以全面考查学生对函数概念和性质的理解。

2.抽象函数的单调性：例1.已知定义在R 上的函数)(x f 对任意x 、R y ∈有()()()f x y f x f y +=+，且当0>x 时0)(<x f（1）试判断函数)(x f 在R 上的单调性；（2）若(1)1f =，()(2)2f x f x --<，求x 的取值范围。

例2.已知定义在R 上的函数)(x f y =，0)0(≠f ，当0>x 时1)(<x f ，且对任意x 、R y ∈有()()()f x y f x f y +=⋅（1）证明1)0(=f ；（2）证明对任意R x ∈，恒有0)(>x f ；（3）判断)(x f 在R 上的单调性；（4）若2(1)(2)1f x f x x +⋅-+>，求x 的取值范围。

例3.若定义域为),0(+∞的函数)(x f 有()()()f xy f x f y =+，且当1>x 时0)(<x f（1）求)1(f ；（2）判断)(x f 在定义域上的单调性；（3）若(2)1f =，求满足不等式()(3)2f x f x +-≥的x 的取值范围。

例4.已知定义在),0(+∞上的函数)(x f y =，(1)0f ≠，当1x >时1)(<x f ，且对任意x 、R y ∈有()()()f xy f x f y =⋅（1）求)1(f ；（2）证明对任意(0,)x ∈+∞，恒有0)(>x f ；（3）判断)(x f 在R 上的单调性；（4）若(1)(1)1f x f x +⋅->，求x 的取值范围。

例5.已知函数)(x f 的定义域为),0(+∞，当),0(+∞∈x 时，恒有x x f f 2)]([=，且过)(x f 图像上任意两点的直线斜率都大于1，求证：（1）)(x f 为增函数； （2）x x f >)(； （3）23)(34<<x x f 证明：（1）对任意1x 、2x 满足210x x <<，恒有1)()(1212>--x x x f x f ，则 0)()(1212>->-x x x f x f ，故)(x f 为增函数。

抽象函数专题（1）抽象函数是指没有明确给出具体的函数表达式，只是给出一些特殊条件的函数 抽象函数知识点：1、抽象函数的定义域：①已知()f x 的定义域，求[]()f g x 的定义域②已知[]()f g x 的定义域，求()f x 的定义域2、抽象函数表达式与函数值3、抽象函数的模型构造①线性函数型抽象函数f （x ）＝kx （k ≠0）----f （x ±y ）＝f （x ）±f （y ）②指数函数型的抽象函数f （x ）＝a x ---- f （x ＋y ）＝f （x ）f （y ）；f （x －y ）＝)()(y f x f ③对数函数型的抽象函数f （x ）＝lo g a x （a >0且a ≠1）-f （x ·y ）＝f （x ）＋f （y ）；f （yx ）＝ f （x ）－f （y ） ④幂函数型的抽象函数2()f x x = ---------()()()f xy f x f y =，()()()xf x f y f y =； 练习题：1、已知函数)(x f 对任意实数x ，y ，均有)()()(y f x f y x f +=+，且当0>x 时，0)(>x f ，2)1(-=-f ，求)(x f 在区间[－2，1]上的值域。

2、定义在R 上的函数)(x f 满足：对任意实数,m n ，总有)()()(n f m f n m f ⋅=+，且当0x >时，1)(0<<x f ．（1）试求)0(f 的值；（2）判断)(x f 的单调性并证明你的结论；（3）试举出一个满足条件的函数)(x f ．3、已知函数)(x f 满足定义域在),0(+∞上的函数，对于任意的),0(,+∞∈y x ，都有)()()(y f x f xy f +=，当且仅当1>x 时，0)(<x f 成立，（1）设),0(,+∞∈y x ，求证)()()(x f y f xy f -=； （2）设),0(,21+∞∈x x ，若)()(21x f x f <，试比较1x 与2x 的大小；（3）解关于x 的不等式[]01)1(2>+++-a x a x f4.已知定义在()()-,00,+∞⋃∞上的函数f(x)对任何x,y 都有f(xy)=f(x)f(y),且f(x)>0,当x>1时,有f(x)<1.（1）判断f(x)的奇偶性（2）判断并证明f(x)在(0,+∞)上的单调性.（3）求解不等式f (23-4x x )≥1抽象函数问题（2）1、下列结论：①函数y =2y =是同一函数；②函数(1)f x -的定义域为[1,2]，则函数2(3)f x 的定义域为；③函数22log (23)y x x =+-的递增区间为(1,)-+∞；④若函数(21)f x -的最大值为3，那么(12)f x -的最小值就是3-其中正确的个数为 ( )A. 0个B. 1个C. 2个D. 3个2、定义在R 上的函数()f x 满足1(0)0,()(1)1,()()52xf f x f x f f x =+-==，且当1201x x ≤<≤时，12()()f x f x ≤，则1()2007f 等于（ ） A. 12 B. 116 C. 132 D. 1643、已知()f x 是定义在R 上的函数，且3()[1()]1()2f x f x f x +-=+，(2)2f =，则()2009f 值为（ ）A. 2+B. 22 D. 2-4、已知(1)(1),()(2)f x f x f x f x +=-=-+，方程()0f x =在[0,1]内有且只有一个根12x =，则()0f x =在区间[]0,2013内根的个数为（ ） A. 2011 B. 1006 C. 2013 D. 1007 5、已知函数()f x 对任意实数x ，y 满足()()()f x y f x f y +=+，且(1)2f ≥.若存在整数m ，使得2(2)40f m m ---+= ，则m 取值的集合为______.6、定义在R 上的函数()f x 满足：(2)()0f x f x ++=，且函数(1)f x +为奇函数，对于下列命题：①函数()f x 满足(4)()f x f x +=；②函数()f x 图象关于点(1,0)对称；③函数()f x 的图象关于直线2x =对称；④函数()f x 的最大值为(2)f ；⑤(2009)0f =. 其中正确的序号为_________.7、定义在R 上的函数()f x ，(0)0f ≠，当0x >时，()1f x >，且对任意实数,a b ，有()()()f a b f a f b +=⋅，求证：(1)(0)1f = (2)证明：()f x 是R 上的增函数；(3)若2()(2)1f x f x x ⋅->，求x 的取值范围.8、已知()f x 是定义在(0,)+∞上的增函数，且满足 ()()()f xy f x f y =+， 1()12f =- (1)求证：(2)1f = (2)求不等式()(3)1f x f x -->的解集.9、已知函数f （x ）对任意实数x 、y 均有f （x ＋y ）＋2＝f （x ）＋f （y ），且当x >0时，f (x )>2，f (3)＝ 5，求不等式3)22(2<--a a f 的解.。

高一数学之抽象函数专题集锦一、选择题（本大题共14小题，共70.0分）1. 设f(x)为定义在R 上的偶函数，且f(x)在[0,+∞)上为增函数，则f(−2)，f(−π)，f(3)的大小顺序是( )A.B. C. D.2. 函数f(x)在(0,+∞)上单调递增，且f(x +2)关于x =−2对称，若f(−2)=1，则f(x −2)≤1的x 的取值范围是( )A. [−2,2]B. (−∞,−2]∪[2,+∞)C. (−∞,0]∪[4,+∞)D. [0,4]3. 已知函数y =f(x)定义域是[−2,3]，则y =f(2x −1)的定义域是( )A. [0,52]B. [−1,4]C. [−12,2]D. [−5,5]4. 函数f(x)在(−∞,+∞)上单调递减，且为奇函数．若f(1)=−1，则满足−1≤f(x −2)≤1的x 的取值范围是( )A. B. C. [0,4] D. [1,3]5. 若定义在R 上的奇函数f(x)在(−∞,0)单调递减，且f(2)=0，则满足xf(x −1)⩾0的x 的取值范围是( )A. [−1,1]∪[3,+∞)B. [−3,−1]∪[0,1]C. [−1,0]∪[1,+∞)D. [−1,0]∪[1,3] 6. 已知f(x)={x 2+4x x ≥0 , 4x −x 2 , x <0若f(2−a 2)>f(a)，则实数a 的取值范围是( ) A. (−2 , 1)B. (−1 , 2)C. (−∞ , −1)⋃(2 , +∞)D. (−∞ , −2)⋃(1 , +∞)7. 已知定义在R 上的函数f(x)满足f(2−x)=f(x)，且在[1,+∞)上为增函数，则下列关系式正确的是A. f(−1)<f(0)=f(2)B. f(0)<f(−1)<f(2)C. f(0)=f(2)<f(−1)D. f(−1)<f(0)<f(2)8. 设函数f(x)={x 2−6x +6,x ⩾03x +4,x <0，若互不相等的实数x 1,x 2,x 3满足f(x 1)=f(x 2)=f(x 3)，则x 1+x 2+x 3的取值范围是( )A. (113,6]B. (203,263)C. (203,263]D. (113,6) 9. f(x)是定义域在(−2,2)上单调递减的奇函数，当f(2−a)+f(2a −3)<0时，a 的取值范围是( )A. (0,4)B. (0,52)C. (12,52)D. (1,52) 10. 设f (x )是定义在R 上的奇函数，且当x ≥0时，f (x )单调递减，若x 1+ x 2>0，则f (x 1)+ f (x 2)的值( )A. 恒为负值B. 恒等于零C. 恒为正值D. 无法确定正负11. 已知偶函数f(x)在区间(0,+∞)上单调增加，则f(2x −1)<f(13)的x 取值范围是( ) A. (13,23). B. [13,23) C. (12,23) D. (12,23] 12. 已知函数y =f(x)定义域是[−2,3]，则y =f(2x −1)的定义域是( )A. [0,52]B. [−1,4]C. [−12,2]D. [−5,5] 13. 若函数f(x)的定义域是[0,1]，则函数f(2x)+f(x +13)的定义域为( )A. [−13,23]B. [−13,12]C. [0,12]D. [0,13] 14. 已知函数f(x)={x 2+4x(x ⩾0)4x −x 2(x <0)，若f (2−a 2)>f(a)，则实数a 的取值范围是( ) A. (−∞,−1)∪(2,+∞)B. (−1,2)C. (−2,1)D. (−∞,−2)∪(1,+∞)二、填空题（本大题共4小题，共20.0分） 15. 设偶函数f(x)在区间[0,+∞)上单调递增，则满足f(2x −1)≤f(1)的x 的取值范围是_____．16. 已知偶函数f(x)在区间[0,+∞)上单调递增，则满足f(2x −1)<f(13)的x 的取值范围是 ．17. 奇函数f(x)的定义域为[−5,5]，当x ∈[0,5]时，f(x)的图象如图所示，则不等式f(x)<0的解集是______________．18. 已知f(x)是定义在R 上的偶函数，且f(x +4)=f(x −2).若当x ∈[−3,0]时，f(x)=6−x ，则f(919)=______．三、解答题（本大题共15小题，共180.0分）19. 设函数f(x)是增函数，对于任意x ，y ∈R 都有f(x +y)=f(x)+f(y)．(1)求f(0)；(2)证明f(x)奇函数；(3)解不等式．20.函数f(x)的定义域为D={x|x≠0}，且满足对于任意x1∈D,x2∈D，有f(x1⋅x2)=f(x1)+f(x2)．(Ⅰ)求f(1 )的值；(Ⅱ)判断f(x)的奇偶性并证明；(Ⅲ)如果f(4)=1，f(3x+1)+f(2x−6)≤3，且f(x)在(0,+∞)上是增函数，求x的取值范围．21.已知函数f(x)=ax2+bx ，且f(1)=2，f(2)=52．(Ⅰ)确定函数f(x)的解析式，并判断奇偶性；(Ⅱ)用定义证明函数f(x)在区间(−∞,−1)上单调递增；(Ⅲ)求满足f(1+2t2)−f(3+t2)<0的实数t的取值范围．22.定义域为R的单调函数f(x)满足f(x+y)=f(x)+f(y)(x,y∈R)，且f(3)=6，(1)求f(0)，f(1)；(2)判断函数f(x)的奇偶性，并证明；(3)若对于任意x∈[12,3]都有f(kx2)+f(2x−1)<0成立，求实数k的取值范围．23.已知y=f(x)是定义域为R的奇函数，当x∈[0,+∞)时，f(x)=x2−2x．(1)写出函数y=f(x)的解析式；(2)若方程f(x)=a恰有3个不同的解，求实数a的取值范围．24.已知函数y=f(x)的定义域为R，对任意a,b∈R，都有f(a+b)=f(a)+f(b)，且当x>0时，f(x)<0恒成立，证明：(Ⅰ)函数y=f(x)是R上的减函数；(Ⅱ)函数y=f(x)是奇函数.25.已知f(x)是定义在[−1,1]上的奇函数，且f(1)=1，若a,b∈[−1,1]，且a+b≠0时，有f(a)+f(b)>0恒成立．a+b(1)用定义证明函数f(x)在[−1,1]上是增函数;)<f(1−x);(2)解不等式：f(x+12(3)若f(x)≤m2−2m+1对所有x∈[−1,1]恒成立，求实数m的取值范围．26.定义域为R的函数f(x)满足，对任意的m，n∈R有f(m+n)=f(m)f(n)，且当x>0时，有0<f(x)<1，f(4)=1．16(1)求f(0)；(2)证明：f(x)在R上是减函数；f(x2)恒成立，求实数a的取值范围．(3)若x>0时，不等式f(x)f(ax)>14)=1，如果对于0<x<y，都有f(x)> 27.已知函数f(x)的定义域是(0,+∞)，且满足f(xy)=f(x)+f(y)，f(12f(y)，(1)求f(1)；(2)解不等式f(−x)+f(3−x)≥−2。

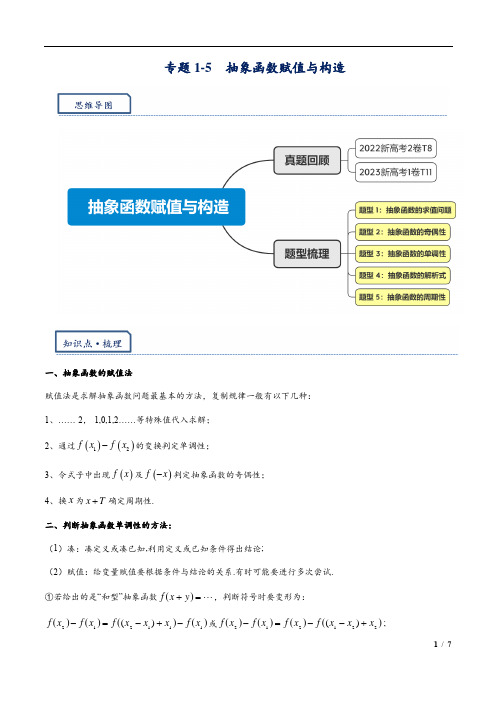
专题1-5 抽象函数赋值与构造一、抽象函数的赋值法赋值法是求解抽象函数问题最基本的方法，复制规律一般有以下几种： 1、……-2，-1,0,1,2……等特殊值代入求解； 2、通过的变换判定单调性；3、令式子中出现及判定抽象函数的奇偶性；4、换为确定周期性. 二、判断抽象函数单调性的方法：（1）凑：凑定义或凑已知,利用定义或已知条件得出结论;（2）赋值：给变量赋值要根据条件与结论的关系.有时可能要进行多次尝试. ①若给出的是“和型”抽象函数，判断符号时要变形为：或;()()12−f x f x ()f x ()−f x x +x T () =+y x f ()()()()111212)(x f x x x f x f x f −+−=−()()()()221212)(x x x f x f x f x f +−−=−②若给出的是“积型”抽象函数，判断符号时要变形为：或. 三、常见的抽象函数模型1、可看做的抽象表达式；2、可看做的抽象表达式（且）；3、可看做的抽象表达式（且）；4、可看做的抽象表达式.2022新高考2卷T8 1．已知函数()f x 的定义域为R ，且()()()(),(1)1f x y f x y f x f y f ++−==，则221()k f k ==∑（ ）A ．3−B ．2−C ．0D ．12023新高考1卷T112．（多选）已知函数()f x 的定义域为R ，()()()22f xy y f x x f y =+，则（ ）．A ．()00f =B ．()10f =C ．()f x 是偶函数D ．0x =为()f x 的极小值点2023·山东青岛·统考三模() =xy f ()()()112112x f x x x f x f x f −⎪⎪⎭⎫ ⎝⎛⋅=−()()()⎪⎪⎭⎫⎝⎛⋅−=−212212x x x f x f x f x f ()()()+=+f x y f x f y ()=f x kx ()()()+=f x y f x f y ()=xf x a 0>a 1≠a ()()()=+f xy f x f y ()log =a f x x 0>a 1≠a ()()()=f xy f x f y ()=af x x 重点题型·归类精讲1．设()f x 为定义在整数集上的函数，()11f =，()20f =，()10f −<，对任意的整数,x y 均有()()()()()11f x y f x f y f x f y +=−+−．则()55f =______．2023·山东滨州·三模2．（多选）已知连续函数()f x 对任意实数x 恒有()()()f x y f x f y +＝＋，当0x ＞时，()0f x ＜，(1)2f ＝－，则以下说法中正确的是（ ） A ．f （0）＝0B ．f (x )是R 上的奇函数C ．f (x )在[－3，3]上的最大值是6D ．不等式()232()(3)4f x f x f x −<+的解集为213xx ⎧⎫<<⎨⎬⎩⎭安徽省皖江名校联盟2024届高三上学期10月第二次联考3．已知函数不是常数函数，且满足以下条件：①，其中；②，则（ ）A ．0B ．1C ．2D ．4．（多选）已知定义在R 上的函数()f x 满足()()()()()()()()2,02,01f xy f x f y f x f y f f f =−−+<≠，且()0f x >，则（ ） A ．()01f =B ．()12f −=C ．()()2f x f x −=D ．()()f x f x −=5．已知函数及其导函数的定义域均为，对任意的，恒有，则下列说法正确的个数是（ ）①；②必为奇函数；③；④若，则.A ．1B ．2C ．3D ．42023·浙江嘉兴·统考模拟6．已知函数的定义域为，且，，则的值是（ ）A ．9B ．10C ．11D ．12(),y f x x =∈R ()()()()f a b f a b f a f b ++−=,a b ∈R ()10f =()2026f −=2−()f x ()f x 'R ,R x y ∈()()()()2f x y f x y f x f y ++−=()00f =()f x '()()00f x f +≥1(1)2f =202311()2n f n ==∑()f x R ()()()()31,00,f x x f x x ⎛⎫=∈−∞+∞ ⎪⎝⎭()()()2f x f y xy f x y ++=+()3f2023届江苏连云港校考7．已知函数，任意，满足，且，则的值为（ ）A ．B ．0C ．2D ．48．已知，都是定义在上的函数，对任意x ，y 满足，且，则下列说法正确的是（ ）A ．B ．函数的图象关于点对称C ．D ．若，则2023绍兴·高二期末9．已知函数的定义域为R ，且，为奇函数，，则（ ） A ． B ． C ．0 D ．10．（多选）已知函数()f x 的定义域为R ,()()()f x y f x f y +=+,则（ ）A ．()00f =B ．()f x 是奇函数 C ．0x =为()f x 的极小值点D ．若()11f =,则()20232023f =11．（多选）设()f x 是定义在R 上的函数，对,x y ∀∈R ，有()()()()22f x y f x y f x f y +−−=++，且()00f ≠，则（ ）A ．()()0f x f x −−=B ．()()40f x f x +−=C ．()()()()02420242f f f f ++++=−()f x x y R ∈，()()()()22f x y f x y f x f y +−=−()()1220f f ==，()()()1290f f f +++2−()f x ()g x R ()()()()()f x y f x g y g x f y −=−()()210f f −=≠()01f =()21g x +()1,0()()110g g +−=()11f =()202311n f n ==∑()f x ()()()28f x f x f ++=()21f x +1122f ⎛⎫= ⎪⎝⎭22112k kf k =⎛⎫−= ⎪⎝⎭∑11−12−212D ．()()()()222212320244048f f f f ++++=12．（多选）已知函数()f x 及其导函数()f x '的定义域均为R ，对任意的,R x y ∈，恒有()()()()2f x y f x y f x f y ++−=，则下列说法正确的有（ ）A ．()00f =B ．()f x '必为奇函数C ．()()00f x f +≥D ．若1(1)2f =，则202311()2n f x ==∑13．已知函数()f x 的定义域为R ，满足()()()()f x y f x y f x f y ++−=⋅，且12f ，则（ ）A ．()02f =B ．()f x 为奇函数C ．()()()()12320232f f f f +++⋅⋅⋅⋅⋅⋅+=−D ．()22f x −≤≤14．（多选）已知定义域为R 的函数()f x 对任意实数,x y 都有()()()()2f x y f x y f x f y ++−=，且102f ⎛⎫= ⎪⎝⎭，则以下结论一定正确的有（ ）A ．()01f =−B ．()f x 是偶函数C ．()f x 关于1,02⎛⎫⎪⎝⎭中心对称D ．()()()1220230f f f +++=15．函数()f x 的定义域为R ，且()()()21f x f x f x +=−+−，()()2f x f x =−，()3651f =−，则()20231k f k ==∑ .16．已知函数()f x 满足：1(1),4()()()()(,R)4f f x f y f x y f x y x y ==++−∈，则()2023f = .17．已知函数()f x 定义域为R ，满足()()()()()11,f f x y f x y f x f y =++−=，则()8f = .18．设()f x 为定义在整数集上的函数，()11f =，()20f =，()10f −<，对任意的整数,x y 均有()()()()()11f x y f x f y f x f y +=−+−．则()55f = ．19．（2024届厦门一中校考）若定义域为R 的奇函数()f x 满足()(1)(1)f x f x f x =++−，且(1)2f =，则(2024)f = ．20．函数()f x 的定义域为R ，对任意,x y ∈R ，恒有()()222x y x y f x f y f f +−⎛⎫⎛⎫+=⋅⎪ ⎪⎝⎭⎝⎭，若()112f =，则()1f −= ，()20221n f n ==∑ ．深圳市宝安区2024届高三上学期10月调研数学试题21．已知函数()f x 的定义域为R ，且()()()()22f x y f x y f x f y +−=−，()13f =，322f x ⎛⎫+ ⎪⎝⎭为偶函数，则（ ） A ．()f x 为偶函数 B ．()23f = C ．()()33f x f x +=−−D ．()202313k f k ==∑专题1-5 抽象函数赋值与构造一、抽象函数的赋值法赋值法是求解抽象函数问题最基本的方法，复制规律一般有以下几种： 1、……-2，-1,0,1,2……等特殊值代入求解； 2、通过的变换判定单调性；3、令式子中出现及判定抽象函数的奇偶性；4、换为确定周期性. 二、判断抽象函数单调性的方法：（1）凑：凑定义或凑已知,利用定义或已知条件得出结论;（2）赋值：给变量赋值要根据条件与结论的关系.有时可能要进行多次尝试. ①若给出的是“和型”抽象函数，判断符号时要变形为：或;()()12−f x f x ()f x ()−f x x +x T () =+y x f ()()()()111212)(x f x x x f x f x f −+−=−()()()()221212)(x x x f x f x f x f +−−=−②若给出的是“积型”抽象函数，判断符号时要变形为：或. 三、常见的抽象函数模型1、可看做的抽象表达式；2、可看做的抽象表达式（且）；3、可看做的抽象表达式（且）；4、可看做的抽象表达式.2022新高考2卷T8 1．已知函数()f x 的定义域为R ，且()()()(),(1)1f x y f x y f x f y f ++−==，则221()k f k ==∑（ ）A ．3−B ．2−C ．0D ．1【答案】A【分析】法一：根据题意赋值即可知函数()f x 的一个周期为6，求出函数一个周期中的()()()1,2,,6f f f 的值，即可解出．【详解】[方法一]：赋值加性质因为()()()()f x y f x y f x f y ++−=，令1,0x y ==可得，()()()2110f f f =，所以()02f =，令0x =可得，()()()2f y f y f y +−=，即()()f y f y =−，所以函数()f x 为偶函数，令1y =得，()()()()()111f x f x f x f f x ++−==，即有()()()21f x f x f x ++=+，从而可知()()21f x f x +=−−，()()14f x f x −=−−，故()()24f x f x +=−，即()()6f x f x =+，所以函数()f x 的一个周期为6．因为()()()210121f f f =−=−=−，()()()321112f f f =−=−−=−，()()()4221f f f =−==−，()()()5111f f f =−==，()()602f f ==，所以一个周期内的()()()1260f f f +++=．由于22除以6余4，() =xy f ()()()112112x f x x x f x f x f −⎪⎪⎭⎫ ⎝⎛⋅=−()()()⎪⎪⎭⎫⎝⎛⋅−=−212212x x x f x f x f x f ()()()+=+f x y f x f y ()=f x kx ()()()+=f x y f x f y ()=xf x a 0>a 1≠a ()()()=+f xy f x f y ()log =a f x x 0>a 1≠a ()()()=f xyf x f y ()=af x x所以()()()()()221123411213k f k f f f f ==+++=−−−=−∑．故选：A ．[方法二]：【最优解】构造特殊函数由()()()()f x y f x y f x f y ++−=，联想到余弦函数和差化积公式()()cos cos 2cos cos x y x y x y ++−=，可设()cos f x a x ω=，则由方法一中()()02,11f f ==知2,cos 1a a ω==，解得1cos 2ω=，取3πω=，所以()2cos3f x x π=，则()()()()2cos 2cos 4cos cos 333333f x y f x y x y x y x y f x f y ππππππ⎛⎫⎛⎫++−=++−== ⎪ ⎪⎝⎭⎝⎭，所以()2cos 3f x xπ=符合条件，因此()f x 的周期263T ππ==，()()02,11f f ==，且()()()()()21,32,41,51,62f f f f f =−=−=−==，所以(1)(2)(3)(4)(5)(6)0f f f f f f +++++=，由于22除以6余4，所以()()()()()221123411213k f k f f f f ==+++=−−−=−∑．故选：A ．【整体点评】法一：利用赋值法求出函数的周期，即可解出，是该题的通性通法；法二：作为选择题，利用熟悉的函数使抽象问题具体化，简化推理过程，直接使用具体函数的性质解题，简单明了，是该题的最优解.2023新高考1卷T112．（多选）已知函数()f x 的定义域为R ，()()()22f xy y f x x f y =+，则（ ）．A ．()00f =B ．()10f =C ．()f x 是偶函数D ．0x =为()f x 的极小值点【答案】ABC【分析】方法一：利用赋值法，结合函数奇遇性的判断方法可判断选项ABC ，举反例()0f x =即可排除选项D.方法二：选项ABC 的判断与方法一同，对于D ，可构造特殊函数2ln ,0()0,0x x x f x x ⎧≠=⎨=⎩进行判断即可.【详解】方法一：因为22()()()f xy y f x x f y =+，对于A ，令0x y ==，(0)0(0)0(0)0f f f =+=，故A 正确.对于B ，令1x y ==，(1)1(1)1(1)f f f =+，则(1)0f =，故B 正确. 对于C ，令1x y ==−，(1)(1)(1)2(1)f f f f =−+−=−，则(1)0f −=，令21,()()(1)()y f x f x x f f x =−−=+−=，又函数()f x 的定义域为R ，所以()f x 为偶函数，故C 正确，对于D ，不妨令()0f x =，显然符合题设条件，此时()f x 无极值，故D 错误. 方法二：因为22()()()f xy y f x x f y =+，对于A ，令0x y ==，(0)0(0)0(0)0f f f =+=，故A 正确.对于B ，令1x y ==，(1)1(1)1(1)f f f =+，则(1)0f =，故B 正确. 对于C ，令1x y ==−，(1)(1)(1)2(1)f f f f =−+−=−，则(1)0f −=， 令21,()()(1)()y f x f x x f f x =−−=+−=，又函数()f x 的定义域为R ，所以()f x 为偶函数，故C 正确，对于D ，当220x y ≠时，对22()()()f xy y f x x f y =+两边同时除以22x y ，得到2222()()()f xy f x f y x y x y=+， 故可以设2()ln (0)f x x x x =≠，则2ln ,0()0,0x x x f x x ⎧≠=⎨=⎩，当0x >肘，2()ln f x x x =，则()212ln (2ln 1)x x x x xf x x =+⋅=+'， 令()0f x '<，得120e x −<<；令0fx，得12e x −>；故()f x 在120,e −⎛⎫ ⎪⎝⎭上单调递减，在12e ,−⎛⎫+∞ ⎪⎝⎭上单调递增，因为()f x 为偶函数，所以()f x 在12,0e −⎛⎫− ⎪⎝⎭上单调递增，在12,e −⎛⎫ ⎪⎝∞⎭−上单调递减，显然，此时0x =是()f x 的极大值，故D 错误.故选：ABC .2023·山东青岛·统考三模1．设()f x 为定义在整数集上的函数，()11f =，()20f =，()10f −<，对任意的整数,x y 均有()()()()()11f x y f x f y f x f y +=−+−．则()55f =______．重点题型·归类精讲【答案】1−【分析】采用赋值的方式可求得()()0,1f f −，令1y =和y x =−可证得()f x 的对称轴和奇偶性，由此可推导得到()f x 的周期性，利用周期性可求得函数值.【详解】令1x y ==，则()()()()()()21001200f f f f f f =+==，()00f ∴=；令2x =，1y =−，则()()()()22212111f f f f =+−=−=，又()10f −<，()11f ∴−=−；令1y =，则()()()()()()10111f x f x f f x f f x +=+−=−，f x 关于直线1x =对称；令y x =−，则()()()()()()()()01110f f x f x f x f x f x f x f x =++−−=+−+=⎡⎤⎣⎦， ()10f x +=不恒成立，()()0f x f x ∴+−=恒成立，f x 为奇函数，()()()2f x f x f x +=−=−，()()()42f x f x f x ∴+=−+=，f x 是周期为4的周期函数，()()()55414111f f f ∴=⨯−=−=−.故答案为：1−.2023·山东滨州·三模2．（多选）已知连续函数()f x 对任意实数x 恒有()()()f x y f x f y +＝＋，当0x ＞时，()0f x ＜，(1)2f ＝－，则以下说法中正确的是（ ） A ．f （0）＝0B ．f (x )是R 上的奇函数C ．f (x )在[－3，3]上的最大值是6D ．不等式()232()(3)4f x f x f x −<+的解集为213xx ⎧⎫<<⎨⎬⎩⎭【答案】ABC【分析】根据函数()f x 对任意实数x 恒有()()()f x y f x f y +=+，令0x y ==，可得(0)0f =，判断奇偶性和单调性，即可判断选项；【详解】解：对于A ，函数()f x 对任意实数x 恒有()()()f x y f x f y +=+， 令0x y ==，可得(0)0f =，A 正确；对于B ，令x y =−，可得(0)()()0f f x f x =+−=，所以()()f x f x =−−，所以()f x 是奇函数；B 正确；对于C ，令x y <，则()()()()()f y f x f y f x f y x −=+−=−， 因为当x ＞0时，f (x )＜0，所以()0f y x −<，即()()0f y f x −<， 所以()f x 在()()0,,,0+∞−∞均递减， 因为()0f x <，所以()f x 在R 上递减；12f ，可得(1)2f −=；令1y =，可得()()12f x f x +=− ()24f =−，()36f =−；()3(3)6f f =−−=，()f x ∴在[3−，3]上的最大值是6，C 正确；对于D ，由不等式2(3)2()(3)4f x f x f x −<+的可得2(3)()()(3)4f x f x f x f x <+++， 即2(3)(23)4f x f x x <++，4(2)f =−，2(3)(23)(2)f x f x x f ∴<++−，则2(3)(52)f x f x <−，2352x x ∴>−，解得：23x <或1x >； D 不对；故选：ABC ． 安徽省皖江名校联盟2024届高三上学期10月第二次联考3．已知函数不是常数函数，且满足以下条件：①，其中；②，则（ ）A ．0B ．1C ．2D ．【答案】D(),y f x x =∈R ()()()()f a b f a b f a f b ++−=,a b ∈R ()10f =()2026f −=2−【分析】先令，得到，再令，得到，根据函数的周期性得到函数的周期为，即可求解.【详解】由题意令，得，又不是常数函数， 所以，再令，得， 即，则， 即，故， 所以函数的周期为，所以， 故选：D.4．（多选）已知定义在R 上的函数()f x 满足()()()()()()()()2,02,01f xy f x f y f x f y f f f =−−+<≠，且()0f x >，则（ ） A ．()01f = B ．()12f −= C ．()()2f x f x −= D ．()()f x f x −=【答案】ABD【分析】由已知，利用赋值法计算判断得解.【详解】定义在R 上的函数()f x 满足()()()()()2f xy f x f y f x f y =−−+，令0x y ==，得()()()20[0]202f f f =−+，而()02f <，则()01f =，A 正确；令x y ==1，得()()()21[1]212f f f =−+，而()()01f f ≠，则()12f =， 令1x y ==−，得()()()21[1]212f f f =−−−+，即()()2[1]21f f −=−，而()0f x >，即()10f −>，则()12f −=，B 正确；令1y =−，得()()()()()112f x f f x f f x −=−−−−+，即有()()()222f x f x f x −=−−+，因此()()f x f x −=，C 错误，D 正确. 故选：ABD5．已知函数及其导函数的定义域均为，对任意的，恒有，则下列说法正确的个数是（ ）0b =()02f =1b =()()2f a f a +=−()y f x =40b =()()()20f a f a f =()y f x =()02f =1b =()()()()111f a f a f a f ++−=()()110f a f a ++−=()()2f a f a +=−()()2f a f a −=−()()4f a f a =+()y f x =4()()()()202624506202f f f f −=+⨯==−=−()f x ()f x 'R ,R x y ∈()()()()2f x y f x y f x f y ++−=①；②必为奇函数；③；④若，则.A ．1B ．2C ．3D ．4【答案】C【分析】利用赋值法可判断①；利用赋值法结合函数奇偶性定义判断②；赋值，令，得出，变量代换可判断③；利用赋值法求出部分函数值，推出其值具有周期性，由此可计算，判断④，即可得答案.【详解】令，则由可得，故或，故①错误；当时，令，则，则，故，函数既是奇函数又是偶函数；当时，令，则，所以，则，即，则为奇函数，综合以上可知必为奇函数，②正确；令，则，故.由于，令，即，即有，故③正确； 对于D ，若，令 ，则，则， 令，则，即，令，则，即， 令，则，即， 令，则，即，令，则，即， 令，则，即， 令，则，即，，()00f =()f x '()()00f x f +≥1(1)2f =202311()2n f n ==∑y x =()()200f x f +≥()f n 20231()n f n =∑0x y ==()()()()2f x y f x y f x f y ++−=()()22020f f =(0)0f =()01f =(0)0f =0y =()()2()(0)0f x f x f x f +==()0f x =()0f x '=()f x '(0)1f =0x =()()2(0)()f y f y f f y +−=()()−=f y f y ()()f y f y −''−=()()f y f y −='−'()f x '()f x 'y x =()()()2202f x f f x +=()()200f x f +≥x ∈R 2,R t x t =∈()()00f t f +≥()()00f x f +≥()112f =1,0x y ==()()()()11210+=f f f f (0)1f =1x y ==()()()22021f f f +=()()1121,222f f +=∴=−2,1x y ==()()()()31212f f f f =+()113,(3)122f f +=−∴=−3,1x y ==()()()()42231f f f f +=()1141,(4)22f f −=−∴=−4,1x y ==()()()()53241f f f f +=()1151,(5)22f f −=−∴=5,1x y ==()()()()64251f f f f +=()116,(6)122f f −=∴=6,1x y ==()()()()75261f f f f +=()1171,(7)22f f +=∴=7,1x y ==()()()()86271f f f f +=()1181,(8)22f f +=∴=−由此可得的值有周期性，且6个为一周期，且 ，故，故④正确， 即正确的是②③④， 故选：C.2023·浙江嘉兴·统考模拟6．已知函数的定义域为，且，，则的值是（ ）A ．9B ．10C ．11D ．12【答案】D【分析】由赋值法先得，再由与关系列式求解． 【详解】中令，则，中令，，则，又中令，则，所以，中，令，则，再令，，则． 故选：D2023届江苏连云港校考7．已知函数，任意，满足，且，则的值为（ ）A ．B ．0C ．2D ．4【答案】C【分析】抽象函数利用特殊值的思路可以得到函数在取奇数和偶数的时候的规律，然后可以得到函数值的和.【详解】令，，则，所以；令，，则，所以；令，则，所以，(),N f n n *∈(1)(2)(3)(4)(5)(6)0f f f f f f +++++=()202311337[(1)(2)(3)(4)(5)(6)](1)2n f n f f f f f f f ==⨯++++++=∑()f x R ()()()()31,00,f x x f x x ⎛⎫=∈−∞+∞ ⎪⎝⎭()()()2f x f y xy f x y ++=+()3f ()00f =()1f ()1f −()()()2f x f y xy f x y ++=+0x y ==()00f =()()()2f x f y xy f x y ++=+1x =1y =−()()()11200f f f +−−==()31f x x f x ⎛⎫= ⎪⎝⎭=1x −()10f −=()12f =()()()2f x f y xy f x y ++=+1x y ==()()22126f f =+=1x =2y =()()()312426412f f f =++=++=()f x x y R ∈，()()()()22f x y f x y f x f y +−=−()()1220f f ==，()()()1290f f f +++2−()f x 2x =1y =()()()()223121f f f f =−()32f =−3x =2y =()()()()2251324f f f f =−=()52f =2y =()()()222f x f x f x +−=()72f =−()92f =.令，，则①，令，，则②，令，，则③，假设，那么由③可知，将，代入②式发现与矛盾，所以不成立，.同理可得当x 为偶数时，. 所以原式=.故选：C.8．已知，都是定义在上的函数，对任意x ，y 满足，且，则下列说法正确的是（ ）A ．B ．函数的图象关于点对称C ．D ．若，则【答案】D【分析】利用赋值法结合题目给定的条件可判断AC ，取可判断B ，对于D ，通过观察选项可以推断很可能是周期函数，结合的特殊性及一些已经证明的结论，想到令和时可构建出两个式子，两式相加即可得出，进一步得出是周期函数，从而可求的值.【详解】解：对于A ，令，代入已知等式得，得，故A 错误；对于B ，取，满足及， 因为，所以的图象不关于点对称， 所以函数的图象不关于点对称，故B 错误；对于C ，令，，代入已知等式得， 可得，结合得，，()()()2112kf k k Z +=−⋅∈3x =1y =()()420f f =4x =2y =()()()2624f f f =5x =1y =()()640f f =()40f ≠()60f =()20f =()60f =()40f ≠()40f ≠()40f =()0f x =()()()()138925f f f f ++++=()f x ()g x R ()()()()()f x y f x g y g x f y −=−()()210f f −=≠()01f =()21g x +()1,0()()110g g +−=()11f =()202311n f n ==∑()()2π2πsin,cos 33f x xg x x ==()f x ()()()(),f x g y g x f y 1y =−1y =()()()11f x f x f x ++−=−()f x ()20231n f n =∑0x y ==()()()()()000000f f g g f =−=()00f =()()2π2πsin,cos 33f x xg x x ==()()()()()f x y f x g y g x f y −=−()()210f f −=≠()3cos 2π10g ==≠()g x ()3,0()21g x +()1,00y =1x =()()()()()11010f f g g f =−()()()()110100f g g f ⎡⎤−=−=⎣⎦()10f ≠()100g −=()01g =再令，代入已知等式得，将，代入上式，得，所以函数为奇函数. 令，，代入已知等式，得， 因为，所以，又因为，所以， 因为，所以，故C 错误；对于D ，分别令和，代入已知等式，得以下两个等式：，，两式相加易得，所以有， 即：，有：， 即：，所以为周期函数，且周期为3，因为，所以，所以，， 所以， 所以，故D 正确.故选：D.【点评】：对于含有的抽象函数的一般解题思路是：观察函数关系，发现可利用的点，以及利用证明了的条件或者选项；抽象函数一般通过赋值法来确定、判断某些关系，特别是有双变量，需要双赋值，可以得到一个或多个关系式，进而得到所需的关系，此过程中的难点是赋予哪些合适的值，这就需要观察题设条件以及选项来决定.2023绍兴·高二期末9．已知函数的定义域为R ，且，为奇函数，，则（ ） 0x =()()()()()00f y f g y g f y −=−()00f =()01g =()()f y f y −=−()f x 1x =1y =−()()()()()21111f f g g f =−−−()()11f f −=−()()()()2111f f g g =−+⎡⎤⎣⎦()()()221f f f =−−=−()()()()1111f f g g −=−+⎡⎤⎣⎦()10f ≠()()111g g +−=−1y =−1y =()()()()()111f x f x g g x f +=−−−()()()()()111f x f x g g x f −=−()()()11f x f x f x ++−=−()()()21f x f x f x ++=−+()()()12f x f x f x =−+−+()()()()()()11120f x f x f x f x f x f x −+=++−−+−+=()()12f x f x −=+()f x ()11f =()21f −=()()221f f =−−=−()()300f f ==()()()1230f f f ++=()()()()()()()2023111232023202311n f n f f f f f f ===++++===∑,x y ,x y ()f x ()()()28f x f x f ++=()21f x +1122f ⎛⎫= ⎪⎝⎭22112k kf k =⎛⎫−= ⎪⎝⎭∑A ．B ．C ．0D ．【答案】B【分析】根据即可得出周期为4，赋值可求出.进而由为奇函数，可推得函数关于点对称，由已知可求出，，，然后即可求得，.进而即可根据周期性得出函数值，求出，即可得出，代入数值，即可得出答案.【详解】由，则， 所以，，周期为4，所以.由，令，则有，所以，. 因为为奇函数，所以，所以，，所以函数关于点对称， 所以，. 令，则.令可得，，所以，所以， 所以，有，即有.令，则有；令，则.综上，，，，. 所以，，所以，. 11−12−212()()()28f x f x f ++=()f x ()20f =()21f x +()y f x =()1,03122f ⎛⎫=− ⎪⎝⎭()00f =()80f =5122f ⎛⎫=− ⎪⎝⎭2721f ⎛⎫=⎪⎝⎭()()()()135741442443444402222m f m m f m m f m m f m ⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2211132122222k kf k f f =⎛⎫⎛⎫⎛⎫−=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑()()()28f x f x f ++=()()()428f x f x f +++=()()4f x f x +=()f x ()()()840f f f ==()()()28f x f x f ++=0x =()()()()2080f f f f +==()20f =()21f x +()()2121f x f x −+=−+()()11f x f x −+=−+()y f x =()1,0()()2f x f x −=−12x =311222f f ⎛⎫⎛⎫=−=− ⎪ ⎪⎝⎭⎝⎭0x =()()200f f =−=()00f =()80f =()()()280f x f x f ++==()()2f x f x +=−12x =511222f f ⎛⎫⎛⎫=−=− ⎪ ⎪⎝⎭⎝⎭32x =731222f f ⎛⎫⎛⎫=−= ⎪ ⎪⎝⎭⎝⎭1114222f m f ⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭3314222fm f ⎛⎫⎛⎫+==− ⎪ ⎪⎝⎭⎝⎭5514222f m f ⎛⎫⎛⎫+==− ⎪ ⎪⎝⎭⎝⎭7714222f m f ⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭()()()()13574144244344442222m f m m f m m f m m f m ⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()()()()11114142434402222m m m m ⎛⎫⎛⎫=+⨯++⨯−++⨯−++⨯= ⎪ ⎪⎝⎭⎝⎭2211111321212222212222222k kf k fff f =⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫−=−+−=+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∑1112122222⎛⎫=⨯+⨯−=− ⎪⎝⎭故选：B.10．（多选）已知函数()f x 的定义域为R ,()()()f x y f x f y +=+,则（ ）A ．()00f =B ．()f x 是奇函数 C ．0x =为()f x 的极小值点 D ．若()11f =,则()20232023f =【答案】ABD【分析】利用赋值法,令0x y ==判断A 得正误;令y x =−,结合奇函数的定义判断B 的正误;举例判断C 的正误;令1y =,则()()11f x f x +=+,再利用累加法即可判断D 的正误. 【详解】令0x y ==，则()()()000f f f =+，所以()00f =，故A 正确; 令y x =−，则()()()0f x x f x f x −=+−=，所以()f x 是奇函数，故B 正确;令()f x x =，其定义域为R ,且()()()f x y f x f y +=+满足题意，因为函数()f x x =为R 上的增函数,所以0x =不是()f x 的极小值点,故C 错误;令1y =,则()()11f x f x +=+,即()()11f x f x +−=,()()()()()()()2023202320222022202120212020f f f f f f f ⎡⎤⎡⎤⎡⎤=−+−+−⎣⎦⎣⎦⎣⎦ ()()()21111112023f f f ++−+=++++=⎡⎤⎣⎦,故D 正确.故选:ABD.11．（多选）设()f x 是定义在R 上的函数，对,x y ∀∈R ，有()()()()22f x y f x y f x f y +−−=++，且()00f ≠，则（ ）A ．()()0f x f x −−=B ．()()40f x f x +−=C ．()()()()02420242f f f f ++++=− D ．()()()()222212320244048f f f f ++++=【答案】ACD【分析】利用赋值法判断函数的奇偶性和周期性，再结合假设法、函数的周期性逐一判断即可. 【详解】A ：在()()()()22f x y f x y f x f y +−−=++中，令0x y ==，则有()()20220f f =⇒=，在()()()()22f x y f x y f x f y +−−=++中，令0x =，则有()()()()()()2200f y f y f f y f x f x −−=+=⇒−−=， 因此本选项正确；B ：若()()40f x f x +−=成立，即有()()04f f =， 在()()()()22f x y f x y f x f y +−−=++中，令2x y ==，则有()()()()()24044000f f f f f −=⇒=⇒=，这与()00f ≠相矛盾，所以假设不成立，因此本选项不正确； C ：在()()()()22f x y f x y f x f y +−−=++中， 以x −代y ，得()()()()0222f f x f x f x −=+−+，以x 代y ，得()()()2202f x f f x −=+，上面两个等式相加，得()()()()()()222202220f x f x f x f x f x f x ⎡⎤+++−+=⇒+++−+=⎣⎦()20f x ⇒+=，或()()220f x f x ++−+=，当()20f x +=时，则有()00f =，显然与()00f ≠矛盾，因此()()220f x f x ++−+=，于是有()()()()()()44()8f x f x f x f x f x f x f x =−−⇒+=−−=−⇒+=， 因此函数()f x 的周期为8，由()()()202060f f f =⇒−=⇒=， 由()()()()440f x f x f f =−−⇒=−， 在()()()()22f x y f x y f x f y +−−=++中，令2,1x y ==，得()()()()()()()()31433103f f f f f f f f −=⇒−=−，令1x y ==，得()()()()()2220330f f f f f −=⇒=−，由()()()()22031f x f x f f ++−+=⇒=−，于是有()()()()()()()()()()2331033023331f f f f f f f f f f ⎧−=−⎪=−⇒=⎨⎪=−⎩， 因为()()2300f f =−≠，所以由()()()3223332f f f =⇒=，于是()02f =−，因此()()()()02460f f f f +++=，()()()()()()02420242530202402f f f f f f ++++=⨯+==−，因此本选项正确；D ：在()()()()22f x y f x y f x f y +−−=++中，令()2N x y n n *==−∈，所以有()()()2240f n f f n −−=，因此有：()()()()22221232024f f f f ++++()()()()()()()()()()2000204040440f f f f f f f f f f =−−+−+−+−++−⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦因为()02f =−，()()220f f −==，()()()()02460f f f f +++=， 函数()f x 的周期为8，所以()()()()22221232024f f f f ++++()050620240f ⎡⎤=⨯+⋅−⎣⎦020*******=+⨯=，因此本选项正确， 故选：ACD.12．（多选）已知函数()f x 及其导函数()f x '的定义域均为R ，对任意的,R x y ∈，恒有()()()()2f x y f x y f x f y ++−=，则下列说法正确的有（ ）A ．()00f =B ．()f x '必为奇函数C ．()()00f x f +≥D ．若1(1)2f =，则202311()2n f x ==∑【答案】BCD【分析】赋值法求()0f 的值，判断A ；赋值法结合导数以及函数奇偶性的定义，判断B ；赋值法结合换元法判断C ；利用赋值法求得(),N f n n *∈的值有周期性，即可求得()20231n f n =∑的值，判断D.【详解】对于A ，令0x y ==，则由()()()()2f x y f x y f x f y ++−=可得()()22020f f =，故(0)0f =或()01f =，故A 错误；对于B ，当(0)0f =时，令0y =，则()()2()(0)0f x f x f x f +==，则()0f x =， 故()0f x '=，函数()f x '既是奇函数又是偶函数；当(0)1f =时，令0x =，则()()2(0)()f y f y f f y +−=，所以()()−=f y f y ， 则()()f y f y −''−=，即()()f y f y −='−'，则()f x '为奇函数， 综合以上可知()f x '必为奇函数，B 正确；对于C ，令y x = ，则()()()2202f x f f x +=，故()()200f x f +≥.由于x ∈R ,令2,R t x t =∈,即()()00f t f +≥，即有()()00f x f +≥，故C 正确；对于D ，若()112f =，令1,0x y == ，则()()()()11210+=f f f f ，则(0)1f = ，令1x y ==，则()()()22021f f f +=，即()()1121,222f f +=∴=−，令2,1x y ==，则()()()()31212f f f f =+，即()113,(3)122f f +=−∴=−， 令3,1x y ==，则()()()()42231f f f f +=，即()1141,(4)22f f −=−∴=−， 令4,1x y ==，则()()()()53241f f f f +=，即()1151,(5)22f f −=−∴=，令5,1x y ==，则()()()()64251f f f f +=，即()116,(6)122f f −=∴=， 令6,1x y ==，则()()()()75261f f f f +=，即()1171,(7)22f f +=∴=，由此可得(),N f n n *∈的值有周期性，且6个为一周期，且(1)(2)(3)(4)(5)(6)0f f f f f f +++++= ， 故()202311337[(1)(2)(3)(4)(5)(6)](1)2n f n f f f f f f f ==⨯++++++=∑，故D 正确， 故选：BCD.13．已知函数()f x 的定义域为R ，满足()()()()f x y f x y f x f y ++−=⋅，且12f ，则（ ）A ．()02f =B ．()f x 为奇函数C ．()()()()12320232f f f f +++⋅⋅⋅⋅⋅⋅+=−D ．()22f x −≤≤【答案】ACD【分析】A.通过赋值，求()0f 的值；B.赋值0x =，即可判断函数的奇偶性；C.赋值1y =，利用函数()()()1f x f x g x −+=的周期性，即可求和；D.通过多次赋值，可证明()24f x ≤，即可判断.【详解】A.令1,0x y ==，有()()()()1110f f f f +=⋅，得()02f =，A 正确；B.令0x =，得()()()()0f y f y f f y +−=⋅，()02f =，则()()−=f y f y ，函数的定义域为R ，所以函数为偶函数，故B 错误；C.令1y =，得()()()()111f x f x f x f ++−=⋅，即()()()()110f x f x f x f x +++−+=⎡⎤⎡⎤⎣⎦⎣⎦， 设()()()1f x f x g x −+=，则()()10g x g x ++=，所以()()()21g x g x g x +=−+=，所以函数()g x 的周期为2，()()()101220g f f =+=−=，()()()3230g f f =+=，…，()()()2023202220230g f f =+=，所以()()()()()0123...20230f f f f f +++++=，()02f =， 所以()()()()123...20232f f f f ++++=−，故C 正确， D.由()()()()f x y f x y f x f y ++−=⋅，()02f =，12f ，令12x y ==，得()()211002f f f ⎛⎫+== ⎪⎝⎭，所以102f ⎛⎫= ⎪⎝⎭， 将y 换成x ，得()()()220f x f f x +=，①，将,x y 换成12x +，得()()212102f x f f x ⎛⎫++=+ ⎪⎝⎭，②，将x 换成122x +，y 换成12，得()()112122022f x f x f x f ⎛⎫⎛⎫++=+⋅= ⎪ ⎪⎝⎭⎝⎭,③, ①+②-③,得()()2212042f f x f x ⎛⎫=++= ⎪⎝⎭，则()24f x ≤，得()22f x −≤≤，故D 正确.故选：ACD【点睛】关键点睛：本题关键的方法是赋值法，尤其是D 选项，通过三次赋值，找到等式间的关系，再可进行判断.14．（多选）已知定义域为R 的函数()f x 对任意实数,x y 都有()()()()2f x y f x y f x f y ++−=，且102f ⎛⎫= ⎪⎝⎭，则以下结论一定正确的有（ ）A ．()01f =−B ．()f x 是偶函数C ．()f x 关于1,02⎛⎫⎪⎝⎭中心对称D ．()()()1220230f f f +++=【答案】BC【分析】根据赋值法，可判断()01f =或()00f =，进而判断A ，根据赋值法结合奇偶性的定义可判断C ，根据偶函数即可判断对称性，根据对称性以及奇偶性可得函数的周期性，进而可判断CD. 【详解】令0x y ==，则()()()()()0020000f f f f f +=⇒=或()01f =，故A 错误， 若()01f =时，令0x =，则=20=f y fy f y f fy f y ，此时()f x 是偶函数，若()00f =时，令0y =，则=20=0f x f x f x f f x ，此时()f x 既是偶函数又是奇函数；因此B 正确，令12x =，则()111112=0=022222f y f y f f y f y f y ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++−=⇒++− ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，所以()f x 关于1,02⎛⎫ ⎪⎝⎭中心对称，故C 正确，由()f x 关于1,02⎛⎫⎪⎝⎭中心对称可得=1f x f x，结合()f x 是偶函数，所以=1=1=2=2f x f x f x f x f x ，所以()f x 的周期为2，令12x y ==，则()()11102=022f f f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，故12=10=0f f f f ，进而()()()()()122022101112=0f f f f f ⎡⎤+++=⨯+⎣⎦，而()2023(1)(0)f f f ==−，由A 选项知()00f =或()01f =，所以()()()1220230f f f +++=或1−，故D 错误.故选：BC15．函数()f x 的定义域为R ，且()()()21f x f x f x +=−+−，()()2f x f x =−，()3651f =−，则()20231k f k ==∑ .【答案】2【分析】根据给定条件，探讨函数()f x 的周期，再结合()()2f x f x =−求出(1),(2),(3)f f f 即可求解作答. 【详解】函数()f x 的定义域为R ，由()()()21f x f x f x +=−+−，得(3)(2)(1)(1)()(1)()f x f x f x f x f x f x f x +=−+−+=++−+=，因此函数()f x 是以3为周期的周期函数，且()(1)(2)0f x f x f x ++++=，即(1)(2)(3)0f f f ++=， 由()3651f =−，得(2)1f =−，又()()2f x f x =−，(3)(0)(2)1f f f ===−，从而(1)(2)(3)2f f f =−−=，所以20231()674(2(1)(2)3[((1]1)))k f f k f f f f =+=⨯=++=∑.故答案为：216．已知函数()f x 满足：1(1),4()()()()(,R)4f f x f y f x y f x y x y ==++−∈，则()2023f = .【答案】14【分析】由已知等式联想到三角公式()()cos cos 2cos cos x y x y x y ++−=，构造函数()1cos 23xf x π=求解. 【详解】由已知等式联想到三角公式()()cos cos 2cos cos x y x y x y ++−=， 注意它们结构相似，通过尝试和调整，构造函数()1cos 23x f x π=，则()111cos 234f π==， ()()()()11cos cos 23323311cos cos 4cos cos 4,332323x y x y f x y f x y x y x y f x f y ππππ⎛⎫⎛⎫++−=++− ⎪ ⎪⎝⎭⎝⎭ππππ==⋅⋅=故函数()1cos 23xf x π=满足题意，而函数()f x 是周期2π6π3T ==的函数，()()()120233376114f f f ∴=⨯+==. 故答案为：14.【点睛】：抽象函数可以选择构造函数（特例构造法），此题主要是联想到三角公式()()cos cos 2cos cos x y x y x y ++−=，并且还要根据1(1)4f =构造出合适的函数()1cos 23x f x π=，再由周期性解决问题，达到富有创造力的解题效果。

抽象函数浅谈对于抽象函数，一直是高中学生遇到的一个难点，现我们对抽象函数进行简单的分析。

题型一：一次函数模型①正比例函数：kx x f y f x f y x f y f x f y x f =⇔⎭⎬⎫-=-+=+)()()()()()()(。

（2019地二，高一月考，T12）例题：已知函数)(x f 对任意的y x ,，都满足函数)()()(y f x f y x f +=+，且满足0>x ，0)(<x f ，试求函数)(x f 的单调性和奇偶性。

②一次函数b kx x f b y f x f y x f +=⇔-+=+)()()()(。

变式题：已知函数)(x f 对任意的y x ,，都满足2)()()(-+=+y f x f y x f ，且满足0>x ，2)(>x f ，求函数的单调性。

题型二：指数函数模型①指数函数模型：x a x f y f x f y x f y f x f y x f =⇔⎪⎭⎪⎬⎫=⋅=+)()()(()()()(。

②指数类函数模型：[]t a x f t t y f x f t y f x f y x f x +=⇔+++-⋅=+)()()()()()(2。

题型三：对数函数模型①对数函数模型：x x f y f x f y x f y f x f y x f a log )()()()()()()(=⇔⎪⎭⎪⎬⎫-=+=⋅。

②对数类函数模型：t x x f t y f x f y x f a +=⇔-+=⋅log )()()()(。

题型四：幂函数模型①幂函数模型：a x x f y f x f y x f y f x f y x f =⇔⎪⎭⎪⎬⎫=⋅=⋅)()()()()()()(。

②幂函数类函数模型：[]t x x f t t y f x f t y f x f y x f a +=⇔+++-⋅=⋅)()()()()()(2。

（2018杭高，高三月考，T22）例题：已知函数)(x f 的定义域是{}0>x x ，并且满足：当1>x 时，2)(>x f ；),0(,21+∞∈∀x x ，都有2)()()()()(212121+--=x f x f x f x f x x f 。

抽象函数压轴题汇总A1．若函数f（x）对∀a，b∈R，同时满足：（1）当a+b＝0时，有f（a）+f（b）＝0；（2）当a+b＞0时，有f（a）+f（b）＞0，则称f（x）为Ω函数．下列函数中：①f（x）＝x﹣sin x，②f（x）＝e x﹣e﹣x，③f（x）＝e x+e﹣x，④op=0，=0，−1，≠0，是Ω函数的为（）A．①②B．②③C．③④D．①④2．已知函数f（x）对任意x，y∈R，都有2f（x+y）＝f（x）f（y），且f（1）＝1，则J0 1op=（）A．2n﹣1B．2−12C．1−12D．2−123．函数f（x）是定义在R上的奇函数，且f（﹣1）＝0，若对任意x1，x2∈（﹣∞，0），且x1≠x2时，都有1o1)−2o2)1−2＜0成立，则不等式f（x）＜0的解集为（）A．（﹣∞，﹣1）∪（1，+∞）B．（﹣1，0）∪（0，1）C．（﹣∞，﹣1）∪（0，1）D．（﹣1，0）∪（1，+∞）4．已知定义在（﹣3，3）上的函数f（x）满足f（x﹣1）＝﹣f（1﹣x），且x≥0时，f（x）＝x3，则f（x）+ 27f（1﹣x）＞0的解集为（）A．∅B．（﹣3，12）C．（﹣2，32）D．（32，3）5．已知函数f（x）是R上的偶函数，对于任意x∈R都有f（x+6）＝f（x）+f（3）成立，当x1，x2∈[0，3]，且x1≠x2时，都有o1)−o2)1−2＞0．给出以下三个命题：①直线x＝﹣6是函数f（x）图象的一条对称轴；②函数f（x）在区间[﹣9，﹣6]上为增函数；③函数f（x）在区间[﹣9，9]上有五个零点．问：以上命题中正确的个数有（）A．0个B．1个C．2个D．3个6．已知定义在R上的奇函数f（x）满足f（x+2）﹣f（﹣x）＝0，且当x∈[0，1]时，f（x）＝log2（x+1），则下列结论正确的是（）①f（x）的图象关于直线x＝1对称；②f（x）是周期函数，且2是其一个周期；③o163)＜o12)；④关于x的方程f（x）﹣t＝0（0＜t＜1）在区间（﹣2，7）上的所有实根之和是12．A．①④B．①②④C．③④D．①②③7．已知定义在R上的函数满足f（x+2）＝﹣f（x），x∈（0，2]时，f（x）＝x﹣sinπx，则J12020 op=（）A．6B．4C．2D．08．函数f（x）满足3f（x）f（y）＝f（x+y）+f（x﹣y）（x，y∈R），且f（1）=13，则f（2020）＝（）A．23B．−23C．−13D．139．定义在R上的函数y＝f（x）满足以下三个条件：①对于任意的x∈R，都有f（x+1）＝f（x﹣1）；②函数y＝f（x+1）的图象关于y轴对称；③对于任意的x1，x2∈[0，1]，都有（f（x1）﹣f（x2））（x1﹣x2）＞0．则f（32）、f（2）、f（3）从小到大的关系是（）A．f（32）＞f（2）＞f（3）B．f（3）＞f（2）＞o32)C．f（32）＞f（3）＞f（2）D．f（3）＞o32)＞o2)10．已知定义在R上的函数f（x），若函数y＝f（x+2）为偶函数，且f（x）对任意x1，x2∈[2，+∞）（x1≠x2），都有o2)−o1)2−1＜0，若f（a）≤f（3a+1），则实数a的取值范围是（）A．[−12，34]B．[﹣2，﹣1]C．(−∞，−12]D．(34，+∞)11．已知函数f（x）在R上是单调函数，且满足对任意x∈R，都有f[f（x）﹣3x]＝4，则f（2）的值是（）A．4B．8C．10D．1212．已知y＝f（x）是定义在R上的偶函数，函数f（x）满足f（4﹣x）＝f（x），又已知f（﹣2）＝2，则f （2022）＝（）A．0B．1C．32D．213．定义在R上的函数f（x）满足对任意的x，y都有f（x+y）＝f（x）+f（y）．设g（x）＝f（x）+sin x﹣x，若g（10）＝2020，则g（﹣10）＝（）A．﹣2020B．2020C．0D．101014．已知定义域为R的函数f（x）的图象关于原点对称，且f（2﹣x）+f（x+6）＝0，当x∈[0，4]时，f（x）=(32)−1，0≤＜2−58+52，2≤≤4，则f（f（2020））+f（2021）＝（）A．−58B．38C．58D．13815．设函数f（x）定义域为全体实数，令g（x）＝f（|x|）﹣|f（x）|，有以下6个论断：①f（x）是奇函数时，g（x）是奇函数；②f（x）是偶函数时，g（x）是奇函数；③f（x）是偶函数时，g（x）是偶函数；④f（x）是奇函数时，g（x）是偶函数；⑤g（x）是偶函数；⑥对任意的实数x，g（x）≤0．那么正确论断的编号是（）A．③④B．①②⑥C．③④⑥D．③④⑤16．已知函数f（x）是定义在R上的偶函数，且f（1﹣x）＝﹣f（1+x），f（0）＝1，则f（0）+f（1）+…+ f（2020）＝（）A．﹣1B．0C．1D．202017．定义在R上的函数y＝f（x）在（﹣∞，1]上单调递减，且f（x+1）是偶函数，则使f（2x﹣1）＞f（3）成立的x的取值范围是（）A．（1，+∞）B．（﹣∞，0）∪（2，+∞）C．（0，1）D．（﹣∞，0）18．已知定义在R上的奇函数f（x），对任意实数x，恒有f（x+3）＝﹣f（x），且当∈(0，32]时，f（x）＝x2﹣6x+8，则f（0）+f（1）+f（2）+…+f（2020）＝（）A．6B．3C．0D．﹣319．已知定义在R上的函数f（x）满足：①f（1）＝0；②对任意x∈R的都有f（﹣x）＝﹣f（x）；③对任意的x1，x2∈（0，+∞）且x1≠x2时，总有o1)−o2)1−2＞0；记g（x）=2op−3o−pK1，则不等式g（x）≤0的解集为（）A．[﹣1，0）∪（0，1）B．（﹣∞，﹣1]∪[0，1）C．[﹣1，0）D．[﹣1，0]20．已知函数f（x+2）（x∈R）为奇函数，且函数y＝f（x）的图象关于直线x＝1对称，当x∈[0，1]时，f（x）=2020，则f（2020）＝（）A．2020B．12020C．11010D．021．设函数f（x）的定义域为（0，+∞），满足f（x+2）＝2f（x），且当x∈（0，2]时，f（x）＝log2（x+2）•log3（x+1），则f（7）＝（）A．1B．2C．6D．822．已知函数f（x）满足f（1﹣x）＝f（1+x），当x≥1时，f（x）＝x−2，则{x|f（x+2）＞1}＝（）A．{x|x＜﹣3或x＞0}B．{x|x＜0或x＞2}C．{x|x＜﹣2或x＞0}D．{x|x＜2或x＞4} 23．已知定义域为R的函数f（x）满足f（﹣x）＝f（x），f（x+2）=1op，当x∈[0，2]时，f（x）＝2log2（x+3），则f（923）＝（）A．16B．923C．4D．124．已知f（x+2）是偶函数，f（x）在（﹣∞，2]上单调递减，f（0）＝0，则f（2﹣3x）＞0的解集是（）A．(−∞，23)∪(2，+∞)B．(23，2)C．(−23，23)D．(−∞，−23)∪(23，+∞)25．已知f（x）是定义域为（﹣∞，+∞）的奇函数，满足f（1﹣x）＝f（1+x），若f（1）＝2，则f（1）+f （2）+f（3）+…+f（2020）＝（）A．50B．2C．0D．﹣5026．已知f（x）是定义在R上的奇函数，且满足f（1﹣x）＝f（1+x），当x∈（0，1]时，f（x）＝log2（x+ 1），则f（2019）＝（）A．1B．﹣1C．0D．log2327．定义在R上的奇函数f（x）满足f（x+1）=−1op，且在（2，3）上f（x）＝4x，则f（2019.5）＝（）A．10B．0C．﹣10D．﹣2028．已知函数f（x）＝lnx+ln（a﹣x）的图象关于直线x＝1对称，则函数f（x）的值域为（）A．（0，2）B．[0，+∞）C．（﹣∞，2]D．（﹣∞，0] 29．已知定义在R上的函数f（x）满足f（﹣x）＝f（x），且函数f（x）在（﹣∞，0）上是减函数，若=o2c23p，=oc124.1)，=o20.8)，则a，b，c的大小关系为（）A．a＜c＜b B．c＜b＜a C．b＜c＜a D．c＜a＜b30．函数f（x）在（0，+∞）单调递增，且f（x+2）关于x＝﹣2对称，若f（﹣2）＝1，则f（x﹣2）≤1的x的取值范围是（）A．[﹣2，2]B．（﹣∞，﹣2]∪[2，+∞）C．（﹣∞，0]∪[4，+∞）D．[0，4]A1．若函数f（x）对∀a，b∈R，同时满足：（1）当a+b＝0时，有f（a）+f（b）＝0；（2）当a+b＞0时，有f（a）+f（b）＞0，则称f（x）为Ω函数．下列函数中：①f（x）＝x﹣sin x，②f（x）＝e x﹣e﹣x，③f（x）＝e x+e﹣x，④op=0，=0，−1，≠0，是Ω函数的为（）A．①②B．②③C．③④D．①④【解析】解：由（1）当a+b＝0时有f（a）+f（b）＝0，即为f（﹣a）＝﹣f（a），则f（x）为R上的奇函数；由（2）当a+b＞0时有f（a）+f（b）＞0，即为a＞﹣b，f（a）＞﹣f（b）＝f（﹣b），可得f（x）为R上的增函数，则函数f（x）为R上的奇函数，且为增函数．由①f（x）＝x﹣sin x，定义域为R，f（﹣x）＝﹣x﹣sin（﹣x）＝﹣x+sin x＝﹣f（x），即有f（x）为奇函数；又f′（x）＝1﹣cos x≥0，可得f（x）为R上的增函数，故①是Ω函数；②f（x）＝e x﹣e﹣x，定义域为R，f（﹣x）＝e﹣x﹣e x＝﹣f（x），即有f（x）为奇函数，又f′（x）＝e x+e﹣x＞0，可得f（x）为R上的增函数，故②是Ω函数；③f（x）＝e x+e﹣x，定义域为R，f（﹣x）＝e﹣x+e x＝f（x），可得f（x）为偶函数，故③不是Ω函数；④op=0，=0，−1，≠0，定义域为R，x≠0时，f（﹣x）=1=−f（x），可得f（x）为奇函数，又f（x）在（﹣∞，0），（0，+∞）递增，但在R上不为增函数，比如f（﹣1）＞f（1），故④不是Ω函数．故选：A．2．已知函数f（x）对任意x，y∈R，都有2f（x+y）＝f（x）f（y），且f（1）＝1，则J0 1op=（）A．2n﹣1B．2−12C．1−12D．2−12【解析】解：令x＝1，y＝0，得2f（1）＝f（1）f（0），则f（0）＝2；令x＝n（n∈N*），y＝1，则有2f（n+1）＝f（n）f（1）＝f（n），∴or1)op=12，∴{f（n）}（n∈N*）为等比数列，公比为12，首项为1，则{1op}（n∈N*）为等比数列，公比为2，首项为1，则J0 1op=1o0)+1o1)+1o2)+⋯+1op=12+1+2+⋯+2K1=12+1×(1−2)1−2=2−12．故选：B．3．函数f（x）是定义在R上的奇函数，且f（﹣1）＝0，若对任意x1，x2∈（﹣∞，0），且x1≠x2时，都有1o1)−2o2)1−2＜0成立，则不等式f（x）＜0的解集为（）A．（﹣∞，﹣1）∪（1，+∞）B．（﹣1，0）∪（0，1）C．（﹣∞，﹣1）∪（0，1）D．（﹣1，0）∪（1，+∞）【解析】解：根据题意，设g（x）＝xf（x），若函数f（x）是定义在R上的奇函数，即f（﹣x）＝﹣f（x），则g（﹣x）＝（﹣x）f（﹣x）＝xf（x）＝g（x），则g（x）为R上的偶函数，若f（﹣1）＝0，则g（﹣1）＝g（1）＝0，又由对任意x1，x2∈（﹣∞，0），且x1≠x2时，都有1o1)−2o2)1−2＜0成立，即o1)−o2)1−2＜0，即函数g（x）在（﹣∞，0）上为减函数，则在（﹣∞，﹣1）上，g（x）＝xf（x）＞0，在（﹣1，0）上，g（x）＝xf（x）＜0，又由x∈（﹣∞，0），则在（﹣∞，﹣1）上，f（x）＜0，在（﹣1，0），f（x）＞0，又由f（x）为奇函数，在在（0，1），f（x）＜0，综合可得：f（x）＜0的解集为（﹣∞，﹣1）∪（0，1）；故选：C．4．已知定义在（﹣3，3）上的函数f（x）满足f（x﹣1）＝﹣f（1﹣x），且x≥0时，f（x）＝x3，则f（x）+27f（1﹣x）＞0的解集为（）A．∅B．（﹣3，12）C．（﹣2，32）D．（32，3）【解析】解：∵f（x﹣1）＝﹣f（1﹣x），令x＝x+1，∴f（x）＝﹣f（﹣x），∴函数f（x）为奇函数，∵x≥0时，f（x）＝x3，∴f（x）＝x3，x∈（﹣3，3），∴f（x）+27f（1﹣x）＝x3+27（1﹣x）3＞0，∴x3＞[3（x﹣1）]3，∵f（x）＝x3为增函数，∴x＞3（x﹣1），∴﹣3＜x＜32，故选：C．5．已知函数f（x）是R上的偶函数，对于任意x∈R都有f（x+6）＝f（x）+f（3）成立，当x1，x2∈[0，3]，且x1≠x2时，都有o1)−o2)1−2＞0．给出以下三个命题：①直线x＝﹣6是函数f（x）图象的一条对称轴；②函数f（x）在区间[﹣9，﹣6]上为增函数；③函数f（x）在区间[﹣9，9]上有五个零点．问：以上命题中正确的个数有（）A．0个B．1个C．2个D．3个【解析】解：根据题意，对于任意x∈R，都有f（x+6）＝f（x）+f（3）成立，令x＝﹣3，则f（﹣3+6）＝f（﹣3）+f（3），又因为f（x）是R上的偶函数，所以f（3）＝0，则有f（x+6）＝f（x），所以f（x）的周期为6；据此分析三个命题：对于①，函数为偶函数，则函数的一条对称轴为y轴，又由函数的周期为6，则直线x＝﹣6是函数f（x）图象的一条对称轴，①正确；对于②，当x1，x2∈[0，3]，且x1≠x2时，都有o1)−o2)1−2＞0，则函数y＝f（x）在[0，3]上为增函数，因为f（x）是R上的偶函数，所以函数y＝f（x）在[﹣3，0]上为减函数，而f（x）的周期为6，所以函数y＝f（x）在[﹣9，﹣6]上为减函数；②错误；对于③，f（3）＝0，f（x）的周期为6，所以f（﹣9）＝f（﹣3）＝f（3）＝f（9）＝0，函数y＝f（x）在[﹣9，9]上有四个零点；③错误；三个命题中只有①是正确的；故选：B．6．已知定义在R上的奇函数f（x）满足f（x+2）﹣f（﹣x）＝0，且当x∈[0，1]时，f（x）＝log2（x+1），则下列结论正确的是（）①f（x）的图象关于直线x＝1对称；②f（x）是周期函数，且2是其一个周期；③o163)＜o12)；④关于x的方程f（x）﹣t＝0（0＜t＜1）在区间（﹣2，7）上的所有实根之和是12．A．①④B．①②④C．③④D．①②③【解析】解：由题意，f（x+2）﹣f（﹣x）＝0，即f（x+2）＝f（﹣x）可知f（x）的图象关于直线x＝1对称，①正确；因为f（x）是奇函数，所以f（x+2）＝f（﹣x）＝﹣f（x），所以f（x+4）＝﹣f（x+2）＝f（x），所以f（x）是周期函数，其一个周期为4，但不能说明2是f（x）的周期，故②错误；由f（x）的周期性和对称性可得o163)=o4+43)=o43)=o23)．又当x∈[0，1]时，f（x）＝log2（x+1），所以f（x）在x∈[0，1]时单调递增，所以o12)＜o23)，即o163)＞o12)，③错误；又x∈[0，1]时，f（x）＝log2（x+1），则可画出f（x）在区间[﹣4，8]上对应的函数图象大致如下．易得f（x）﹣t＝0（0＜t＜1）即f（x）＝t（0＜t＜1）在区间（﹣2，7）上的根分别关于1，5对称，故零点之和为2×（1+5）＝12，④正确．故选：A．7．已知定义在R上的函数满足f（x+2）＝﹣f（x），x∈（0，2]时，f（x）＝x﹣sinπx，则J12020 op=（）A．6B．4C．2D．0【解析】解：因为x∈（0，2]时，f（x）＝x﹣sinπx，所以f（1）＝1﹣sinπ＝1，f（2）＝2﹣sin2π＝2，因为f（x+2）＝﹣f（x），所以f（0）＝﹣f（2）＝﹣2，f（﹣1）＝﹣f（1）＝﹣1，所以f（﹣1）+f（0）+f（1）+f（2）＝0．因为f（x+2）＝﹣f（x），将x换为x+2，则f（x+4）＝﹣f（x+2），所以f（x）＝f（x+4），即函数的周期为4，所以J12020 op=505×[f（﹣1）+f（0）+f（1）+f（2）]＝0．故选：D．8．函数f（x）满足3f（x）f（y）＝f（x+y）+f（x﹣y）（x，y∈R），且f（1）=13，则f（2020）＝（）A．23B．−23C．−13D．13【解析】解：取x＝1，y＝0，得3f（0）f（1）＝f（1）+f（1）=23，∴f（0）=23，取x＝n，y＝1，有3f（n）f（1）＝f（n+1）+f（n﹣1），即f（n）＝f（n+1）+f（n﹣1），同理：f（n+1）＝f（n+2）+f（n），∴f（n+2）＝﹣f（n﹣1），∴f（n）＝﹣f（n﹣3）＝f（n﹣6）所以函数是周期函数，周期T＝6，故f（2020）＝f（3×336+4）＝f（4）．∵3f（x）f（y）＝f（x+y）+f（x﹣y）令x＝y＝1，得3f2（1）＝f（2）+f（0），可得f（2）=−13，令x＝2，y＝1，得3f（2）f（1）＝f（3）+f（1），解得f（3）=−23，令x＝3，y＝1，得3f（3）f（1）＝f（4）+f（2），解得f（4）=−13．∴f（2020）=−13；故选：C．9．定义在R上的函数y＝f（x）满足以下三个条件：①对于任意的x∈R，都有f（x+1）＝f（x﹣1）；②函数y＝f（x+1）的图象关于y轴对称；③对于任意的x1，x2∈[0，1]，都有（f（x1）﹣f（x2））（x1﹣x2）＞0．则f（32）、f（2）、f（3）从小到大的关系是（）A．f（32）＞f（2）＞f（3）B．f（3）＞f（2）＞o32)C．f（32）＞f（3）＞f（2）D．f（3）＞o32)＞o2)【解析】解：由①对于任意的x∈R，都有f（x+1）＝f（x﹣1）；得函数为周期函数，且周期为2，由②函数y＝f（x+1）的图象关于y轴对称；得函数的图象关于直线x＝1对称，由③对于任意的x1，x2∈[0，1]，都有（f（x1）﹣f（x2））（x1﹣x2）＞0得函数在[0，1]为增函数，则f（32）＝f（12），f（2）＝f（0），f（3）＝f（1），又因为0＜12＜1，所以f（0）＜f（12）＜f（1），即f（2）＜f（32）＜f（3），故选：D．10．已知定义在R上的函数f（x），若函数y＝f（x+2）为偶函数，且f（x）对任意x1，x2∈[2，+∞）（x1≠x2），都有o2)−o1)2−1＜0，若f（a）≤f（3a+1），则实数a的取值范围是（）A．[−12，34]B．[﹣2，﹣1]C．(−∞，−12]D．(34，+∞)【解析】解：根据题意，函数y＝f（x+2）为偶函数，则函数f（x）的图象关于x＝2对称，f（x）对任意x1，x2∈[2，+∞）（x1≠x2），都有o2)−o1)2−1＜0，则函数f（x）在[2，+∞）上为减函数，则f（a）≤f（3a+1）⇔|a﹣2|≥|3a+1﹣2|，即|a﹣2|≥|3a﹣1|，解可得：−12≤a≤34，即a的取值范围为[−12，34]．故选：A．11．已知函数f（x）在R上是单调函数，且满足对任意x∈R，都有f[f（x）﹣3x]＝4，则f（2）的值是（）A．4B．8C．10D．12【解析】解：∵对任意x∈R，都有f[f（x）﹣3x]＝4，且函数f（x）在R上是单调函数，故f（x）﹣3x＝k，即f（x）＝3x+k，∴f（k）＝3k+k＝4，解得：k＝1，故f（x）＝3x+1，∴f（2）＝10，故选：C．12．已知y＝f（x）是定义在R上的偶函数，函数f（x）满足f（4﹣x）＝f（x），又已知f（﹣2）＝2，则f（2022）＝（）A．0B．1C．32D．2【解析】解：根据题意，y＝f（x）是定义在R上的偶函数且满足f（4﹣x）＝f（x），则有f（4﹣x）＝f（﹣x），变形可得f（x+4）＝f（x），则f（x）是周期为4的周期函数，则f（2022）＝f（﹣2+506×4）＝f（﹣2）＝2；故选：D．13．定义在R上的函数f（x）满足对任意的x，y都有f（x+y）＝f（x）+f（y）．设g（x）＝f（x）+sin x﹣x，若g（10）＝2020，则g（﹣10）＝（）A．﹣2020B．2020C．0D．1010【解析】解：∵有f（x+y）＝f（x）+f（y），∴f（0+0）＝f（0）+f（0）＝f（0），即f（0）＝0，令y＝﹣x，则有f（x﹣x）＝f（x）+f（﹣x）＝f（0）＝0即f（﹣x）＝﹣f（x），即f（x）是奇函数，若g（x）＝f（x）+sin x﹣x，g（10）＝2020，则g（10）＝f（10）+sin10﹣10＝2020，则g（﹣10）＝f（﹣10）﹣sin10+10＝﹣f（10）﹣sin10+10，两式相加得：0＝2020+g（﹣10），得g（﹣10）＝﹣2020，故选：A．14．已知定义域为R的函数f（x）的图象关于原点对称，且f（2﹣x）+f（x+6）＝0，当x∈[0，4]时，f（x）=(32)−1，0≤＜2−58+52，2≤≤4，则f（f（2020））+f（2021）＝（）A．−58B．38C．58D．138【解析】解：根据题意，定义域为R的函数f（x）的图象关于原点对称，即函数f（x）为奇函数，则有f （﹣x）＝﹣f（x），又由f（2﹣x）+f（x+6）＝0，则有﹣f（x﹣2）+f（x+6）＝0，即f（x+6）＝f（x﹣2），变形可得f（x+8）＝f（x），即函数f（x）是周期为8的周期函数，则f（2020）＝f（4+2016）＝f（4），f（2021）＝f（﹣3+2024）＝f（﹣3）＝﹣f（3），又由当x∈[0，4]时，f（x）=(32)−1，0≤＜2−58+52，2≤≤4，则f（4）＝0，f（3）=58；则f（2020）＝f（4）＝0，则有f（f（2020））＝f（0）＝0；故f（f（2020））+f（2021）＝0−58=−58；故选：A．15．设函数f（x）定义域为全体实数，令g（x）＝f（|x|）﹣|f（x）|，有以下6个论断：①f（x）是奇函数时，g（x）是奇函数；②f（x）是偶函数时，g（x）是奇函数；③f（x）是偶函数时，g（x）是偶函数；④f（x）是奇函数时，g（x）是偶函数；⑤g（x）是偶函数；⑥对任意的实数x，g（x）≤0．那么正确论断的编号是（）A．③④B．①②⑥C．③④⑥D．③④⑤【解析】解：根据题意，g（x）＝f（|x|）﹣|f（x）|，依次分析6个判断：对于①f（x）是奇函数时，有f（﹣x）＝﹣f（x），则g（﹣x）＝f（|﹣x|）﹣|f（﹣x）|＝f（|x|）﹣|f（x）|＝g（x），g（x）是偶函数，故①错误；对于②f（x）是偶函数时，有f（﹣x）＝f（x），则g（﹣x）＝f（|﹣x|）﹣|f（﹣x）|＝f（|x|）﹣|f（x）|＝g（x），g（x）是偶函数，故②错误；③f（x）是偶函数时，f（﹣x）＝f（x），则g（﹣x）＝f（|﹣x|）﹣|f（﹣x）|＝f（|x|）﹣|f（x）|＝g（x），g（x）是偶函数，故③正确；④f（x）是奇函数时，f（﹣x）＝﹣f（x），则g（﹣x）＝f（|﹣x|）﹣|f（﹣x）|＝f（|x|）﹣|f（x）|＝g（x），g（x）是偶函数，故④正确；⑤g（x）＝f（|x|）﹣|f（x）|，而g（﹣x）＝f（|﹣x|）﹣|f（﹣x）|＝f（|x|）﹣|f（﹣x）|，则g（x）不一定是偶函数，⑤错误；⑥设f（x）＝x+5，则f（|﹣2|）＝f（2）＝7，f（﹣2）＝（﹣2）+5＝3，|f（﹣2）|＝3，则g（﹣2）＝f（|﹣2|）﹣|f（﹣2）|＝7﹣3＞0，⑥错误；综上可得，③④正确；故选：A．16．已知函数f（x）是定义在R上的偶函数，且f（1﹣x）＝﹣f（1+x），f（0）＝1，则f（0）+f（1）+…+f （2020）＝（）A．﹣1B．0C．1D．2020【解析】解：根据题意，f（x）满足f（1﹣x）＝﹣f（1+x），即函数f（x）图象关于点（1，0）对称，则有f（x+2）＝﹣f（﹣x），又由f（x）为偶函数，则f（﹣x）＝f（x），即有f（x+2）＝﹣f（x），则有f（x+4）＝﹣f（x+2）＝f（x），即函数f（x）为周期为4的周期函数，f（0）＝1，则f（2）＝﹣f（0）＝﹣1，f（1）+f（3）＝0，则有f（0）+f（1）+f（2）+f（3）＝0，则f（0）+f（1）+…+f（2020）＝[f（0）+f（1）+f（2）+f（3）]×505+f（2020）＝f（0）＝1；故选：C．17．定义在R上的函数y＝f（x）在（﹣∞，1]上单调递减，且f（x+1）是偶函数，则使f（2x﹣1）＞f（3）成立的x的取值范围是（）A．（1，+∞）B．（﹣∞，0）∪（2，+∞）C．（0，1）D．（﹣∞，0）【解析】解：根据题意，f（x+1）是偶函数，则函数f（x）的图象关于直线x＝1对称，若y＝f（x）在（﹣∞，1]上单调递减，则f（x）在[1，+∞）上为增函数，f（2x﹣1）＞f（3）⇒|2x﹣2|＞|3﹣1|，解可得x＜0或x＞2，即x的取值范围是（﹣∞，0）∪（2，+∞）；故选：B．18．已知定义在R上的奇函数f（x），对任意实数x，恒有f（x+3）＝﹣f（x），且当∈(0，32]时，f（x）＝x2﹣6x+8，则f（0）+f（1）+f（2）+…+f（2020）＝（）A．6B．3C．0D．﹣3【解析】解：根据题意，对任意实数x，恒有f（x+3）＝﹣f（x），则有f（x+6）＝﹣f（x+3）＝f（x），即函数f（x）是周期为6的周期函数，又由f（x）为定义在R上的奇函数，则f（0）＝0，则f（3）＝﹣f（0）＝0，又由当∈(0，32]时，f（x）＝x2﹣6x+8，则f（1）＝3，f（2）＝f（﹣1+3）＝﹣f（﹣1）＝f（1）＝3，f（4）＝f（1+3）＝﹣f（1）＝﹣3，f（5）＝f（2+3）＝﹣f（2）＝﹣3，则有f（0）+f（1）+f（2）+f（3）+f（4）+f（5）＝0，f（0）+f（1）+f（2）+…+f（2020）＝[f（0）+f（1）+f（2）+…+f（5）]×336+f（0）+f（1）+f（2）+f（3）+f（4）＝f（2）＝3；故选：B．19．已知定义在R上的函数f（x）满足：①f（1）＝0；②对任意x∈R的都有f（﹣x）＝﹣f（x）；③对任意的x1，x2∈（0，+∞）且x1≠x2时，总有o1)−o2)1−2＞0；记g（x）=2op−3o−pK1，则不等式g（x）≤0的解集为（）A．[﹣1，0）∪（0，1）B．（﹣∞，﹣1]∪[0，1）C．[﹣1，0）D．[﹣1，0]【解析】解：根据题意，f（x）满足对任意x∈R的都有f（﹣x）＝﹣f（x），即函数f（x）为奇函数，则有f（0）＝0；又由对任意的x1，x2∈（0，+∞）且x1≠x2时，总有o1)−o2)1−2＞0，即函数f（x）在（0，+∞）上为增函数，若f（1）＝0，则在区间（0，1）上，f（x）＜0，在区间（1，+∞）上，f（x）＞0，又由f（x）为奇函数，则在区间（﹣∞，﹣1）上，f（x）＜0，在区间（﹣1，0）上，f（x）＞0，则g（x）≤0即g（x）=2op−3o−pK1=5op K1≤0，即op＜0−1＞0或op＞0−1＜0或op=0−1≠0，解可得：﹣1≤x≤0，即不等式g（x）≤0的解集为[﹣1，0]；故选：D．20．已知函数f（x+2）（x∈R）为奇函数，且函数y＝f（x）的图象关于直线x＝1对称，当x∈[0，1]时，f （x）=2020，则f（2020）＝（）A．2020B．12020C．11010D．0【解析】解：根据题意，函数f（x+2）为奇函数，即函数f（x）的图象关于点（2，0）对称，则有f（﹣x）＝﹣f（x+4），函数y＝f（x）的图象关于直线x＝1对称，则f（﹣x）＝f（2+x），变形可得：f（x+4）＝﹣f（x+2），即f（x+2）＝﹣f（x），则有f（x+4）＝f（x），即函数f（x）是周期为4的周期函数，f（2020）＝f（0+505×4）＝f（0）＝0；故选：D．21．设函数f（x）的定义域为（0，+∞），满足f（x+2）＝2f（x），且当x∈（0，2]时，f（x）＝log2（x+2）•log3（x+1），则f（7）＝（）A．1B．2C．6D．8【解析】解：根据题意，f（x）满足f（x+2）＝2f（x），则f（7）＝2f（5）＝4f（3）＝8f（1），又由当x∈（0，2]时，f（x）＝log2（x+2）•log3（x+1），则f（1）＝log23•log32＝1，则f（7）＝8f（1）＝8；故选：D．22．已知函数f（x）满足f（1﹣x）＝f（1+x），当x≥1时，f（x）＝x−2，则{x|f（x+2）＞1}＝（）A．{x|x＜﹣3或x＞0}B．{x|x＜0或x＞2}C．{x|x＜﹣2或x＞0}D．{x|x＜2或x＞4}【解析】解：由f（1﹣x）＝f（1+x），得函数关于x＝1对称，当x≥1时，f（x）＝x−2，则f（x）为增函数，且f（2）＝2﹣1＝1，由f（x）＞1得x＞2，由对称性知当x＜1时，由f（x）＞1得x＜0，综上f（x）＞1得x＞2或x＜0，由f（x+2）＞1得x+2＞2或x+2＜0，得x＞0或x＜﹣2，即不等式的解集为{x|x＜﹣2或x＞0}，故选：C．23．已知定义域为R的函数f（x）满足f（﹣x）＝f（x），f（x+2）=1op，当x∈[0，2]时，f（x）＝2log2（x+3），则f（923）＝（）A．16B．923C．4D．1【解析】解：因为定义域为R的函数f（x）满足f（﹣x）＝f（x），所以函数f（x）是偶函数，又因为f（x+2）=1op，所以f（x+4）=1or2)=11op=f（x），所以函数f（x）的周期是4，所以f（923）＝f（4×230+3）＝f（3）＝f（﹣1）＝f（1），因为当x∈[0，2]时，f（x）＝2log2（x+3），所以f（923）＝f（1）＝2log24＝4，故选：C．24．已知f（x+2）是偶函数，f（x）在（﹣∞，2]上单调递减，f（0）＝0，则f（2﹣3x）＞0的解集是（）A．(−∞，23)∪(2，+∞)B．(23，2)C．(−23，23)D．(−∞，−23)∪(23，+∞)【解析】解：根据题意，f（x+2）是偶函数，则函数f（x）的图象关于直线x＝2对称，又由f（x）在（﹣∞，2]上单调递减，则f（x）在[2，+∞）上递增，又由f（0）＝0，则f（2﹣3x）＞0⇒f（2﹣3x）＞f（0）⇒|3x|＞2，解可得：x＜−23或x＞23，即不等式的解集为（﹣∞，−23）∪（23，+∞）；故选：D．25．已知f（x）是定义域为（﹣∞，+∞）的奇函数，满足f（1﹣x）＝f（1+x），若f（1）＝2，则f（1）+f （2）+f（3）+…+f（2020）＝（）A．50B．2C．0D．﹣50【解析】解：根据题意，f（x）是定义域为（﹣∞，+∞）的奇函数，则f（﹣x）＝﹣f（x），且f（0）＝0；又由f（1﹣x）＝f（1+x）即有f（x+2）＝f（﹣x），则f（x+2）＝﹣f（x），进而得到f（x+4）＝﹣f（x+2）＝f（x），f（x）为周期为4的函数，若f（1）＝2，可得f（3）＝f（﹣1）＝﹣f（1）＝﹣2，f（2）＝f（0）＝0，f（4）＝f（0）＝0，则f（1）+f（2）+f（3）+f（4）＝2+0﹣2+0＝0，则f（1）+f（2）+f（3）+…+f（2020）＝505×[f（1）+f（2）+f（3）+f（4）]＝0；故选：C．26．已知f（x）是定义在R上的奇函数，且满足f（1﹣x）＝f（1+x），当x∈（0，1]时，f（x）＝log2（x+1），则f（2019）＝（）A．1B．﹣1C．0D．log23【解析】解：根据题意，f（x）满足f（1﹣x）＝f（1+x），则有f（x+2）＝f（﹣x），又由f（x）为奇函数，则f（x+2）＝f（﹣x）＝﹣f（x），则有f（x+4）＝﹣f（x+2）＝f（x），即函数f（x）是周期为4的周期函数，则f（2019）＝f（﹣1+5×505）＝f（﹣1）＝﹣f（1），又由当x∈（0，1]时，f（x）＝log2（x+1），则f（1）＝log2（1+1）＝1，则f（2019）＝﹣f（1）＝﹣1；故选：B．27．定义在R上的奇函数f（x）满足f（x+1）=−1op，且在（2，3）上f（x）＝4x，则f（2019.5）＝（）A．10B．0C．﹣10D．﹣20【解析】解：根据题意，函数f（x）满足f（x+1）=−1op，则f（x+2）=−1or1)=f（x），即函数f（x）是周期为2的周期函数，则f（2019.5）＝f（2022﹣2.5）＝f（﹣2.5），又由f（x）为奇函数，则f（﹣2.5）＝﹣f（2.5）＝﹣4×2.5＝﹣10，则f（2019.5）＝﹣10，故选：C．28．已知函数f（x）＝lnx+ln（a﹣x）的图象关于直线x＝1对称，则函数f（x）的值域为（）A．（0，2）B．[0，+∞）C．（﹣∞，2]D．（﹣∞，0]【解析】解：根据题意，对于函数f（x）＝lnx+ln（a﹣x），有f（a﹣x）＝ln（a﹣x）+ln[a﹣（a﹣x）]＝lnx+ln（a﹣x）＝f（x），则函数f（x）的图象关于直线x=2对称，若函数f（x）＝lnx+ln（a﹣x）的图象关于直线x＝1对称，则有2=1，则a＝2，则f（x）＝lnx+ln（2﹣x）＝ln（2x﹣x2），其定义域为（0，2），设t＝2x﹣x2，则y＝lnt，又由t＝﹣（x﹣1）2+1，0＜x＜2，则有0＜t≤1，则y＝lnt≤0，即函数f（x）的值域为（﹣∞，0]；故选：D．29．已知定义在R上的函数f（x）满足f（﹣x）＝f（x），且函数f（x）在（﹣∞，0）上是减函数，若=o2c23p，=oc14.1)，=o20.8)，则a，b，c的大小关系为（）A．a＜c＜b B．c＜b＜a C．b＜c＜a D．c＜a＜b【解析】解：根据题意，函数f（x）满足f（﹣x）＝f（x），则函数f（x）为偶函数，a＝f（2cos23）＝f（2cos3）＝f（1），b＝f（c124.1）＝f（log24.1）c＝f（20.8），又由函数f（x）在（﹣∞，0）上是减函数，则f（x）在（0，+∞）上为增函数，且1＜20.8＜2＜log24.1，则a＜c＜b；故选：A．30．函数f（x）在（0，+∞）单调递增，且f（x+2）关于x＝﹣2对称，若f（﹣2）＝1，则f（x﹣2）≤1的x的取值范围是（）A．[﹣2，2]B．（﹣∞，﹣2]∪[2，+∞）C．（﹣∞，0]∪[4，+∞）D．[0，4]【解析】解；根据题意，f（x+2）关于x＝﹣2对称，则f（x）为偶函数，且f（﹣2）＝f（2）＝1，则f（x﹣2）≤1⇒f（|x﹣2|）≤f（|﹣2|），又f（x）在（0，+∞）单调递增，所以|x﹣2|≤2，解可得0≤x≤4；故选：D．。

高考抽象函数技巧总结由于函数概念比较抽象.学生对解有关函数记号()f x 的问题感到困难.学好这部分知识.能加深学生对函数概念的理解.更好地掌握函数的性质.培养灵活性；提高解题能力.优化学生数学思维素质。

现将常见解法及意义总结如下： 一、求表达式： 1.换元法：即用中间变量表示原自变量x 的代数式.从而求出()f x .这也是证某些公式或等式常用的方法.此法解培养学生的灵活性及变形能力。

例1：已知 ()211xf x x =++,求()f x . 解：设1x u x =+,则1u x u =-∴2()2111u u f u u u-=+=--∴2()1xf x x -=- 2.凑合法：在已知(())()fg xh x =的条件下.把()h x 并凑成以()g u 表示的代数式.再利用代换即可求()f x .此解法简洁.还能进一步复习代换法。

例2：已知3311()f x x xx+=+.求()f x 解：∵22211111()()(1)()(()3)f x x x x x xx x x x+=+-+=++-又∵11||||1||x x x x +=+≥ ∴23()(3)3f x x x x x =-=-.(|x |≥1)3.待定系数法：先确定函数类型.设定函数关系式.再由已知条件.定出关系式中的未知系数。

例3． 已知()f x 二次实函数.且2(1)(1)f x f x x ++-=+2x +4,求()f x .解:设()f x =2ax bx c ++.则22(1)(1)(1)(1)(1)(1)f x f x a x b x c a x b x c ++-=+++++-+-+=22222()24ax bx a c x x +++=++比较系数得2()41321,1,2222a c a abc b +=⎧⎪=⇒===⎨⎪=⎩∴213()22f x x x =++ 4.利用函数性质法:主要利用函数的奇偶性,求分段函数的解析式.例4.已知y =()f x 为奇函数,当 x >0时,()lg(1)f x x =+,求()f x解:∵()f x 为奇函数.∴()f x 的定义域关于原点对称.故先求x <0时的表达式。

2025高三一轮加强专题4：抽象函数一、单选题1．定义在R 上的函数()f x 满足对任意实数,x y 都有()()()1f x y f x f y +=+-，若0x >时，()1f x >，则()f x （）A ．先单调通淢后单调递增B ．在R 上单调递增C ．在R 上单调通减D ．单调性不确定2．已知函数()f x 的定义域为R ，()()()f a f b f a ab b -=-，则（）A ．()00f =B ．()12f =C ．()1f x -为偶函数D ．()1f x -为奇函数3．已知定义在R 上的函数()f x 满足()()()()2f x y f x y f x f y +-=+，且()00f ≠，则下列结论中错误的是（）A ．()01f =B ．()y f x =为奇函数C ．()y f x =不存在零点D ．()()2f x f x =4．已知函数()f x 的定义域为R ，且()()2222f f x y x y y f f x +-⎛⎫⎛⎫⋅=- ⎪ ⎪⎝⎭⎝⎭，122f x ⎛⎫+ ⎪⎝⎭的图像关于直线12x =对称，()11f =，()f x 在[]1,0-上单调递增，则下列说法中错误的是（）A ．()()240f f +=B ．()f x 的一条对称轴是直线32x =C ．()202342f f ⎛⎫> ⎪⎝⎭D ．()202411k f k ==∑5．已知函数()f x 的定义域为R ，函数()()()11F x f x x =+-+为偶函数，函数()()231G x f x =+-为奇函数，则下列说法错误的是（）A ．函数()f x 的一个对称中心为()2,1B ．()01f =-C ．函数()f x 为周期函数，且一个周期为4D ．()()()()12346f f f f +++=6．已知函数()f x 定义域为R ，且()()()22yf x xf y xy y x -=-，下列结论成立的是（）A ．()f x 为偶函数B ．()22f =-C ．()f x 在[]1,2上单调递减D ．()f x 有最大值二、多选题7．已知定义在(,0)(0,)-∞+∞ 上的函数()f x 满足()()1()f x f y f xy y x xy--=++，则（）A ．()f x 是奇函数B ．()f x 在(,0)-∞上单调递减C ．()f x 是偶函数D ．()f x 在(0,)+∞在上单调递增8．定义在R 上的非常数函数()f x 的导函数为()f x '，若()2f x +为偶函数且()()23f x f x ++=.则下列说法中一定正确的是（）A ．()f x 的图象关于直线2x =对称B ．6是函数()f x 的一个周期C ．()312f =D ．()f x '的图象关于直线3x =对称9．已知函数()f x 及其导函数()f x '的定义域都是R ，若函数()f x 的图象关于点31,2⎛⎫ ⎪⎝⎭对称，()f x '为偶函数，则（）A ．312f ⎛⎫= ⎪⎭'⎝B ．()()12123f x f x -++=C ．()f x '的图象关于直线1x =对称D ．()f x '的最小周期是110．已知函数()f x 的定义域为R ，且()10f =，若()()()2f x y f x f y +=++，则下列说法正确的是（）A ．()14f -=-B ．()f x 有最大值C ．()20244048f =D ．函数()2f x +是奇函数11．已知()f x ，()g x 都是定义在R 上的函数，对任意实数x ，y 满足()()()()2f x y f x y g x f y +--=，()()210f f +=且()()210f f ⋅≠，则下列结论正确的是A ．()00f =B ．()112g =-C ．()f x 为奇函数D ．()202412024n f n ==∑12．已知函数()f x （()f x 不恒为零），其中()f x '为()f x 的导函数，对于任意的,x y ∈R ，满足()()()()22f x y f x y f x f y +-=-，且()()11,20f f ==，则（）A ．()f x 是偶函数B ．()1f x '+关于直线1x =对称C ．()20,f n n =∈ND ．81()1k f k ==-∑13．已知函数()f x 的定义域为R ，()11f =，()()()()()f x y f x f y f x f y +=++，则（）A ．()01f =-B ．()()0f x f x -≤C ．()()2f x y f x =+为奇函数D ．115212122k k f =-⎛⎫< ⎪⎝⎭∑参考答案：1．B【分析】利用函数单调性的定义即可判断.【详解】任取12x x <，令211,x x x y x =-=，则()()()()212111f x f x f x x x f x -=-+-()()()()21112111f x x f x f x f x x =-+--=--，因为210x x ->，所以()211f x x ->，所以()()210f x f x ->，所以()f x 在R 上单调递增.故选：B.2．D【分析】对于A ，令0b =，可求出(0)f 进行判断，对于B ，令1a b ==，可求出(1)f 进行判断，对于CD ，令0,a b x ==，可求出()f x ，从而可求出()1f x -，进而可判断其奇偶性.【详解】对于A ，令0b =，则()()()00f a f f a -=，得()()010f a f -=⎡⎤⎣⎦，所以()0f a =或()01f =，当()0f a =时，()()()f a f b f a ab b -=-不恒成立，所以()01f =，所以A 错误，对于B ，令1a b ==，则()()()1110f f f -=，得(1)[(1)1]0f f -=，所以()10f =，或()11f =，由选项A 可知()10f ≠，所以()11f =，所以B 错误，对于CD ，令0,a b x ==，则()()()00f f x f x -=-，由选项A 可知()01f =，所以()1f x x =-，所以()111f x x x -=--=-，令()()1g x f x x =-=-，则()()g x x g x -==-，所以()g x 为奇函数，即()1f x -为奇函数，所以C 错误，D 正确，故选：D 3．B【分析】根据题意，结合抽象函数的赋值法，列出方程，逐项判定，即可求解.【详解】对于A 中，由2()()()()f x y f x y f x f y +-=+，令0x y ==，可得22(0)2(0)f f =，因为(0)0f ≠，所以(0)1f =，所以A 不符合题意；对于B 中，函数()f x 的定义域为全体实数，由(0)1f =，显然不符合()()f x f x -=-，所以函数()f x 不是奇函数，所以B 符合题意；对于C 中，由2()()()()f x y f x y f x f y +-=+，令0y =，可得22()()(0)f x f x f =+，即22()()10f x f x --=，解得()1f x =或1()2f x =-，所以函数()y f x =没有零点，所以C 不符合题意；对于D 中，由2()()()()f x y f x y f x f y +-=+，令y x =，可得2(2)(0)()()f x f f x f x =+，所以2(2)2()f x f x =，即(2)()f x f x =，所以D 不符合题意.故选：B ．4．D【分析】令0x y ==，可求得()00f =，令x y =-，可得()()f x f x -=-，利用已知可得()f x 关于32x =对称，可判断B ；可求得函数的周期为6，()f x 关于()3,0对称，计算可判断AD ；由题意可得()f x 在[]2,4上单调递减，可判断C.【详解】()()2222x y x y f x f y f f +-⎛⎫⎛⎫⋅=- ⎪ ⎪⎝⎭⎝⎭，令0x y ==，可得()()2200000022f f f f +-⎛⎫⎛⎫⋅=- ⎪ ⎪⎝⎭⎝⎭，解得()00f =；令x y =-，()()2222x x x x f x f x f f -+⎛⎫⎛⎫⋅-=- ⎪ ⎪⎝⎭⎝⎭，则()()()2f x f x f x ⋅-=-，∴()()f x f x -=-，∴()f x 为奇函数；∵122f x ⎛⎫+ ⎪⎝⎭的图像关于12x =对称，()()11332121222222f x f x f x f x ⎛⎫⎛⎫⎛⎫⎛⎫-+=++⇒-=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,∴()f x 关于32x =对称，故B 正确；∴3322f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭，∴()()3()f x f x f x -=+=-，∴()6(3)()f x f x f x +=-+=，即()f x 的周期为6，∵()f x 关于32x =对称，可得()f x 关于()3,0对称∴()()600f f ==，()()511f f =-=-，()()411f f =-=-，()30f =，()()211f f ==，所以()()240f f +=，2024()337[(1)(2)(3)(4)(5)(6)](1)(2)2f k f f f f f f f f =+++++++=∑小，故A 正确，D 错误；∵202377(1686)222f f f ⎛⎫⎛⎫=+⨯= ⎪⎪⎝⎭⎝⎭，又()f x 在[]1,0-上单调递增∴()f x 在[]2,4上单调递减，所以7(4)2f f ⎛⎫> ⎪⎝⎭，即()202342f f ⎛⎫> ⎪⎝⎭，故C 正确.故选：D.5．C【分析】对于A ，由()G x 为奇函数，则()()G x G x -=-，再将()()231G x f x =+-代入化简可求出对称中心；对于B ，由选项A 可得(2)1f =，再由()F x 为偶函数可得(1)(1)2f x f x x +--=，令1x =可求出(0)f ；对于C ，由()f x 的图象关于点(2,1)对称，结合(0)1f =-求出(4)f 进行判断；对于D ，利用赋值法求解判断.【详解】对于A ，因为()()231G x f x =+-为奇函数，所以()()G x G x -=-，即(23)1[(23)1]f x f x --=-+-，所以(23)(23)2f x f x -++=，所以(2)(2)2f x f x -++=，所以函数()f x 的图象关于点(2,1)对称，所以A 正确，对于B ，在(2)(2)2f x f x -++=中，令0x =，得2(2)2f =，得(2)1f =，因为函数()()()11F x f x x =+-+为偶函数，所以()()F x F x -=，所以()()()()1111f x x f x x ---=+-+，所以(1)(1)2f x f x x +--=，令1x =，则(2)(0)2f f -=，所以1(0)2f -=，得(0)1f =-，所以B 正确，对于C ，因为函数()f x 的图象关于点(2,1)对称，(0)1f =-，所以(4)3f =，所以(0)(4)f f ≠，所以4不是()f x 的周期，所以C 错误，对于D ，在(2)(2)2f x f x -++=中令1x =，则(1)(3)2f f +=，令2x =，则(0)(4)2f f +=，因为(0)1f =-，所以(4)3f =，因为(2)1f =，所以()()()()12346f f f f +++=，所以D 正确，故选：C【点睛】关键点点睛：此题考查抽象函数的奇偶性、对称性和周期性，解题的关键是由已知条件化简后利用赋值法分析判断，考查计算能力，属于较难题.6．D【分析】利用题设结合赋值法可得出()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+，进而结合二次函数性质一一判断各选项，即可得答案.【详解】由于函数()f x 的定义域为R ，且()()()22yf x xf y xy y x -=-，令2y =，则()()()24222f x xf x x -=-，得()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+，2x =时，()()2212222f f +⎡⎤⎣⎦=-⨯+恒成立，无法确定()22f =-，B 不一定成立；由于()22f =-不一定成立，故()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+不一定为偶函数，A 不确定；由于()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+的对称轴为()1212x f =⋅+⎡⎤⎣⎦与[]1,2的位置关系不确定，故()f x 在[]1,2上不一定单调递减，C 不确定，由于()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+表示开口向下的抛物线，故函数()f x 必有最大值，D 正确.故选：D【点睛】关键点睛：解答本题的关键是利用赋值法确定函数()()2112221f x x f x ⎡⎤+⎢⎥⎣=⎦-+，进而结合二次函数性质求解.7．AB【分析】令1x y ==-，求出()1f ，令1x y ==，求出()1f -，再分别令1y =-和1y =，即可求出函数()f x 的解析式，进而可得函数性质.【详解】定义在(,0)(0,)-∞+∞ 上的函数()f x 满足()()1()f x f y f xy y x xy--=++，令1x y ==-，则()()1211f f =-+，所以()113f =，令1x y ==，则()()1211f f =-+，所以()113f -=-，令1y =-，则()()()()()1111233f f x f x f x f x xx x x x-=--+-=--+-=---，所以()13f x x-=-，令1y =，则()()()111111333f f x f x xx x x x x-=-++=--+=，所以()13f x x =，因为()()13f x f x x-=-=-，且定义域关于原点对称，所以函数()f x 是奇函数，由反比例函数的单调性可得函数()13f x x=在(,0)-∞和(0,)+∞上单调递减.故选：AB.8．ACD【分析】根据偶函数的性质即可求解A ，根据4是函数()f x 的一个周期，利用反证法即可求解B ，由赋值法求解C ，求导，即可判断D.【详解】对于A ：因为()2f x +是偶函数，所以()()22f x f x -+=+，即()f x 的图象关于直线2x =对称，所以A 正确；对于B ：由()()23f x f x ++=得()()243f x f x +++=，所以()()4f x f x =+，即4是函数()f x 的一个周期，若6也为函数()f x 的一个周期，则2为函数()f x 的一个周期，那么()()()232f x f x f x ++==，即()32f x =为常数函数，不合题意，所以B 错误；对于C ：由A 可知()()13f f =，对于()()23f x f x ++=可令1x =得()()133f f +=，所以()312f =，所以C 正确；对于D ：由A 可得()()22f x f x -+=+，求导可得()()220f x f x ''++-=即()()40f x f x ''+-=，对于()()23f x f x ++=求导可得()()20f x f x '+'+=，所以()()42f x f x -='+'，即函数()f x '的图像关于直线3x =对称，所以D 正确；故选：ACD.9．BC【分析】用举反例的方法得选项A ，D 错误，再由对称性和对称性与周期性之间的关系对剩余选项逐一分析即可.【详解】因为()f x '为偶函数，函数()f x 的图象关于点31,2⎛⎫⎪⎝⎭对称，对于函数() 1.5f x x =，显然其图象关于点31,2⎛⎫⎪⎝⎭对称，且() 1.5f x '=，故() 1.5f x '=为偶函数，即() 1.5f x x =满足条件()f x '为偶函数，且其图象关于点31,2⎛⎫⎪⎝⎭对称，但33122f ⎛⎫=⎪⎭'≠ ⎝，故A 错误；()f x '的最小正周期不是1，D 错误；函数()f x 的图象关于点31,2⎛⎫⎪⎝⎭对称，()()113f t f t ∴-++=，令2t x =，得()()12123f x f x -++=，故B 正确；函数()f x 的图象关于点31,2⎛⎫⎪⎝⎭对称，()(2)3f x f x ∴=--+，两边求导得：()()2f x f x ''=-，()f x ∴'的图象关于直线1x =对称,故C 正确；故选：BC.10．AD【分析】根据题意，利用抽象函数的性质，及赋值法并结合选项，即可逐项判定，从而求解.【详解】对于A 中，令0x y ==，可得()02f =-，令1,1x y ==-，则()()()11112f f f -=-++，解得()14f -=-，所以A 正确；对于B 中，令121,x x y x x ==-，且12x x <，则()()()1211212f x x x f x f x x +-=+-+，可得()()()21212f x f x f x x -=-+，若0x >时，()2f x >-时，()()210f x f x ->，此时函数()f x 为单调递增函数；若0x <时，()2f x <-时，()()210f x f x -<，此时函数()f x 为单调递减函数，所以函数()f x 不一定有最大值，所以B 错误；对于C 中，令1y =，可得()()()()1122f x f x f f x +=++=+，即()()12f x f x +-=，所以()()()()()()()2024202420232023202232f f f f f f f ⎡⎤⎡⎤⎡⎤=-+-++-⎣⎦⎣⎦⎣⎦ ()()()2112023204046f f f ⎡⎤+-+=⨯+=⎣⎦，所以C 错误；对于D 中，令y x =-，可得()()()02f f x f x =+-+，可得()()220f x f x ++-+=，即()()22f x f x +=--+⎡⎤⎣⎦，所以函数()2f x +是奇函数，所以D 正确；故选：AD.【点睛】关键点点睛：本题主要是对抽象函数利用赋值法，去求解出()14f -=-，及证明函数()2f x +是奇函数.11．ABC【分析】令0y =即可判断A ；令1x y ==即可判断B ；令1x =可得()(1)(1)f x f x f x =--+，结合奇函数的定义即可判断C ；由选项C ，令1x x =-可得(1)()(2)f x f x f x -=+-，求出()f x 的周期即可求解.【详解】()()2()()f x y f x y g x f y +--=.A ：令0y =，得()()2()(0)0f x f x g x f -==，则(0)0f =，故A 正确；B ：令1x y ==，得(2)(0)2(1)(1)f f g f -=，即(2)2(1)(1)f g f =，又(2)(1)0f f +=且(2)(1)0f f ≠，所以2(1)(1)(1)0g f f +=，解得1(1)2g =-，故B 正确；C ：令1x =，得(1)(1)2(1)()f y f y g f y +--=，即(1)(1)()f y f y f y +--=-，得()(1)(1)f y f y f y =--+，所以()(1)(1)f x f x f x =--+，得()(1)(1)f x f x f x -=+--，所以()()0f x f x +-=，则()f x 为奇函数，故C 正确；D ：由选项C 知()(1)(1)f x f x f x =--+，又(1)(1)f x f x -+=--，得()(1)(1)f x f x f x =-+--①，令x 替换成1x -，得(1)()(2)f x f x f x -=+-②，①②相加，得(1)(2)0f x f x --+-=，则(2)(1)(1)f x f x f x -=---=+，得()(3)f x f x =+，即()f x 的周期为3，所以(0)(3)0f f ==，因为(1)(2)(3)0,202467432f f f ++==⨯+，所以20241()(1)(2)(3)(2024)(1)(2)0n f n f f f f f f ==++++=+=∑ ，故D 错误.故选：ABC【点睛】思路点睛：对于含有,x y ，的抽象函数的一般解题思路是：观察函数关系，发现可利用的点，以及利用证明了的条件或者选项；抽象函数一般通过赋值法来确定、判断某些关系，特别是有,x y 双变量，需要双赋值，可以得到一个或多个关系式，进而得到所需的关系.此过程中的难点是赋予哪些合适的值，这就需要观察题设条件以及选项来决定.12．BCD【分析】对于A ：结合赋值法与函数奇偶性的定义计算；对于B ：结合复合函数导数公式与对称性可对于CD ：借助赋值法结合周期性分析求解.【详解】因为()f x 的定义域为R对于选项A ：令0x y ==，可得()()()()2200000f f f f =-=，即()00f =，令0x =，可得()()()()()2220f y f y f f y f y -=-=-，且()f y 不恒为零，则()()f y f y -=-，即()()f x f x -=-，所以()f x 是奇函数，故A 错误；对于选项B ：令11x ty t=+⎧⎨=-⎩，可得22(2)(2)(1)(1)0f f t f t f t =+--=，即22(1)(1)f x f x +=-，即22()(2)f x f x =-，可得()(2)f x f x =±-，令2x =，可得2(2)(2)()f y f y f y +-=-，即2(2)(2)()f x f x f x +-=-，当()(2)0f x f x =-≠时，有()()()2f x f x f x +=-=-，所以(2)(2)()()0f x f x f x f x ++-=-+=；当()(2)0f x f x =--≠，有(2)()f x f x +=，可得(2)(2)()()0f x f x f x f x ++-=-=，当()(2)0f x f x =-=，结合()()f x f x -=-，有()(2)f x f x -=--，可得()(2)0f x f x =-+=，所以(2)(2)0f x f x ++-=；综上所述：(2)(2)0f x f x ++-=，两边同时求导可得(2)(2)f x f x +=-''，可知()f x '关于直线2x =对称，所以(1)f x '+关于直线1x =对称，故B 正确；对于选项C ：由选项B 可知：()(2)f x f x =±-，若()()(2)2f x f x f x =-=--，即()(2)f x f x +=-，可得()()(4)2f x f x f x +=-+=，可知4为()f x 的周期；若()()(2)2f x f x f x =--=-，即()(2)f x f x +=，可得()()(4)2f x f x f x +=+=，可知4为()f x 的周期；综上所述：4为()f x 的周期.且()()200f f ==，所以()20,f n n =∈N ，故C 正确；对于选项D ：由选项B 可知：(2)(2)0f x f x ++-=，令1x =，可得(3)(1)0f f +=，可得()()()()12340f f f f +++=，结合周期性可得()()()81()1011k f k f f f =-=-+=-=-∑，故D 正确.故选：BCD.【点睛】方法点睛：函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性，在解题中根据问题的条件通过变换函数的解析式或者已知的函数关系，推证函数的性质，根据函数的性质解决问题．13．BCD【分析】利用赋值法求得()0f 即可判断A ；利用赋值可得()2222x x f x f f ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，并且判断出()1f x ≠-，由不等式的性质可得()10f x +>，即可判断B ；利用函数的奇偶性以及()0g 的值即可判断C ；利用等比数列的判定可得()f n的通项公式，利用等比数列的求和公式可得1152121252k k f =-⎛⎫= ⎪⎝⎭∑，即可判断D ．【详解】令1x =，0y =，则()()()()()11010f f f f f =++，将()11f =代入得()200f =，即()00f =，故A 错误；由()00f =，令y x =-可得()()()()0f x f x f x f x =+-+-，若存在x 使得()1f x =-，则上式变为01=-，显然不成立，所以()1f x ≠-，又()2221122222x x x x x f x f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+=+=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，因为()1f x ≠-，所以()1f x >-，将()()()()0f x f x f x f x =+-+-整理为()()()()1f x f x f x -+=-，因为()1f x >-，即()10f x +>，所以()()0f x f x -≤，故B 正确；令()()()()R 2f x g x x f x =∈+，则()()()()()()()()()()()()()()()202222f x f x f x f x f x f x g x g x f x f x f x f x +-+--+-=+==+-++-+，且()()()00002f g f ==+，所以()g x 为奇函数，故C 正确；当*n ∈N 时，()()()()()()11121f n f n f f n f f n +=++=+，()()1121f n f n ++=+，所以(){}1f x +是以2为首项，2为公比的等比数列，所以()12n f n +=，由()2112x f x f ⎛⎫+=+ ⎪⎝⎭可知2122n n f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，因为12n f ⎛⎫>- ⎪⎝⎭，所以()*221N 2n n f n ⎛⎫=-∈ ⎪⎝⎭，所以)521111155222111221215252212k k k k f -==-⎛⎫-⎛⎫=-=-=-< ⎪ ⎪-⎝⎭⎝⎭∑∑，故D 正确；故选：BCD ．【点睛】关键点点睛：关键是充分利用函数的奇偶性，等比数列的判定与证明以及等比数列的前n 项和进行分析，由此即可顺利得解．。