下载文档原格式
网络计划优化案例费用优化在一个建设项目中，有多个任务需要按照一定的顺序执行，而每个任务的执行需要一些资源投入，比如人力、材料、设备等，同时每个任务的执行时间也是不同的。
为了充分利用资源、缩短项目总工期，并降低项目成本，需要对网络计划进行优化。
首先，我们需要绘制网络计划图，将各个任务按照任务执行的前后关系连接起来，形成一个网络计划。
网络计划图可以清晰地显示每个任务的持续时间、紧前任务和紧后任务等信息。
然后，我们可以利用关键路径法来确定项目的关键路径。
关键路径是指影响整个项目工期的一条路径，即在该路径上的任务不能延迟，否则将导致整个项目工期延长。
确定了关键路径后，我们可以对这条路径上的任务进行优化，以缩短项目总工期。
接下来，我们可以利用资源平衡法来对项目的资源分配进行优化。
资源平衡法是指在满足任务时间要求的前提下，合理调整任务执行时间，以实现资源的合理利用和最小化费用的目标。
具体操作可以参考以下步骤：1.根据任务执行所需的资源量和资源使用限制，计算每个任务执行所需的资源量。
2.制定资源分配策略，即确定每个任务每个时间段所需的资源量。
3.按照资源分配策略，结合网络计划图，制定资源分配计划。
4.对资源分配计划进行优化，调整任务执行时间，以实现资源的合理利用和最小化费用的目标。
在进行资源分配优化时，需要注意以下几点：1.合理利用资源：根据资源的供需情况，尽量避免资源的浪费或过度使用。
2.优化资源分配计划：根据项目实际情况，灵活调整资源分配计划，以达到最小化费用的目标。
3.控制项目总工期：通过调整任务执行顺序和时间，缩短项目总工期，降低项目成本。
4.风险评估与控制：在优化资源分配计划的过程中，要充分考虑项目风险，制定相应的风险评估与控制措施。
通过以上的优化措施，我们可以最大限度地缩短项目总工期，并降低项目成本。
但是需要注意的是，在进行优化时，需要充分考虑项目实际情况，并量化和评估各个因素的影响，以确保优化方案的可行性和有效性。
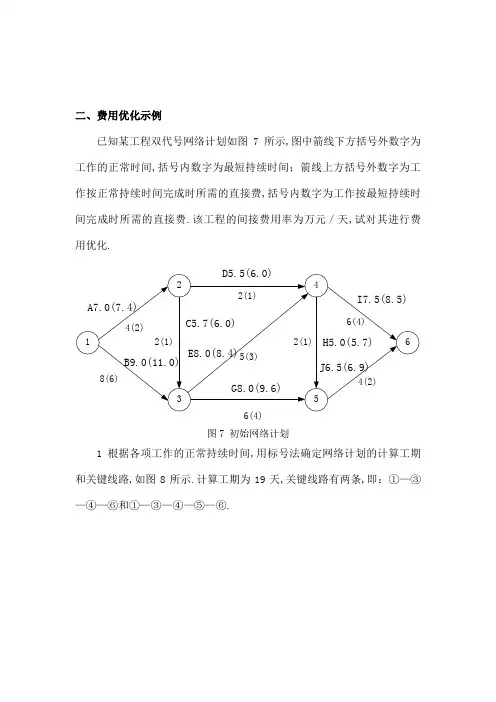
二、费用优化示例已知某工程双代号网络计划如图7所示,图中箭线下方括号外数字为工作的正常时间,括号内数字为最短持续时间；箭线上方括号外数字为工作按正常持续时间完成时所需的直接费,括号内数字为工作按最短持续时间完成时所需的直接费.该工程的间接费用率为万元／天,试对其进行费用优化.图7 初始网络计划1根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图8所示.计算工期为19天,关键线路有两条,即：①—③—④—⑥和①—③—④—⑤—⑥.(①,4)(①,8)(④,15)(③,13)图8 初始网络计划中的关键线路2计算各项工作的直接费用率：△C1-2=∕4-2=万元∕天△C1-3=∕8-6=万元∕天△C1-2=∕4-2=万元∕天△C2-3=万元∕天△C2-4=万元∕天△C3-4=万元∕天△C3-5=万元∕天△C4-5=万元∕天△C4-6=万元∕天△C5-6=万元∕天3计算工程总费用：①直接费总和：Cd=++++++++=万元；②间接费总和：Ci=×19=万元；③工程总费用：Ct = Cd+Ci=+=万元.4通过压缩关键工作的持续时间进行费用优化优化过程见表1：1第一次压缩从图8可知,该网络计划中有两条关键线路,为了同时缩短两条关键线路的总持续,有以下四个压缩方案：①压缩工作B,直接费用率为万元／天；②压缩工作E,直接费用率为万元／天；③同时压缩工作H和工作I,组合直接费用率为：+=万元／天；④同时压缩工作I和工作J,组合直接费用率为：+=万元／天.在上述压缩方案中,由于工作E的直接费用率最小,故应选择工作E为压缩对象.工作E的直接费用率万元／天,小于间接费用率0,8万元／天,说明压缩工作E可使工程总费用降低.将工作E的持续时间压缩至最短持续时间3天,利用标号法重新确定计算工期和关键线路,如图9所示.此时,关键工作E被压缩成非关键工作,故将其持续时间延长为4天,使成为关键工作.第一次压缩后的网络计划如图10所示.图中箭线上方括号内数字为工作的直接费用率.(①,8)(④,14)图9 工作E压缩至最短时的关键线路(③,12)(①,4)图10 第一次压缩后的网络计划2第二次压缩从图3-44可知,该网络计划中有三条关键线路,即：①—③—④—⑥、①—③—④—⑤—⑥和①—③—⑤—⑥.为了同时缩短三条关键线路的总持续时间,有以下五个压缩方案：①压缩工作B,直接费用率为万元／天；②同时压缩工作E和工作G,组合直接费用率为+=万元／天；③同时压缩工作E和工作J,组合直接费用率为：+=万元／天；④同时压缩工作G、工作H和工作J,组合直接费用率为：++=万元／天；⑤同时压缩工作I和工作J,组合直接费用率为：+=万元／天.在上述压缩方案中,由于工作E和工作J的组合直接费用率最小,故应选择工作E和工作J作为压缩对象.工作E和工作J的组合直接费用率万元／天,小于间接费用率万元／天,说明同时压缩工作E和工作J可使工程总费用降低.由于工作E的持续时间只能压缩1天,工作J的持续时间也只能随之压缩1天.工作E和工作J的持续时间同时压缩1天后,利用标号法重新确定计算工期和关键线路.此时,关键线路由压缩前的三条变为两条,即：①—③—④—⑥和①—③—⑤—⑥.原来的关键工作H未经压缩而被动地变成了非关键工作.第二次压缩后的网络计划如图11所示.此时,关键工作E的持续时间已达最短,不能再压缩,故其直接费用率变为无穷大.(①,8)(③,14)图11 第二次压缩后的网络计划3第三次压缩从图11可知,由于工作E不能再压缩,而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下三个压缩方案：①压缩工作B,直接费用率为万元／天；②同时压缩工作G和工作I,组合直接费用率为+ =万元／天；③同时压缩工作I和工作J,组合直接费用率为：+=万元／天.在上述压缩方案中,由于工作I和工作J的组合直接费用率最小,故应选择工作I和工作J作为压缩对象.工作I和工作J的组合直接费用率万元∕天,小于间接费用率万元∕天,说明同时压缩工作I和工作J可使工程总费用降低.由于工作J的持续时间只能压缩1天,工作I的持续时间也只能随之压缩1天.工作I和工作J的持续时间同时压缩l天后,利用标号法重新确定计算工期和关键线路.此时,关键线路仍然为两条,即：①—③—④—⑥和①—③—⑤—⑥.第三次压缩后的网络计划如图12所示.此时,关键工作／的持续时间也已达最短,不能再压缩,故其直接费用率变为无穷大.(①,4)(③,11) Array (①,8)(③,14)图12 第三次压缩后的网络计划4第四次压缩：从图3-46可知,由于工作E和工作／不能再压缩,而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下两个压缩方案：①压缩工作B,直接费用率为万元／天；②同时压缩工作G和工作I,组合直接费用率为+=万元∕天.在上述压缩方案中,由于工作B的直接费用率最小,故应选择工作B作为压缩对象.但是,由于工作B的直接费用率万元∕天,大于间接费用率万元／天,说明压缩工作B会使工程总费用增加.因此,不需要压缩工作B,优化方案已得到,优化后的网络计划如图13所示.图中箭线上方括号内数字为工作的直接费.(①,4)(①,8)(③,14)(③,11)图13 费用优化后的网络计划5计算优化后的工程总费用①直接费总和：Cd0=++++++++= 万元；②间接费总和：Ci0=×16=万元；③工程总费用：Ct0 = Cd0+ CiO= +=万元.优化表表1。
第四节网络计划优化网络计划优化, 就是在满足一定条件下, 利用时差来平衡时间、资源与费用三者的关系, 寻求工期最短、费用最低、资源利用最好的网络计划过程。
但是, 目前还没有使这三个方向因素同时优化的数学模型。
目前能进行的网络计划优化是时间优化、时间—费用优化和时间—资源优化。
一、时间优化时间优化就是不考虑人力、物力、财力资源的限制。
这种情况通常发生在任务紧急、资源有保障的情况。
由于工期由关键路线上活动的时间所决定, 压缩工期就在于如何压缩关键路线上活动的时间。
缩短关键路线上活动时间的途径有: ①利用平行、交叉作业缩短关键活动的时间；②在关键路线上赶工。
由于压缩了关键路线上活动的时间, 会导致原来不是关键路线的路线成为关键路线。
若要继续缩短工期, 就要在所有关键路线上赶工或进行平行交叉作业。
随着关键路线的增多, 压缩工期所付出的代价就变大。
因此, 单纯地追求工期最短而不顾资源的消耗是不可取的。
二、时间—费用优化时间—费用优化就是在使工期尽可能短的同时, 也使费用尽可能少。
能够实现时间—费用优化的原因是, 工程总费用可以分为直接费用和间接费用两部分, 这两部分费用随工期变化而变化的趋势是相反的。
C(一)直接费用D直接费用是指能够直接计入成本计算对象的费用, 如直接工人工资, 原材料费用等。
直接费用随工期的缩短而增加。
一项活动如果按正常工作班次进行, 其延续时间称为正常时间, 记为；所需费用称为正常费用, 记为。
若增加直接费用投入, 就可以缩短这项活动所需的时间, 但活动所需时间不可能无限缩短。
如加班加点, 一天也只有24小时, 生产设备有限, 投入更多的人力也不会增加产出。
称赶工时间条件下活动所需最少时间为极限时间, 记为；相应所需费用为极限费用, 记为。
直接费用与活动时间之间的关系如图8.4—1所示。
为简化处理, 可将活动时间—费用关系视为一种线性关系。
在线性假定条件下, 活动每缩短一个单位时间所引起直接费用增加称为直接费用变化率. 记为。
