高斯光束与准直器简介
- 格式:ppt
- 大小:1.06 MB
- 文档页数:31





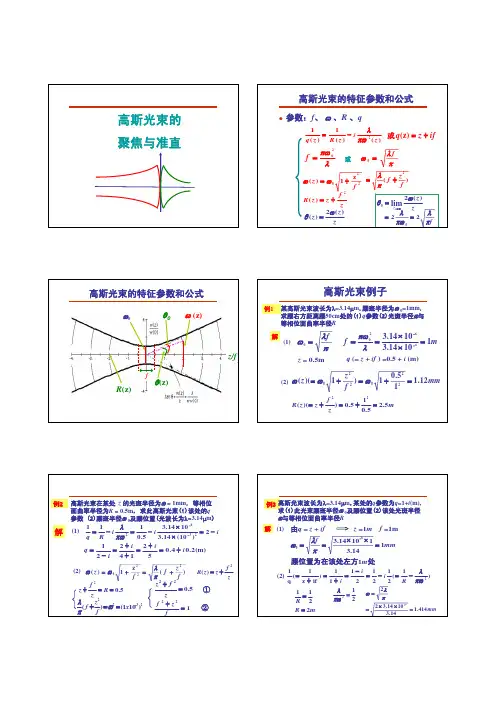
![第7讲 高斯光束的聚焦和准直[优质PPT]](https://uimg.taocdn.com/0b8981bb02d276a200292ef0.webp)

第八章 现代光学系统随着激光技术、光纤技术和光电技术的不断发展,各种不同的用途的新型光学系统相继出现,例如激光光学系统、付里叶光学系统、扫描光学系统等。
为能全面地了解这些光学系统的成像特性和设计要求,本章就上述几种新型光学系统作一简要介绍。
§8-1 激光光学系统一、高斯光束的特性激光作为一种光源,其光束截面内的光强分布式不均匀的,激光束波面上各点的振幅是不相等的,其振幅A 与光束截面半径r 的函数关系为:220r A A e ω-=其中A 0为光束截面中心的振幅;ω为一个与光束截面半径有关的参数;r 为光束截面半径。
由上式可以看出光束波面的振幅A 呈高斯型函数分布,如图8-1所示,所以激光光束又称为高斯光束。
图8-1 高斯光束截面当r =ω时,0A A e=,说明高斯光束的名义截面半径ω是当振幅A 下降到中心振幅0A 的1/e 时所对应的光束截面半径。
二、高斯光束的传播高斯光束的截面半径、波面曲率半径和位相因子是高斯光束传播中的三个重要参数。
1、高斯光束的截面半径高斯光束截面半径()z ω的表达式为:()1220201z z λωωπω⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦ 从图8-2中可以看出,高斯光束在均匀的透明介质中传播时,其光束截面半径()z ω与z 不成线性关系,而是一种非线性关系,这与同心光束在均匀介质中的传播完全不同。
图8-2高斯光束传播2、高斯光束的波面曲率半径高斯光束的波面曲率半径表达式为:()2201R z z z πωλ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦高斯光束在传播过程中,光束波面的的曲率半径由无穷逐渐变小,达到最小后又开始变大,直至达到无限远时变成无穷大。
3、高斯光束的位相因子高斯光束的位相因子表达式为:()20zz arctg λπωΦ=高斯光束的截面半径轨迹为一对双曲线,双曲线的渐近线可以表示高斯光束的远场发散程度,如图8-3所示。
图8-3 高斯光束的发散角高斯光束的孔径角为:tg λθπω= 4、高斯光束传播的复参数表示假设有一个复参数()q z ,并令()()()211i q z R z z λπω=-当z =0时,得()()()211000i q R λπω=-因为()0R =∞,()00ωω=所以()2000q q i πωλ==- 把()2201R z z z πωλ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦和()2220201z z λωωπω⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦代入式()()()211i q z R z z λπω=-得()0q z q z =+这与同心球面光束沿z 轴传播时,其表达式为0R R z =+有相同的表达形式。

文章来源: /schemes/scheme-27.htm在自由空间型的光无源器件(如光隔离器、光环形器、光开关等)中,输入和输出光纤端面必须间隔一定距离,以便在光路中插入一些光学元件,从而实现器件功能。
从光纤输出的高斯光束(实际为近高斯光束,可以高斯光束近似处理),束腰半径较小而发散角较大,两根光纤之间的直接耦合损耗对其间距极其敏感,光纤准直器扮演这样一种功能,将从光纤输出的光准直为腰斑较大而发散角较小的光束,以增加对轴向间距的容差,如图 4 所示,从图 2(c)(d)亦可看出准直器对轴向容差的改善。
光纤准直器的结构和参数光纤准直器的结构参数如图 5 所示,因光纤头端面的 8 度斜角,造成输出光束与准直器轴线存在夹角θ,称为点精度。
图 6 所示为两准直器的理想耦合情况,二者的输出光场完全重合,其间距为准直器的工作距离Zw。
准直器输出高斯光束的束腰距离其端面Zw/2,束腰直径为2ωt,而高斯光束的发散角与其束腰直径成反比关系。
到此我们介绍了光纤准直器的三个主要参数:工作距离、点精度和光斑尺寸。
光纤准直器的设计方法光纤准直器的基本原理是,将光纤端面置于准直透镜的焦点处,使光束得到准直,然后在焦点附近轻微调节光纤端面位置,得到所需工作距离,因此准直器的工作距离与光纤头和透镜的间距 L相关。
光纤准直器的设计方法是,根据实际需求确定准直器的工作距离,依据高斯光束传输理论,确定光纤头和透镜间距 L并计算光斑尺寸,然后依据光线理论计算准直器的点精度。
具体设计步骤如下:a) 确定所需工作距离Zw;b) 列出从光纤端面至输出光束束腰位置的近轴光线传输矩阵;下面以 Grin-Lens准直器为例:c) 列出输出光束束腰位置的 q 参数;高斯光束的传输可用 q 参数及 ABCD法则来描述,如下图公式所示:一般考虑光纤端面高斯光束的模场半径为ω0且波面曲率半径为R0=∞,因此光纤端面的q参数为:根据 ABCD法则,输出光束束腰位置的 q 参数为:d) 确定光纤头与透镜间距 L;在输出光束束腰位置,波面曲率半径为R3=∞即 1/q3的实部为 0纵观以上推导过程,q3中只包含一个变量L。


光纤准直器原理曾孝奇一.模型光纤准直器通过透镜能实现将从发散角较大(束腰小)的光束转换为发散角较小(束腰大)的光束,从而以较低损耗耦合进入其他光学器件。
在这里,我们将从光纤中的出射光束认为是基模高斯光束;光纤准直器基本模型如下:图1 光纤准直器原理示意图其中,(i=0,1,2,3)为高斯光束的q参数,q参数定义为:,(1),,;(2)图1中,(i=0,1,2,3)分别表示光纤端面,透镜入射面,透镜出射面,和出射光束的束腰处的q参数,而和分别表示透镜变换前后的束腰;l表示光纤端面与透镜间隔,l w为准直器的设计工作距离。
二.理论分析根据ABCD理论,高斯光束q参数经透镜变换后,,(3)而且,,,,。
这样,我们可以得到经过透镜后的束腰大小:,(4)工作距离:,(5)方程(5)是关于l的二次方程,为使得l有实根,方程(5)的判别式应该不小于零,从而我们可以得到:,(6)方程(6)表示准直器的工作距离有上限,就是一个最大工作距离。
此时,我们得到:。
分析:不论对于何种透镜,准直器的出射光斑和工作距离都取决于透镜的传输矩阵ABCD;对于给定的透镜,它们还跟入射光斑大小和光纤端面与透镜间的距离l有关,也就是说,对于给定的入射光束和给定的透镜,我们可以通过在透镜焦距附近改变l来实现不同的工作距离。
在实际制作准直器当中,我们正是通过这种方法来实现不同的工作距离的。
进一步地,如果我们需要定量计算准直器的出射束腰和工作距离,需要具体知道不同透镜的ABCD系数。
对于G Lens(自聚焦透镜,通常为0.23P),它的ABCD矩阵为:,(7)其中,透镜的透镜的轴线折射率,L为透镜的中心厚度,为透镜的聚焦常数。
由于G Lens的ABCD系数取决于,L和,因而,适当选择这些参数,同样能改变准直器的出射光斑大小和工作距离。
对于C lens(厚透镜),它的传输矩阵为:。
(8)三.实例分析本小组采用C lens已制作的一些准直器,C lens参数如下:曲率半径R=1.2mm,透镜长度L=2.5mm,C lens采用SF11材料,在1550nm处折射率n=1.744742。