2020年中考数学动态问题分项破解专题01 动点问题中的最值、最短路径问题(教师版)
- 格式:docx
- 大小:370.20 KB
- 文档页数:11
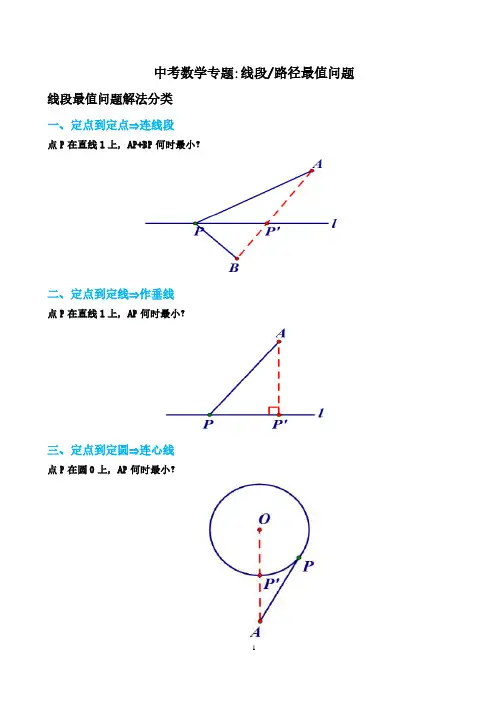
中考数学专题:线段/路径最值问题线段最值问题解法分类一、定点到定点⇒连线段点P在直线l上,AP+BP何时最小?二、定点到定线⇒作垂线点P在直线l上,AP何时最小?三、定点到定圆⇒连心线点P在圆O上,AP何时最小?线段最值问题一般转化为上述三个问题.例题赏析:1.如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN 的周长最小值为.思路:把点P分别沿OA、OB翻折得P1、P2,周长即为P1M+MN+P2N,转化为求P1、P2两点之间最小值,得△PMN最小值为P1P2=OP=6.2.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是.思路:点N沿AD翻折至AC上,BM+MN=BM+MN',转化为求点B到直线AC的连线最小值,即BN'⊥AC时,最小值为2√2.3.如图,矩形ABCD中,AB=2,BC=3,以A为圆心、1为半径画圆,E是⊙A上一动点,F是BC 上的一动点,则FE+FD的最小值是.思路:点D沿BC翻折至D',DF+EF=D'F+EF,转化为求点D'到圆A上各点的最小距离,易求D'E=4.4.抛物线y=3/5x2-18/5x+3与直线y=3/5x+3相交于A、B两点,点M是线段AB上的动点,直线PM∥y轴,交抛物线于点N.在点M运动过程中,求出MN的最大值.思路:设M(m,3/5m2-18/5m+3),N(m,3/5m+3),用函数关系式表示MN=(3/5m+3)-(3/5m2-18/5m+3)=21/5m-3/5m2,求得最大值即可.5.在菱形ABCD中,对角线AC=8,BD=6,点E、F分别是边 AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是思路:点E沿AC翻折,转化为点到点的距离.(将军饮马问题实质就是通过翻折转化为定点到定点的问题)6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O 的最大距离为 .思路:取AB中点E,连接DE、OE,由两点间线段最短,得OD≤OE+DE,最大为1+√2.7.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP 沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是简解:B'点运动路径为以C为圆心,BC为半径的圆弧,转化为点到圆的最短距离AC-B'C=1.8.如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为 .思路:正六边形最大半径为1/2,与正方形中心重合,E点运动路径为圆,转化为求点到圆的最短距离,如下图.9.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是 .思路:D是定点,C是直线AC上的动点,转化为求点到线的最短距离.10.在△ABC中,AB=AC=5,cos∠ABC=3/5,将△ABC绕点C顺时针旋转,得到△A'B'C,点E是BC上的中点,点F为线段AB上的动点,在△A'B'C绕点C顺时针旋转过程中,点F的对应点是F',求线段EF'长度的最大值与最小值的差.思路:先确定线段A'B'的运动轨迹是圆环,外圆半径为BC,内圆半径为AB边上的高,F'是A'B'上任意一点,因此F'的运动轨迹是圆环内的任意一点,由此转化为点E到圆环的最短和最长距离.E到圆环的最短距离为EF2=CF2-CE=4.8-3=1.8,E到圆环的最长距离为EF1=EC+CF1=3+6=9,其差为7.2.问:何时需要作辅助线翻折其中的定点(定线或定圆)?答:当动点所在直线不在定点(定线或定圆)之间时,需把定点(定线或定圆)沿动点所在直线翻折以使定点(定线或定圆)处于动点所在直线的两侧,从而便于连接相关线段或作垂线与动点所在直线找到交点.如上述例3,动点F所在直线不在定圆A和定点D之间,因而需把D点沿BC翻折至D',即可转化为定点D'到定圆A的最短距离,另外亦可把圆A沿BC翻折至另一侧,同样可以转化为定点D到定圆A'的最短距离,如下图.关键方法:动中求定,动点化定线;以定制动,定点翻两边.(1)动中求定,动点化定线:如例7、例8、例10,动点所在路径未画出时需先画出动点所在轨迹,一般动点所在轨迹为线或圆.(2)以定制动,定点翻两边:如例1、例2、例3、例5,定点(线或圆)在动点所在直线同侧时需翻折至两侧,转化为上述三种关系.练1、如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。

专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点,它贯穿于整个初中数学,自数轴起始,至几何图形的存在性、几何图形的长度及面积的最值,函数的综合类题目,无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变,而其中又有一些技巧性很强的数学思想(转化思想),本专题以几个基本的知识点为经,以历年来中考真题为纬,由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间,线段最短;2. 垂线段最短;3. 若A、B是平面直角坐标系内两定点,P是某直线上一动点,当P、A、B在一条直线上时,PA PB 最大,最大值为线段AB的长(如下图所示);(1)单动点模型作图方法:作已知点关于动点所在直线的对称点,连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示,P是x轴上一动点,求P A+PB的最小值的作图.P 是∠AOB 内一点,M 、N 分别是边OA 、OB 上动点,求作△PMN 周长最小值.作图方法:作已知点P 关于动点所在直线OA 、OB 的对称点P ’、P ’’,连接P ’P ’’与动点所在直线的交点M 、N 即为所求.5. 二次函数的最大(小)值()2y a x h k =-+,当a >0时,y 有最小值k ;当a <0时,y 有最大值k .二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. (详见精品例题解析) 三、精品例题解析例1. (2019·凉山州)如图,正方形ABCD 中,AB =12,AE =3,点P 在BC 上运动(不与B 、C 重合),过点P 作PQ ⊥EP ,交CD 于点Q ,则CQ 的最大值为例2. (2019·凉山州)如图,已知A 、B 两点的坐标分别为(8,0),(0,8). 点C 、F 分别是直线x =-5和x 轴上的动点,CF =10,点D 是线段CF 的中点,连接AD 交y 轴于点E ,当△ABE 面积取最小值时,tan ∠BAD =( )OA .817 B . 717 C . 49 D . 59例3. (2019·南充)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,AB =24,BC =5,给出结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;②△OAB 的面积的最大值为144;③当OD 最大时,点D 的坐标为)2626125,262625(,其中正确的结论是 (填写序号).例4. (2019·天津)已知抛物线2y x bx c =-+(b 、c 为常数,b >0)经过点A (-1,0),点M (m ,0)是x 轴正半轴上的动点,若点Q (1,2Q b y +2QM +b 的值.例5. (2019·舟山)如图,一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上,边AC 与EF 重合,12AC cm .当点E 从点A 出发沿AC 方向滑动时,点F 同时从点C 出发沿射线BC 方向滑动.当点E 从点A 滑动到点C 时,点D 运动的路径长为 cm ;连接BD ,则△ABD 的面积最大值为 2cm .例6. (2019·巴中)如图,在菱形ABCD 中,连接BD 、AC 交于点O ,过点O 作OH ⊥BC 于点H ,以O 为圆心,OH 为半径的半圆交AC 于点M .(1)求证:DC是圆O的切线;(2)若AC=4MC,且AC=8,求图中阴影部分面积;(3)在(2)的前提下,P是线段BD上的一动点,当PD为何值时,PH+PM的值最小,并求出最小值.B D。

专题15最短路径问题模型一. 两点之间,线段最短模型二. “将军饮马”模型三. 双动点模型四. 垂线段最短【例1】(2019·河南南阳一模)如图,已知一次函数y=12x+2的图象与x轴、y轴交于点A、C,与反比例函数y=kx的图象在第一象限内交于点P,过点P作PB⊥x轴,垂足为B,且△ABP的面积为9.(1)点A的坐标为,点C的坐标为,点P的坐标为;(2)已知点Q在反比例函数y=kx的图象上,其横坐标为6,在x轴上确定一点M,是的△PQM的周长最小,BA'O求出点M的坐标.【分析】(1)根据一次函数的解析式求得A、C坐标,由S△ABP=12·AB·BP=9,设P点坐标为(m,12m+2),代入得到点P坐标;(2)先根据反比例函数解析式求得Q点坐标,作Q点(或P点)关于x轴的对称点Q’(P’),连接PQ’(QP’)与x轴的交点即为点M,用待定系数法求出直线PQ’(QP’的解析式).【解析】解:(1)在y=12x+2中,当x=0时,y=2;y=0时,x=-4,∴A点坐标为(-4,0),C点坐标为(0,2),设P点坐标为(m,12m+2),m>0,则AB=m+4,BP=12m+2,∵S△ABP=12·AB·BP=9,即12×(m+4)(12m+2)=9,解得:m=2或m=-10(舍),∴点P的坐标为(2,3);(2)如图,作点Q关于x轴的对称点Q’,连接PQ’交x轴于点M,此时,△PQM的周长最小,6,-1),设直线PQ’的解析式为:y=mx+b,得:23 61m bm b+=⎧⎨+=-⎩,解得:15mb=-⎧⎨=⎩,即直线PQ’的解析式为:y=-x+5,当y=0时,x=5,即M点坐标为(5,0),∴当△PQM的周长最小时,M点坐标为(5,0).【变式1-1】(2017·新野一模)已知抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),C三点.直线y=mx+12交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.(1)求抛物线的解析式;(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)∵抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),∴20 4220a ba b-+=⎧⎨++=⎩,解得a=﹣1,b=1,∴抛物线的解析式为y=﹣x2+x+2.(2)直线y=mx+12交抛物线与A、Q两点,将A(﹣1,0)代入得:m=12,∴直线AQ的解析式为y=12x+12.设点P的横坐标为n,则P(n,﹣n2+n+2),N(n,12n+12),F(n,0),∴PN=﹣n2+n+2﹣(12n+12)=﹣n2+12n+32,NF=12n+12,∵PN=2NF,即﹣n2+12n+32=2×(12n+12),解得:n=﹣1或12.当n=﹣1时,点P与点A重合,舍去.故点P的坐标为(12,94).(3)∵y=﹣x2+x+2,=﹣(x﹣12)2+94,∴M(12,94).∵A、C关于直线DE对称,∴连接AM交直线DE与点G,连接CG、CM,此时,△CMG的周长最小,设直线AM的函数解析式为y=kx+b,将A(﹣1,0),M(12,94)代入并解得:k=32,b=32,∴直线AM的函数解析式为y=32x+32,∵D为AC的中点,∴D(﹣12,1).可得直线AC的解析式为:y=2x+2,直线DE的解析式为y=﹣12x+34.将y=﹣12x+34与y=32x+32联立,解得:x=﹣38,y=1516.∴在直线DE上存在点G,使△CMG的周长最小,G(﹣38,1516).【变式1-2】(2019·三门峡二模)已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D 是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD =m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.图1 图2【答案】见解析.【解析】解:(1)证明:由旋转性质,得:∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=∴△BDE的周长最小值为:+4.1.(2018·焦作一模)如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.(1)填空:抛物线的解析式为,点C的坐标;(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标;(3)如图2,当点P位于抛物线的对称轴的右侧,若将△APQ沿AP对折,点Q的对应点为点Q',请直接写出当点Q'落在坐标轴上时点P的坐标.图1 图2【答案】(1)y=﹣x2+3x+4,(﹣1,0);(2)(3)见解析.【解析】解:(1)∵抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),∴-16a+4b+c=0,c=4,解得:b=3,c=4,∴抛物线解析式为y=﹣x2+3x+4,当y=0时,﹣x2+3x+4=0,解得x=﹣1,x=4,即C(﹣1,0);答案为:y=﹣x2+3x+4;(﹣1,0);(2)∵△AQP∽△AOC,∴AQ AOPQ CO=4,即AQ=4PQ,设P(m,﹣m2+3m+4),则PQ=|4﹣(﹣m2+3m+4|=|m2﹣3m|,∴4|m2﹣3m|=m,解得:m1=0(舍去),m2=134,m3=114,∴P点坐标为(134,5116)或(114,7516).(3)设P(m,﹣m2+3m+4),∵抛物线对称轴为:x =32, ∴m >32, ①当点Q ′落在x 轴上时,延长QP 交x 轴于H ,则PQ =m 2﹣3m ,由折叠性质知:∠AQ ′P =∠AQP =90°,AQ ′=AQ =m ,PQ ′=PQ =m 2﹣3m , ∵∠AQ ′O =∠Q ′PH , ∴△AOQ ′∽△Q ′HP , ∴'''OA AQ Q B PQ =, 即24'3m Q B m m=-,得:Q ′B =4m ﹣12, ∴OQ ′=12﹣3m ,在Rt △AOQ ′中,由勾股定理得:42+(12﹣3m )2=m 2, 解得:m 1=4,m 2=5,即P 点坐标为(4,0),(5,﹣6); ②当点Q ′落在y 轴上,此时以点A 、Q ′、P 、Q 所组成的四边形为正方形, ∴PQ =PQ ′, 即|m 2﹣3m |=m ,得m 1=0(舍去),m 2=4,m 3=2, P 点坐标为(4,0),(2,6), 综上所述,点P 的坐标为(4,0)或(5,﹣6)或(2,6).2.(2019·中原名校大联考)如图,直线y =﹣x +5与x 轴交于点B ,与y 轴交于点C ,抛物线y =﹣x 2+bx +c 与直线y =﹣x +5交于B ,C 两点,已知点D 的坐标为(0,3)(1)求抛物线的解析式;(2)点M ,N 分别是直线BC 和x 轴上的动点,则当△DMN 的周长最小时,求点M ,N 的坐标.【答案】见解析.【解析】解:(1)在y=﹣x+5中,当x=0,y=5,当y=0,x=5,点B、C的坐标分别为(5,0)、(0,5),将(5,0)、(0,5),代入y=﹣x2+bx+c,并解得:b=4,c=5即二次函数表达式为:y=﹣x2+bx+5.(2)在y=﹣x2+bx+5中,当y=0时,x=﹣1或5,∴A(﹣1,0),OB=OC=2,∴∠OCB=45°;过点D分别作x轴和直线BC的对称点D′(0,﹣3)、D″,∵∠OCB=45°,∴CD″∥x轴,点D″(2,5),连接D′D″交x轴、直线BC于点N、M,此时△DMN的周长最小,设直线D’D’’的解析式为:y=mx+n将D′(0,﹣3),D″(2,5),代入解得:m=4,n=-3,直线D’D’’的解析式为:y=4x﹣3,∴N(34,0).联立y=4x﹣3,y=﹣x+5得:x=85,y=175,即M(85,175).3.(2017·预测卷)已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数123y=图象上一点.将△AOB绕B点旋转至△A′O′B处.(1)求m的值;(2)求当AO′最短和最长时A′点的坐标.【答案】见解析.【解析】解:(1)∵C(m,6)为反比例函数123y=图象上一点,∴m=23;(2)当AO′最短时A′点的坐标(2+65,85),当AO′最长时A′点的坐标(2﹣65,﹣85).①当点O′在线段AB上时,AO′最短,过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,∵O′N∥OA,∴''BN O N O B OB OA AB==,即'2425 BN O N==∴BN=25,O′N=45.由∠A′MO′=∠A′O′B=∠O′NB=90°,得:∠MA′O′=∠NO′B,∴△A′MO′∽△O′NB,∴''2 'A M O MO N BN==,∴A′M,O′M即A’();②当点O′在线段AB延长线上时,AO′最长,同理可得:(2).4.(2017·郑州一模)如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O 于点Q,则PQ的最小值为()A B C.2D.3【答案】A.【解析】解:由垂线段最短知,当OP⊥l时,OP取最小值,而由PQ PQ取最小值,过点O作OP⊥l于P,过P作⊙O的切线PQ,切点为Q,连接OQ,则OP=3,OQ=2,∵PQ切⊙O于点Q,∴∠OQP=90°,由勾股定理得:PQ,即PQ,故答案为:A .5.(2019·许昌月考)如图,在菱形ABCD 中,∠ABC =60°,AB =2,点P 是这个菱形内部或边上的一点,若以点P 、B 、C 为顶点的三角形是等腰三角形,则P 、D (P 、D 两点不重合)两点间的最短距离为 .【答案】 2.【解析】解:(1)BC 为腰,且∠PCB 为顶角时,以C 为圆心,以BC 为半径画弧,点P 在弧上,由题意知,点P 在菱形外或与A 、D 重合,不符合题意;(2)以BC 为腰,且∠PBC 为顶角时,点P 在以B 为圆心,以AB 为半径的圆上,则PD 的最小值为:BD -BC BC -BC ﹣2;(3)BC 为底时,则点P 在线段BC 的垂直平分线上,由垂线段最短知,PD 最小为:1+1=2;∵2<2,∴PD 的最小值为:﹣2.6.(2019·郑州外国语模拟)在平面直角坐标系中,抛物线y =-x 2+bx +c 经过点A 、B 、C ,已知A (-1,0),C (0,3).(1)求抛物线的解析式;(2)如图,抛物线的顶点为E ,EF ⊥x 轴于F ,N 是直线EF 上一动点,M (m ,0)是x 轴上一个动点,请直接写出CN +MN +12MB 的最小值.【答案】见解析.【解析】解:(1)将A (-1,0),C (0,3)代入y =-x 2+bx +c 得:103b c c --+=⎧⎨=⎩,解得:23b c =⎧⎨=⎩,即抛物线的解析式为:y =-x 2+2x +3;(2)首先构造出12MB ,将AB 绕点B 顺时针旋转30°,交y 轴于H ,过M 作MG ⊥BH 于G ,则MG =12MB ,CN +MN +12MB 的最小值即CN +MN +MG 的最小值, 由图可知,当C 、N 、M 、G 共线,且CG ⊥BH 时,取得最小值,即∠HCG =30°,∵OB =3,∠ABH =30°,∴AH H (0),∴CH∴CG =CH ·cos ,即CN +MN +12MB 的最小值为32. 7.(2019·郑州实验中学模拟)如图,已知抛物线y =﹣x 2+bx +c 与一直线相交于A (1,0)、C (﹣2,3)两点,与y 轴交于点N ,其顶点为D .(1)求抛物线及直线AC 的函数关系式;(2)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值;(3)在对称轴上是否存在一点M ,使△ANM 的周长最小.若存在,请求出△ANM 周长的最小值;若不存在,请说明理由.【答案】见解析.【解析】解:(1)将A (1,0),C (﹣2,3)代入y =﹣x 2+bx +c ,得:10423b c b c -++=⎧⎨--+=⎩,解得:23b c =-⎧⎨=⎩, ∴抛物线的函数解析式为:y =﹣x 2﹣2x +3;设直线AC 的解析式为:y =kx +n ,将A (1,0),C (﹣2,3)代入y =kx +n ,得:k +n =0,-2k +n =3,解得:k =-1,n =1,即直线AC 的解析式为y =﹣x +1.(2)过点P 作PF ∥y 轴交直线AC 于点F ,设点P (x ,﹣x 2﹣2x +3),则点F (x ,﹣x +1),(﹣2<x <1)∴PF =﹣x 2﹣2x +3﹣(﹣x +1)=﹣x 2﹣x +2.∴S △APC =12(x A -x C )•PF =﹣32x 2﹣32x +3 =﹣32(x +12)2+278. ∴当x =﹣12时,△APC 的面积取最大值,最大值为278. (3)当x =0时,y =﹣x 2﹣2x +3=3,∴点N 的坐标为(0,3).由y =﹣x 2﹣2x +3=﹣(x +1)2+4,得:抛物线的对称轴为x =﹣1.∴点C ,N 关于抛物线的对称轴对称,设直线AC 与抛物线的对称轴的交点为点M ,∴MN=CM,∴AM+MN=AM+MC=AC,此时△ANM周长有最小值.由勾股定理得:AC=,AN=∴C△ANM=AM+MN+AN=AC+AN=∴△ANM周长的最小值为8.(2018·郑州预测卷)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.(1)求抛物线的解析式;(2)连接CB交EF于点M,连接AM交OC于点R,连接AC,求△ACR的周长;(3)设G(4,-5)在该抛物线上,P是y轴上一动点,过点P作PH⊥EF于点H,连接AP,GH,问AP+PH +HG是否有最小值?如果有,求出点P的坐标;如果没有,请说明理由.【答案】见解析.【解析】解:(1)∵四边形OCEF为矩形,OF=2,EF=3,∴C (0,3),E (2,3).将C (0,3),E (2,3)代入y=-x2+bx+c得:b=2,c=3,∴抛物线的解析式为:y=-x2+2x+3;(2)在y=-x2+2x+3中,当y=0时,x1=-1,x2=3,∴A(-1,0),B(3,0),∵AO=1,CO=3,∴在Rt△AOC中,由勾股定理得:AC ∵CO=BO=3,∴∠OBC=∠OCB=45°,∴FM=BF=1,∵RO∥MF,∠RAO=∠MAF,∴△ARO∽△AMF,∴RO AOMF AF=,得RO=13,∴CR=OC-OR=3-13=83,AR,∴△ACR的周长为:AC+CR+AR=83+;(3)取OF中点A′,连接A′G交直线EF的延长线于点H,过点H作HP′⊥y轴于点P′,连接AP′,当P在P′处时,AP+PH+HG最小,A′(1,0),设直线A′G的解析式为:y=kx+m,将G(4,-5),A′(1,0)代入得:k=53-,b=53,∴直线A′G的解析式为:y=53-x+53.当x=2时,y=53 -,即点H的坐标为(2,53 -),∴符合题意的点P的坐标为(0,53 -).9. (2019·郑州联考)如图,在平面直角坐标系中,抛物线y2x-与x轴交于A,C(A在C 的左侧),点B 在抛物线上,其横坐标为1,连接BC ,BO ,点F 为OB 中点.(1)求直线BC 的函数表达式;(2)若点D 为抛物线第四象限上的一个动点,连接BD ,CD ,点E 为x 轴上一动点,当△BCD 的面积的最大时,求点D 的坐标,及|FE ﹣DE |的最大值.【答案】见解析.【解析】解:(1)在y2x -y =0,解得:x 1=32,x 2=72, ∴A (32,0),C (72,0) 当x =1时,y =即B (1,,设直线BC 的解析式为y =kx +b得:702k b k b ⎧+=⎪⎨+=⎪⎩,解得5k b ⎧=⎪⎪⎨⎪=⎪⎩, 直线BC 的解析式为y=x. (2)设点D (m,255-+),则点H (m,5-m+5) 过点D 作DH ⊥x 轴交BC 于点H ,HD =5-m +5﹣(255-+)=294m ⎫-+⎪⎝⎭ S △BCD =12×DH ×(x C -x B ) =54DH , ∴当m =94时,HD 取最大值,此时S △BCD 的面积取最大值.此时D (94. 作D 关于x 轴的对称点D ′则D ′(94), 连接D ′H 交x 轴于一点E ,此时|D ′E ﹣FE |最大,最大值为D ′F 的长度,∵F (12)∴D ′F ,即|FE ﹣DE |. 10.(2019·三门峡一模)反比例函数k y x=(k 为常数,且k ≠0)的图象经过点A (1,3),B (3,m ). (1)求反比例函数的解析式及点B 的坐标;(2)在x 轴上找一点P ,使P A +PB 的值最小,求满足条件的点P 的坐标.【答案】见解析.【解析】解:(1)将点A(1,3)代入kyx=得:k=3,即反比例函数解析式为:3yx =,将点B(3,m)代入3yx=得:m=1,即B(3,1).(2)作点A关于x轴的对称点A’(1,-3),连接A’B交x轴于点P,此时P A+PB最小,如图所示,设直线A’B的解析式为:y=kx+b,∴331k bk b+=-⎧⎨+=⎩,解得:25kb=⎧⎨=-⎩,即直线A’B的解析式为:y=2x-5,当y=0时,x=52,即P(52,0).ABO x y。
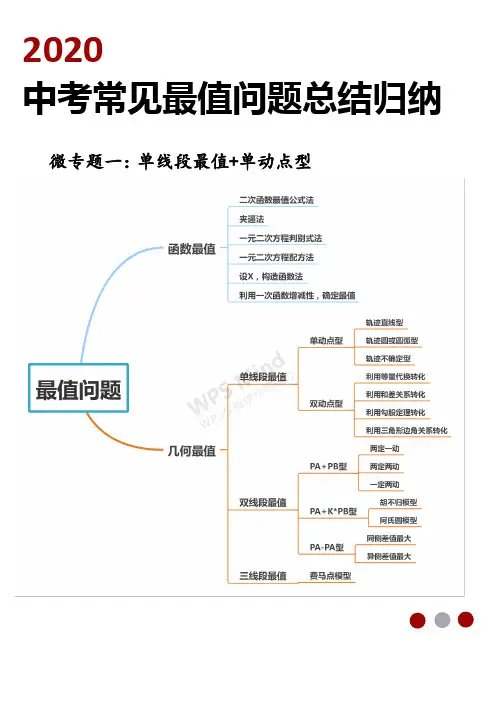
2020中考常见最值问题总结归纳微专题一:单线段最值+单动点型WORKINGPLAN微专题一:单线段最值+单动点型类型一:动点轨迹--直线型考法指导动点轨迹为一条直线时,利用“垂线段最短”求最值。
(1)当动点轨迹确定时可直接运用垂线段最短求最值(2)当动点轨迹不易确定是直线时,可通过以下三种方法进行确定①观察动点运动到特殊位置时,如中点,端点等位置时是否存在动点与定直线的端点连接后的角度不变,若存在该动点的轨迹为直线。
②当某动点到某条直线的距离不变时,该动点的轨迹为直线。
③当一个点的坐标以某个字母的代数式表示时,若可化为一次函数,则点的轨迹为直线。
【典例精析】例题1.(2020·全国初三单元测试)如图,矩形ABCD 中,4AB =,6BC =,点P 是矩形ABCD 内一动点,且∆∆=PAB PCD S S ,则PC PD +的最小值为_____.【答案】【详解】 ABCD 为矩形,AB DC ∴=又=PAB PCD S S∴点P 到AB 的距离与到CD 的距离相等,即点P 线段AD 垂直平分线MN 上,连接AC ,交MN 与点P ,此时PC PD +的值最小,且PC PD AC +====故答案为:【针对训练】1.(2018·湖北中考真题)如图,等腰Rt △ABC 中,斜边AB 的长为2,O 为AB 的中点,P 为AC 边上的动点,OQ ⊥OP 交BC 于点Q,M 为PQ 的中点,当点P 从点A 运动到点C 时,点M 所经过的路线长为( )A.4 B.2 C .1 D .2【答案】C【详解】连接OC ,作PE ⊥AB 于E,MH ⊥AB 于H,QF ⊥AB 于F ,如图,∵△ACB 为到等腰直角三角形,∴AC=BC=2,∠A=∠B=45°, ∵O 为AB 的中点,∴OC ⊥AB,OC 平分∠ACB,OC=OA=OB=1,∴∠OCB=45°,∵∠POQ=90°,∠COA=90°,∴∠AOP=∠COQ,在Rt △AOP 和△COQ 中A OCQ AO COAOP COQ ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴Rt △AOP ≌△COQ,∴AP=CQ,易得△APE 和△BFQ 都为等腰直角三角形,∴∴PE+QF=2,CQ+BQ,=2BC=2 ∵M 点为PQ 的中点,∴MH 为梯形PEFQ 的中位线,∴MH=12,PE+QF,=12, 即点M 到AB 的距离为12, 而CO=1,∴点M 的运动路线为△ABC 的中位线,∴当点P 从点A 运动到点C 时,点M 所经过的路线长=12AB=1, 故选C,2.(2017·江苏中考真题)如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为______,【答案】【详解】解:如图,由题意可知点C运动的路径为线段AC′,点E运动的路径为EE′,由平移的性质可知AC′=EE′,在Rt,ABC′中,易知AB=BC′=6,,ABC′=90°,,EE′=AC故答案为:3.如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;(2)连接AE,当AE的长最小时,求CD的长.【答案】(1)见解析;(2)【详解】解:(1)补全图形如图1所示,AD=BE,理由如下:∵∵ABC是等边三角形,∵AB=BC=AC,∵A=∵B=60°,由旋转的性质得:∵ACB=∵DCE=60°,CD=CE,∵∵ACD=∵BCE,∵∵ACD∵∵BCE(SAS),∵AD=BE.(2)如图2,过点A作AF∵EB交EB延长线于点F.∵∵ACD∵∵BCE,∵∵CBE=∵A=60°,∵点E的运动轨迹是直线BE,根据垂线段最短可知:当点E与F重合时,AE的值最小,此时CD=CE=CF,∵∵ACB=∵CBE=60°,∵AC∵EF,∵AF∵BE,∵AF∵AC,在Rt∵ACF中,,∵CD=CF=类型二:动点轨迹--圆或圆弧型考法指导动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。


2020中考数学几何专题突破模块四:动点最值问题1.(2019·安徽中考真题)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是()A.0 B.4 C.6 D.82.(2018·贵州中考真题)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG 长的最小值为_____.3.(2019·吉林中考真题)如图,在矩形ABCD 中,4,3AD cm AB cm ==,E 为边BC 上一点,BE AB =,连接AE .动点P Q 、从点A 同时出发,点P 以2/cm s 的速度沿AE 向终点E 运动;点Q 以2/cm s 的速度沿折线AD DC -向终点C 运动.设点Q 运动的时间为()x s ,在运动过程中,点P ,点Q 经过的路线与线段PQ 围成的图形面积为()2y cm .⑴AE =________cm ,EAD ∠=________°;⑵求y 关于x 的函数解析式,并写出自变量x 的取值范围; ⑶当54PQ cm =时,直接写出x 的值.4.(2019·湖北中考真题)如图,AB 是O 的直径,M 、N 是弧AB (异于A 、B )上两点,C 是弧MN 上一动点,ACB ∠的角平分线交O 于点D ,BAC ∠的平分线交CD 于点E .当点C 从点M 运动到点N 时,则C 、E 两点的运动路径长的比是( )A 2B .2πC .32D 55.(2019·湖南中考真题)如图,点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA (不包括端点)上运动,且满足AE CG =,AH CF =. (1)求证:AEH CGF ∆≅∆;(2)试判断四边形EFGH 的形状,并说明理由.(3)请探究四边形EFGH 的周长一半与矩形ABCD 一条对角线长的大小关系,并说明理由.6.(2020·湖南)如图,△ABC 中,AB =AC =10,tanA =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则55CD BD +的最小值是( )A .25B .45C .53D .107.(2019·陕西中考真题)如图,在正方形ABCD 中,AB=8,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且BM=6. P 为对角线BD 上一点,则PM —PN 的最大值为___.8.(2019·南省衡阳市)如图,在等边△ABC中,AB=6cm,动点P从点A出发以l cm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为以t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.(1)当t为何值时,△BPQ为直角三角形;(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;(3)求DE的长;(4)取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B′PM,连接AB′,当t 为何值时,AB'的值最小?并求出最小值.9.(2019•吉林省长春市)如图,在Rt△ABC中,∠C=90°,AC=20,BC=15.点P从点A 出发,沿AC向终点C运动,同时点Q从点C出发,沿射线CB运动,它们的速度均为每秒5个单位长度,点P到达终点时,P、Q同时停止运动.当点P不与点A、C重合时,过点P作PN⊥AB于点N,连结PQ,以PN、PQ为邻边作□PQMN.设□PQMN与△ABC重叠部分图形的面积为S,点P的运动时间为t秒.(1)①AB的长为;②PN的长用含t的代数式表示为.(2)当□PQMN为矩形时,求t的值;(3)当□PQMN与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式;(4)当过点P且平行于BC的直线经过□PQMN一边中点时,直接写出t的值.10.(2019•江苏省苏州市)已知矩形ABCD 中,AB =5cm ,点P 为对角线AC 上的一点,且AP =25cm .如图①,动点M 从点A 出发,在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s ),APM ∆的面积为S (cm ²),S 与t 的函数关系如图②所示:(1)直接写出动点M 的运动速度为 /cm s ,BC 的长度为 cm ;(2)如图③,动点M 重新从点A 出发,在矩形边上,按原来的速度和方向匀速运动.同时,另一个动点N 从点D 出发,在矩形边上沿着D C B →→的方向匀速运动,设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C ),动点M 、N 相遇后立即停止运动,记此时APM DPN ∆∆与的面积为()()2212,S cm S cm .①求动点N 运动速度()/v cm s 的取值范围;②试探究12S S ⋅是否存在最大值.若存在,求出12S S ⋅的最大值并确定运动速度时间x 的值;若不存在,请说明理由.①(图)PBCDAS (cm²)t (s )②图O2.57.511.(2019•江苏省扬州市)如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG 运动,点Q沿折线BC﹣CG运动(与点G不重合),在运动过程中始终保持线段PQ∥A B.设PQ与AB之间的距离为x.(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为;②在运动过程中,求四边形AMQP的最大面积;(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.12.(2019•山东省青岛市)已知:如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD垂直平分A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t(s)(0<t<5),解答下列问题:(1)当t为何值时,点E在∠BAC的平分线上?(2)设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.13.(2019•天津市)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB 相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;②当3≤S≤53时,求t的取值范围(直接写出结果即可).。


专题 09 动点类题目图形最值问题研究题型一:矩形中的相似求解例 1.( 2019·绍兴) 如图,矩形 ABCD 中, AB=a , BC=b ,点 M 、 N 分别在边 AB 、 CD上,点 E 、 F 分别在边 BC 、 AD 上, MN 、EF 交于点 P. 记 k=MN:EF.( 1)若 a : b 的值为 1,当 MN ⊥ EF 时,求 k 的值 .( 2)若 a : b 的值为 1,求 k 的最大值和最小值 .2( 3)若 k 的值为 3,当点 N 是矩形的极点,∠MPE =60°, MP=EF=3 PE 时,求 a :b 的值 .AFD NMBEC题型二:二次函数中几何图形最值求解 例 2.( 2019·衡阳) 如图,二次函数y =x 2+bx+c 的图象与 x 轴交于点 A (﹣ 1, 0)和点 B(3, 0),与 y 轴交于点 N ,以 AB 为边在 x 轴上方作正方形 ABCD ,点 P 是 x 轴上一动点,连接 CP ,过点 P 作 CP 的垂线与y 轴交于点 E .(1)求该抛物线的函数关系表达式;(2)当点 P 在线段 OB (点 P 不与 O 、B 重合)上运动至哪处时,线段OE 的长有最大值?并求出这个最大值;( 3)在第四象限的抛物线上任取一点M ,连接 MN 、MB .请问: △ MBN 的面积可否存在最大值?若存在,求出此时点M 的坐标;若不存在,请说明原由.题型三:二次函数中面积最值的求解例 3.( 2019·自贡)如图,已知直线AB 与抛物线C : y ax 2 2x c 订交于点A( -1,0)和点 B( 2,3)两点 .(1)求抛物线 C 函数表达式;(2)若点 M 是位于直线AB 上方抛物线上的一动点,以MA、MB为相邻的两边作平行四边形 MANB ,当平行四边形 MANB 的面积最大时,求此时平行四边形MANB 的面积 S 及点 M的坐标;(3)在抛物线 C 的对称轴上可否存在定点F,使抛物线 C 上任意一点 P 到点 F 的距离等于到直线y 17F 的坐标;若不存在,请说明原由 .的距离,若存在,求出定点4题型四:反比率函数中面积最值的求解例 4.( 2018·扬州一模)如图1,反比率函数y= k( x> 0)的图象经过点A( 23, 1),射x线 AB 与反比率函数图象交于另一点B( 1,a),射线 AC 与 y 轴交于点C,∠ BAC=75°,AD ⊥ y 轴,垂足为 D .(1)求 k 的值;(2)求 tan∠ DAC 的值及直线AC 的解析式;(3)如图 2, M 是线段 AC 上方反比率函数图象上一动点,过M 作直线 l⊥ x 轴,与 AC 相交于点 N,连接 CM,求△ CMN 面积的最大值.题型五:反比率函数中面积最值的求解例 5.( 2019·达州)如图 1,已知抛物线 y=- x2+bx+c 过点 A(1,0), B(- 3,0).(1)求抛物线的解析式及其极点 C 的坐标;(2)设点 D 是 x 轴上一点,当tan(∠ CAO+∠ CDO ) =4 时,求点 D 的坐标;(3)如图 2,抛物线与 y 轴交于点 E,点 P 是该抛物线上位于第二象限的点,线段PA 交BE 于点 M,交 y 轴于点 N,△ BMP 和△ EMN 的面积分别为m、 n,求 m- n 的最大值 .题型六:二次函数中最值及最短路径题型例 6.(2019·绵阳)在平面直角坐标系中,将二次函数y=ax2( a>0)的图象向右平移 1 个单位,再向下平移 2 个单位,获取以以下图的抛物线,该抛物线与x 轴交于点 A、 B(点 A 在点 B 的左侧),OA=1,经过点 A 的一次函数 y=kx+b( k≠0)的图象与 y 轴正半轴交于点C,且与抛物线的另一个交点为D,△ ABD 的面积为 5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点 E 在一次函数的图象下方,求△ACE 面积的最大值,并求出此时点E 的坐标;(3)若点 P 为 x 轴上任意一点,在( 2)的结论下,求PE+ 3PA 的最小值.5例 7.( 2019·潍坊)如图,在平面直角坐标系xoy 中, O 为坐标原点,点A( 4, 0),点 B (0, 4),△ ABO 的中线 AC 与 y 轴交于点 C,且⊙M 经过 O, A, C 三点.(1)求圆心 M 的坐标;(2)若直线 AD 与⊙ M 相切于点 A,交 y 轴于点 D,求直线 AD 的函数表达式;(3)在过点 B 且以圆心M 为极点的抛物线上有一动点P,过点 P 作 PE∥ y 轴,交直线AD 于点 E.若以 PE 为半径的⊙ P 与直线 AD 订交于另一点 F .当 EF = 4 5 时,求点 P 的坐标.答案与解析题型一:矩形中的相似求解例1.( 2019·绍兴)如图,矩形 ABCD 中, AB=a, BC=b,点 M、 N 分别在边 AB、 CD 上,点 E、 F 分别在边BC、 AD 上, MN 、EF 交于点 P. 记 k=MN:EF.(1)若 a: b 的值为 1,当 MN ⊥ EF 时,求 k 的值 .(2)若 a: b 的值为1,求 k 的最大值和最小值 . 2( 3)若 k 的值为 3,当点 N 是矩形的极点,∠MPE =60°, MP=EF=3 PE 时,求 a:b 的值.A FDNMB E C【解析】( 1)当 a: b=1 时,可得四边形ABCD 为正方形,由MN ⊥ EF ,可证 MN =EF ,即 k=1;( 2)先确定 MN 和 EF 的取值范围,当 MN 取最大值, EF 取最小值时, k 的值最大,否则反之;( 3)依照 N 是矩形极点,分两种情况谈论,即N 分别与 D 点和 C 点重合,依照不同样图形求解 .【答案】见解析.【解析】解:( 1)当 a:b=1 时,即 AB=BC,∵四边形 ABCD 是矩形,∴四边形 ABCD 是正方形,过 F 作 FG ⊥ BC 于 G,过 M 作 MH ⊥CD 于 H,以以下图所示,A FDNMHBG E C ∵MN⊥ EF ,∴∠ NMH =∠ EFG ,∵∠ MHN =∠ FGE =90°, MH =FG ,∴△ MNH ≌△ FEG ,∴MN=EF ,即 k=1;( 2)由题意知: b=2a,所以得: a≤EF ≤5a,2a≤MN ≤5a ,所以当 MN 取最大值, EF 取最小值时, k 取最大值,为 5 ;25当 MN 取最小值, EF 取最大值时, k 取最小值,为;5( 3)以以下图所示,A F DP NMBEC连接 FN ,ME,设PE=x,则 EF =MP=3x, PF=2x,MN =3EF=9 x, PN=6x,∴PF PN PE PM又∵∠ FPN =∠ MPE,∴△ FPN∽△ EPM ,∴∠ PFN=∠ PEM,∴FN∥ ME ,①当 N 点与 D 点重合时,由FN ∥ ME 得, M 点与 B 点重合,AF(N)DP HB C (M )E过F 作 FH ⊥ BD 于 H ,∵∠ MPE=60°,∴∠ PFH =30°,∴ PH=x , FH = 3x , BH=BP+PH=4x , DH =5x ,在 Rt △ DFH 中, tan ∠FDH =3 ,5即 a:b=3;5②当 N 点与 C 点重合时,过A FDM H PBE(N ) C过点 E 作 EH ⊥ MN 于 H ,连接 EM ,则 PH =x ,EH= 3x , CH=PC+PH =13x ,在 Rt △ ECH 中, tan ∠ECH =3 , 13∵ ME ∥ FC ,∴∠ MEB=∠ FCB=∠ CFD ,∵∠ B=∠ D ,∴△ MEB ∽△ CFD ,∴CD FC=2,MB MECD 2BM 2 3即 a:b=BC;BC13综上所述, a:b 的值为3 或 2 3 .513题型二:二次函数中几何图形最值求解例 2.( 2019·衡阳) 如图,二次函数y =x 2+bx+c 的图象与 x 轴交于点 A (﹣ 1, 0)和点 B(3, 0),与 y 轴交于点 N ,以 AB 为边在 x 轴上方作正方形 ABCD ,点 P 是 x 轴上一动点,连接 CP ,过点 P 作 CP 的垂线与 y 轴交于点 E .(1)求该抛物线的函数关系表达式;(2)当点 P 在线段 OB (点 P 不与 O 、B 重合)上运动至哪处时,线段OE 的长有最大值?并求出这个最大值;( 3)在第四象限的抛物线上任取一点M ,连接 MN 、MB .请问: △ MBN 的面积可否存在最大值?若存在,求出此时点M 的坐标;若不存在,请说明原由.【解析】( 1)将点 A 、B 的坐标代入二次函数解析式求解; ( 2)由 △ POE ∽△ CBP 得出比率 线段,可表示 OE 的长,利用二次函数的性质可求出线段 OE 的最大值;(3)过点 M 作 MH ∥ y轴交 BN 于点 H ,由 S △MNB =S △BMH +S △MNH 即可求解. 【答案】见解析 .【解析】解:( 1) ∵抛物线 y = x 2+bx+c 经过 A (﹣ 1, 0), B ( 3, 0),1 b c 09 3bc ,0 解得:b 2 c,3抛物线函数关系表达式为y = x 2﹣2x ﹣ 3;( 2)由题意知: AB = OA+OB = 4,在正方形 ABCD 中, ∠ ABC = 90°, PC ⊥ BE , ∴∠ OPE+∠ CPB = 90°,∠CPB +∠ PCB = 90°, ∴∠ OPE =∠ PCB ,又∵∠ EOP = ∠ PBC = 90°,∴△ POE ∽△ CBP ,∴BC OP ,BP OE∴4 x , 3 xOE2∴OE =1x 2 3x1 x 3 9 ,44 216当 x3时,即 OP =3时线段 OE 长有最大值,最大值为9 .2216(3)存在.如图,过点 M 作 MH ∥y 轴交 BN 于点 H ,∴N 点坐标为( 0,﹣ 3),设直线 BN 的解析式为 y =kx+b ,3k b 0 ∴,b3∴直线 BN 的解析式为y =x ﹣ 3,设 M ( m , m 2﹣2m ﹣ 3),则 H ( m , m ﹣ 3), ∴MH = m ﹣ 3﹣( m 2 ﹣2m ﹣3)=﹣ m 2+3 m ,∴S △MNB =S △BMH +S △MNH =11 m 2m 2 3m3 27 ,2228∴a = 3时, △ MBN 的面积有最大值,最大值是27,此时 M 点的坐标为( 3,15).2824题型三:二次函数中面积最值的求解例 3.( 2019·自贡) 如图,已知直线 AB 与抛物线 C : y ax 2 2xc 订交于点 A ( -1,0)和点 B ( 2,3)两点 .(1)求抛物线 C 函数表达式;(2)若点 M 是位于直线 AB 上方抛物线上的一动点, 以 MA 、MB 为相邻的两边作平行四边的坐标;(3)在抛物线 C 的对称轴上可否存在定点 F ,使抛物线 C 上任意一点 P 到点 F 的距离等于到直线 y17 F 的坐标;若不存在,请说明原由 .的距离,若存在,求出定点4【答案】见解析 .【解析】解:( 1)把 A ( -1,0),B ( 2,3)代入抛物线得:a 2 c 04a 4 c 3解得a 1c 3∴抛物线的函数表达式为:y=-x 2+2x+3( 2)∵ A ( -1,0), B ( 2,3),∴直线 AB 的解析式为: y=x+1,以以下图所示,过 M 作 MN ∥ y 轴交 AB 于 N ,设 M(m,- m 2+2m+3), N(m,m+1) ,( -1< m <2)∴MN =- m 2+m+2,∴S △△△ 1x A ) MNABM =S AMN +S BMN = ( x B2∴S △ ABM =1( m 2 m 2)33 (m 1 ) 227 ,22 28∴当1 时, △ ABM 的面积有最大值 27,而 S □MANB△ ABM27 ,此时1 7 m8=2S=M (, )242 2( 3)存在,点 F (1,15)4原由以下:抛物线极点为D ,则 D ( 1,4),则极点 D 到直线 y17 的距离为 1 ,174 4设 F (1, n) 、 P(x, x 22x 3) ,设 P 到直线 y的距离为 PG.4则 PG=17( x 2 2 x3) x 22x 5 ,44∵P 为抛物线上任意一点都有 PG=PF ,∴当 P 与极点 D 重合时,也有 PG=PF .此时 PG= 1,即极点 D 到直线 y17 的距离为 1 ,44 41∴PF =DF = ,∴ F (1,15) ,4∵PG=PF ,∴PG 2=PF 2, ∵ PF 2( x 1)2(15x 2 2x 3)2( x 1)2(x 22x3 )244PG 2( x 22x 5) 2(15 43)25)2∴ (x 1)2x 2 2x 3)2 ( x 1)2( x 2 2 x (x 22x44 4整理化简可得 0x=0,∴当 F (1,15) 时,无论 x 取任何实数,均有 PG=PF .4题型四:反比率函数中面积最值的求解k例 4.( 2018·扬州一模) 如图 1,反比率函数 y= x ( x > 0)的图象经过点 A (2 3, 1),射线 AB 与反比率函数图象交于另一点 B ( 1, a ),射线 AC 与 y 轴交于点 C ,∠ BAC=75°,AD ⊥y 轴,垂足为 D . (1)求 k 的值;(2)求 tan ∠ DAC 的值及直线 AC 的解析式;(3)如图 2, M 是线段 AC 上方反比率函数图象上一动点,过 M 作直线 l ⊥ x 轴,与 AC 相交于点 N ,连接 CM ,求 △ CMN 面积的最大值.11【答案】见解析.【解析】解:( 1)∵将 A(2 3 , 1)代入反比率函数y=k ,x∴k= 2 3 ;(2)由( 1)知,反比率函数解析式为y=2 3,x∵点 B( 1, a)在反比率函数y=23 的图象上,x∴a= 2 3 ,∴点 B( 1, 2 3 )过 B 作 BE⊥ AD 于 E,以以下图所示,则AE=BE =2 3 ﹣1.∴∠ ABE=∠ BAE=45°又∵∠ BAC=75°,∴∠ DAC =30°3∴DC = tan30°·AD= 2 3 = 2,∴OC= 1,即 C( 0,﹣ 1)设直线 AC 的解析式为y=kx+b12∴ 2 3kb 1 ,b1解得k3 3 b1∴直线 AC 的解析式为 y = 3 x ﹣ 13( 3)设 M ( m ,2 3), N ( m , 3m ﹣ 1)m3则 MN =2 3- (3 m ﹣ 1)=2 3﹣ 3 m+1,m3 m 3∴S △CMN = 1 (23 ﹣ 3 m+1) m =﹣ m 2+ m+2m 3=﹣3( m ﹣ 3 ) 2+ 9 3628当 m =3时, △ CMN 的面积有最大值,最大值为9 3 .28题型五:反比率函数中面积最值的求解例 5.( 2019·达州) 如图 1,已知抛物线 y=- x 2+bx+c 过点 A(1,0), B(- 3,0).(1)求抛物线的解析式及其极点 C 的坐标;(2)设点 D 是 x 轴上一点,当tan (∠ CAO+∠ CDO ) =4 时,求点 D 的坐标;(3)如图 2,抛物线与 y 轴交于点 E ,点 P 是该抛物线上位于第二象限的点,线段PA 交BE 于点 M ,交 y 轴于点 N , △ BMP 和 △ EMN 的面积分别为 m 、 n ,求 m - n 的最大值 .【答案】见解析 .2【解析】解:( 1)把点( 1,0),(﹣ 3, 0)代入 y =﹣ x +bx+c ,得,0 1 b c , 0 9 3bc解得 b =﹣ 2, c = 3,2 2,∴y =﹣ x ﹣ 2x+3 =-( x+1) +4∴此抛物线解析式为: y =﹣ x 2﹣2x+3,极点 C 的坐标为(﹣ 1, 4);13(2)由( 1)知:抛物线对称轴为x =﹣ 1,设抛物线对称轴与x 轴交于点 H , H (﹣ 1, 0),在 Rt △ CHO 中, CH =4, OH = 1,∴ t an ∠COH = CH=4,OH∵∠ COH = ∠ CAO+∠ ACO ,∴当 ∠ ACO = ∠ CDO 时,tan ( ∠CAO+∠CDO )= tan ∠ COH = 4,以以下图所示,当点 D 在对称轴左侧时,∵∠ ACO =∠ CDO , ∠ CAO =∠ CAO ,∴△ AOC ∽△ ACD ,∴ AC AO ,AD AC∵AC = 2 5 , AO = 1,∴AD = 20, OD = 19,∴D (﹣ 19, 0);当点 D 在对称轴右侧时,点D 关于直线 x = 1 的对称点 D'的坐标为( 17, 0),∴点 D 的坐标为(﹣ 19,0)或( 17, 0);( 3)设 P ( a ,﹣ a 2﹣ 2a+3),设直线 PA 的解析式为: y=kx+b ,将 P ( a ,﹣ a 2﹣ 2a+3), A ( 1, 0)代入 y = kx+b ,ak ba 2 2a 3 k b,解得, k =﹣ a ﹣ 3, b = a+3 ,∴ y =(﹣ a ﹣ 3) x+a+3,当 x = 0 时, y = a+3,∴ N ( 0,a+3),14以以下图所示,∵m=S △ BPM = S △BPA ﹣ S 四边形 BMNO ﹣ S △AON , n=S △EMN = S △EBO ﹣ S 四边形 BMNO ,∴m - n = S △BPA ﹣ S △EBO ﹣ S △AON= 1×4×(﹣ a 2﹣ 2a+3)﹣ 1 ×3×3﹣ 1×1×( a+3) 2 2 2=﹣ 2( a+ 9 ) 2+ 81,8 32 ∴当 a =﹣ 9 时, m - n 有最大值81.832题型六:二次函数中最值及最短路径题型例 6.(2019·绵阳) 在平面直角坐标系中,将二次函数y=ax 2( a >0)的图象向右平移1 个单位,再向下平移 2 个单位,获取以以下图的抛物线,该抛物线与 x 轴交于点 A 、 B (点 A在点 B 的左侧) ,OA=1,经过点 A 的一次函数 y=kx+b ( k ≠0)的图象与 y 轴正半轴交于点 C ,且与抛物线的另一个交点为D , △ ABD 的面积为 5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点 E 在一次函数的图象下方,求 △ACE 面积的最大值,并求出此时点 E 的坐标;(3)若点 P 为 x 轴上任意一点,在(2)的结论下,求PE+ 3PA 的最小值.5【答案】见解析 .【解析】解:( 1)由平移知,平移后获取的抛物线解析式为y=a ( x-1)2 -2,∵OA=1,15∴点 A 的坐标为( -1,0),代入抛物线的解析式得, 4a-2=0 ,得: a= 1,2∴抛物线的解析式为 y1 x 1 21 x2 x3 .2 ,即 y222令 y=0,解得 x 1=-1 , x 2 =3,∴B ( 3,0),∴AB =OA +OB=4,∵△ ABD 的面积为 5,1∴S △ ABD = AB ·y D =5∴ y D = 5,25 1 x 2 x 3 ,解得 x 1=-2, x 2=4,2225∴D ( 4, ),设直线 AD 的解析式为 y=kx+b ,∴ 4kb5k12 ,2 ,解得:k b 0b1 2∴直线 AD 的解析式为: y=1x+ 1 . 2 2( 2)过点 E 作 EM ∥y 轴交 AD 于 M ,以以下图所示,设 E ( a , 1a 2- a - 3 ), M (a , 1 a+ 1),2 2 2 2∴ME = - 1a 2+ 3a+2 ,2 2∴S △ ACE =S △ AME - S △CME =- 1 ( a 2- 3a - 4) =- 1 ( a - 3 ) 2+25,44 2 1616∴当 a= 3 时, △ ACE 的面积有最大值,最大值是25,此时 E 点坐标为( 3 , 15 ).21628( 3)作 E 关于 x 轴的对称点 F ,连接 EF 交 x 轴于点 G ,过点 F 作 FH ⊥ AE 于点 H ,交轴于点 P ,∴AG = 5 , EG = 15,2 8AG 4 ∴,EG3∵∠ AGE=∠ AHP =90° ∴sin ∠= PHEG 3EAGAE,AP53∴PH = AP ,∵E 、 F 关于 x 轴对称,∴PE =PF ,3∴PE + 5 AP=FP+HP=FH ,此时 FH 最小,∵ E F =15, ∠AEG =∠ HEF ,4∴sin ∠ AEG=sin ∠ HEF =AGFH4 AEAE 5∴FH =3.即 PE+ 3PA 的最小值是3. 5例 7.( 2019·潍坊) 如图,在平面直角坐标系 xoy 中, O 为坐标原点,点A ( 4, 0),点 B( 0, 4),△ ABO 的中线 AC 与 y 轴交于点 C ,且 ⊙M 经过 O , A , C 三点.( 1)求圆心 M 的坐标;( 2)若直线 AD 与 ⊙ M 相切于点 A ,交 y 轴于点 D ,求直线 AD 的函数表达式;(3)在过点B 且以圆心 M 为极点的抛物线上有一动点 P ,过点 P 作 PE ∥ y 轴,交直线 AD于点 E .若以 PE 为半径的 ⊙ P 与直线 AD 订交于另一点 F .当 EF = 4 5 时,求点 P 的坐标.17【答案】见解析.【解答】解:( 1)∵ AC 为△ ABO 的中线,点B( 0,4),∴点 C(0, 2),∵点 A( 4, 0),点M 为线段 AC 的中点,即 M( 2, 1);(2)∵⊙P 与直线 AD ,则∠ CAD = 90°,设∠ CAO=α,则∠ CAO=∠ ODA=∠ PEH =α,tan∠ CAO=OC1αα5, cosα=25 ,OA2= tan ,则 sin=55AC= 10 ,则 CD=AC= 10,sin则 D ( 0,﹣ 8),设直线 AD 的解析式为: y= mx+n:b8得:,解得: k=2, b=- 8,4k b 0直线 AD的表达式为: y=2x﹣ 8;(3)抛物线的表达式为:y= a( x﹣ 2)2+1,3将点 B 坐标代入上式并解得:a=,故抛物线的表达式为:y=3x2﹣ 3x+4,41过点 P 作 PH ⊥ EF,则 EH =EF= 2 5 ,18(完满版)2020年中考数学动向问题图形最值问题研究(含答案) 21 / 21 cos ∠PEH = EH cos 2 5PE 5得: PE = 5,设点 P ( x , 3 x 2﹣ 3x+4),则点 E ( x ,2x ﹣ 8),4则 PE = 3 x 2﹣ 3x+4 ﹣ 2x+8=5,4解得 x = 14 或 2(舍),3则点 P ( 14 , 19 ).3 3 19。

2020中考常见最值问题总结归纳微专题一:单线段最值+单动点型WORKING PLAN微专题一:单线段最值+单动点型类型一:动点轨迹--直线型考法指导动点轨迹为一条直线时,利用“垂线段最短”求最值。
(1)当动点轨迹确定时可直接运用垂线段最短求最值(2)当动点轨迹不易确定是直线时,可通过以下三种方法进行确定 ①观察动点运动到特殊位置时,如中点,端点等位置时是否存在动点与定直线的端点连接后的角度不变,若存在该动点的轨迹为直线。
②当某动点到某条直线的距离不变时,该动点的轨迹为直线。
③当一个点的坐标以某个字母的代数式表示时,若可化为一次函数,则点的轨迹为直线。
【典例精析】例题1.(全国初三单元测试)如图,矩形ABCD 中,4AB =,6BC =,点P 是矩形ABCD 内一动点,且∆∆=PAB PCD S S ,则PC PD +的最小值为_____.【详解】ABCD为矩形,∴=AB DCS S又=PAB PCD∴点P到AB的距离与到CD的距离相等,即点P线段AD垂直平分线MN上,+的值最小,连接AC,交MN与点P,此时PC PD+====且PC PD AC故【针对训练】1.(湖北中考真题试卷)如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P 为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C 时,点M所经过的路线长为()A B C.1D.2C【详解】连接OC ,作PE ⊥AB 于E,MH ⊥AB 于H,QF ⊥AB 于F ,如图,∵△ACB 为到等腰直角三角形,∴AC=BC=2,∠A=∠B=45°, ∵O 为AB 的中点,∴OC ⊥AB,OC 平分∠ACB,OC=OA=OB=1,∴∠OCB=45°,∵∠POQ=90°,∠COA=90°,∴∠AOP=∠COQ,在Rt △AOP 和△COQ 中A OCQ AO COAOP COQ ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴Rt △AOP ≌△COQ,∴AP=CQ,易得△APE 和△BFQ 都为等腰直角三角形,∴PE=2AP=2CQ,QF=2BQ, ∴PE+QF=2,CQ+BQ,=2∵M 点为PQ 的中点,∴MH 为梯形PEFQ 的中位线,∴MH=12,PE+QF,=12,即点M到AB的距离为1 2,而CO=1,∴点M的运动路线为△ABC的中位线,∴当点P从点A运动到点C时,点M所经过的路线长=12AB=1,故选C,2.(2017·江苏中考真题试卷)如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB 方向从点A运动到点B,则点E运动的路径长为______,【详解】解:如图,由题意可知点C运动的路径为线段AC′,点E运动的路径为EE′,由平移的性质可知AC′=EE′,在Rt,ABC′中,易知AB=BC′=6,,ABC′=90°,,EE′=AC故3.如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;(2)连接AE,当AE的长最小时,求CD的长.(1)见解析;(2)【详解】解:(1)补全图形如图1所示,AD=BE,理由如下:∵∵ABC是等边三角形,∵AB=BC=AC,∵A=∵B=60°,由旋转的性质得:∵ACB=∵DCE=60°,CD=CE,∵∵ACD=∵BCE,∵∵ACD∵∵BCE(SAS),∵AD=BE.(2)如图2,过点A作AF∵EB交EB延长线于点F.∵∵ACD∵∵BCE,∵∵CBE=∵A=60°,∵点E的运动轨迹是直线BE,根据垂线段最短可知:当点E与F重合时,AE的值最小,此时CD=CE=CF,∵∵ACB=∵CBE=60°,∵AC∵EF,∵AF∵BE,∵AF∵AC,在Rt∵ACF中,,∵CD=CF=类型二:动点轨迹--圆或圆弧型考法指导动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。
![(完整版)初中数学[最短路径问题]典型题型及解题技巧](https://uimg.taocdn.com/078676f277a20029bd64783e0912a21614797f76.webp)
(完整版)初中数学[最短路径问题]典型题型及解题技巧初中数学[最短路径问题]典型题型及解题技巧最短路径问题中,关键在于,我们善于作定点关于动点所在直线的对称点,或利用平移和展开图来处理。
这对于我们解决此类问题有事半功倍的作用。
理论依据:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”“立体图形展开图”。
教材中的例题“饮马问题”,“造桥选址问题”“立体展开图”。
考的较多的还是“饮马问题”。
知识点:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
一、两点在一条直线异侧例:已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
解:连接AB,线段AB与直线L的交点P ,就是所求。
(根据:两点之间线段最短.)二、两点在一条直线同侧例:图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A 关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C 就是所求的点.三、一点在两相交直线内部例:已知:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.解:分别作点A关于OM,ON的对称点A′,A″;连接A′,A″,分别交OM,ON于点B、点C,则点B、点C即为所求分析:当AB、BC和AC三条边的长度恰好能够体现在一条直线上时,三角形的周长最小例:如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)解:1.将点B沿垂直与河岸的方向平移一个河宽到E,2.连接AE交河对岸与点M,则点M为建桥的位置,MN为所建的桥。
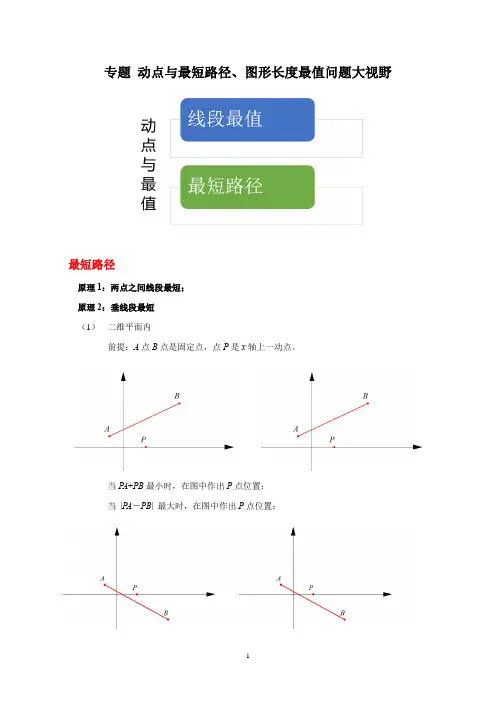
专题动点与最短路径、图形长度最值问题大视野最短路径原理1:两点之间线段最短;原理2:垂线段最短(1)二维平面内前提:A点B点是固定点,点P是x轴上一动点。
当P A+PB最小时,在图中作出P点位置;当|P A-PB| 最大时,在图中作出P点位置;当P A+PB最小时,在图中作出P点位置;当|P A-PB| 最大时,在图中作出P点位置;(2)立体图形中常见的有立方体、长方体、楼梯、树木绕绳问题解决方法:将立体图形曲面展开成平面图形,标出起始位置,借助勾股定理求解。
题型一、线段最值问题例1. 【2019·福州市晋安区期末】如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,点E是AB上的点,以AC为对角线的平行四边形AECF,则EF的最小值是()A.5B.4C.1.5D.3【答案】D.【解析】解:∵在Rt△ABC中,∠B=90°,∴BC⊥AB,∵四边形AECF是平行四边形,∴OE=OF,OA=OC,∴当OE取最小值时,线段EF最短,此时OE⊥AB,即OE是△ABC的中位线,∴OE=12BC=1.5,∴EF=2OE=3,即EF的最小值是3.故答案为:D.例2. 【2019·宿迁市期末】在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为______cm.【答案】24 5.【解析】解:∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴△ABC为直角三角形,∠A=90°,∵PE⊥AB于E,PF⊥AC于F,∴∠AEP=∠AFP=90°,∴四边形AEPF为矩形,连接AP,如图,EF=AP,当AP⊥BC时,AP的值最小,此时AP=245,∴EF的最小值为245.例3. 【2019·宜昌市期中】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是()A.2B.6C.﹣2D.4【答案】A.【解析】解:由题意知,点B’的轨迹是以E为圆心,BE的长为半径的圆弧,当B’、E、D共线时,B’D的值最小,最小值为:DE-BE2,故答案为:A.例4. 【2109·福州市期中】如图,平面内三点A、B、C,AB=4,AC=3,以BC 为对角线作正方形BDCE,连接AD,则AD的最大值是.【答案】2【解析】解:将△BAD绕点D顺时针旋转90°,得到△DCM,易证,△ADM是等腰直角三角形,AD=AM,2当A、C、M共线时,且C在A、M之间时,AM的长度最大,最大为7,∴AD.例5. 【2019·厦门大学附中期末】如图,在平面直角坐标系中,已知A(2,0),B(5,0),点P为线段AB外一动点,且P A=2,以PB为边作等边△PBM,则线段AM的最大值为()A.3B.5C.7D【答案】B.【解析】解:如图,点P 的轨迹为以A 为圆心,以OA 为半径的圆,点M 的轨迹为以点O ’为圆心以EF 的长为直径的圆,∴O ′(72), ∴AO ′=3,当点M 在AO ′的延长线上时,AM 的值最大,最大值为3+2=5,故答案为:B .题型二、最短路径问题例1.【2019·十堰市外国语期末】如图,在菱形ABCD 中,对角线AC =8,BD =6,点E ,F 分别是边AB ,BC 的中点,点P 在AC 上运动,在运动过程中,存在PE +PF 的最小值,则这个最小值是( )A .3B .4C .5D .6【答案】C .【解析】解:设AC 交BD 于O ,作E 关于AC 的对称点N ,连接NF ,交AC 于P ,则此时EP +FP 的值最小,∴PN =PE ,∵四边形ABCD是菱形,∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,∵E为AB的中点,∴N在AD上,且N为AD的中点,∵AD∥CB,∴∠ANP=∠CFP,∠NAP=∠FCP,∵AD=BC,N为AD中点,F为BC中点,∴AN=CF,∴△ANP≌△CFP,∴AP=CP,即P为AC中点,∵O为AC中点,∴P、O重合,即NF过O点,∵AN∥BF,AN=BF,∴四边形ANFB是平行四边形,∴NF=AB,∵AC⊥BD,OA=12AC=4,BO=12BD=3,由勾股定理得:AB=2+BO2=5,故答案为:C.例2. 【2019·厦门市期中】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△P AB=13S矩形ABCD,则点P到A、B两点之间的距离之和P A+PB的最小值是【答案】【解析】解:设△ABP边BA上的高为h,∵S△P AB=13S矩形ABCD,∴h=2,即动点P的运动轨迹是与AB平行,且与AB距离为2的直线,不妨设这条直线为l,作A点关于直线l的对称点E,连接AE,BE,则BE的长度即为所求的最短距离,由勾股定理,得:BE=即P A+PB的最小值是故答案为:例3. 【2019·遵义市期中】如图,已知圆柱底面的周长为6cm,圆柱高为3cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()cm.A.B.C D.6【答案】B.【解析】解:如图,把圆柱的侧面展开,得到矩形,这圈金属丝的周长最小为2AC的长度.由题意得:AB=3cm,BC=BC′=3cm,∴AC=cm,这圈金属丝的周长最小值为:2AC=cm.故答案为:B.例4. 【2019·北京101中学期末】如图,在△ABC中,AB=BC=4,S△ABC=P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为______.【答案】【解析】解:命题:在直角三角形中,若一条直角边是斜边长的一半,则该直角边所对的角为30°(证明略);如图,过点A作AH⊥BC交CB的延长线于H,∵AB=CB=4,S△ABC=,∴AH=,∴∠HAB=30°,∠ABH=60°,∴∠ABC=120°,∵∠BAC=∠C=30°,作点P关于直线AC的对称点P′,过P′作P′Q⊥BC于Q交AC于K,则P′Q的长度=PK+QK的最小值,∴∠P′AK=∠BAC=30°,∴∠HAP′=90°,∴∠H=∠HAP′=∠P′QH=90°,∴四边形AP′QH是矩形,∴P′Q=AH=即PK+QK的最小值为,故答案为:【刻意练习】1. 【2019·抚顺市期中】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为.【答案】125.【解析】连接BP∵∠B=∠D=90°,AD=3,CD=4,∴AC=5,∵PE⊥BC于点E,PF∥BC,∠B=90°,∴四边形PEBF是矩形;∴EF=BP,由垂线段最短可得BP⊥AC时,线段EF的值最小,1 2BC•AB=12AC•CP,即12×4×3=12×5•CP,CP=125.故答案为:125.2. 【2019·鞍山市期末】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.B.25C.+5D.35【答案】B.【解析】解:将长方体展开,连接A、B,根据两点之间线段最短,(1)如图,BD=10+5=15,AD=20,由勾股定理得:AB=25.(2)如图,BC=5,AC=20+10=30,由勾股定理得,AB=(3)如图:BD=CD+BC=20+5=25,AD=10,由勾股定理得:AB=由于25<故答案为:B.3. 【2019·临洮县期中】如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F 是AC上一动点,则EF+BF的最小值为.【解析】解:连接DB,DE,设DE交AC于M,连接MB,DF,∵四边形ABCD是菱形,∴AC,BD互相垂直平分,∴点B关于AC的对称点为D,∴FD=FB,∴FE+FB=FE+FD≥DE,所以当点F运动到点M时,取等号,△ABD是等边三角形,E为AB的中点,∴DE⊥AB,∴AE =12AD =1,DE∴EF +BF4. 【2019·成都市期末】如图,△ABC ,△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,将△ADE 绕点A 在平面内自由旋转,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点,若AD =3,AB =7,则线段MN 的取值范围是______.【答案】MN ≤≤【解析】解:∵点P ,M 分别是CD ,DE 的中点,∴PM =12CE ,PM ∥CE ,同理,PN =12BD ,PN ∥BD ,∵△ABC ,△ADE 均为等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,∴△ABD ≌△ACE (SAS ),∴BD =CE ,∴PM =PN ,∴△PMN 是等腰三角形,∵PM ∥CE ,PN ∥BD ,∴∠DPM =∠DCE ,∠PNC =∠DBC ,∵∠DPN =∠DCB +∠PNC =∠DCB +∠DBC ,∴∠MPN =∠DPM +∠DPN=∠DCE +∠DCB +∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC=90°,∴△PMN是等腰直角三角形,∴PM=PN=12 BD,∴MN=2BD,∴点D在线段AB上时,BD最小,最小值为4,MN的最小值点D在BA延长线上时,BD最大,最大值为10,MN的最大值为,故答案为:MN≤≤5. 【2019·武汉市期末】如图,在菱形ABCD中,E为AB中点,P是BD上一个动点,则下列线段的长度等于P A+PE最小值的是()A.BCB.CEC.DED.AC【答案】B.【解析】解:在菱形ABCD中,A与C关于直线BD对称,连接EC,与BD交于点P,此时P A+PE=CP+EP=CE值最小,故答案为:B.6. 【2019·固始县期末】如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是()A.3√1+πB.3√2D.3√1+π2C.3√4+π22【答案】C.【解析】解:(1)蚂蚁可以沿A-B-C的路线爬行,AB+BC=6,(2)把圆柱侧面展开,展开图如图所示,在Rt△ADC中,∠ADC=90°,CD=AB=3,AD=1.5π,AC=√AD2+CD2=3√4+π2<6,2故答案为:C.7. 【2019·黄石期中】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为()B.√2C.2√2D.3√2A.2【答案】A.【解析】解:如图,作EH⊥x轴于H,连接CE,∵∠AOD=∠ADE=∠EHD=90°,∴∠ADO+∠EDH=90°,∠EDH+∠DEH=90°,∴∠ADO=∠DEH,∵AD=DE,∴△ADO≌△DEH(AAS),∴OA=DH=OC,OD=EH,∴OD=CH=EH,∴∠ECH=45°,过点O作OE′⊥CE,则△OCE′是等腰直角三角形,∵OC=3,∴OE′=由垂线段最短,知OE故答案为:A.8.【2019·广州市番禺区期末】如图一个圆柱,底圆周长10cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行______cm.【解析】解:将圆柱展开,侧面为矩形,如图所示:∵底面圆的周长为10cm,∴AC=5cm,∵高BC=4cm,∴AB=√AC2+BC2=√41cm.故答案为:√41.9. 【2019·桑植县期末】如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.(1)若直线AB解析式为y=-2x+12,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.【答案】见解析.【解析】解:(1)①联立y=-2x+12,y=x,解得:x=y=4,即点C的坐标为(4,4);②在y=-2x+12中,当x=0时,y=12,当y=0时,-2x+12=0,x=6,∴点B(0,12),A(6,0),则△OAC的面积为:12×6×4=12;(2)∵ON平分∠AOC,AB⊥ON,∴ON是线段AC的垂直平分线,∴AQ=CQ,∴AQ+PQ=CQ+PQ,当C、Q、P共线,且CP⊥OA时,AQ+PQ取最小值,最小值为△OAC边OA上的高,∵△OAC的面积为6,OA=4,∴△OAC边OA上的高=2×6÷4=3.∴AQ+PQ存在最小值,最小值为3.10.【2019·泉州市期末】已知:AC是菱形ABCD的对角线,且AC=BC.(1)如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.①求证:△PBE是等边三角形;②若BC=5,CE=4,PC=3,求∠PCE的度数;(2)连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值.【答案】见解析.【解析】解:(1)①∵四边形ABCD是菱形∴AB=BC,∵AC=BC,∴AB=BC=AC,∴△ABC等边三角形,∴∠ABC=60°,由旋转知BP=BE,∠PBE=∠ABC=60°,∴△PBE是等边三角形;②由①知AB=BC=5,由旋转知△ABP≌△CBE,∴AP=CE=4,∠APB=∠BEC,∵AP2+PC2=42+32=25=AC2,∴△ACP是直角三角形,∴∠APC=90°,∴∠APB+∠BPC=270°,∵∠APB=∠CEB,∴∠CEB+∠BPC=270°,∴∠PBE+∠PCE=90°,∵∠PBE=∠ABC=60°,∴∠PCE=90°-60°=30°;(2)如图,将△ADG绕着点D顺时针旋转60°得到△A'DG',由旋转知△ADG≌△A'DG',∴A'D=AD=4,G'D=GD,A'G'=AG,∵∠G'DG=60°,G'D=GD,∴△G'DG是等边三角形,∴GG'=DG,∴AG+EG+DG=A'G'+EG+GG'∵当A'、G'、G、E四点共线时,A'G'+EG+G'G的值最小,即AG+EG+DG的值最小,∵∠A'DA=60°,∠ADE=12∠ADC=30°,∴∠A'DE=90°,∴AG+EG+DG=A'G'+EG+G'G=A'E=5,∴AG+EG+DG的最小值为5.11.【2019·宿迁市期末】如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.(1)点A坐标为______;点B坐标为______;点C坐标为______;(2)画出△ABC关于原点对称的△A1B1C1;(3)已知M(1,4),在x轴上找一点P,使|PM-PB|的值最大(写出过程,保留作图痕迹),并写出点P 的坐标______.【答案】(1)(-1,0);(-2,-2);(-4,-1);(2)见解析;(3)(-5,0).【解析】解:(1)由图象可知点A(-1,0),点B(-2,-2),点C(-4,-1);(2)如图所示:(3)作点B关于x轴的对称点F(-2,2),连接MF交x轴于P,点P就是所求的点,理由:在x轴上任意取一点P1,∵|P1M-P1B|=|P1M-P1F|≤FM,∴|PM-PB|的最大值为线段FM的长度,设直线FM解析式为:y=kx+b,把F、M两点坐标代入,得:k+b=1,-2k+b=2,解得:23103kb⎧=⎪⎪⎨⎪=⎪⎩,即直线FM解析式为:y=210 33x+,当y=0时,x=-5,即点P坐标为(-5,0).故答案为:(-5,0).。
动点最值专题动点最值专题近几年有关“线段最值”的中考试题层出不穷,形式多样,往往综合了几何变换、函数等方面的知识,具有一定的难度,具有很强的探索性,通过研究发现,这些问题尽管形式多样、背景复杂、变化不断,但都可以通过几何变换转化为常见的基本问题.最值题目类型多:作图、计算;有求差最大,求和最小;求周长最小、求时间最短;求最值、已知最值求待定系数等;对称载体多:几乎涉及到初中全部的轴对称图形(角、线段、等腰三角形、等腰梯形、菱形、正方形、抛物线、圆、坐标轴).我们知道“对称、平移、旋转”是三种保形变换。
通过这三种几何变换可以实现图形在保持形状、大小不变的前提下而使其位置发生变化,具有更紧凑的位置关系或组合成新的有利论证的基本图形.通过几何变换移动线段的位置是解决最值问题的有效手段,题目是千变万化的,但是运用几何变换把最值问题转化为基本问题却是不变的。
数学问题是千变万化的,几何变换的应用也不是单一的,有些问题需要多种变换的组合才能解决,看看以下策略对解决问题能否奏效。
(1)去伪存真。
刨去不变的线段,看清楚究竟是几段和的最小值问题,必须仔细研究题目的背景,搞清楚哪些是动点、哪些是定点、哪些是定长。
(2)科学选择。
捕捉题目的信号,探索变换的基础,选择变换的手段.平移把不“连”的线段“接”起来,旋转把“碰头”的线段“展”开来重“接”,对称把在同侧的线段翻折过去重组,因此“不连——平移、碰头——旋转、同侧——对称”是一般的思路;对称变换的基础是轴对称图形,平移变换的基础是平行线,旋转变换的基础是等线段,所以选择哪种几何变换还要看题目中具备何种变换的基础信息。
(3)怎么变换?对称变换一般以动点所在直线为对称轴,构建定点(直线)的对称点(直线),如有多个动点就必须作多次变换;平移一般是移动没有公共端点的两条线段中的某一条,与另一条对“接”;旋转变换一般以定点为旋转中心旋转60°或90°。
(4)怎么求值?几何变换成了“两折线”或“三折线”后,根据“两点之间线段最短”或“垂线段最短”把“折线”转“直”,找出最短位置,求出最小值。
1专题七;最短路径一一费马点问题【导例引入】耳例:如團,拒形Ara 中.AB=2yβ9 Bc=& P 为矩形內一点,连接% PB. PC 、则【方法指引】费尔刃法国业余数学家,拥有业余数学之王的称号,也罡解析几何的发明者N —・≡5 点一一就定到三角形的三个顶点的距蔑之和最小的点〈如图;点的点F 〉・费尔马偉论:(1)对于一个各甬不超过120°的三角形,费勻点是对各边的张角都是120°的点,<2)对于有一个角超过120°的三角形,费勻点就足这个內鸽的顶点•下面筒亘说明如何找点P 使ΘJ∆ABC 三个顶点的艇冉之和PA+豚PC 悬小?这颈杲所i 胃的费尔T 问题・指引:如图2,把△佃绕/点逆时针旋转60°得到△护「,连接歹•则△/加为 等边三角形,Ap= PP , , P' C' =PC,所以丹+/+应=PP ■ F 班P ,C .点L 可看成是独段M 绕/点逆时什施转60°而得的定点,BC i 为定长,所咲当易P )F , C f 四点在同一直结上时,PA^PB^最小• 这时Z^=ISO Q -OPF =iεθ"-03^=120" , ∆APOΛA P f C =IEo Q -AAP 孩 180°- 60° =120φ > /5^360° -Z^-厶怒360° -120" -120° =120° 费2点的轨点:费巳点与3个顶点连成的线段是:勾通3点的最短路线,【导例解析分折】将△陀绕点C 逆时针旋转60° ,得到△陀,连接彤,屁,AC,则D- 4≠PA 畑PC 的最小值是(的长即为所求•庄旋传为性质可知△阮罡等丈三角形、:∙PC=PF∙•:际EF, :.PA\PB\PC=PA^FF\EF.••・当人P f F, 0共线时,刊+砂ZT的誉最小•AB 0T四边形ABCD^^->> :. ZABC=^・・・・询1厶0=荒=丁・:.ZACB=30Q, AC=2AB=4∖^.'.,Z SCF= 60o, .∙.Z用疋=90°・.∙∕5=J (“): + 6: =20.故选:B.【例题精讲】类型一;与二角形有关的费巧点例1.如團,在中,P为平面內一点、,连结必,PB, FC,分别以兀和祐为一边向右作等丈三角形HFQf^ACD.【探究】求证:Bf=PC' AO=PA【应用】若Be=SAC=E Z⅛g=60>,W l I PA^PB^的最小值罡 _ (用②0表示)【分析】【探究】生竽边三隹形的性话得出砂处AC=CD. FC=W ZPOif=A^CD=60° ,得出Z◎二上竝力证明△/加M血得^MD=PAi【应用】连接由全等三角形的性原得出AACP^ZJX2!> AC=CD-O,求出NEQ=ZZ^Zra120°、作 DFLBC 于 F ,则Z 胞=90°,在 RtAQV 7 中,由直角三1 1 yβ 1角形的性庚得出CF=2A C=⅝, DF=V 3CF=Nb,求出BF=α+⅝,由勾股定理求出M= λIBF T TEF=√α2 + αb + b∖ ,即可得出结论.类型二:与四边形有关的费耳点倂2 .已知正万形辺内一动点£到儿B t C 三点的距區之和的最小背为√7+.B,求此正方形的边长•【分析】:连按AC,发现点£到儿B f 。
2020年中考数学二轮专项复习——四边形、动点、最值问题压轴题型1、如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是。
解:【分析】连接CP,当点E,P,C在同一直线上时,AP+PE的最小值为CE长,依据△ABF≌△CDE,即可得到AP+EP最小值等于线段AF的长.如图,连接CP,由AD=CD,∠ADP=∠CDP=45°,DP=DP,可得△ADP≌△CDP,∴AP=CP,∴AP+PE=CP+PE,∴当点E,P,C在同一直线上时,AP+PE的最小值为CE长,此时,由AB=CD,∠ABF=∠CDE,BF=DE,可得△ABF≌△CDE,∴AF=CE,∴AP+EP最小值等于线段AF的长,【点评】本题考查的是轴对称,最短路线问题,根据题意作出A关于BD的对称点C是解答此题的关键.2、【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是.【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是.解:猜想:∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO,在△AOE和△COF中,,∴△AEO≌△CFO(AAS),∴四边形CDEF的面积=S△ACD=▱ABCD的面积=4;故答案为:4;探究:∵四边形ABCD是菱形,∴AD∥BC,AO=CO AC=2.5,BO=BD=5,∠AOD=90°,∴AB=AC=,∠OAE=∠OCF,∠OEA=∠OFC,在△AOE于△COF中,,∴△AOE≌△COF(AAS),∵AC⊥BD,∴S四边形ABFE=S△ABC=AC•BO=××5=.应用:延长AC到E使CE=AC=3,在△ABC与△CDE中,,∴△ABC≌△CDE(SAS),∴∠E=∠BAC=90°,∴DE=,∴S△ABD=S△ADE=AE•DE=×6×2=6.故答案为:63、如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C 沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为.【分析】首先证明DC′≠DA,只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.构建方程即可;②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件;【解答】解:由题意DE=EC=EC′=1,∴DC′<1+1∴DC′≠DA,只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.∵AE=AE,AD=AC′,DE=DC′,∴△ADE≌△AC′E,∴∠ADE=∠AC′E=90°,∵∠C=∠FC′E=90°,∴∠AC′E+∠FC′E=180°,∴A、C′、F共线,设CF=x,则BF=2﹣x,AF=2+x,在Rt△ABF中,22+(2﹣x)2=(2+x)2,解得x=.②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件,此时CF=1.综上所述,满足条件的CF的长为或1.故答案为或1.【点评】本题考查翻折变换、正方形的性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的首先思考问题,属于中考填空题中的压轴题.4、如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB ⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.(1)线段AB,BC,AC的长分别为AB=,BC=,AC=;(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答,我选择题.A:①求线段AD的长;②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.B:①求线段DE的长;②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,∴A(4,0),C(0,8),∴OA=4,OC=8,∵AB⊥x轴,CB⊥y轴,∠AOC=90°,∴四边形OABC是矩形,∴AB=OC=8,BC=OA=4,在Rt△ABC中,根据勾股定理得,AC==4,故答案为:8,4,4;(2)A、①由(1)知,BC=4,AB=8,由折叠知,CD=AD,在Rt△BCD中,BD=AB﹣AD=8﹣AD,根据勾股定理得,CD2=BC2+BD2,即:AD2=16+(8﹣AD)2,∴AD=5,②由①知,D(4,5),设P(0,y),∵A(4,0),∴AP2=16+y2,DP2=16+(y﹣5)2,∵△APD为等腰三角形,∴Ⅰ、AP=AD,∴16+y2=25,∴y=±3,∴P(0,3)或(0,﹣3)Ⅱ、AP=DP,∴16+y2=16+(y﹣5)2,∴y=,∴P(0,),Ⅲ、AD=DP,25=16+(y﹣5)2,∴y=2或8,∴P(0,2)或(0,8).B、①、由A①知,AD=5,由折叠知,AE=AC=2,DE⊥AC于E,在Rt△ADE中,DE==,②、∵以点A,P,C为顶点的三角形与△ABC全等,∴△APC≌△ABC,或△CPA≌△ABC,∴∠APC=∠ABC=90°,∵四边形OABC是矩形,∴△ACO≌△CAB,此时,符合条件,点P和点O重合,即:P(0,0),如图3,过点O作ON⊥AC于N,易证,△AON∽△ACO,∴,∴,∴AN=,过点N作NH⊥OA,∴NH∥OA,∴△ANH∽△ACO,∴,∴,∴NH=,AH=,∴OH=,∴N(,),而点P2与点O关于AC对称,∴P2(,),同理:点B关于AC的对称点P1,同上的方法得,P1(﹣,),即:满足条件的点P的坐标为:(0,0),(,),(﹣,).5、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.(1)求证:△OBP与△OPA相似;(2)当点P为AB中点时,求出P点坐标;(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.解:(1)证明:∵AB是过点P的切线,∴AB⊥OP,∴∠OPB=∠OPA=90°;(1分)∴在Rt△OPB中,∠1+∠3=90°,又∵∠BOA=90°∴∠1+∠2=90°,∴∠2=∠3;(1分)在△OPB中△APO中,∴△OPB∽△APO.(2分)(2)∵OP⊥AB,且PA=PB,∴OA=OB,∴△AOB是等腰三角形,∴OP是∠AOB的平分线,∴点P到x、y轴的距离相等;(1分)又∵点P在第一象限,∴设点P(x,x)(x>0),∵圆的半径为2,∴OP=,解得x=或x=﹣(舍去),(2分)∴P点坐标是(,).(1分)(3)存在;①如图设OAPQ为平行四边形,∴PQ∥OA,OQ∥PA;∵AB⊥OP,∴OQ⊥OP,PQ⊥OB,∴∠POQ=90°,∵OP=OQ,∴△POQ是等腰直角三角形,∴OB是∠POQ的平分线且是边PQ上的中垂线,∴∠BOQ=∠BOP=45°,∴∠AOP=45°,设P(x,x)、Q(﹣x,x)(x>0),(2分)∵OP=2代入得,解得x=,∴Q点坐标是(﹣,);(1分)②如图示OPAQ为平行四边形,同理可得Q点坐标是(,﹣).(1分)6、如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连结AD,以AD为一边且在D的右侧作正方形ADEF,解答下列问题:(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),如图2,线段CF,BD之间的位置关系为,数量关系为;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动(如图4)当∠ACB=时,CF⊥BC(点C,F 重合除外)?(3)若AC=4,BC=3.在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.解:(1)CF⊥BD,CF=BD,理由如下:∵四边形ADEF是正方形,∴∠DAF=90°,AD=AF,∵AB=AC,∠BAC=90°,∴∠BAD+∠DAC=∠CAF+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴CF=BD,∴∠B=∠ACF,∴∠B+∠BCA=90°,∴∠BCA+∠ACF=90°,即CF⊥BD;故答案为:CF⊥BD,CF=BD;②当点D在BC的延长线上时,①的结论仍成立.如图2,由正方形ADEF得:AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC.∴∠DAB=∠FAC.又∵AB=AC,∴△DAB≌△FAC(SAS).∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°.∴∠BCF=∠ACB+∠ACF=90°,∴CF⊥BD;(2)当∠BCA=45°时,CF⊥BD;理由如下:如图3,过点A作AC的垂线与CB所在直线交于G,∵∠ACB=45°,∴△AGC等腰直角三角形,∴AG=AC,∠AGC=∠ACG=45°,∵AG=AC,AD=AF,∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,∴∠GAD=∠FAC,∴△GAD≌△CAF(SAS),∴∠ACF=∠AGD=45°,∴∠GCF=∠GCA+∠ACF=90°,∴CF⊥BC;故答案为:45°;(3)过点A作AQ⊥BC交CB的延长线于点Q,如图4所示:∵DE与CF交于点P时,此时点D位于线段CQ上,∵∠BCA=45°,AC=4,∴△ACQ是等腰直角三角形,∴AQ=CQ=4.设CD=x,则DQ=4﹣x,∵∠ADB+∠ADE+∠PDC=180°且∠ADE=90°,∴∠ADQ+∠PDC=90°,又∵在直角△PCD中,∠PDC+∠DPC=90°∴∠ADQ=∠DPC,∵∠AQD=∠DCP=90°∴△AQD∽△DCP,∴=,即=.解得:CP=﹣x2+x=﹣(x﹣1)2+1.∵0<x≤3,∴当x=1时,CP有最大值1,即线段CP长的最大值为1.7、如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交BO于H,连接OG,CG.(1)求证:AH=BE;(2)试探究:∠AGO的度数是否为定值?请说明理由;(3)若OG⊥CG,BG=2,求S△OGC的值.解析:(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠AOB=∠BOE=90°,∵AF⊥BE,∴∠GAE+∠AEG=∠OBE+∠AEG=90°.∴∠GAE=∠OBE,在△AOH和△BOE中,,∴△AOH≌△BOE(ASA),∴AH=BE.(2)解:∠AGO的度数为定值,理由如下:∵∠AOH=∠BGH=90°,∠AHO=∠BHG,∴△AOH∽△BGH,∴=,∴=,∵∠OHG=∠AHB,∴△OHG∽△AHB,∴∠AGO=∠ABO=45°,即∠AGO的度数为定值.(3)解:∵∠ABC=90°,AF⊥BE,∴∠BAG=∠FBG,∠AGB=∠BGF=90°,∴△ABG∽△BFG,∴=,∴AG•GF=BG2=20,∵△AHB∽△OHG,∴∠BAH=∠GOH=∠GBF.∵∠AOB=∠BGF=90°,∴∠AOG=∠GFC,∵∠AGO=45°,CG⊥GO,∴∠AGO=∠FGC=45°.∴△AGO∽△CGF,∴=,∴GO•CG=AG•GF=20.∴S△OGC=CG•GO=10.8、已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.(1)DE的长为.(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.解:(1)∵四边形ABCD是矩形∴AB=CD=4,AD=BC=6,CD⊥BC在Rt△DCE中,DE===5 故答案为5.(2)若△ABP与△DCE全等∴BP=CE或AP=CE当BP=CE=3时,则t==3秒当AP=CE=3时,则t==13秒∴求当t为3秒或13秒时,△ABP和△DCE全等.(3)若△PDE为等腰三角形则PD=DE或PE=DE或PD=PE当PD=DE时,∵PD=DE,DC⊥BE∴PC=CE=3∵BP=BC﹣CP=3∴t==3当PE=DE=5时,∵BP=BE﹣PE∴BP=9﹣5=4∴t==4当PD=PE时,∴PE=PC+CE=3+PC∴PD=3+PC在Rt△PDC中,DP2=CD2+PC2.∴(3+PC)2=16+PC2∴PC=∵BP=BC﹣PC∴BP=∴t==综上所述:当t=3秒或4秒或秒时,△PDE为等腰三角形.9、在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3(1)直接写出点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式;(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)过B作BG⊥OA于点G,在Rt△ABG中,利用勾股定理可求得BG的长,则可求得B点坐标;(2)由条件可求得E点坐标,利用待定系数法可求得直线DE的解析式;(3)当OD为边时,则MO=OD=5或MD=OD=5,可求得M点坐标,由MN∥OD,且MN=OD可求得N点坐标;当OD为对角线时,则MN垂直平分OD,则可求得M、N的纵坐标,则可求得M的坐标,利用对称性可求得N点坐标.【解答】解:(1)如图1,过B作BG⊥OA于点G,∵BC=3,OA=6,∴AG=OA﹣OG=OA﹣BC=6﹣3=3,在Rt△ABG中,由勾股定理可得AB2=AG2+BG2,即(3)2=32+BG2,解得BG=6,∴OC=6,∴B(3,6);(2)由OD=5可知D(0,5),∵B(3,6),OE=2BE,∴E(2,4),设直线DE的解析式是y=kx+b把D(0,5)E(2,4)代入得,∴直线DE的解析式是y=﹣x+5;(3)当OD为菱形的边时,则MN=OD=5,且MN∥OD,∵M在直线DE上,∴设M(t,﹣t+5),①当点N在点M上方时,如图2,则有OM=MN,∵OM2=t2+(﹣t+5)2,∴t2+(﹣t+5)2=52,解得t=0或t=4,当t=0时,M与D重合,舍去,∴M(4,3),∴N(4,8);②当点N在点M下方时,如图3,则有MD=OD=5,∴t2+(﹣t+5﹣5)2=52,解得t=2或t=﹣2,当t=2时,N点在x轴下方,不符合题意,舍去,∴M(﹣2,+5),∴N(﹣2,);当OD为对角线时,则MN垂直平分OD,∴点M在直线y=2.5上,在y=﹣x+5中,令y=2.5可得x=5,∴M(5,2.5),∵M、N关于y轴对称,∴N(﹣5,2.5),综上可知存在满足条件的点N,其坐标为(4,8)或(﹣5,2.5)或(﹣2,).【点评】本题为一次函数的综合应用,涉及勾股定理、待定系数法、菱形的性质、分类讨论及方程思想.在(2)中求得E点坐标是解题的关键,在(3)中求得M点的坐标是解题的关键,注意分类讨论.本题考查知识点较多,综合性较强,难度较大.10、如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.计算:(1)当点E与点D重合时,△BDF的面积为;当点E为CD的中点时,△BDF的面积为.证明:(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想;运用:(3)如图2,设BF与CD相交于点H,若△DFH的面积为,求正方形CEFG的边长.解:计算:(1)∵当点E与点D重合时,∴CE=CD=6,∵四边形ABCD,四边形CEFG是正方形,∴DF=CE=AD=AB=6,∴S△BDF=×DF×AB=18,如图,连接CF,∵四边形ABCD和四边形CEFG均为正方形;∴∠CBD=∠GCF=45°,∴BD∥CF,∴S△BDF=S△BDC=S正方形ABCD=×36=18,故答案为:18,18;证明:(2)S△BDF=S正方形ABCD,理由:连接CF.∵四边形ABCD和四边形CEFG均为正方形,∴∠CBD=∠GCF=45°,∴BD∥CF,∴S△BDF=S△BDC=S正方形ABCD;运用:(3)如图2,∵S△BDF=S正方形ABCD=×36=18,且S△BDF=S△BDH+S△DFH,∴S△BDH=18﹣=,∴×DH×6=,∴DH=,∴S△BDH=××EF=,∴EF=4∴正方形CEFG的边长为4.11、已知如图,点C、D在线段AF上,AD=CD=CF,∠ABC=∠DEF=90°,AB∥EF.(1)若BC=2,AB=2,求BD的长;(2)求证:四边形BCED是平行四边形.(1)解:∵∠ABC=90°,∴AC===2,∵AD=CD,∴BD=AC=;(2)证明:∵AD=CD=CF,∴DF=AC=2,∵∠DEF=90°,∴CE=DF=,∴BD=CE,∵AB∥EF,∴∠A=∠F,在△ABC和△FED中,,∴△ABC≌△FED(AAS),∴BC=ED,∵BD=CE,∴四边形BCED是平行四边形.12、如图,在矩形ABCD中,M是BC上一点,EF垂直平分AM,分别交BC,AM,AD于点E,O,F,连接AE,MF.(1)求证:四边形AEMF是菱形;(2)若AB=6,H为AB的中点,连接OH交AE于点P,OH+OA=9,求△OPE的周长.(1)证明:∵EF垂直平分AM,∴AE=EM,OA=OM.∵四边形ABCD是矩形,∴AD∥BC.∴∠AFO=∠MEO,在△OF和△MOE中,,∴△AOF≌△MOE(AAS).∴OF=OE.∴四边形AEMF是平行四边形.∵AE=EM.∴四边形AEMF是菱形;(2)解:∵O、H分别为AM、AB的中点,∴BM=2OH,AM=2OA,∴AM+BM=2OA+2OH=18.设BM=x,则AM=18﹣x,在Rt△ABM中,由勾股定理得:62+x2=(18﹣x)2,解得:x=8,∴BM=8,AM=10.∴OA=AM=5,设EM=m,则BE=8﹣m,AE=EM=m,在Rt△ABE中,由勾股定理得:62+(8﹣m)2=m2,解得:m=,∴AE=EM=在Rt△AOE中,EO===.∵OP∥EM,∴==1,∴AP=PE,∴OP=EM=,∵PE=AE=,∴△OPE的周长=EO+PE+OP=++=10.。
2020中考数学(选择题难题突破)(含答案)备战中考数学选择题难题突破类型⼀:动点函数类1.如图,点P是菱形ABCD边上的⼀动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△P AD的⾯积为y,P点的运动时间为x,则y关于x的函数图象⼤致为( )A B C D2.如图,在正⽅形ABCD中,点P从点A出发,沿着正⽅形的边顺时针⽅向运动⼀周,则△APC的⾯积y与点P运动的路程x之间形成的函数关系图象⼤致是( )A BCD3.如图,已知正三⾓形ABC 的边长为2,E ,F ,G 分别是AB ,BC ,CA 上的点,且AE =BF =CG ,设△EFG 的⾯积为y ,AE 的长为x ,则y 关于x 的函数图象⼤致是( )4.如图,在Rt △AOB 中,AB △OB ,且AB =OB =3,设直线x =t 截此三⾓形所得阴影部分的⾯积为S ,则S 与t 之间的函数关系的图象为下列选项中A BCD的( )5.如图,正△ABC 的边长为4,点P 为BC 边上的任意⼀点(不与点B ,C 重合),且△APD =60°,PD 交AB 于点D .设BP =x ,BD =y ,则y 关于x 的函数图象⼤致是( )6.如图,△ABC 是等腰直⾓三⾓形,△A =90°,BC =4,点P 是△ABC 边上⼀动点,沿B →A →C 的路径移动,过点P 作PD △BC 于点D ,设BD =x ,△BDP 的⾯积为y ,则下列能⼤致反映y 与x 函数关系的图象是( )7.如图,边长分别为1和2的两个等边三⾓形,开始它们在左边重合,⼤三⾓形固定不动,然后把⼩三⾓形⾃左向右平移直⾄移出⼤三⾓形外停⽌.设⼩三⾓形移动的距离为x ,两个A B CD三⾓形重叠⾯积为y,则y关于x的函数图象是( )A BC D8.如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的⾯积为y,那么y与x之间的函数关系的图象⼤致是( )A BC D9.如图,正⽅形ABCD的边长为2 cm,动点P,Q同时从点A出发,在正⽅形的边上,分别按A→D→C,A→B→C的⽅向,都以1 cm/s的速度运动,到达点C运动终⽌,连接PQ,设运动时间为x s,△APQ的⾯积为y cm2,则下列图象中能⼤致表⽰y与x的函数关系的是( )A BC D10.如图,在菱形ABCD中,△B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当⼀个点停⽌运动时,另⼀个点也随之停⽌.设△APQ的⾯积为y,运动时间为x秒,则下列图象能⼤致反映y与x之间函数关系的是( )A BC D11.如图,△O的半径为1,AD,BC是△O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin△APB=y,那么y与x之间的关系图象⼤致是( )12.如图,在Rt△PMN中,△P=90°,PM=PN,MN=6 cm,在矩形ABCD中,AB=2 cm,BC=10 cm,点C和点M重合,点B,C(M),N在同⼀直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1 cm的速度向右移动,⾄点C与点N重合为⽌,设移动x秒后,矩形ABCD与△PMN重叠部分的⾯积为y,则y与x的⼤致图象是( )A B C D13.早上,⼩明从家⾥步⾏去学校,出发⼀段时间后,⼩明妈妈发现⼩明的作业本落在家⾥,便带上作业本骑车追赶,途中追上⼩明两⼈稍作停留,妈妈骑车返回,⼩明继续步⾏前往学校,两⼈同时到达.设⼩明在途的时间为x,两⼈之间的距离为y,则下列选项中的图象能⼤致反映y与x之间关系的是( )14.从甲地到⼄地的铁路路程约为615千⽶,⾼铁速度为300千⽶/时,直达;动车速度为200千⽶/时,⾏驶180千⽶后,中途要停靠徐州10分钟.若动车先出发半⼩时,两车与甲地之间的距离y(千⽶)与动车⾏驶时间x(⼩时)之间的函数图象为( )15.⼩聪步⾏去上学,5分钟⾛了总路程的1,估6计步⾏不能准时到校,于是他改乘出租车赶往学校,他的⾏程与时间关系如图所⽰(假定总路程为1,出租车匀速⾏驶),则他到校所花的时间⽐⼀直步⾏提前了( )A.16分钟B.18分钟C.20分钟D.24分钟类型⼆:⼏何综合类1.如图,已知正⽅形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;①S△CDF=4S△CEF;①S△ADF=2S△CEF;①S△ADF=2S△CDF.其中正确的是( )A.①①B.①①C.①①D.①①2.如图,正⽅形ABCD的边长为4,延长CB⾄E使EB=2,以EB为边在上⽅作正⽅形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N,K,则下列结论:△△ANH △△GNF ;△△AFN =△HFG ;△FN =2NK ;△S △AFN △S △ADM =1△4.其中正确的结论有( )A .1个B .2个C .3个D .4个强化训练3.如图,ABCD 是正⽅形,E ,F 分别是DC ,CB 的延长线上的点,且DE=BF .连接AE ,AF ,EF ,AC ,EF 交AB 于点G.则下列结论:①△ADE △△ABF ; ①△AEF=45°;①若AB=3,DE=13DC ,则S △AEF =54;①若AB=2,E 为DC 的中点,则EF AC =√102.其中正确结论的有( )A .1个B .2个C .3 个D .4 个4.如图,已知E ,F 分别为正⽅形ABCD 的边AB ,BC 的中点,AF 与DE 交于点M ,设AB=4,则下列结论:①△AME=90°;①△BAF=△EDB;①MD=2AM=4EM;MF.其中正确结论的有()①AM=23A.4个B.3个C.2个D.1个5.如图,已知△ABCD的对⾓线AC,BD交于点O,DE平分△ADC交BC于点E,交AC于点F,且△BCD=60°, BC=2CD,连接OE.下列结论:=BD·CD;①OE①AB; ①S平⾏四边形ABCD①AO=2BO; ①S△DOF=2S△EOF.其中成⽴的有( )A.1个B.2个C.3个D.4个6.如图,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若△COB=60°,FO=FC,则下列结论:①FB垂直平分OC;①△EOB△△CMB;①DE=EF;①S△AOE①S△BCM=2①3.其中正确结论的有( )A.4个B.3个C.2个D.1个7.如图,AB为△O的直径,BC为△O的切线,弦AD△OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是△O的切线;①CO△DB;①△EDA△△EBD;①ED·BC=BO·BE.其中正确结论的有( )A.4个B.3个C.2个D.1个类型三:函数综合类1.已知k1<0的图象⼤致是( )xA B C D2.⼆次函数y=ax2+bx+c(a≠0)的⼤致图象如图,关于该⼆次函数,下列说法错误的是( )A.函数有最⼩值B.对称轴是直线x=12C.当x<1时,y随x的增⼤⽽减⼩D.当-12时,y>0强化训练3.如图,在平⾯直⾓坐标系中,矩形ABCD的顶点A,D分别在x轴、y轴上,对⾓线BD△x轴,反⽐例函数(k>0,x>0)的图象经过矩形对⾓线的交点E.若点y=kxA(2,0),D(0,4),则k的值为()A.16B.20C.32D.404.已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y=c的图象为x( )5.⼀次函数y=ax+b与反⽐列函数y=c的图象如图所⽰,则⼆次函数xy=ax2+bx+c的⼤致图象是( )6.若函数y=k与y=ax2+bx+c的图象如图所⽰,则函数y=kx+b的⼤致图x象为( )7.在平⾯直⾓坐标系中,⼆次函数y=ax2+bx+c(a≠0)的图象如图所⽰,现给以下结论:△abc<0;△c+2a<0;△9a-3b+c=0;△a-b≥m(am+b)(m 为实数);△4ac-b2<0.其中结论错误的有( )A.1个B.2个C.3个D.4个类型四:图形变换类1.如图,在菱形ABCD中,AC=6√2,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最⼩值是( )C.2√6D.4.52.如图,在△ABC中,△BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连接AD,则下列结论不⼀定正确的是( )A.AE=EFB.AB=2DEC.△ADF和△ADE的⾯积相等D.△ADE和△FDE的⾯积相等3.如图,在正⽅形ABCD中,E是BC边上的⼀点,BE=4,EC=8,将正⽅形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,FC,现在有如下4个结论:△△EAG=45°;△FG=FC;△FC△AG;△S△GFC=14.其中正确结论的有( )A.1个B.2个C.3个D.4个4.如图,在等腰直⾓三⾓形ABC中,△BAC=90°,⼀个三⾓尺的直⾓顶点与BC边的中点O重合,且两条直⾓边分别经过点A和点B,将三⾓尺绕点O按顺时针⽅向旋转任意⼀个锐⾓,当三⾓尺的两直⾓边与AB,AC分别交于点E,F时,下列结论中错误的是( )A.AE+AF=ACB.△BEO+△OFC=180°C.OE+OF=√22BCD.S四边形AEOF =12S△ABC5.如图,在Rt△ABC中,△ACB=90°,△ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )A.√7B.2√2类型五:求阴影⾯积类1.如图,在正⽅形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的⾯积是( )A.18+36πB.24+18πC.18+18πD.12+18π2.如图,将半径为2,圆⼼⾓为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O',B',连接BB',则图中阴影部分的⾯积是( )A.2π3B.2√3?π3C.2√3?2π3D.4√3?2π33.如图,在半径为6的△O中,点A,B,C都在△O上,四边形OABC是平⾏四边形,则图中阴影部分的⾯积为( )A.6πB.3√3πC.2√3πD.2π4.如图,在菱形ABCD中,点E是BC的中点,以C为圆⼼、CE为半径作弧,交CD于点F,连接AE,AF.若AB=6,△B=60°,则阴影部分的⾯积为( )A.9√3-3πB.9√3-2πC.18√3-9πD.18√3-6π选择题难题突破类型⼀:动点函数类1.B2.C【强化训练】4.D5.C6.B7.B8.D9.A10.B11.C12.A 13.B14.A15.C类型⼆:⼏何综合类1.C 2.C【强化训练】3.B4.B5.C6.B7.A类型三:函数综合类1.A 2.D【强化训练】3.B4.C5.A6.C7.A类型四:图形变换类1.C 2.C 3.B 4.C 5.A 类型五:求阴影⾯积类1.C 2.C 3.A 4.A。
专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点,它贯穿于整个初中数学,自数轴起始,至几何图形的存在性、几何图形的长度及面积的最值,函数的综合类题目,无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变,而其中又有一些技巧性很强的数学思想(转化思想),本专题以几个基本的知识点为经,以历年来中考真题为纬,由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间,线段最短;2. 垂线段最短;3. 若A 、B 是平面直角坐标系内两定点,P 是某直线上一动点,当P 、A 、B 在一条直线上时,PA PB最大,最大值为线段AB 的长(如下图所示);(1)单动点模型作图方法:作已知点关于动点所在直线的对称点,连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示,P 是x 轴上一动点,求P A +PB 的最小值的作图.P 是∠AOB 内一点,M 、N 分别是边OA 、OB 上动点,求作△PMN 周长最小值.作图方法:作已知点P 关于动点所在直线OA 、OB 的对称点P ’、P ’’,连接P ’P ’’与动点所在直线的交点M 、N 即为所求.5. 二次函数的最大(小)值()2y a x h k =-+,当a >0时,y 有最小值k ;当a <0时,y 有最大值k .二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. (详见精品例题解析) 三、精品例题解析例1. (2019·凉山州)如图,正方形ABCD 中,AB =12,AE =3,点P 在BC 上运动(不与B 、C 重合),过点P 作PQ ⊥EP ,交CD 于点Q ,则CQ 的最大值为【答案】4.【解析】解:∵PQ ⊥EP ,∴∠EPQ =90°,即∠EPB +∠QPC =90°,∵四边形ABCD 是正方形,∴∠B =∠C =90°,∠EPB +∠BEP =90°,∴∠BEP =∠QPC ,∴△BEP ∽△CPQ ,O。
专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点,它贯穿于整个初中数自数轴起始,至几何图形的存在性、几何图形的长度及面积的最值,函数的综合类题目,无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变,而其中又有一些技巧性很强的数学思想(转化思想),本专题以几个基本的知识点为经,以历年来中考真题为纬,由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间,线段最短;2. 垂线段最短;3. 若A、B是平面直角坐标系内两定点,P是某直线上一动点,当P、A、B在一条直线上时,PA PB 最大,最大值为线段AB的长(如下图所示);(1)单动点模型作图方法:作已知点关于动点所在直线的对称点,连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示,P是x轴上一动点,求P A+PB的最小值的作图.P 是∠AOB 内一点,M 、N 分别是边OA 、OB 上动点,求作△PMN 周长最小值.作图方法:作已知点P 关于动点所在直线OA 、OB 的对称点P ’、P ’’,连接P ’P ’’与动点所在直线的交点M 、N 即为所求.5. 二次函数的最大(小)值()2y a x h k =-+,当a >0时,y 有最小值k ;当a <0时,y 有最大值k .二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. (详见精品例题解析) 三、精品例题解析例1. (2019·凉山州)如图,正方形ABCD 中,AB =12,AE =3,点P 在BC 上运动(不与B 、C 重合),过点P 作PQ ⊥EP ,交CD 于点Q ,则CQ 的最大值为【答案】4.【解析】解:∵PQ ⊥EP ,∴∠EPQ =90°,即∠EPB +∠QPC =90°,∵四边形ABCD 是正方形,∴∠B =∠C =90°,∠EPB +∠BEP =90°,∴∠BEP =∠QPC ,∴△BEP ∽△CPQ ,O∴BE BP CP CQ=,∵AB=12,AE=3,∴BE=9,设CQ=y,BP=x,CP=12-x,(0<x<12)∴912xx y=-,即()()21216499x xy x-==--+,∴当x=6时,y有最大值为4,即CQ的最大值为4.【点睛】此题为“一线三直角模型”,解题方法为相似三角形性质求解,综合利用二次函数的性质求解最值问题.例2.(2019·自贡)如图,已知A、B两点的坐标分别为(8,0),(0,8). 点C、F分别是直线x=-5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取最小值时,tan ∠BAD=()A.817B.717C.49D.59【答案】B.【解析】解:S△ABE=142BE OA BE ⨯⨯=,当BE取最小值时,△ABE面积为最小值.设x=-5与x轴交于点G,连接DG,因为D为CF中点,△CFG为直角三角形,所以DG=15 2CD=,∴D点的运动轨迹为以G为圆心,以5半径的圆上,如图所示由图可知:当AD与圆G相切时,BE的长度最小,如下图,过点E作EH⊥AB于H,∵OG=5,OA=8,DG=5,在Rt△ADG中,由勾股定理得:AD=12,△AOE∽△ADG,∴AO AD OE DG=,求得:OE=10 3,由OB=OA=8,得:BE=143,∠B=45°,AB=∴EH=BH=,AH=AB-BH,∴tan ∠BAD=717EH AH ==, 故答案为B .【点睛】此题解题的关键是找到△ABE 面积最小时即是AD 与D 的远动轨迹圆相切的时刻. 进而构造以∠BAD 为内角的直角三角形,利用勾股定理求出边长,代入三角函数定义求解.例3. (2019·南充)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,AB =24,BC =5,给出结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;①①OAB 的面积的最大值为144;①当OD 最大时,点D 的坐标为)2626125,262625(,其中正确的结论是 (填写序号).【答案】①①.【解析】解:根据题意可知:OE =12AB =12, 即E 的轨迹为以O 为圆心以12为半径的四分之一圆(第一象限的部分),根据弧长公式,得点E 的路径长为:9012180π⨯⨯=6π,故①错误; 因为AB =24,当斜边AB 上的高取最大值时,①OAB 的面积取最大值,点O 在以AB 为直径的圆上(圆心为E ),当OE ⊥AB 时,斜边AB 上的高最大,所以①OAB 的面积取最大值为:124122⨯⨯=144,故②正确; 连接OE 、DE ,得:OD≤OE+DE,当O、E、D三点共线时取等号,即OD的最大值为25,如图,过点D作DF⊥y轴于F,过点E作EG⊥y轴于G,可得:25DF OD==,即:1225EG DF=,512AF ADEG AE==,即:51125AF EG DF==,设DF=x,在Rt△ADF中,由勾股定理得:221255x x⎛⎫+=⎪⎝⎭,解得:x=26,在Rt△ODF中,由勾股定理得:OF=26,即点D的坐标为)2626125,262625(,故③正确.综上所述,答案为:②③.例4.(2019·天津)已知抛物线2y x bx c=-+(b、c为常数,b>0)经过点A(-1,0),点M(m,0)是x轴正半轴上的动点.若点Q(1,2Qb y+2QM+b的值.【答案】见解析.【解析】解:∵2y x bx c =-+经过点A (-1,0),∴1+b +c =0,即21y x bx b =---∵点Q (1,2Q b y +)在抛物线2y x bx c =-+上, ∴324Q by =--, 即13,224bQ b ⎛⎫+-- ⎪⎝⎭,∵b >0,∴Q 点在第四象限,22QM AM QM ⎫+=+⎪⎝⎭所以只要构造出2AM QM ⎛⎫+ ⎪⎝⎭2QM +的最小值取N (1,0),连接AN ,过M 作MG ⊥AN 于G ,连接QM ,如图所示,△AGM 为等腰直角三角形,GM =2AM ,即当G 、M 、Q 三点共线时,GM +MQ 2QM +取最小值,此时△MQH 为等腰直角三角形,∴QM 324b⎫+⎪⎭,GM =2AM =()12m +()322=2122244b QM AM QM m ⎛⎫⎤⎫+=++++= ⎪⎥⎪⎭⎝⎭⎣⎦ ①∵QH =MH ,∴324b +=12b m +-,解得:m =124b - ②联立①②得:m =74,b =4.2QM +的最小值为4时,b =4.2QM +转化为2AM QM ⎫+⎪⎝⎭,进而根据两点之间线段最短及等腰三角形性质求解. 例5. (2019·舟山)如图,一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上,边AC 与EF 重合,12AC cm =.当点E 从点A 出发沿AC 方向滑动时,点F 同时从点C 出发沿射线BC 方向滑动.当点E 从点A 滑动到点C 时,点D 运动的路径长为 cm ;连接BD ,则△ABD 的面积最大值为 2cm .【答案】 【解析】解:如图1所示,当E 运动至E ’,F 滑动到F ’时,图1过D ’作D ’G ⊥AC 于G ,D ’H ⊥BC 交BC 延长线于点H ,可得∠E ’D ’G =∠F ’D ’H ,D ’E ’=D ’F ’,∴Rt △E ’D ’G ≌Rt △F ’D ’H ,∴D ’G =G ’H ,D '∴D ’在∠ACH 的角平分线上,即C ,D ,D ’三点共线.通过分析可知,当D ’E ’⊥AC 时,DD ’的长度最大,随后返回初始D 点,如图2所示,D 点的运动路径为D →D ’→D ,行走路线长度为2DD ’;图2∵∠BAC =30°,AC =12,DE =CD∴BC=CD =DE=由图知:四边形E ’CF ’D ’为正方形,CD ’=EF =12,∴DD ’=CD ’-CD =12-D 点运动路程为2DD ’=24-图3如图3所示,当点D 运动至D ’时,△ABD ’的面积最大,最大面积为:'''''''ABC AE D BD F E CF D S S S S ++-△△△正方形=(((211112222⨯+⨯--⨯⨯=-【点睛】准确利用全等、角平分线判定得到D 点的运动轨迹是关键,利用三角函数及勾股定理求解,计算较为繁琐,尤其是利用割补法求解三角形的面积时对学生计算能力要求较高,此题难度较大,新颖不失难度.BD'BD'例6. (2019·巴中)如图,在菱形ABCD 中,连接BD 、AC 交于点O ,过点O 作OH ⊥BC 于点H ,以O 为圆心,OH 为半径的半圆交AC 于点M .(1)求证:DC 是圆O 的切线;(2)若AC =4MC ,且AC =8,求图中阴影部分面积;(3)在(2)的前提下,P 是线段BD 上的一动点,当PD 为何值时,PH +PM 的值最小,并求出最小值.【答案】见解析.【解析】(1)证明:过点O 作ON ⊥CD 于N ,AC 是菱形ABCD 的对角线,∴AC 平分∠BCD ,∵OH ⊥BC ,ON ⊥CD ,∴OH =ON ,又OH 为圆O 的半径,∴ON 为圆O 的半径,即CD 是圆O 的切线.(2)由题意知:OC =2MC =4,MC =OM =2,即OH =2,在Rt △OHC 中,OC =2OH ,可得:∠OCH =30°,∠COH =60°,B D11 由勾股定理得:CH==23OCH OMHS S S π-=△阴影扇形(3)作点M 关于直线BD 的对称点M ’,连接M ’H 交BD 于点P , 可知:PM =PM ’即PH +PM =PH +PM ’=HM ’,由两点之间线段最短,知此时PH +PM 最小, ∵OM ’=OM =OH ,∠MOH =60°,∴∠MM ’H =30°=∠HCM ,∴HM ’=HC=即PH +PM的最小值为在Rt △M ’PO 及Rt △COD 中,OP =OM ’ tan 30°=3,OD =OC tan 30°即PD =OP +OD=B D。