中考数学专题复习-轨迹问题

最值模型之瓜豆模型(原理)直线轨迹型动点轨迹问题是中考和各类模拟考试的重要题型，学生受解析几何知识的局限和思维能力的束缚，该压轴点往往成为学生在中考中的一个坎，致使该压轴点成为学生在中考中失分的集中点。

掌握该压轴题型的基本图形，构建问题解决的一般思路，是中考专题复习的一个重要途径。

本专题就最值模型中的瓜豆原理(动点轨迹为直线型)进行梳理及对应试题分析，方便掌握。

【模型解读】瓜豆原理：若两动点到某定点的距离比是定值，夹角是定角，则两动点的运动路径相同。

动点轨迹基本类型为直线型和圆弧型，本专题受教学进程影响，估只对瓜豆原理中的直线型轨迹作讲解。

主动点叫瓜，从动点叫豆，瓜在直线上运动，豆也在直线_上运动；瓜在圆周上运动，豆的轨迹也是圆。

古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”。

模型1、运动轨迹为直线1)如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？解析：当P点轨迹是直线时，Q点轨迹也是一条直线．理由：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．2)如图，在△APQ中AP=AQ，∠PAQ为定值，当点P在直线BC上运动时，求Q点轨迹？解析：当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形。

理由：当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q点的起始位置和终点位置，连接即得Q点轨迹线段。

【最值原理】动点轨迹为一条直线时，利用“垂线段最短”求最值。

1)当动点轨迹已知时可直接运用垂线段最短求最值；2)当动点轨迹未知时，先确定动点轨迹，再垂线段最短求最值。

3)确定动点轨迹的方法(重点)②当某动点到某条直线的距离不变时，该动点的轨迹为直线；③当一个点的坐标以某个字母的代数式表示时，若可化为一次函数，则点的轨迹为直线；④观察动点运动到特殊位置时，如中点，端点等特殊位置考虑；⑤若动点轨迹用上述方法不都合适，则可以将所求线段转化(常用中位线、矩形对角线、全等、相似)为其他已知轨迹的线段求最值。

学习-----好资料更多精品文档中考数学核心知识专题复习----轨迹问题探究符合一定条件的动点所形成的图形，或者说，符合一定条件的点的全体所组成的集合，叫做满足该条件的点的轨迹六种常用的基本轨迹：①到已知线段的两个端点距离相等的点的轨迹是这条线段的垂直平分线。

②到已知角的两边距离相等的点的轨迹是这个角的平分线。

③到已知直线的距离等于定长的点的轨迹是与这条直线平行，且与已知直线的距离等于定长的两条直线。

④到两条平行线距离相等的点的轨迹是和这两条平行线平行且到这两条平行线距离相等的一条直线。

⑤到定点的距离等于定长的点轨迹是与定点为圆心，定长为半径的圆。

⑥和已知线段的两个端点的连线的夹角等于已知角的点的轨迹是以已知线段为弦，所含圆周角等于已知角的两段弧（端点除外）。

一、 尺规作图：轨迹法确定动点位置1） 已知AOB ∠,求作点P ，使得点P 到角两边距离相等，且满足OP=22） 已知AOB ∠和直线L,在直线L 上确定点P ，使得使得点P 到角两边距离相等 3）已知AOB ∠和线段CD,使得点P 到角两边距离相等且满足PC=PD 4) 已知线段AB 和直线L ，在直线L 上确定点P 使得060=∠APB 1) 2)OBOOBAB学习-----好资料 更多精品文档3) 4)二 交轨法应用1.在正方形ABCD 中，E 为AD 边上一点，以BE 边所在直线为折痕将ABE ∆对折之PBE ∆位置。

若AB=2，且PC=1.1) 不全图形2) 求tan ∠PCD 的值2．如图，在Rt △ABC 中，∠CAB =90°，∠ACB=300，BC =8，D 为线段AB 上的动点，过点A 作AH ⊥CD 于点H ，连接BH ，则 ② 求AB 的长②求BH 的最小值。

3．等边三角形ABC 的边长为6，在AC ，BC 边上各取一点E ，F ，连接AF ，BE 相交于点P ．且AE =CF ；A AB C DH学习-----好资料更多精品文档（1）求证：AF =BE ，并求∠APB 的度数； （2）若AE =2，试求AP •AF 的值；（3）当点E 从点A 运动到点C 时，试求点P 经过的路径长．4．如图，以G （0，1）为圆心，半径为2的圆与x 轴交于A ，B 两点，与y 轴交于C ，D 两点，点E 为⊙G 上一动点，CF AE 于F ．当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长5．如图，已知AB =10，P 是线段AB 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等边△ACP 和△PDB ，连接 CD ，设CD 的中点为G ，当点P 从点A 运动到点B 时， 求点G 移动路径的长学习-----好资料 更多精品文档6.问题探究：（1）请在图①的正方形ABCD 内，画出使∠APB=90°的一个点，并说明理由．（2）请在图②的正方形ABCD 内（含边），画出使∠APB=60°的所有的点P ，并说明理由． 问题解决：（3）如图③，现在一块矩形钢板ABCD ，AB=4，BC=3．工人师傅想用它裁出两块全等的、面积最大的△APB 和△CP′D 钢板，且∠APB=∠CP'D=60度．请你在图③中画出符合要求的点和，并求出△APB 的面积（结果保留根号）．三、坐标系中的动点问题动点P(a,2)的运动轨迹是____________________________________________________动点P(a,a+2)的运动轨迹是__________________________________________________动点P （a,a 2-2a ）的运动轨迹是_________________________________________________1．在平面直角坐标系中，A （2，0）、B （0，3）， 过点B 作直线∥x 轴，点P (,3)a 是直线上的动点，以AP 为边在AP 右侧作等腰Rt APQ ， ∠APQ =90°，直线AQ 交y 轴于点C ． （1）当a =1时，求点Q 的坐标（2）当点P 在直线上运动时，点Q 也随之运动．当a = _______ 时，AQ +BQ 的值最小为 _________ ．8．如图，△AOB 是直角三角形，∠AOB =90°，OB =2OA ，点A 在反比例函数1y x的图象上．设点B 的坐标为(,)m n ，则n 与m 的等量关系是______________．更多精品文档。

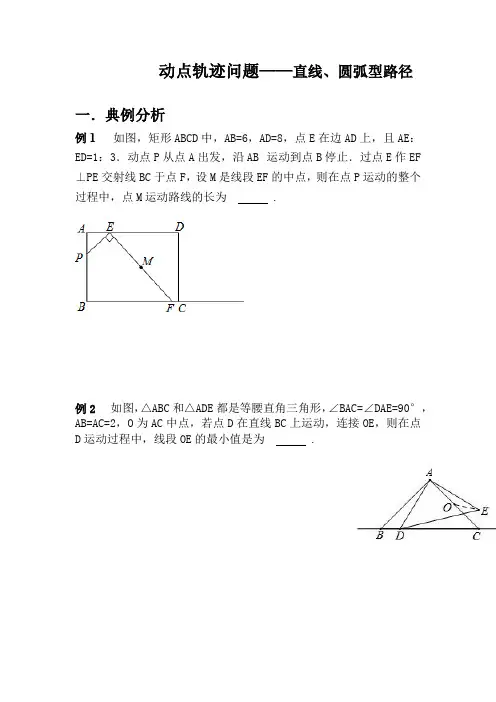
动点轨迹问题——直线、圆弧型路径一．典例分析例1如图，矩形ABCD中，AB=6，AD=8，点E在边AD上，且AE：ED=1：3．动点P从点A出发，沿AB 运动到点B停止．过点E作EF ⊥PE交射线BC于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为 .例2如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=2，O为AC中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值是为 .例3如图，在等腰Rt△ABC中，AC=BC=22，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B 时，点M运动的路径长是 .例4 在正方形ABCD中，AD=2，点E从点A出发向终点D运动，点F从D出发向终点C运动，且始终保持AE=DF.连接AF，BE交于点P，则点P运动的路径长是 .三、巩固练习1. 如图，在Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点D 是平面内的一个动点，且AD=2，M 为BD 的中点，在D 点运动过程中，线段CM 长度的取值范围是 .1题图 2题图 3题图2. 如图，等边三角形ABC 中，BC=6，D 、E 是边BC 上两点，且BD=CE=1，点P 是线段DE 上的一个动点，过点P 分别作AC 、AB 的平行线交AB 、AC 于点M 、N ，连接MN 、AP 交于点G ，则点P 由点D 移动到点E 的过程中，线段BG 扫过的区域面积为 .3. 如图，以G （0，1）为圆心，半径为2的圆与x 轴交于A 、B 两点，与y 轴交于C 、D 两点，点E 为⊙G 上一动点，CF ⊥AE 于F ．若点E 从在圆周上运动一周，则点F 所经过的路径长为 .4. 如图，已知点A 是第一象限内横坐标为32的一个定点，AC ⊥x 轴于点M ，交直线y=﹣x 于点N ．若点P 是线段ON 上的一个动点，∠APB=30°，BA ⊥PA ，则点P 在线段ON 上运动时，A 点不变，B 点随之运动．求当点P 从点O 运动到点N 时，点B 运动的路径是 ．4题图 5题图 6题图5. 如图，在边长为3的等边三角形ABC 中，P 为AC 边上一动点，Q 为线段PC 上一点，∠PBQ=30°，D 为BQ 延长线上一点，PD=PB. 当点P 从点A 运动到AP=31AC 时，点D 经过的路线长为 .6. 如图，在△ABC 中，∠ABC=90°，AB=AC=2，线段BC 上一动点P 从点C 开始运动，到点B停止，以AP 为边在AC 的右侧作等边△APQ ，则点Q 运动的路径长为 .7. （2018 花都区一模 ）已知,如图1，正方形ABCD 的边长为5，点E 、F 分别在边AB 、AD 的延长线上,且BE DF =，连接EF .（1）证明：EF AC ⊥；（2）将AEF ∆绕点A 顺时针方向旋转，当旋转角α满足045α︒<<︒时，设EF 与射线AB交于点G ，与AC 交于点H ，如图2所示，试判断线段FH ，HG ，GE 的数量关系，并说明理由.（3）若将AEF ∆绕点A 旋转一周，连接DF 、BE ，并延长EB 交直线DF 于点P ，连接PC ，试说明点P 的运动路径并求线段PC 的取值范围.8. （2017 越秀区期末25题）如图，在平面直角坐标系xoy 中，点A （0,3），B （5,3）.点P （x ，0）是x 轴正半轴上的一个动点，以BP 为直径作圆Q 交x 轴于点C ，圆Q 与直线AC 交于点D ，连接PD 、BD ，过点P 作PE ∥BD 交圆Q 于点E ，连接BE.（1）求证：四边形BDPE 是矩形；（2）设矩形BDPE 的面积为S ，试求S 关于x 的函数关系式，写出x 的取值范围，并判断S 是否存在最大值或最小值？若存在，求出这个最大值或最小值，若不存在，请说明理由；（3）当0≤x ≤5时，求点E 移动路线的长.备用图9.（2018 越秀区期末25题）如图1所示，正方形ABCD的边长为2，点E、F分别为边AB、AD的中点，如图2所示，将△AEF绕点A逆时针旋转α（0°<α 90°），射线BE、DF相交于点P.（1）求证：△ABE≌△ADF；（2）如图2，在△AEF旋转过程中，若射线BE恰好通过AD的中点H，求PF的长；（3）如图3，若将△AEF从图1的位置旋转至AE⊥BE，试求点P在旋转过程中的运动路径长.10.如图，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连结EG、FG．（1）设AE＝x时，△EGF的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；（2）P是MG的中点，请直接写出点P运动路线的长．11.如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA＝4，OC＝2．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P 到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA．（1）请用含t的代数式表示出点D的坐标；（2）求t为何值时，△DPA的面积最大，最大为多少？（3）在点P从O向A运动的过程中，△DPA能否成为直角三角形？若能，求t的值；若不能，请说明理由；（4）请直接写出随着点P的运动，点D运动路线的长.12.如图，直角坐标系中，已知点A（2，4），B（5，0），动点P从B点出发沿BO向终点O运动，动点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了x秒．（1）Q点的坐标为( , )（用含x的代数式表示）；（2）当x为何值时，△APQ是一个以AP为腰的等腰三角形？（3）记PQ的中点为G．请你直接写出点G随点P，Q运动所经过的路线的长度．13. 已知△ABC 是等腰直角三角形，AC=BC=2，D 是边AB 上的一动点（A 、B 两点除外），将△CAD 绕点C 按逆时针方向旋转角α得到△CEF ，其中点E 是点A 的对应点，点F 是点D 的对应点．（1）如图1，当α=90°时，G 是边AB 上一点，且BG=AD ，连接GF ．求证：GF ∥AC ；（2）如图2，当90°≤α≤180°时，AE 与DF 相交于点M ．①当点M 与点C 、D 不重合时，连接CM ，求∠CMD 的度数；②设D 为边AB 的中点，当α从90°变化到180°时，求点M 运动的路径长．14. 已知抛物线 ()023:21≠-+=a bx ax y C 经过点A （1,0）和B （-3,0）. （1）求抛物线1C 的解析式，并写出其顶点C 的坐标；（2）如图1，把抛物线1C 沿着直线AC 方向平移到某处时得到抛物线2C ,此时点A ，C 分别平移到点D ，E 处.设点F 在抛物线1C 上且在x 轴的上方，若△DEF 是以EF 为底的等腰直角三角形，求点F 的坐标.（3）如图2，在（2）的条件下，设点M 是线段BC 上一动点，EN ⊥EM 交直线BF 于点N ，点P 为线段MN 的中点，当点M 从点B 向点C 运动时：①tan ∠ENM 的值如何变化？请说明理由；②点M 到达点C 时，直接写出点P 经过的路线长.15.如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点．P(0，m)是线段OC上一个动点(点C除外)，直线PM交AB的延长线于点D．(1)求点D的坐标(用含m的代数式表示)；(2)当△ADP是等腰三角形时，求m的值；(3)设过点P、M、B的抛物线与x轴的正半轴交于点E，过点O作直线ME的垂线，垂足为H(如图2)．当点P从原点O向点C运动时，点H也随之运动．请直接写出点H所经过的路径长(不写解答过程)．16.问题探究：（1）请在图①的正方形ABCD内，画出使∠APB=90°的一个点，并说明理由．（2）请在图②的正方形ABCD内（含边），画出使∠APB=60°的所有的点P，并说明理由．问题解决：（3）如图③，现在一块矩形钢板ABCD，AB=4，BC=3．工人师傅想用它裁出两块全等的、面积最大的△APB和△CP′D钢板，且∠APB=∠CP'D=60度．请你在图③中画出符合要求的点和，并求出△APB的面积（结果保留根号）．17.如图，△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，AC=2，AD=1，F为BE 的中点．（1）如图1，当边AD与边AB重合时，连接DF，求证：DF⊥CF；（2）若∠BAE=135°，如图2，求CF2的值；（3）将△ADE绕点A旋转一周，直接写出点F运动路径的长。

瓜豆原理中动点轨迹直线型最值问题以及逆向构造【专题说明】近些年的中考中，经常出现动点的运动轨迹类问题，通常出题以求出轨迹的长度或最值最为常见。

很多考生碰到此类试题常常无所适从，不知该从何下手。

动点轨迹问题是中考的重要压轴点.受学生解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的一个黑洞.掌握该压轴点的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径.本文就动点轨迹问题的基本图形作一详述.动点轨迹基本类型为直线型和圆弧型.其实初中阶段如遇求轨迹长度仅有2种类型：“直线型”和“圆弧型”（两种类型中还会涉及点往返探究“往返型”），对于两大类型该如何断定，通常老师会让学生画图寻找3处以上的点来确定轨迹类型进而求出答案，对于填空选择题而言不外乎是个好方法，但如果要进行说理很多考生难以解释清楚。

瓜豆原理：一个主动点，一个从动点（根据某种约束条件，跟着主动点动），当主动点运动时，从动点的轨迹相同．只要满足：1.两“动”，一“定”；2.两动点与定点的连线夹角是定角3.两动点到定点的距离比值是定值。

【引例】（选讲）如图，△APQ是等腰直角三角形，∠P AQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q点的起始位置和终点位置，连接即得Q点轨迹线段．【模型总结】必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．结论：P、Q两点轨迹所在直线的夹角等于∠P AQ（当∠P AQ≤90°时，∠P AQ等于MN与BC夹角）P、Q两点轨迹长度之比等于AP:AQ（由△ABC∽△AMN，可得AP:AQ=BC:MN）如图，D 、E 是边长为4的等边三角形ABC 上的中点，P 为中线AD 上的动点，把线段PC 绕C 点逆时针旋转60°，得到P ’，EP ’的最小值【分析】结合这个例题我们再来熟悉一下瓜豆模型第一层：点P ’运动的轨迹是直线吗？第二层：点P ’的运动长度和点P 的运动长度相同吗？第三层：手拉手模型怎么构造？第四层：分析∠CAP 和∠CBP ’第五层：点P 和点P ’轨迹的夹角和旋转角的关系P'P'P'总共提到了3种处理方式： 1.找始末，定轨迹2.在轨迹上找一点旋转，构造手拉手模型，再通过角度相等得到从动点轨迹.3.反向旋转相关定点，构造手拉手模型，代换所求线段，即逆向构造. 那么什么具体选择什么方法更合适呢？我们再看一道例题 【例题2 宿迁中考】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE ＝1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．现在，我们分别用上面提到的3种策略来处理这个题目策略一：找始末，定轨迹我们分别以BE ，AE 为边，按题目要求构造等边三角形得到G 1与G 2，连接G 1与G 2得到点G 的轨迹，再作垂线CH 得到最小值.前面提到过从动点轨迹和主动点轨迹的夹角与旋转角有关，我们可以调用这个结论，得到∠AMG 1＝60°，BABABABA22进一步得到△MBG 1为等腰三角形后，求CH 就不难了.策略二：在点F 轨迹上找一点进行旋转.我们分别对A ，B 顺时针旋转60°，构造手拉手模型，再通过角度相等得到从动点轨迹，对A 点旋转会得到一个正切值为14的角，即1tan tan 4∠G M E =∠A FE=，然后进一步算出最值【简证】311202EM AE EN NEC IC ⇒°⇒∠,则5=2CH对B 点旋转得到∠EMG ＝∠FBE ＝90°，相对来说要容易一些.策略三：反向旋转相关定点，构造手拉手模型，代换所求线段.将点C 逆时针旋转60°，得到点H ，易证△CGE ≌△HFE ，则有CG ＝HF ，作MH ⊥AB 于M ，HM 即为所求．相比之下，先求轨迹后再求垂线段时，比较麻烦，而反向旋转代换所求线段感觉清爽很多.BABA如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE ＝1，F 为AB 边上的一个动点，连接EF ，以EF 为底向右侧作等腰直角△EFG ，连接CG ，则CG 的最小值为 ．如图，正方形ABCD 的边长为4，E 为BC 上一点，F 为AB 边上一点，连接EF ，以EF 为底向右侧作等腰直角△EFG ，连接CG ，则AG 的最小值为 ．1.如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，点D是BC边的中点，点P是AC边上一个动点，连接PD，以PD为边在PD的下方作等边△PDQ，连接CQ．则CQ的最小值是2.如图，在矩形ABCD中，AB＝5，BC＝5 3,点P在线段BC上运动（含B、C两点），连接AP，以点A 为中心，将线段AP逆时针旋转60°到AQ，连接DQ，则线段DQ的最小值为3、如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转,使∠1=∠2,且过点D作DG⊥PG,连接CG.则CG最小值为瓜豆原理中动点轨迹直线型最值问题以及逆向构造【专题说明】近些年的中考中，经常出现动点的运动轨迹类问题，通常出题以求出轨迹的长度或最值最为常见。

中考压轴专题：轨迹圆问题
考点考查背景：
•在强调综合能力全面发展的前提下，中学数学会越来越注重数学逻辑分析，此类问题通常需要学生能够在辨别基本模型的前提下，分析轨迹问题基本成立条件，结合基本模型的形成原理以及题目要求，综合运用最值以及轨迹长问题的解决方法完成对题目的辨别/分析/解决，从而达到最终目的；
考点辨别解析：
•定义法-平面内某一动点到定点的距离定值；
•定弦直角-动点处线段夹角90°恒成立，根据直径所对圆周角是直角，可知点的运动轨迹是以线段为直径的半圆；
•定弦定角-动点处线段夹角定值（非直角）恒成立，根据同弦所对圆周角是定值，反向推定可知点的运动轨迹是以线段为弦的半圆；
考点方法突破：
此类题型的分析推定方向界定在以下两个方向
•动点处线段长度定值-定义法轨迹圆问题；
•动点处角度定值-定弦直角/定弦定角；
考点结果导向分析：
•最值类问题-定点到动点线段长度最值；
•轨迹长问题-动点轨迹长度；。

❖ 共线类最值问题 ✧ 单动点共线最值1. 如图，正△ABC 的边长为2，过点B 的直线l ⊥AB ，且△ABC 与△A ′BC ′关于直线l 对称，D 为线段BC ′上一动点，则AD+CD 的最小值是（ ）2．如图Rt △ABC 中，AB=BC=4，D 为BC 的中点，在AC 边上存在一点E ，连接ED,EB ，则△BDE 周长的最小值为（ ）A ．52B ．32C ．252+D ．232+3。

已知菱形OABC 在平面直角坐标系的位置如图所示,顶点A （5,0)，OB=45，点P 是对角线OB 上的一个动点，D （0，1）,当CP+DP 最短时，点P 的坐标为( )A 。

(0，0） B.（1,21） C 。

（56,53) D.(710，75）4。

如图,已知在矩形ABCD 中，AB=4,BC=2,点M ，E 在AD 上,点F 在边AB 上，并且DM=1，现将△AEF 沿着直线EF 折叠，使点A 落在边CD 上的点P 处，则当PB+PM 的和最小时，ME 的长度为( ）A ．4B ．23C ．32D ．32+A ．31B ．94C ．32D ．95✧ 多动点最值1．如图，已知等边△ABC 的边长为8，点D 为AC 的中点,点E 为BC 的中点,点P 为BD 上一动点，则PE+PC 的最小值为( )A ．3B ．24C ．32D ．342．如图，已知正比例函数y=kx （k ＞0）的图象与x 轴相交所成的锐角为70°，定点A 的坐标为(0,4），P 为y 轴上的一个动点，M 、N 为函数y=kx （k ＞0)的图象上的两个动点,则AM+MP+PN 的最小值为( ） A ．2 B ．4 C ．32 D ．3✧ 动线段类型1. 如图，矩形ABCD中，AB=4，BC=8,E为CD边的中点，点P、Q为BC边上两个动点，且PQ=2，当BP=________时,四边形APQE的周长最小．2．如图，已知平面直角坐标系，A、B两点的坐标分别为A（2,-3)，B（4，-1）．若C（a，0），D（a+3，0)是x轴上的两个动点，则当a=___________时，四边形ABDC的周长最短．翻折衍生的圆弧轨迹问题1。

专题十一：连锁轨迹——动点在直线（线段）上产生的动点轨迹类问题探究专题导例已知，如图Rt△AB C中，∠ACB＝90°，AC＝3，BC＝4，D、E分别是AC、BC的中点，连接DE，M是DE上一动点，点M从点D开始沿DE向终点E运动，在运动过程中AM的中点移动的路径长为．【分析】取AD的中点P，AE的中点Q，连接PQ，根据勾股定理得到AB＝5，根据三角形中位线定理计算即可．如果：①动点的初始位置②动点的中途位置③动点的终止位置三点在一条直线上，那么可以初步判断动点的运动路径是．导例答案解：取AD的中点P，AE的中点Q，连接PQ，∵∠ACB＝90°，AC＝3，BC＝4，∴AB＝＝5，∵D、E分别是AC、BC的中点，∴DE＝AB＝，∵P、Q分别是AD、AE的中点，∴PQ＝DE＝，∴AM的中点移动的路径长为，故答案为：．典例剖析类型一：动点产生的路径与最值问题例1．如图，△AB C中，∠ABC＝90°，AB＝BC＝4，D为BC边上一动点，点O是正方形ADEF的中心，当点D沿BC边从点B运动到点C时，点O运动的路径长为．【分析】以点B为原点建立如图所示坐标系，作EG⊥x轴，证△ABD≌△DGE得AB＝DG＝4、BD ＝EG＝a，从而得E（4+a，a），根据线段的中点坐标知O（，），从而知点O在直线y＝x 上，由0≤a≤4知点O的横坐标2≤x≤4、纵坐标满足2≤y≤4，根据两点间的距离公式可得答案．类型二：动点产生的路径长问题例2．如图，在Rt△AB C中，∠C＝90°，AC＝8，BC＝6，D为AB边上的动点，过点D作DE⊥AB 交边AC于点E，过点E作EF⊥DE交BC于点F，连接DF．（1）当AD＝4时，求EF的长度；（2）求△DEF的面积的最大值；（3）设O为DF的中点，随着点D的运动，则点O的运动路径的长度为．【分析】（1）由勾股定理可求AB＝10，通过证明△AED∽△ABC，可得＝，可求AE＝5，CE ＝3，通过△CEF∽△ACB，可得＝，即可求EF的长度；（2）设AD＝x，由相似三角形的性质可可得DE＝•BC＝x，EF＝•AB＝10﹣x，由三角形的面积公式可得S△DEF＝DE•EF＝﹣x2+x＝﹣（x﹣）2+6，由二次函数的性质可求△DEF的面积的最大值；（3）以点A为原点，AB为x轴建立平面直角坐标系，设AD＝t，则点D坐标（t，0），点E（t，t），点F（10﹣t，t），由中点坐标公式可求点O坐标，由t的取值范围可求点O的运动路径的长度．专题突破1．如图，在△AB C中，∠B＝45°，∠C＝60°，且AB＝，M是边BC上的一个动点，连接AM，P 为AM的中点，当M点从点B运动到点C的过程中，P点的运动路线长为（）A．1+B．1﹣πC．+D．2. 如图，在矩形ABC D中，已知AB＝2cm，BC＝4cm，现有一根长为2cm的木棒EF紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则木棒EF的中点P在运动过程中所围成的图形的面积为（）A．（8﹣π）cm2B．4cm2C．（3+π）cm2D．8cm23.已知线段AB＝12，C、D是AB上两点，且AC＝DB＝2，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为4.如图，等腰直角△AB C中，AC＝BC＝3，P为斜边AB上一动点，D为BC延长线上一点，以点D为直角顶点作直角△PQD，并且使∠DPQ＝30°，则当点P从点A运动到点B时，点Q运动的路径长为．5.如图，矩形ABC D中，AB＝4，AD＝6，点E在边AD上，且AE：ED＝1：2．动点P从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交射线BC于点F．设点M是线段EF的中点，则在点P运动的整个过程中，点M的运动路径长为．6．如图，在△AB C中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿着CA以每秒3cm的速度向A点运动，设运动时间为x秒．（1）x为何值时，PQ∥BC；（2）是否存在某一时刻，使△APQ∽△CQB？若存在，求出此时AP的长；若不存在，请说明理由；7.如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．（1）若AP＝1，则AE＝；（2）①求证：点O一定在△APE的外接圆上；②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；（3）在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．8．如图，正方形ABCD的边长为2，动点E从点A出发，沿边AB﹣BC向终点C运动，以DE为边作正方形DEFG（点D、E、F、G按顺时针方向排列）．设点E运动的速度为每秒1个单位，运动的时间为x秒．（1）如图1，当点E在AB上时，求证：点G在直线BC上；（2）设正方形ABCD与正方形DEFG重叠部分的面积为S，求S与x之间的函数关系式；（3）直接写出整个运动过程中，点F经过的路径长．9．如图，平面直角坐标系中，直线AB：y＝﹣x+b交y轴于点A（0，1），交x轴于点B．过点E （1，0）作x轴的垂线EF交AB于点D，P是直线EF上一动点，且在点D的上方，设P（1，n）．（1）直线AB的表达式为；（2）求△ABP的面积（用含n的代数式表示）；（3）当S△ABP＝2时，以PB为边在第一象限作等腰直角三角形BPC，请直接写出点C的坐标．10．如图，在矩形ABC D中，AB＝2，BC＝4，M是AD的中点，动点E在线段AB上，连接EM并延长交射线CD于点F，过点M作EF的垂线交BC于点G，连接EG、FG．（1）求证：△AME≌△DMF；（2）在点E的运动过程中，探究：①△EGF的形状是否发生变化？若不变，请判断△EGF的形状，并说明理由；②线段MG的中点H运动的路程最长为多少？（直接写出结果）（3）设AE＝x，△EGF的面积为S．①当S＝6时，求x的值；②直接写出点E的运动过程中S的变化范围．11．如图，正方形ABCD的边长为4，点E从点A出发，沿AB运动到点B停止．（1）如图1，当E是AB的中点，F是AD上的一点，且AF＝AD，求证：CE平分∠BCF．（2）如图2，若点Q是AD的中点，连接EQ并延长交射线CD于点G，过Q作EG的垂线交射线BC于点P，连接PE、PG．①设AE＝x时，△PEG的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围．②若点M是PQ的中点，请直接写出点M的运动的路线的长．12．在平面直角坐标系中，A（2，0）、B（0，3），过点B作直线l∥x轴，点P（a，3）是直线上的动点，以AP为边在AP右侧作等腰Rt△APQ，∠APQ＝Rt∠，直线AQ交y轴于点C．（1）当a＝时，求点Q的坐标．（2）当P A+PO最小时，求a．专题十一答案：轨迹之点在直线（线段）上运动问题探究例1．解：如图，以点B为原点，BC所在直线为x轴建立平面直角坐标系，过点E作EG⊥x轴于点G，连接AE，根据题意知，点A（0，4）、C（4，0），∵∠ABD＝∠ADE＝∠DGE＝90°，∴∠ADB+∠EDG＝∠ADB+∠DAB＝90°，∴∠DAB＝∠EDG，在△ABD和△DGE中，∵，∴△ABD≌△DGE（AAS），∴AB＝DG＝4，BD＝EG，设BD＝EG＝a，则BG＝BD+DG＝4+a，∴点E（4+a，a），∵点O为正方形ADEF的中心，即点O为AE的中点，∴点O（，），即O（，），则无论a为任意实数，点O的横纵坐标相等，即点O在直线y＝x上，∵0≤a≤4，∴2≤≤4，即点O的横坐标2≤x≤4、纵坐标满足2≤y≤4，则点O的运动路径长为＝2，故答案为：2．例2．解：（1）∵在Rt△AB C中，∠C＝90°，∴AB＝＝10．∵DE⊥AB，∴∠EDA＝90°．∵∠A＝∠A，∠EDA＝∠C＝90°，∴△AED∽△ABC，∴＝．∴AE＝•AB＝5．∴CE＝AC﹣AE＝8﹣5＝3．∵DE⊥AB，∴∠DEF＝90°．∵∠EDA＝∠DEF＝90°，∴EF∥A B．∴△CEF∽△ACB，∴＝．∴EF＝•AB＝．（2）设AD＝x．∵△AED∽△ABC，∴＝＝．∴DE＝•BC＝x，AE＝•AB＝x．∴CE＝AC﹣AE＝8﹣x．∵△CEF∽△ACB，∴＝．∴EF＝•AB＝10﹣x．∴S△DEF＝DE•EF＝﹣x2+x＝﹣（x﹣）2+6．∴当x＝时，S△DEF取最大值为6．因此，△DEF的面积的最大值为6．（3）如图，以点A为原点，AB为x轴建立平面直角坐标系，设AD＝t，则点D坐标（t，0），点E（t，t），点F（10﹣t，t）∵点O是DF的中点，∴点O（5+t，t）∴点O在直线y＝上运动，∵过点D作DE⊥AB交边AC于点E，∴0≤t≤∴当t＝0时，点O坐标为（5，0）当t＝时，点O坐标为（，）∴点O的运动路径的长度＝＝故答案为：专题突破答案1.解：如图作AH⊥BC于H．在Rt△ABH中，∵AB＝，∠B＝45°，∴AH＝BH＝1，在Rt△ACH中，∵AH＝1，∠C＝60°，∴CH＝＝，∴BC＝1+当点M与B重合时，点P与A B中点E重合，当点M与C重合时，点P与F重合，∴点P的运动轨迹是△ABC的中位线EF，∴EF＝BC＝+．故选：C．2. 解：如图，∵P是EF的中点，∴BP＝EF＝×2＝1（cm），∵AB＝2，∴点P在运动过程中所围成的图形的面积为长方形的面积减去四个扇形的面积，：又∵四个扇形的面积正好等于一个相同半径的圆的面积，∴4×2﹣π•12＝8﹣π（cm2）．故选：A．3.解：如图，分别延长AE、BF交于点M，∵∠A＝∠DPF＝60°，∴AM∥PF，∵∠B＝∠EP A＝60°，∴BM∥PE，∴四边形PEMF为平行四边形，∴EF与MP互相平分．∵G为EF的中点，∴G正好为PM的中点，即在P的运动过程中，G始终为PM的中点，∴G的运行轨迹为△MCD的中位线H I，∵H I＝CD＝×（12﹣2﹣2）＝4，∴G点移动的路径长度为4．故答案为：44.解：如图，过点D作DK⊥AD，使得∠DAK＝30°，连接AK，KQ．∵∠ADK＝90°，∠DAK＝30°，∴＝，∵∠PDQ＝90°，∠DPQ＝30°，∴＝，∴＝，∵∠ADK＝∠PDQ＝90°，∴∠ADP＝∠KDQ，∴△ADP∽△KDQ，∴＝＝，∠DAP＝∠DKQ，∴当则当点P从点A运动到点B时，点Q运动的轨迹是线段KQ，∵点P的运动路径是3，∴点Q的运动路径是3÷＝．故答案为．5.解：如图，当P与A重合时，点F与K重合，此时点M在H处，当点P与B重合时，点F与G重合，点M 在N处，点M的运动轨迹是线段HN．在Rt△AE B中，AE＝2，AB＝4，∴BE＝＝2，∵△AEB∽△EBG，∴＝，∴BG＝＝10，∵BK＝AE＝2，∴KG＝BG﹣BK＝8，∴HN＝KG＝4，∴点M的运动路径的长为4．故答案为4．6．解：(1)∵PQ∥BC，∴∠AQP＝∠C.又∵∠A＝∠A，∴△APQ∽△ABC，∴＝，即＝，解得x＝.即当x＝时，PQ∥B C.(2)能相似．∵AB＝BC，∴∠A＝∠C，∴△APQ和△CQB相似可能有以下两种情况：①△APQ∽△CQB，可得＝，即＝，解得x＝.经检验，x＝是上述方程的解．∴当AP＝4x＝cm时，△APQ∽△CQB；②△APQ∽△CBQ，可得＝，即＝，解得x＝5或x＝－10(舍去)．经检验，x＝5是上述方程的解．∴当AP＝4x＝20 cm时，△APQ∽△CBQ.综上所述，当AP的长为cm或20 cm时，△APQ与△CQB相似．7.（1）解：∵四边形ABCD、四边形PEFG是正方形，∴∠A＝∠B＝∠EPG＝90°，PF⊥EG，AB＝BC＝4，∠OEP＝45°，∴∠AEP+∠APE＝90°，∠BPC+∠APE＝90°，∴∠AEP＝∠BPC，∴△APE∽△BCP∴，即，解得：AE＝；故答案为：；（2）①证明：如图3，取PE的中点Q，连接AQ，OQ，∵∠POE＝90°，∴OQ＝PE，∵△APE是直角三角形，∴点Q是Rt△APE外接圆的圆心，∴AQ＝PE，∴OQ＝AQ，∴点O一定在△APE的外接圆上；（到圆心的距离等于半径的点必在此圆上）②解：连接OA、AC，如图1所示：∵四边形ABCD是正方形，∴∠B＝90°，∠BAC＝45°，∴AC＝＝4，∵A、P、O、E四点共圆，∴∠OAP＝∠OEP＝45°，∴点O在AC上，当P运动到点B时，O为AC的中点，OA＝AC＝2，即点O经过的路径长为2；（3）解：设△APE的外接圆的圆心为M，作MN⊥AB于N，如图2所示：则MN∥AE，∵ME＝MP，∴AN＝PN，∴MN＝AE，设AP＝x，则BP＝4﹣x，由（1）得：△APE∽△BCP，∴，即，解得：AE＝x﹣x2＝﹣（x﹣2）2+1，∴x＝2时，AE的最大值为1，此时MN的值最大＝×1＝，即△APE的圆心到AB边的距离的最大值为．8．（1）证明：∵四边形ABCD与四边形DEFG都是正方形，∴AD＝CD，DE＝DG，∠ADE+∠EDC＝∠EDC+∠CDG＝90°，∴∠ADE＝∠CDG，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴∠DCG＝∠DAE＝90°，∵∠DCB＝90°，∴∠DCG+∠DCB＝180°，∴点G在直线BC上；（2）解：①当点E在AB边上时，过点E作EK∥AD，交CD于点K，如图1所示：则AC∥EK∥AD，∴∠HEK＝∠EHB，∠DEK＝∠EDA，∵∠EHB+∠BEH＝90°，∠EDA+∠AED＝90°，∠HEK+∠DEK＝90°，∴∠EDA＝∠BEH，∠AED＝∠EHB，∴△ADE∽△BEH，∴＝，即＝，∴BH＝，S＝正方形ABCD的面积﹣△ADE的面积﹣△BEH的面积＝2×2﹣×2×x﹣×（2﹣x）×＝；②当点E在BC边上时，S＝△DEC的面积＝×2×（4﹣x）＝4﹣x；（3）解：由（1）知，当点E在AB上时，点G在直线BC上，当点E与B点重合时，点F的位置如图2所示：点F运动的路径为BF；同理，点E在BC上时，当点E与C点重合时，点F运动的路径为FG；∵BD＝＝＝2，∴BF+FG＝2BD＝4，∴点F运动的路径长为4．9．解：（1）∵y＝﹣x+b经过A（0，1），∴b＝1，∴直线AB的解析式是y＝﹣x+1；故答案为：y＝﹣x+1；（2）过点A作AM⊥PD，垂足为M，则有AM＝1，∵x＝1时，y＝﹣x+1＝，P在点D的上方，∴PD＝n﹣，S PD•AM＝，由点B（3，0），可知点B到直线x＝1的距离为2，即△BDP的边PD上的高长为2，∴S△BPD＝PD×2＝n﹣，∴S△P AB＝S△APD+S△BPD＝n﹣+n﹣＝n﹣1；（3）当S△ABP＝2时，n﹣1＝2，解得n＝2，∴点P（1，2）．∵E（1，0），∴PE＝BE＝2，∴∠EPB＝∠EBP＝45°．第1种情况，如图1，∠CPB＝90°，BP＝PC，过点C作CN⊥直线x＝1于点N．∵∠CPB＝90°，∠EPB＝45°，∴∠NPC＝∠EPB＝45°，在△CNP与△BEP中，，∴△CNP≌△BEP，∴PN＝NC＝EB＝PE＝2，∴NE＝NP+PE＝2+2＝4，∴C（3，4）．第2种情况，如图2∠PBC＝90°，BP＝BC，过点C作CF⊥x轴于点M．∵∠PBC＝90°，∠EBP＝45°，∴∠CBM＝∠PBE＝45°，在△CBP与△PBE中，，∴△CBM≌△PBE．∴BF＝CF＝PE＝EB＝2，∴OF＝OB+BF＝3+2＝5，∴C（5，2）．第3种情况，如图3，∠PCB＝90°，CP＝EB，∴∠CPB＝∠EBP＝45°，在△PCB和△PE B中，，∴△PCB≌△PEB（SAS），∴PC＝CB＝PE＝EB＝2，∴C（3，2）．∴以PB为边在第一象限作等腰直角三角形BPC，点C的坐标是（3，4）或（5，2）或（3，2）．10．解：（1）在矩形ABC D中，AB∥CD，∴∠A＝∠FDM＝90°，∠AEM＝∠DFM，又∵M是AD的中点，∴AM＝DM，∴△AME≌△DMF（AAS）；（2）①△EGF的形状不发生变化，是等腰直角三角形，理由如下：如图1，过点M作MN⊥BC于点N，则∠NMD＝∠FMG＝90°，MN＝AB＝AD＝MD，∴∠NMD﹣∠MDG＝∠FMG﹣∠MDG，即∠FMD＝∠GMN，又∵∠MNG＝∠MDF＝90°，∴△MNG≌△MDF（ASA），∴MG＝MF，∴∠MGF＝45°，∵MG垂直平分EF，∴GF＝GE，∴∠EGM＝∠MGF＝45°，∴∠EGF＝90°，∴△EGF的形状不发生变化，是等腰直角三角形；②如图2，由题意知，MG的运动路线是从MN开始，至MC结束，∴点H的运动路程是如图所示的HO，∵H是MN的中点，O是MC的中点，∴HO＝NC＝1，∴线段MG的中点H运动的路程最长为1；（3）①由（1）和（2）知，△AME≌△DMF≌△NMG，∴AE＝NG＝x，BE＝2﹣x，∴EG2＝BE2+BG2＝（2﹣x）2+（2+x）2＝8+2x2，∴S△EGF＝EG2＝（8+2x2）＝x2+4，∴当S＝6时，x＝（取正值）；②由题意知，0≤x≤2，∴当x＝0时，S有最小值4；当x＝2时，S有最大值8，故S的取值范围为：4≤S≤8．11．解：（1）过点E作EG⊥CF于G，连接EF，∵AF＝AD，E是AB的中点，AB＝AD＝4，∴AF＝1，FD＝3，AE＝BE＝2，∴CF＝＝＝5，∵S△EFC＝4×4﹣×4×2﹣×2×1﹣×3×4＝5，∴S△EFC＝×CF×EG＝5，∴EG＝2＝BE，且EG⊥CF，EB⊥BC，∴CE平分∠BCF；（2）设CP＝a，∵四边形ABCD是正方形，∴∠GDQ＝∠BAQ＝90°，∵点Q是AD的中点，∴DQ＝AQ，∵∠DQG＝∠AQB，∴△GDQ≌△BAQ（ASA），∴DG＝AB＝4，∴CG＝CD+DG＝4+x，在Rt△BPE中，PE2＝BE2+BP2＝（4﹣x）2+（4+a）2，在Rt△GCP中，GP2＝CP2+CG2＝（4+x）2+a2，∵PE＝PG，∴a＝2x﹣2，PQ2＝PE2﹣QE2＝4x2+16，∴PQ＝，∴S＝y＝××＝2x2+8（其中0≤x≤4）（3）如图，MM′即为M点运动的距离；当点E与点A重合时，∵PQ⊥EQ，∠BAQ＝∠ABP＝90°，∴四边形ABPQ是矩形，∴BP＝AQ＝2，当点E与点B重合时，由（2）可得P'E'＝P'G，DG＝AB＝4，∴CG＝8，∵P'G2＝P'C2+CG2，∴P'E'2＝（P'E'﹣4）2+64，∴P'E'＝10，∴P'P＝8，∵点M，点M'分别是QP，QP'的中点，∴MM'＝PP'＝4，∴点M的运动的路线的长为4．12．解：（1）过点P作PE⊥OA，垂足为E，过点Q作QF⊥BP，垂足为F，如图1．∵BP∥OA，PE⊥OA，∴∠EPF＝∠PEO＝90°．∵∠APQ＝90°，∴∠EP A＝∠FPQ＝90°﹣∠APF．在△PEA和△PFQ中，∴△PEA≌△PFQ．∴PE＝PF，EA＝QF．∵a＝，∴P（，3）．∴OE＝BP＝，PE＝3．∵A（2，0），∴OA＝2，∴EA＝0.5．∴PF＝3，QF＝0.5．∴点Q的坐标为（4.5，3.5）．（2）如图2，作O点关于直线l的对称点O′，连接AO′，交直线l于点P，此时OP＝O′P，∴P A+PO＝P A+PO′，∴AO′是P A+PO的最小值，∵点B的坐标为（0，3）．∴点O′（0，6），．设直线AO′为y＝kx+6，代入A（2，0）得，0＝2k+6，解得k＝﹣3，∴直线AO′为y＝﹣3x+6，把y＝3代入得，3＝﹣3x+6，解得x＝1，∴P（1，3），∴当P A+PO最小时，a＝1．。

初三轨迹问题解题技巧如下：
1. 直接法：根据动点所满足的等量关系列出方程，通过化简得到轨迹方程。

2. 定义法：根据各种已知曲线（直线、圆、圆锥曲线等）的定义，结合题意直接设出这些曲线的方程，再利用已知条件求出方程中各项系数的方法。

3. 相关点法：当曲线上一个动点的变动与另外一个动点相关时，可用曲线上该动点的坐标表示出另外一个点的坐标，把此点的坐标代入制约条件就可得到所求曲线的方程，这种方法就叫相关点法（又叫代入法）。

4. 参数法：参数法就是把曲线上动点的坐标先用相关参数表示出来，然后消去参数就得到。

以上是初三轨迹问题解题的一些技巧，希望对解决您的问题有所帮助。