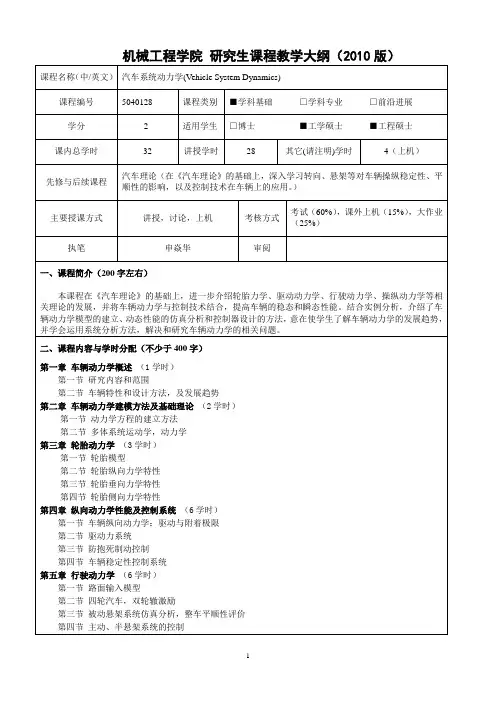
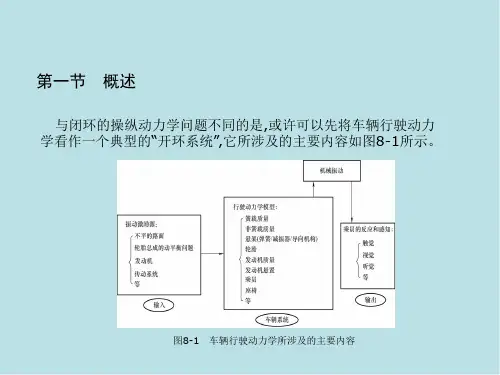
S (n) G0n p (8 3)
式中,G0为路面谱密度不平度系数,其大小随路面的粗糙程度而递增;指数p 表示双对数坐标下谱密度曲线的斜率。有些情况下,路面谱密度公式包含的 斜率可能不连续,如图8-6所示的实测路面谱就有两段不同斜率的情况[5], 这时,式(8-3)则可写成如下形式:
S (n)
4.6×10-7
2.75
支路
5.6×10-7
3.15
MIRA石子路① 1.7×10-5
5.9
斜率 p2
— 1.16 2.42 1.55
下截止 空(间cyc频le率/mn)0/
0.01 0.01 0.01 0.04
断点处 空(间cyc频le率/mn)d/
— 0.30 0.20 0.16
如果仅以基本行驶模型分析为目的,通常式(8-3)表示的单斜率路面输入模 型基本上就可满足要求。假如不平度系数G0按表8-3取值,则斜率p值通常 取2~2.5为宜。
图8-5 由实测路面位移到频域表达的分析过程
显然,低频长波通常有较大的振幅,而高频短波具有较小的振幅。图8-6所示的 实际路面的频谱密度图就清晰地表明了这一点。
图8-6 实测的典型主干道路面谱密度
国际标准化组织推荐采用路面功率谱密度来描述路面不平度的统计特性,并制 定了《机械振动—地面车辆—测量数据报告方法》标准,为单道或多道路面不平度 测量数据提供了统一报告方法,适用于乡道、街道、公路以及非路面的不平度测量 的数据处理。ቤተ መጻሕፍቲ ባይዱ
S(f)= G0n p = G0u p1 (8-5)
u
fp
式中,f为时间频率;u为恒定的车辆行驶速度。
对于线性车辆模型来说,式(8-5)表示的路面模型可直接用来作为频域分