里德伯常数的测定
- 格式:pdf
- 大小:71.30 KB
- 文档页数:3


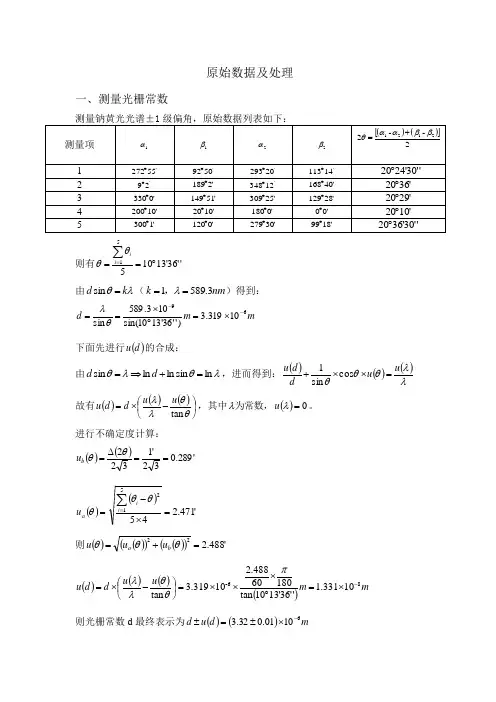
原始数据及处理一、测量光栅常数测量钠黄光光谱±1级偏角,原始数据列表如下: 测量项 1α1β2α2β()()[]2--22121ββααθ+=1 '55272︒'5092︒ '20293︒'14113︒ ''30'2420︒ 2 '29︒ '2189︒ '12348︒ '40168︒ '3620︒ 3 '0330︒ '51149︒ '25309︒ '28129︒ '2920︒ 4 '10200︒ '1020︒ '0180︒ '00︒'1020︒ 5'1300︒'0120︒'30279︒'1899︒''30'3620︒则有''36'1310551︒==∑=i iθθ由λθk d =sin (nm k 3.5891==λ,)得到:m m d 6910319.3)''36'1310sin(103.589sin --⨯=︒⨯==θλ下面先进行()d u 的合成:由λθλθln sin ln ln sin =+⇒=d d ,进而得到:()()()λλθθθu u d d u =⨯⨯+cos sin 1 故有()()()⎪⎭⎫⎝⎛-⨯=θθλλtan u u d d u ,其中()0=λλu 为常数,。
进行不确定度计算:()()'289.032'1322==∆=θθb u ()=θa u ()'471.245512=⨯-∑=i i θθ则()()()()()'488.222=+=θθθb a u u u()()()()m m u u d d u 86-10331.1''36'1310tan 18060488.210319.3tan -⨯=︒⨯⨯⨯=⎪⎭⎫ ⎝⎛-⨯=πθθλλ 则光栅常数d 最终表示为()()m d u d 61001.032.3-⨯±=±二、测量里德伯常数根据巴尔末系公式()⋯=⎪⎭⎫⎝⎛-=5,4,3121122n n R H λ以及λθk d =sin 可以得到: ()2141ln ln sin ln ln ln nR d k H -+=--θ由于可视为常数与k n ,可以化简为:()()()⎪⎭⎫⎝⎛--⨯=θθtan u dd u R R u H H1、1级红光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '21230︒'1850︒ '40207︒'3927︒ ''30'2111︒ 2 '26296︒ '24116︒'44273︒'4293︒'2011︒则有''45'2011221︒=+=θθθ里德伯常数1722100971.11389.01sin 1312111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i4-21210209.212⨯=⨯-∑=θθ()()()()()4-2210775.2⨯=+=θθθb a u u u则得到()()()141081.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)8.11.1097(-⨯±=±m R u R H H 2、1级蓝光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '38351︒'38171︒ '268︒'26188︒ '248︒ 2'3581︒ '33261︒'2998︒'25278︒''30'268︒则有rad 1470.0''15'258221=︒=+=θθθ里德伯常数1722100958.11875.01sin 1412111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i 4-21210040.212⨯=⨯-∑=θθ()()()()()4-2210642.2⨯=+=θθθb a u u u则得到()()()141002.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)0.18.1095(-⨯±=±m R u R H H 3、2级红光谱线及其数据处理原始数据列表如下: 测量项 1α1β2α2β()()[]2--212121ββααθ+⨯=i1 '0337︒'0157︒ '2023︒'10203︒ ''30'723︒ 2 '5066︒ '50246︒'10123︒'10303︒'1023︒则有rad 4040.0''45'823221=︒=+=θθθ里德伯常数1722100981.11389.01sin 2312111-⨯=⨯=-⨯=m d R H θλ进行不确定度的计算:()()rad u b 4-10679.1'289.032'1322⨯===∆=θθ ()=θa u ()rad i i 4-21210506.312⨯=⨯-∑=θθ()()()()()4-2210887.3⨯=+=θθθb a u u u则得到()()()141044.1tan -⨯=⎪⎭⎫ ⎝⎛--⨯=m u dd u R R u H H θθ里德伯常数最终表示为()1410)4.11.1098(-⨯±=±m R u R H H 4、通过加权平均值来获得H R 的最佳值:()()()()173123121009667.11-==⨯==∑∑m R u R u R R i Hi i Hi HiH()()()1431210741.011-=⨯==∑m R u R u i Hi H则获得里德伯常数的最佳表达式()()14107.07.1096-⨯±=±m R u R H H 与里德伯常数标准值534.10973731=H R 相比较,其相对误差为%0641.0%100=⨯-=HHH R R R E ,相对误差已经很小。


光栅单色仪计算里德伯常量
里德伯常量(Rydberg constant)是一个物理常量,它表示了由原子能级组成的光谱线之
间的精确关系。
它是研究光谱学和原子性质的基本工具,是光栅单色仪计算时不可或缺的参数。
光栅单色仪计算里德伯常量的方法是利用光栅单色仪把原子发出的单色光信号分解成多条
精密的光谱线来测量这些光谱线之间的相对位置和强度,通过特定的仪器和物理量测来推断里
德伯常量的值。
此外,光栅单色仪计算里德伯常量的原理也可以用于计算更高的精度。
它主要利用光谱分
析仪对原子发射的对应到某一波长的单色光进行检测,而位置分辨率则取决于设备的品质。
根
据光谱参数和原子能级构成,可以将里德伯常数计算出来。
光栅单色仪计算里德伯常量时,还可以使用同步加载等特殊方式,采用选择性发射技术,
将线性光源与磁场的有效结合,帮助实现更高的精度,获得更精准的里德伯常量值。
当然,光栅单色仪计算里德伯常量的时候,仪器的质量仍然非常重要,质量好的仪器才能
得到更高的精度。
因此,在购买光栅单色仪来计算里德伯常量时,需要用户选择高品质仪器,
以保证精度要求。

由钠原子光谱测定里德伯常数
里德伯常数是物理学中一个重要的常数,它是电荷和电场之间的关系,它的值决定了电荷和电场之间的关系。
里德伯常数的值是由钠原子光谱测定的。
钠原子光谱测定里德伯常数的原理是:当钠原子处于电场中时,它会受到电场的影响,电子会从原子的低能级跃迁到高能级,从而产生光谱线。
根据光谱线的频率,可以计算出里德伯常数的值。
钠原子光谱测定里德伯常数的实验步骤是:首先,将钠原子放入真空容器中,然后在容器中施加电场,使钠原子处于电场中,最后,用光谱仪测量钠原子发出的光谱线,根据光谱线的频率计算出里德伯常数的值。
钠原子光谱测定里德伯常数的结果表明,里德伯常数的值为2.17×10^-
18J·m,这个值与其他实验结果相符,说明钠原子光谱测定里德伯常数是一种可靠的方法。
总之,钠原子光谱测定里德伯常数是一种可靠的方法,它可以准确测定里德伯常数的值,为物理学的研究提供了重要的参考。

氢原子光谱和里德伯常量测定 —-以及实验数据处理方法的选择摘要: (3)Abstract:Key words: (3)1.实验背景 (3)2. 实验要求 (3)2.1实验重点 (3)2.2实验要点 (3)3.实验原理 (4)3.1光栅及其衍射 (4)3.2光栅的色散本领与色散分辨本领 (5)3.3氢原子光谱 (6)4.测量结果的加权平均 (7)5.实验仪器介绍 (8)6.实验内容 (8)7.实验数据记录及处理 (8)1.光栅常数测量 (9)2.氢原子光谱测里德波尔常数 (10)3.色散率和色分辨本领 (12)8.不同的数据处理方法 (13)8. 1 波数为因变量的一般直线拟合 (13)8.2波长为因变量的直线拟合 (14)8.3加权平均法求RH (14)8. 4 波数为因变量的过原点直线的加权拟合 (14)9.实验感想与总结 (14)10.参考文献 (15)摘要:关键字:Abstract:Key words:1.实验背景衍射光栅在现代光谱分析中具有重要应用。
无论发射光谱仪器,还是吸收光谱仪器中的色散元件,大多使用性能优良的光栅。
光栅的刻槽密度可达4800条/mm。
进入纳米科学范围,属于光、机、电结合的高科技领域。
衍射光栅作为各种光谱仪器的核心元件,广泛应用于石油化工、医药卫生、食品、生物、环保等国民经济和科学研究的诸多部门。
光谱分析就是利用物质发射的光谱对其元素组成做出分析和判断,它在诸如地质找矿、冶金成分的分析、材料的超纯检测或微量元素识别等国民经济和教学科研各部门被广泛才用。
在高科技领域,如各种激光器特别是强激光核聚变、航空航天遥感成像光谱仪、同步辐射光束线等,都需要各种特殊光栅。
现代高科技的发展,使光栅有了更广泛的重要应用,许多高科技项目应用的特种光栅还有待于进一步开发。
发射光谱有三种类型:线状光谱、带状光谱和连续光谱。
氢原子光谱是一种典型的线状光谱,它是量子力学理论得以建立的最重要的是要基础之一。

里德伯常量是原子物理学中的基本物理常量之一。
为一经验常数,一般取R=1.097373157×10^7m-1。
里德伯常量起初是在为表示氢原子光谱的里德伯公式中引入的,1/λ=R[(1/n2)-(1/m2)]。
其中的R,即里德伯常量,实验测得的数值为:R=1.0967758×10^7m-1。
1913年波尔推导出其理论值,为R=1.09737315689396×10^7 m-1,与实验值吻合得很好。
后来,波尔引入约化质量,计算出理论值R=10967757.8m-1。
相关历史
1885年,瑞士数学教师约翰·雅各布·巴尔默(J.J.Balmer)在一篇论文中报告了氢原子光谱的一个经验规律:1/λ=R[(1/21)-(1/n1)],同时得出里德伯常量的近似数值。
1908年,德国物理学家弗里德里希·帕邢(Friedrich Paschen)发现了氢原子光谱的帕邢系。

棱镜分光计测量里德堡常数
棱镜分光计测量里德堡常数,以氢灯为光源,利用棱镜分光计,通过测定氢原子巴尔末谱系中三条可见光谱线的波长来测定里德堡常数。
测量结果误差小于0.5%,实现了使用普通常规仪器测量波谱常数。
实验时,先利用光栅测量汞光灯8 条谱线的波长(表1)利用镜分光计测出棱镜顶角及汞灯8 条谱线对应的最小偏向角,计算出棱镜对不同波长的折射率(表2), 作出棱镜的色散曲线,利用柯西公式对实验所得色散曲线进行拟合。
给出色散公式(图1)。
再以氢灯为光源、用棱镜分光计测出棱镜对氢原子进的最小偏向角,计算出相应的折射率(表3).然后由色散公式求出氢原子此 3 条谱线对应的波长。
将入a,入 6.入y代入原子巴尔末线系的公式(2(4),求得里德堡常数R(表4)。

氢原子光谱和里德伯常数的测定基础物理实验研究性报告一、实验目的1.掌握氢原子光谱测定方法。
2.理解和测定氢原子光谱系列。
3.通过测定氢原子光谱系列来计算里德伯常数。
4.分析实验结果并对其进行讨论。
二、实验原理1.氢原子光谱2.里德伯常数里德伯常数是描述氢原子光谱的重要物理常数,用于计算光谱线的频率和能级之间的能量差。
三、实验装置和材料1.光谱仪:用于测定氢原子光谱的波长。
2.氢放电装置:用于产生氢原子光谱。
3.高频电源:用于提供激发氢原子的电磁场。
4.精密光栅:用于分光。
5.光电倍增管:用于探测光信号。
四、实验步骤1.调整光谱仪和测定仪器,确保仪器的准确性和稳定性。
2.打开氢放电装置,产生氢原子光谱。
3.使用光谱仪测定不同波长的氢原子光谱,并记录光谱线的位置。
4.根据光谱线的位置和光谱系列的特点,确定氢原子光谱系列。
5.根据光谱系列和波长的关系,计算里德伯常数。
6.重复实验多次,计算平均值,并进行误差分析。
五、实验结果1.根据光谱线的位置,确定氢原子光谱系列为巴耳末系列。
2.根据巴耳末系列的波长和能级公式,计算里德伯常数的值。
六、实验分析和讨论七、实验结论通过本实验的研究,我们成功测定了氢原子的光谱并计算了里德伯常数。
实验结果与理论值相符,验证了实验方法的准确性和可靠性。
同时,根据实验结果可以进一步了解氢原子的能级结构,并研究光谱与能级之间的关系。
八、实验总结本实验通过测定氢原子光谱和计算里德伯常数的方法,深入研究了氢原子的光谱现象和能级结构。
通过实验的方法和结果,我们对氢原子的能级、波长和光谱系列有了更深入的理解。
同时,实验还进一步验证了实验方法的准确性和可靠性。
通过本次实验的学习,我们进一步掌握了基础物理实验的重要方法和技巧,并对物理实验的研究方法有了更深入的了解。

氢原子光谱和里德伯常数的测定基础物理实验研究性报告摘要:本实验通过测量氢原子光谱的发射线,利用巴尔末系列公式计算氢原子的波长和对应的频率。
通过计算求得里德伯常数。
实验结果显示,通过对氢原子光谱发射线的精确测量计算,我们得到了一个非常接近理论值的里德伯常数。
引言:在物理学中,氢原子光谱和里德伯常数是非常重要的研究内容。
氢原子的光谱可以通过精确测量发射线的波长和频率来研究。
里德伯常数是描述氢原子光谱的一个重要参数。
本实验通过测定氢原子光谱的发射线,计算出里德伯常数。
实验方法:1.实验仪器:用于测量光谱的光栅仪、频率计、电源等。
2.实验步骤:a.首先调整光谱仪的位置和角度,以确保获得清晰的光谱。
b.通过频率计测量氢原子光谱发射线的频率。
c.使用巴尔末系列公式计算波长,并计算对应的频率。
d.根据计算结果,得出里德伯常数。
实验结果与讨论:通过实验测量的氢原子光谱发射线的频率,我们计算得到了氢原子的波长和对应的频率。
利用计算结果,我们得到了里德伯常数的数值,并与理论值进行对比。
实验结果显示,我们得到的里德伯常数非常接近理论值。
结论:本实验通过测量氢原子光谱的发射线,计算出了里德伯常数。
实验结果显示,通过对氢原子光谱发射线的精确测量计算,我们得到了一个非常接近理论值的里德伯常数。
这个实验为研究氢原子的光谱和里德伯常数提供了有力的支持。
1. Griffiths, D. J. (2024). Introduction to quantum mechanics. Cambridge University Press.2. Cao, G. Z., Shu, S. B., & Gao, W. B. (1981). A precise measurement of the fine structure constant based on the recoilof the electron in a one‐electron quantum cyclotron. Applied Physics Letters, 39(8), 691-692.。
基础物理实验研究性报告题目:氢原子光谱和里德伯常数的测定2012年4月28日氢原子光谱和里伯德常数的测定【摘要】:本实验把作为分光元件的光栅和精密测角仪分光仪联合起来进行氢光谱的观察与测量,从而测得了氢原子光谱巴耳末系的波长,采用加权平均确定了里德伯常数。
除此之外,还进行了一些讨论。
【关键字】:氢原子光谱;分光仪;里德伯常数【abstract 】:This experiment as a spectral components of the grating and precision Angle measuring instrument spectrometers for hydrogen combined spectrum of the observation and measurement, which were measured and the ear of the hydrogen atom spectrum of the wavelength, the weighted average determined the rydberg constant. In addition, also made some discussions.【key words 】: hydrogen atoms spectrum; Spectrometers; Rydberg constant目录一、实验原理 (1)1、光栅及其衍射 (1)2、光栅的色散分辨本领与色分辨本领 (2)3、氢原子光谱 (3)二、实验仪器 (4)1、分光仪 (4)2、投射光栅 (4)3、钠灯及电源 (4)4、氢灯及电源 (4)三、实验步骤 (4)1、调节分光仪 (4)2、调节光栅 (4)3、测光栅常数 (5)4、测量氢原子里德伯常数 (5)四、数据处理 (5)1、用钠灯测光栅常数 (5)2、用氢灯测定里德伯常数 (6)3、计算钠黄光角色散率和分辨本领 (7)五、实验讨论 (8)六、参考文献 (8)一、实验原理 1、光栅及其衍射波绕过光栅而传播的现象称为衍射。
氢原子光谱和里德伯常数的测量Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】氢原子光谱和里德伯常数的测量第一作者 XXX第二作者 XXX指导老师:XXX一、实验要求实验重点○1巩固、提高从事光学实验和使用光学仪器的能力(分光仪的调整和使用)○2掌握光栅的基本知识和方法○3了解氢原子光谱的特点并使用光栅衍射测量巴尔末系的波长和里德伯常数○4巩固与扩展实验数据处理的方法——测量结果的加权平均,不确定度和误差的计算,实验结果的讨论等1、 预习思考题○1如何由()出发证明:在相邻的两个主极大之间由N-1个极小,N-1个次极大;N 越大,主极大的角宽度越小答:光栅衍射可以看作是单缝衍射和多缝干涉干涉的综合。
当平面单色光正入射到光栅上时,其衍射光振幅的角分布正比于单缝衍射因子sin αα和缝间干涉因子sin sin N ββ的乘积,及沿着 θ方向的的衍射光强220sin sin ()()()sin N I I αβθαβ=,式中sin sin ,,a d N θθαβλλ==是光栅的总缝数。
当sin 0β=时,sin N β也等于0,sin sin N N ββ=,()I θ形成干涉极大;当sin 0N β=但sin 0β≠时,()0I θ=,为干涉极小。
它说明:两个相邻的主极大之间有N-1个极小,N-2个次极大;N 数越多,主极大的角宽度越小。
○2 氢原子里德伯常数的理论值等于什么氢原子光谱的巴尔末系中对应的n=3,4,5的3条谱线应当是什么颜色答:理论值±)1m -。
谱线分别是红色、蓝色、与紫色。
○3 总结分光仪调整的关键步骤,在调整望远镜接受平行光、望远镜光轴垂直仪器主轴、平行光管射出平行光、平行光管主轴垂直仪器主轴的过程中应分别调整什么调整完成的标志又是什么答:分别应该调整目镜与载物台;载物台调平螺母;狭缝套筒与平行光管的水平调节螺母。
氢原子光谱中的里德堡常数测量【实验目的】1. 掌握SBP300型光栅光谱仪的工作原理和使用方法,学习识谱和谱线测量等基本技术。
2. 通过所测得的氢(氘)原子光谱在可见和近紫外区的波长验证巴尔末公式并准确测出 氢(氘)的里德伯常数。
3.测出氢、氘同位素位移,理解测量质子与电子质量比的方法。
【实验原理】1913年玻尔提出了氢原子模型并进一步假设:(1) 电子在原子中沿特殊轨道运动时电子处于稳定状态,虽然电子绕核作加速运动,但不会随意吸收和发射辐射,故将这些态称为定态.(2) 当一个电子以某种方式从一个定态m E 向另一个定态n E 跃迁时,原子就会吸收或发射 光子。
光子的频率为:hE E mn -=ν 而当电子从状态n E 跃迁到m E 时,就发射出同频率的光子。
由于m E ,n E 都是不连续的值,因此光子的频率也是分立的,故可以知道原子光谱为线状光谱。
(3)为了简单起见,电子运动的轨道选择为一些圆形轨道,但电子在这些轨道运动时的角动量是)2/(πh = 的整数倍,即角动量是量子化的:n hnmvr L ===π2, n = 1, 2, 3 … 根据玻尔假设,结合经典电学和力学,很容易求得氢原子中电子能级的大小。
电子在轨道上运动时,核对它的静电吸引力提供向心力。
对于圆周运动,则有20224r e r v m πε= 2024mv e r πε=根据玻尔角动量量子化假设mvn r =故有:2024mve mv n πε= 则:ncn e v απε==0242022204n a men r == πε 式中α为精细结构常数,0a 为玻尔半径。
电子的能量为动能与势能之和,当它在第n 个轨道运动时,能量为:222040228421nh me r e mv E n επε-=-= 由上可见,无论是电子的轨道半径r 、运动速度v ,还是电子的能量E ,它们均是分立的。
1=n 的状态称为氢原子的基态,2≥n 的态称为激发态。
氢原子光谱和里德伯常数测量综合探究第一作者:班级学号姓名第二作者:班级学号姓名日期:2013年5月22日目录摘要 (1)1实验目的 (2)2 实验原理 (3)2.1分光仪的调整 (3)2.2光栅及其衍射 (4)2.3光栅的色散本领与色分辨本领 (6)2.4 氢原子光谱 (8)3实验仪器 (10)4实验内容 (11)4.1调节分光仪 (11)4.2调节透射光栅 (13)4.3测光栅常数 (13)4.4测量氢原子里德伯常数 (13)5实验数据处理 (14)5.1光栅常数d的测量 (14)5.2氢原子光谱测里德伯常数 (15)5.3误差分析 (18)6实验数据处理再分析 (19)6.1波数为因变量的直线拟合 (19)6.2 等权平均法 (19)7总结与讨论 (21)7.1分光仪调节经验总结 (21)7.1.1 分光仪粗调方法 (21)7.1.2 十字反射像的寻找方法 (21)7.1.3调节望远镜光轴与分光仪轴垂直正交 (22)7.2固定透射光栅的技巧 (23)7.3实测谱线具有一定宽度的原因分析 (23)7.4钠黄双线能否被观测到分开的探讨以及不确定度进一步讨论 (23)8实验感想 (26)9 参考文献 (27)摘要:氢原子光谱是一种典型的线状光谱,是量子理论得以建立的最重要的实验基础之一。
该实验把作为分光元件的光栅和精密测角仪器的分光仪结合起来进行氢光谱的观察与测量。
本文通过介绍实验的原理、步骤、仪器,并对实验数据进行不同方式的处理与对比及最后结果的进一步探讨。
此外,还分析了分光仪调整方法、调整技巧以及在实验过程中未能观察到钠黄双线被分辨的原因等。
借助进一步研究该实验综合性地梳理了分光仪、光栅以及氢原子光谱的知识。
关键词:氢原子光谱分光仪钠黄光双线加权平均1巩固提高从事光学实验和使用光学仪器的能力;2掌握光栅的基本知识和使用方法;3了解氢原子光谱的特点并用光栅衍射测量巴耳末系的波长和里德伯常数;4巩固与扩展分光仪调节,实验数据的处理方法,及测量结果的加权平均,不确定度和误差计算,实验结果的讨论等。
里德伯常数的测定
氢原子的光谱现在按波长(或波数)大小的排列次序上显示出简单的规律性,测量氢灯各光谱线的波长值可以来了解原子的能级结构。
本实验用分光计测量氢原子的光谱线波长,并通过巴尔末公式推算里德伯常数。
原理
氢原子的光谱线在可见光区共有四条,分别用αH (红线)βH (蓝绿线)γ
H (青线)和δH (紫线)记号来标志。
他们的波数ν(波长λ的倒数)可以准确地用实验公式
)121(
2
2n R H −=ν
(1)
表示,式中n 是大于2的整数,即3,4,5,…每一个数代表一条谱线,而H R 是一个实验常数,称为里德伯常数。
式(1)就是著名的巴尔末公式。
若利用分光计准确的测定上述四条谱线的波长,并分别代入(1)式,即可由实验方法确定里德伯常数。
此外,根据玻尔关于原子构造的量子假设,里德伯常数与原子内部若干微观量和有关物理普适常数的关系是:
)
1(83
20
4
H
H M m m
h ce e R +=
(2)
式中e 为电子电荷,m 为电子质量,H M 为氢原子核的质量,
5
.18361
=H M m ,c 为光在真空中的传播速度,0ε为真空介电常数,h 为普朗克常数。
由此算出里德伯常数的理论值 m R H /1009678.17×=
实验内容
1﹑以钠灯为光源,利用分光计及光栅测出衍射角,再算得光栅常数。
2﹑用氢气放电管作为光源,分别测出氢原子三条谱线(αH ,βH ,γH )所对
应的衍射角αϕ、βϕ、γϕ,并由此求得他们的波长αλ,βλ,γλ(人眼对δH 线很不灵敏,故不作测量)
利用式(1)计算里德伯常数的实验值。
例1.利用钠灯测量光栅的光栅常数。
当nm 3.589=λ,测得光栅常数为 3(1.67740.0004)10d d mm σ−±=±×
2.用氢气放电管作为光源,测出氢原子三条谱线波长αλ,βλ,γλ所对应的1±级,
零级衍射光的位置读数见表一。
表一
λ
+1级读数 -1级读数 零级读数
1窗口读数 2窗口读数 1窗口读数 2窗口读数 1窗口读数
2窗口读数
红线(αλ)
215410′′′°215410′′′°215400′′′°215410′′′°215410′′′° 35410′′′°35410′′′°35410′′′°354130′′′°354030′′′° 169380′′′°169390′′′°169390′′′°169390′′′°169390′′′° 349370′′′°349380′′′°349380′′′°349380′′′°349390′′′° 192390′′′°192400′′′°192400′′′°192400′′′°192400′′′° 123930′′′°12400′′′
°12400′′′
°12400′′′°124030′′′°
平均 215.680° 35.683° 169.647° 349.633° 192.663° 12.667°
蓝线(βλ)
209300′′′°2093030′′′°209300′′′°2093030′′′°209300′′′° 292930′′′°29300′′′°29300′′′°29300′′′°29300′′′° 1754930′′′°175490′′′°175490′′′°175490′′′°1754930′′′° 355490′′′
°3554930′′′
°355490′′′°355490′′′°3554930′′′°
平均 209.503° 29.498° 175.817° 355.820°
青线(γλ)
207390′′′°207390′′′
°2073930′′′°207390′′′°2073930′′′° 27390′′′°27390′′′°273930′′′°27390′′′
°27390′′′° 177390′′′°177400′′′°1774030′′′°1774030′′′°177400′′′° 093357′
′′
004357′
′′
004357′′′ 0304357′′′ 0304357′′′
平均 207.653° 27.652° 177.667° 357.667°
由表一可以分别计算这三根谱线的衍射角,波长及里德伯常数见表二。
表二
ϕϕσ±
λλσ±(A
) 1
()H RH
R mm σ−± α 23.021°±0.003° 6559.8±1.6 1097.6±3 β 16.842°±0.003° 4860.0±1.7 1097.4±4 γ 14.944°±0.003°
4339.7±1.7
1097.3±4
H R 的平均值及标准偏差为
7
ˆ(1.09750.0001)10/H R R m σ±=±×。
思考题
1. 氢原子在可见区、红外区、紫外区的所有谱线可统一用一个简单的公式表示:
2211
(H oi R n n
ν
=− 式中oi n =1﹑2﹑3﹑… ;n=oi n +1﹑oi n +2…。
根据什么原则来选定各氢光谱线的n 的可能值?又怎么来判别某个n 值的可能值是正确值?oi n 又怎么求得呢?(提示:可作2
1
n ν
− 图线来判断所选定n 的正确性及求得oi n 。
) 2.光谱中若出现不属于氢的谱线,应如何判断?。