非线性最小二乘平差
- 格式:doc
- 大小:512.50 KB
- 文档页数:24

最小二乘法设(x 1, y 1 ), (x 2, y 2), …, (x n, y n)是直角平面坐标系下给出的一组数据,若x 1<x 2<…<x n,我们也可以把这组数据看作是一个离散的函数。
根据观察,如果这组数据图象“很象”一条直线(不是直线),我们的问题是确定一条直线y = bx +a ,使得它能"最好"的反映出这组数据的变化。
最小二乘法是处理各种观测数据进行测量平差的一种基本方法。
如果以不同精度多次观测一个或多个未知量,为了求定各未知量的最可靠值,各观测量必须加改正数,使其各改正数的平方乘以观测值的权数的总和为最小。
因此称最小二乘法。
所谓“权”就是表示观测结果质量相对可靠程度的一种权衡值。
法国数学家勒让德于1806年首次发表最小二乘理论。
事实上,德国的高斯于1794年已经应用这一理论推算了谷神星的轨道,但迟至1809年才正式发表。
此后他又提出平差三角网的理论,拟定了解法方程式的方法等。
为利用最小二乘法测量平差奠定了基础。
最小二乘法也是数理统计中一种常用的方法,在工业技术和其他科学研究中有广泛应用。
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1、x2, y2... xm , ym);将这些数据描绘在x -y直角坐标系中(如图1), 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)其中:a0、a1 是任意实数为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用(式1-1)计算值(Y计= a0+a1X)的离差(Yi-Y计)的平方和`〔∑(Yi - Y计)2〕最小为“优化判据”。
令: φ = ∑(Yi - Y计)2 (式1-2)把(式1-1)代入(式1-2)中得:φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)当∑(Yi-Y计)平方最小时,可用函数φ 对a0、a1求偏导数,令这两个偏导数等于零。


最小二乘平差最小二乘平差(Least Squares Adjustment)是测量数据处理中的一种常用方法,用于对测量观测数据进行最优估计。
通过该方法可以减小测量误差,提高测量精度,对于工程测量、测绘、地理信息系统等领域具有重要的应用价值。
原理介绍最小二乘平差的原理基于最小化观测量与观测值之间的残差平方和。
在测量过程中,常常会存在观测误差、系统误差等不确定因素,这些因素会导致观测值与真实值之间存在差异。
最小二乘平差通过对所有观测值进行加权,使得观测值与真实值之间的差异最小化。
设有n个观测值,每个观测值的观测量为O,真实值为T,观测误差为e。
则最小二乘平差的目标是找到最优的拟合/估计值x,使得:formula1通过对以上目标进行求解,可以得到最优的拟合/估计值x。
其中,观测值和真实值之间的关系可以通过各种数学模型进行描述,例如线性模型、非线性模型等。
应用场景最小二乘平差在测量数据处理中有广泛的应用。
以下是一些常见的应用场景:1.三角测量:在工程测量中,常用三角测量方法测量不同点之间的距离、角度等。
利用最小二乘平差,可以修正测量误差,提高测量精度。
2.高程测量:在测绘、地理信息系统中,通常需要测量地点的高程信息。
最小二乘平差可以对高程测量数据进行优化处理,提高高程测量的精度。
3.GPS定位:全球卫星定位系统(GPS)在导航、地图绘制等领域有着广泛的应用。
最小二乘平差可用于对GPS观测数据进行处理,提高定位的准确性。
4.建筑变形监测:在建筑工程中,对于建筑物的变形监测和建筑物的结构健康状况评估,最小二乘平差可用于对监测数据进行处理,及时发现异常情况。
实现方法最小二乘平差的实现方法有多种,常用的包括:1.高斯-马尔可夫模型:基于线性模型,通过最小二乘法对观测数据进行拟合估计。
该方法适用于满足高斯分布假设的情况。
2.递归最小二乘法:将观测数据分为多个子集,通过递归的方式对子集数据进行最小二乘拟合,然后合并得到最终的拟合结果。


光束法平差
光束法平差是测量学和测绘学中应用最广泛的一种平差方法,它以一组未知观测量解决地面测量所需要求解的问题为核心,建立一种系统的求解未定参数的数学模型,以便进行数据处理和分析。
光束平差应用范围广泛,是空间测量系统性能评价和空间位置测量准确性计算的一种重要工具。
光束法平差是一种逐步求解的解析平差方法,是一种数学最优化的空间数据优化的工具,为空间位置测量精度评价和尺寸变换等、求解空间多项式曲线拟合以及平面多项式曲线拟合等等提供了可靠而有效的计算方法。
光束法平差建立在非线性最小二乘拟合基础上,是以观测数据作为解决问题的核心,这些数据可以来自测量的结果,也可以来自GPS定位系统、近地表面导航系统甚至基于图像的定位系统。
其最主要的特点是,通过将观测数据转化成未定参数的无量纲模型,以最小二乘拟合的方式求解未定参数及其误差。
光束法平差存在种种优缺点,其优点有: 1)光束法可以以一种系统性的方式求解任意给定的空间测量问题,及其未定参数和误差;2)可以有效地处理不能解被定的观测数据,耦合的影响;3)可定义可操纵的误差类型;4)可以快速、可靠地进行数据处理和分析。
光束法平差的缺点是:1)被观测数据集必须有一定数量才能计算;2)模型参数需要相同模型;3)对于相对较大的观测量,计算时间会很长;4)受限于光束法本身定义的范围,无法很好地处理不符合本质原理的被观测量数据集。
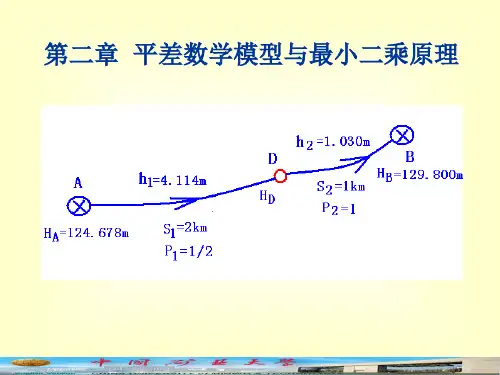

非线性最小二乘平差6-1问题的提出经典平差是基于线性模型的平差方法。
然而在现实世界中,严格的线性模型并不多见。
测量上大量的数学模型也是非线性模型。
传统的线性模型平差中的很多理论在非线性模型平差中就不一定适用;线性模型平差中的很多结论在非线性模型平差中就不一定成立;线性模型平差中的很多优良统计性质在非线性模型平差中就不一定存在。
例如,在线性模型平差中,当随机误差服从正态分布时,未知参数X的最小二乘估计具有一致无偏性和方差最小性。
但在非线性模型平差中,即使随机误差严格服从正态分布,未知参数X的非线性最小二乘估计也是有偏的。
其方差一般都不能达到最小值。
对于测量中大量的非线性模型,在经典平差中总是进行线性近似(经典的测量平差中称之为线性化),即将其展开为台劳级数,并取至一次项,略去二次以上各项。
如此线性近似,必然会引起模型误差。
过去由于测量精度不高,线性近似所引起的模型误差往往小于观测误差,故可忽略不计。
随着科学技术的不断发展,现在的观测精度已大大提高,致使因线性近似所产生的模型误差与观测误差相当,有些甚至还会大于观测误差。
例如,GPS载波相位观测值的精度很高,往往小于因线性近似所产生的模型误差。
因此,用近似的理论、模型、方法去处理具有很高精度的观测结果,从而导致精度的损失,这显然是不合理的。
现代科学技术要求估计结果的精度尽可能高。
这样,传统线性近似的方法就不一定能满足当今科学技术的要求。
另外,有些非线性模型对参数的近似值十分敏感,若近似值精度较差,则线性化会产生较大的模型误差。
由于线性近似后,没有顾及因线性近似所引起的模型误差,而用线性模型的精度评定理论去评定估计结果的精度,从而得到一些虚假的优良统计性质,人为地拔高了估计结果的精度。
鉴于上述各种原因,对非线性模型平差进行深入的研究是很有必要的。
非线性模型的平差和精度估计以及相应的误差理论研究也是当前国内外测绘界研究的前沿课题之一。
电子教材 > 第六章非线性模型平差 > 6-2 非线性模型平差原理一、非线性误差方程测量中大量的观测方程是非线性方程。

附不等式约束的总体最小二乘迭代算法汪奇生;杨根新【摘要】基于惩罚函数和测量平差中权的思想,提出了附不等式约束的总体最小二乘平差模型,即利用惩罚函数对不等式约束方程构造约束权,通过零权和无限权将不等式约束转换为等式约束,从而将不等式约束平差准则转化为传统的测量平差准则.同时,根据非线性最小二乘平差理论,用构造结构矩阵的方法来顾及系数矩阵的结构性,推导了附不等式约束的总体最小二乘迭代算法.该算法迭代格式与传统的间接平差类似,只需经过若干次迭代便能得到最优解.【期刊名称】《大地测量与地球动力学》【年(卷),期】2016(036)012【总页数】5页(P1100-1104)【关键词】不等式约束;EIV模型;总体最小二乘;迭代算法;惩罚函数【作者】汪奇生;杨根新【作者单位】湖南软件职业学院建筑工程学院,湘潭市开源路1号,411100;云南国土资源职业学院测绘地理信息学院,昆明市经牛路2号,650217【正文语种】中文【中图分类】P207总体最小二乘(total least squares)是一种能同时考虑系数矩阵误差的方法[1],受到各领域学者的广泛关注。
在测量数据处理中,总体最小二乘估计方法对应的平差模型为EIV(errors in variables)模型。
对于EIV模型的解算,国内外学者进行了深入研究[2-9]。
其中,文献[2]运用拉格朗日原理首次提出总体最小二乘的迭代法,文献[3]针对线性回归系数矩阵含有常数列提出了其总体最小二乘解,文献[4-8]研究了加权总体最小二乘算法并应用于测量数据处理。
除此之外,一些学者还研究了扩展总体最小二乘的一些其他算法[9]。
以上算法都没有考虑参数估计时的先验信息。
当存在某些先验信息时,可根据先验信息对参数附加某种约束。
如果约束是等式,则可以构建附有等式约束的总体最小二乘模型(equality constrained EIV,ECEIV)。
对于ECEIV模型的解算,文献[10-12]进行了详细论述。

最小二乘模糊度降相关平差法最小二乘模糊度降相关平差法(Least Squares Ambiguity Resolution Method, LSAR)是GNSS(全球导航卫星系统)精密定位中常用的一种方法,用于解决载波相位观测中的模糊度问题。
本文将详细介绍最小二乘模糊度降相关平差法的原理、步骤以及在GNSS精密定位中的应用。
一、原理在GNSS定位中,观测到的载波相位是包含了模糊度和测量噪声的结果,而模糊度是导致定位精度降低的主要原因。
最小二乘模糊度降相关平差法通过将载波相位观测值进行线性组合,并将模糊度作为参数引入到平差过程中,通过最小化残差和协方差矩阵来估计出最优的模糊度解,并提高定位精度。
具体来说,最小二乘模糊度降相关平差法的思想是通过构建一个适当的模糊度模型,将载波相位观测值与模糊度之间的关系建立起来。
通过对观测方程进行线性化,可以得到一个待估计参数为模糊度的线性方程组。
然后应用最小二乘法,通过最小化残差的平方和,将模糊度解与其他相关参数一起估计出来。
二、步骤最小二乘模糊度降相关平差法的具体步骤如下:1.构建模糊度模型:根据载波相位观测值的性质和预先设置的条件,构建模糊度模型。
常用的模型包括单差模型、双差模型和三差模型等。
2.线性化观测方程:将模糊度模型引入到载波相位观测方程中,并对观测方程进行线性化处理。
线性化的目的是为了将非线性观测方程转化为线性方程,以便于进行最小二乘平差。
3.构建设计矩阵:根据线性化后的观测方程,构建设计矩阵,其中每一行对应一个观测方程,每一列对应一个参数。
4.建立权阵:根据观测方程的精度信息,建立相应的权阵。
权阵可以用来加权处理观测方程,提高最小二乘平差的精度。
5.最小二乘平差:应用最小二乘法,通过最小化残差的平方和,估计模糊度解和其他相关参数。
同时,可以计算出参数的最佳估计值以及其协方差矩阵。
6.模糊度固定:根据最小二乘估计得到的模糊度解,进行模糊度固定。
模糊度固定是指将模糊度取整为最接近的整数值,以恢复精密定位。

土地测绘中平差计算的原理和方法土地测绘是一门通过测量、记录和分析地球表面特征的科学和技术。
在土地测绘中,平差计算是一个重要的步骤,它可以帮助我们准确地确定地图上的地理位置和边界。
本文将讨论土地测绘中平差计算的原理和方法。
平差计算的原理基于一个重要的概念,即误差传递。
在土地测绘中,无论是测量仪器的误差还是人为因素的误差,都会影响测量结果的准确性。
平差计算的目的就是通过对误差进行分析和修正,从而提高测量结果的精度。
平差计算的方法有多种,其中最常用的是最小二乘法。
最小二乘法通过最小化误差平方和的方式,找到最优解。
在土地测绘中,最小二乘法可以用于确定地理位置的坐标和边界的位置。
在进行平差计算之前,首先需要收集和整理测量数据。
这些数据可以包括测量仪器的读数、角度和距离等信息。
然后,对这些数据进行误差分析,找出可能存在的误差来源。
例如,测量仪器的读数可能存在零偏误差,而人为因素可能引入随机误差。
接下来,通过最小二乘法来进行平差计算。
最小二乘法的基本原理是将实测值与理论值之间的差异最小化。
通过建立一个数学模型,可以将测量数据和误差项联系起来。
然后,利用最小二乘法的公式,可以求解出误差的最小二乘估计值,从而得到最优解。
在平差计算中,还需要考虑一些特殊情况和修正因素。
例如,在地球曲率的影响下,地图上的直线实际上是一个弧线。
因此,在计算边界位置时,需要考虑地球曲率修正。
此外,地球表面的不规则性也会对平差计算产生影响,需要进行适当的修正。
除了最小二乘法,还有其他一些常用的平差计算方法。
例如,加权平差方法可以根据不同的误差来源,为每个观测量分配不同的权重。
这样可以更好地反映不同观测量的精确度。
此外,非线性平差方法可以应用于具有非线性关系的测量数据,如形状复杂的地表。
总之,平差计算在土地测绘中起着至关重要的作用。
通过对误差进行分析和修正,可以提高测量结果的精度和准确性。
最小二乘法是最常用的平差计算方法之一,它通过最小化误差平方和的方式,找到最优解。
误差理论综述与最小二乘法讨论摘要:本文对误差理论和有关数据处理的方法进展综述。
并且针对最小二乘法〔LS〕的创立、开展、思想方法等相关方面进展了研究和总结。
同时,将近年开展起来的全面最小二乘法(TLS)同传统最小二乘法进展了比照。
1.误差的有关概念对科学而言,各种物理量都需要经过测量才能得出结果。
许多物理量的发现,物理常数确实定,都是通过精细测量得到的。
任何测试结果,都含有误差,因此,必须研究,估计和判断测量结果是否可靠,给出正确评定。
对测量结果的分析、研究、判断,必须采用误差理论,它是我们客观分析的有力工具1.1测量根本概念一个物理量的测量值应由数值和单位两局部组成。
按实验数据处理的方式,测量可分为直接测量、间接测量和组合测量。
直接测量:可以用测量仪表直接读出测量值的测量。
间接测量:有些物理量无法直接测得,需要依据待测物理量与假设干直接测量量的函数关系求出。
组合测量:如有假设干个待求量,把这些待求量用不同方法组合起来进展测量,并把测量结果与待求量之间的函数关系列成方程组,用最小二乘法求出这个待求量的数值,即为组合测量。
1.2误差根本概念误差是评定测量精度的尺度,误差越小表示精度越高。
假设*物理量的测量值为y,真值为Y,则测量误差dy=y-Y。
虽然真值是客观存在的,但实际应用时它一般无从得知。
按照误差的性质,可分为随机误差,系统误差和粗大误差三类。
随机误差:是同一测量条件下,重复测量中以不可预知方式变化的测量误差分量。
系统误差:是同一测量条件下,重复测量中保持恒定或以可预知方式变化的测量误差分量。
粗大误差:指超出在规定条件下预期的误差。
1.3等精度测量的随机误差当对同一量值进展屡次等精度的重复测量,得到一系列的测量值,每个测量值都含有误差,这些误差的出现没有特定的规律,但就误差的总体而言,却有统计规律。
正态分布通过对大量的测量数据的观察,人们发现测量列的随机误差有以下几个特征:(1)绝对值相等的正误差与负误差出现的次数相等,即误差的对称性;(2)绝对值小的误差比绝对值大的误差出现的次数多,即误差的单峰性;(3)在一定的测量条件下,随机误差的绝对值不会超过一定界限,即误差的有界性;(4)随着测量次数的增加,随机误差的算术平均值趋于零,即误差的抵偿性。
最小二乘平差原理csdn
最小二乘平差原理是一种常用于数据处理和参数估计的方法。
它
是通过最小化观测值与预测值之间的差异的平方和来求解未知参数的
最优值。
最小二乘平差原理的基本思想是,通过建立一个数学模型来描述
观测量与待估参数之间的关系,然后使用观测数据进行模型参数的估计。
在建模过程中,通常会假设观测误差满足一定的概率分布,常见
的是假设观测误差服从正态分布。
根据这些假设,可以通过最小化观
测值与模型预测值之间的差异的平方和来求解最优的参数估计。
最小二乘平差原理在测量和定位领域有着广泛的应用。
例如,在
测量大地水准面时,可以通过观测水准仪的高程差来求解待估的地理
坐标,而最小二乘平差原理可以帮助我们优化地求解参数估计。
在全
球导航卫星系统(GNSS)定位中,最小二乘平差原理可以帮助我们估
计接收机钟差、卫星轨道参数等。
最小二乘平差原理的求解一般采用数值计算方法,例如最常见的
是利用矩阵运算来求解。
通过求解观测方程组,可以得到最优的参数
估计值及其相关参数,如方差、协方差等。
最小二乘平差原理是一种较为经典的数学处理方法,它的应用广
泛且成熟。
在实际应用中,我们需要根据具体的问题和数据特点,合
理地选取模型、构建观测方程组,才能得到准确可靠的参数估计结果。
它在测量、定位、导航等领域都有重要作用,是科学研究和工程实践
中不可或缺的重要工具之一。
非线性最小二乘的遗传算法与常规算法的比较
范辉辉;孙罗庆
【期刊名称】《地理空间信息》
【年(卷),期】2013(000)004
【摘要】为克服线性经典平差的不足,对非线性最小二乘进行了研究,主要将遗传算法应用于非线性模型参数估计领域,并采用阻尼最小二乘法和高斯-牛顿法对同一观测数据进行了处理,且对解算结果进行了比较。
【总页数】2页(P150-151)
【作者】范辉辉;孙罗庆
【作者单位】江西理工大学建筑与测绘工程学院,江西赣州341000; 广东省国土资源测绘院,广东广州510500;辽宁工程技术大学测绘与地理科学学院,辽宁阜新,123000
【正文语种】中文
【中图分类】P207
【相关文献】
1.求解非线性最小二乘全局解基于最速下降法和遗传算法的混合算法 [J], 赵明旺
2.基于遗传算法的维修时间分布参数非线性最小二乘估计 [J], 曾海军;陆中;戎翔;孙有朝
3.遗传算法改进及其在非线性最小二乘平差中的应用 [J], 谷川;张岳
4.混合遗传算法及其在非线性最小二乘估计中的应用 [J], 李春风
5.基于多群体遗传算法的非线性最小二乘估计 [J], 刘德玲;马志强
因版权原因,仅展示原文概要,查看原文内容请购买。
常用的地基沉降计算方法汇总
一、常见的地基沉降计算方法
1.简单光滑法
简单光滑法是最简单的地基沉降分析法,主要用于计算下拔法线和位移规律的变化。
方法是根据沉降点的实测观测值进行直线拟合,得出拟合的光滑曲线,再以该曲线为基础,求出焊接立柱等传感器沉降量。
2.三参数法
三参数法是地基沉降计算中较为常用的法则,又叫微分平差法和三参数最小二乘法,是在观测数据的基础上,拟合出一条光滑曲线来模拟测点的沉降曲线,以达到计算沉降量的目的。
3.非线性最小二乘法
非线性最小二乘法是对三参数法的一种改进,同时加入时间变量,以不同的时间作为参数,拟合出不同时间的沉降曲线,更加准确的计算沉降量。
4.指数衰减法
指数衰减法是将沉降衰减视为指数衰减的形式,将沉降量变化视为指数函数的形式,以此作为拟合曲线,最终计算出沉降量。
5.萜烯函数法
萜烯函数法是实验自由度较大的地基沉降计算方法,它能够有效的拟合沉降点中有抛物线变化的沉降曲线,以此计算出沉降量。
6.经验函数法
经验函数法是最常见的地基沉降计算方法,它基于对历史经验的总结,归纳出一系列复杂的沉降曲线。
最小二乘法平差公式最小二乘法平差公式呀,这可是个在数学和统计学领域里相当重要的家伙!咱们先来说说啥是最小二乘法平差公式。
简单来讲,它就是用来找到一组数据的最佳拟合直线或者曲线的方法。
比如说,咱们有一堆测量数据,这些数据可能有点杂乱无章,但咱们想找出一个规律来,这时候最小二乘法平差公式就派上用场啦。
我记得有一次,我带着学生们做一个物理实验,测量小车在不同时间内移动的距离。
同学们那叫一个兴奋,认认真真地记录着每一个数据。
可等数据出来一看,哎呀,那叫一个参差不齐。
这可咋办呢?我就跟他们说:“别着急,咱们用最小二乘法平差公式来找出规律。
”然后我就开始一步一步地给他们讲解。
咱们先设一个线性方程,比如 y = a + bx ,这里的 a 和 b 就是咱们要找的参数。
然后呢,根据测量的数据,咱们列出一堆方程,通过一番计算,就能求出a 和b 的值啦。
在这个过程中,有些同学一开始有点懵,觉得这公式太复杂。
我就跟他们说:“别害怕,就把它当成一个解谜的游戏,咱们一点点来。
”慢慢地,大家都跟上了节奏,最后算出了结果,找到了小车移动距离和时间的关系。
再深入点说,最小二乘法平差公式可不只是能处理线性关系哦,对于一些非线性的问题,咱们也可以通过巧妙的变换,把它转化成线性的,然后再用这个公式。
比如说,要是数据看起来像是符合抛物线的规律,咱们可以设个方程 y = a + bx + cx²,照样能用最小二乘法来搞定。
在实际应用中,像工程测量、经济数据分析、科学研究等等好多领域都离不开它。
比如说,建筑师在设计大楼的时候,要根据测量的地形数据来确定地基的形状和高度,这时候最小二乘法平差公式就能帮助他们找到最合适的设计方案。
还有在市场调研中,分析产品销量和价格之间的关系,也能用到这个公式。
通过对大量的数据进行处理,找到那个最优的拟合曲线,就能为企业的决策提供有力的支持。
总之啊,最小二乘法平差公式虽然看起来有点复杂,但只要咱们掌握了它,就能在一堆杂乱的数据中找到有用的信息,发现隐藏的规律。
非线性最小二乘平差
6-1问题的提出
经典平差是基于线性模型的平差方法。
然而在现实世界中,严格的线性模型并不多见。
测量上大量的数学模型也是非线性模型。
传统的线性模型平差中的很多理论在非线性模型平差中就不一定适用;线性模型平差中的很多结论在非线性模型平差中就不一定成立;线性模型平差中的很多优良统计性质在非线性模型平差中就不一定存在。
例如,在线性模型平差中,当随机误差服从正态分布时,未知参数X 的最小二乘估计具有一致无偏性和方差最小性。
但在非线性模型平差中,即使随机误差严格服从正态分布,未知参数X的非线性最小二乘估计也是有偏的。
其方差一般都不能达到最小值。
对于测量中大量的非线性模型,在经典平差中总是进行线性近似(经典的测量平差中称之为线性化),即将其展开为台劳级数,并取至一次项,略去二次以上各项。
如此线性近似,必然会引起模型误差。
过去由于测量精度不高,线性近似所引起的模型误差往往小于观测误差,故可忽略不计。
随着科学技术的不断发展,现在的观测精度已大大提高,致使因线性近似所产生的模型误差与观测误差相当,有些甚至还会大于观测误差。
例如,GPS载波相位观测值的精度很高,往往小于因线性近似所产生的模型误差。
因此,用近似的理论、模型、方法去处理具有很高精度的观测结果,从而导致精度的损失,这显然是不合理的。
现代科学技术要求估计结果的精度尽可能高。
这样,传统线性近似的方法就不一定能满足当今科学技术的要求。
另外,有些非线性模型对参数的近似值十分敏感,若近似值精度较差,则线性化会产生较大的模型误差。
由于线性近似后,没有顾及因线性近似所引起的模型误差,而用线性模型的精度评定理论去评定估计结果的精度,从而得到一些虚假的优良统计性质,人为地拔高了估计结果的精度。
鉴于上述各种原因,对非线性模型平差进行深入的研究是很有必要的。
非线性模型的平差和精度估计以及相应的误差理论研究也是当前国内外测绘界研究的前沿课题之一。
电子教材> 第六章非线性模型平差> 6-2 非线性模型平差原理
一、非线性误差方程
测量中大量的观测方程是非线性方程。
比如导线测量中,以待定点坐标为未知参数的角度观测方程和边长观测方程分别为:
(6-2-1)
式中:为待定点坐标的真值,分别为角度观测值和边长观测值的真误差。
角度观测值和边长观测值的观测方程(6-2-1)式是待定点坐标真值()的非线性函数。
又如在GPS伪距测量中,第j颗卫星至测站k的几何距离的观测方程为:
也是测站点k的待定坐标真值()的非线性函数。
一般地,用L表示的观测向量,用表示的未知参数向量的真值,用△表示的真误差向量,则非线性观测方程可写为:
(6-2-2)
式中: ,是由n个的非线性函数组成的的向量;。
(6-2-2)式就是我们所要讨论的一般的非线性模型。
在一般的非线性模型(6-2-2)式中,用未知参数向量和真误差向量的估计值代替其真值,得非线性误差方程如下:
(6-2-3)
式中:V为观测值的改正数向量(残差向量);为参数向量的估值。
二、非线性模型平差
由非线性误差方程(6-2-3)式知,非线性误差方程(6-2-3)式中仅有n个方程,而有n+t个未知数(n个观测值的改正数和t个参数)。
因此非线性误差方程(6-2-3)式是非线性不定方程组,有无穷组解。
在这无穷组解中,必然有一组解能使
(6-2-4)
我们将满足(6-2-4)式的一组解作为最优解,并称(6-2-4)式所确定的为的一个非线性最小二乘[23]估计。
本书中将求解非线性最小二乘估计的过程称为非线性模型平差。
可见,非线性模型平差与线性模型平差的是完全一致的。
(6-2-4)式的几何意义就是观测空间至解空间的距离最短,或者说是解轨迹π上离观测值L最近的点(见图6-1)。
L到π的距离就是‖V‖。
图6-1
在非线性模型(6-2-3)式中,若存在一阶连续偏导数,且的非线性最小二乘估计量存在,则残差向量V在处垂直于切空间T(见图6-1)[24]。
一、非线性最小二乘估计的近似解。