用MATLAB作线性和非线性最小二乘法拟合

matlab最小二乘法求参数一、引言最小二乘法是数学中常见的一个工具，它用于寻找最适合一组数据的函数参数。

在非线性回回归和多元线性回归中，最小二乘法是非常有用的一种工具。

MATLAB是一种流行的计算机解释型编程语言，广泛应用于科学、工程、财务等领域。

Matlab中有许多内置的函数，支持最小二乘法。

本文介绍如何在Matlab中使用最小二乘法函数lsqcurvefit或lsqnonlin求解函数参数。

二、最小二乘法最小二乘法是用于寻找数据点到拟合函数直线或曲线之间的最小平方距离的方法，通常用于回归分析中。

它是一种优化问题，可以通过优化算法来解决。

最小二乘法通常用于线性和非线性回归分析。

在线性回归中，拟合的函数是线性函数; 而在非线性回归中，拟合的函数也可以是任意函数。

在这种情况下，最小二乘法可以通过非线性优化方法来解决。

假设有N个数据点(x1,y1),(x2,y2),...(xn,yn)，我们想要找到一个函数f(x,θ)来逼近这些数据点，其中θ是函数的参数。

最小二乘法的目标是使f(x,θ)与y尽可能接近。

误差函数可以定义为:E(θ)=∑i=1^N[f(xi,θ)-yi]^2最小二乘法的目标是最小化误差函数θ*=argmin(E(θ))为了寻找θ，我们可以使用最小二乘法优化算法。

有两种方法可以解决这个问题：线性最小二乘法（LLS）和非线性最小二乘法（NLS）。

三、线性最小二乘法在线性最小二乘法中，函数f(x,θ)是线性的，可以表示为:f(x,θ)=θ1x1+θ2x2+...+θmxm 其中θ=(θ1,θ2,...,θm)是待定的函数参数。

在这种情况下，误差函数可以写成E(θ)=∑i=1^N(θ1x1i+θ2x2i+...+θmxmi-yi)^2我们可以将误差函数写成矩阵形式。

假设我们有一个m×N的矩阵X，它由输入数据点(x1i,x2i,..,xmi)构成，我们还有长度为N的y向量。

随着m的增加参数数量增加，此时，我们的优化问题变成了θ*=argmin||Xθ-y||^2此处||.||表示二范数，即向量各分量的平方和的平方根。

使用Matlab进行数据拟合的方法概述：数据拟合是数据分析中常用的一种技术，它通过找到适合特定数据集的数学模型，在给定数据范围内预测未知变量的值。

在科学研究、工程分析和金融建模等领域，数据拟合起到了至关重要的作用。

而Matlab作为一种强大的数值计算工具，提供了丰富的函数和工具箱来实现各种数据拟合方法。

本文将介绍几种常见的使用Matlab进行数据拟合的方法。

一、线性回归线性回归是一种基本的数据拟合方法，它用于建立自变量和因变量之间的线性关系。

Matlab中可以使用`polyfit`函数来实现线性拟合。

具体步骤如下：1. 导入数据集。

首先需要将数据集导入到Matlab中，可以使用`importdata`函数读取数据文件。

2. 根据自变量和因变量拟合一条直线。

使用`polyfit`函数来进行线性拟合，返回的参数可以用于曲线预测。

3. 绘制拟合曲线。

使用`plot`函数绘制原始数据点和拟合曲线，比较其拟合效果。

二、多项式拟合多项式拟合是一种常见的非线性拟合方法，它通过拟合多项式函数来逼近原始数据集。

Matlab中使用`polyfit`函数同样可以实现多项式拟合。

具体步骤如下：1. 导入数据集。

同线性回归一样，首先需要将数据集导入到Matlab中。

2. 选择多项式次数。

根据数据集的特点和实际需求，选择适当的多项式次数。

3. 进行多项式拟合。

使用`polyfit`函数，并指定多项式次数，得到拟合参数。

4. 绘制拟合曲线。

使用`plot`函数绘制原始数据点和拟合曲线。

三、非线性拟合有时候，数据集并不能通过线性或多项式函数来准确拟合。

这时，需要使用非线性拟合方法，通过拟合非线性方程来逼近原始数据。

Matlab中提供了`lsqcurvefit`函数来实现非线性拟合。

具体步骤如下：1. 导入数据集。

同样，首先需要将数据集导入到Matlab中。

2. 定义非线性方程。

根据数据集的特点和实际需求，定义适当的非线性方程。

matlab拟合数组
在MATLAB中，可以使用多种方法来拟合数组，这取决于数据的特性和拟合的需求。

以下是一些常用的拟合方法：
1. 多项式拟合，可以使用`polyfit`函数进行多项式拟合。

该函数可以拟合出一个多项式函数，使其最小二乘误差最小化。

2. 线性回归，使用`fitlm`函数进行线性回归拟合。

该函数可以拟合出一个线性模型，适用于线性关系较为明显的数据。

3. 非线性拟合，使用`fit`函数进行非线性拟合。

该函数可以拟合出各种非线性模型，例如指数、对数、幂函数等。

4. 样条拟合，可以使用`csaps`函数进行样条拟合。

样条拟合可以更好地拟合出数据中的曲线特征，尤其是在数据中存在较大的波动时效果更佳。

5. 自定义模型拟合，如果数据符合特定的模型，也可以使用`fit`函数结合自定义的模型进行拟合。

在进行拟合时，需要注意选择合适的拟合方法和模型，以及合理地评估拟合效果，避免过拟合或欠拟合的问题。

此外，还需要注意处理数据中的异常值和缺失值，以确保拟合结果的准确性和可靠性。

总之，MATLAB提供了丰富的拟合工具和函数，可以根据具体的数据特点和拟合需求选择合适的方法进行数组拟合。

希望这些信息能对你有所帮助。

matlab最小二乘法拟合直线【导言】直线拟合是数据分析和数学建模中常用的方法之一，而最小二乘法则是在直线拟合中最常用的方法之一。

在本文中，将介绍使用Matlab进行最小二乘法拟合直线的步骤和原理，并就此主题进行深入的探讨。

【正文】一、最小二乘法简介最小二乘法是一种数学优化方法，它通过最小化误差的平方和来寻找函数与观测数据之间的最佳拟合。

在直线拟合中，最小二乘法的目标是找到一条直线，使得所有观测数据点到直线的距离之和最小。

1. 确定拟合的模型在直线拟合中，我们的模型可以表示为：Y = a*X + b，其中a和b为待求参数，X为自变量，Y为因变量。

2. 计算误差对于每一个观测数据点(x_i, y_i)，计算其到直线的垂直距离d_i，即误差。

误差可以表示为：d_i = y_i - (a*x_i + b)。

3. 求解最小二乘法问题最小二乘法的目标是最小化所有观测数据点到直线的距离之和，即最小化误差的平方和：min Σ(d_i^2) = min Σ(y_i - (a*x_i + b))^2。

通过求解该最小化问题，可以得到最佳拟合的直线斜率a和截距b的值。

二、Matlab实现最小二乘法拟合直线的步骤下面将介绍使用Matlab进行最小二乘法拟合直线的基本步骤。

1. 导入数据需要将实验数据导入Matlab。

可以使用matlab自带的readtable函数从文件中读取数据，也可以使用xlsread函数直接从Excel文件中读取数据。

2. 数据预处理在进行最小二乘法拟合直线之前，先对数据进行预处理。

一般情况下，可以对数据进行去除异常值、归一化等操作，以确保数据的准确性和可靠性。

3. 拟合直线使用Matlab的polyfit函数可以实现直线拟合。

polyfit函数可以拟合输入数据的曲线或平面，并返回拟合参数。

在拟合直线时，需要指定拟合的阶数，对于直线拟合，阶数为1。

4. 绘制拟合直线使用Matlab的plot函数可以将拟合的直线绘制出来，以便于观察拟合效果。

在Matlab中，最小二乘法是一种常见的数学拟合技术，可以用来拟合直线，曲线甚至更复杂的函数。

通过最小二乘法，可以找到最适合数据点的直线方程，从而能够更好地分析和预测数据之间的关系。

在本文中，我将详细介绍如何在Matlab中使用最小二乘法来拟合直线，并输出直线方程。

我们需要准备一组数据点。

假设我们有一组横坐标和纵坐标的数据点，分别用变量x和y表示。

接下来，我们可以使用Matlab中的polyfit函数来进行最小二乘拟合。

该函数的语法如下：```matlabp = polyfit(x, y, 1);```其中，x和y分别代表数据点的横坐标和纵坐标，而1代表要拟合的直线的次数，即一次函数。

执行该语句后，变量p将会存储拟合出的直线的系数，即直线方程y = ax + b中的a和b。

在接下来的内容中，我将详细讨论如何通过最小二乘法拟合直线，并输出直线方程。

具体而言，我们将从如何准备数据、使用polyfit函数进行拟合、得到直线方程以及如何应用和解释直线拟合结果等方面进行全面分析。

一、数据准备在使用最小二乘法拟合直线之前，首先要准备一组数据点。

这些数据点应该是具有一定规律性的，从而能够通过直线拟合来揭示数据之间的关系。

在这一部分，我将详细介绍如何准备数据，并重点关注数据的合理性和可靠性。

1.1 数据收集要拟合直线，首先需要收集一组数据点。

这些数据点可以来源于实验观测、实际测量或者模拟计算等方式。

在收集数据时，需要保证数据的准确性和完整性。

还需要考虑数据的分布范围和密度，以便更好地反映数据之间的关系。

1.2 数据预处理在拟合直线之前，通常需要对数据进行一定的预处理。

这可能包括去除异常值、处理缺失数据，甚至进行数据变换等操作。

在这一步中，我将介绍如何进行数据预处理，并强调预处理对最终拟合结果的影响。

二、最小二乘拟合当数据准备工作完成后，就可以使用polyfit函数进行最小二乘拟合了。

在这一部分，我将详细介绍polyfit函数的使用方法，并解释其背后的数学原理。

MATLAB实例：多元函数拟合（线性与⾮线性）MATLAB实例：多元函数拟合(线性与⾮线性)作者：凯鲁嘎吉 - 博客园更多请看：之前写过⼀篇博⽂，是。

现在⽤拟合多元函数，实现线性拟合与⾮线性拟合，其中⾮线性拟合要求⾃定义拟合函数。

下⾯给出三种拟合⽅式，第⼀种是多元线性拟合(回归)，第⼆三种是多元⾮线性拟合，实际中第⼆三种⽅法是⼀个意思，任选⼀种即可，推荐第⼆种拟合⽅法。

1. MATLAB程序fit_nonlinear_data.mfunction [beta, r]=fit_nonlinear_data(X, Y, choose)% Input: X ⾃变量数据(N, D)， Y 因变量(N, 1)，choose 1-regress, 2-nlinfit 3-lsqcurvefitif choose==1X1=[ones(length(X(:, 1)), 1), X];[beta, bint, r, rint, states]=regress(Y, X1)% 多元线性回归% y=beta(1)+beta(2)*x1+beta(3)*x2+beta(4)*x3+...% beta—系数估计% bint—系数估计的上下置信界% r—残差% rint—诊断异常值的区间% states—模型统计信息rcoplot(r, rint)saveas(gcf,sprintf('线性曲线拟合_残差图.jpg'),'bmp');elseif choose==2beta0=ones(7, 1);% 初始值的选取可能会导致结果具有较⼤的误差。

[beta, r, J]=nlinfit(X, Y, @myfun, beta0)% ⾮线性回归% beta—系数估计% r—残差% J—雅可⽐矩阵[Ypred,delta]=nlpredci(@myfun, X, beta, r, 'Jacobian', J)% ⾮线性回归预测置信区间% Ypred—预测响应% delta—置信区间半⾓plot(X(:, 1), Y, 'k.', X(:, 1), Ypred, 'r');saveas(gcf,sprintf('⾮线性曲线拟合_1.jpg'),'bmp');elseif choose==3beta0=ones(7, 1);% 初始值的选取可能会导致结果具有较⼤的误差。

关于采用matlab进行指定非线性方程拟合的问题(1)※1。

优化工具箱的利用函数描述LSQLIN 有约束线性最小二乘优化LSQNONNEG 非负约束线性最小二乘优化问题当有约束问题存在的时候，应该采用上面的方法代替Polyfit与反斜线（\）。

具体例子请参阅优化工具箱文档中的相应利用这两个函数的例子。

d. 非线性曲线拟合利用MATLAB的内建函数函数名描述FMINBND 只解决单变量固定区域的最小值问题FMINSEARCH 多变量无约束非线性最小化问题（Nelder-Mead 方法）。

下面给出一个小例子展示一下如何利用FMINSEARCH1．首先生成数据>> t=0:.1:10;>> t=t(:);>> Data=40*exp(-.5*t)+rand(size(t)); % 将数据加上随机噪声2．写一个m文件，以曲线参数作为输入，以拟合误差作为输出function sse=myfit(params,Input,Actural_Output)A=params(1);lamda=params(2);Fitted_Curve=A.*exp(-lamda*Input);Error_Vector=Fitted_Curve-Actural_Output;%当曲线拟合的时候，一个典型的质量评价标准就是误差平方和sse=sum(Error_Vector.^2);%当然，也可以将sse写作：sse=Error_Vector(:)*Error_Vector(:);3．调用FMINSEARCH>> Strarting=rand(1,2);>> options=optimset('Display','iter');>> Estimates=fiminsearch(@myfit,Strarting,options,t,Data);>> plot(t,Data,'*');>> hold on>> plot(t,Estimates(1)*exp(-Estimates(2)*t),'r');Estimates将是一个包含了对原数据集进行估计的参数值的向量。

最小二乘法拟合matlab
最小二乘法拟合MATLAB
最小二乘法是一种有效地估计未知参数值的统计学方法，它假定误差服从正态分布，然后进行极大似然估计。

下面我们就来介绍一下如何使用MATLAB来拟合最小二乘法。

1.第一步：绘制出要拟合的数据，这里我们绘制出了一个简单的抛物线数据：
x=[-3 -2 -1 0 1 2 3];
y=[6 3 1 0 -2 -4 -7];
plot(x,y);
2.第二步：根据你要拟合的函数，构建出你所要拟合的模型。

这里，我们想拟合一条抛物线：y=ax2+bx+c ;
3.第三步：定义拟合函数：
fun=@(x,xdata)x(1)*xdata.^2+x(2)*xdata+x(3);
4.第四步：调用最小二乘法函数：
[x,resnorm,residual,exitflag,output,lambda,jacobian]=lsqcur vefit(fun,[1 1 1],x,y);
现在你已经可以看到拟合函数的参数了：
x的值为[1.7, 0.3, -1.5]，
而拟合函数为： y=1.7x2+0.3x-1.5
因此，使用MATLAB调用最小二乘法可以很方便地拟合出任意复
杂的函数，并且可以得到准确的参数值。

---------------------------------------------------------------最新资料推荐------------------------------------------------------ matlab最小二乘法的非线性参数拟合（精荐）matlab 最小二乘法的非线性参数拟合 matlab 最小二乘法的非线性参数拟合首先说一下匿名函数：在创建匿名函数时，Matlab 记录了关于函数的信息，当使用句柄调用该函数的时候，Matlab 不再进行搜索，而是立即执行该函数，极大提高了效率。

所以首选匿名函数。

具体拟合时可以使用的方法如下：1 曲线拟合工具箱1 曲线拟合工具箱提供了很多拟合函数，使用简单非线性拟合 nlinfit 函数 clear all; x1=[0.4search 或优化工具箱提供的极小化函数求解。

在 Matlab 中，曲线拟合工具箱也提供了曲线拟合的图形界面操作。

在命令提示符后键入：cftool，即可根据数据，选择适当的拟合模型。

\命令\命令 1.假设要拟合的多项式是：y=a+b*x+c*x.首先建立设计矩阵 X：X=[ones(size(x)) x x]; 执行：para=X\y para 中包含了三个参数：para(1)=a;para(2)=b;para(3)=c; 这种方法对于系数是线性的模型也适应。

1 / 102.假设要拟合：y=a+b*exp(x)+cx*exp(x) 设计矩阵 X 为 X=[ones(size(x)) exp(x) x.*exp(x.)]; para=X\y 3.多重回归(乘积回归) 设要拟合： y=a+b*x+c*t，其中 x 和 t 是预测变量，y 是响应变量。

设计矩阵为 X=[ones(size(x)) x t] %注意 x,t 大小相等！para=X\y polyfit 函数polyfit 函数 polyfit 函数不需要输入设计矩阵，在参数估计中，polyfit 会根据输入的数据生成设计矩阵。

一、引言在科学和工程领域中，拟合曲线是一种重要的数学工具，它用于寻找一条曲线，使得该曲线最好地描述已知的数据点或者模拟实验结果。

MATLAB作为一种强大的数学计算软件，拥有丰富的拟合曲线的算法和工具。

本文将介绍MATLAB中拟合曲线的算法，包括常见的线性拟合、多项式拟合、非线性拟合等。

二、线性拟合1. 线性拟合是指采用线性方程来拟合已知数据点的方法。

在MATLAB 中，可以使用polyfit函数来实现线性拟合。

该函数的基本语法如下： p = polyfit(x, y, n)，其中x和y分别代表已知数据点的横坐标和纵坐标，n代表拟合多项式的阶数。

函数返回一个长度为n+1的向量p，其中p(1)、p(2)分别代表拟合多项式的系数。

2. 通过polyfit函数可以实现对数据点的线性拟合，得到拟合曲线的系数，并且可以使用polyval函数来计算拟合曲线在指定点的取值。

该函数的基本语法如下：yfit = polyval(p, x)，其中p代表拟合曲线的系数向量，x代表待求取值的点，yfit代表拟合曲线在该点的取值。

三、多项式拟合1. 多项式拟合是指采用多项式方程来拟合已知数据点的方法。

在MATLAB中，可以使用polyfit函数来实现多项式拟合，和线性拟合类似。

不同之处在于，可以通过调整多项式的阶数来适应不同的数据特性。

2. 除了使用polyfit函数进行多项式拟合外，MATLAB还提供了Polytool工具箱，它是一个方便的图形用户界面，可以用于拟合已知数据点并可视化拟合曲线。

使用Polytool工具箱，用户可以直观地调整多项式的阶数和观察拟合效果，非常适合初学者和快速验证拟合效果。

四、非线性拟合1. 非线性拟合是指采用非线性方程来拟合已知数据点的方法。

MATLAB中提供了curvefitting工具箱，其中包含了众多非线性拟合的工具和算法，例如最小二乘法、最大似然法、拟合优度计算等。

通过该工具箱，用户可以方便地进行各种复杂数据的非线性拟合。

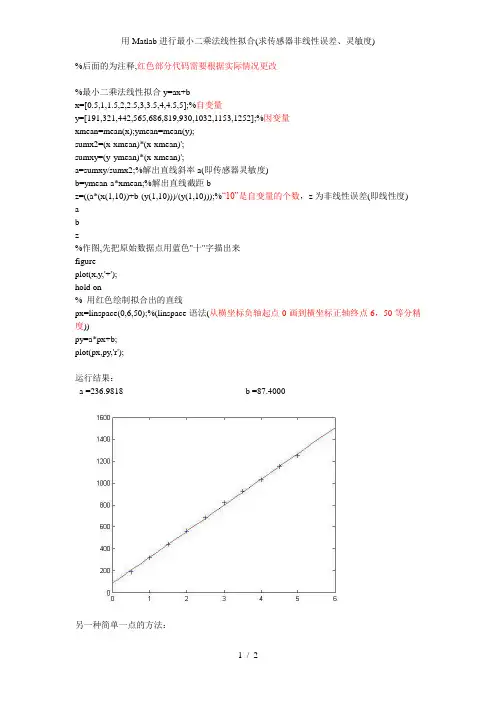
%后面的为注释,红色部分代码需要根据实际情况更改%最小二乘法线性拟合y=ax+bx=[0.5,1,1.5,2,2.5,3,3.5,4,4.5,5];%自变量y=[191,321,442,565,686,819,930,1032,1153,1252];%因变量xmean=mean(x);ymean=mean(y);sumx2=(x-xmean)*(x-xmean)';sumxy=(y-ymean)*(x-xmean)';a=sumxy/sumx2;%解出直线斜率a(即传感器灵敏度)b=ymean-a*xmean;%解出直线截距bz=((a*(x(1,10))+b-(y(1,10)))/(y(1,10)));%“10”是自变量的个数，z为非线性误差(即线性度)abz%作图,先把原始数据点用蓝色"十"字描出来figureplot(x,y,'+');hold on% 用红色绘制拟合出的直线px=linspace(0,6,50);%(linspace语法(从横坐标负轴起点0画到横坐标正轴终点6，50等分精度))py=a*px+b;plot(px,py,'r');运行结果：a =236.9818b =87.4000另一种简单一点的方法：%最小二乘法线性拟合y=ax+bx=[0.5,1,1.5,2,2.5,3,3.5,4,4.5,5];%自变量y=[191,321,442,565,686,819,930,1032,1153,1252];%因变量p=polyfit(x,y,1);p运行结果：p =236.9818 87.4000。

文章标题：深入解析MATLAB三元函数曲线拟合一、引言MATLAB是一种强大的数学软件工具，广泛应用于科学与工程领域。

三元函数曲线拟合作为其中一项重要功能，可以通过拟合已知的数据点，找到最合适的函数曲线来描述这些数据点的分布规律。

在本文中，我们将深入探讨MATLAB中的三元函数曲线拟合，包括其原理、方法和实际应用。

二、原理解析1. 三元函数曲线拟合的基本概念三元函数曲线拟合是指通过一组离散的点数据，找到一个函数曲线，使得这些数据点到该曲线的距离最小，从而能够较好地拟合现有的数据分布情况。

2. MATLAB中的三元函数曲线拟合方法MATLAB提供了多种方法来进行三元函数曲线拟合，包括最小二乘法、非线性最小二乘法、曲线拟合工具箱等。

这些方法各有特点，可根据实际需求进行选择。

3. 实例分析接下来，我们通过一个具体的示例来说明MATLAB中三元函数曲线拟合的过程。

假设有一组数据点(x,y)，我们希望通过三元函数曲线拟合来找到最适合的函数曲线 y=f(x)。

我们可以先选择合适的拟合方法，然后利用MATLAB提供的函数进行拟合操作，最终得到拟合的函数曲线。

三、实践应用1. 科学研究三元函数曲线拟合在科学研究中有着广泛的应用，例如在物理实验数据处理、生物学分析等方面发挥着重要作用。

2. 工程领域在工程领域，三元函数曲线拟合可以通过拟合已有的传感器测量数据，从而提供有效的模型来描述系统的工作状态并进行预测。

3. 金融与经济在金融与经济学领域，三元函数曲线拟合可以用于预测市场走势、分析经济数据等重要应用。

四、个人观点和总结通过对MATLAB中的三元函数曲线拟合进行深入探讨和实例分析，我深切感受到了其在科学与工程领域的重要性。

合理选择方法、充分理解原理，并结合实际问题进行应用是十分关键的。

我相信，在今后的学习和工作中，将会进一步加深对这一领域的理解，并能够灵活地应用于实际问题的解决中。

通过本文的阐述，相信读者们对MATLAB中的三元函数曲线拟合有了更深入的了解，希望本文能够对大家有所帮助。

matlab拟合函数MATLAB拟合函数概述：MATLAB是一种功能强大的科学计算软件，可以用于各种数学建模和数据分析任务。

其中一个常见的任务是使用MATLAB进行数据拟合。

数据拟合是根据给定的数据点，找到一个适当的数学模型来描述这些数据，并通过调整模型的参数来最好地拟合数据。

本文将介绍在MATLAB中进行数据拟合的方法和技巧。

数据拟合方法：在MATLAB中，有许多不同的拟合方法可以使用，根据数据的特性和所需的模型形式来选择适当的方法。

1. 线性拟合：线性拟合是最简单的拟合方法之一，适用于线性关系的数据。

在MATLAB中，可以使用polyfit函数进行线性拟合。

该函数使用最小二乘法来找到最佳的线性拟合曲线。

以下是一个简单的示例：```matlabx = [1, 2, 3, 4, 5];y = [4, 7, 9, 12, 15];coefficients = polyfit(x, y, 1);```这将生成一个一次多项式的系数，表示最佳拟合曲线的斜率和截距。

2. 多项式拟合：如果数据的关系不是线性的，可以使用多项式拟合来逼近数据。

可以使用polyfit函数，将拟合曲线的阶数设为所需的多项式的阶数。

以下是一个示例：```matlabx = [1, 2, 3, 4, 5];y = [4, 7, 9, 12, 15];degree = 2; % 二次多项式拟合coefficients = polyfit(x, y, degree);```这将生成一个二次多项式的系数，表示最佳的二次拟合曲线。

3. 曲线拟合：对于更复杂的数据关系，可以使用曲线拟合方法。

在MATLAB中，可以使用curvefit工具箱来进行曲线拟合。

该工具箱提供了多种曲线模型和拟合算法，例如曲线拟合、曲面拟合和非线性最小二乘拟合等。

以下是一个简单的示例：```matlabx = [1, 2, 3, 4, 5];y = [4, 7, 9, 12, 15];fun = @(x)(a*x.^2 + b*x + c); % 自定义的曲线模型starting_guess = [1, 1, 1]; % 初始猜测值fitted_coefficients = lsqcurvefit(fun, starting_guess, x, y);```这将使用最小二乘法找到最佳的曲线拟合参数。

方便大家使用的最小二乘法曲线拟合的Matlab程序非常方便用户使用,直接按提示操作即可;这里我演示一个例子:(红色部分为用户输入部分,其余为程序运行的结果,结果图为Untitled.fig,Untitled2.fig) 请以向量的形式输入x,y.x=[1,2,3,4]y=[3,4,5,6]通过下面的交互式图形，你可以事先估计一下你要拟合的多项式的阶数，方便下面的计算.polytool()是交互式函数,在图形上方[Degree]框中输入阶数,右击左下角的[Export]输出图形回车打开polytool交互式界面回车继续进行拟合输入多项式拟合的阶数m = 4Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 72In zxecf at 64输出多项式的各项系数a = 0.0200000000000001a = -0.2000000000000008a = 0.7000000000000022a = 0.0000000000000000a = 2.4799999999999973输出多项式的有关信息 SR: [4x5 double]df: 0normr: 2.3915e-015Warning: Zero degrees of freedom implies infinite error bounds.> In polyval at 104In polyconf at 92In zxecf at 69观测数据拟合数据x y yh1.0000 3.0000 3.00002.0000 4.0000 4.00003 5 54.0000 6.0000 6.0000剩余平方和 Q = 0.000000标准误差 Sigma = 0.000000相关指数 RR = 1.000000请输入你所需要拟合的数据点，若没有请按回车键结束程序.输入插值点x0 = 3输出插值点拟合函数值 y0 = 5.0000>>结果：untitled.figuntitled2.fig一些matlab优化算法代码的分享代码的目录如下：欢迎讨论1.约束优化问题：minRosen(Rosen梯度法求解约束多维函数的极值)(算法还有bug) minPF(外点罚函数法解线性等式约束)minGeneralPF(外点罚函数法解一般等式约束)minNF(内点罚函数法)minMixFun(混合罚函数法)minJSMixFun(混合罚函数加速法)minFactor(乘子法)minconPS(坐标轮换法)(算法还有bug)minconSimpSearch(复合形法)2.非线性最小二乘优化问题minMGN(修正G-N法)3.线性规划：CmpSimpleMthd(完整单纯形法)4.整数规划(含0-1规划)DividePlane(割平面法)ZeroOneprog(枚举法)5.二次规划QuadLagR(拉格朗日法)ActivedeSet(起作用集法)6.辅助函数(在一些函数中会调用)minNT(牛顿法求多元函数的极值)Funval(求目标函数的值)minMNT(修正的牛顿法求多元函数极值)minHJ(黄金分割法求一维函数的极值)7.高级优化算法1）粒子群优化算法(求解无约束优化问题)1>PSO(基本粒子群算法)2>YSPSO(待压缩因子的粒子群算法)3>LinWPSO(线性递减权重粒子群优化算法)4>SAPSO(自适应权重粒子群优化算法)5>RandWSPO(随机权重粒子群优化算法)6>LnCPSO(同步变化的学习因子)7>AsyLnCPSO(异步变化的学习因子)(算法还有bug)8>SecPSO(用二阶粒子群优化算法求解无约束优化问题)9>SecVibratPSO(用二阶振荡粒子群优化算法求解五约束优化问题)10>CLSPSO(用混沌群粒子优化算法求解无约束优化问题)11>SelPSO(基于选择的粒子群优化算法)12>BreedPSO(基于交叉遗传的粒子群优化算法)13>SimuAPSO(基于模拟退火的粒子群优化算法)2)遗传算法1>myGA(基本遗传算法解决一维约束规划问题)2>SBOGA(顺序选择遗传算法求解一维无约束优化问题)3>NormFitGA(动态线性标定适应值的遗传算法求解一维无约束优化问题)4>GMGA(大变异遗传算法求解一维无约束优化问题)5>AdapGA(自适应遗传算法求解一维无约束优化问题)6>DblGEGA(双切点遗传算法求解一维无约束优化问题)7>MMAdapGA(多变异位自适应遗传算法求解一维无约束优化问题)自己编写的马尔科夫链程序A 代表一组数据序列一维数组本程序的操作对象也是如此t=length(A); % 计算序列“A”的总状态数B=unique(A); % 序列“A”的独立状态数顺序，“E”E=sort(B,'ascend');a=0;b=0;c=0;d=0;for j=1:1:ttLocalization=find(A==E(j)); % 序列“A”中找到其独立状态“E”的位置for i=1:1:length(Localization)if Localization(i)+1>tbreak; % 范围限定elseif A(Localization(i)+1)== E(1)a=a+1;elseif A(Localization(i)+1)== E(2)b=b+1;elseif A(Localization(i)+1)== E(3)c=c+1;% 依此类推，取决于独立状态“E”的个数elsed=d+1;endendT(j,1:tt)=[a,b,c,d]; % “T”为占位矩阵endTT=T;for u=2:1:ttTT(u,:)= T(u,:)- T(u-1,:);endTT; % 至此，得到转移频数矩阵Y=sum(TT,2);for uu=1:1:ttTR(uu,:)= TT(uu,:)./Y(uu,1);endTR % 最终得到马尔科夫转移频率/概率矩阵% 观测序列马尔科夫性质的检验：N=numel(TT);uuu=1;Col=sum(TT,2); % 对列求和Row=sum(TT,1); % 对行求和Total=sum(Row); % 频数总和for i=1:1:ttfor j=1:1:ttxx(uuu,1)=sum((TT(i,j)-(Row(i)*Col(j))./Total).^2./( (Row(i)*Col(j)). /Total));uuu=uuu+1; % 计算统计量x2endendxx=sum(xx)。

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 用MatLab画图(最小二乘法做曲线拟合) 用 MatLab 画图(最小二乘法做曲线拟合) 帮朋友利用实验数据画图时，发现 MatLab 的确是画图的好工具，用它画的图比Excel光滑、精确。

利用一组数据要计算出这组数据对应的函数表达式从而得到相应图像，MatLab 的程序如下：x=[1 5 10 20 30 40 60 80] y=[15. 4 33. 9 42. 2 50. 556 62. 7 72 81. 1] plot(x, y, ‘ r*’ ) ; legend(‘ 实验数据(xi, yi) ‘ ) xlabel(‘ x’ ) , ylabel(‘ y’ ) , title(‘ 数据点(xi, yi) 的散点图’ ) syms a1 a2 a3 x=[15 10 20 30 40 60 80]; fi=a1. *x. +a2. *x+a3 y=[15. 4 33.9 42. 2 50. 5 56 62. 7 72 81. 1] fi =[a1+a2+a3,25*a1+5*a2+a2+(400*a1+20*a2+a3-101/2) +(900*a1+30*a2+a3-56) +(1600*a1+40*a2+a3-627/10) +(3600*a1+60*a2+a3-72)+(6400*a1+80*a2+a3-811/10) ; Ja1=diff(J, a1) ;Ja2=diff(J, a2) ; Ja3=diff(J, a3) ; Ja11=simple(Ja1) ,Ja21=simple(Ja2) , Ja31=simple(Ja3) A=[114921252, 1656252, 26052; 1656252, 26052, 492; 26052, 492, 16]; B=[9542429/5, 166129/5, 4138/5]; C=B/A, f=poly2sym(C) xi=[1 5 10 20 3040 60 80] ; y=[15. 4 33. 9 42. 2 50. 5 56 62. 7 72 81. 1]; n=length(xi) ; f=-0. 0086. *xi. +1. 3876. *xi+23. 1078;1 / 6x=1: 1/10: 80; F=-0. 0086. *x. +1. 3876. *x+23. 1078; fy=abs(f-y) ; fy2=fy. ; Ew=max(fy) , E1=sum(fy) /n,E2=sqrt((sum(fy2) ) /n) plot(xi, y, ‘ r*’ ) , hold on, plot(x, F, ‘ b-’ ) , hold off legend(‘ 数据点(xi, yi) ‘ , ‘ 拟合曲线f(x) = -0. 0086x +1. 3876x+23. 1078’ ) , xlabel(‘ x’ ) , ylabel(‘ y’ ) , title(‘ 实验数据点(xi, yi) 及拟合曲线f(x) ‘ ) 下图是程序运行后得到的：Su7Tw8VxaW ybXAcZB d#Cf!Eg%FhGj*Ik(Jl-Kn+M o0Np2Or3Ps4R t6Sv7Tw8VxaWzbXAcZBe#Cf! Eg%Fi Gj*Ik)Jl-Kn+Mo1Np2Or3Qs4Rt6Sv7 Uw8Vx aWzbYAc ZBe#Df!Eg%FiHj*Ik) Jm-Kn +Mo1Nq2Or3Qs 5Rt6Sv7Uw9VxaWzbYAdZBe#D f$Eg%F iHj(I k) Jm-Ln+Mo1Nq2Pr3Qs5Ru6S v7Uw9V yaWzbY AdZCe#Df$Eh%FiHj(Il) Jm-Ln0Mo1Nq2Pr4 Qs5Ru6Tv8Uw9VyaXzbYAdZCe !Df$Eh %GiHj (Il) Km-Ln0Mp1Nq2Pr4Qt5Ru 6Tv8U x9VyaXz cYAdZCe! Dg$Eh%Gi*Hj(Il) Km+Ln0M p1Oq2P r4Qt5Su6Tv8Ux9WyaXzcYBdZ Ce!Dg$Fh%Gi* Hk(Il) Km+Lo0Mp1Oq3Pr4Qt5 Su7Tv8Ux9Wyb XzcYBd#Ce!Dg$FhGi*Hk(Jl ) Km+L o0Np1Oq 3Ps4Rt 5Su7Tw8Ux9WybXAcY Bd#Cf!Dg$FhGj*Hk(Jl-Km+Lo0Np2Oq3Ps4 Rt6Su7Tw8Vx9 WybXAcZBd#Cf!Eg$FhGj*Ik (Jl-Kn +Lo0Np2Or3Ps4Rt6Sv7Tw8VxaWybXA cZBe#Cf!Eg%F hGj*Ik) Jl-K n+Mo0Np2Or3Q s4Rt6Sv 7Uw8V xaWzbXAcZBe# D f! Eg%FiGj* Ik) Jm- Kn+Mo1 Nq2Or3Qs5Rt6Sv7Uw9VxaWzb YAcZBe#Df$Eg %FiHj*Ik)---------------------------------------------------------------最新资料推荐------------------------------------------------------ Jm-Ln+Mo1Nq2Pr 3Qs5Ru 6Sv7Uw 9VyaWzbYAdZBe#Df$Eh%FiH j(Ik) J m-Ln0M o1Nq2Pr4Qs5Ru6Tv7Uw9VyaX zbYAdZC e#Df$ Eh%GiHj(Il) Jm-Ln0Mp1Nq2 Pr4Qt5Ru6Tv8 Uw9VyaXzcYAdZCe!Df$Eh%Gi *Hj(Il) Km+Ln 0Mp1Oq2Pr4Qt5Su6Tv8Ux9Vy aXzcYB dZCe!D g$Eh%Gi*Hk(Il) Km+Lo0Mp1O q3Pr4Qt5Su7Tv8Ux9WyaXzc Y Bd#Ce!Dg$Fh %Gi*Hk( Jl) Km +Lo0Np1Oq3Ps 4 Qt5Su7Tw8Ux 9WybXzcYBd#C f!Dg$FhGi*H k (Jl-Km+Lo0N p2Oq3Ps4Rt5S u7Tw8Vx9WybX AcYBd#Cf! Eg$ FhGj*Ik (Jl- Kn+Lo0Np2Or3 P s4Rt6Su7Tw8 VxaWybXA cZBd #Cf!Eg%FhGj * Ik) Jl-Kn+Mo 0Np2Or3Qs4Rt 6Sv7Tw8VxaWz bXAcZBe#Cf!E g%FiGj*Ik) J m-Kn+Mo1Np2O r 3Qs5Rt6Sv7U w8VxaWzbYAcZ Be#Df! Eg%Fi H j*Ik) Jm-Ln+ Mo1Nq2O r3Qs5 Ru6Sv7Uw9Vxa W zbYAdZBe#Df $Eh%Fi Hj(Ik ) Jm-Ln0Mo1Nq 2Pr3Qs5Ru6Tv 7Uw9Vya WzbYA dZCe#Df$Eh%G iHj(Il) Jm-L n0Mp1Nq2Pr4Q s5Ru6Tv8Uw9V ya XzbYAdZCe! Df$Eh%Gi*Hj( Il) Km-Ln0Mp1 Oq 2Pr4 Qt5Ru6Tv8Ux9Vy aXz cYAdZCe!Dg$E h%G i*Hk(Il) K m+Ln0Mp1O q3P r4Qt5Su6Tv8U x9WyaXzcYBd# Ce!Dg$Fh% Gi* Hk(Jl) Km+Lo0 Mp1Oq3Ps4Qt5 Su7Tv8Ux9Wyb XzcYBd#Cf! Dg $F hGi*Hk(Jl -Km+Lo0N p1Oq 3Ps4Rt5Su7Tw 8U x9WybXAcYB d#Cf!Eg$F hG j*Hk(Jl-Kn+Lo0Np2O q3Ps4Rt 6Su7Tw8Vx9WybXAcZBd#Cf!E g%FhGj*Ik(J l-Kn+Mo0Np2O r3Ps4Rt6Sv7T w8Vxa WzbXAcZ Be#Cf! Eg%Fi Gj*Ik) Jl-Kn+ Mo1Np2Or3Qs4 Rt6Sv7Uw8VxaWzbYAcZBe#Df !Eg%FiHj*Ik )3 / 6Jm-Kn+Mo1Nq2Or3Qs5Rt6Sv 7Uw9Vx aWzbYA dZBe#Df$Eg%FiHj(Ik) Jm-L n+Mo1Nq2Pr3Q s5Ru6Sv7Uw9VyaWzbYAdZCe# Df$Eh %FiHj( Il) Jm-Ln0Mo1Nq2Pr4Qs5Ru6 Tv8Uw9VyaXzb YAdZCe!Df$Eh%GiHj(Il) Km -Ln0Mp 1Nq2Pr 4Qt5Ru6Tv8Ux9VyaXzcYAdZC e!Dg$E h%Gi*H j(Il) Km+Ln0Mp1Oq2Pr4Qt5S u6Tv8U x9WyaX zcYBdZCe! Dg$Fh%Gi*Hk(Il) Km+Lo0Mp1Oq3 Pr4Qt5Su7Tv8Ux9WybXzcYBd #Ce!D g$FhGi *Hk(Jl ) Km+Lo0Np1Oq3Ps4R t5Su7Tw8Ux9T v7Uw9VyaXzbYAdZCe#Df$Eh% GiHj( Il) Jm- Ln0Mp1Nq2Pr4Qs5Ru6Tv8Uw9 VyaXzcY AdZCe !Df$Eh%Gi*Hj(Il) Km-Ln0Mp 1Oq2Pr 4Qt5Ru 6Tv8Ux9VyaXzcYBdZCe! Dg$E h%Gi*Hk(Il) K m+Ln0Mp1Oq3Pr4Qt5Su6Tv8U x9WyaX zcYBd# Ce!Dg$Fh%Gi*Hk(Jl) Km+Lo0 Mp1Oq3P s4Qt5 Su7Tw8Ux9Wyb X zcYBd#Cf!Dg $FhGi*Hk(Jl -Km+Lo0Np1Oq3Ps4Rt5Su7Tw 8Vx9Wy bXAcYB d#Cf! Eg$FhGj*Hk(Jl-Kn+L o0Np2O q3Ps4R t6Su7Tw8VxaWybXAcZBd#Cf! Eg%Fh Gj*Ik( Jl-Kn+Mo0Np2Or3Ps4Rt6Sv7 Tw8Vxa WzbXAc ZBe#Cf!Eg%FiGj*Ik) Jl-Kn +Mo1Np2Or3Qs 5Rt6Sv7Uw8Vx a WzbYAcZBe#D f! Eg%FiHj*Ik) Jm-Kn+Mo1 Nq 2Or3Qs5Ru6 Sv7Uw9Vx aWzb YAdZBe#Df$Eg %F iHj(Ik) Jm -Ln+Mo1N q2Pr 3Qs5Ru6Tv7Uw 9VyaWzbYAdZC e#Df$Eh%FiH j(Il) Jm-Ln0M o1Nq2Pr4Qs5R u6Tv8Uw9VyaX zbYAdZCe! Df$ E h%GiHj(Il) Km-Ln0Mp 1Oq2 Pr4Qt5Ru6Tv8 U x9VyaXzcYAd ZCe!Dg$E h%Gi *Hj(Il) Km+Ln 0Mp1Oq3Pr4Qt 5Su6Tv8Ux9Wy aXzcYBdZCe!D g $Fh%Gi*Hk(I l)---------------------------------------------------------------最新资料推荐------------------------------------------------------ Km+Lo0Mp1O q3Ps4Qt5Su7T v 8Ux9WybXzcY Bd#Ce! D g$Fh Gi*Hk(Jl) Km+ L o0Np1Oq3Ps4 Rt5Su7T w8Ux9 WybXAcYBd#Cf !Dg$FhGj*Hk (Jl-Km+ Lo0Np 2Oq3Ps4Rt6Su 7Tw8Vx9WybXA cZBd#Cf ! Eg$F hGj*Ik(Jl-K n+Mo0Np2Or3P s4Rt6Sv 7Tw8V xaWybXAcZBe# C f!Eg% FhGj*Ik) Jl-K n+Mo 1Np2Or3Qs4Rt 6Sv 7Uw8VxaWz bXAcZBe#D f!E g%FiGj*Ik) J m- Kn+Mo1Nq2O r3Qs5Rt6Sv7U w9VxaWzbYAcZ Be#Df$Eg%Fi Hj*Ik) Jm-Ln+ Mo1Nq2Pr3Qs5 Ru6Sv7Uw9Vya WzbYAdZBe#Df $Eh%FiHj(Il ) Jm -Ln0Mo1Nq 2Pr4Qs5Ru 6Tv 7Uw9VyaXzbYA dZCe#Df$Bd#C f! Eg%FhGj*I k(Jl-Kn+Mo0Np2O r3Qs4Rt 6Sv7Tw8VxaWzbXAcZBe#Cf!E g%FiGj*Ik) J l-Kn+Mo1Np2O r3Qs5Rt6Sv7U w8Vxa WzbYAcZ Be#Df! Eg%Fi Hj*Ik) Jm-Kn+ Mo1Nq2Or3Qs5 Ru6Sv7Uw9VxaWzbYAdZBe#Df $Eg%FiHj(Ik ) Jm-Ln0Mo1Nq2Pr3Qs5Ru6Tv 7Uw9Vy aWzbYA dZCe#Df$Eh%FiHj(Il) Jm-L n0Mp1Nq2Pr4Q s5Ru6Tv8Uw9VyaXzbYAdZCe! Df$Eh %GiHj( Il) Km-Ln0Mp1Oq2Pr4Qt5Ru6 Tv8Ux9VyaXzc YAdZCe!Dg$Eh%Gi*Hj(Il) Km +Ln0Mp 1Oq3Pr 4Qt5Su6Tv8Ux9WyaXzcYBdZC e!Dg$F h%Gi*H k(Jl) Km+Lo0Mp1Oq3Ps4Qt5S u7Ts5R u6Sv7U w9VyaWzbYAdZBe#Df$Eh%Fi Hj(Ik)Jm-Ln0 Mo1Nq2Pr4Qs5Ru6Tv7Uw9Vya XzbYA dZCe#Df $Eh%Gi Hj(Il) Jm-Ln0Mp1N q2Pr4Qt5Ru6T v8Uw9VyaXzcYAdZCe!Df$Eh% Gi*Hj( Il) Km- Ln0Mp1Oq2Pr4Qt5Su6Tv8Ux9 VyaXzcY BdZCe !Dg$Eh%Gi*Hk(Il) Km+Ln0Mp 1Oq3Pr4Qt5Su5 / 67Tv8Ux9WyaXzcYBd#Ce! Dg$F h%Gi*Hk (Jl) K m+Lo0Np1Oq3Ps4Qt5Su7Tw8U x9WybX zcYBd# Cf!Dg$FhGi*Hk(Jl-Km+Lo0 Np2Oq3Ps4Rt5 Su7Tw8Vx9WybXAcYBd#Cf!Eg $FhGj*Hk(Jl -Kn+Lo0Np2Or3Ps4Rt6Su7Tw 8VxaWy bXAcZB d#Cf! Eg%FhG j*Ik(Jl-Kn+M o0Np2O r3Qs4R t6Sr4Qt5Su6Tv8Ux9WyaXzcY BdZCe!Dg$Fh% Gi*Hk(Il) Km+Lo0Mp1Oq3Pr4 Qt5Su7Tv8Ux9 WybXzcYBd#Ce! Dg$FhGi*Hk (Jl) Km +Lo0Np 1Oq3Ps4Rt5Su7Tw8Ux9WybXA cYBd#Cf!Dg$FhGj*Hk(Jl- K m+Lo0Np2Oq3 Ps4Rt6Su7Tw8 Vx9WybXAcZBd # Cf!Eg$FhGj *Ik(Jl- Kn+Lo 0Np2Or3Ps4Rt 6Sv7Tw8VxaWy bXAcZBe#Cf!E g%FhGj*Ik) J l-Kn+Mo0Np2O r3Qs4Rt6Sv7U w8VxaWzbXAcZ B e#Df!Eg%Fi Gj*Ik) J m-Kn+ Mo1Nq2Or3Qs5 R t6Sv7Uw9Vxa WzbYAcZB e#Df $Eg%Ff! Dg$Fh Gi*Hk(Jl-Km +Lo0Np1Oq3Ps 4Rt5Su7Tw8Vx 9W ybXAcYBd#C f!Eg$Fh Gj*H k(Jl-Kn+Lo0N p2Oq3Ps4Rt6S u7Tw8Vxa WybX AcZBd#Cf!Eg% F hGj*Ik(Jl- Kn+Mo0N p2Or3 Ps4Rt6Sv7Tw8 V xaWzbXAcZBe #Cf!Eg% FiGj *Ik) Jl-Kn+Mo 1Np2Or3Qs5Rt 6Sv7Uw8V xaWz bYAcZBe#Df!E g%FiHj*Ik) J m-Kn+Mo1Nq2O r3Qs5Ru6Sv7U w9VxaW zbYAdZBe#Df$Eg %Fi Hj(Ik) Jm-Ln +M o1Nq2Pr3Qs 5Ru6Tv7U w9Vy aWzbYAdZCe#D f$Eh%FiHj(I l) Jm-Ln0Mo1N q2Pr4Qs5Or3P s4Rt6Su7Tw8V xaWybXAcZ Be# Cf! Eg%FhGj* I。

matlab中的一些经典算法在MATLAB中，有许多经典算法可以用于各种数学和工程问题。

以下是一些常见的经典算法：1. 最小二乘法（Least Squares Method），用于拟合数据和解决过定系统的线性方程组。

MATLAB中的`polyfit`和`lsqcurvefit`函数可以实现最小二乘拟合。

2. 快速傅里叶变换（Fast Fourier Transform, FFT），用于信号处理和频域分析。

MATLAB中的`fft`函数可以对信号进行快速傅里叶变换。

3. 线性规划（Linear Programming），用于优化问题的求解，例如最大化/最小化线性目标函数的线性约束问题。

MATLAB中的`linprog`函数可以用于线性规划求解。

4. 非线性最小二乘法（Nonlinear Least Squares），用于拟合非线性模型到数据。

MATLAB中的`lsqnonlin`函数可以用于非线性最小二乘拟合。

5. 最优化算法（Optimization Algorithms），MATLAB提供了许多优化算法，包括梯度下降、共轭梯度、拟牛顿等算法，用于解决无约束和约束优化问题。

6. 插值算法（Interpolation），MATLAB中的`interp1`和`interp2`函数可以用于一维和二维数据的插值。

7. 微分方程求解（Differential Equation Solving），MATLAB中的`ode45`和`ode15s`等函数可以用于求解常微分方程和偏微分方程。

8. 图像处理算法（Image Processing Algorithms），MATLAB提供了丰富的图像处理工具箱，包括滤波、边缘检测、图像分割等经典算法。

以上列举的算法只是 MATLAB 中众多经典算法的一小部分，它们在数学建模、信号处理、优化、图像处理等领域有着广泛的应用。

希望这些信息能够帮助到你。

matlab 阻抗最小二乘法“最小二乘法”（Least Squares）是一种数学优化方法，用于解决线性方程组或者非线性方程组的问题。

在MATLAB中，最小二乘法可通过使用内置函数lsqcurvefit 或者nlinfit 来实现。

这两个函数用于非线性最小二乘法的拟合问题。

lsqcurvefit 用于对非线性方程进行曲线拟合，使用的是Gauss-Newton 算法。

% 定义模型函数function y = model(params, x)a = params(1);b = params(2);y = a * x + b;end% 定义初始参数值params0 = [0, 0];% 定义数据xData = [1, 2, 3, 4, 5];yData = [2, 3, 4, 5, 6];% 最小二乘拟合params = lsqcurvefit(@model, params0, xData, yData); disp(params);nlinfit 用于非线性模型的参数估计。

matlabCopy code% 定义模型函数function y = model(params, x)a = params(1);b = params(2);y = a * x + b;end% 定义初始参数值params0 = [0, 0];% 定义数据xData = [1, 2, 3, 4, 5];yData = [2, 3, 4, 5, 6];% 最小二乘拟合params = nlinfit(xData, yData, @model, params0);disp(params);在上面的例子中，我们定义了一个简单的一次线性模型 y = a * x + b，然后通过最小二乘法来拟合数据集 (xData, yData)，从而估计参数 a 和 b 的值。

matlab最小二乘法的非线性参数拟合首先说一下匿名函数：在创建匿名函数时，Matlab记录了关于函数的信息，当使用句柄调用该函数的时候，Matlab不再进行搜索，而是立即执行该函数，极大提高了效率。

所以首选匿名函数。

具体拟合时可以使用的方法如下：1 曲线拟合工具箱提供了很多拟合函数，使用简单非线性拟合nlinfit函数clear all;x1=[0.4292 0.4269 0.381 0.4015 0.4117 0.3017]';x2=[0.00014 0.00059 0.0126 0.0061 0.00425 0.0443]';x=[x1 x2];y=[0.517 0.509 0.44 0.466 0.479 0.309]';f=@(p,x)2.350176*p(1)*(1-1/p(2))*(1-(1-x(:,1).^(1/p(2))).^p(2)).^2.*(x(:,1).^ (-1/p(2))-1).^(-p(2)).*x(:,1).^(-1/p(2)-0.5).*x(:,2);p0=[8 0.5]';opt=optimset('TolFun',1e-3,'TolX',1e-3);%[p R]=nlinfit(x,y,f,p0,opt)2 最小二乘法在曲线拟合中比较普遍。

拟合的模型主要有1.直线型2.多项式型3.分数函数型4.指数函数型5.对数线性型6.高斯函数型一般对于LS问题，通常利用反斜杠运算“\”、fminsearch或优化工具箱提供的极小化函数求解。

在Matlab中，曲线拟合工具箱也提供了曲线拟合的图形界面操作。

在命令提示符后键入：cftool，即可根据数据，选择适当的拟合模型。

“\”命令1.假设要拟合的多项式是：y=a+b*x+c*x^2.首先建立设计矩阵X：X=[ones(size(x)) x x^2];执行：para=X\ypara中包含了三个参数：para(1)=a;para(2)=b;para(3)=c;这种方法对于系数是线性的模型也适应。