下载文档原格式
1.计算下面长方体的表面积和体积。
（单位：厘米）解：长方体的表面积：（9×6+9×5+6×5）×2=258（平方厘米）长方体的体积：9×5×6=270（立方厘米）2.计算下面图形的体积。
（单位：分米）3.2×12.5×3=40×3=120（立方分米）3.计算下面图形的表面积。
（单位：厘米）4×4×6=16×6=96（平方厘米）4.求下面图形的表面积和体积。
表面积=（5×5+5×3+5×3）×2+2×2×6-2×2×2=（25+15+15）×2+24-8=126（平方厘米）体积=5×5×3+2×2×2=83（立方厘米）5.求下面图形的表面积和体积。
（单位：dm）表面积=6×6×6=216dm²体积=6×6×6-2×3×2=204dm³6.下图是一个长方体的展开图，测量需要的数据，并求长方体的表面积和体积。
表面积：(2.7×1.7+2.7×0.9+1.7×0.9)×2=17.1(平方厘米) 体积：2.7×1.7×0.9=4.131(立方厘米)7.如图是一个正方体的表面展开图，求原来正方体的表面积和体积。
解：6÷3=2（cm）S表=2×2×6=24(cm²)V体=2×2×2=8(cm³)8.一块长方形铁皮（如图），从四个角各切掉一个边长为3cm 的正方形，然后做成盒子．这个盒子用了多少铁皮？它的容积有多少？解：①26×21﹣3×3×4=510（平方厘米）②（26﹣3×2）×（21﹣3×2）×3=（26﹣6）×（21﹣6）×3=20×15×3=900（立方厘米）答：这个盒子用了510平方厘米铁皮；它的容积是900立方厘米.6.计算下面图形的表面积和体积。
六年级下册体积与表面积同学们，在六年级下册的数学学习中，体积与表面积可是非常重要的知识点哦！咱们先来说说体积。
体积呀，简单来说，就是一个物体所占空间的大小。
想象一下，一个盒子能装多少东西，这就是盒子的体积。
那怎么计算体积呢？对于长方体，体积等于长乘以宽乘以高。
比如说，有一个长方体，长是 5 厘米，宽是 3 厘米，高是 2 厘米，那它的体积就是 5×3×2 ＝ 30 立方厘米。
再看看正方体，它的长、宽、高都相等，所以正方体的体积就是棱长的立方。
假如一个正方体的棱长是 4 厘米，那它的体积就是 4×4×4 ＝ 64 立方厘米。
接下来，咱们聊聊圆柱体。
圆柱体的体积等于底面积乘以高。
底面积怎么算呢？是圆的面积，也就是π乘以半径的平方。
假如一个圆柱体，底面半径是 3 厘米，高是 5 厘米，先算出底面积是 314×3×3 ＝2826 平方厘米，体积就是 2826×5 ＝ 1413 立方厘米。
然后是圆锥体，它的体积是等底等高圆柱体体积的三分之一。
比如说，有一个圆锥和一个圆柱，底面半径和高都一样，圆柱体积是 90 立方厘米，那圆锥的体积就是 90÷3 ＝ 30 立方厘米。
说完体积，咱们再讲讲表面积。
表面积就是一个物体表面的总面积。
长方体的表面积等于（长×宽＋长×高＋宽×高）×2。
还是用前面那个长方体举例，表面积就是（5×3 ＋ 5×2 ＋ 3×2）×2 ＝ 62 平方厘米。
正方体的表面积就简单多啦，因为六个面都一样，所以是棱长×棱长×6。
比如一个棱长为 5 厘米的正方体，表面积就是 5×5×6 ＝ 150 平方厘米。
圆柱体的表面积稍微复杂一点，它由两个底面和一个侧面组成。
底面是两个圆，侧面展开是一个长方形。
假如圆柱体底面半径是2 厘米，高是 6 厘米，底面积是 2×314×2×2 ＝ 2512 平方厘米，侧面积是2×314×2×6 ＝ 7536 平方厘米，表面积就是 2512×2 ＋ 7536 ＝ 1256 平方厘米。
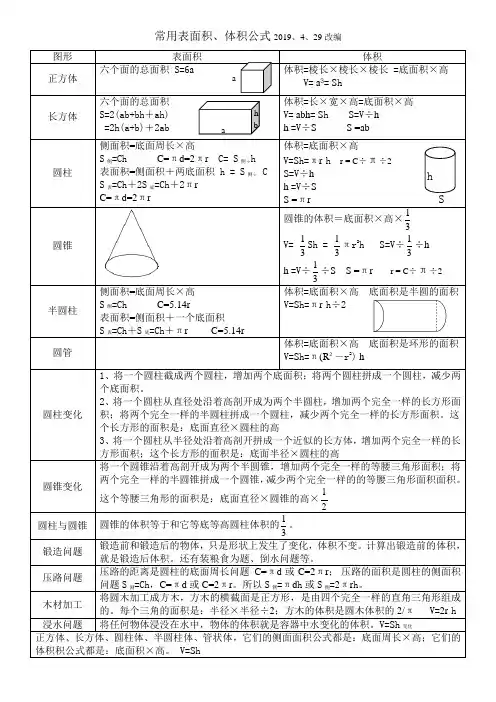
常用表面积、体积公式2019、4、29改编图形 表面积体积正方体六个面的总面积 S=6a ² 体积=棱长×棱长×棱长 =底面积×高V= a 3= S h长方体六个面的总面积 S=2(ab+bh ＋ah) =2h(a+b)＋2ab体积=长×宽×高=底面积×高 V= abh = S h S =V ÷h h =V ÷S S =ab 圆柱侧面积=底面周长×高S 侧=Ch C=πd=2πr C= S 侧÷h 表面积=侧面积＋两底面积 h = S 侧÷ C S 表=Ch ＋2S 底=Ch ＋2πr ² C=πd=2πr体积=底面积×高 V=S h=πr ²h r = C ÷π÷2 S =V ÷h h =V ÷S S =πr ²圆锥圆锥的体积＝底面积×高×13V= 13Sh = 13πr 2h S =V ÷13÷hh =V ÷13÷S S =πr ² r = C ÷π÷2半圆柱侧面积=底面周长×高 S 侧=Ch C=5.14r表面积=侧面积＋一个底面积 S 表=Ch ＋S 底=Ch ＋πr ² C=5.14r 体积=底面积×高 底面积是半圆的面积 V=S h=πr ²h ÷2圆管体积=底面积×高 底面积是环形的面积 V=S h=π(R ²－r 2) h圆柱变化 1、将一个圆柱截成两个圆柱，增加两个底面积；将两个圆柱拼成一个圆柱，减少两个底面积。
2、将一个圆柱从直径处沿着高剖开成为两个半圆柱，增加两个完全一样的长方形面积；将两个完全一样的半圆柱拼成一个圆柱，减少两个完全一样的长方形面积。
第27讲表面积与体积（一）一、知识要点小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。
从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。
因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。
在解答立体图形的表面积问题时，要注意以下几点：（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。
（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。
反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。
（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。
二、精讲精练【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？这是一道开放题，方法有多种：①按图27-1所示，沿着一条棱挖，剩下部分的表面积为592平方厘米。
图27--1②按图27-2所示，在某个面挖，剩下部分的表面积为632平方厘米。
图27--2③按图27-3所示，挖通某两个对面，剩下部分的表面积为672平方厘米。
图27--3练习1：1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体，剩下部分的表面积是多少？2、把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后，表面积会发生怎样的变化？图27—4【例题2】把19个棱长为3厘米的正方体重叠起来，如图27-4所示，拼成一个立体图形，求这个立体图形的表面积。
要求这个复杂形体的表面积，必须从整体入手，从上、左、前三个方向观察，每个方向上的小正方体各面就组合成了如下图形（如图27-5所示）。
第28讲表面积与体积（二）一、知识要点解答立体图形的体积问题时，要注意以下几点：（1）物体沉入水中，水面上升部分的体积等于物体的体积。
把物体从水中取出，水面下降部分的体积等于物体的体积。
这是物体全部浸没在水中的情况。
如果物体不全部浸在水中，那么派开水的体积就等于浸在水中的那部分物体的体积。
（2）把一种形状的物体变为另一种形状的物体后，形状变了，但它的体积保持不变。
（3）求一些不规则形体体积时，可以通过变形的方法求体积。
（4）求与体积相关的最大、最小值时，要大胆想象，多思考、多尝试，防止思维定。
二、精讲精练【例题1】有大、中、小三个正方体水池，它们的内边长分别为6米、3米、2米。
把两堆碎石分别沉在中、小水池里，两个水池水面分别升高了6厘米和4厘米。
如果将这两堆碎石都沉在大水池里，大水池的水面升高多少厘米？中、小水池升高部分是一个长方体，它的体积就等同于碎石的体积。
两个水池水面分别升高了6厘米和4厘米，两堆碎石的体积就是3×3×0.06+2×2×0.04=0.7（立方米）。
把它沉到大水池里，水面升高部分的体积也就是0.7立方米，再除以它的底面积就能求得升高了多少厘米。
3×3×0.06+2×2×0.04=0.7（立方米）0.7÷6的平方=7/360（米）=1又17/18（厘米）答：大水池的水面升高了1又17/18厘米。
练习1：1、有大、中、小三个正方体水池，它们的内边长分别为4米、3米、2米。
把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4厘米和11厘米，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？2、用直径为20厘米的圆钢，锻造成长、宽、高分别为30厘米、20厘米、5厘米的长方体钢板，应截取圆钢多长（精确到0.1厘米）？3、将表面积为54平方厘米、96平方厘米、150平方厘米的三个铁质正方体熔铸成一个大正方体（不计损耗），求这个大正方体的体积。
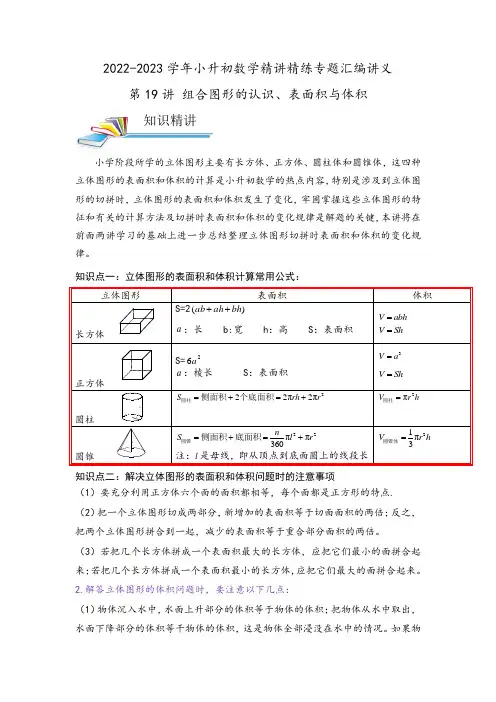
2022-2023学年小升初数学精讲精练专题汇编讲义第19讲 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体，这四种立体图形的表面积和体积的计算是小升初数学的热点内容，特别是涉及到立体图形的切拼时，立体图形的表面积和体积发生了变化，牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键，本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。
知识点一：立体图形的表面积和体积计算常用公式： 立体图形 表面积体积 长方体S=2)(bh ah ab ++a ：长 b:宽 h ：高 S ：表面积 V abh = V Sh = 正方体S=26a a ：棱长 S ：表面积 3V a = V Sh = 圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱圆锥 22ππ360n S l r =+=+圆锥侧面积底面积 注：l 是母线，即从顶点到底面圆上的线段长 21π3V r h =圆锥体 知识点二：解决立体图形的表面积和体积问题时的注意事项（1）要充分利用正方体六个面的面积都相等，每个面都是正方形的特点.（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍；反之，把两个立体图形拼合到一起，减少的表面积等于重合部分面积的两倍。
（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来；若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。
2.解答立体图形的体积问题时，要注意以下几点：（1）物体沉入水中，水面上升部分的体积等于物体的体积；把物体从水中取出，水面下降部分的体积等干物体的体积，这是物体全部浸没在水中的情况。
如果物h r hr 知识精讲体不全部浸在水中，那么排开水的体积就等于浸在水中的那部分物体的体积. （2）把一种形状的物体变为另一种形状的物体后，形状变了，但它的体积保持不变.（3）求一些不规则物体体积时，可以通过变形的方法求体积。
（六年级）备课教员：第十二讲表面积与体积一、教学目标：知识目标1.进一步理解表面积和体积的含义，掌握常见几何体的表面积的计算方法；能力目标1.进一步加深对相关体积单位实际大小的认识，发展学生的空间观念。
2.在解决问题的过程中，发展学生灵活地应用相关数学知识和方法的能力。
情感目标1.进一步感受数学知识和方法的应用价值,激发学习数学的兴趣。
2.进一步感受数学与生活的密切联系，体会学习数学的重要性。
二、教学重点：进一步加深对相关体积单位实际大小的认识，发展学生的空间观念。
三、教学难点：掌握常见几何体的表面积的计算方法；四、教学准备：PPT、长方形硬纸片、圆形纸片各一张五、教学过程：第一课时（50分钟）一、导入（5分)【设计意图：通过实验观察，让学生深入地意识到体积基础公式是底面积×高，提高学生的空间想象力】师：老师手中有两张纸片，看纸片上贴的是什么？生：红包。
师：你们想要红包吗？每个红包里面的东西都不一样哦。
生：想要。
师：红包不是你们想要就能要。
想获得红包就得经过老师的考验。
这里2张长方形的纸片，老师想看到一个圆柱体和一个长方体？哪位同学告诉老师怎么办？上来操作给老师看看。
生：……（长方形纸片快速地上下平移，我们可以看到一个长方体，圆形纸片水平的快速地上下平移我们可以看到一个圆柱体。
）师：这两位同学想象力非常棒，这两个红包就给这两位优秀的同学，看看里面是什么？生：……师：唉，老师再问问你们，拿着长方形这张纸上移，到这个点高度停止，它运动的轨迹是不是这一段，就是它形成的长方体的高？圆形纸片呢？（不断地平移，加强学生的空间观念）生：……师：不错，那这个形成的长方体和圆柱体底面积是不是就是纸片的面积？生：是的。
师：好像立体图形和平面图形也是有些联系的哦，那我们进一步了解立体图形的奥妙吧。
【探究新知，引入新课：学生已经学习过了小学所有的立体图形，长方体、正方体、圆柱、圆锥，本堂主要是对该知识点进行整理和巩固，并应用到实际解决问题中】【板书课题：表面积与体积】二、探索发现授课（40分）（一）例题1：（10分）一个棱长为20厘米的正方体木块，从它的上方挖去一个半径为5厘米，高10厘米的圆柱形木块，这个木块剩下部分的表面积是多少？讲解重点：回顾和整理正方体、圆柱体概念和表面积计算公式，及了解圆柱体表面积推导过程。
第27周表面积与体积（一）专题简析：小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。
从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。
因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。
在解答立体图形的表面积问题时，要注意以下几点：（1 ）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。
（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。
反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。
（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。
例题1:从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？这是一道开放题，方法有多种：①按图27-1所示，沿着一条棱挖，剩下部分的表面积为592平方厘米。
②按图27-2所示，在某个面挖，剩下部分的表面积为632平方厘米。
图27--2③按图27-3所示，挖通某两个对面，剩下部分的表面积为672平方厘米。
图27--3练习1：1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体，剩下部分的表面积是多少？2、把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后，表面积会发生怎样的变化？例题2：把19个棱长为3厘米的正方体重叠起来，如图27-4所示，拼成一个立体图形，求这个立体图形的表面积要求这个复杂形体的表面积，必须从整体入手，从上、左、前三个方向观察，每个方向上的小正方体各面就组合成了如下图形（如图27-5所示）而从另外三个方向上看到的面积与以上三个方向的面积是相等的。
整个立体图形的表面积可米用（S上+S左+S前）X 2来计算。
（3X 3X 9+3X 3X 8+3X 3X 10）X 2=(81+72+90)X 2=243 X 2=486 (平方厘米)答：这个立体图形的表面积是486平方厘米。
练习2:1用棱长是1厘米的立方体拼成图27-6所示的立体图形。
求这个立体图形的表面积。
2、一堆积木（如图27-7所示），是由16块棱长是2厘米的小正方体堆成的。
它们的表面积是多少平方厘米？3、一个正方体的表面积是384平方厘米，把这个正方体平均分割成64个相等的小正方体。
每个小正方体的表面积是多少平方厘米？例题3：把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体，拼成一个大长方体，这个大长方体的表面积最少是多少平方厘米？把两个相同的大长方体拼成一个大厂房体，需要把两个相同面拼合，所得大厂房体的表面积就减少了两个拼合面的面积。
要使大长方体的表面积最小，就必须使两个拼合面的面积最大，即减少两个9X7的面。
（9X 9+9X 4+7X 4）X 2X 2—9X 7X 2=（63+36+28）X 4—126=508—126=382 （平方厘米）答：这个大厂房体的表面积最少是382平方厘米。
练习3：1、把底面积为20平方厘米的两个相等的正方体拼成一个长方体，长方体的表面积是多少？2、将一个表面积为30平方厘米的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体。
求大长方体的表面积是多少。
3、用6块（如图27-8所示）长方体木块拼成一个大长方体，有许多种做法，其中表面积最小的是多少平方厘米？例题4：一个长方体，如果长增加2厘米，则体积增加40立方厘米；如果宽增加3厘米, 则体积增加90立方厘米；如果高增加4厘米，则体积增加96立方里，求原长方体的表面积。
我们知道：体积=长乂宽X高；由长增加2厘米，体积增加40立方厘米，可知宽X 高=40-2=20 （平方厘米）；由宽增加3厘米，体积增加90立方厘米，可知长X高=90 -3=30 （平方厘米）；由高增加4厘米，体积增加96立方厘米，可知长X宽=96-4=24（平方厘米）。
而长方体的表面积=（长X宽+长X高+宽X高）X2= （20+30+24）X2=148 （平方厘米）。
即40 - 2=20 （平方厘米）90 - 3=30 （平方厘米）96 - 4=24 （平方厘米）（30+20+24 X 2=74 X 2=148 （平方厘米）答：原长方体的表面积是148平方厘米。
练习4:1、一个长方体，如果长减少2厘米，则体积减少48立方厘米；如果宽增加5厘米, 则体积增加65立方厘米；如果高增加4厘米，则体积增加96立方厘米。
原来厂房体的表面积是多少平方厘米？2、一个厂房体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，其表面积减少了120平方厘米。
原来厂房体的体积是多少立方厘米？3、有一个厂房体如下图所示，它的正面和上面的面积之和是209。
如果它的长、宽、高都是质数，这个长方体的体积是多少？例题5：如图27-10所示，将高都是1米，底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体。
求这个物体的表面积。
如果分别求出三个圆柱的表面积，再减去重叠部分的面积，这样计算比较麻烦。
实际上三个向上的面的面积和恰好是大圆柱的一个底面积。
这样，这个物体的表面积就等于一个大圆柱的表面积加上中、小圆柱的侧面积。
3.14 X 1.5 X 1.5 X 2+2X 3.14 X 1.5 X 1+2X 3.14 X 1 X 1+2X 3.14 X 0.5 X 1 =3.14 X(4.5+3+2+1)=3.14 X 10.5=32.97 （平方米）答：这个物体的表面积是32.97平方米。
练习5：1、 一个棱长为40厘米的正方体零件（如图27-11所示）的上、下两个面上，各有 一个直径为4厘米的圆孔，孔深为10厘米。
求这个零件的表面积。
2、 用铁皮做一个如图27-12所示的工件（单位：厘米），需用铁皮多少平方厘米？3、 如图27-13所示，在一个立方体的两对侧面的中心各打通一个长方体的洞，在 上、下侧面的中心打通一个圆柱形的洞。
已知立方体棱长为 10厘米，侧面上的洞口是 边长为4厘米的正方形，上、下侧面的洞口是直径为 4厘米的圆，求该立方体的表面积 和体积（口取3.14 ）。
练21、从三个不同的方向看，得到图答 27- 1：从上往下看 从前往后看 从左往右看(1 X 1 X 12+1 X 1 X 8+1X 1 X 7)X 2 = 54 平方厘米I 15不图 27—12 答案：练11、 切下一块后，切口处的表面减少了前、后、上面 3个1X 1的正方形，新增加了左右 下面三个1 X 1的正方形，所以表面积大小不变。
2、 4X 4X 6-2X 2X 2 = 92 平方厘米3、 中心挖去的洞的体积是：12X 3X 3- 13X 2= 7立方厘米，挖洞后木块的体积：33- 7 =20立方厘米，中心挖洞后每面增加的面积是 12X 4- 12 = 3平方厘米，挖洞后木块 的表面积：（32+3）X 6= 72平方厘米。
2、 (2X 2X 9+2X 2X 9+2X 2X 7)X 2 = 200 平方厘米3、因为64= 4X4X4,所以大正方形的棱长等于小正方形棱长的4被，那么大正方体的表面积是小正方体的4X 4= 16倍，小正方体的表面积是：384- 16= 24平方厘米练31、将正方体分为两个长方体，表面积就增加了2个30十6= 15平方厘米，拼成大正方体，表面积将减少两个拼合面的面积，正好是1个30十6= 15平方厘米，所以大长方体的表面积是30+30+6= 35平方厘米。
2、要是表面积最小，就要尽可能地把大的面拼合在一起。
表面积最小的拼法有如图答27- 2两种：表面积都是(3X 3+3X 4X 2)X 2 = 66平方厘米。
3、设大长方体的宽和高为x分米，长为2x分米，左面和右面的面积就是x2平方分米。
其余的面积为2x2平方分米，根据题意，大长方体的表面积是：8X2+8 X 2x2= 600 x =5大长方体的体积是：5X 5X 2X 5 = 250立方分米练41、 (48- 2+65- 5+96- 4)X 2= 122 平方厘米2、减少的表面积实质是高度分别为2厘米和3厘米的前、后、左、右四个面的面积之和。
把两个合并起来，用120-( 2+3)= 24厘米，求到正方体底面的周长，正方体的棱长就是24- 4= 6厘米。
圆长方体的体积是：6X 6X(6+3+2)= 396立方厘米3、长方体正面及上面的面积之和恰好等于这个长方体的长X(宽+高)，209= 11X 19,所以长=11，宽+高=19，或长=19，宽+高=11，根据题意，宽和高只能是17和2,长方体的体积就是11X 17X 2 = 374练51、402X 6+3.14X 4X 10X 2 = 9651.2 平方厘米2、用两个同样的工件可拼成图答27- 3的圆柱体。
3.14X 15X( 46+54)十2 = 2355 平方厘米3、立方体的表面积和是：6X 102-42X 4-2X 3.14X(2 ) 2= 510.88平方厘米打洞后增加的面积是：2 4 23.14X4X( 10-4) +4X( 10-4)X 4X 2+4 X 2-3.14X(- ) X 2 = 274.24 平方厘米表面积是：510.88+274.24= 785.12平方厘米。
