当前位置：文档之家 › 第9章 SPSS 20.0回归分析讲解

第9章 SPSS 20.0回归分析讲解

  • 格式：ppt
  • 大小：145.00 KB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

第9章SPSS线性回归分析

第9章SPSS线性回归分析

第9章SPSS线性回归分析1.线性回归分析概述线性回归分析是一种广泛应用于统计学和数据分析领域的方法，它用于研究自变量与因变量之间的线性关系。

线性回归模型基于一条直线的假设，通过最小化残差平方和来估计各个回归系数，并利用这些系数进行预测和推断。

SPSS是一款强大的统计分析软件，提供了丰富的功能和工具，使得线性回归分析变得更加简单和高效。

2.数据准备在进行线性回归分析之前，需要准备好相关的数据。

SPSS可以导入各种类型的数据文件，包括Excel、CSV等格式。

在导入数据之后，可以对数据进行预处理，如缺失值处理、异常值处理等。

3.构建线性回归模型在SPSS中，构建线性回归模型非常简单。

首先选择“回归”菜单下的“线性”选项，然后将所需要的自变量和因变量选择到相应的框中。

SPSS还提供了多种方法来选择自变量，如逐步回归、逐步回归法等。

选择好自变量之后，点击“确定”按钮，即可得到回归模型结果。

4.分析回归模型在得到回归模型结果之后，需要对模型进行分析。

SPSS提供了丰富的结果输出，包括参数估计值、显著性检验、模型拟合度等。

需要注意的是，线性回归模型的可靠性需要通过一系列统计检验进行验证，如F统计量、t统计量、残差分析等。

5.模型诊断6.预测与推断线性回归模型可以用于预测和推断，SPSS也提供了相应的功能。

在SPSS中可以输入自变量的数值，从而得到相应的因变量预测值。

此外，SPSS还可以进行参数估计的推断，包括置信区间和假设检验等。

7.扩展与应用除了简单的线性回归模型，SPSS还支持复杂的线性回归模型，如多重回归分析、多元回归分析等。

此外，SPSS还可以进行模型的改进和优化，如加入交互项、非线性变换等。

这些扩展功能在实际应用中非常有用，可以提高模型的解释力和预测能力。

总结：本章介绍了SPSS中的线性回归分析方法，包括模型构建、结果分析、模型诊断、预测与推断等。

SPSS提供了丰富的功能和工具，使得线性回归分析变得更加简单和高效。

第九章 SPSS的线性回归分析

第九章 SPSS的线性回归分析

第九章 SPSS的线性回归分析线性回归分析是一种常用的统计方法，用于探索自变量与因变量之间的线性关系。

在SPSS中，进行线性回归分析可以帮助研究者了解变量之间的关系，并预测因变量的数值。

本文将介绍如何在SPSS中进行线性回归分析，并解释如何解释结果。

一、数据准备。

在进行线性回归分析之前，首先需要准备好数据。

在SPSS中，数据通常以数据集的形式存在，可以通过导入外部文件或手动输入数据来创建数据集。

确保数据集中包含自变量和因变量的数值，并且数据的质量良好，没有缺失值或异常值。

二、进行线性回归分析。

在SPSS中进行线性回归分析非常简单。

首先打开SPSS软件，然后打开已经准备好的数据集。

接下来，依次点击“分析”-“回归”-“线性”，将自变量和因变量添加到相应的框中。

在“统计”选项中，可以选择输出各种统计信息，如残差分析、离群值检测等。

点击“确定”按钮后，SPSS会自动进行线性回归分析，并生成相应的结果报告。

三、解释结果。

线性回归分析的结果报告包括了各种统计信息和图表，需要仔细解释和分析。

以下是一些常见的统计信息和图表：1. 相关系数，线性回归分析的结果报告中通常包括了自变量和因变量之间的相关系数，用来衡量两个变量之间的线性关系强度。

相关系数的取值范围为-1到1，接近1表示两个变量呈正相关，接近-1表示呈负相关，接近0表示无相关。

2. 回归系数，回归系数用来衡量自变量对因变量的影响程度。

回归系数的符号表示自变量对因变量的影响方向，系数的大小表示影响程度。

在结果报告中，通常包括了回归系数的估计值、标准误、t值和显著性水平。

3. 残差分析，残差是因变量的观测值与回归方程预测值之间的差异，残差分析可以用来检验回归模型的拟合程度。

在结果报告中，通常包括了残差的分布图和正态概率图，用来检验残差是否符合正态分布。

4. 变量间关系图，在SPSS中，可以生成自变量和因变量之间的散点图和回归直线图，用来直观展示变量之间的线性关系。

SPSS回归分析讲义

SPSS回归分析讲义
其取值。 • 拟合二分类变量的Logistic回归模型的参数问题可通过Logistic变换转换为拟合线性
模型的参数。
第29页/共42页
• 诊断发现运营不良的金融商业机构 下表列出了66家公司的一些运营的财务比率，其中33家在2年后破产，另外33家在同
期保持偿付能力。用变量X1、X2、X3拟合一个Logistic回归模型。
第11页/共42页
• 结果解读 • 模型拟合度检验
第12页/共42页
• 方差分析表
第13页/共42页
• 回归分析结果
第14页/共42页
• 残差统计量检验
第15页/共42页
• 雇员对其主管满意度的调查
第16页/共42页
• 结果解读
共线性检验
第17页/共42页
• 共线性检验指标
第18页/共42页
• 在金融界，最关心的是企业的“健康”状况。自变量是公司的各项财务指标。而因变量 即是公司的偿付能力（破产＝0，有偿付能力＝1）。
第27页/共42页
• 二分类变量Logistic回归简介
第28页/共42页
◆ 注意 • 二分类变量Logistic回归其核心思想是对因变量二值取一的概率建模而不是直接预测
第34页/共42页
6.5 非线性回归—— Nonlinear过程
• 非线性回归简介
• 线性回归模型：回归参数是线性的，【Linear】过程。
• 内蕴线性（拟线性）回归模型：其回归参数不是线性的，但是可以通过转换变为线性的 参数，【Curve Estimation】过程。
• 非线性回归模型：其回归参数不是线性的，也不能通过转换的方法将其变为线性的参数， 【Nonlinear】过程。
第35页/共42页

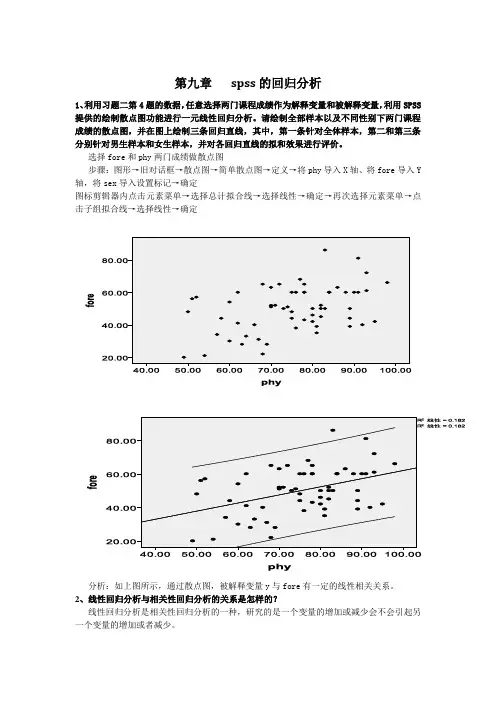
第九章 spss的回归分析

第九章 spss的回归分析

第九章spss的回归分析1、利用习题二第4题的数据，任意选择两门课程成绩作为解释变量和被解释变量，利用SPSS 提供的绘制散点图功能进行一元线性回归分析。

请绘制全部样本以及不同性别下两门课程成绩的散点图，并在图上绘制三条回归直线，其中，第一条针对全体样本，第二和第三条分别针对男生样本和女生样本，并对各回归直线的拟和效果进行评价。

选择fore和phy两门成绩做散点图步骤：图形→旧对话框→散点图→简单散点图→定义→将phy导入X轴、将fore导入Y 轴，将sex导入设置标记→确定图标剪辑器内点击元素菜单→选择总计拟合线→选择线性→确定→再次选择元素菜单→点击子组拟合线→选择线性→确定分析：如上图所示，通过散点图，被解释变量y与fore有一定的线性相关关系。

2、线性回归分析与相关性回归分析的关系是怎样的？线性回归分析是相关性回归分析的一种，研究的是一个变量的增加或减少会不会引起另一个变量的增加或者减少。

3、为什么需要对线性回归方程进行统计检验？一般需要对哪些方面进行检验？线性回归方程能够较好地反映被解释变量和解释变量之间的统计关系的前提是被解释变量和解释变量之间确实存在显著的线性关系。

回归方程的显著性检验正是要检验被解释变量和解释变量之间的线性关系是否显著，用线性模型来描述他们之间的关系是否恰当。

一般包括回归系数的检验，残差分析等。

4、SPSS多元线性回归分析中提供了哪几种解释变量筛选策略？包括向前筛选策略、向后筛选策略和逐步筛选策略。

5、先收集到若干年粮食总产量以及播种面积、使用化肥量、农业劳动人数等数据，请利用建立多元线性回归方程，分析影响粮食总产量的主要因素。

数据文件名为“粮食总产量.sav”。

步骤：分析→回归→线性→粮食总产量导入因变量、其余变量导入自变量→确定结果如图：Variables Entered/Removed bModel Variables Entered Variables Removed Method1 农业劳动者人数(百万人),总播种面积(万公顷), 风灾面积比例(%), 粮食播种面积(万公顷), 施用化肥量(kg/公顷), 年份a. Entera. All requested variables entered.b. Dependent Variable: 粮食总产量(y万吨)ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 2.025E9 6 3.375E8 414.944 .000aResidual 2.278E7 28 813478.405Total 2.048E9 34a. Predictors: (Constant), 农业劳动者人数(百万人), 总播种面积(万公顷), 风灾面积比例(%),粮食播种面积(万公顷), 施用化肥量(kg/公顷), 年份b. Dependent Variable: 粮食总产量(y万吨)Coefficients aModel UnstandardizedCoefficients StandardizedCoefficientst Sig.B Std. Error Beta1 (Constant) -613605.817 230903.867 -2.657 .013年份304.688 119.427 .402 2.551 .016粮食播种面积(万公顷) .736 .782 .053 .942 .354总播种面积(万公顷) 1.939 .650 .111 2.984 .006施用化肥量(kg/公顷) 141.077 11.186 .755 12.612 .000风灾面积比例(%) -307.209 51.870 -.174 -5.923 .000-5.121 22.286 -.038 -.230 .820 农业劳动者人数(百万人)a. Dependent Variable: 粮食总产量(y万吨)分析：如以上4个表所示，影响程度来由大到小依次是风灾面积、使用化肥量、总播种面积和年份。

[课件]SPSS回归分析过程详解()PPT

[课件]SPSS回归分析过程详解()PPT
SPSS回归分析过程详解 (ppt)
回归分析的概念
寻求有关联（相关）的变量之间的关系 主要内容：



从一组样本数据出发，确定这些变量间的定 量关系式 对这些关系式的可信度进行各种统计检验 从影响某一变量的诸多变量中，判断哪些变 量的影响显著，哪些不显著 利用求得的关系式进行预测和控制
回归分析的模型
按是否线性分：线性回归模型和非线性回归模型 按自变量个数分：简单的一元回归，多元回归 基本的步骤：利用SPSS得到模型关系式，是否 是我们所要的，要看回归方程的显著性检验（F 检验）和回归系数b的显著性检验(T检验)，还要 看拟合程度R2 (相关系数的平方,一元回归用R Square，多元回归用Adjusted R Square)
我们只讲前面3个简单的（一般教科书的讲法）
10.1 线性回归(Liner)
一元线性回归方程: y=a+bx


a称为截距 b为回归直线的斜率 用R2判定系数判定一个线性回归直线的拟合程度：用来说明用自变 量解释因变量变异的程度（所占比例）
b0为常数项 b1、b2、…、bn称为y对应于x1、x2、…、xn的偏回归系数 用Adjusted R2调整判定系数判定一个多元线性回归方程的拟合程度： 用来说明用自变量解释因变量变异的程度（所占比例）
逐步回归方法的基本思想
对全部的自变量x1,x2,...,xp,按它们对Y贡献的大小进 行比较，并通过F检验法，选择偏回归平方和显著的变 量进入回归方程，每一步只引入一个变量，同时建立 一个偏回归方程。当一个变量被引入后，对原已引入 回归方程的变量，逐个检验他们的偏回归平方和。如 果由于引入新的变量而使得已进入方程的变量变为不 显著时，则及时从偏回归方程中剔除。在引入了两个 自变量以后，便开始考虑是否有需要剔除的变量。只 有当回归方程中的所有自变量对Y都有显著影响而不需 要剔除时，在考虑从未选入方程的自变量中，挑选对Y 有显著影响的新的变量进入方程。不论引入还是剔除 一个变量都称为一步。不断重复这一过程，直至无法 剔除已引入的变量，也无法再引入新的自变量时，逐 步回归过程结束。

第九章 回归分析

第九章 回归分析
第九章 一元线性回归
经济与管理学院
教学要求
• 一、教学重点 • 回归分析的基本假设；运用SPSS进行线性 回归分析 • 二、教学难点 • 回归分析的原理 • 三、教学方式 • 课堂教学＋实践环节 • 四、课时数 • 12学时
第一节 相关回归分析的基本概念
西藏大学 经济与管理学 院
一、基本概念 （一）现象间的依存关系 函数关系 相关关系
第九章
经济与管理学 院
这样的方程有意义吗？
第九章
第三节 一元回归方程的检验
一、方差的分解
西藏大学 经济与管理学 院
yi y yi i i y y y
第九章
180 160 140 120 100 80 60 40 20 0 0 200000 400000 600000 800000 1000000
第九章
（二）相关关系的种类
1、直线相关与曲线相关 见图1，图2 2、 单相关与复相关 （1）单相关（一元相关） （2）复相关（多元相关）
西藏大学 经济与管理学 院
农 作 物 产 量 f 气 温, 降 雨 量, 阳 光, 施 肥 量
3、正相关与负相关
第九章
经济与管理学 院
180 160 140 120 100 80 60 40 20 0 0 200000 400000 600000 800000 1000000 1200000
第九章
二、回归分析的类别
一元回归 多元回归 线性回归 非线性回归
西藏大学 经济与管理学 院
回 归 分 析
第九章
三、一元线性回归方程的确定
西藏大学 经济与管理学 院
对于具有线性关系的两个变量，我们可以写成：
yi a b xi

邓铸《心理统计学与SPSS应用》笔记和课后习题详解-第9~13章【圣才出品】

第9章线性回归分析9.1 复习笔记一、回归分析概述（一）回归分析的意义在相关变量间建立预测方程式的统计学方法叫回归分析，包括线性和非线性、一元和多元的回归分析。

回归分析中变量之间的地位是不对等的，分为自变量和因变量。

回归分析是指建立自变量与因变量之间的关系模型，这个模型也叫回归方程。

（二）回归分析的基本逻辑1．回归分析的基本逻辑（1）自变量与因变量的关系首先假设因变量与一个或一些自变量之间具有某种数量关系。

用来表示预测值的平均值，则有y i=f（x1，x2，…，x k）+εi，（公式9-2）（2）回归分析的核心任务回归分析的核心任务是建立因变量与自变量之间的预测关系，即建立它们之间确定的函数关系，并尽可能地评估预测误差的大小。

2．回归分析的基本程序（1）提出假设的回归模型首先确定自变量与因变量。

（2）获取数据资料通过实验或大量的实际观测及调查，取得较为可靠的数据资料。

此项工作是研究者进行回归分析的前提和基础，其数据质量决定回归分析工作的质量。

（3）估计回归方程的函数形式①利用所获取的大量数据资料，先用直观的方式分析变量关系的形态；②根据函数拟合方式，确定应通过何种数学模型来概括回归线。

（4）回归方程的参数估计①“最佳拟合”回归方程最佳拟合原则就是误差平方和达到最小，Q表示误差平方和，在回归分析也称为剩余平方和：②最小二乘法回归分析最核心的任务就是依据观测的实际数据，按照最小原则确定函数中的参数。

（5）回归方程的有效性检验①含义根据样本数据建立起回归方程后，应对其进行各种检验，看其是否真实地反映了因变量与自变量之间的数量关系。

②内容a．回归方程的显著性检验；b．回归方程的拟合优度检验；c．回归系数的显著性检验。

③目的回归方程有效性检验的目的是考察回归方程预测的因变量值与实际观测的因变量值之间相关程度的高低。

相关越高，说明预测值与实际观测值越具有一致性，回归方程越能有效地反映自变量与因变量之间的变化关系。

第九章SPSS回归分析


第3步：启动分析过程。点击【分析】【 回归】【线性】菜单命令，打开如图所示 的对话框。
第4步：设置分析变量。设置因变量：在左边变量 列表中选“成就动机分数”，选入到“因变量”框 中。设置自变量：在左边变量列表中选“智商分数 ”变量，选入“自变量”框中。如果是多元线性回 归，则可以选择多个自变量。
第八个表：残差统计
第九个：标准化残差的概率图
[分析]：由此图可知，所有的点都比较靠近对角线 ，结合前面第八个表中的标准化残差为0.892，小 于2，因此可以认为残差是正态的。
由于自我效能感、服从领导满意度、同事人际敏感 、工作技能水平、个人信心指数这几个变量的回归 系数所对应的sig值不显著，在回归分析中需要删 除这几个变量，然后再建立回归方程。因此在SPSS 中接着再次进行回归分析。
分析：此例属于一元线性回归，一般先做两个变量 之间的散点图进行简单地观测。若散点图的趋势大 概呈线性关系，可以建立线性方程；若不呈线性分 布，可建立其它方程模型，并比较R2来确定选择其 中一种最佳方程式。
一元线性回归方程的原假设为：所建立的回归方程 无效，回归方程中来自总体自变量的系数为0。
第9步：重复前面SPSS的操作步骤，从第2步至第6 步。在第3步将自我效能感、服从领导满意度、同 事人际敏感、工作技能水平、个人信心指数这几个 变量从自变量移出，由于SPSS软件中还保存了刚才 第4、5、6步的操作内容，此时只需要再点击【确 定】按钮，输出分析结果。其中模型摘要、回归方 程、回归系数表如下：
第4步：设置分析参数。单击【统计】按钮，打开“ 线性回归：统计”对话框，可以选择输出的统计量 如图所示。
在“回归系数”栏，选择“估算值”。
在对话框的右边，有五个复选框：
（1）“模型拟合”是系统默认项，输出复相关系数 R、R2及R2修正值，估计值的标准误，方差分析表。 （2）“R方变化量”:增加进入或剔除一个自变量时 ， R2的变化。

用SPSS做回归分析ppt课件

从而用以进行预测或控制，达到指导生产活动的目的。
例1、某医学研究所对30个不同年龄的人的血压（高 压）进行了测量，得到如下数据：
年龄 39 47 45 47 65 45 67 42 67 56 36 50 39 21 44 血压 144 120 138 145 162 142 170 124 158 154 136 142 120 120 116 年龄 64 56 59 34 42 48 45 17 20 19 53 63 29 25 69 血压 162 150 140 110 128 130 135 114 116 124 158 144 130 125 175
初步分析作图察看按statisticsregressionlinear顺序展开对话框将y作为因变量选入dependent框中然后将其他变量选入作为自变量选入independents框中method框中选择stepwise逐渐回归作为分析方式单击statistics按钮进展需求的选择单击continue前往回归模型的建立被引入与被剔除的变量回归方程模型编号引入回归方程的自变量称号从回归方程被剔除的自变量称号回归方程中引入或剔除自变量的根据结果分析由复相关系数r0982阐明该预告模型高度显著可用于该地域大春粮食产量的短期预告常用统计量方差分析表回归方程为
在最优的方程中，所有变量对因变量Y的影响都应 该是显著的，而所有对Y影响不显著的变量都不包含 在方程中。选择方法主要有：
•逐步筛选法(STEPWISE) (最常用) •向前引入法(FORWARD) •向后剔除法(BACKWARD)等
逐步回归的基本思想和步骤：
开始
对不在方程中的变 量考虑能否引入？
能 引入变量
X1 137. 0 148. 0 154. 0 157. 0 153. 0 151. 0 151. 0 154. 0 155. 0 155. 0 156. 0 155. 0 157. 0 156. 0 159. 0 164. 0 164. 0 156. 0

《spss学习第9章》课件

《spss学习第9章》PPT课件
欢迎大家来到《spss学习第9章》PPT课件！在这个课程中，我们将深入学习 回归分析的基础、进阶和实战应用。让我们一起开始这个精彩的学习之旅吧！
回归分析基础
1
什么是回归分析
了解回归分析的概念和基本原理，掌握
简单回归与多元回归
2
其在数据分析中的重要性。
区分简单回归和多元回归分析的不同，
非线性回归分析
了解非线性回归分析的概念和应 用，以适应各种复杂的数据模式。
回归分析实战
1 数据准备
学习如何准备和清理回归 分析所需的数据，以确保 结果的准确性。
2 模型建立与分析
探索如何构建和分析回归 模型，以预测和解释数据 中的相关变量。
3 结果解释与展示
学习如何解释和展示回归 分析的结果，以便向其他 人传达研究发现。
结束语
感谢大家参与《spss学习第9章》PPT课件！通过这个课程，希望大家对回归分析有了更深入的理解，并能应 用于实际的数据分析工作中。祝大家取得好成果！
理解它们在实际应用中的用途。
3
相关系数与回归系数
研究与解释回归模型中的相关系数和回
回归模型诊断学习如何对回归模型进行诊断，以检验 其有效性和准确性。
回归分析进阶
变量选择方法
探索不同的变量选择方法，以找 到对回归模型最具影响力的自变 量。
线性回归分析
深入研究线性回归分析，并学习 如何解释和评估模型的结果。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.残差的独立性分析
残差独立性分析可以通过以下三种方式实 现： 一、绘制残差序列的序列图 二、计算残差的自相关系数 三、Durbin—Watson 检验
3. 异方差分析 一、绘制残差图
可以通过绘制残差图分析是否存在异方差。 二、等级相关分析 得到残差序列后首先对其取绝对值，然后 分别计算出残差和解释变量的
• 9.2.5.1 变量筛选问题
在多元线性回归分析中，模型中应引入多少 解释变量是需要重点研究的。如果引入的变 量较少，回归方程将无法很好地解释说明被 解释变量的变化。但是也并非引入的变量越 多越好，因为这些变量之间可能存在多重共 线性。因此有必要采取一些策略对变量引入 回归方程加以控制和筛选。多元回归分析中， 变量的筛选一般有向前筛选、向后筛选、逐 步筛选三种基本策略。
• 9.2.4.1 回归方程的拟合优度检验
• 对于一元线性回归方程
一元线性回归方程的拟合优度检验采用 R2 统计 量。该统计量称为判定系数或决定系数，数学 定义为:
n
( yi y)2
n

( yi y)2
R2 =
i 1 n
1
i 1 n
( yi y)2
( yi y)2
• 9.2.1一元线性回归模型
一元线性回归模型是指只有一个解释变量的 线性回归模型，用于揭示被解释变量与另一个 解释变量之间的线性关系。现实社会经济现象 中，某一事物（被解释变量）总会收到多方面 因素（多个解释变量）的影响。一元线性回归 分析是在不考虑其他影响因素或在是比较理想 化的分析。一元线性回归数学模型是
• 9.1.1 回归线和回归模型
利用样本数据获得回归线通常可采用两类 方法：第一，局部平均；第二，函数拟合。
• 9.1.2 回归分析的一般步骤 1确定回归方程中的解释变量和被解释变量 2确定回归模型 3建立回归方程 4对回归方程进行各种检验 5利用回归方程进行预测
9.2 线性回归分析
• 观察被解释变量和一个多个解释变量的散点 图，当发现与的线性回归模型。在线性回归 分析中，根据模型中解释变量的个数，可将 线性回归模型分成一元线性回归模型和多元 线性回归模型，相应的分析称为一元线性回 归分析和多元线性回归分析。
• 对于多元线性回归方程
多元线性回归方程显著性检验的零假设 是 ：i 0 ，即第个偏回归系数与零无显著差异。 它意味着当偏回归系数为 =0时i ，无论取值如何 变化都不会引起的线性变化，所有无法解释的线 性变化，它们不存在线性关系。
• 9.2.4.4 残差分析
所谓的残差是指由回归方程计算所得的预测值与实际样
第九章 回归分析
※回归分析概述 ※线性回归分析 ※曲线估计 ※二项Logistic回归 ※案例分析
9.1 回归分析概述
回归分析是一种应用极为广泛的数量分析方 法。它用于分析事物之间的统计关系，侧重 考察变量之间的数量变化规律，并通过回归 方程的形式描述和反映这种关系，帮助人们 准确把握变量受其他一个或多个变量影响程 度，进而为预测提供科学依据。
i 1
i 1
• 对于多元线性回归方程 多元线性回归方程的拟合优度检验采用 R2统计 量。该统计量称为调整的判定系数或调整的决 定系数，数学定义为
SSE
2
R =1-
n
p 1
SST
n 1
• 9.2.4.2 回归方程的显著性检验
对于一元线性回归方程检验采用统计量， 其数学定义为
n
( yi y)2
线性回归方程确定后的任务是利用已经收 集到的样本数据，根据一定的统计拟合准 则，对方程中的各个参数进行估计。普通 最小二乘就是一种最为常见的统计拟合准 则，在该准则下得到的回归参数的估计称 为普通最小二乘估计。
• 9.2.4 回归方程的统计检验
通过样本数据建立回归方程后一半不能立 即用于对实际问题的分析和预测，通常要 进行各种统计检验，主要包括回归方程的 拟合优度检验、回归方程的显著性检验、 回归系数的显著性检验、残差分析等。
y 0 1x
9.2.2多元线性回归模型 多元线性回归模型是指有多个解释变量的线 性回归模型，用于揭示被解释变量与其他多 个解释变量之间的线性关系。多元线性回归 的数学模型是
y 0 1x1+2 x2 + p xp
• 9.2.3 回归参数的普通最小二乘估计
F= n
i 1
( yi yi )2 / (n 2)
i 1
• 对于多元线性回归方程 检验采用统计量，其数学定义为
n
( yi y)2 / p
F= n
i 1
( yi yi )2 / (n p 1)
i 1
• 9.2.4.3 回归系数的显著性检验
• 回归系数的显著性检验的主要目的是研究 回归方程中的每个解释变量与被解释变量 之间是否存在显著性的线性关系，也就是 研究解释变量能否有效地解释被解释变量 的线性变化，它们能否保留在线性回归方 程中。
秩，最后计算Spearman 等级相关系数，并 进行等级相关分析。
• 9.2.5 多元回归分析中的其他问题
在多元回归分析中，由于解释变量会受 众多因素的共同影响，需要由多个解释变 量解释的，于是会出现诸如此类的问题： 多个变量是否都能够进入线性回归模型， 解释变量应以怎样的策略和顺序进行方程， 方程中多个解释变量之间是否存在多重共 线性等。
• 回归系数显著性检验是围绕回归系数（或 偏回归系数）估计值得抽样分布展开的， 由此构造服从某种理论分布的检验统计量， 并进行检验。
• 对于一元线性回归方程
一元线性回归方程的回归系数显著性检验的 零假设是 1=0 ，即回归系数与零无显著差异。 它意味着，当回归系数为0时，无论取值如何变 化都不会引起的线性变化，无法解释的线性变 化，它们之间不存在线性关系。
本值之间的差距，定义为ei yi yi yi (0 1 x1i 2 x2i p xpi )
1.残差均值为0的正态分布分析
当前面的讨论中知道，当解释变量取某个特定的值时， 对应的残差必然有正有负，但总体上应服从以0为均值的 正态分布。可以通过绘制残差图对该问题进行分析。残 差图也是一直散点图。图中一般横坐标是解释变量（也 可以是被解释变量的预测值），纵坐标为残差。