实验五 迭代与分形

实验名称：迭代与分形专业：信息工程班级：09级四班姓名：序号：29，38提交日期：2011年4月29日一、实验目的与要求1．认识Fibonacci数列，体验发现其通项公式的过程；2．了解matlab软件中进行数据显示与数据拟合的方式；3．掌握matlab软件中plot, polyfit等函数的基本用法；4．提高对数据进行分析与处理的能力。

二、问题描述几何学研究的对象是客观世界中物体的形状。

传统欧氏几何学的研究对象，都是规则并且光滑的，比如：直线、曲线、曲面等。

但客观世界中物体的形状，并不完全具有规则光滑等性质，因此只能近似当作欧氏几何的对象，比如：将凹凸不平的地球表面近似为椭球面。

虽然多数情况下通过这样的近似处理后，能够得到符合实际情况的结果，但是对于极不规则的形态，比如：云朵、烟雾、树木等，传统的几何学就无能为力了。

如何描述这些复杂的自然形态？如何分析其内在的机理？这些就是分形几何学所面对和解决的问题。

三、问题解决（1）对一个等边三角形，每条边按照Koch曲线的方式进行迭代，产生的分形图称为Koch雪花。

编制程序绘制出它的图形，并计算Koch雪花的面积，以及它的分形维数。

（2）自己构造生成元（要有创意），按照图形迭代的方式产生分形图，用计算机编制程序绘制出它的图形，并计算其分形维数。

1、程序如下：function plottrkoch(a,k)％函数，a为迭代0次的三角形的边长，k为迭代次数p=[0 0;a 0;a/2 a/2*sqrt(3);0 0];n=3;A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)];for s=1:kj=0;for i=1:nq1=p(i,:);q2=p(i+1,:);d=(q2-q1)/3;j=j+1;r(j,:)=q1;j=j+1;r(j,:)=q1+d;j=j+1;r(j,:)=q1+d+d*A';j=j+1;r(j,:)=q1+2*d;endn=4*n;clear pp=[r;q2];endmianji=sqrt(3)*(1+3*(1-(4/9)^k)/5)/4*a^2％计算迭代k次后的面积大小weishuD=log(4)/log(3)％计算维数plot(p(:,1),p(:,2))axis equal当k=1时当k=3时当k=5时因为是Koch曲线，所以维数d=ln4÷ln3=1.2619计算面积：假设最初的正三角形边长为1，则其周长为，面积为。

《数学实验》报告学院：电子信息学院专业班级：信息工程电联班学号：姓名：实验名称：迭代与分析实验日期：2016/05/031．实验目的了解分形几何的基本特性了解通过迭代方式产生分形图的方法欣赏美妙的分形艺术了解分形几何的简单应用2．实验任务对一条横向线段，先将其等分成4段，然后将第2段向上平移，将第3段向下平移，再将4段的相邻端点连接起来，迭代一次后变成下图。

继续迭代得到的分形图，称为Minkowski香肠。

编制程序绘制出它的图形，并计算它的分形维数。

图1Minkowski香肠1次迭代3．实验过程3.1实验原理通过观察该图形可以得知，该图形的相似形个数为8，边长放大倍数为4。

所以要把八条边进行迭代运行，同时把每个点的坐标放入数组中。

3.2算法与编程minkowski的算法代码：function plotminkowski(k)p=[0,0;10,0];n=1;A=[0,1;-1,0];for s=1:kj=0;for i=1:nq1=p(i,:);q2=p(i+1,:);d=(q2-q1)/4;j=j+1;r(j,:)=q1;j=j+1;r(j,:)=q1+d;j=j+1;r(j,:)=q1+d+d*A;j=j+1;r(j,:)=q1+2*d+d*A;j=j+1;r(j,:)=q1+2*d;j=j+1;r(j,:)=q1+2*d-d*A;j=j+1;r(j,:)=q1+3*d-d*A;j=j+1;r(j,:)=q1+3*d;endn=8*n;clear p;p=[r;q2];endfigureplot(p(:,1),p(:,2)) %显示各结点的连线图axis equal3.3计算结果或图形执行命令行：plotminkowski(4)输出图形：图3.3.1四次迭代的minkowski分形图执行命令行：plotminkowski(3)输出图形：图3.3.2三次迭代的minkowski分形图执行命令行：plotminkowski(1)输出图形：图3.3.3一次迭代的minkowski分形图3.4结果分析相似形个数：m=8边长倍数：c=4minkowski分形维度d=ln m/ln c=1.54. 实验总结和实验感悟通过这次实验，我们以迭代的方式来体验生成分形图的过程，从而对分形几何有了一个直观的了解，并感受美丽的分形图案。

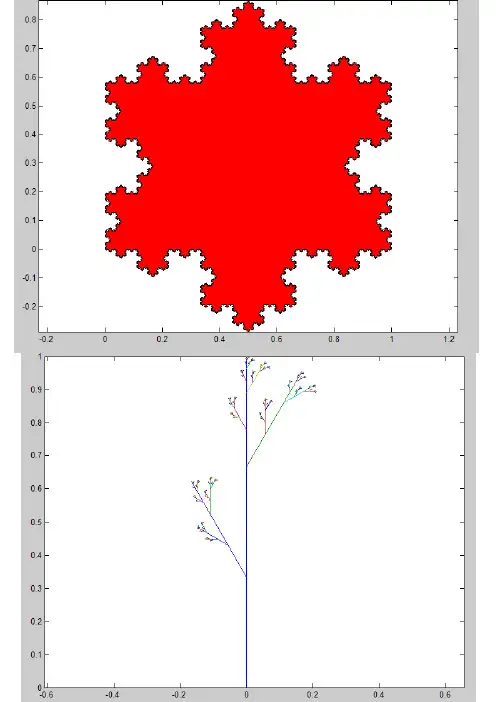
数学实验实验练习3.1对一个等边三角形，每条边按照Koch曲线的方式进行迭代，产生的分形图称为Koch雪花。

实验练习3.2对一条竖向线段，在三分之一点处，向左上方向画一条线段，在其三分之二分点处，向右上方向再画一条线段，线段长度都是原来的三分之一，夹角都为30度。

代码3.1Homework1.mfunction homework1(d,a) % d为图形基础边长，a为图形阶数A=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)]; %正负30°旋转因子p=[0,0;[0,0]+[d,0]*A';(0+d),0;0,0]; %分形点列矩阵n=3;if n~=1for s=1:(a-1)j=0;for i=1:n %一直线段新增3点q1=p(i,:);q2=p(i+1,:);d=(q2-q1)/3;j=j+1;r(j,:)=q1;j=j+1;r(j,:)=q1+d;j=j+1;r(j,:)=q1+d+d*A';j=j+1;r(j,:)=q1+2.*d;endclear pp=[r;q2];n=4*n;endendfill(p(:,1),p(:,2),'r')axis equal代码3.2Homework2.mfunction homework2(n) %n为图形阶数，一阶是长度为1的竖直直线born=[0;1i];plot(born); %画出主树干hold onzhuan=[exp(1i*pi/6),exp(-1i*pi/6)]; %正负30°旋转因子if n~=1for s=1:(n-1)j=0;b=0;sizeb=size(born);hua=zeros(2,2*3^(s-1)); %装要画出的线段构成的矩阵r=zeros(2,3^s); %装成为新生枝的主干的矩阵for a=1:sizeb(2)p1=born(1,a); %分主干的根点p2=born(2,a); %分主干的顶点d=(p2-p1)/3;j=j+1;hua(1,j)=p1+d; %要画出的分支线段装进hua矩阵hua(2,j)=p1+d+d*zhuan(1);b=b+1;r(1,b)=hua(1,j); %要要成为新分主干的线段装进r矩阵r(2,b)=hua(2,j);j=j+1;hua(1,j)=p1+2*d;hua(2,j)=p1+2*d+d*zhuan(2);b=b+1;r(1,b)=hua(1,j);r(2,b)=hua(2,j);b=b+1;r(1,b)=p1+2*d;r(2,b)=p2;endplot(hua); %画出新分支hold onclear huaborn=r; %装进新的分主干clear rendendaxis equal。

一、实验目的：1、初步认识迭代，体会迭代思想的重要性。

2、通过在mathematica 环境下编写程序，利用迭代的方法求解方程的根、线性方程组的解、非线性方程组的解。

3、了解分形的的基本特性及利用mathematica 编程生成分形图形的基本方法， 在欣赏由mathematica 生成的美丽的分形图案的同时对分形几何这门学科有一个直观的了解。

从哲理的高度理解这门学科诞生的必然性，激发读者探寻科学真理的兴趣。

4、从一个简单的二次函数的迭代出发，利用mathematica 认识混沌现象及其所 蕴涵的规律。

5、.进一步熟悉Mathematic 软件的使用，复习总结Mathematic 在数学作图中的应用，为便于研究数学图像问题提供方便，使我们从一个新的视角去理解数学问题以及问题的实际意义。

6、在学习和运用迭代法求解过程中，体会各种迭代方法在解决问题的收敛速度上的异同点。

二、实验的环境：学校机房，mathematica4环境三、实验的基本理论和方法：1、迭代（一）—方程求解函数的迭代法思想：给定实数域上光滑的实值函数)(x f 以及初值0x 定义数列1()n n x f x +=， ,3,2,1,0=n ， (1)n x ， ,3,2,1,0=n ，称为)(x f 的一个迭代序列。

（1）方程求根给定迭代函数)(x f 以及初值0x 利用（1）迭代得到数列n x ， ,3,2,1,0=n .如果数列收敛到某个*x ，则有)(**x f x =. (2)即*x 是方程)(x f x =的解。

由此启发我们用如下的方法求方程0)(=x g 的近似解。

将方程0)(=x g 改写为等价的方程)(x f x =， (3) 然后选取一初值利用（1）做迭代。

迭代数列n x 收敛的极限就是方程0)(=x g 的解。

为了使得迭代序列收敛并尽快收敛到方程0)(=x g 的某一解的条件是迭代函数)(x f 在解的附近的导数将的绝对值尽量小，因此迭代方程修订成x x f x h x )1()()(λλ-+== (4) 选取λ使得|)(|x h '在解的附近尽量小. 为此, 我们可以令,01)()(=-+'='λλx f x h得)(11x f '-=λ. 于是 1)()()(-'--=x f x x f x x h . 特别地,如果取x x g x f +=)()(, 则可得到迭代公式 .,1,0,)()(1 ='-=+n x g x g x x n n n n (5) （2）线性方程组的数值解的迭代求解理论与矩阵理论给定一个n 元线性方程组⎪⎩⎪⎨⎧=++=++,,1111111n n nn n n n b x a x a b x a x a (6)或写成矩阵的形式,b Ax = (7) 其中)(ij a A =是n 阶方阵,T n x x x x ),,(21 =及T n b b b b ),,,(21 =均为n 维列向量.熟知，当矩阵A 的行列式非零时，以上的方程组有唯一解.如何有效，快速地寻求大型的线性方程组的数值解释科学工程计算中非常重要的任务.而迭代法常常是求解这些问题的有效方法之一。

迭代：分形姓名：学号：班级：数学与应用数学4班实验报告实验目的：以迭代的观点介绍分形的基本特性以及生成分形图形的基本方法，使读者在欣赏美丽的分形图案的同时对分形几何这门学科有一个直观的了解，并从哲理的高度理解这门学科诞生的必然，激发读者探寻科学真理的兴趣。

实验环境：Mathematica软件实验基本理论和方法：在19世纪末及20世纪初，一些数学家就构造出一些边界形状极不光滑的图形，而这类图形的构造方式都有一个共同的特点，即最终图形F都是按照一定的规则R通过对初始图形不断修改得到的。

其中最有代表性的图形是Koch曲线，Koch曲线的构造方式是：给定一条直线段，将该直线段三等分，并将中间的一段用以该线段为边的等边三角形的另外两条边代替，得到图形，然后再对图形中的每一小段都按上述方式修改，以至无穷。

则最后得到的极限曲线即是所谓的Koch曲线。

生成元：Koch曲线的修改规则R是将每一条直线段用一条折线代替，我们称为该分形的生成元。

分形的基本特性完全由生成元确定，因此，给定一个生成元，我们就可以生成各种各样的分形图形。

Julia集绘制方法：（1）设定初值p，q，一个最大的迭代次数N，图形的分辨率的大小a，b，和使用的颜色数(如K=16)（或者给定灰度级L）；（2）设定一个上界值；（3）将矩形区域分成的网格，分别以每个网格点，，，，作为初值利用riter做迭代（实际上，只需对满足的初值点做迭代）。

如果对所有，，则将图形的像素点用黑色显示，否则，如果从迭代的某一步开始有，则用modK种颜色显示相应像素（或者用相应的灰度级显示）。

Mandelbrot集绘制方法：设定一个最大的迭代次数N，图形的分辨率的大小a，b，和使用的颜色数(如K=16)（或者给定灰度级L）；（2）设定一个上界值；（3）将矩形区域分成的网格，分别以每个网格点，，，，作为参数值利用riter做迭代（实际上，只需对的初值点做迭代），每次迭代的初值均取为。

《数学实验》报告学院：电子与信息学院专业班级：通信工程4班学号：*************名：***实验名称：迭代与分形实验日期：2013.04.7第三次实验1． 实验内容1.对一个等边三角形，每条边按照Koch 曲线的方式进行迭代，产生的分形图称为Koch 雪花。

编制程序绘制出它的图形，并计算Koch 雪花的面积，以及它的分形维数。

2． 实验过程方法一仿照Koch 曲线代码对三角形的每条边进行Koch 曲线化，函数的输入参数有三角形的边长R 和迭代次数k,输出Koch 雪花图形以及雪花所围面积S.KochSnow 面积推导如下所示：迭代次数k 面积S0: S=24r1: 2+ (13R)2*32: 2+ (13R)2*3 + 13)2R)2*323: S=4R 2+ 4(13R)2*3 + 4((13)2R)2*32 + 4((13)3R)2*33 ``````N: R 2+ 13R)2*3 + ((13)2R)2*32 + ((13)3R)2*33+…((13)n R)2*3n 如此相加下去，当N 无穷时，S 将为无穷大源代码如下：function kochsnow(R,k) %R为正三角形边长，k为迭代次数p01=[0,0];p02=[R/2,sqrt(3)*R/2];p03=[R,0]; %3个起始点S = 0; % S为面积，开始设为0 for line=0:2 %依次对3条边进行Koch曲线运算if line==0;p=[p01;p02];elseif line==1;p=[p02;p03];else line==2;p=[p03;p01];endn=1; %存放线段的数量，初始值为1A=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)]; %变换矩阵用于计算新的结点for s=1:kj=0; % j为行数for i=1:nq1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3;j=j+1;r(j,:)=q1; %原起点存入rj=j+1;r(j,:)=q1+d; %新1点存入rj=j+1;r(j,:)=q1+d+d*A'; %新2点存入rj=j+1;r(j,:)=q1+2*d; %新3点存入rendn=4*n; %全部线段迭代一次后，线段数量乘4clear p %清空p ，注意：最后一个终点q2不在r中p=[r;q2]; %一条边的全部结点clear rendif line==0; %把第一条边的全部结点放在aa=p;elseif line==1; %把第二条边的全部结点放在bb=p;else line==2; %把第三条边的全部结点放在cc=p;endendall=[a;b;c]; %三条边全部结点放入all plot(all(:,1),all(:,2)) %连接各个结点fill(all(:,1),all(:,2),'g')%填充所围区域for i=0:k %计算KochSnow的面积S = S + (3^(0.5-i))*0.25*(R^2);endSaxis equalKoch雪花图形输入半径R=2K=0时是正三角形此时面积为 1.7321K=1时是正六边形此时面积为 2.3094 K=2时的koch雪花此时面积为 2.5019K=3时的Koch雪花此时面积为 2.5660 K=4时的Koch雪花此时面积为 2.5874分形维数：根据迭代的规律得到：相似形个数：m=6 边长放大倍数：c=3，d m c=÷=÷=1.631ln ln ln6ln3方法2只生成一次Koch曲线，然后对生成的Koch曲线进行旋转变换，旋转3次即可得到所需图形。

几何画板迭代详解之:迭代与分形几何佛山市南海区石门中学谢辅炬分形的特点是,整体与部分之间存在某种自相似性，整体具有多种层次结构。

分形图片具有无可争议的美学感召力，特别是对于从事分形研究的科学家来说。

欣赏分形之美当然也要求具有一定的科学文化知识，但相对而言，分形美是通俗易懂的.分形就在我们身边，我们身体中的血液循环管道系统、肺脏气管分岔过程、大脑皮层、消化道小肠绒毛等等都是分形，参天大树、连绵的山脉、奔涌的河水、漂浮的云朵等等,也都是分形。

人们对这些东西太熟悉了，当然熟悉不等于真正理解。

分形的确贴近人们的生活,因而由分形而来的分形艺术也并不遥远，普通人也能体验分形之美。

因为分形几何的迭代的原像一般不止一个，而且均为多映射迭代，为了叙述的方便，我们先作以下两个约定。

1.用（A，B，C）表示有顺序的两点A、B和C.2.(A,B,C)(D,E,F,),(G,H,I)表示A映射到D，B映射到D，C映射到F,然后添加映射A映射到G,B映射到H,C映射到I，如此类推。

【Sierpinski三角形】波兰著名数学家谢尔宾斯基在1915-1916年期间，为实变函数理论构造了几个典型的例子，这些怪物常称作“谢氏地毯"、“谢氏三角”、“谢氏海绵”、“谢氏墓垛"。

如今，几乎任何一本讲分形的书都要提到这些例子。

它们不但有趣,而且有助于形象地理解分形。

著名的Sierpinski三角形，它是很有代表性的线性分形，具有严格的自相似特点。

不断连接等边三角形的中点，挖去中间新的小三角形进行分割——-随着分割不断进行Sierpinski三角形总面积趋于零，总长度趋于无穷。

Sierpinski三角形在力学上也有实用价值，Sierpinski 三角形结构节省材料，强度高，例如埃菲尔铁塔的结构与它就很相似。

【步骤】1.在平面上任意画一个三角形ABC,取三边中点为D、E、F，连接DEF.2.新建参数n＝33.顺次选择B，C,A三点和参数n，作深度迭代,(B,C,A)(D,F,A)⇒。

一、实验目的1. 理解分形的基本概念及其在自然界和科学中的应用。

2. 掌握分形图形的生成方法，包括迭代和递归。

3. 通过计算机实现Koch曲线、Sierpinski三角形和Cantor集等经典分形图形。

4. 分析分形图形的几何特性，如自相似性、无限细节和分形维数。

二、实验原理分形是一种具有无限复杂性和自相似性的几何形状。

它可以通过迭代和递归的方法生成，具有以下特点：1. 自相似性：分形图形的任何部分都与整体具有相似的结构。

2. 无限细节：分形图形在放大后仍然具有复杂的结构。

3. 分形维数：分形维数介于传统几何维数（如一维、二维、三维）之间，可以用来描述分形图形的复杂程度。

三、实验内容1. Koch曲线实验目的：生成Koch曲线，观察其自相似性和无限细节。

实验步骤：- 选择一条初始线段。

- 将线段等分为三部分，删除中间部分，并在两侧各添加一个等长的线段，形成60度角。

- 对新形成的四个线段重复上述步骤。

实验结果：通过迭代，Koch曲线逐渐呈现出复杂的结构，表现出自相似性和无限细节。

2. Sierpinski三角形实验目的：生成Sierpinski三角形，观察其自相似性和无限细节。

实验步骤：- 选择一个等边三角形作为初始图形。

- 在每个等边三角形的每个顶点处，向下作等边三角形的高，将其等分为三个小三角形。

- 保留中间的小三角形，删除其余部分。

实验结果：通过迭代，Sierpinski三角形逐渐呈现出复杂的结构，表现出自相似性和无限细节。

3. Cantor集实验目的：生成Cantor集，观察其分形维数和无限细节。

实验步骤：- 选择一个线段作为初始图形。

- 将线段等分为三部分，删除中间部分。

- 对新形成的两个线段重复上述步骤。

实验结果：通过迭代，Cantor集逐渐呈现出复杂的结构，具有无限细节。

其分形维数为ln(2)/ln(3) ≈ 0.6309，介于一维和二维之间。

四、实验结果与分析1. 通过实验，我们成功生成了Koch曲线、Sierpinski三角形和Cantor集等经典分形图形，验证了分形的基本概念和特性。

实验（五）：分形1. 用计算机绘制出koch曲线的图形。

你能否自己构造一些生成元，并由此绘出相应的分形图形？任取分形图形的一个局部并将它放大，它同原来的分形图形有什么联系？代码：function result=kochsnow(a,b,n) if (b(1)-a(1))^2+(b(2)-a(2))^2<n plot([a(1) b(1)],[a(2) b(2)])hold on; elsec=[a(1)+(b(1)-a(1))/3 a(2)+(b(2)-a(2))/3]; d=[a(1)+2*(b(1)-a(1))/3a(2)+2*(b(2)-a(2))/3]; alpha=atan((d(2)-c(2))/(d(1)-c(1)));l=sqrt((d(2)-c(2))^2+(d(1)-c(1))^2); if(alpha>=0&(d(1)<c(1))|(alpha<=0&(d(1)<c(1))))alpha=alpha+pi; ende(1)=c(1)+cos(alpha+pi/3)*l; e(2)=c(2)+sin(alpha+pi/3)*l; result=0;kochsnow(a,c,n); kochsnow(d,b,n); kochsnow(c,e,n); kochsnow(e,d,n);end end clear clc n=input(请输入次数: ); a=[0 0]; b=[130 0]; c=[b(1)/2 b(1)*sqrt(3)/2]; kochsnow(a,c,n); kochsnow(c,b,n); kochsnow(b,a,n); 2012秋数学实验实验（5）：分形页第 1 页共 10 实验（五）：分形运行结果：请输入次数: 6120100 806040200-20-40-20020406080100120140 （放大后可知其变化规律是一样的。

数学实验报告综合实验迭代学院：数学与信息科学学院班级： 09级数学（4）班姓名：***学号：***综合实验——迭代给定实数域上光滑的实值函数()f x 以及初值0x 定义数列1(),0,1,n n x f x n +==⋅⋅⋅，n x ，0,1,n =⋅⋅⋅，称为()f x 的一个迭代数列.函数的迭代是数学研究中的一个非常重要的思想工具.哪怕是对一个相当简单的函数进行迭代，都可以产生异常复杂的行为，并由此而衍生了一些崭新的学科分支，如分型与混沌.同时，迭代在各种数值计算方法以及其他学科领域的诸多算法中处于核心的地位.我们将通过一系列实验介绍迭代在诸多领域的应用。

一、迭代（方程求解）二、迭代（分形）③按Shift 和Enter 键运行。

运行结果：redosierpinski ptlist_List : Blockt mp ,i,pnum Length ptlist3 ,For i 0,i pnum,i i 1,tmp Join t mp, ptlist3i 1,ptlist 3i 1 ptlist 3i 2 2, ptlist 3i 1 ptlist 3i 3 2, ptlist 3i 1 ptlist3i 2 2,ptlist 3i 2 ,ptlist 3i 2 ptlist 3i 3 2, ptlist 3i 1 ptlist 3i 3 2, ptlist3i 2ptlist3i 32,ptlist 3i 3 ;tmpshowsierpinski ptlist_List : Blockt mp ,i,pnum Length ptlist3 ,For i 0,i pnum,i i 1,AppendTo t mp,Polygonptlist3i 1,ptlist3i 2ptlist3i 3;Show G raphics t mp ,AspectRatio 1 GoldenRat po1 1,0 , 1,0 , 0,Sqrt 3;showsierpinski Nest r edosierpinski,po1,4三、复变函数迭代1.510.5-0.5-1-1.5-1.5-1-0.500.511.510.5-0.5-1-1.5-1.5-1-0.500.51 0.30.20.1-0.1-0.7-0.65-0.6-0.55-0.5-0.45四、迭代（混沌）五、迭代（几何形状的构造）。

分形图形学实验报告指导实验报告要求1. 实验名称2. 实验目的、要求3. 实验主要内容（某某算法的实现）4. 实验过程（程序流程图、源代码）5. 实验结果（附上打印的图形）6. 实验小结实验报告一一般分形图形生成实验目的1. koch曲线、sierpinski三角形、cantor集的计算机实现2. 掌握用迭代、递归生成分形实验内容及步骤1、 koch曲线函数：plot(x1,y1) –(x2,y2) （画直线函数）sin( ) （正弦函数）cos( ) （余弦函数）arctan( ) （反正切函数）12、 sierpinski三角形函数： plot(x1,y1) –(x2,y2) （画直线函数）sin( ) （正弦函数）cos( ) （余弦函数）23、 cantor集3实验报告二 l系统语言生成分形图形实验目的1. 掌握用l系统语言生成分形2. koch曲线、sierpinski三角形、cantor集的l系统实现4实验内容及步骤1. 编写程序用l系统语言生成分形图形1) 编写程序生成koch曲线:初始图形是一条线段，生成过程是将线段中间1/3向外折起。

程序伪码如下：kochcurve { ；柯赫曲线angle 6 ；角度增量是60°axiom f ；初始图形是一单位线段f=f+f--f+f ；产生式是将线段中间1/3折起} ；结束2) 用l系统再次生成sierpinski三角。

生成sierpinski三角的伪码如下：hilbert{ ；sierpinski三角，1996-12 angle 4 axiom y ；初始串为任意字母y x=-yf+xfx+fy- ；第一个生成规则y=+xf-yfy-fx+ ；第二个生成规则，由以上规则不断代换 } 3) 模拟草本植物。

注意这里出现了“括号”——可以方便地表示树枝，伪码如下：herbplant { ；生成植物，本程序使用了括号angle 14axiom zz=zfx［+z］［-z］x=x［-fff］［+fff］fx}5篇二：光学实验报告建筑物理——光学实验报告实验一：材料的光反射比、透射比测量实验二：采光系数测量实验三：室内照明实测实验小组成员：指导老师：日期：2013年12月3日星期二实验一、材料的光反射比和光透射比测量一、实验目的与要求室内表面的反射性能和采光口中窗玻璃的透光性能都会直接或间接的影响室内光环境的好坏，因此，在试验现场采光实测时，有必要对室内各表面材料的光反射比，采光口中透光材料的过透射比进行实测。