2020年复变函数与积分变换第9章
- 格式:ppt
- 大小:4.14 MB
- 文档页数:55

1. 求下列信号的离散傅里叶变换。
()()(01).n x n a u n a a =<<为实数,解:1()()()(),1jwjwnjwnjw n jwn n n X e x n ea n eae ae ∞∞∞----=-∞=-∞=-∞====-∑∑∑幅度谱为21/21(),(12cos )jw X e a a w =+- 相位谱为sin ()arg ()arctan.1cos jw a ww X e a wφ==--2.求1, 1;().0, 1.n n x n Z n ≥⎧=⎨<⎩ 的变换解:该序列是一个右边序列,由定义得11().n n X z z n∞-==∑因为11211d ()11()(), 1.d n n n n X z n z z z z n z z ∞∞----===-=-=>-∑∑ 则()ln ln(1)ln.1z X z z z z=--=-3.求长度为N 的有限长序列00()(), 0x n n n n N δ=-<<的DFT.解:由定义得21()()()N jnk NN n X k x n eR k π--==∑2100()()N jnk NN n n n eR k πδ--==-∑02(),jn k NN eR k π-=其中()N R k 为矩形序列.4. 已知x(n )是N 点有限长序列,X(k)=DFT[x(n)].现将长度变为rN 点的有限长序列y(n),(), 01;()0, 1.x n n N y n N n rN ≤≤-⎧=⎨≤≤-⎩ 试求rN 点的DFT[y(n)]与X(k)的关系. 解:由21()[()](),01,N jnk Nn X k DFT x n x n ek N π--===≤≤-∑可得(1)1()[()]()()r N N nk nkrNrN n n Y k DFT y n y n Wx nW --=====∑∑ 210(),,0,1,, 1.k N j n N rn k x n eX k lr l N ar π--=⎛⎫====- ⎪⎝⎭∑所以在一个周期内,()Y k 的抽样点数是()X k 的r 倍,相当于在()X k 的每两个之间插入1r -个其他的数值(比一定为零),而当k 为r 的整数l 倍时,()Y k 与k X r ⎛⎫⎪⎝⎭相等.5.已知X(k),Y(k )是两个N 点的实序列x(n),y(n)的DFT 值,今需要从X(k),Y(k)求x(n),y(n)的值,为了提高运算效率,试用一个N 点IFFT 运算一次完成. 解:依据题意()(),()(),x n X k y n Y k ⇔⇔取序列()()(),Z k X k jY k =+对()Z k 作N 点IFFT 可得序列()z n .又根据DFT 的性质[][][]IDFT ()()IDFT ()IDFT ()()().X k jY k X k j Y k x n jy n =+=+=+由原题可知,(),()x n y n 都是实序列.再根据()()()z n x n jy n =+,可得[]()Re ()x n z n =以及[]()Im ().y n z n =6.如果一台计算机的速度为平均每次复乘5 μs ,每次复加0.5 μs ,用它来计算512点的DFT[x(n)],问:直接计算需要多长时间?用FFT 需要多长时间?解:(1)直接计算 复乘所需时间62621510510512 1.31072();T N s --=⨯⨯=⨯⨯=复加所需时间6620.510(1)0.510512(5121)0.130816().T N N s --=⨯⨯⨯-=⨯⨯⨯-=所以12 1.441536().T T T s =+=(2)用FFT 计算 复乘所需时间66122512510log 510log 5120.01152();22N T N s --=⨯⨯=⨯⨯= 复加所需时间662220.510log 0.510512log 5120.002304().T N N s --=⨯⨯=⨯⨯=所以120.013824().T T T s =+=。

复变函数与积分变换(修订版)主编:马柏林(复旦大学出版社)——课后习题答案习题一1. 用复数的代数形式a +ib 表示下列复数π/43513;;(2)(43);711i i e i i i i i-++++++.①解i 4πππe cos isin 44-⎛⎫⎛⎫⎛⎫=-+- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭②解: ()()()()35i 17i 35i 1613i 7i 11+7i 17i 2525+-+==-++-③解: ()()2i 43i 834i 6i 510i ++=-++=+ ④解: ()31i 1335=i i i 1i 222-+-+=-+2.求下列各复数的实部和虚部(z =x +iy )(z a a z a -∈+); 33311;;;.22n z i ⎛⎛-+-- ⎝⎭⎝⎭①: ∵设z =x +iy则()()()()()()()22i i i i i i x a y x a y x y a x a y z a z a x y a x a y x a y -++-⎡⎤⎡⎤+--+-⎣⎦⎣⎦===+++++++ ∴()22222Re z a x a y z a x a y ---⎛⎫= ⎪+⎝⎭++,()222Im z a xyz a x a y-⎛⎫=⎪+⎝⎭++. ②解: 设z =x +iy ∵()()()()()()()()323222222223223i i i 2i i 22i33iz x y x y x y x y xy x y x x y xy y x y x y x xy x y y =+=++=-++⎡⎤=--+-+⎣⎦=-+- ∴()332Re 3z x xy =-,()323Im 3z x y y =-.③解:∵(()(){}33232111313188-+⎡⎤⎡⎤==--⋅-⋅+⋅-⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭()180i 18=+=∴Re 1=⎝⎭, Im 0=⎝⎭. ④解:∵()()(()2332313131i 8⎡⎤--⋅-⋅+⋅-⎢⎥⎣⎦=⎝⎭()180i 18=+=∴Re 1=⎝⎭, Im 0=⎝⎭. ⑤解: ∵()()1,2i 211i,kn kn k k n k ⎧-=⎪=∈⎨=+-⋅⎪⎩. ∴当2n k =时,()()Re i 1kn=-,()Im i 0n=;当21n k =+时,()Re i 0n =,()()Im i 1kn =-.3.求下列复数的模和共轭复数12;3;(2)(32);.2ii i i +-+-++①解:2i -+==2i 2i -+=--②解:33-=33-=-③解:()()2i 32i 2i 32i ++=++=()()()()()()2i 32i 2i 32i 2i 32i 47i ++=+⋅+=-⋅-=-④解:1i 1i 22++==()1i 11i222i ++-⎛⎫== ⎪⎝⎭4、证明:当且仅当z z =时,z 才是实数.证明:若z z =,设i z x y =+,则有 i i x y x y +=-,从而有()2i 0y =,即y =0 ∴z =x 为实数.若z =x ,x ∈ ,则z x x ==. ∴z z =.命题成立.5、设z ,w ∈ ,证明: z w z w ++≤证明∵()()()()2z w z w z w z w z w +=+⋅+=++()()22222Re z z z w w z w wz zw z w w z wz w =⋅+⋅+⋅+⋅=++⋅+=++⋅()2222222z w z wz w z w z w ++⋅=++⋅=+≤∴z w z w ++≤.6、设z ,w ∈ ,证明下列不等式. ()2222Re z w z z w w +=+⋅+ ()2222Re z w z z w w -=-⋅+()22222z w z w z w++-=+并给出最后一个等式的几何解释.证明:()2222Re z w z z w w +=+⋅+在上面第五题的证明已经证明了.下面证()2222Re z w z z w w -=-⋅+.∵()()()()222z w z w z w z w z w z z w w z w-=-⋅-=--=-⋅-⋅+()222Re z z w w =-⋅+.从而得证.∴()22222z w z w z w ++-=+几何意义:平行四边形两对角线平方的和等于各边的平方的和.3352π2π;;1;8π(1);.cos sin 7199i i i i +⎛⎫--+ ⎪+⎝⎭ ①解:()()()()35i 17i 35i 7i 117i 17i +-+=++-3816i 198i e 5025i θ⋅--==其中8πarctan 19θ=-.②解:e i i θ⋅=其中π2θ=.π2e i i =③解:ππi i 1e e -==④解:()28π116ππ3θ-+==-.∴()2πi 38π116πe--+=⋅⑤解:32π2πcos isin 99⎛⎫+ ⎪⎝⎭ 解:∵32π2πcosisin 199⎛⎫+= ⎪⎝⎭.∴322πi π.3i 932π2πcos isin 1e e 99⋅⎛⎫+=⋅= ⎪⎝⎭8.计算:(1)i 的三次根;(2)-1的三次根;(3)的平方根.⑴i 的三次根. 解:()13ππ2π2πππ22cos sin cosisin 0,1,22233++⎛⎫+=+= ⎪⎝⎭k k i k∴1ππ1cosisin i 662=+=+z .2551cos πisin πi 662=+=+z3991cos πisin πi 662=+=-z ⑵-1的三次根 解:()()132π+π2ππcos πisin πcosisin 0,1,233k k k ++=+=∴1ππ1cos isin 332=+=z 2cos πisin π1=+=-z3551cos πisin π332=+=-z的平方根. 解:πi 4e ⎫⎪⎪⎝⎭∴)()1π12i 44ππ2π2π44e6cos isin 0,122k k k ⎛⎫++ ⎪=⋅+= ⎪⎝⎭∴π11i 8441ππ6cos isin 6e 88⎛⎫=⋅+=⋅ ⎪⎝⎭z911πi 8442996cos πisin π6e 88⎛⎫=⋅+=⋅ ⎪⎝⎭z . 9.设2πe,2inz n =≥. 证明:110n z z -+++=证明:∵2πi e nz ⋅= ∴1n z =,即10n z -=.∴()()1110n z z z --+++=又∵n ≥2. ∴z ≠1 从而211+0n z z z -+++=11.设Γ是圆周{:},0,e .i z r r a c r z c α=>=+-令:Im 0z a L z b β⎧-⎫⎛⎫==⎨⎬⎪⎝⎭⎩⎭, 其中e i b β=.求出L β在a 切于圆周Γ的关于β的充分必要条件. 解:如图所示.因为L β={z : Im z a b -⎛⎫⎪⎝⎭=0}表示通过点a 且相切,则CA ⊥L β.过C 作直线平行L β,则有∠BCD =β,∠ACB =90° 故α-β=90°所以L β在α处切于圆周T 的关于β的充要条件是α-β=90°.12.指出下列各式中点z 所确定的平面图形,并作出草图.(1)arg π;(2);1(3)1|2;(4)Re Im ;(5)Im 1 2.z z z z i z z z z ==-<+<>><且解:(1)、argz =π.表示负实轴.(2)、|z -1|=|z |.表示直线z =12.(3)、1<|z +i|<2解:表示以-i 为圆心,以1和2为半径的周圆所组成的圆环域。


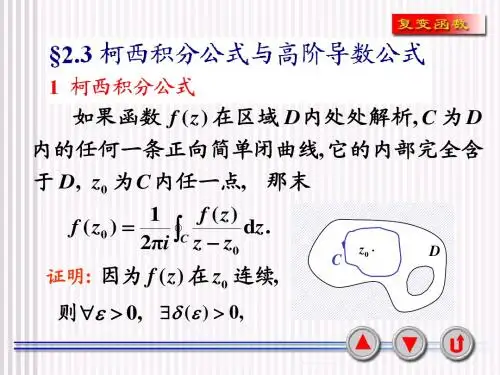



![[优选文档]复变函数与积分变换详细PPT](https://uimg.taocdn.com/7611a3d90b4c2e3f572763f8.webp)


2371 引言复变函数的物理背景非常鲜明,这是因为在流体力学和电动力学中,它有着最重要的向量场特征,它将力学、数学物理等许多方面的理论和实际问题紧密联系起来。
在复变函数理论基础之上,人们以特定形式积分的方法建立起函数之间的某种对应关系,这就是积分变换方法。
电子信息类专业《复变函数与积分变换》课程的教学研究郜东宁(兰州城市学院电子与信息工程学院 甘肃 兰州 730070)【摘要】《复变函数与积分变换》作为电子信息类专业的一门必修课程,主要任务是培养学生的创新思维、理论与实践相结合的能力。
本文根据该课程的现状,从教学手段、教学方法和考核方法等方面进行教学改革、完善教学体系,并将其融入实际教学中,收到很好的教学效果。
【关键词】《复变函数与积分变换》;教学改革;理论与实践【中图分类号】O174.5 【文献标识码】A 【文章编号】1009-5624(2020)07-0237-02总结学生在练习中出现的问题,教会学生掌握灵活的操作方法。
通过这种教学模式,能够有效锻炼学生的操作能力与思维能力,从而促进教学质量与效率提高[1]。
3 以课堂任务驱动学生开展课堂学习在任务驱动教学方法下,学生需要通过完成教师布置的学习任务掌握知识内容,整个完成任务的过程,就是学生学习的过程。
在整个任务驱动学习模式下,关键在于教师为学生布置的学习任务,任务的质量直接关系到学生的学习状态与最终的学习效果。
教师在为学生设计教学任务时,要考虑到中职计算机信息技术的教学标准与目的,将实际生活内容融入到信息技术教学中,与其他课程知识有机的联系在一起,以学生的生活与学习为基础,为学生制定学习任务。
通过这样的方式能够让学生感受到计算机信息技术的生活性与实用性,从而拉近学生与计算机信息技术之间的距离,激发学生对信息技术知识的好奇心与探索欲,此时学生自己动手参与到计算机信息技术课堂中。
教师在为学生布置学习任务后,不要急于为学生进行讲解,而是给学生预留出足够的空间与时间,让学生以通过自主思考与合作学习的方式,共同探究学习任务,从而调动学生的学习热情与参与课堂的积极性。
复变函数与积分变换西安科技大学智慧树知到答案2024年第一章测试1.设为复数,则方程的解是()A:B:C:D:答案:B2.满足不等式的所有点构成的集合是()A:无解区域B:有界闭区域C:无界闭区域D:有界区域答案:C3.在时极限()A:0B:不存在C:-1D:1答案:B4.设则()A:B:C:D:答案:D5.函数在点处连续的充要条件是()A:和在处连续B:在处连续C:在处连续D:在处连续答案:A第二章测试1.若函数在区域内解析,则也在内解析。
()A:对 B:错答案:B2.若函数在处满足柯西-黎曼条件,则在处解析。
()A:错 B:对答案:A3.若函数在区域内解析,且也在内解析,则是常数。
()A:错 B:对答案:B4.函数的基本周期为。
()A:错 B:对答案:B5.设则。
()A:对 B:错答案:A第三章测试1.一个解析函数在圆心处的值等于它在圆周上的平均值。
()A:错 B:对答案:B2.复积分与路径无关的充要条件是其右端两个对坐标的曲线积分都与积分路径无关。
()A:对 B:错答案:A3.一个解析函数不仅有一阶导数,而且有任意阶导数,它的值也可用函数在边界上的值通过积分来表示。
()A:对 B:错答案:A4.解析函数的实部和虚部都不是调和函数。
()A:对 B:错答案:B5.解析函数的实部是虚部的共轭调和函数。
()A:对 B:错答案:B第四章测试1.若幂级数在处收敛,那么该级数在处的敛散性为()A:不能确定B:发散C:条件收敛D:绝对收敛答案:D2.级数的收敛半径为()A:0.5B:C:2D:答案:D3.复数列收敛于的充要条件是,()A:对 B:错答案:A4.若收敛。
()A:对 B:错答案:B5.在某一个圆环域解析的函数展开的洛朗级数是唯一的。
()A:错 B:对答案:B第五章测试1.是函数的()A:3级极点B:2级极点C:本性奇点D:可去奇点答案:B2.是函数的()A:本性奇点B:4级极点C:3级极点D:可去奇点答案:B3.为函数的级极点的充分必要条件,是可表示为的形式,其中在点解析。
教案复变函数与积分变换课程教案填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;复变函数与积分变换课程教案填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;复变函数与积分变换课程教案填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;填表说明:1. 每项页面大小可自行添减;2. 课次为授课次序,填1、2、3……等;3. 授课方式填理论课、实验课、讨论课、习题课等;。