二次函数中求直角三角形的方法

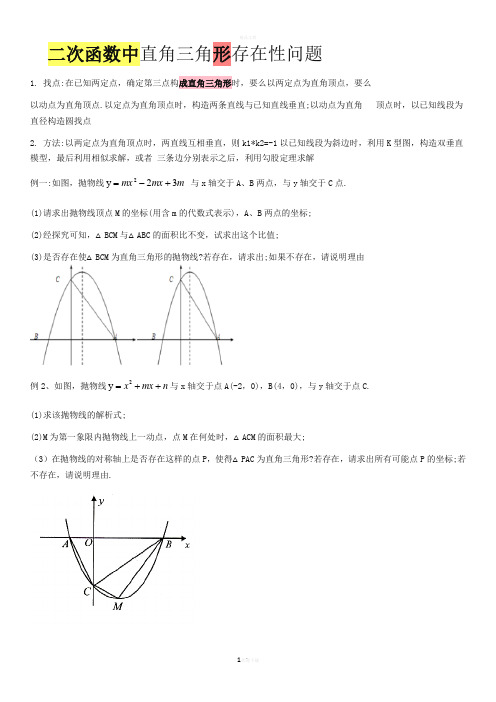
二次函数中直角三角形存在性问题1. 找点:在已知两定点，确定第三点构成直角三角形时，要么以两定点为直角顶点，要么以动点为直角顶点.以定点为直角顶点时，构造两条直线与已知直线垂直;以动点为直角 顶点时，以已知线段为直径构造圆找点2. 方法:以两定点为直角顶点时，两直线互相垂直，则k1*k2=-1以已知线段为斜边时，利用K 型图，构造双垂直模型，最后利用相似求解，或者 三条边分别表示之后，利用勾股定理求解例一:如图，抛物线m mx mx 32y 2+-= 与x 轴交于A 、B 两点，与y 轴交于C 点.(1)请求出抛物线顶点M 的坐标(用含m 的代数式表示)，A 、B 两点的坐标;(2)经探究可知，△BCM 与△ABC 的面积比不变，试求出这个比值;(3)是否存在使△BCM 为直角三角形的抛物线?若存在，请求出;如果不存在，请说明理由例2、如图，抛物线n mx x ++=2y 与x 轴交于点A(-2，0)，B(4，0)，与y 轴交于点C.(1)求该抛物线的解析式;(2)M 为第一象限内抛物线上一动点，点M 在何处时，△ACM 的面积最大;（3）在抛物线的对称轴上是否存在这样的点P ，使得△PAC 为直角三角形?若存在，请求出所有可能点P 的坐标;若不存在，请说明理由.2.如图，抛物线mx x 2y 2-=(m ＞0)与x 轴的另一个交点为A ，过P(1，-m)作PM ⊥x 轴于点M ，交抛物线于点B ．点B 关于抛物线对称轴的对称点为C ．（1）若m=2，求点A 和点C 的坐标；（2）令m ＞1，连接CA ，若△ACP 为直角三角形，求m 的值；（3）在坐标轴上是否存在点E ，使得△PEC 是以P 为直角顶点的等腰直角三角形？若存在，求出点E 的坐标；若不存在，请说明理由．3. 如图，抛物线2y 2++=bx ax 与x 轴交于点A(1，0)和B(4，0)．（1）求抛物线的解析式；（2）若抛物线的对称轴交x 轴于点E ，点F 是位于x 轴上方对称轴上一点，FC ∥x 轴，与对称轴右侧的抛物线交于点C ，且四边形OECF 是平行四边形，求点C 的坐标；（3）在（2）的条件下，抛物线的对称轴上是否存在点P ，使△OCP 是直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．4、在平面直角坐标系中，抛物线()k x k x --+=1y 2与直线y=kx+1交于A ，B 两点，点A 在点B 的左侧． （1）如图1，当k=1时，直接写出A ，B 两点的坐标；（2）在（1）的条件下，点P 为抛物线上的一个动点，且在直线AB 下方，试求出△ABP 面积的最大值及此时点P 的坐标；（3）如图2，抛物线()k x k x --+=1y 2（k ＞0）与x 轴交于点C 、D 两点（点C 在点D 的左侧），在直线y=kx+1上是否存在唯一一点Q ，使得∠OQC=90°？若存在，请求出此时k 的值；若不存在，请说明理由．5.如图，直线y=x+2与抛物线62++=bx ax y （a ≠0）相交于A （2，2）和B(4，m)，点P 是线段AB 上异于A 、B 的动点，过点P 作PC ⊥x 轴于点D ，交抛物线于点C ．(1）求抛物线的解析式；（2）是否存在这样的P 点，使线段PC 的长有最大值，若存在，求出这个最大值；若不存在，请说明理由；（3）求△PAC 为直角三角形时点P 的坐标．6、如图，抛物线c bx ax y ++=2经过A(-3，0)、C(0，4)，点B 在抛物线上，CB ∥x 轴，且AB 平分∠CAO ．（1）求抛物线的解析式；（2）线段AB 上有一动点P ，过点P 作y 轴的平行线，交抛物线于点Q ，求线段PQ 的最大值；（3）抛物线的对称轴上是否存在点M ，使△ABM 是以AB 为直角边的直角三角形？如果存在，求出点M 的坐标；如果不存在，说明理由．。

求直角三角形的方法中的特定函数在二次函数中求直角三角形的方法中，可以使用特定的函数来计算直角三角形的各个属性，例如边长、角度、面积等。

这些函数可以帮助我们快速准确地解决直角三角形相关的问题。

本文将详细介绍几个常用的函数，包括函数的定义、用途和工作方式等。

1. 求斜边长的函数求斜边长的函数是用来计算直角三角形斜边的长度的。

根据勾股定理，直角三角形的斜边长度可以通过已知的两个直角边的长度来计算。

函数的定义如下：def hypotenuse(a, b):"""计算直角三角形的斜边长:param a: 直角三角形的直角边a的长度:param b: 直角三角形的直角边b的长度:return: 直角三角形的斜边长"""c = math.sqrt(a**2 + b**2)return c该函数接受两个参数a和b，分别表示直角三角形的直角边a和直角边b的长度。

函数内部使用勾股定理来计算斜边的长度，并返回结果。

2. 求角度的函数求角度的函数是用来计算直角三角形中某个角度的大小的。

根据三角函数的定义，我们可以通过已知的两个直角边的长度来计算角度的大小。

函数的定义如下：def angle(a, b):"""计算直角三角形中的角度:param a: 直角三角形的直角边a的长度:param b: 直角三角形的直角边b的长度:return: 直角三角形中的角度（弧度制）"""radians = math.atan(a / b)return radians该函数接受两个参数a和b，分别表示直角三角形的直角边a和直角边b的长度。

函数内部使用反正切函数来计算角度的大小，并返回结果（以弧度制表示）。

3. 求面积的函数求面积的函数是用来计算直角三角形的面积的。

根据直角三角形的面积公式，我们可以通过已知的两个直角边的长度来计算面积。

二次函数中的三角形一．与三角形面积例1：如图，已知在同一坐标系中，直线22k y kx =+-与y 轴交于点P ，抛物线k x k x y 4)1(22++-=与x 轴交于)0,(),0,(21x B x A 两点。

C 是抛物线的顶点。

（1）求二次函数的最小值（用含k 的代数式表示）； （2）若点A 在点B 的左侧，且021<⋅x x 。

①当k 取何值时，直线通过点B ；②是否存在实数k ，使ABC ABP S S ∆∆=？如果存在，请求出此时抛物线的解析式；如果不存在，请说明理由。

例2：已知抛物线)1(3)4(2-+---=m x m x y 与x 轴交于A 、B 两点，与y 轴交于C 点， （1）求m 的取值范围；（2）若0<m ，直线1-=kx y 经过点A ，与y 轴交于点D ，且25=⋅BD AD ，求抛物线的解析式； （3）若A 点在B 点左边，在第一象限内，（2）中所得的抛物线上是否存在一点P ，使直线P A 平分ACD ∆的面积？若存在，求出P 点的坐标；若不存在，请说明理由。

例3．已知矩形ABCD 中，AB ＝2，AD ＝4，以AB 的垂直平分线为x 轴，AB 所在的直线为y 轴，建立平面直角坐标系(如图)。

(1)写出A 、B 、C 、D 及AD 的中点E 的坐标；(2)求以E 为顶点、对称轴平行于y 轴，并且经过点B 、C 的抛物线的解析式； (3)求对角线BD 与上述抛物线除点B 以外的另一交点P 的坐标；(4)△PEB 的面积S △PEB 与△PBC 的面积S △PBC 具有怎样的关系？证明你的结论。

A BC DO E x y(第25题图)例4.如图1，已知直线12y x =-与抛物线2164y x =-+交于AB ，两点． （1）求A B ，两点的坐标；（2）求线段AB 的垂直平分线的解析式；（3）如图2，取与线段AB 等长的一根橡皮筋，端点分别固定在A B ，两处．用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动，动点P 将与A B ，构成无数个三角形，这些三角形中是否存在一个面积最大的三角形？如果存在，求出最大面积，并指出此时P 点的坐标；如果不存在，请简要说明理由．二．与三角形形状例5. 如图，抛物线254y ax ax =-+经过ABC △的三个顶点，已知BC x ∥轴，点A 在x 轴上，点C 在y 轴上，且AC BC =．（1）求抛物线的对称轴；（2）写出A B C ，，三点的坐标并求抛物线的解析式；（3）探究：若点P 是抛物线对称轴上且在x 轴下方的动点，是否存在PAB △是等腰三角形．若存在，求出所有符合条件的点P 坐标；不存在，请说明理由．图2图1例 6.如图①，在平面直角坐标系中，点A 的坐标为(12)，，点B 的坐标为(31)，，二次函数2y x =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的一个抛物线的函数表达式： （任写一个即可）．（2）平移抛物线1l ，使平移后的抛物线过A B ，两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式．（3）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABK ABC S S =△△，求点K 的坐标．（4）请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ，使ABP △为等腰三角形．若存在，请判断点P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明师．x 图①x 图②x 图③例7. 已知：如图，抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点． （1）求抛物线的函数关系式；（2）若过点C 的直线y kx b =+与抛物线相交于点E （4，m ），请求出△CBE 的面积S 的值； （3）在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标；（4）除（3）中所求的0P 点外，在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形？若存在，请求出一共有几个满足条件的点P （要求简要说明理由，但不证明）；若不存在这样的点P ，请说明理由．例8.如图，在直角坐标系中，点A 的坐标为(－2，0)，连接OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ． (1)求点B 的坐标；(2)求经过A 、O 、B 三点的抛物线的解析式； (3)在(2)中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由；(4)如果点P 是(2)中的抛物线上的动点，且在x 轴的下方， 那么△P AB 是否有最大面积？若有，求出此时P 点的坐标及△P AB 的最大面积；若没有，请说明理由．(注意：本题中的结果均保留根号)(第25题图)三．二次函数与三角形相似 例9：已知一次函数1243--=x y 的图象分别交x 轴、y 轴于A 、C 两点， （1）求出A 、C 两点的坐标；（2）在x 轴上找出点B ，使ACB ∆∽AOC ∆，若抛物线过A 、B 、C 三点，求出此抛物线的解析式； （3）在（2）的条件下，设动点P 、Q 分别从A 、B 两点同时出发，以相同速度沿AC 、BA 向C 、A 运动，连结PQ ，使m AP =，是否存在m 的值，使以A 、P 、Q 为顶点的三角形与ABC ∆相似，若存在，求出所有m 的值；若不存在，请说明理由。

二次函数中等腰直角三角形 -回复
您好，关于二次函数中等腰直角三角形，我们可以通过以下步骤来解决：
1. 二次函数一般式：$y=ax^2+bx+c$。

2. 因为中位线长度为右腰，所以这个中位线对应的$x$可以用平移的方法求出：设中位线长度为$t$，则该中位线对应的$x$值为$-\frac{b}{2a}+t$。

3. 由直角三角形性质可知，斜边的平方等于直角腰的平方和，即$(\frac{t}{2})^2+(at^2+c)^2=(\frac{t}{2}+b)^2$。

4. 将第3步中的方程式化简后解出$t$，再带回第2步中的式子，求出该中位线对应的$x$值。

5. 根据对称性，可以得出第二条中位线的长度与第一条中位线相等，且对应的$x$值也相等。

6. 根据中位线长度与底边长度相等的定义，可以得出三角形的底边长度为$2\times(\frac{t}{2}+b)$。

7. 最终，我们就可以得出该等腰直角三角形的底边长、两条直角边长及其顶点的坐标。

希望以上解释能够解决您的问题，任何疑问，请随时追问。

1、已知抛物线与x轴交于A、 B两点，与y轴交于点C．是否存在实数a，使得△ABC为直角三角形．若存在，请求出a的值；若不存在，请说明理由．由，解得，．∴点A、B的坐标分别为（-3，0），（，0）．∴，，．∴，，．〈ⅰ〉当时，∠ACB＝90°．由，得．解得．∴当时，点B的坐标为（，0），，，．于是．∴当时，△A BC为直角三角形．〈ⅱ〉当时，∠ABC＝90°．2：如图，抛物线与x轴交与A(1,0),B(-3，0)两点，顶点为D。

交Y轴于C，在抛物线第二象限图象上是否存在一点M，使△MBC是以∠BCM为直角的直角三角形，若存在，求出点P的坐标。

若没有，请说明理由抛物线y=-x^2+bx+c与x轴交予A(1,0),B(-3,0)两点,得-1+b+c=0-9-3b+c=0得b=-2,c=3该抛物线的解析式y=-x^2-2x+3点C为（0.3）△ABC的面积为1/2AB*OC=6设在抛物线第二象限图象上存在点M(x0,y0)使△MBC是以∠BCM为直角的直角三角形则x0<0,y0>0y0=-x0^2-2x0+3(1)再由MB^2=MC^2+BC^2得(x0+3)^2+(y0-0)^2=(x0-0)^2+(y0-3)^2+(0+3)^2+(3-0)^2(2)(3)由（1）和（2）可解得y0=3,x0=0或者y0=4，x0=-1又x0<0,y0>0所以y0=4，x0=-1在抛物线第二象限图象上存在点M(-1,4)使△MBC是以∠BCM为直角的直角三角形.3：（2012云南）如图，在平面直角坐标系中，直线交x轴于点P，交y轴于点A．抛物线的图象过点E（-1，0），并与直线相交于A、B两点（1）求抛物线的解析式（关系式）；（2）过点A作AC⊥AB交x轴于点C，求点C的坐标；（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．解答：解：（1）直线解析式为y=x+2，令x=0，则y=2，∴A（0，2），∵抛物线y=x2+bx+c的图象过点A（0，2），E（﹣1，0），∴，解得．∴抛物线的解析式为：y=x2+x+2．（2）∵直线y=x+2分别交x轴、y轴于点P、点A，∴P（6，0），A（0，2），∴OP=6，OA=2．∵AC⊥AB，OA⊥OP，∴Rt△OCA∽Rt△OPA，∴，∴OC=，又C点在x轴负半轴上，∴点C的坐标为C（，0）．（3）抛物线y=x2+x+2与直线y=x+2交于A、B两点，令x2+x+2=x+2，解得x1=0，x2=，∴B（，）．如答图①所示，过点B作BD⊥x轴于点D，则D（，0），BD=，DP=6﹣=．点M在坐标轴上，且△MAB是直角三角形，有以下几种情况：①当点M在x轴上，且BM⊥AB，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AB，BD⊥x轴，∴，即，解得m=，∴此时M点坐标为（，0）；②当点M在x轴上，且BM⊥AM，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AM，易知Rt△AOM∽Rt△MDB，∴，即，化简得：m2﹣m+=0，解得：x1=，x2=，∴此时M点坐标为（，0），（，0）；（说明：此时的M点相当于以AB为直径的圆与x轴的两个交点）③当点M在y轴上，且BM⊥AM，如答图②所示．此时M点坐标为（0，）；④当点M在y轴上，且BM′⊥AB，如答图②所示．设M′（0，m），则AM=2﹣=，BM=，MM′=﹣m．易知Rt△ABM∽Rt△MBM′，∴，即，解得m=，∴此时M点坐标为（0，）．综上所述，除点C外，在坐标轴上存在点M，使得△MAB是直角三角形．符合条件的点M有5个，其坐标分别为：（，0）、（，0）、（，0）、（0，）或（0，）．4：（2012?河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线经过A、B两点．（1）写出点A、点B的坐标；（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；（3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．解：（1）抛物线y=﹣x2+x+4中：令x=0，y=4，则 B（0，4）；令y=0，0=﹣x2+x+4，解得 x1=﹣1、x2=8，则 A（8，0）；∴A（8，0）、B（0，4）．△ABC中，AB=AC，AO⊥BC，则OB=OC=4，∴C（0，﹣4）．由A（8，0）、B（0，4），得：直线AC：y=﹣x+4；依题意，知：OE=2t，即 E（2t，0）；∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；S=S△ABC+S△PAB=×8×8+×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；∴当t=2时，S有最大值，且最大值为64．（3）∵PM∥y轴，∴∠AMP=∠ACO＜90°；而∠APM是锐角，所以△PAM若是直角三角形，只能是∠PAM=90°；由A（8，0）、C（0，﹣4），得：直线AC：y=x﹣4；所以，直线AP可设为：y=﹣2x+h，代入A（8，0），得：﹣16+h=0，h=16∴直线AP：y=﹣2x+16，联立抛物线的解析式，得：，解得、∴存在符合条件的点P，且坐标为（3，10）．5：（2012?海南）如图，顶点为P（4，-4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，（1）求该二次函数的关系式；（2）若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：①证明：∠ANM=∠ONM；②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．1）∵二次函数图象的顶点为P（4，－4），∴设二次函数的关系式为。

二次函数直角三角形二次函数是一种常见的数学模型，其图像呈现出连续的曲线，可以用于描述许多实际问题，如物体的运动轨迹、物体的抛射运动、电子电路等。

而直角三角形是一个三角形中的一种特殊情况，其中一个角为90度。

在这篇文章中，我们将讨论二次函数与直角三角形之间的关系，以及如何利用二次函数和三角函数求解直角三角形问题。

一、二次函数二次函数是一种以自变量x的二次多项式的形式表示的函数，其一般式为：y=ax²+bx+c，其中a、b、c为常数，且a≠0。

二次函数的图像通常呈现出抛物线状，其开口向上或向下取决于系数a的正负性。

当a>0时，抛物线开口朝上；当a<0时，抛物线开口朝下。

二、二次函数与直角三角形之间的关系二次函数可以用于描述许多物理问题，如自由落体运动、抛体运动等。

这些物理问题中通常包含有物体的高度、速度、加速度等数值。

而这些数值往往与直角三角形有直接关系。

例如，在自由落体运动中，当一个物体从高度h自由落下时，其高度与时间的关系可以表示为二次函数y=-gt²/2 + h，其中g为重力加速度，t为时间。

同时，当物体与地面碰撞时，其速度可以表示为v=gt，即与时间t存在线性关系。

这些物理问题中的二次函数常常与直角三角形有关，我们可以将物体高度与时间关系中的高度看作直角三角形中的斜边，将时间看作直角三角形中的一条直角边，将落地时的高度看作直角三角形中的另一条直角边。

这样，我们就可以将二次函数转化为三角函数的形式，利用三角函数求解直角三角形的问题。

三、利用三角函数求解直角三角形的问题在直角三角形中，我们通常会用三角函数来计算三角形的各边和角度的大小。

其中最常用的三角函数包括正弦函数、余弦函数和正切函数。

通过利用三角函数可以快速地求解直角三角形的各项参数，如角度、斜边、直角边以及三角形的面积等。

下面是利用三角函数求解直角三角形的常用公式：1.正弦定理：a/sin(A)=b/sin(B)=c/sin(C)。

抛物线中的直角三角形基本题型：已知AB ，抛物线()02≠++=a c bx ax y ，点P 在抛物线上（或坐标轴上，或抛物线的对称轴上），若ABP ∆为直角三角形，求点P 坐标。

分两大类进行讨论：（1）AB 为斜边时（即PA PB ⊥）：点P 在以AB 为直径的圆周上。

（2）AB 为直角边时，分两类讨论：①以A ∠为直角时（即AP AB ⊥）：②以B ∠为直角时（即BP BA ⊥）：利用两点的斜率公式求出AB k ，因为两直线垂直斜率乘积为1-，进而求出PA （或PB ）的斜率k ；进而求出PA （或PB ）的解析式；将PA （或PB ）的解析式与抛物线（或坐标轴，或抛物线的对称轴）的解析式联立即可求出点P 坐标。

典型例题：例1、在平面直角坐标系xOy 中，已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 左侧)，与y 轴交于点C ，其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ，且COS∠BCO＝10。

（1）求抛物线的解析式；(2)在此抛物线上是否存在异于点C 的点P ，使以N 、P 、C 为顶点的三角形是以NC 为一条直角边的直角三角形？若存在，求出点P 的坐标：若不存在，请说明理由；(3)过点A 作x 轴的垂线，交直线MC 于点Q.若将抛物线沿其对称轴上下平移，使抛物线与线段NQ ?（2009年成都）例2、如图，抛物线两点轴交于与B A x bx ax y ,32-+=，与y 轴交于点C ，且OA OC OB 3==．（I ）求抛物线的解析式；（II ）探究坐标轴上是否存在点P ，使得以点C A P ,,为顶点的三角形为直角三角形？若存在，求出P 点坐标，若不存在，请说明理由；（III ）直线131+-=x y 交y 轴于D 点，E 为抛物线顶点．若α=∠DBC ，βαβ-=∠求,CBE 的值．例3、在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，且点A （0，2），点C （－1，0），如图所示，抛物线22y ax ax =+-经过点B 。